8
Fuzzy Computation
Computation is about calculating or enumerating mechanically. Typically, the word mechanically means that one builds a device and sets it in motion in order to perform the desired calculation or enumeration. Many and different real or conceptual devices capable of performing computations have been proposed. Most of them operate in a crisp environment and in a crisp manner. However, there are some devices that profit from the use of vagueness in their overall operation. These devices and the related theory are described in this chapter. The material presented in this chapter is based on [220, 274].
8.1 Automata, Grammars, and Machines
A finite automaton can be seen as a machine equipped with scanning head that can read the contents of sequence of cells, while the head can move in only one direction. At any moment, the machine is in a state. Initially, the scanning head is positioned on the leftmost cell, while a number of symbols are printed on consecutive cells starting with the leftmost cell. Also, the machine enters a default initial state. Each machine is associated with a number of transition rules. A transition rule has the general form ![]() , where
, where ![]() and
and ![]() are states and
are states and ![]() is a symbol. The meaning of this rule is that if the automaton is in state
is a symbol. The meaning of this rule is that if the automaton is in state ![]() , it will enter state
, it will enter state ![]() only if the next symbol is
only if the next symbol is ![]() . When the machine starts, it reads the first symbol and if there is a transition rule that includes this symbol and the current state, then the scanning head moves to the right and the machine enters a new state. If the machine enters the final state, then it accepts the input and terminates. The machine may suspend without completion when no transition rule applies. The alphabet of the machine consists of the symbols that the scanning head can recognize. The following figure shows a finite automaton with two states whose alphabet is
. When the machine starts, it reads the first symbol and if there is a transition rule that includes this symbol and the current state, then the scanning head moves to the right and the machine enters a new state. If the machine enters the final state, then it accepts the input and terminates. The machine may suspend without completion when no transition rule applies. The alphabet of the machine consists of the symbols that the scanning head can recognize. The following figure shows a finite automaton with two states whose alphabet is ![]() .
.

The symbols in the circles are the states, the symbol in the double circle is the accepting state, and the symbols over the arcs are the symbols that the automaton consumes. Thus, this is a compact way to write the various transition rules. This automaton determines if an input sequence of symbols over its alphabet contains an even number of ![]() 's. For example, if the input is the sequence “
's. For example, if the input is the sequence “![]() ”, then the following table shows what has to be done in order to have this sequence accepted by this automaton.
”, then the following table shows what has to be done in order to have this sequence accepted by this automaton.
| Current state | Unread symbols | Transition rule |
| Input accepted! |
More generally, automata are able to examine whether character sequences or just strings belong to some formal language.
Typically, a language is defined by a grammar:
Grammars are classified as follows:
- Unrestricted grammars. There are no restrictions on the form of the production rules.
- Context‐sensitive grammars. The relation
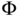 contains only productions of the form
contains only productions of the form 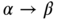 , where
, where  , and in general,
, and in general, 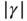 is the length of the string
is the length of the string  .
. - Context‐free grammars. The relation
 contains only productions of the form
contains only productions of the form  , where
, where  and
and  .
. - Regular grammars. The relation
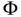 contains only productions of the form
contains only productions of the form 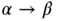 , where
, where 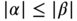 ,
,  , and
, and 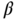 has the form
has the form 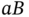 or
or  , where
, where  and
and  .
.
Syntactically complex languages can be defined by means of grammars. To each class of languages, there is a class of automata (machines) that accept (i.e., they can answer the decision problem “![]() ?,” where
?,” where ![]() is a string and
is a string and ![]() is a language) this class of languages, which are generated by the respective grammars. In particular, finite automata accept languages generated by regular grammars, push‐down automata accept languages generated by context‐free grammars, linear bounded automata accept languages generated by context‐sensitive grammars, and Turing machines accept recursive languages, that is, a subclass of the class of languages generated by unrestricted grammars.
is a language) this class of languages, which are generated by the respective grammars. In particular, finite automata accept languages generated by regular grammars, push‐down automata accept languages generated by context‐free grammars, linear bounded automata accept languages generated by context‐sensitive grammars, and Turing machines accept recursive languages, that is, a subclass of the class of languages generated by unrestricted grammars.
A Turing machine is a conceptual computing device consisting of an infinite tape, a controlling device, and a scanning head (see Figure 8.1). The tape is divided into an infinite number of cells. The scanning head can read and write symbols in each cell. The symbols are elements of a set ![]() ,
, ![]() , which is called the alphabet. Usually, there is an additional symbol,
, which is called the alphabet. Usually, there is an additional symbol, ![]() , called the blank symbol, and when this symbol is written on a cell by the scanning head, the effect of this operation is the erasure of the symbol that was printed on this particular cell. At any moment, the machine is in a state
, called the blank symbol, and when this symbol is written on a cell by the scanning head, the effect of this operation is the erasure of the symbol that was printed on this particular cell. At any moment, the machine is in a state ![]() , which is a member of a finite set
, which is a member of a finite set ![]() ,
, ![]() . The controlling device is actually a look‐up table that is used to determine what the machine has to do next at any given moment. In particular, the action a machine has to take depends on its current state and the symbol that is printed on the cell the scanning head has just finished scanning. If no action has been specified for a particular combination of state and symbol, the machine halts. Usually, the control device is specified by a finite set of quadruples, which are special cases of expressions.
. The controlling device is actually a look‐up table that is used to determine what the machine has to do next at any given moment. In particular, the action a machine has to take depends on its current state and the symbol that is printed on the cell the scanning head has just finished scanning. If no action has been specified for a particular combination of state and symbol, the machine halts. Usually, the control device is specified by a finite set of quadruples, which are special cases of expressions.
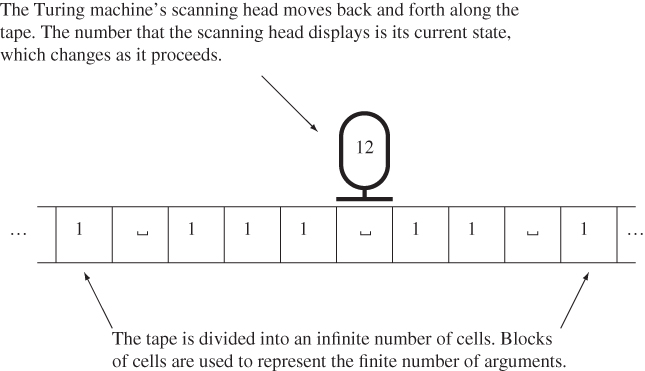
Figure 8.1 A typical Turing machine.
A quadruple can have one of the following forms:
Note that ![]() and
and ![]() . The quadruple (8.1) specifies that if the machine is in state
. The quadruple (8.1) specifies that if the machine is in state ![]() and the cell that the scanning head scans contains the symbol
and the cell that the scanning head scans contains the symbol ![]() , then the scanning head replaces
, then the scanning head replaces ![]() by
by ![]() and the machine enters state
and the machine enters state ![]() . The quadruples (8.2) and (8.3) specify that if the machine is in state
. The quadruples (8.2) and (8.3) specify that if the machine is in state ![]() and the cell that the scanning head scans contains the symbol
and the cell that the scanning head scans contains the symbol ![]() , then the scanning head moves to the cell to the left of the current cell, or to the cell to the right of the current cell, respectively, and the machine enters the state
, then the scanning head moves to the cell to the left of the current cell, or to the cell to the right of the current cell, respectively, and the machine enters the state ![]() . Sometimes the following quadruple is also considered:
. Sometimes the following quadruple is also considered:
This quadruple is particularly useful if we want to construct a Turing machine that will compute relatively computable functions. These quadruples provide a Turing machine with a means of communicating with an external agency that can give correct answers to questions about a set ![]() . In particular, when a machine is in state
. In particular, when a machine is in state ![]() and the cell that the scanning head scans contains the symbol
and the cell that the scanning head scans contains the symbol ![]() , then the machine can be thought of as asking the question, “Is
, then the machine can be thought of as asking the question, “Is ![]() ?” Here
?” Here ![]() is the number of
is the number of ![]() 's that are printed on the tape. If the answer is “yes,” then the machine enters state
's that are printed on the tape. If the answer is “yes,” then the machine enters state ![]() ; otherwise it enters state
; otherwise it enters state ![]() . Turing machines equipped with such an external agency are called oracle machines, and the external agency is called an oracle.
. Turing machines equipped with such an external agency are called oracle machines, and the external agency is called an oracle.
Turing machines are used to compute the value of functions ![]() that take values in
that take values in ![]() . Each argument
. Each argument ![]() , is represented on the tape by preprinting the symbol
, is represented on the tape by preprinting the symbol ![]() on
on ![]() consecutive cells. Typically, such a block of cells is denoted by
consecutive cells. Typically, such a block of cells is denoted by ![]() . Argument representations are separated by a blank cell (i.e., a cell on which the symbol
. Argument representations are separated by a blank cell (i.e., a cell on which the symbol ![]() is printed), while all other cells are empty (i.e., the symbol
is printed), while all other cells are empty (i.e., the symbol ![]() has been preprinted on each cell). It is customary to represent such a block of cell with the expression
has been preprinted on each cell). It is customary to represent such a block of cell with the expression
If ![]() is an expression, then
is an expression, then ![]() will denote the number of
will denote the number of ![]() contained in
contained in ![]() . In addition,
. In addition,
It is also customary to use the symbol 1 for ![]() . Thus, the sequence
. Thus, the sequence ![]() will be represented by the following three blocks of 1's:
will be represented by the following three blocks of 1's:
The machine starts at state ![]() and the scanning head is placed atop the leftmost 1 of a sequence of
and the scanning head is placed atop the leftmost 1 of a sequence of ![]() blocks of 1's. If the machine has reached a situation in which none or more than one quadruple is applicable, the machine halts. Once the machine has terminated, the result of the computation is equal to the number of cells on which the symbol
blocks of 1's. If the machine has reached a situation in which none or more than one quadruple is applicable, the machine halts. Once the machine has terminated, the result of the computation is equal to the number of cells on which the symbol ![]() is printed.
is printed.
Although the description presented so far is quite formal for our own taste, still fuzzy versions of the Turing machine are extensions of the “standard” formal definition that is given below.
Note that here we have defined a machine that has a unidirected tape and not a bidirectional tape. One can get the bidirectional version by eliminating all references to the ![]() symbol.
symbol.
A configuration of ![]() is an element from
is an element from
where ![]() denotes strings that are formed by concatenating a string that belongs to
denotes strings that are formed by concatenating a string that belongs to ![]() with a string that belongs to
with a string that belongs to ![]() . If
. If ![]() is a configuration, then
is a configuration, then ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Moreover, this configuration means that a machine
. Moreover, this configuration means that a machine ![]() is in state
is in state ![]() , the content of the tape is
, the content of the tape is ![]() , and the scanning head sits atop the
, and the scanning head sits atop the ![]() th cell, where
th cell, where ![]() is the length of string
is the length of string ![]() . The initial configuration is
. The initial configuration is ![]() , where
, where ![]() is the input fed to the machine. A configuration whose state component is in
is the input fed to the machine. A configuration whose state component is in ![]() is called a halted configuration.
is called a halted configuration.
A step is a relation ![]() on the set of configurations defined as follows:
on the set of configurations defined as follows:
 , if
, if  ;
; , if
, if 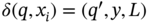 ;
;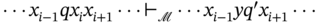 , if
, if 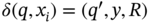 ; and
; and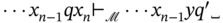 , if
, if  .
.
A computation by ![]() is a sequence of configurations
is a sequence of configurations ![]() , for some
, for some ![]() such that
such that
A computation from ![]() to
to ![]() can be written compactly as
can be written compactly as ![]() .
.
A computation by ![]() on input
on input ![]() is a series of actions that start at configuration
is a series of actions that start at configuration ![]() and is either infinite (i.e. nonterminating) or stops at configuration
and is either infinite (i.e. nonterminating) or stops at configuration ![]() , where
, where ![]() . Assume that
. Assume that ![]() , where
, where ![]() is the accepting state and
is the accepting state and ![]() is the rejecting state. Then, a computation is called accepting if it finishes in the configuration
is the rejecting state. Then, a computation is called accepting if it finishes in the configuration ![]() and rejecting if it finishes in the configuration
and rejecting if it finishes in the configuration ![]() . Furthermore, if a computation on input
. Furthermore, if a computation on input ![]() is accepting or rejecting, we say that the corresponding machine accepts or rejects
is accepting or rejecting, we say that the corresponding machine accepts or rejects ![]() , respectively. More generally, the words accepted by
, respectively. More generally, the words accepted by ![]() form a formal language
form a formal language ![]() .
.
8.2 Fuzzy Languages and Grammars
Suppose that ![]() is an alphabet. Then, a fuzzy formal language (or just fuzzy language) is a fuzzy subset of
is an alphabet. Then, a fuzzy formal language (or just fuzzy language) is a fuzzy subset of ![]() . If we have a set of nonterminal symbols,
. If we have a set of nonterminal symbols, ![]() , and a set of terminal symbols,
, and a set of terminal symbols, ![]() , such that
, such that ![]() , then a fuzzy language is a fuzzy subset of
, then a fuzzy language is a fuzzy subset of ![]() .
.
Assume that ![]() and
and ![]() are two fuzzy languages over
are two fuzzy languages over ![]() . Then, the union of
. Then, the union of ![]() and
and ![]() is the fuzzy language denoted by
is the fuzzy language denoted by ![]() and defined by
and defined by
Similarly, the intersection of ![]() and
and ![]() is the fuzzy language denoted by
is the fuzzy language denoted by ![]() and defined by
and defined by
The concatenation of ![]() and
and ![]() is the fuzzy language denoted by
is the fuzzy language denoted by ![]() and defined by
and defined by
Since the operators ![]() and
and ![]() are distributive, concatenation is associative. Note that
are distributive, concatenation is associative. Note that ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Suppose that ![]() is a fuzzy language in
is a fuzzy language in ![]() . Then, the fuzzy subset
. Then, the fuzzy subset ![]() of
of ![]() defined by
defined by
is called the Kleene closure of ![]() .
.
A fuzzy grammar includes a set of rules for generating the elements of a fuzzy language. More specifically, a fuzzy grammar ![]() is a quadruple
is a quadruple ![]() where
where ![]() is a set of fuzzy production rules and everything else is as in Definition 8.1.2. The elements of
is a set of fuzzy production rules and everything else is as in Definition 8.1.2. The elements of ![]() are expressions of the form
are expressions of the form
where ![]() and
and ![]() is the plausibility degree that
is the plausibility degree that ![]() can generate
can generate ![]() . Also, we write
. Also, we write ![]() to designate that this is the plausibility degree of rule of the form
to designate that this is the plausibility degree of rule of the form ![]() . Given the rewriting rule (8.5) and two arbitrary strings
. Given the rewriting rule (8.5) and two arbitrary strings ![]() and
and ![]() in
in ![]() , then we have
, then we have
and ![]() is said to be directly derivable from
is said to be directly derivable from ![]() . Suppose that
. Suppose that ![]() and
and
where ![]() , then
, then ![]() is derivable from
is derivable from ![]() in
in ![]() . This is usually written as
. This is usually written as
The following expression
is called a derivation chain from ![]() to
to ![]() .
.
A fuzzy grammar ![]() generates a fuzzy language
generates a fuzzy language ![]() . Given a string
. Given a string ![]() consisting of terminal symbols, we say that it is in
consisting of terminal symbols, we say that it is in ![]() if and only if
if and only if ![]() is derivable from
is derivable from ![]() . The membership degree of
. The membership degree of ![]() in
in ![]() is given by
is given by
where the least upper bound is taken over all derivation chains from ![]() to
to ![]() . This means that (8.6) defines
. This means that (8.6) defines ![]() as a fuzzy subset of
as a fuzzy subset of ![]() . Also, if
. Also, if ![]() and
and ![]() are equal fuzzy sets, then the grammars
are equal fuzzy sets, then the grammars ![]() and
and ![]() are equivalent. Naturally, it is important to know whether we can compute
are equivalent. Naturally, it is important to know whether we can compute ![]() using Eq. (8.6):
using Eq. (8.6):
Similar to crisp grammars, fuzzy grammars are classified as follows:
- Fuzzy unrestricted grammars. Production rules are of the form
 ,
, 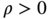 , where
, where 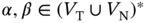 .
. - Fuzzy context‐sensitive grammars. Production rules are of the form
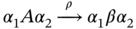 ,
, 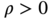 , where
, where 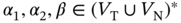 ,
,  , and
, and 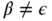 . The production rule
. The production rule 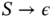 is also allowed.
is also allowed. - Fuzzy context‐free grammars. Production rules are of the form
 ,
,  ,
, 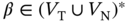 ,
,  , and
, and  .
. - Fuzzy regular grammars. Productions are of the form
 or
or 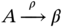 ,
, 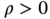 , where
, where  and
and 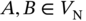 . In addition, the rule
. In addition, the rule  is allowed.
is allowed.
The following result states that fuzzy context‐sensitive and hence also fuzzy context‐free and fuzzy regular grammars are recursive.
8.3 Fuzzy Automata
In general, a fuzzy automaton, or more formally, a fuzzy finite state automaton is, a triple ![]() , where
, where ![]() is the set of states,
is the set of states, ![]() is the set of input symbols and
is the set of input symbols and ![]() is a fuzzy subset of
is a fuzzy subset of ![]() , that is,
, that is, ![]() . Both
. Both ![]() and
and ![]() are finite nonempty sets and
are finite nonempty sets and ![]() is the set of all finite words of elements of
is the set of all finite words of elements of ![]() .
.
The pair ![]() is called a strong homomorphism if
is called a strong homomorphism if
for all ![]() and all
and all ![]() .
.
Suppose that ![]() and
and ![]() are two fuzzy finite state automata. Also, suppose that
are two fuzzy finite state automata. Also, suppose that ![]() is a finite set and
is a finite set and ![]() is a function. Assume that
is a function. Assume that ![]() and
and ![]() are the projection maps of
are the projection maps of ![]() onto
onto ![]() ,
, ![]() . Then, we define
. Then, we define ![]() as follows:
as follows:
for all ![]() and for all
and for all ![]() . Then,
. Then, ![]() is called the general direct product of
is called the general direct product of ![]() and
and ![]() and it is usually denoted by
and it is usually denoted by ![]() .
.
Assume that ![]() and
and ![]() are two fuzzy finite state automata. Also, assume that
are two fuzzy finite state automata. Also, assume that ![]() is a function and
is a function and ![]() . Define
. Define
as follows: for all ![]() ,
,
Then, ![]() is a fuzzy finite state automaton, it is called the cascade product of
is a fuzzy finite state automaton, it is called the cascade product of ![]() and
and ![]() and we write
and we write ![]() .
.
As before, let ![]() and
and ![]() be two fuzzy finite state automata. Also, let
be two fuzzy finite state automata. Also, let ![]() be a function. In addition, let
be a function. In addition, let
be a function such that for all ![]() ,
,
Then, ![]() is a fuzzy finite state automaton.
is a fuzzy finite state automaton. ![]() is called the wreath product of
is called the wreath product of ![]() and
and ![]() .
.
Subsystems and strong subsystems are special cases of subautomata:
We can also compose automata.
Mansoor Doostfatemeh and Stefan C. Kremer [104] had presented a new definition for fuzzy automata. A number of reasons (i.e. membership assignment, output mapping, multi‐membership resolution, and the concept of acceptance for fuzzy automata) necessitated the introduction of this new definition:
The authors have presented a multi‐membership resolution algorithm, but we are not going to present it here. But let us see how some simple fuzzy automata can be described as general fuzzy automata.
8.4 Fuzzy Turing Machines
The first general description of a fuzzy Turing machine was given by Zadeh [306]. He presumed that a fuzzy algorithm should contain vague commands (Zadeh used the term “fuzzy commands,” but in order to be consistent with the terminology used in this book, we will call them “vague commands”). Accordingto Zadeh, the following are examples of simple vague commands:
- Set
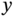 approximately equal to 10, if
approximately equal to 10, if 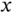 is approximately equal to 5.
is approximately equal to 5. - If
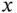 is large, increase
is large, increase  by several units.
by several units. - If
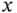 is large, increase
is large, increase 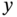 by several units; if
by several units; if 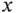 is small, decrease
is small, decrease  by several units; otherwise keep
by several units; otherwise keep  unchanged.
unchanged.
This command is vague, because the text that appears slanted corresponds to fuzzy sets. For example, the numbers that are approximately equal to 10 or 5 are two different fuzzy sets. Based on this, Zadeh vaguely described a fuzzy Turing machine as one where instructions are performed to a degree. A number of concrete proposals followed (see Ref. [275] for a detailed presentation of all these proposals), however, we will only present the one by Jiří Wiedermann [298] since it is the most complete presentation and the most interesting of all previous attempts. Wiedermann's machine is a nondeterministic fuzzy Turing machine with hypercomputational capabilities. In a nutshell, Wiedermann has shown that his machine can solve problems no ordinary Turing machine can solve.
A configuration gives
- the position of the scanning head,
- what is printed on the tape, and
- the current state of the machine.
If ![]() and
and ![]() are two configurations, then
are two configurations, then ![]() means that
means that ![]() is reachable in one step from
is reachable in one step from ![]() with a plausibility degree that is equal to
with a plausibility degree that is equal to ![]() if and only if there is a
if and only if there is a ![]() such that
such that ![]() , and by which the machine goes from
, and by which the machine goes from ![]() to
to ![]() . When a machine starts with input some string
. When a machine starts with input some string ![]() , the characters of the string are printed on the tape starting from the leftmost cell; the scanning head is placed atop the leftmost cell, and the machine enters state
, the characters of the string are printed on the tape starting from the leftmost cell; the scanning head is placed atop the leftmost cell, and the machine enters state ![]() . If
. If
then ![]() is reachable from
is reachable from ![]() in
in ![]() steps. Assume that
steps. Assume that ![]() is reachable from
is reachable from ![]() in
in ![]() steps, then the plausibility degree of this computational path is
steps, then the plausibility degree of this computational path is
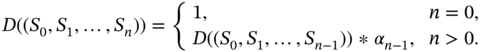
Obviously, the value that is computed with this formula depends on the specific path that is chosen. Since the machine is nondeterministic, it is quite possible that some configuration ![]() can be reached via different computational paths. Therefore, when a machine starts from
can be reached via different computational paths. Therefore, when a machine starts from ![]() and finishes at
and finishes at ![]() in
in ![]() steps, the plausibility degree of this computational path, which is called a computation, should be equal to the maximum of all possible computation paths:
steps, the plausibility degree of this computational path, which is called a computation, should be equal to the maximum of all possible computation paths:
In other words, the plausibility degree of the computation is equal to the plausibility degree of the computational path that is most likely to happen.
Assume that a machine starts from configuration ![]() with
with ![]() as input. Then, a computational path
as input. Then, a computational path ![]() is an accepting path of configurations if the state of
is an accepting path of configurations if the state of ![]() is
is ![]() . In addition, the string
. In addition, the string ![]() is accepted with degree equal to
is accepted with degree equal to ![]() .
.
Also,
The class of all fuzzy languages accepted by a fuzzy Turing machine, in the sense just explained, with (classically) computable ![]() ‐norms is denoted by
‐norms is denoted by ![]() .
.
There have been some arguments against the validity of this proof, but we will not discuss it further (see Ref. [275] for details). In addition, there are some results (e.g. the existence of a universal fuzzy Turing machine) that are discussed in [275, 278].
8.5 Other Fuzzy Models of Computation
Fuzzy Turing machines and fuzzy automata are not the only fuzzy models of computation, however, they are the ones that keep busy most researchers. Indeed, there are models of computation that are based on fuzzy multisets.
It is not difficult to see that any fuzzy multiset ![]() is actually characterized by a function
is actually characterized by a function
which is obtained from the former function by uncurrying it. However, one can demand that for each element ![]() , there is only one membership degree and one multiplicity. In other words, a “fuzzy multiset”
, there is only one membership degree and one multiplicity. In other words, a “fuzzy multiset” ![]() should be characterized by a function
should be characterized by a function ![]() . To distinguish these structures from fuzzy multisets, we will call them multi‐fuzzy sets [271]. Given a multi‐fuzzy set
. To distinguish these structures from fuzzy multisets, we will call them multi‐fuzzy sets [271]. Given a multi‐fuzzy set ![]() , the expression
, the expression ![]() denotes that there are
denotes that there are ![]() copies of
copies of ![]() that belong to
that belong to ![]() with a degree that is equal to
with a degree that is equal to ![]() . A generalization of this definition was presented in [273]:
. A generalization of this definition was presented in [273]:
By substituting ![]() with
with ![]() in the previous definition, the resulting structures will be called
in the previous definition, the resulting structures will be called ![]() ‐multi‐fuzzy sets.
‐multi‐fuzzy sets.
Assuming that ![]() is an
is an ![]() ‐fuzzy hybrid set, then we can define the following two functions: the multiplicity function
‐fuzzy hybrid set, then we can define the following two functions: the multiplicity function ![]() and the degree function
and the degree function ![]() . Clearly, if
. Clearly, if ![]() , then
, then ![]() and
and ![]() . Note that it is equally easy to define the corresponding functions for an
. Note that it is equally easy to define the corresponding functions for an ![]() ‐multi‐fuzzy set.
‐multi‐fuzzy set.
In order to give the basic properties of fuzzy hybrid sets, it is necessary to define the notion of subsethood. Before, going on with this definition, we will introduce the partial order ![]() over
over ![]() , which is defined as follows, for all
, which is defined as follows, for all ![]() :
:
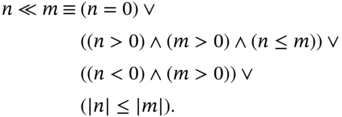
Here ![]() and
and ![]() denote the classical logical conjunction and disjunction operators, respectively. In addition, the symbols
denote the classical logical conjunction and disjunction operators, respectively. In addition, the symbols ![]() and
and ![]() are the well‐known ordering operators, and
are the well‐known ordering operators, and ![]() is the absolute value of
is the absolute value of ![]() .
.
Note that ![]() is an alternative form of
is an alternative form of ![]() , which will be used in the rest of this section. Let us now proceed with the definition of the notion of subsethood for
, which will be used in the rest of this section. Let us now proceed with the definition of the notion of subsethood for ![]() ‐fuzzy hybrid sets:
‐fuzzy hybrid sets:
Note that for all ![]() ,
, ![]() if
if ![]() is “less than or equal” to
is “less than or equal” to ![]() in the sense of the partial order defined over
in the sense of the partial order defined over ![]() . The definition of subsethood for
. The definition of subsethood for ![]() ‐multi‐fuzzy sets is more straightforward:
‐multi‐fuzzy sets is more straightforward:
Let us now present the definitions of union and sum of ![]() ‐multi‐fuzzy sets:
‐multi‐fuzzy sets:
P system is a model of computation, inspired by the way cells live and function. The model is built around the notion of nested compartments surrounded by porous membranes (hence the term membrane computing). It is quite instructive to think of the membrane structure as a bubbles‐inside‐bubbles structure, where we have a bubble that contains bubbles, which, in turn, contain other bubbles, etc. Initially, each compartment contains a number of possible repeated objects (i.e. a multiset of objects). Once “computation” commences, the compartments exchange objects according to a number of multiset processing rules that are associated with each compartment; in the simplest case, these processing rules are just multiset rewriting rules. The activity stops when no rule can be applied anymore. The result of the computation is equal to the number of objects that reside within a designated compartment called the output membrane.
In [271], a fuzzified version of P systems was presented. The basic idea behind this particular attempt to fuzzify P systems is the substitution of one or all ingredients of a P system with their fuzzy counterparts. From a purely computational point of view, it turns out that only P systems that process multi‐fuzzy sets are interesting, the reason being the fact that these systems are capable of computing (positive) real numbers. By replacing the multi‐fuzzy sets employed in the first author's previous work with ![]() ‐multi‐fuzzy sets, the computational power of the resulting P systems will not be any “greater,” nevertheless, these systems may be quite useful in modeling living organisms. But, things may get really interesting if we consider P systems with
‐multi‐fuzzy sets, the computational power of the resulting P systems will not be any “greater,” nevertheless, these systems may be quite useful in modeling living organisms. But, things may get really interesting if we consider P systems with ![]() ‐fuzzy hybrid sets, in general. Here we are going to give only the definition of these systems. For a full exposition see Ref. [275].
‐fuzzy hybrid sets, in general. Here we are going to give only the definition of these systems. For a full exposition see Ref. [275].
Fuzzy multisets have been also used to define fuzzy multiset grammars (see Ref. [259] and references therein). These grammars are recognized by special kinds of automata. In what follows, ![]() will denote the set of all multisets whose universe is the set
will denote the set of all multisets whose universe is the set ![]() . Also, given two multisets
. Also, given two multisets ![]() , then
, then ![]() and
and ![]() .
.
A configuration of a fuzzy multiset finite automaton ![]() is a pair
is a pair ![]() , where
, where ![]() and
and ![]() denote the current state and the current multiset, respectively. Transitions in a fuzzy multiset finite automaton are described with the help of configurations. The transition from configuration
denote the current state and the current multiset, respectively. Transitions in a fuzzy multiset finite automaton are described with the help of configurations. The transition from configuration ![]() leads to configuration
leads to configuration ![]() with membership degree
with membership degree ![]() if there exists a multiset
if there exists a multiset ![]() with
with ![]() ,
, ![]() and
and ![]() . This transition is written as
. This transition is written as ![]() .
.
