Appendix A
Probability Review
A.1 Standard Probability Theory
A.1.1 Probability Space
A probability space (Ω, 
, 
) is the provision of:
- A set of all possible outcomes ω ∈ Ω, sometimes called states of Nature
- A σ-algebra, that is, a set of measurable events A ∈
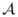, which (1) contains ∅, (2) is stable by complementation (
) and (3) is stable by countable unions (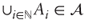
) - A probability measure :
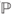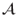→ [0, 1], which (1) satisfies 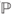(Ω) = 1 and (2) is countably additive (
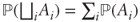where 
denotes disjoint union)
A.1.2 Filtered Probability Space
A filtered probability space (Ω, 
, (
t), ) is a probability space equipped with a filtration (t), which is an increasing sequence of σ-algebras (for any t ≤ t′:t ⊆ t′ ⊆ 
). Informally the filtration represents “information” garnered through time.
A.1.3 Independence
Two events (A, B) ∈ 
2 are said to be independent whenever their joint probability is the product of individual probabilities:
A.2 Random Variables, Distribution, and Independence
A.2.1 Random Variables
A random variable is a function X: Ω → 
mapping every outcome with a real number, such that the event {X ≤ x} ∈ 
for all x ∈ . The notation X ∈ 
is often used to indicate that X satisfies the requirements for a random variable with respect to the σ-algebra 
.
The cumulative distribution function of X is then 
, which is always defined. In most practical applications the probability mass function 
or density function 
(often denoted 
as well) contains all the useful information about X.
The mathematical expectation of X, if it exists, is then:
- In general:
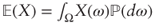; - For clearly discrete random variables:
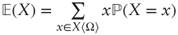; - For random variables with density fX:
.
The law of the unconscious statistician states that if X has density fX the expectation of an arbitrary function g(X) is given by the inner product of fX and g:
if it exists.
The variance of X, if it exists, is defined as 
, and its standard deviation as 
.
A.2.2 Joint Distribution and Independence
Given n random variables X1,…, Xn, their joint cumulative distribution function is:
and each individual cumulative distribution function 
is then called “marginal.”
The n random variables are said to be independent whenever the joint cumulative distribution function of any subset is equal to the product of the marginal cumulative distribution functions:
The covariance between two random variables X, Y is given as:
and their correlation coefficient is defined as: 
. If X, Y are independent, then their covariance and correlation is zero but the converse is not true. If ρ = ± 1 then 
.
The variance of the sum of n random variables X1,…, Xn is:
If X, Y are independent with densities fX, fY, the density of their sum X + Y is given by the convolution of marginal densities:
A.3 Conditioning
Conditioning is a method to recalculate probabilities using known information. For example, at the French roulette the initial Ω is {0, 1,…, 36} but after the ball falls into a colored pocket, we can eliminate several possibilities even as the wheel is still spinning.
The conditional probability of an event A given B is defined as:
Note that 
if A, B are independent.
This straightforwardly leads to the conditional expectation of a random variable X given an event B:
Generally, the conditional expectation of X given a σ-algebra ⊆ 
can be defined as the random variable Y ∈ such that:
or equivalently: 
. 
can be shown to exist and to be unique with probability 1.
The conditional expectation operator shares the usual properties of unconditional expectation (linearity; if X ≥ Y then 
; Jensen's inequality; etc.) and also has the following specific properties:
- If X ∈ 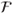then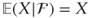
- If X ∈ 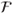and Y is arbitrary then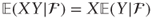
- Iterated expectations: if 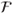1 ⊆ 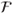2 are σ-algebras then
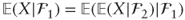. In particular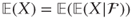 
A.4 Random Processes and Stochastic Calculus
A random process, or stochastic process, is a sequence (Xt) of random variables. When Xt ∈ t for all t the process is said to be (t)-adapted.
The process (Xt) is called a martingale whenever for all t < t′: 
.
The process (Xt) is said to be predictable whenever for all t: Xt ∈ t− (Xt is knowable prior to t).
The path of a process (Xt) in a given outcome ω is the function 
.
A standard Brownian motion or Wiener process (Wt) is a stochastic process with continuous paths that satisfies:
- W0 = 0
- For all t < t′ the increment Wt′ − Wt follows a normal distribution with zero mean and standard deviation
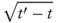
- Any finite set of nonoverlapping increments
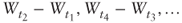is independent.
An Ito process (Xt) is defined by the stochastic differential equation:
where W is a standard Brownian motion, (at) is a predictable and integrable process, and (bt) is a predictable and square-integrable process.
The Ito-Doeblin theorem states that a C2 function (f(Xt)) of an Ito process is also an Ito process with stochastic differential equation:
