Solutions Manual
This Solutions Manual includes answers to all of the end of chapter problems found in this book (except for a few coding problems where the numerical answer is provided in the text).
Chapter 1: Exotic Derivatives
1.1 “Free” Option
- The option is not really free because we may end up at a loss at and above the strike price. (See Figure S.1.)
- The replicating portfolio would include selling x digital calls struck at K at price p and buying a vanilla call struck at K for the premium of m. In order for the portfolio to have zero cost we must have
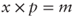 .
. - The cost of one digital call using the Black-Scholes model with the given parameters is $0.5398. The premium of the vanilla call from the Black-Scholes model is $7.97. Solving for x we get
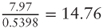 .
.
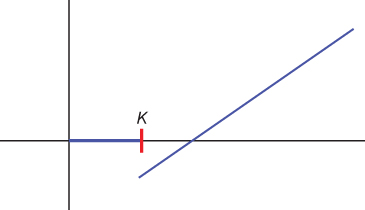
Figure S.1 “Free” option payoff.
1.2 Autocallable
Answer: ![]() .
.
1.3 Geometric Asian Option
- From Ito-Doeblin we have
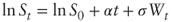 where α = r − q − ½σ2. Substituting into the definition of AT we get:
where α = r − q − ½σ2. Substituting into the definition of AT we get:
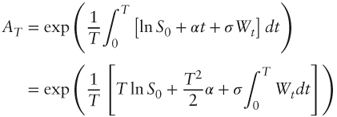
- which yields the required expression for AT after simplifications.
- From Ito-Doeblin, we get
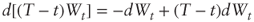 , which yields the required result after integration of both sides over [0, T]. The distribution of
, which yields the required result after integration of both sides over [0, T]. The distribution of 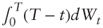 is thus normal with zero mean and variance
is thus normal with zero mean and variance 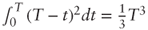 .
. - Substituting
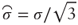 and
and 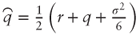 we need to show that ln AT is normally distributed with mean:
we need to show that ln AT is normally distributed with mean:
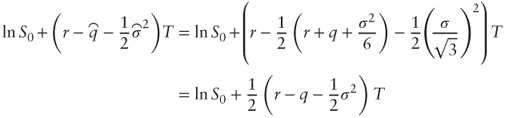
- and variance
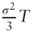 . Indeed the mean matches the expression from question (a), and using question (b) we find that the variance of
. Indeed the mean matches the expression from question (a), and using question (b) we find that the variance of 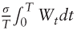 is
is 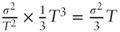 as required.
as required.
1.4 Change of Measure
We have ![]() with
with ![]() . Since
. Since ![]() we have after substitution:
we have after substitution:
But ![]() and thus
and thus ![]()
![]() . Expanding the second squared bracket and cancelling terms we are left with
. Expanding the second squared bracket and cancelling terms we are left with ![]() as required.
as required.
1.6 Siegel's Paradox
- Straightforward application of Ito-Doeblin.
- The “risk-neutral” dynamics of 1/X from question (a) correspond to the dollar risk-neutral measure, in which 1/X is non tradable (number of euros per dollar). The paradox is resolved by introducing the euro risk-neutral measure where 1/X follows the process:
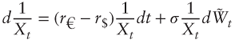
In the dollar risk-neutral measure, 1/X is the price of the dollar-euro exchange rate quanto dollar. Following the notations of Section 1.2.4 and defining S = 1/X, we have ρ = −1 and η = σ; thus the drift of S quanto dollar under the dollar risk-neutral measure is r€ − r$ − ρση = r€ − r$ + σ2 as required.
Chapter 2: The Implied Volatility Surface
2.1 No Call or Put Spread Arbitrage Condition
We know the upper bound is:
and we know that ![]() so after rearranging terms we get:
so after rearranging terms we get:
We know the lower bound is:
and we know that ![]() so we get
so we get
From put-call parity: ![]() , and thus:
, and thus:
Putting them together we get:
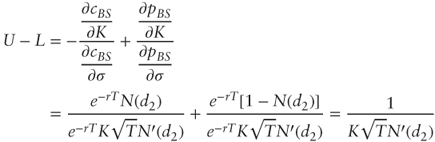
Furthermore ![]() and
and ![]()
Thus:
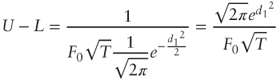
as required.
2.2 No Butterfly Spread Arbitrage Condition
- Identities:
- We have:
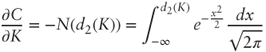
Differentiating with respect to K:
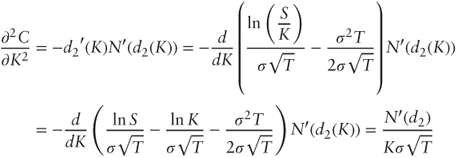
as required.
Differentiating
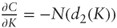 with respect to σ:
with respect to σ: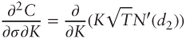
Using the chain rule:
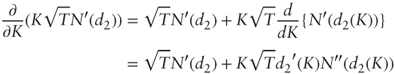
But:
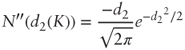
Substituting
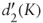 and
and 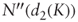 :
: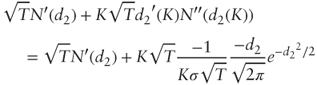
Using the fact that
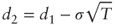 , we get:
, we get: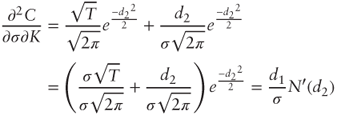
- Differentiating
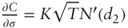 with respect to σ:
with respect to σ:
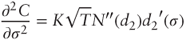
We have:
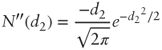
and:
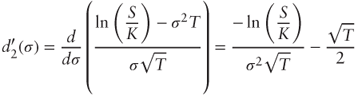
Substituting back into
 :
: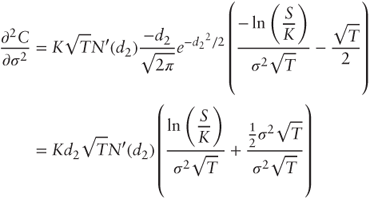
Factoring by
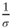 and recognizing d1 we obtain as required:
and recognizing d1 we obtain as required: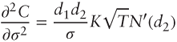
- First-order derivative:
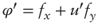 . Second-order derivative:
. Second-order derivative:
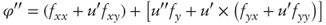
- which yields the required result after noting that fxy = fyx by Schwarz's theorem.
- Applying the second-order chain rule:
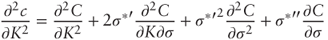
Substituting the identities from (a) we get the required result after further straightforward algebra.
- After simplifications
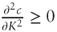 is equivalent to:
is equivalent to:
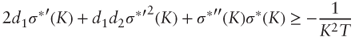
2.3 Sticky True Delta Rule
- Applying the chain rule:
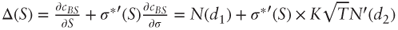 , whence the required result after substituting K = 1 and T = 1.
, whence the required result after substituting K = 1 and T = 1. - If
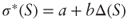 then
then 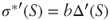 and thus
and thus 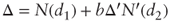 yielding the required result after appropriate substitutions.
yielding the required result after appropriate substitutions. - c. Because Δ′ > 0 (call delta goes up as S goes up) and b < 0 (volatility goes down as S and Δ go up) the sticky true delta rule would produce a lower delta than Black-Scholes.
Chapter 3: Implied Distributions
3.1 Overhedging Concave Payoffs
Assume f(K1) = 0 for simplicity. From left to right: start with f′(K1) calls struck at K1 so as to be tangential to the payoff; add ![]() calls struck at K2 such that the portfolio matches the payoff f(K3) at K3; then add
calls struck at K2 such that the portfolio matches the payoff f(K3) at K3; then add ![]() calls struck at K3 so as to be tangential to the payoff after K3; and so on (see Figure S.2).
calls struck at K3 so as to be tangential to the payoff after K3; and so on (see Figure S.2).

Figure S.2 Over-hedging concave payoffs.
3.2 Perfect Hedging with Puts and Calls
From Section 3.2:
Splitting the integral at F and using terminal put-call parity ![]() we get:
we get:
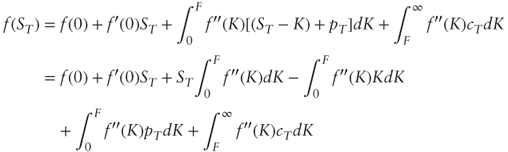
But ![]() , and:
, and:
After substitutions and simplifications we get:
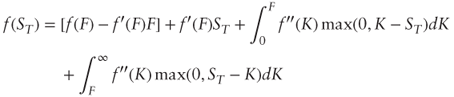
Thus:
because ![]() .
.
3.3 Implied Distribution and Exotic Pricing
-
- Answer: ≈ .1043
- Answer: ≈ 1.0789
- Answer: ≈ .2693
- Answer: ≈ .0211. Vanilla overhedge with strikes 0.5, 0.9, 1, 1.1, 1.3, 1.7: Quantities are 0, 0, 0.0100, 0.1200, 0.6700, and 1.5200 (see Figure S.3).
-
- (i Answer: approximately $0.8965.
- (ii Answer: approximately $0.8626.
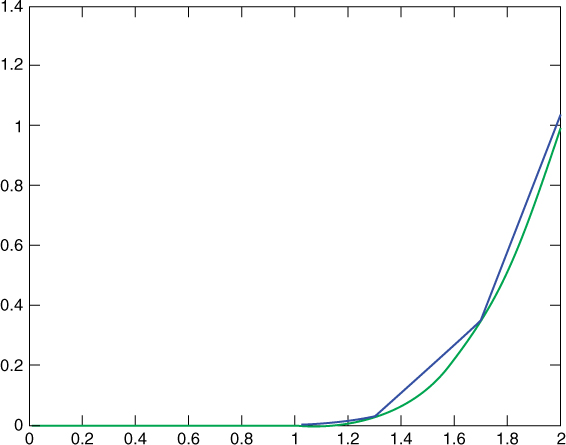
3.5 Path-Dependent Payoff
- For example: forward start option, Asian option.
- Pseudo-code:
- Loop for i = 1 to N:
- Generate and calculate
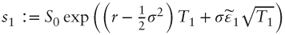
- Generate
 and
and 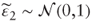 independently and calculate
independently and calculate
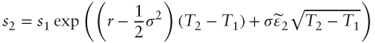
- Calculate
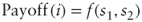
- Generate and calculate
- Return
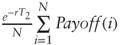
- Loop for i = 1 to N:
- We only know the marginal distributions of
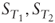 but we are missing the conditional implied distribution of
but we are missing the conditional implied distribution of 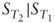 .
.
3.6 Delta
From ![]() we get
we get ![]() and thus:
and thus:
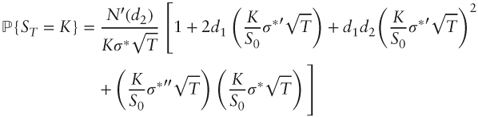
atm_vol = SVI(1);
atm_vol1 = SVI(1/(1+epsilon));
price = 0;
for i=1:n
normal = randn;
x = exp(atm_vol*normal*sqrt(T) - 0.5*atm_vol∧2*T);
x1 = (1+epsilon)*exp(atm_vol1*normal*sqrt(T) − 0.5*atm_vol1∧2*T);
price = (i-1)/i*price + Payoff(x)*ImpDist(x) …
/ lognpdf(x,-0.5*atm_vol∧2*T,atm_vol*sqrt(T)) / i;
price1 = (i-1)/i*price1 + Payoff(x1)*ImpDist(x1) …
/ lognpdf(x1,-0.5*atm_vol1∧2*T,atm_vol1*sqrt(T)) / i;
end
delta = price − price1
Chapter 4: Local Volatility and Beyond
4.1 From Implied to Local Volatility
- We rewrite Equation (4.1) by solving for
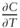 after using the result from Problem 2.4.2(c) for
after using the result from Problem 2.4.2(c) for 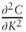 .
.
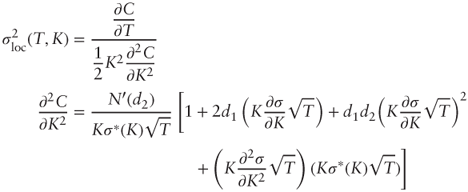
Take
 and derive with respect to T:
and derive with respect to T: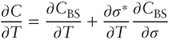
We are given
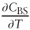 and
and 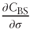 so:
so: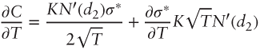
We then plug in
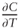 and
and 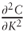 into Equation (4.1):
into Equation (4.1):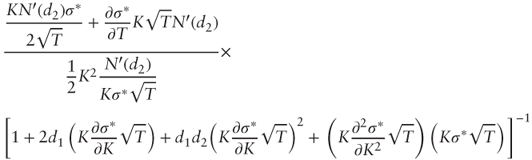
By dividing both numerator and denominator by
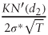 , we obtain the desired Equation (4.2):
, we obtain the desired Equation (4.2):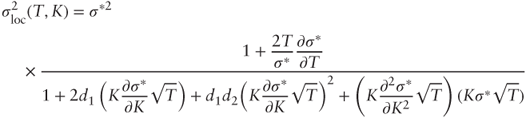
- Replace
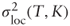 with
with 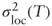 so we now have:
so we now have:
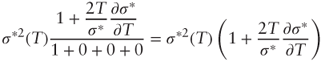
Now using the Hint:
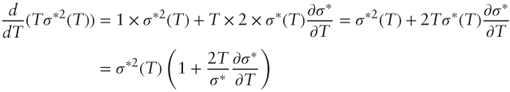
Thus
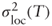 =
= 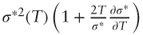 and by integration we find that:
and by integration we find that: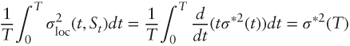
as required.
- To establish the hint, note that
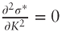 by linearity of σ*, and substitute
by linearity of σ*, and substitute 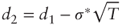 . Differentiating
. Differentiating 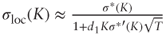 with respect to K we obtain:
with respect to K we obtain:
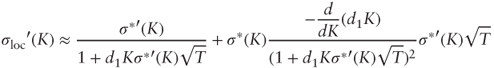
Near the money both denominators are close to 1; furthermore
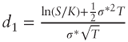 gives
gives 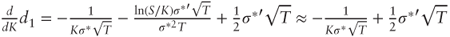 . After substitution and simplification:
. After substitution and simplification: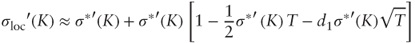
whose leading term is
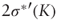 .
.
4.2 Market Price of Volatility Risk
- The delta-hedged portfolio Π is long one option and short
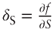 units of S. Thus:
units of S. Thus:
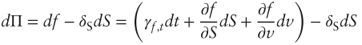
- which yields the required result after cancelling terms.
- We have:
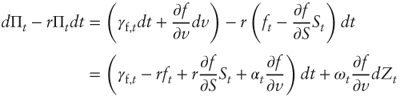
But
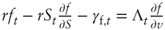 which yields the required result after substitution and simplifications.
which yields the required result after substitution and simplifications. - Conditional expectation:
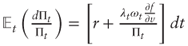 . Conditional standard deviation:
. Conditional standard deviation:
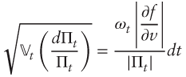
Thus
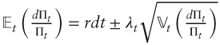 , that is, at time t the risk-neutral expected return on the delta-hedged portfolio is the risk-free interest rate plus a positive or negative risk premium, which is proportional to the risk of the portfolio, with proportionality coefficient λ. This result applies to any option and λ is independent from the particular option chosen, which is why it is called the market price of volatility risk.
, that is, at time t the risk-neutral expected return on the delta-hedged portfolio is the risk-free interest rate plus a positive or negative risk premium, which is proportional to the risk of the portfolio, with proportionality coefficient λ. This result applies to any option and λ is independent from the particular option chosen, which is why it is called the market price of volatility risk.
4.3 Local Volatility Pricing
- Figure S.4 shows a graph of the corresponding local volatility surface.
- Using Monte Carlo simulations:
- “Capped quadratic” option:
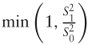 ; answer: 0.76949
; answer: 0.76949 - Asian at-the-money-call:
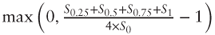 ; answer: 0.1242
; answer: 0.1242 - Barrier call:
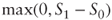 if S always traded above 80 using 252 daily observations, 0 otherwise. Answer: 12.87577
if S always traded above 80 using 252 daily observations, 0 otherwise. Answer: 12.87577
- “Capped quadratic” option:
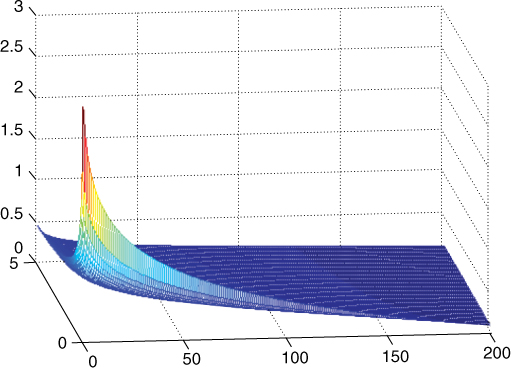
Figure S.4 Local volatility surface.
Chapter 5: Volatility Derivatives
5.1 Delta-Hedging P&L Simulation
- Positive Path: See Figure S.5
Negative Path: See Figure S.5
- Average P&L: −$11,663.80 (see Figure S.6)
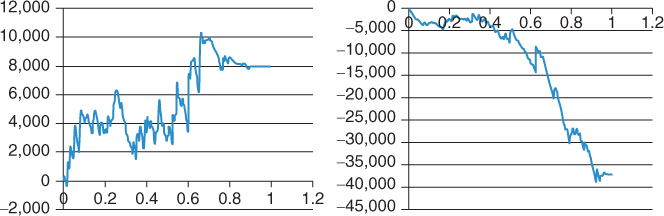
Figure S.5 Cumulative P&L: positive and negative paths.
Figure S.6 Distribution of final cumulative P&L.
5.2 Volatility Trading with Options
- (i) If σ is constant then
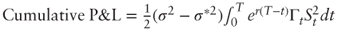 . For a vanilla call Γ > 0 and thus the cumulative P&L is always positive.
. For a vanilla call Γ > 0 and thus the cumulative P&L is always positive.
(ii) We have
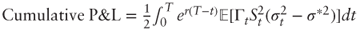 . By iterated expectations:
. By iterated expectations: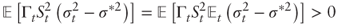
- The aggregate cumulative P&L is:
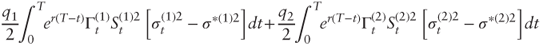
As a sum of two independent normal distributions the aggregate distribution is normal with parameters:
- Mean: q1m1 + q2m2
- Standard deviation:
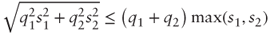
This result sheds light on the diversification effect obtained by delta-hedging several options within an option book: the expected income is the sum of individual delta-hedging P&Ls, but it is less risky than delta-hedging a single position.
5.4 Generalized Variance Swaps
- From Ito-Doeblin:
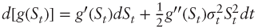 . But
. But 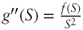 ; rearranging terms we get:
; rearranging terms we get: 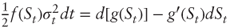 . Integrating over [0, T] yields the desired result.
. Integrating over [0, T] yields the desired result.
Thus generalized variance may be replicated by a combination of cash, two derivative contracts paying off g(ST) at maturity, and dynamically trading S to maintain a short position of 2g′(St) at all times. Taking expectations we find that the fair value is:
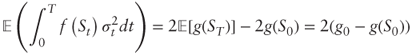
since
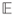 (dWt) = 0.
(dWt) = 0. - From Problem 3.4.2 we get:
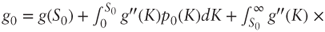
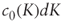 whence the required formula after substituting
whence the required formula after substituting 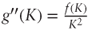 and annualizing.
and annualizing. - For the corridor varswap
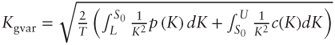
5.5 Call on Realized Variance
- Solving for vt we have:
 Thus vt is lognormally distributed with mean
Thus vt is lognormally distributed with mean 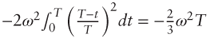 and standard deviation
and standard deviation 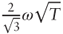 . From Black's formula we have
. From Black's formula we have 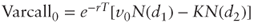 where
where 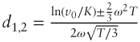 . At the money this simplifies to
. At the money this simplifies to 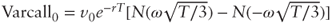 which yields the required formula because N(x) − N(−x) = 2N(x) − 1.
which yields the required formula because N(x) − N(−x) = 2N(x) − 1. - For x ≈ 0 we have
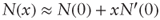 .
.
Chapter 6: Introducing Correlation
6.1 Lower Bound for Average Correlation
- Substitute x = e in
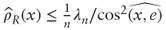 .
. - Because
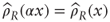 we have
we have 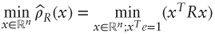 . Define the Lagrangian
. Define the Lagrangian 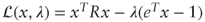 . The first-order condition yields
. The first-order condition yields 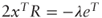 that is,
that is, 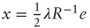 . The constraint eTx = 1 then gives the value of λ and we get the required result after substitution and simplification.
. The constraint eTx = 1 then gives the value of λ and we get the required result after substitution and simplification. - (i) By spectral decomposition:
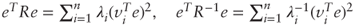 . Furthermore, Parseval's identity states that
. Furthermore, Parseval's identity states that 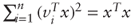 for any x, and thus
for any x, and thus 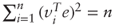 . Scaling by appropriate constants we obtain the required result.
. Scaling by appropriate constants we obtain the required result.
(ii) Rewrite
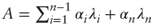 and make the approximation that for i = 1,…, n − 1:
and make the approximation that for i = 1,…, n − 1: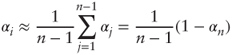
which is justified by the fact that αn ≈ 1 since vn and e are assumed to form a tight angle. Proceed similarly for H.
6.2 Geometric Basket Call
- We have:
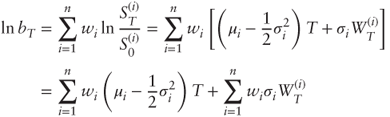
- where
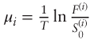 is the annualized risk-neutral drift of S(i). As a sum of normal variables ln bT is normally distributed with mean
is the annualized risk-neutral drift of S(i). As a sum of normal variables ln bT is normally distributed with mean 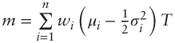 and variance:
and variance:
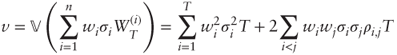
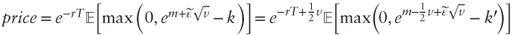 where
where 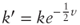 . Using Black's formula:
. Using Black's formula: 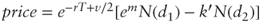 with
with 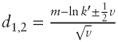 . Further simplifications are possible.
. Further simplifications are possible.
6.4 Continuously Monitored Correlation
After substitution, we have by Cauchy-Schwarz:
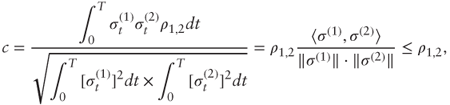
where ![]() .
.
Chapter 7: Correlation Trading
7.1
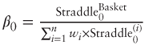 is positive because straddles always have a positive payoff and thus price. It must be less than 1 because of the triangle inequality:
is positive because straddles always have a positive payoff and thus price. It must be less than 1 because of the triangle inequality: 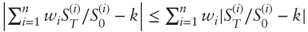
- Use the proxy
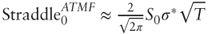
7.2
- From the Black-Scholes PDE
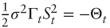 . Applying Ito-Doeblin to Θ:
. Applying Ito-Doeblin to Θ: 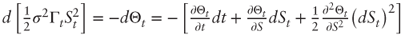 . Taking expectations we get:
. Taking expectations we get:
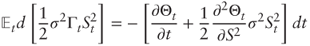
- which vanishes because Greeks must also satisfy the Black-Scholes PDE.
7.3
At time 0 the portfolio value is ![]() , and the vega of each component is
, and the vega of each component is ![]() . Hence the portfolio vega is
. Hence the portfolio vega is ![]() .
.
Chapter 8: Local Correlation
8.1 Implied Correlation
Implied correlation is constant iff ![]() , i.e., iff
, i.e., iff ![]() , whence the required result after simplifications.
, whence the required result after simplifications.
8.2 Dynamic Local Correlation I
When D = I and U = eeT Langnau's alpha is:
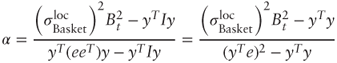
where ![]() . Define
. Define ![]() and divide both the numerator and denominator of the above expression by B to get:
and divide both the numerator and denominator of the above expression by B to get:
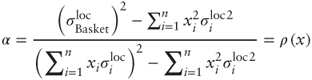
It is easy to verify that ![]() .
.
Chapter 9: Stochastic Correlation
9.2
- The process clearly remains within [0,1] because it is continuous and its drift and volatility coefficients vanish at 0 and 1. Let us show that the bound 0 is nonattracting:
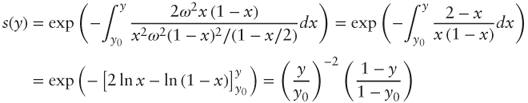
Thus
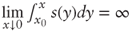 since
since 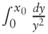 diverges. A similar analysis shows that the bound 1 is also nonattracting.
diverges. A similar analysis shows that the bound 1 is also nonattracting. - We want to find f(x), g(x) such that:
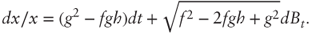
Thus we must solve:
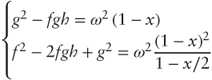
Taking ratios we get
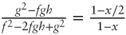 ; dividing both numerator and denominator by g2 on the left-hand side we obtain
; dividing both numerator and denominator by g2 on the left-hand side we obtain 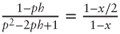 . Solving for p after substituting
. Solving for p after substituting 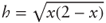 we find
we find 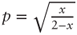 , that is,
, that is, 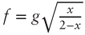 . Substituting in
. Substituting in 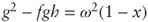 and simplifying we get
and simplifying we get 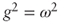 , and thus
, and thus 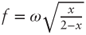 .
. - This model is not suitable for several reasons: it has only one parameter ω, which leaves little freedom for parameterization, and the volatility of basket variance f is lower than the volatility of constituent variance g, which is contrary to empirical observation.
