Chapter 24

Answers

      1.           −4, −3, −1, 0, 4

The number −4 has a greater absolute value than −3, so it's farther to the left on the number line. And −3 has a greater absolute value than −1.

      2.           −3, −2, 0, 1, 3

The number −3 has a greater absolute value than −2, so it's farther to the left on the number line.

      3.          

The number −5 has a greater absolute value than −1, so it's farther to the left on the number line. The number is between −2 and −3. And the number is between 0 and 1.

      4.          

The number −4 has a greater absolute value than −2, so it's farther to the left on the number line. And the number is between −1 and −2.

      5.          

The number is about 1.7, and the number is about −1.4, which is between −1 and −2. The number −4 has a greater absolute value than −1.4, so it's farther to the left on the number line.

      6.          

The number is about 1.7, and the number is equal to −3.5, which is between −3 and −4.

      7.           4

Absolute value asks for the distance of the number from 0. The value of −4 is 4 units to the left of 0.

      8.           7.6

Absolute value asks for the distance of the number from 0. The value of −7.6 is 7.6 units to the left of 0.

      9.           −2

First find the absolute value of the −2 within the absolute value symbols.

|−2| = 2

Then find the opposite of that answer.

−(2) = −2

      10.          

First find the absolute value of the within the absolute value symbols.

Then find the opposite of that answer.

      11.           −6

The signs are the same, so you find the sum of the absolute values of the numbers, 4 + 2 = 6, and then attach their negative sign. The answer is −6.

      12.           −2

The signs are different, so first you find the difference between the absolute values of the numbers, 4 − 2 = 2, and then you attach the sign of the number with the greater absolute value, the −4. The answer is −2.

      13.           2

The signs are different, so first you find the difference between the absolute values of the numbers, 4 − 2 = 2, and then you attach the sign of the number with the greater absolute value, the +4. The answer is +2.

      14.           −2

The signs are different, so first you find the difference between the absolute values of the numbers, 5 − 3 = 2, and then you attach the sign of the number with the greater absolute value, the −5. The answer is −2.

      15.           0

The signs are different, so you find the difference between the absolute values of the numbers, 6 − 6 = 0. The number 0 has no sign, so the answer is 0.

      16.           5

The signs are different, so first you find the difference between the absolute values of the numbers, 7 − 2 = 5, and then you attach the sign of the number with the greater absolute value, the +7. The answer is 5.

      17.           −1

First, add the two negative numbers together, −4 + −2 = −6.

Now the problem looks like this: 5 + (−6).

Add the two numbers with the different signs by finding the difference between their absolute values, 6 − 5 = 1. Attach the sign of the number with the greater absolute value, the −6. The answer is −1.

      18.           2

Add the two negative numbers together to get −4. Then add the two positive numbers together to get 6.

The sum of −4 and 6 is +2, because you find the difference between the absolute values of the numbers and attach the sign of the number with the greater absolute value.

      19.           2

Add the first two numbers together by finding the difference between their absolute values, 1. Next, add the last two numbers together by finding the difference between their absolute values, 1.

Finally, add the two results together: 1 + 1 = 2.

      20.           −11

Add the four negative numbers together by finding the sum of their absolute values: 4 + 5 + 6 + 7 = 22. Attached a negative sign to the sum: −22.

Now add the two positive numbers together: 7 + 4 = 11.

The sum of the two results, −22 + 11, is found by finding the difference between the absolute values, 22 − 11 = 11. The sign of the final answer is negative, because the −22 has the greater absolute value. So the answer is −11.

      21.           −10

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the 6 to −6. Then do the addition problem: −4 + (−6).

The signs are the same, so you find the sum of the absolute values of the numbers and then apply the negative sign. The answer is −10.

      22.           15

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the −8 to +8. Then do the addition problem:

7 + (+8).

The signs are the same, so you find the sum of the absolute values of the numbers.

      23.           3

This is just a simple subtraction problem involving two positive numbers. Subtract as usual.

      24.           −5

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the −4 to +4. Then do the addition problem:

−9 + (+4).

The signs are different, so you find the difference of the absolute values of the numbers and then apply the sign of the larger value. The answer is −5.

      25.           −14

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the 7 to −7. Then do the addition problem:

−7 + (−7).

The signs are the same, so you find the sum of the absolute values of the numbers and then apply the negative sign. The answer is −14.

      26.           0

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the −7 to +7. Then do the addition problem:

−7 + (+7).

The signs are different, so you find the difference of the absolute values of the numbers, 7 − 7 = 0.

      27.           5

Create an equivalent addition problem by changing the subtract to add and the sign of the −2 to +2. Then do the addition problem: 3 + (+2).

The signs are the same, so you find the sum of the absolute values of the numbers.

      28.           −1

First find the opposite of the −2 in the brackets, giving you +2. Then, create an equivalent addition problem by changing the subtraction sign to addition and the sign of the 3 to −3. Then do the addition problem:

2 + (−3).

The signs are different, so you find the difference of the absolute values of the numbers and apply the sign of the larger value. The answer is −1.

      29.           8

First, find the opposite of the −4 in the brackets, giving you +4. Then create an equivalent addition problem by changing the subtraction sign to addition and the sign of the −4 in the parentheses to +4. Then do the addition problem:

4 + (+4).

The signs are the same, so you find the sum of the absolute values of the numbers.

      30.           5

Create an equivalent addition problem by changing the subtraction sign to addition and the sign of the −5 in the parentheses to +5. Then do the addition problem:

0 + (+5).

The number 0 is the additive identity, so adding it to +5 does not change the value of the +5.

      31.           −6

The product of 2 and 3 is 6.

There's one negative sign (odd number), so the product is negative.

      32.           20

The product of 4 and 5 is 20.

There are two negative signs (even number), so the product is positive.

      33.           −30

The product of 5 and 6 is 30.

There's one negative sign (odd number), so the product is negative.

      34.           −3

The product of 3 and 1 is 3.

There's one negative sign (odd number), so the product is negative.

      35.           49

The product of 7 and 7 is 49.

There are two negative signs (even number), so the product is positive.

      36.           −64

The product of 8 and 8 is 64.

There's one negative sign (odd number), so the product is negative.

      37.           10

The product of 6 and is

There are two negative signs (even number), so the product is positive.

      38.           −15

The product of 20 and is

There is one negative sign (odd number), so the product is negative.

      39.           0

The product of any number and 0 is 0.

      40.           1

The product of 1·1·1·1 is 1.

There are four negative signs (even number), so the product is positive.

      41.           −3

When you divide 6 by 2, you get 3.

There is one negative sign (odd number), so the quotient is negative.

      42.           2

When you divide 8 by 4, you get 2.

There are two negative signs (even number), so the quotient is positive.

      43.           −4

When you divide 12 by 3, you get 4.

There is one negative sign (odd number), so the quotient is negative.

      44.           4

When you divide 60 by 15, you get 4.

There are two negative signs (even number), so the quotient is positive.

      45.           0

When you divide 0 by any number (other than 0), the answer is 0.

      46.           −5

When you divide 5 by 1, you get 5.

There is one negative sign (odd number), so the quotient is negative.

      47.           2

First, find the product of the two numbers in the denominator.

2(−4) = −8

Now divide −16 by −8.

When you divide 16 by 8, you get 2.

There are two negative signs (even number), so the quotient is positive.

      48.           −1

First, find the product in the numerator and in the denominator.

In the numerator, 2(−6)(−1) = 12, because there are an even number of negative signs.

In the denominator, 4(−3) = −12, because there's only one (odd number) negative sign.

Now divide 12 by −12, and you get −1, because there's one negative sign.

A good way to check the sign of your answer is to just count the number of negative signs in the original problem. You see three negative signs (odd number), so the final result should be negative.

      49.           −4

First, find the product in the numerator and in the denominator.

In the numerator, −4(−3)(−2)(−1) = 24, because there are an even number of negative signs.

In the denominator, 6(−1) (−1) (−1)= −6, because there are an odd number of negative signs.

Now divide 24 by −6, and you get −4, because there's one negative sign.

A good way to check the sign of your answer is to just count the number of negative signs in the original problem. You see seven negative signs, so the final result should be negative.

      50.           1

One way to solve this would be to find the products of the numerator and denominator, separately and then divide. Both the numerator and denominator have products of 36, so, when you divide, you get 1. There are an even number of negative signs so the answer is positive.

Another way to handle the problem is to divide out (reduce) all the equal factors in the numerator and denominator. The two 2's and two 3's all divide out, leaving you with 1.

      51.           4

First, perform the subtraction inside the parentheses.

6 − (5 − 3) = 6 − (2)

Now subtract.

6 − 2 = 4

      52.           −4

First, perform the subtraction inside the parentheses.

(4 − 3) − 5 = (1) − 5

Now subtract.

1 − 5 = −4

      53.           20

First, perform the subtraction inside the parentheses.

5[6 + (3 − 5)] = 5[6 + (−2)]

Add the two numbers inside the brackets.

= 5[4]

Now multiply.

= 20

      54.           0

First, perform the subtraction inside the parentheses.

8{3 − [4 + (5 − 6)]} = 8{3 − [4 + (− 1)]}

Next, add the numbers inside the brackets.

= 8{3 − [3]}

Add the two numbers inside the braces.

= 8{0}

The product of 0 and anything is 0.

      55.           2

First, subtract the two numbers in the numerator.

Then divide to get 2.

      56.           −6

First, subtract the two numbers in the denominator.

Then, when dividing to get −6, the quotient is negative, because there is one negative sign.

      57.           1

First, subtract the two numbers in the parentheses.

Next, subtract the two numbers in the numerator, and then the two numbers in the denominator.

Dividing a number by itself, you get 1.

      58.           1

First, do the two subtractions inside the parentheses.

Now subtract the two numbers in the numerator, and then the two numbers in the denominator.

Dividing a number by itself, you get 1.

      59.           2

First, find the difference of the numbers under the radical.

The square root of 4 is 2.

      60.           4

First, subtract the numbers in the numerator, and then subtract the numbers under the radical sign.

Next, find the square root of 4.

The final division gives you 4.

      61.           −1

First, subtract the numbers in the numerator under the radical sign, and then subtract the numbers in the denominator.

The square root of 1 is 1.

Dividing 1 by −1 gives you −1, because there's one negative sign.

      62.           −6

First, find the difference between the two numbers inside the absolute value symbol.

|5 − 6| − 7 = |−1| − 7

Now evaluate the result inside the absolute value symbol.

|−1| − 7 = 1 − 7

Subtracting, you get −6.

      63.           2

First, find the difference between the two numbers inside the absolute value symbol.

5 − 14 − 7| = 5 − |−3|

Now evaluate the result inside the absolute value symbol.

5 − |−3|= 5 − 3

Subtracting, you get 2.

      64.           2

First, subtract the numbers under the radical, and then subtract the numbers inside the absolute value symbol.

The square root of 16 is 4, and the absolute value of −2 is 2.

Dividing, you get 2.

      65.           14 − 2y

Multiply the 2 times each term in the parentheses. Be sure to carry the negative sign along with the y.

2(7) + 2(−y) = 14 − 2y

      66.           −6x − 24

Multiply the −6 times each term in the parentheses.

−6(x) + −6(4) = −6x − 24

      67.           −3x + 1

Multiply the −3 times each term in the parentheses.

      68.           6 − 12y

Multiply each term in the parentheses by . Be sure to carry the subtraction sign along with the second term.

      69.           xy − 6x

Multiply each term in the parentheses by x. Be sure to carry the subtraction sign along with the second term.

x(y) + x(−6) = xy − 6x

      70.           −4x² + 8xy − 12x

Multiply each term in the parentheses by −4x.

−4x(x) + −4x(−2y) + −4x(3)

= −4x² + 8xy − 12x

      71.           2 − 8 + 9 = 3

Multiply each fraction in the parentheses by 12.

      72.           −20x + 2

Multiply each term in the parentheses by −5.

      73.           90

Regroup the 47 with the −47; their sum is 0.

(47 + (−47)) + 90 = 0 + 90 = 90

      74.           −6

Regroup the 23 with the −23; their sum is 0.

−6 + (23 − 23) = −6 + 0 = −6

      75.           29

Regroup the two fractions, which are reciprocals of one another. Their product is 1.

      76.           811

Regroup the and the 15 together. They're reciprocals, and their product is 1.

      77.           20

Regroup the 19 and −19 together. Their sum is 0.

16 + (19 + (−19)) + 4 = 16 + 0 + 4 = 20

      78.           77

Regroup the −53.2 and 53.2 together. Their sum is 0.

77 + (−53.2 + 53.2) = 77 + 0 = 77

      79.           47

Reverse the order of the 47 and 16. Then add the −16 and 16, which are additive inverses.

−16 + 16 + 47 = (−16 + 16) + 47 = 0 + 47 = 47.

      80.          

Reverse the order of the first two fractions. Then the two additive inverses can be combined to give you 0.

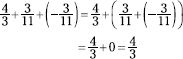
      81.           673

Reverse the last two numbers. Then you have additive inverses that can be combined to give you 0.

432 − 432 + 673 = 0 + 673 = 673

      82.          

Reverse the second two fractions. The product of a fraction and its reciprocal is 1.

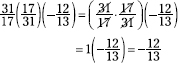
      83.          

Reverse the two fractions. Then multiply the times 18 before multiplying the result times .

      84.           4

Reverse the −3 and 4, and then reverse the 23 and 3.

4 + −3 + 23 + 3 − 23

= 4 + −3 + 3 + 23 − 23

Associate the two pairs of additive inverses and simplify.

= 4 + (−3 + 3) + (23 − 23) = 4 + 0 + 0 = 4

      85.           −4x

First, distribute the 4 over the terms in the parentheses.

−32 + 4(8 − x) = −32 + 32 − 4x

The first two terms have a sum of 0.

0 − 4x = −4x

      86.           −5x

First, distribute the −5 over the two terms in the parentheses.

−5(x − 2) − 10 = −5x + 10 − 10

The last two terms have a sum of 0.

−5x + 0 = −5x

      87.           48

First, distribute the 48 over the two terms in the parentheses.

Now reverse the first and second terms.

48 + 8x − 8x

The second two terms have a sum of 0.

48 + 0 = 48

      88.           −x

First, distribute the over the two terms in the parentheses.

The sum of the second two terms is 0.

−x + 0 = −x

      89.           y

First distribute the −2 over the terms in the first parentheses, and distribute the 3 over the terms in the second parentheses.

−2(3) + −2(y) + 3(y) + 3(2) = −6 − 2y + 3y + 6

Move the first term all the way to the right.

− 2y + 3y + 6 − 6

The first two terms combine, and the last two terms have a sum of 0.

y + 0 = y

      90.          

First reverse the last two terms.

Now write the middle fraction as the product of two fractions, one of them , and write the last fraction as the product of two fractions, one of them .

Grouping the pairs of reciprocals together,

      91.          

Find a common denominator, and change each fraction to an equivalent fraction using that denominator.

Since the denominators are relatively small, find the common denominator by multiplying them together, 6 × 5 = 30.

Find the sum of the numerators; then change the answer to a mixed number.

      92.          

Find a common denominator, and change each fraction to an equivalent fraction using that denominator.

You can find the least common denominator by checking multiples of the larger denominator, 25. When you get to 25 × 6 = 150, you have a number divisible by 15, also.

Find the difference between the numerators; then reduce the fraction.

      93.          

Find a common denominator for the two fractions, and change each fraction to an equivalent fraction using that denominator.

You can find the least common denominator by checking multiples of the larger denominator, 8. When you get to 8 × 3 = 24, you have a number divisible by 6, also.

Add the whole numbers together, then the fractions.

The fractional part of the answer is improper. Change the to , and then add the whole number part to the rest of the answer.

      94.          

Find a common denominator for the two fractions, and change each fraction to an equivalent fraction using that denominator.

You can find the least common denominator by checking multiples of the larger denominator, 10. When you get to 10 × 3 = 30, you have a number divisible by 6, also.

The numerator of the second fraction is larger than the numerator it's being subtracted from, so you borrow one, , from the 6 in the first number and add it on to the fraction.

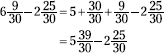
Now subtract the whole numbers and then the fractions by finding the difference between the numerators. Then reduce the fraction.

      95.          

First, find a common denominator for the four fractions, and change each fraction to an equivalent fraction using that denominator. The four denominators have no factors in common, so the least common denominator will be their product, 840.

Next, find the sum of the first two fractions. Then find the sum of the second two fractions, but place a subtraction sign in front of that result.

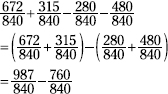
Subtract the two fractions.

      96.          

First, find a common denominator for the three fractions in the problem, and change each fraction to an equivalent fraction using that denominator. The fractions have common factors, so just try multiples of the largest denominator, the 12. The number 24 is the least common denominator.

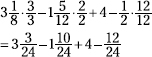
Next, add the first mixed number and the 4 together. Then add the two negative numbers together and put a subtraction sign in front of the result.

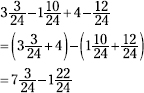
The numerator in the second number is larger than that in the first, so borrow from the 7 to create an equivalent number.

Now perform the subtraction.

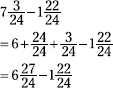
      97.          

Before multiplying the two numerators and the two denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiplying the two numerators and the two denominators:

      98.          

Before multiplying the two numerators and the two denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the two numerators and the two denominators:

      99.          

First, change each mixed number to an improper fraction.

Before multiplying the two numerators and the two denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the two numerators and the two denominators.

Now rewrite the answer as a mixed number.

      100.          

First, change each mixed number to an improper fraction.

Before multiplying the three numerators and the three denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

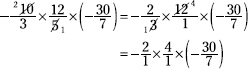
Multiply the numerators and the denominators.

Now rewrite the answer as a mixed number.

      101.          

First, change the division problem to an equivalent multiplication problem using the reciprocal of the second fraction.

Now, before multiplying the numerators and the denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the numerators and the denominators.

Finally, rewrite the improper fraction as a mixed number.

      102.          

First, rewrite the mixed numbers as improper fractions.

Next, change the division problem to an equivalent multiplication problem using the reciprocal of the second fraction.

Now, before multiplying the numerators and the denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the numerators and the denominators.

Finally, rewrite the improper fraction as a mixed number.

      103.          

First, rewrite the whole number and mixed number as improper fractions.

Next, change the division problem to an equivalent multiplication problem using the reciprocal of the second fraction.

Now, before multiplying the numerators and the denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the numerators and the denominators.

Finally, rewrite the improper fraction as a mixed number.

      104.          

First, rewrite the integer and mixed number as improper fractions.

Next, change the division problem to an equivalent multiplication problem using the reciprocal of the second fraction.

Now, before multiplying the numerators and the denominators, reduce the fractions — dividing one numerator and one denominator by the same number.

Multiply the numerators and the denominators.

Finally, rewrite the improper fraction as a mixed number.

      105.          

Multiply the numerator and denominator by 3. This is, essentially, multiplying by 1. Be sure to distribute the 3 over both terms in the denominator.

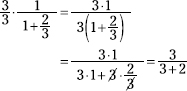
Now simplify the denominator.

Another technique for solving this type of problem is to add the two numbers in the denominator.

Write the result as an improper fraction.

Then multiply the numerator by the reciprocal of this new denominator.

      106.          

Multiply the numerator and denominator by 6. This is the least common denominator of the two fractions in the problem. Be sure to distribute the 6 over both terms in the denominator.

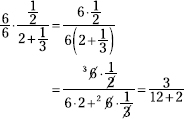
Now simplify the denominator.

Another technique for solving this type of problem is to add the two numbers in the denominator, write the result as an improper fraction, and then multiply the numerator by the reciprocal of this new denominator.

      107.          

Subtract the two fractions in the denominator by first creating common denominators.

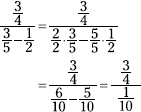
Now multiply the numerator by the reciprocal of the denominator.

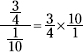
Reduce the fractions before multiplying and convert the final product to a mixed number.

Another technique for solving this type of problem is to multiply the numerator and denominator by the least common denominator of all the fractions. In this case, it would be 20.

      108.          

Subtract the two fractions in the denominator, and change the mixed number in the numerator to an improper fraction.

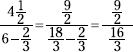
Now multiply the numerator by the reciprocal of the denominator.

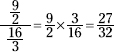
Another technique for solving this type of problem is to multiply the numerator and denominator by the least common denominator of all the fractions. In this case, it would be 6.

      109.          

Multiply the numerator and denominator by x. This is the denominator of the only fraction and is, essentially, multiplying by 1. Be sure to distribute the x over both terms in the denominator.

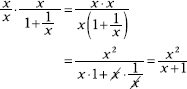
Another technique for solving this type problem is to add the two terms in the denominator and then multiply the numerator by the reciprocal of this new denominator.

      110.          

Subtract the two fractions in the numerator, and change the whole number in the denominator to an improper fraction.

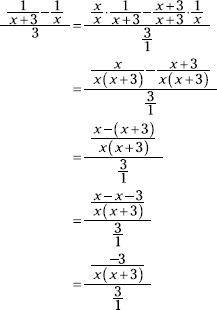
Now multiply the numerator by the reciprocal of the denominator.

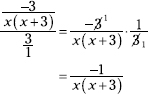
Another technique for solving this type problem is to multiply the numerator and denominator by the least common denominator of all the fractions. In this case, it would be x(x + 3).

      111.           438.0401

When adding or subtracting decimal numbers, you need to line up the decimal points to align the digits having the same place value.

      112.           10.277

When adding or subtracting decimal numbers, you need to line up the decimal points to align the digits having the same place value.

Add 0's after the 4, and then subtract.

      113.           1.043x

When adding like terms, you combine the coefficients of the variables. So you add 1 and 0.043 and make the sum be the new coefficient of the x.

When adding or subtracting decimal numbers, you need to line up the decimal points to align the digits having the same place value.

So the sum is 1.043x.

      114.           0.588y

When subtracting like terms, you combine the coefficients of the variables. So you subtract 5.3 minus 4.712 and make the difference be the new coefficient of the y.

When adding or subtracting decimal numbers, you need to line up the decimal points to align the digits having the same place value.

So the difference is 0.588y.

      115.           0.2408

When multiplying decimal numbers, count the number of digits to the right of the decimal point in the multipliers. That will be the number of digits to the right of the decimal point in the answer. Then multiply the numbers together without considering their decimal points. Place the decimal in the final answer.

4.3 has one digit to the right of the decimal point.

0.056 has three digits to the right of the decimal.

The sum of those digits is four, which you need for the answer.

Multiplying 43 × 56 (the 0's in front of the 5 and 6 aren't necessary), you get 2408. You need four digits to the right of the decimal point, so that gives you 0.2408.

      116.           −34.155

When multiplying decimal numbers, count the number of digits to the right of the decimal point in the multipliers. That will be the number of digits to the right of the decimal point in the answer. Then multiply the numbers together without considering their decimal points. Place the decimal in the final answer.

6.21 has two digits to the right of the decimal point.

−5.5 has one digit to the right of the decimal.

The sum of those digits is three, which you need for the answer.

Multiplying 621 × 55, you get 34155. You need three digits to the right of the decimal point, so that gives you 34.155.

There's one negative sign in the problem, so the answer is negative.

      117.           0.0332x²

In multiplication of algebraic expressions, the coefficients get multiplied together, and the variables get multiplied.

When multiplying decimal numbers, count the number of digits to the right of the decimal point in the multipliers. That will be the number of digits to the right of the decimal point in the answer. Then multiply the numbers together without considering their decimal points. Place the decimal in the final answer.

8.3 has one digit to the right of the decimal point.

0.004 has three digits to the right of the decimal.

The sum of those digits is four, which you need for the answer.

Multiplying 83 × 4, you get 332. You need four digits to the right of the decimal point, so add a 0 in front of the first 3, giving you 0.0332.

Now multiply the x variables to get x².

      118.           1.665y³

In multiplication of algebraic expressions, the coefficients get multiplied together, and the variables get multiplied.

When multiplying decimal numbers, count the number of digits to the right of the decimal point. That will be the number of digits to the right of the decimal point in the answer. Then multiply the numbers together without considering their decimal points. Place the decimal in the final answer.

3.7, −4.5, and −0.1 each have just the one digit to the right of the decimal point.

The sum of those digits is three, which you need for the answer.

Multiplying 37 × 45 × 1, you get 1665. You need three digits to the right of the decimal point, giving you 1.665.

Now multiply the y variables to get y³.

There are two negative numbers in the problems, so the sign of the product is positive.

      119.           730

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing 36.5 by 0.05, move the decimal point two places to the right. You'll have to add a 0 after the 5 in the dividend.

Becomes:

      120.           0.13

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing 0.143 by 1.1, move the decimal point one place to the right.

Becomes:

      121.           ≈487.805

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing 6 by 0.0123, move the decimal point four places to the right.

Becomes:

The problem doesn't divide evenly, so round to three decimal places, giving you approximately 487.805 for an answer.

      122.           ≈ −23.529

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing −72 by 3.06, move the decimal point two places to the right. You have to add two 0's to the end of the dividend.

Becomes:

The problem doesn't divide evenly, so round to three decimal places, giving you approximately −23.529 for an answer.

      123.           ≈48.333

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing 1.45 by 0.03, move the decimal point two places to the right.

Becomes:

The problem doesn't divide evenly, so round to three decimal places, giving you approximately 48.333 for an answer.

The decimal is a non-terminating, repeating decimal which is equivalent to , so the answer can also be written as 48.

      124.           ≈1821.622

When dividing decimal numbers, you want to divide with a whole number. So move the decimal point in the divisor to the right to form a whole number, and then move the decimal point in the dividend that same number of places. Place a decimal point above the dividend's new decimal position for the quotient.

Dividing 67.4 by 0.037, move the decimal point three places to the right. You have to add two 0's after the 4 in the dividend.

Becomes:

The problem doesn't divide evenly, so round to three decimal places, giving you approximately 1821.622 for an answer.

The decimal is a non-terminating, repeating decimal which is equivalent to , so the answer can also be written as 1821.

      125.           0.125

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal terminates, so 0.125 is the exact equivalent value.

      126.           0.28

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal terminates, so 0.28 is the exact equivalent value.

      127.           0.0792

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal terminates, so 0.0792 is the exact equivalent value.

      128.           0.0006

When the denominator is a power of 10, the decimal equivalent will have the value of the numerator with as many digits to the right of the decimal point as there are 0s in the denominator. In this case, you write 6 in the fourth place after the decimal, giving you the equivalent decimal of 0.0006.

      129.           0.444444...

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal repeats. The decimal equivalent can be written as 0.444444. or as 0.4 to show that the 4 repeats.

      130.           0.727272...

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal repeats. The decimal equivalent can be written as 0.727272... or as to show that the 72 repeats.

      131.           0.810810...

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal repeats. The decimal equivalent can be written as 0.810810... or as to show that the 810 repeats.

      132.           0.08910891...

Divide the numerator by the denominator. Add zeros to the dividend, and keep dividing until the decimal part of the answer either terminates or repeats.

This decimal repeats. The decimal equivalent can be written as 0.08910891... or as to show that the 0891 repeats.

      133.          

When changing a terminating decimal to an equivalent fraction, write the digits to the right of the decimal point over a power of ten with the same number of 0's as the number of digits to the right of the decimal point. Reduce the fraction if possible.

For 0.75, write 75 over 100 and reduce the fraction.

      134.          

When changing a terminating decimal to an equivalent fraction, write the digits to the right of the decimal point over a power of ten with the same number of 0's as the number of digits to the right of the decimal point. Reduce the fraction if possible.

For 0.875, write 875 over 1000 and reduce the fraction.

      135.          

When changing a terminating decimal to an equivalent fraction, write the digits to the right of the decimal point over a power of ten with the same number of 0's as the number of digits to the right of the decimal point. Reduce the fraction if possible.

For 0.0008..., write 8 over 10000 and reduce the fraction.

      136.          

When changing a terminating decimal to an equivalent fraction, write the digits to the right of the decimal point over a power of ten with the same number of 0's as the number of digits to the right of the decimal point. Reduce the fraction if possible.

For 0.1525, write 1525 over 10000 and reduce the fraction.

      137.          

When changing a repeating decimal (in which all the digits are part of the repeater) to an equivalent fraction, write the repeating digits over a number with as many 9's as digits that repeat. Reduce the fraction if possible.

For 0.888..., write 8 over 9. This fraction is already in lowest terms.

      138.          

When changing a repeating decimal (in which all the digits are part of the repeater) to an equivalent fraction, write the repeating digits over a number with as many 9's as digits that repeat. Reduce the fraction if possible.

For 0.636363..., write 63 over 99; then reduce the fraction.

      139.          

When changing a repeating decimal (in which all the digits are part of the repeater) to an equivalent fraction, write the repeating digits over a number with as many 9's as digits that repeat. Reduce the fraction if possible.

For 0.261261..., write 261 over 999; then reduce the fraction.

      140.          

When changing a repeating decimal (in which all the digits are part of the repeater) to an equivalent fraction, write the repeating digits over a number with as many 9's as digits that repeat. Reduce the fraction if possible.

For 0.285714285714..., write 285714 over 999999; then reduce the fraction.

      141.           243

Since the bases are the same, add the exponents.

3² · 3³ = 3²⁺³ = 3⁵ = 243

      142.           32

Since the bases are the same, add the exponents.

2⁻¹ · 2⁶ = 2⁻¹⁺⁶ = 2⁵ = 32

      143.           16

Since the bases are the same, add the exponents. The number 4 is written 4¹.

4.4² · 4⁻¹ = 4^1+2+(−1) = 4² = 16

      144.           125

Since the bases are the same, add the exponents. The number 5 is written 5¹.

5 · 5⁻³ · 5⁵ = 5^1+(−3)+5 = 5³ = 125

      145.           36

Since the bases are the same, subtract the exponents.

      146.           8

Since the bases are the same, subtract the exponents.

The number 2 is written 2¹.

      147.           27

Since the bases are the same, subtract the exponents.

      148.           125

Since the bases are the same, subtract the exponents.

The number 5 is written 5¹.

      149.          

Since the bases are the same, subtract the exponents.

To write this without a negative exponent, move the base to the denominator.

      150.           3

Since the bases are the same, subtract the exponents.

      151.           64

Multiply the exponents.

(2²)³ = 2⁽²⁾⁽³⁾ = 2⁶ = 64

      152.           81

Multiply the exponents.

(3²)² = 3⁽²⁾⁽²⁾ = 3⁴ = 81

      153.           16

Multiply the exponents.

      154.           9

Multiply the exponents.

      155.           25

Multiply the exponents.

(5⁻²)⁻¹ = 5^(−2)(−1) = 5² = 25

      156.           64

Multiply the exponents.

(2⁻³)⁻² = 2^(−3)(−2) = 2⁶ = 64

      157.          

Multiply the exponents.

To write this without a negative exponent, move the base to the denominator.

      158.           256

Multiply the exponents.

      159.          

Multiply the exponents.

To write this without a negative exponent, move the base to the denominator.

      160.           6

Multiply the exponents.

      161.           2

First multiply the two factors in the numerator by adding the exponents.

Now divide by subtracting the exponents.

      162.          

First multiply the two factors in the numerator by adding the exponents.

Now divide by subtracting the exponents.

Rewrite without the negative exponent.

      163.           4

First raise the power in the parentheses to the power outside the parenthesis by multiplying exponents.

4⁻³(4²)² = 4⁻³(4⁴)

Now multiply by adding the exponents.

4⁻³(4⁴) = 4¹ = 4

      164.          

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

Now multiply by adding the exponents.

Rewrite without the negative exponent.

      165.          

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

Now multiply by adding the exponents.

Rewrite without the negative exponent.

      166.          

First raise the power in the parentheses to the power outside the parentheses by multiplying exponents.

Now divide by subtracting the exponents.

4³ ÷ (4⁶) = 4⁻³

Rewrite without the negative exponent and simplify.

      167.           128

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

(2⁻³)⁻⁴ ÷ (2³)²(2⁴)^1/4 = 2¹² ÷ (2⁶)(2¹)

Now work from left to right — first dividing and then multiplying (subtracting and then adding exponents).

      168.           16

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

(4²)^−1/2(2³)² = (4⁻¹)(2⁶)

Now change the 4 to a power of 2.

Raise the power in the brackets to the power outside the brackets by multiplying exponents.

=(2⁻²)(2⁶)

Now multiply by adding the exponents.

= 2⁴ = 16

      169.           9

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

(6^1/2)⁴ ÷ (4^−1/2)⁻² = (6²) ÷ (4¹)

Don't bother to change to the same bases — just evaluate the expression.

(6²) ÷ (4¹) = 36 ÷ 4 = 9

      170.           131,072

First raise each of the powers in the parentheses to the power outside the parentheses by multiplying exponents.

(2²)³(2³)² ÷ (2²)²(2³)³ = (2⁶)(2⁶) ÷ (2⁴)(2⁹)

Now move from left to right, performing the operations.

= (2¹²) ÷ (2⁴)(2⁹)

= 2⁸(2⁹)

= 2¹⁷

Don't forget that, when operations are on the same level, such as multiplication and division, you move from left to right performing the operations.

      171.           4

Change the 4 to a power of 2.

2⁴ · 4⁻¹ = 2⁴ · (2²)⁻¹

Raise the power to a power by multiplying the exponents.

= 2⁴ · 2⁻²

Multiply by adding the exponents.

= 2² = 4

      172.           81

Change the 27 to a power of 3.

3⁻² · 27² = 3⁻² · (3³)²

Raise the power to a power by multiplying the exponents.

= 3⁻² · 3⁶

Multiply by adding the exponents.

= 3⁴ = 81

      173.           256

Change the 4 and 8 to powers of 2.

4^1/3 · 8² · 2^4/3 = (2²)^1/3 · (2³)² · 2^4/3

Raise the powers to powers by multiplying the exponents.

= 2^2/3 · 2⁶ · 2^4/3

Multiply by adding the exponents.

= 2^2/3+6+4/3 = 2^6/3+6 = 2⁸ = 256

      174.          

Change the 25 to a power of 5.

5³ · 25⁻² = 5³ · (5²)²

Raise the power to a power by multiplying the exponents.

= 5³ · 5⁻⁴

Multiply by adding the exponents.

      175.          

Change the 4 to a power of 2, and find the cube root of 8 — which is 2.

(4⁻³)²(8^1/3) = ((2²)⁻³)² · 2

Simplify the powers of 2 by multiplying all three.

= 2⁻¹² · 2

Multiply by adding the exponents.

      176.           243

Change the 9 and 27 to powers of 3.

Raise the powers to powers.

= 3⁻⁴ · 3⁹

Multiply by adding the exponents.

= 3⁵ = 243

      177.          

Write the 6 as the product of 2 and 3; then apply the power to each factor.

Group the factors of 2 and 3 together; then multiply the like bases by adding their exponents.

      178.           3

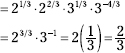
Write the 12 as the product of 3 and 4; then apply the power to each factor.

12⁻¹ · 3² · 4 = (3 · 4)⁻¹ · 3² · 4

= 3¹ · 4⁻¹ · 3² · 4

Group the factors of 3 and 4 together; then multiply the like bases by adding their exponents.

= 3⁻¹ · 3² · 4⁻¹ · 4¹

= 3¹ · 4⁰ = 3 · 1 = 3

      179.          

Rewrite the 32 and 8 as powers of 2.

Raise the powers.

= 2^5/2 · 2^−9/2

Now multiply by adding the exponents.

      180.          

Rewrite the 49 as a power of 7.

49^−1/3(7²)^−1/6 = (7²)^−1/3(7²)^−1/6

Raise the powers.

= 7^−2/3 · 7^−1/3

Multiply by adding the exponents.

      181.           8 × 106

Multiply the coefficients together and the powers of 10 together.

      182.           5.1 × 10²

Multiply the coefficients together and the powers of 10 together.

      183.           4.8 × 10¹¹

Multiply the coefficients together and the powers of 10 together.

For the answer to be in scientific notation, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (4.8 × 10¹) × 10¹⁰

= 4.8 × (10¹ × 10¹⁰) = 4.8 × 10¹¹

      184.           4.5 × 10⁻⁶

Multiply the coefficients together and the powers of 10 together.

For the answer to be in scientific notation, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (4.5 × 10¹) × 10⁻⁷

= 4.5 × (10¹ × 10⁻⁷) = 4.5 × 10⁻⁶

      185.           3.328 × 10¹

Multiply the coefficients together and the powers of 10 together.

For the answer to be in scientific notation, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (3.328 × 10¹) × 10⁰

= 3.328 × (10¹ × 10⁰) = 3.328 × 10¹

      186.           3 × 10²

Divide the coefficients and the powers of 10 separately.

Remember, when you divide numbers with the same base, you subtract the exponents.

      187.           5 × 10⁵

Divide the coefficients and the powers of 10 separately.

Remember, when you divide numbers with the same base, you subtract the exponents.

Also, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (5 × 10⁻¹) × 10⁶

= 5 × (10⁻¹ × 10⁶) = 5 × 10⁵

      188.           1.7 × 10⁰

Divide the coefficients and the powers of 10 separately.

(5.1 × 10⁻²) ÷ (3 × 10⁻²) = (5.1 ÷ 3) × (10⁻² ÷ 10⁻²)

= 1.7 × 10⁰

Remember, when you divide numbers with the same base, you subtract the exponents.

      189.           9 × 10¹¹

Divide the coefficients and the powers of 10 separately.

Remember, when you divide numbers with the same base, you subtract the exponents.

Also, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (9 × 10⁻¹) × 10¹²

= 9 × (10⁻¹ × 10¹²) = 9 × 10¹¹

      190.           1.25 × 10⁻³

Divide the coefficients and the powers of 10 separately.

(1 × 10⁻¹⁷) ÷ (8 × 10⁻¹⁵) = (1 ÷ 8) × (10⁻¹⁷ ÷ 10⁻¹⁵)

= 0.125 × 10⁻²

Remember, when you divide numbers with the same base, you subtract the exponents.

Also, the coefficient has to be a number between 1 and 10, so rewrite it as such a number times a power of 10. Then multiply the powers of 10 again.

= (1.25 × 10⁻¹) × 10⁻²

= 1.25 × (10⁻¹ × 10⁻²) = 1.25 × 10⁻³

      191.          

The expression can be written .

Simplifying,

      192.          

The expression can be written .

Simplifying,

      193.          

The expression can be written .

Simplifying,

.

      194.          

The expression can be written .

Simplifying,

      195.          

First simplify the two radicals.

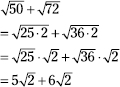
Now add the radicals by adding the multipliers.

      196.          

First simplify the two radicals.

Now add the radicals by subtracting the multipliers.

      197.          

Multiply both the numerator and denominator by the radical in the denominator.

Now simplify the radical in the denominator and reduce the fraction.

      198.          

Multiply both the numerator and denominator by the radical in the denominator.

Now simplify the radical in the denominator and reduce the fraction.

      199.          

Multiply both the numerator and denominator by the radical in the denominator.

Now simplify the radical in the denominator and reduce the fraction.

      200.          

Multiply both the numerator and denominator by the radical in the denominator.

Now simplify both radicals and reduce the fraction.

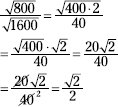
      201.          

Multiply both the numerator and denominator by the radical in the denominator.

Now simplify both radicals and reduce the fraction.

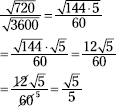
      202.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the denominator and simplify.

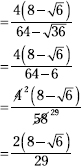
      203.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the denominator and simplify.

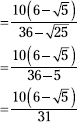
      204.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the denominator and simplify.

      205.          

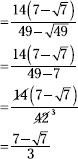
Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the denominator and simplify.

      206.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the denominator and simplify.

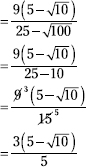
      207.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the numerator and denominator and simplify.

That's it. Nothing combines, and nothing reduces.

      208.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the numerator and denominator and simplify.

      209.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the numerator and denominator and simplify.

      210.          

Multiply both the numerator and denominator by the conjugate of the binomial in the denominator.

Now multiply in the numerator and denominator and simplify.

      211.           a^5/3

The cube root is written with an exponent of .

Now multiply the exponents.

      212.           4^3/7

The seventh root is written with an exponent of .

Now multiply the exponents.

      213.           a⁵

The fifth root is written with an exponent of .

Now multiply the exponents and simplify.

      214.           x⁵

The third root is written with an exponent of .

Now multiply the exponents and simplify.

      215.          

The square root is written with an exponent of .

      216.          

The cube root is written with an exponent of .

      217.           4

Find the root, and then raise the result to the power.

      218.           8

Find the root, and then raise the result to the power.

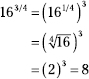
      219.           81

Find the root, and then raise the result to the power.

      220.           243

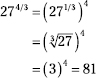
Find the root, and then raise the result to the power.

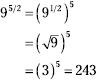
      221.           32

Find the root, and then raise the result to the power.

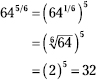
      222.           25

Find the root, and then raise the result to the power.

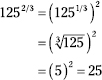
      223.          

Find the root, and then raise the result to the power.

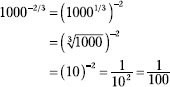
      224.          

Find the root, and then raise the result to the power.

      225.          

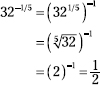
First write the power of the fraction as a fraction with powers in the numerator and denominator.

In both numerator and denominator, find the root, and then raise the result to the power.

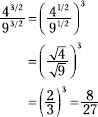
      226.          

First “flip” the fraction to make the exponent a positive number.

Now write the power of the fraction as a fraction with powers in the numerator and denominator.

In both numerator and denominator, find the root.

      227.           4

The number 16 is a perfect fourth power, so change 16 to a power of 2, the radical to a fractional exponent, and multiply the powers.

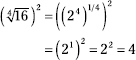
      228.           729

Since 81 isn't a perfect sixth power, change the radical to a fractional exponent and multiply the powers.

Now rewrite as a root and power and solve.

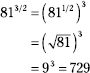
      229.           512

Since 64 isn't a perfect fourth power, change the radical to a fractional exponent and multiply the powers.

Now rewrite as a root and power and solve.

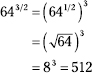
      230.          

Since 100 isn't a perfect cube, change the radical to a fractional exponent and multiply the powers.

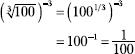
      231.           4

First rewrite the numbers under the radicals as powers of 2.

Now write each radical as a fractional power.

= (2⁸)^1/6(2²)^1/3

Raise the powers to the powers and simplify.

2^8/6 · 2^2/3 = 2^4/3 · 2^2/3

Multiply by adding the exponents and simplify.

2^4/3 · 2^2/3 = 2^6/3 = 2² = 4

      232.           27

First rewrite the numbers under the radicals as powers of 3.

Now write each radical as a fractional power.

= (3³)^1/2(3⁴)^1/3(3¹)^1/6

Raise the powers to the powers.

= 3^3/2 · 3^4/3 · 3^1/6

Now multiply by adding the exponents and simplify.

= 2^3/2+4/3+1/6 = 3^9/6+8/6+1/6

= 3^18/6 = 3³ = 27

      233.          

First rewrite the numbers under the radicals as powers of 2.

Now write each radical as a fractional power.

Raise the powers to the powers and simplify.

Now divide by subtracting the exponents and simplify.

      234.          

First rewrite the numbers under the radicals as powers of 3.

Now write each radical as a fractional power.

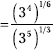
Raise the powers to the powers.

Now divide by subtracting the exponents and simplify.

      235.          

The bases are the same, so add the exponents.

6^10/3 · 6^1/3 6^10/3+1/3 = 6^11/3

Now rewrite the power as the sum of a whole number and a fraction.

= 6^9/3+2/3 = 6^3+2/3

Rewrite again as a product and simplify.

= 6³ · 6^2/3 = 216 · 6^2/3

As a radical expression, this is written as .

      236.          

The bases are the same, so add the exponents.

5^3/4 · 5^15/4 = 5^3/4+15/4 = 5^18/4 = 5^9/2

Now rewrite the power as the sum of a whole number and a fraction.

= 5^8/2+1/2 = 5^4+1/2

Rewrite again as a product and simplify.

= 5⁴ · 5^1/2 = 625 · 5^1/2

As a radical expression, this is written as .

      237.          

The bases are the same, so subtract the exponents.

Now rewrite the power as the sum of a whole number and a fraction.

= 8^7/7+2/7 = 8^1+2/7

Rewrite again as a product and simplify.

= 8¹ · 8^2/7 = 8 · 8^2/7

As a radical expression, this is written as .

      238.          

The bases are the same, so subtract the exponents.

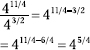
Now rewrite the power as the sum of a whole number and a fraction.

= 4^4/4+1/4 = 4^1+1/4

Rewrite again as a product and simplify.

= 4¹ · 4^1/4

As a radical expression, this is written as .

      239.           9

First rewrite the bases as powers of 3 and simplify the factors.

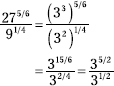
The bases are now the same, so subtract the exponents.

3^5/2−1/2 = 3^4/2 = 3² = 9

      240.           1

First rewrite the bases as powers of 2 and simplify the factors.

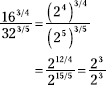
The bases are now the same, so subtract the exponents.

= 2³⁻³ = 2⁰ = 1

      241.           2

First rewrite the bases as powers of 2 and simplify the factors.

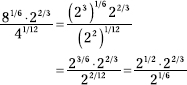
The bases are now the same, so add the exponents in the numerator.

Divide by subtracting the exponents.

= 2^7/6−1/6 = 2^6/6 = 2¹ = 2

      242.           25

First rewrite the bases as powers of 5 and simplify the factors.

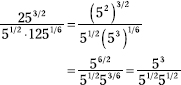
The bases are now the same, so add the exponents in the denominator.

Divide by subtracting the exponents.

= 5³⁻¹ = 5² = 25

      243.           4.4

First rewrite the radical as the product of an integer and a radical.

Now substitute the decimal approximation for the radical and multiply.

≈ 2(2.2) = 4.4

      244.           17

First rewrite the radical as the product of an integer and a radical.

Now substitute the decimal approximation for the radical and multiply.

≈ 10(1.7) = 17

      245.           8.5

First rewrite the radical as the product of an integer and a radical.

Now substitute the decimal approximation for the radical and multiply.

≈ 5(1.7) = 8.5

      246.           16.8

First rewrite the radical as the product of an integer and a radical.

Now substitute the decimal approximation for the radical and multiply.

≈ 12(1.4) = 16.8

      247.           7

First rewrite the radicals as the products of an integer and a radical. Then find the sum.

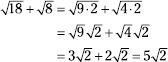
Now substitute the decimal approximation for the radical and multiply.

≈ 5(1.4) = 7.0

      248.           2.2

First rewrite the radicals as the products of an integer and a radical. Then find the difference.

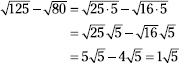
Now substitute the decimal approximation for the radical and multiply.

≈ 1(2.2) = 2.2

      249.           2.38

First rewrite the radical as a product.

Now replace the radicals with the respective approximations.

      250.           3.08

First rewrite the radical as a product.

Now replace the radicals with the respective approximations.

      251.           10a

Add the coefficients: (4 + 6)a = 10a

      252.           8xy

Add and subtract the coefficients:

(9 + 4 − 5)xy = 8xy

      253.           3z + 4

Rearrange the terms with like-terms together.

5z − 2z − 3 + 7

Perform the operations on the like-terms.

3z + 4

      254.           −2y + 1

Rearrange the terms with like-terms together.

6y − 8y + 4 − 3

Perform the operations on the like-terms.

−2y + 1

      255.           11a − 4ab − 3

Rearrange the terms with like-terms together.

7a + 4a + 2b − 2b + ab − 5ab − 3

Perform the operations on the like-terms.

11a − 4ab − 3

      256.           7x² − 3x + 2

Rearrange the terms with like-terms together.

3x² + 4x² + 2x − 5x − 1 + 3

Perform the operations on the like-terms.

7x² − 3x + 2

      257.           9 − 3z − 8ab + 6b

Rearrange the terms with like-terms together.

9 + 4 − 4 − 3z − 7ab − ab + 6b

Perform the operations on the like-terms.

9 − 3z − 8ab + 6b

      258.           x + 10 − y − z²

Rearrange the terms with like-terms together.

x + 3 + 4 + 5 − 2 − y − z²

The only like-terms are the constants.

Perform the operations on the like-terms.

x + 10 − y − z²

      259.           12x

Multiply the two constants.

(4.3)x = 12x

      260.           −45y

Multiply the two constants.

(−9.5)y = −45y

      261.           4x

Reduce the fraction by dividing common factors.

      262.           −4

Reduce the fraction by dividing common factors.

      263.           12x²y³

Multiply the constants together. Add exponents when multiplying like variables.

(3 · 4)(x · x)(y · y²)

= 12x²y³

      264.           −15y³z³

Multiply the constants together. Add exponents when multiplying like variables.

(−5 · 3)(y · y²)(z² · z)

= −15y³z³

      265.           7a

Reduce the fraction by dividing common factors.

      266.           2b

Reduce the fraction by dividing common factors.

      267.           20

Multiply first.

= 2 + 18

Then add.

= 20

      268.           7

Divide first.

= 9 − 2

Then subtract.

= 7

      269.           −6

Do the two multiplications first.

= 6 + (−12)

Then add.

= −6

      270.           −4

Do the two divisions first.

= −2 − 2

Then subtract.

= −4

      271.           19

Evaluate the two roots first.

= 5(2) + 3(3)

Next do the two multiplications.

= 10 + 9

Now add.

= 19

      272.           −3

Find the root first.

= 7 − 2(5)

Now multiply.

= 7 − 10

Finally, subtract.

= −3

      273.           −1

Do the multiplication and division.

= 6 − 8 + 2 − 1

Now subtract, add, and subtract — working from left to right.

= −2 + 2 − 1

= 0 − 1

= −1

      274.           15

Do the division and multiplication.

= 4 + 12 − 1

Now add and subtract, working from left to right.

= 16 − 1

= 15

      275.           10

First multiply.

= 10 − 4 − 8 + 12

Now subtract, subtract and add, working from left to right.

= 6 − 8 + 12

= −2 + 12

= 10

      276.           32

First do the two divisions and two multiplications, in order from left to right.

= 6 ÷ 3 + 3 · 2 · 5

= 2 + 3 · 2 · 5

= 2 + 6 · 5

= 2 + 30

Now add.

= 32

      277.           12

First do the subtraction in the parentheses.

= 4(3)

Now multiply.

= 12

      278.           −5

First do the addition in the parentheses.

= 5(−1)

Now multiply.

= −5

      279.           2

First add the terms in the numerator.

Now divide.

= 2

      280.           4

First add the two terms in the denominator.

Now divide.

= 4

      281.           20

First add the two numbers under the radical.

Now find the square root.

= 5(4)

Finally, multiply.

= 20

      282.           21

First subtract the two numbers under the radical.

Now find the square root.

= 7(3)

Now multiply.

= 21

      283.           7

First subtract the two numbers in the parentheses.

= 3 + 2(2)

Next multiply.

= 3 + 4

Now add.

= 7

      284.           −20

First add the two numbers in the parentheses.

= 8 − 7(4)

Next multiply.

= 8 − 28

Now subtract.

= −20

      285.           −12

First add the two sets of numbers in the parentheses.

= 4(7) − 8(5)

Next do the two multiplications.

= 28 − 40

Finally, subtract.

= −12

      286.           13

First add and subtract in the denominators.

Next do the two divisions.

= 1 + 12

Now add.

= 13

      287.           12

Replace the x in the expression with −2.

3(−2)2

Using the order of operations, first raise −2 to the power of 2.

= 3(4)

Now multiply.

= 12

      288.           14

Replace the x in the expression with −3.

−5(−3) − 1

Using the order of operations, first multiply.

= 15 − 1

Now subtract.

= 14

      289.           −8

Replace the x variables in the expression with 4.

4(2 − 4)

Using the order of operations, subtract in the parentheses.

= 4(−2)

Now multiply.

= −8

      290.           −4

Replace the x variables in the expression with −2.

Using the order of operations, first simplify in the numerator and denominator separately.

Now divide.

= −4

      291.           14

Replace the l in the expression with 4 and the w with 3.

2(4 + 3)

Using the order of operations, first add the terms in the parentheses.

= 2(7)

Now multiply.

= 14

You'll use this formula to find the perimeter of a rectangle.

      292.           18

Replace the b in the expression with 9 and the h with 4.

Even though the order of operations says to multiply from left to right, in order, you can take advantage of the associative property of multiplication and group the 9 and 4 together.

Multiply the numbers in the parentheses.

Now multiply.

= 18

You get the same answer if you multiply the three numbers in order, but doing this grouping saves having to deal with fractions.

This formula is used to find the area of a triangle.

      293.           34

Replace the a₀ in the expression with 4, the n with 11, and the d with 3.

4 + (11 − 1)(3)

Using the order of operations, first subtract the terms in the parentheses.

= 4 + (10)(3)

Now multiply.

= 4 + 30

Finally, add.

= 34

This is a formula you can use to find the nth term in an arithmetic sequence.

      294.           104

Replace the C in the expression with 40.

Using the order of operations, first multiply.

= 72 + 32

Now add.

= 104

This is the formula you use to change degrees Celsius (centigrade) to degrees Fahrenheit.

      295.           2700

Replace the A in the expression with 100, the r with 2, the n with 1, and the t with 3.

Using the order of operations, first do the division in the parentheses.

= 100(1 + 2)⁽¹⁾⁽³⁾

Now add the terms in the parentheses.

= 100(3)⁽¹⁾⁽³⁾

Now multiply the two factors in the exponent.

= 100(3)³

Now raise the 3 to the 3rd power.

= 100(27)

Finally, multiply.

= 2700

This is the compound interest formula, although “doubling” your money sounds pretty risky!

      296.           6

Replace the x in the expression with 6, the a with 4, the b with 3, and the c with 5.

Using the order of operations, first find all the differences in the parentheses.

Now multiply the four factors under the radical.

Now find the square root.

= 6

This is Heron's formula for finding the area of a triangle.

      297.           6

Multiply 3·2·1 = 6

      298.           714

First write:

(6·5·4·3·2·1) − (3·2·1)

Multiply all the terms on either side of the subtraction symbol.

= 720 − 6

Now subtract.

= 714

      299.           12

First write:

Rather than multiplying and then dividing, first reduce the fraction.

      300.           120

First write:

Rather than multiplying and then dividing, first reduce the fraction.

      301.           11

Replace each x in the rule with 2.

f(2) = (2)² + 3(2) + 1

First raise the power.

f(2) = 4 + 3(2) + 1

Now multiply.

f(2) = 4 + 6 + 1

Finally, add.

f(2) = 11

      302.           6

Replace each x in the rule with −1.

g(−1) = 9 − 3(−1)²

First raise the power.

g(−1) = 9 − 3(1)

Now multiply.

g(−1) = 9 − 3

Finally, subtract

g(−1) = 6

      303.           3

Replace x in the rule with −4.

First subtract.

Finally, find the root.

h(−4) = 3

      304.           3

Replace x in the rule with 10.

First subtract the terms in the numerator.

Now divide.

k(10)= 3

      305.           16

Replace each x in the rule with 2.

n(2) = (2)³ + 2(2)²

Raise the two powers.

n(2) = 8 + 2(4)

Next multiply.

n(2) = 8 + 8

Now add.

n(2) = 16

      306.           9

Replace each x in the rule with 3.

Now square the 3.

Next, add the two terms in the parentheses.

Multiply the two factors in the numerator.

Finally, divide.

p(3) = 9

      307.           30

First replace each x in the rule with 4.

q(4) = 4! + (4 − 1)!

Subtract the two terms in the parentheses.

q(4) = 4! + (3)!

Now compute the factorial operations.

q(4) = 4·3·2·1 + 3·2·1

= 24 + 6

Finally, add.

q(4) = 30

      308.           2

First replace each x in the rule with 8.

Square the 8 in the numerator.

Multiply the two factors in the denominator.

Do the subtraction and addition.

And now divide.

r(x) = 2

      309.           8

Replace each x in the rule with −3.

Subtract and add.

And now divide.

t(−3) = 8

      310.           5

Replace the x in the rule with 4.

Square the 4.

Multiply.

And subtract.

Finally, find the root.

w(4) = 5

      311.           6x + 12

Multiply:

3(2x) + 3(4)

= 6x + 12

      312.           −20y + 24

Multiply:

−4(5y) − 4(−6)

= −20y + 24

      313.           7x² − 14x + 21

Multiply:

7(x²) + 7(−2x) + 7(3)

= 7x² − 14x + 21

      314.           −8z + 4

Multiply:

      315.           35

Multiply:

      316.           29

Dividing:

      317.           −45

Dividing:

      318.           1 + 2a − 3a²

Dividing:

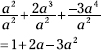
      319.           3x − 4y + 6z

Dividing:

      320.           5x² − 6xy + 8y²

Dividing:

      321.           ax + x − 2a − 2

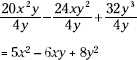
(a + 1)x + (a + 1)(−2)

= ax + x − 2a − 2

      322.           yz² − 4z² + 7y − 28

(y − 4)z² + (y − 4)(7)

= yz² − 4z² + 7y − 28

      323.           xy + 2y − 2x − 4

(x + 2)y + (x + 2)(− 2)

= xy + 2y − 2x − 4

      324.           x⁵ − 7x³ − 8x² + 56

(x² − 7)x³ + (x² − 7)(− 8)

= x⁵ − 7x³ − 8x² + 56

      325.           x⁴ − y⁸

(x² + y⁴)x² + (x² + y⁴)(− y⁴)

= x⁴ + x²y⁴ − x²y⁴ − y⁸

= x⁴ − y⁸

      326.           x² − x − 6

First: x · x = x²

Outer: x · 2 = 2x

Inner: −3 · x = −3x

Last: −3 · 2 = −6

x² + 2x − 3x − 6 = x² − x − 6

      327.           y² + 10y + 24

First: y · y = y²

Outer: y · 4 = 4y

Inner: 6 · y = 6y

Last: 6 · 4 = 24

y² + 4y + 6y + 24 = y² + 10y + 24

      328.           6x² − 13x + 6

First: 2x · 3x = 6x²

Outer: 2x · (−2) = −4x

Inner: −3 · 3x = −9x

Last: −3 · (−2) = 6

6x² − 4x − 9x + 6 = 6x² − 13x + 6

      329.           3z² − 20z + 32

First: z · 3z = 3z²

Outer: z · (−8) = −8z

Inner: −4 · 3z = −12z

Last: −4 · (−8) = 32

3z² − 8z − 12z + 32 = 3z² − 20z + 32

      330.           20x² + 2x − 6

First: 5x · 4x = 20x²

Outer: 5x · (−2) = − 10x

Inner: 3 · 4x = 12x

Last: 3 · (−2) = −6

20x² − 10x + 12x − 6 = 20x² + 2x − 6

      331.           21y² − 16y − 16

First: 3y · 7y = 21y²

Outer: 3y · 4 = 12y

Inner: −4 · 7y = −28y

Last: −4 · 4 = −16

21y² + 12y − 28y − 16 = 21y² − 16y − 16

      332.           x⁴ − 1

First: x² · x² = x⁴

Outer: x² · 1 = x²

Inner: −1 · x² = −x²

Last: −1 · 1 = −1

x⁴ + x² − x² − 1 = x⁴ − 1

      333.           6y⁶ − y³ − 2

First: 2y³ · 3y³ = 6y⁶

Outer: 2y³ · (−2) = −4y³

Inner: 1 · 3y³ = 3y³

Last: 1 · (−2) = −2

6y⁶ − 4y³ + 3y³ − 2 = 6y⁶ − y³ − 2

      334.           64x² − 49

First: 8x · 8x = 64x²

Outer: 8x · 7 = 56x

Inner: −7 · 8x = −56x

Last: −7 · 7 = −49

64x² + 56x − 56x − 49 = 64x² − 49

      335.           4z⁴ − 9

First: 2z² · 2z² = 4z⁴

Outer: 2z² · (−3) = −6z²

Inner: 3 · 2z² = 6z²

Last: 3 · (−3) = −9

4z⁴ − 6z² + 6z² − 9 = 4z⁴ − 9

      336.           x³ + x² − 5x + 3

(x + 3)x² + (x + 3)(−2x) + (x + 3)(1)

= x³ + 3x² − 2x² − 6x + x + 3

= x³ + x² − 5x + 3

      337.           y³ + y² − 2y − 8

(y − 2)y² + (y − 2)(3y) + (y − 2)(4)

= y³ − 2y² + 3y² − 6y + 4y − 8

= y³ + y² − 2y − 8

      338.           2z³ + 3z² + 15z + 7

(2z + 1)z² + (2z + 1)z + (2z + 1)(7)

= 2z³ + z² + 2z² + z + 14z + 7

= 2z³ + 3z² + 15z + 7

      339.           8x³ + 2x² − 2x − 3

(4x − 3)(2x²) + (4x − 3)(2x) + (4x − 3)(1)

= 8x³ − 6x² + 8x² − 6x + 4x − 3

= 8x³ + 2x² − 2x − 3

      340.           3y³ + 14y² − 44y + 35

(y + 7)(3y²) + (y + 7)(−7y) + (y + 7)(5)

= 3y³ + 21y² − 7y² − 49y + 5y + 35

= 3y³ + 14y² − 44y + 35

      341.           x² + 10x + 25

Using the form (a + b)² = a² + 2ab + b²,

a²: x²

2ab: 2(x)(5) = 10x

b²: 25

So the square is x² + 10x + 25.

      342.           y² − 12y + 36

Using the form (a + b)² = a² + 2ab + b²,

a²: y²

2ab: 2(y)(−6) = −12y

b²: 36

So the square is y² − 12y + 36.

      343.           16z² + 24z + 9

Using the form (a + b)² = a² + 2ab + b²,

a²: (4z)² = 16z²

2ab: 2(4z)(3) = 24z

b²: 9

So the square is 16z² + 24z + 9.

      344.           25x² − 20x + 4

Using the form (a + b)² = a² + 2ab + b²,

a²: (5x)² = 25x²

2ab: 2(5x)(−2) = −20x

b²: 4

So the square is 25x² − 20x + 4.

      345.           64x² + 16xy + y²

Using the form (a + b)² = a² + 2ab + b²,

a²: (8x)² = 64x²

2ab: 2(8x)(y) = 16xy

b²: y²

So the square is 64x² + 16xy + y².

      346.           x³ + 6x² + 12x + 8

First, write the coefficients from the fourth row of Pascal's triangle.

1 3 3 1

Now, add the decreasing powers of x.

1x³ 3x² 3x¹ 1x⁰

Next, add the increasing powers of 2.

1x³(2)⁰ 3x²(2)¹ 3x¹(2)² 1x⁰(2)³

Finally, simplify the terms and add them together.

= x³ + 6x² + 12x + 8

      347.           y³ − 12y² + 48y − 64

First, write the coefficients from the fourth row of Pascal's triangle.

1 3 3 1

Now, add the decreasing powers of y.

1y³ 3y² 3y¹ 1y⁰

Next, add the increasing powers of −4.

1y³(−4)⁰ 3y²(−4)¹ 3y¹(−4)² 1y⁰(−4)³

Finally, simplify the terms and add them together.

= y³ − 12y² + 48y − 64

      348.           27z³ + 54z² + 36z + 8

First, write the coefficients from the fourth row of Pascal's triangle.

1 3 3 1

Now, add the decreasing powers of 3z.

1(3z)³ 3(3z)² 3(3z)¹ 1(3z)⁰

Next, add the increasing powers of 2.

1(3z)³(2)⁰ 3(3z)²(2)¹ 3(3z)¹(2)² 1(3z)⁰(2)³

Finally, simplify the terms and add them together.

= 27z³ + 54z² + 36z + 8

      349.           8x⁶ + 12x⁴ + 6x² + 1

First, write the coefficients from the fourth row of Pascal's triangle.

1 3 3 1

Now, add the decreasing powers of 2x².

1(2x²)³ 3(2x²)² 3(2x²)¹ 1(2x²)⁰

Next, add the increasing powers of 1.

1(2x²)³(1)⁰ 3(2x²)² (1)¹ 3(2x²)¹(1)² 1(2x²)⁰(1)³

Finally, simplify the terms and add them together.

= 8x⁶ + 12x⁴ + 6x² + 1

      350.           a⁶ − 3a⁴b + 3a²b² − b³

First, write the coefficients from the fourth row of Pascal's triangle.

1 3 3 1

Now, add the decreasing powers of a².

1(a²)³ 3(a²)² 3(a²)¹ 1(a²)⁰

Next, add the increasing powers of −b.

1(a²)³(−b)⁰ 3(a²)²(−b)¹ 3(a²)¹(−b)¹ 1(a²)⁰(−b)³

Finally, simplify the terms and add them together.

= a⁶ − 3a⁴b + 3a²b² − b³

      351.           x⁴ + 12x³ + 54x² + 108x + 81

First, write the coefficients from the fourth row of Pascal's triangle.

1 4 6 4 1

Now, add the decreasing powers of x.

1x⁴ 4x³ 6x² 4x¹ 1x⁰

Next, add the increasing powers of 3.

1x⁴(3)⁰ 4x³(3)¹ 6x²(3)² 4x¹(3)³ 1x(3)⁴

Finally, simplify the terms and add them together.

= x⁴ + 12x + 54x² + 108x + 81

      352.           y⁵ − 10y⁴ + 40y³ − 80y² + 80y − 32

First, write the coefficients from the sixth row of Pascal's triangle.

1 5 10 10 5 1

Now, add the decreasing powers of y.

1y⁵ 5y⁴ 10y³ 10y² 5y¹ 1y⁰

Next, add the increasing powers of −2.

1y⁵(−2)⁰ 5y⁴(−2)¹ 10y³(−2)² 10y²(−2)³ · · ·

· · · 5y¹(−2)⁴ 1y⁰(−2)⁵

Finally, simplify the terms and add them together.

= y⁵ − 10y⁴ + 40y³ − 80y² + 80y − 32

      353.           z⁶ + 6z⁵ + 15z⁴ + 20z³ + 15z² + 6z + 1

First, write the coefficients from the seventh row of Pascal's triangle.

1 6 15 20 15 6 1

Now, add the decreasing powers of z.

1z⁶ 6z⁵ 15z⁴ 20z³ 15z² 6z¹ 1z⁰

Next, add the increasing powers of 1.

1z⁶(1)⁰ 6z⁵(1)⁰ 15z⁴(1)⁰ 20z³(1)⁰ · · ·

· · · 15z²(1)⁰ 6z¹(1)⁰ 1z⁰(1)⁰

Finally, simplify the terms and add them together.

= z⁶ + 6z⁵ + 15z⁴ + 20z³ + 15z² + 6z + 1

      354.           a⁷ + 7a⁶b¹ + 21a⁵b² + 35a⁴b³ + 35a³b⁴ + 21a²b⁵ + 7ab⁶ + b⁷

First, write the coefficients from the eighth row of Pascal's triangle.

1 7 21 35 35 21 7 1

Now, add the decreasing powers of a.

1a⁷ 7a⁶ 21a⁵ 35a⁴ 35a³ 21a² 7a¹ 1a⁰

Next, add the increasing powers of b.

1a⁷b⁰ 7a⁶b¹ 21a⁵b² 35a⁴b² 35a³b⁴ ···

··· 21a²b⁵ 7a¹b⁶ la⁰b⁷

Finally, simplify the terms and add them together.

= a⁷ + 7a⁶b¹ + 21a⁵b² + 35a⁴b⁴ + 35a³b⁴ + 21a²b⁵ + 7ab⁶ + b⁷

      355.           x⁷ − 14x⁶ + 84x5 − 280x⁴ + 560x³ − 672x² + 448x − 128

First, write the coefficients from the eighth row of Pascal's triangle.

1 7 21 35 35 21 7 1

Now, add the decreasing powers of x.

1x⁷ 1x⁶ 21x⁵ 35x⁴ 35x³ 21x² 7x⁰ 1x⁰

Next, add the increasing powers of −2.

1x⁷(−2)⁰ 7x⁶(−2)¹ 21x⁵(−2)² 35x⁴(−2)³ 35x³(−2)⁴ ···

··· 21x² (−2)⁵ 7x⁶ (−2)⁶ 1x⁰(−2)⁷

Finally, simplify the terms and add them together.

= x⁷ − 14x⁶ + 84x⁵ − 280x⁴ + 560x³ − 672x² + 448x − 128

      356.           256z⁴ + 256z³ + 96z² + 16z + 1

First, write the coefficients from the fifth row of Pascal's triangle.

1 4 6 4 1

Now, add the decreasing powers of 4z.

1(4z)⁴ 4(4z)³ 6(4z)² 4(4z)¹ 1(4z)⁰

Next, add the increasing powers of 1.

1(4z)⁴(1)⁰ 4(4z)³(1)¹ 6(4z)²(1)² 4(4z)¹(1)³ 1(4z)⁰(1)⁴

Finally, simplify the terms and add them together.

= 256z⁴ + 256z³ + 96z² + 16z + 1

      357.           243y⁵ − 810y⁴ + 1080y³ − 720y² + 240y − 32

First, write the coefficients from the seventh row of Pascal's triangle.

1 5 10 10 5 1

Next, add the increasing powers of 3y.

1(3y)⁵ 5(3y)⁴ 10(3y)³ 10(3y)² 5(3y)¹ 1(3y)⁰

Next, add the increasing powers of −2.

1(3y)⁵(−2)⁰ 5(3y)⁴(−2)¹ 10(3y)³(−2)² 10(3y)²(−2)³ ···

··· 5(3y)¹(−2)⁴ 1(3y)⁰(−2)⁵

Finally, simplify the terms and add them together.

= 243y⁵ − 810y⁴ + 1080y³ − 720y² + 240y − 32

      358.           64x⁶ + 576x⁵ + 2160x⁴ + 4320x³ + 4860x² + 2916x + 729

First, write the coefficients from the seventh row of Pascal's triangle.

1 6 15 20 15 6 1

Now, add the decreasing powers of 2x.

1(2x)⁶ 6(2x)⁵ 15(2x)⁴ 20(2x)³ ···

··· 15(2x)² 6(2x)¹ 1(2x)⁰

Next, add the increasing powers of 3.

1(2x)⁶(3)⁰ 6(2x)⁵(3)¹ 15(2x)⁴(3)² 20(2x)³(3)³ ···

··· 15(2x)²(3)⁴ 6(2x)¹(3)⁵ 1(2x)⁰ (3)⁶

Finally, simplify the terms and add them together.

= 64x⁶ + 576x⁵ + 2160x⁴ + 4320x³ + 4860x² + 2916x + 729

      359.           81x⁴ + 216x³y + 216x²y² + 96xy³ + 16y⁴

First, write the coefficients from the fifth row of Pascal's triangle.

1 4 6 4 1

Now, add the decreasing powers of 3x.

1(3x)⁴ 4(3x)³ 6(3x)² 4(3x)¹ 1(3x)⁰

Next, add the increasing powers of 2y.

1(3x)⁴(2y)⁰ 4(3x)³(2y)² 6(3x)²(2y)² 4(3x)¹(2y)³ 1(3x)⁰(2y)⁴

Finally, simplify the terms and add them together.

= 81x⁴ + 216x³y + 216x²y² + 96xy³ + 16y⁴

      360.           32z⁵ − 240z⁴w + 720z³w² − 1080z²w³ + 810zw⁴ − 243w⁵

First, write the coefficients from the sixth row of Pascal's triangle.

1 5 10 10 5 1

Now, add the decreasing powers of 2z.

1(2z)⁵ 5(2z)⁴ 10(2z)³ 10(2z)¹ 5(2z)¹ 1(2z)⁰

Next, add the increasing powers of −3w.

1(2z)⁵(−3w)⁰ 5(2z)⁴(−3w)¹ 10(2z)³(−3w)² ···

··· 10(2z)²(−3w)³ 5(2z)¹(−3w)⁴ 1(2z)⁰(−3w)⁵

Finally, simplify the terms and add them together.

= 32z⁵ − 240z⁴w + 720z³w² − 1080z²w³ + 810zw⁴ − 243w⁵

      361.           x³ − 1

(x − 1)x² + (x − 1)x + (x − 1)(1)

= x³ − x² + x² − x + x − 1

= x³ − 1

      362.           y³ + 8

(y + 2)y² + (y + 2)(−2y) + (y + 2)(4)

= y³ + 2y² − 2y² − 4y + 4y + 8

= y³ + 8

      363.           z³ − 64

(z − 4)z² + (z − 4)(4z) + (z − 4)(16)

= z³ − 4z² + 4z² − 16z + 16z − 64

= z³ − 64

      364.           27x³ − 8

(3x − 2)(9x²) + (3x − 2)(6x) + (3x − 2)(4)

= 27x³ − 18x² + 18x² − 12x + 12x − 8

= 27x³ − 8

      365.           125z³ + 8w³

(5z + 2w)(25z²) + (5z + 2w)(−10zw) + (5z + 2w)(4w²)

= 125z³ + 50wz² − 50wz² − 20w²z + 20w²z + 8w³

= 125z³ + 8w³