6
ENDOGENOUS TECHNICAL CHANGE IN ALTERNATIVE THEORIES OF GROWTH AND DISTRIBUTION
Daniele Tavani
Department of Economics Colorado State University
Luca Zamparelli
Department of Social and Economic Sciences Sapienza University of Rome
1. Introduction
The analysis of the role of technological change in the growth process is of central importance in classical political economy. In his Wealth of Nations, Adam Smith (1776[1981]) famously emphasized increasing returns and specialization as the main driver of economic progress, while in the third volume of Capital, Marx focused on the profit-driven motive to innovation in capitalist economies, and the corresponding conflictual nature of labor productivity growth (Marx, 1867). With the marginalist revolution and its main concern with the allocation of scarce resources over competing needs, technical progress fell out of fashion and was either assumed away or to take place exogenously, as it is the case in the (augmented) Solow (1956) model. Only in the early 1990s, a revived interest in the endogenous determinants of technical change enabled the introduction of insights by Schumpeter (1942) into dynamic neoclassical general equilibrium growth models (Romer, 1990; Grossman and Helpman, 1991; Aghion and Howitt, 1992). These theories have defined endogenous technical change as: (i) explained within the model rather than assumed to occur; (ii) costly to generate so that the problem of allocating resources to R&D becomes of crucial importance; (iii) dependent on preferences, in particular as it pertains to the allocation between current and future consumption, and on policy action.
Before the advent of endogenous growth, the neoclassical scene was dominated by the Solow growth model and its optimal growth counterpart (Ramsey, 1928; Cass, 1965; Koopmans, 1965). As pointed out by Jones and Romer (2010), one reason for the success of the neoclassical growth model was its ability to match the Kaldor facts of long-run growth (Kaldor, 1961). Among those, here, we are mostly concerned with: (a) the constancy of factor shares in the long run; (b) a purely labor-augmenting profile of technical change; (c) an increasing capital intensity, and (d) the constancy of the output/capital ratio. In order to be consistent with the Kaldor facts, the neoclassical theory hinges crucially on the use of a smooth aggregate production function, and the resulting choice of the technique of production that equates the factor marginal products to factor prices.
The Cambridge capital controversy of the 1960s has warned in a definitive way about the logical shortcomings of neoclassical aggregate capital theory. While the neoclassical prescriptions about factor substitution and the distribution of income hold true in a one-good economy, it is not possible to deduct an aggregate production function with decreasing real marginal product of capital from an economy with heterogeneous capital goods (Samuelson, 1966; Garegnani, 1970). Thus, the Cambridge critique had disruptive implications for the neoclassical theory of growth and distribution. Not surprisingly, at the time when the capital debate was occurring, non-neoclassical economists began to look again at the process of technical change, as opposed to capital/labor substitution, in order to provide an alternative view of distribution compatible with the Kaldor facts, but at the same time immune from the pitfalls of the marginalist theory. Key examples of these efforts are the induced innovation hypothesis by Charles Kennedy (Kennedy, 1964), and Nicholas Kaldor's technical progress function (Kaldor, 1957).
Although neither Kaldor's nor Kennedy's view of technical change ever became mainstream, they laid the foundations for more recent work by economists working in alternative traditions toward modeling the interplay between the factor distribution of income and the evolution of labor productivity over time. This survey is meant to summarize the last two and a half decades of alternative literature on balanced growth models that reject the notion of an aggregate production function with well-defined marginal products, but whose long-run equilibria are consistent with the Kaldor facts. We will distinguish between classical-Marxian and post-Keynesian models, and analyze the implications that different model closures have for income distribution and productivity growth. Using these alternative models, we will look at three viewpoints on the evolution of technology: (i) a Kaldorian technical progress function, in which labor productivity grows in line with capital accumulation; (ii) a classical-Marxian technical progress function, where labor productivity growth depends on factor shares; and (iii) a technical progress function that relates labor productivity growth with tightness in the labor market. In addition, we provide an account of recent non-mainstream research on costly innovation—both private and public—and of an unbalanced growth model featuring a declining output/capital ratio with a strong Marxian flavor.
These broadly categorized alternative theories are compared with neoclassical exogenous and endogenous growth: despite a number of strong differences, there are striking similarities between the approaches. Broadly, the differences pertain with the basic question about what drives the pace of technical progress, as well as the assumptions regarding factor substitution and full employment (or the lack thereof). Neoclassical theories emphasize the role of intertemporal saving preferences and deviations from competitive markets, while alternative theories are concerned with income distribution, the state of the labor market, and investors' behavior and expectations as the main drivers of growth. On the other hand, the main common element is that endogenous technical change requires the natural rate of growth to be sensitive to investment decisions; but similarities can also be found in the very formal aspects of the long-run solutions to the various models. By highlighting both similarities and differences, this survey serves the purpose of focusing the debate between competing theories on their relative merits and shortcomings, thus offering an even playing field toward greater engagement between the different traditions (Setterfield, 2014).
The paper is organized as follows. Section 2 reviews exogenous and endogenous mainstream growth theories in order to provide a benchmark for comparison. Section 3 looks at three different specifications of endogenous technical change used in the alternative literature, while Sections 4 and 5 study their implications for different model closures: classical supply side closures with either exogenous distribution or labor supply, vis à vis two post-Keynesian accumulation closures (Kaleckian and Kaldorian, respectively). Section 6 reviews recent contributions that introduce mainstream endogenous growth insights in classical and post-Keynesian models. Section 7 concludes.
2. Neoclassical Growth Theory
2.1 Common Elements
The neoclassical (or marginalist) theory determines output and income distribution taking technology, consumer preferences, and endowments of productive factors as exogenous variables. This structure produces a few foundational elements common to both exogenous and endogenous growth. First, all models presuppose Say's law thus omitting any considerations about the role of aggregate demand in the growth process: growth is determined by supply factors alone. The existence of a continuum of techniques of production ensures that it is possible to substitute one factor with another until their endowments are fully employed: excess supply of one input would produce a reduction in its price, thus favoring the adoption of a technique of production that employs the factor more intensively. Second, income distribution is determined by the relative scarcity of the productive factors. The interaction between technology and factor endowments determines the equilibrium marginal product of each factor, which equals its rate of remuneration via profit-maximization by firms. Due to decreasing marginal products, relative factor prices decrease in the relative factors supply. Third, the society's preferences with regard to consumption and savings affect the endowment of the accumulable factors of production, and therefore output growth and income distribution. Fourth, the economic environment is typically (although not universally) modeled with the aid of a representative agent, who earns a salary as worker and receives interest income as the owner of capital assets. Thus, there is no class distinction in the economy: incomes are differentiated according to their source, not by the social class to which they accrue.
2.2 Exogenous Growth
Both the Solow (1956) growth model and its Ramsey–Cass–Koopmans counterpart featuring an endogenous saving rate (Ramsey, 1928; Cass, 1965; Koopmans, 1965) see technical change as purely exogenous. In fact, under the assumption of perfectly competitive goods and factors markets as well as marginal productivity pricing of capital and labor, neoclassical growth requires technical change to be generated outside the model because there are no resources left to innovate if both factors of production are paid their marginal product. This follows from Euler's theorem: if, for a given level of technology ![]() , output Y is produced according to a constant returns to scale and twice continuously differentiable function of capital and labor
, output Y is produced according to a constant returns to scale and twice continuously differentiable function of capital and labor ![]() , Euler's theorem implies that FKK + FLL = Y, where Fi is the marginal product of factor i. Hence, remunerating capital and labor takes up the entire national product, and no resources are left to finance the production of technology-improving innovations. Accordingly, the growth rate of technology
, Euler's theorem implies that FKK + FLL = Y, where Fi is the marginal product of factor i. Hence, remunerating capital and labor takes up the entire national product, and no resources are left to finance the production of technology-improving innovations. Accordingly, the growth rate of technology ![]() is necessarily exogenous. Focusing on balanced growth and assuming that technical progress is labor augmenting (Uzawa, 1961), we can rewrite the production function as F(K, AL), where AL is a measure of labor in efficiency units, or effective workers. Let k ≡ K/(AL). Then, output per effective worker is y ≡ Y/(AL) = f(k). Population grows at the constant rate n > 0 and, as we will assume throughout the whole paper, capital does not depreciate. The steady state of the Solow model solves
is necessarily exogenous. Focusing on balanced growth and assuming that technical progress is labor augmenting (Uzawa, 1961), we can rewrite the production function as F(K, AL), where AL is a measure of labor in efficiency units, or effective workers. Let k ≡ K/(AL). Then, output per effective worker is y ≡ Y/(AL) = f(k). Population grows at the constant rate n > 0 and, as we will assume throughout the whole paper, capital does not depreciate. The steady state of the Solow model solves
The left-hand side of equation (1) features the constant long-run output/capital ratio, which increases in the growth rate of the effective labor force n + gA and decreases in the saving rate.
While growth is exogenous, income distribution is endogenous: the long-run capital intensity (in efficiency units) kss regulates both factor prices and factor shares. Under marginal productivity pricing, the interest rate r equals the marginal product of capital, and in the long run r = f′(kss). Factor shares, on the other hand, coincide with the respective output elasticities: letting ω be the wage share in national income, its long-run value is ωss = 1 − f′(kss)kss/f(kss), where f′(kss)kss/f(kss) is the elasticity of output with respect to capital (that is, the share of profits). Therefore, all relevant measures of income distribution are endogenous as they depend on the capital/labor ratio, save for the special (though admittedly popular) Cobb–Douglas case where output elasticities, and therefore income shares, are parametrically constant throughout the entire growth path. The saving rate and the exogenous growth rate of technology influence the long-run distribution of income by affecting the steady-state capital intensity in opposite ways. The direction of such influence is regulated by the elasticity of substitution between factors of production σ, defined as the percentage increase in the capital/labor ratio due to a percentage increase in the ratio of marginal products (in turn, equal to the wage/interest rate ratio). When σ < 1 (![]() ), an increase in the wage/interest rate ratio produces a less (more) than proportional boost in the capital/output ratio, so that the wage share increases (decreases). The long-run capital intensity increases in the saving rate: therefore, an increase in s raises (lowers) the long-run wage share if σ < 1 (
), an increase in the wage/interest rate ratio produces a less (more) than proportional boost in the capital/output ratio, so that the wage share increases (decreases). The long-run capital intensity increases in the saving rate: therefore, an increase in s raises (lowers) the long-run wage share if σ < 1 (![]() ). The opposite is true for the growth rate of technology, which is inversely related with the steady-state capital/labor ratio. Finally, when σ = 1, we are in the Cobb–Douglas case.
). The opposite is true for the growth rate of technology, which is inversely related with the steady-state capital/labor ratio. Finally, when σ = 1, we are in the Cobb–Douglas case.
2.3 Endogenous Growth
Starting in the early 1990s, mainstream economists have investigated the role of ideas in generating increasing returns that allow for sustained economic growth in the long run. The endogenous growth models that followed, either based on increasing product variety (Romer, 1990) or increasing product quality (Grossman and Helpman, 1991; Aghion and Howitt, 1992), produce endogenous technical change that is fully explained within the model, and is affected by saving behavior and policy action. The enterprise was made possible by abandoning perfect competition in favor of monopolistic competition. By discovering new ideas, innovators are granted a patent and make the monopolistic profits necessary to cover the cost of R&D investment.
A version of the Romer (1990) model that allows an appreciation of the endogenous nature of technical change is the following. Consider a three-sector economy (final sector, intermediate goods sector, and R&D sector) with a constant, fully employed labor force. The final (manufacturing) good is produced competitively according to
where LY is the number of manufacturing workers, xi denotes the intermediate durable input i rented in the production of the final good, A is a measure of product variety or the number of existing intermediate input in the economy, and α ∈ (0, 1) is an elasticity parameter. One unit of raw capital can be transformed in one unit of any intermediate input, and therefore the total amount of intermediate inputs is equal to the economy's capital stock: ∫A0xidi = K. As it will be clear just below, the symmetric structure of the model ensures that all intermediate inputs are demanded in the same amount; therefore, xi = x, K = Ax, and Y = AL1 − αYxα. This last way of writing the production function shows that output is linear in A, the number of intermediate inputs. Alternatively, one can see that the number of varieties plays the role of labor-augmenting technology in the aggregate production function. In fact, given x = K/A, we have Y = (ALY)1 − αKα. Since the marginal product of each intermediate input is independent of all the others, diminishing returns to capital can be overcome if accumulation results in an increase in the number of intermediate inputs rather than in the amount of each input produced.
Firms in the intermediate goods sector acquire from the R&D sector an infinitely-lived patent on the new variety of input they produce. Therefore, they operate under monopolistic conditions. Each firm chooses the profit-maximizing supply of its intermediate good, given a downward sloping inverse demand curve for its product p(x), the one-to-one production technology, and the cost of capital r. The demand curve equals the marginal product of intermediate goods: p(x) = ∂Y/∂x = αL1 − αYxα − 1, and profits to be maximized are π = p(x)x − rx. The solution is ![]() , and monopolists earn strictly positive profits, equal across all sectors:
, and monopolists earn strictly positive profits, equal across all sectors:
Technological advancements, on the other hand, are developed in the competitive R&D sector. Here, LA workers are employed to produce new ideas according to
which means that the productivity of each R&D worker, βA, is linear in the stock of the existing ideas.1 Labor moves freely between R&D and final production, and all workers are paid the same wage, equal to the marginal product of labor in the final sector: w = (1 − α)Y/LY. If the allocation of workers between the two sectors is constant, and ρ ∈ (0, 1) is the fraction of workers in R&D, to be determined within the model, the growth rate of technology is:
which makes it clear that economic policy aimed at increasing the number of scientists has permanent growth effects. In fact, the allocation of workers between R&D and manufacturing represents the economy's choice between current consumption versus long-run growth, and it may be affected by means of taxes and subsidies to either sector.
If the research sector is competitive with free entry, the flow of profits in R&D must be zero. The value of an innovation is given by π/r, the discounted value of profit flow at the market interest rate r. Since one worker produces βA ideas in the unit time, an R&D firm employing LA workers is faced with the following zero-profit condition:
We can now solve for the rate of return as a simple function of the elasticity of demand faced by the monopolist α, the R&D productivity parameter β, and the number of workers in the final good sector (1 − ρ)L as follows:
To see the effect of the saving rate on long-run growth observe that, with a constant saving rate s ∈ (0, 1) for simplicity, the growth rate of capital is

Next, the balanced growth condition gK = gA yields the share of workers in the R&D sector as
A higher saving rate shifts the allocation of workers in favor of the R&D sector, because society prefers to improve future technology over current consumption. Since the growth rate of technology is linear in the number of researchers, a higher saving rate determines a permanent increase in the growth rate of the economy in contrast with the Solow model.
Consider also the implications of this class of models for income distribution. The labor share in output is endogenous as it depends on the fraction of workers in the R&D sector. In fact, using the wage equation above together with the labor market clearing condition, we have:
Equation (7) shows that the wage share increases in the saving rate. The wage rate is determined in the final good sector as the marginal product of labor, which, in turn, decreases in the share of workers in that sector: a higher saving rate shifts the composition of the labor force toward R&D, thus making final good-producing workers more productive and increasing wages. Finally, notice that the output/capital ratio is inversely related to the saving rate, just like in the neoclassical exogenous growth model. In fact, Y/K = λL/(s + α), decreasing in the saving rate.
Kurz and Salvadori (1998) insightfully noted that income distribution in early neoclassical endogenous growth models depends on technology and profit-maximization only, and it is therefore exogenous. Our account is not inconsistent with their conclusion, once a fundamental difference in the assumptions of the models under consideration is singled out. In our analysis, the factor of production responsible for sustained growth (ideas) requires labor, a scarce input, in order to be produced. In the models considered by Kurz and Salvadori (1998), on the other hand, no original input is involved in the accumulation of the factors responsible for endogenous growth, whether these be physical capital, human capital, or ideas. The difference is thus reconciled here by simply assuming that innovations are produced using foregone consumption (in terms of final output) rather than labor; the latter is fully employed in producing the final good. Equations (2) and (3) become Y = L1 − α∫A0xiαdi and ![]() , where ρ′ is the share of income invested in R&D effort (Aghion and Howitt, 2010). The marginal product of labor is now FL = w = (1 − α)Y/L, so that the wage share ω = 1 − α is independent of the saving rate.
, where ρ′ is the share of income invested in R&D effort (Aghion and Howitt, 2010). The marginal product of labor is now FL = w = (1 − α)Y/L, so that the wage share ω = 1 − α is independent of the saving rate.
A crucial implication of the growth equation (4) is that the growth rate increases with the size of the labor force. This feature is known as the scale effect property of first-generation endogenous growth models and with population growing at a rate n > 0 implies an explosive growth rate. The scale effect property was questioned on empirical grounds by Jones (1995): he proposed a specification for the growth rate of varieties featuring a less-than proportional spillover from past discoveries. With
the growth rate of ideas is:
Balanced growth requires a constant growth rate. Differentiating (9) with respect to time and imposing ![]() yields
yields
Economic growth is therefore explained within the model, but is independent of savings and policy. For this reason, this class of models is commonly referred to as semi-endogenous. On the one hand, technical change is the outcome of profit-maximizing behavior, but, on the other hand, its long-run determinants are purely exogenous (technology and population growth) just like in the Solow model.2 Regarding income distribution, the semi-endogenous model delivers an endogenous labor share increasing in the saving rate.
As a final observation, the comparison of endogenous vs. semi-endogenous growth models highlights the importance of the spillover generated by past discoveries in the production of new ideas, or alternatively the lack of robustness of the assumptions required to generate endogenous growth (Solow, 1994, 2007). With constant returns to ideas (the reproducible factor), growth is endogenous: thriftier consumers or innovation subsidies that increase the share of scientists in the overall labor force will have permanent growth effects. With diminishing returns, neither savings nor innovation subsidies have permanent effects on growth. In the language of dynamical system theory, endogenous growth models are structurally unstable: their conclusions are not robust to slight modifications in the elasticity parameter of the innovation technology.
3. Alternative Theories of Growth and Distribution
3.1 Common Elements
Even though different contributions have emphasized different aspects of the interplay between growth and distribution in the long run, there are a few common elements that span almost universally throughout the non-mainstream literature. A first feature is the use of a Leontief aggregate production function combining fixed proportions of capital and labor in producing output:
where B denotes the ratio of potential output (Yp) to capital, A is labor productivity, and u ≡ Y/Yp is a measure of capacity utilization. Such production technology is not always explicitly assumed but it is functional as a critical tool toward mainstream economics, in that: (a) it implies a rejection of marginal productivity theory as marginal products are not defined, and (b) it allows for less than full employment of both capital and labor. In fact, because factor demands are inelastic to factor prices, there is no market-based equilibrating mechanism toward full utilization of all factors of productions. Thus, even when there is full utilization of capital—that is, when u = 1—the production technology allows for structural unemployment of labor. When effective demand is not strong enough to ensure full capacity utilization, that is, when u < 1, both capital and labor are unemployed.
A second, distinctive element of non-conventional theories is their focus on class as a defining feature of capitalist economies. The distinction between workers, on the one hand, and owners of the capital goods (capitalists), on the other hand, brings the functional income distribution front and center in the analysis. Given the production technology, the inverse relationship between wages and profits is represented by the distributive curve:
where ω ≡ wL/Y = w/A. The class distinction pertains also to different saving behavior: workers and capitalists have different propensities to save so that sw < sπ ≡ s. Throughout the analysis, we will use a simplified version of differential savings by assuming sw = 0.3
A third common feature is that technical change is (with some exceptions discussed in Section 6) costless. In the neoclassical endogenous growth literature, producing new technologies requires to allocate scarce resources to R&D investment, and is therefore costly. On the contrary, the problem of resource allocation toward the financing of innovation technology is seldom addressed in alternative treatments of economic growth, and technical change is basically explained within the model as an externality, whether it occurs through learning-by-doing or responds to either income distribution or employment, as it will be clear just below.
3.2 Approaches to Technical Change
In general, technological change can be represented by changes in the productivity of both labor and capital. However, balanced growth with constant returns to scale in production requires ![]() : capital productivity must remain constant in the long run, as shown by Uzawa (1961), and recently re-emphasized by Schlicht (2006); Jones and Scrimgeour (2008); Irmen (2016). For this reason, most models (with the exceptions discussed in Sections 4.3 and 4.4) simply assume a constant potential output/capital ratio, and only focus on labor productivity growth gA.
: capital productivity must remain constant in the long run, as shown by Uzawa (1961), and recently re-emphasized by Schlicht (2006); Jones and Scrimgeour (2008); Irmen (2016). For this reason, most models (with the exceptions discussed in Sections 4.3 and 4.4) simply assume a constant potential output/capital ratio, and only focus on labor productivity growth gA.
We will then investigate three possible routes to model improvements in labor productivity. The first one is known as Kaldor-Verdoorn law, and it states that technical change is directly related either to capital accumulation or to output growth. Verdoorn (1949) explored empirically the relation between productivity growth and output growth; while Kaldor (1957) formulated the technical progress function, where labor productivity growth depends on the growth of capital stock per worker. The basic idea, however, has been a mainstay in the understanding of economic development since the inception of political economy, when Adam Smith linked productivity growth to the division of labor in turn limited by the size of the market (Smith, 1776[1981]). Later, Marshall (1920), Young (1928) and Arrow (1962) all related labor productivity to the economy's scale of production and capital stock through the concepts of external economies of scale, macroeconomic increasing returns, and learning by doing. Here, we will adopt two linear versions of the law: productivity growth depends either on the growth rate of aggregate capital stock or on the growth rate of capital per worker. Since alternative theories assume the fixed coefficient production function in (11) and that technical change (except in Sections 4.3 and 4.4) leaves capital productivity constant over time, we can use capital growth (gK) instead of output growth (gY) to state the Verdoorn law:
Denoting the growth rate of labor demand by gL, the technical progress function in terms of capital per worker can be written as
with ϕ1 ∈ (0, 1).4 As noted by several commentators (see, for example, Black, 1962) right after Kaldor proposed the technical progress function, (17) can be obtained from a Cobb–Douglas per-capita production function with exogenous technical change: ![]() with ϕ0 denoting the growth rate of the scale parameter A0. Our analysis will show, however, that equation (14) has implications on growth and distribution that are quite non-neoclassical, once it is coupled with alternative closures.
with ϕ0 denoting the growth rate of the scale parameter A0. Our analysis will show, however, that equation (14) has implications on growth and distribution that are quite non-neoclassical, once it is coupled with alternative closures.
A second option consists in postulating that labor-saving technical change depends on the labor share. This relation fits well with the notion of cost-minimization, and is founded in the classical-Marxian analysis of the choice of technique. New techniques of production are adopted only if they do not decrease the profit rate at the given real wage (Okishio, 1961); when the wage share (i.e., a firm's unit labor cost) rises, an increase in labor productivity is necessary if the firm wants to prevent a reduction in its rate of profit. Thus, labor-saving innovation is a way to re-establish profitability in the face of rising labor costs. Some of the contributions belonging to this tradition allow for variable capital productivity, and we will analyze them separately in Sections 4.3 and 4.4. For now, it is enough to focus on a constant output/capital ratio while assuming a direct relationship running from the wage share to the growth rate of labor productivity:
as in Taylor (1991) and Dutt (2013a).
A third strand of recent literature (Dutt, 2006; Flaschel and Skott, 2006; Sasaki, 2010; Palley, 2012; Setterfield, 2013a) has looked at labor market tightness—as measured by the employment rate—as a driver of technical change. Shortages of labor would push firms to adopt innovations that save on labor requirements. This approach is conceptually similar to the one just discussed, because it builds on the implicit assumption that a tight labor market reduces firms' profit margins. However, we will see in Sections 5.1 and 5.2 that the focus on the labor market as opposed to distribution is favored within the Keynesian demand-led growth framework, as it is instrumental in reconciling actual and potential growth rates. Given the exogenous labor supply N, denote the employment rate by e ≡ L/N. We can therefore represent this approach to technical change as5
Observe that equations (13)–(16) all arise from a general specification of the kind ![]() , which exhibits the linear spillover of existing technologies that we discussed regarding the neoclassical endogenous growth case.
, which exhibits the linear spillover of existing technologies that we discussed regarding the neoclassical endogenous growth case.
Finally, we will discuss two cases in which capital productivity is not always constant. The output/capital ratio might vary along the transitional dynamics toward the balanced growth path, as the model evolves toward a constant long-run output/capital ratio: such would be the case with induced technical change we will study in Section 4.3.1. Alternatively, the rejection of balanced growth has led authors to focus on the case of capital-using technical change involving negative capital productivity growth. Combined with a classical closure, a falling output/capital ratio determines a falling rate of profit: for this reason, such a pattern is typically referred to as Marx-biased technical change (MBTC) (Foley and Michl, 1999, chapter 7): we analyze it in Section 4.4. Both cases establish a direct causal relation between the labor share and labor productivity growth, and therefore belong to the tradition summarized by equation (15).
3.3 Balanced Growth with Endogenous Technical Change
Roy Harrod's essay on dynamic economics (Harrod, 1939) is conventionally seen as the beginning of modern growth theory. A stylized account of his contribution would define three different growth rates: the actual growth rate giK, or the ratio of investment to capital stock; the “warranted” rate gsK, which is the ratio of savings to capital stock; and the “natural” rate gp, equal to the sum of population growth and exogenous labor productivity growth. The Harrodian analysis devises two problems. First, full employment is the exception rather than the norm: the economy needs to expand at its natural rate to keep a steady employment rate, but nothing ensures this will happen because the determinants of the warranted and natural rate are unrelated. Second, there are no self-correcting mechanisms capable of dampening deviations of the actual rate from the warranted rate: this is known as the Harrodian instability problem. To some extent, the development of the theory of economic growth can be seen as an attempt to address these two issues. Our focus here is to investigate how the introduction of endogenous technical change affects the solution that different economic traditions have given to the first Harrodian problem.
Given the analytical framework described in Section 3.1, the warranted growth rate is
while the natural rate of growth is
Notice that gp also represents a rate of growth of potential output, since it is a measure of the overall growth in factors supply. The actual rate of growth of capital stock is theory-specific: below, we distinguish between the classical tradition, on the one hand, and post-Keynesian traditions on the other, in turn, drawing a difference between Kaleckian models and Kaldorian models.
The classical tradition is founded on the acceptance of Say's law, the notion that supply creates its own demand at the aggregate level. This principle is satisfied when all savings are automatically invested in capital accumulation, and it is equivalent to impose full utilization of capital stock: u = 1. In fact, there is no independent investment function, and we can directly assume
A crucial element of post-Keynesian economics, instead, is an investment demand function that is independent of saving behavior. In the (neo-) Kaleckian tradition, investment depends on utilization as a proxy for aggregate demand (an accelerator effect), and a measure of profitability. The latter determinant is justified either through the fact that a firm's current profits provide a source of internal funds that finance capital accumulation without resorting to credit markets, or can be used as an indication of future profitability. While early authors have used a specification involving the profit rate as the main determinant of investment demand (Taylor, 1985, 1991), after Bhaduri and Marglin (1990), neo-Kaleckian economists have focused on the profit share. Accordingly, the investment function can be written as follows:
Finally, the Kaldorian tradition emphasizes the role of exports as the ultimate source of autonomous aggregate demand. Since labor productivity growth improves an economy's competitiveness, thus providing access to a larger share of global demand, we can assume that investment rises with labor productivity growth:
In fact, (20) can be seen as a reduced-form investment demand function in an open economy, where the coefficient λ captures trade-related factors such as the foreign trade multiplier and the price-elasticity of exports (see Setterfield, 2013b, for a derivation). We keep the intercept term γ to facilitate the comparison with the Kaleckian framework. In both (19) and (20), γ can be interpreted as the autonomous growth rate of investment demand—Keynes' animal spirits.
The equality giK = gKs defines the short-run equilibrium growth rate g*. On the other hand, balanced growth requires that g* = gp, or we would face the first Harrodian problem with cumulative disequilibrium in the labor market. Below, we explore the implications for growth and distribution of different specification of gA for classical and post-Keynesian economics.
4. Classical Closures
As already mentioned, all the contributions falling within the classical tradition presuppose Say's law, thus imposing full utilization of installed capacity in the general framework. The main differences pertain to models featuring a distributive closure and endogenous growth, as opposed to models featuring an exogenous labor supply closure and endogenous income distribution.
4.1 Distributive Closure
The classical-Marxian tradition has emphasized the role of the reserve army of labor in keeping the labor share in check. The most notable example in development economics is that of a dual economy with a large rural sector providing a basically unlimited pool of labor from which a small but growing manufacturing sector can draw (Lewis, 1954). A dual economy is not labor-constrained: rather, it is capital stock to be the limiting factor for growth. Accordingly, the classical closure consists in assuming a perfectly elastic labor supply at the going wage share. Income distribution is exogenous, and the wage share is fixed at its conventional value (Foley and Michl, 1999):
On the other hand, capital stock is assumed to be utilized at its normal rate: u = 1. This model delivers endogenous growth even without technical change. In fact, the growth rate is simply
Because there is no constraint arising from the size of the labor force, the rate at which the economy grows is governed by capital accumulation only. Labor supply is endogenous and it accommodates labor demand: ![]() . Notice the similarity of the steady state of this model with the Romer model using foregone consumption as an input to R&D: both models deliver an endogenous growth rate that increases in the saving rate, coupled with an exogenous distribution.
. Notice the similarity of the steady state of this model with the Romer model using foregone consumption as an input to R&D: both models deliver an endogenous growth rate that increases in the saving rate, coupled with an exogenous distribution.
In this context, endogenous technical change adds very little to the analysis, as shown in Dutt (2011) and Dutt (2013a); in fact, the role of technical change is simply to determine the growth of employment through the long-run condition g* = gp = gL + gA. Assume, for example, that technology evolves according to (14): labor productivity growth is gA = ϕ0/(1 − ϕ1), and is therefore semi-endogenous; while employment growth satisfies ![]() . Similarly, if we model gA through the Marxian motive described in (15), we find
. Similarly, if we model gA through the Marxian motive described in (15), we find ![]() . In both cases, a higher saving rate as well as a higher profit share increase the growth rate of employment, while improvements in the innovation technology have the opposite effect. The third route to technical change (16) is incompatible with this framework: with unlimited labor supply, the employment rate is undefined.
. In both cases, a higher saving rate as well as a higher profit share increase the growth rate of employment, while improvements in the innovation technology have the opposite effect. The third route to technical change (16) is incompatible with this framework: with unlimited labor supply, the employment rate is undefined.
4.2 Labor Supply Closure
The classical model has also been investigated under the assumption of exogenous labor supply (Pasinetti, 1974; Foley and Michl, 1999, chapter 6). The important question that this framework is called to answer is how adjustments in income distribution can maintain a constant employment rate in the absence of capital/labor substitution. When technical change is exogenous, the long-run equilibrium condition g* = gp yields the Goodwin (1967) steady-state income distribution 1 − ωss = (n + gA)/sB, which would be same in the Pasinetti (1962) model if technical change were introduced. The saving rate and labor productivity growth have opposite effects on the wage share. An increase in the saving propensity s lowers the profit share and the profit rate. The reason is that higher savings translate into higher long-run investment and employment growth. Given the exogenous growth rate of labor supply, a faster pace of accumulation puts pressure on wages relative to labor productivity, so that the wage share increases. Higher labor productivity growth, on the contrary, lowers the economy's labor requirements and the wage share falls as a consequence.
Let us now investigate the implications of endogenous technical change. When gA follows (14), balanced growth yields
with gA = ϕ0/(1 − ϕ1). Not much changes in terms of income distribution: the labor share increases in the saving rate, and the only difference is that the role of exogenous labor productivity growth is played by the technological parameters of the technical progress function. Long-run technical change, on the other hand, is of the semi-endogenous variety: it is explained within the model, but it is independent of economic parameters (see Taylor, 2004, chapter 5). Strikingly, this model delivers implications about long-run growth and distribution that are virtually identical to those found in the Jones (1995) model. In fact, as we will discuss in Section 5.2, this is also the same steady state of a closed-economy Kaldor growth model with endogenous technical change.
When labor productivity follows the Marxian motive as in (15), income distribution still needs to adjust to satisfy the long-run balance g* = gp. Accordingly, ωss solves
The effect of the saving preferences on income distribution is the same as before: total differentiation of (24) shows dωss/ds > 0. A higher saving rate increases capital accumulation; maintaining the balance in the labor market requires either a reduction in the profit share or an increase in labor productivity, which is also achieved through a higher wage share. On the other hand, technical change and growth are fully endogenous as gA = f[ωss(s)]: the higher wage share that follows the increase in the saving rate has a positive effect on labor productivity growth. A comparison with the exogenous distribution model is instructive. With a conventionally determined wage share, capital accumulation is never constrained by labor supply. Conversely, the labor supply poses a binding constraint to capital accumulation in this model, but the constraint is loosened by the fact that investment can increase the growth rate of labor productivity through the distributive channel. We are not aware of contributions that investigated this result, which reaffirms the classical vision according to which effective labor is de facto endogenously produced by the capitalist system;6 Dutt (2013a) studied this specification in the classical model of growth, but only under the conventional wage share assumption.
Finally, we can explore the implications of imposing (16), even though this specification of technical change has not been implemented in the literature. The balanced growth condition becomes
and it provides an equilibrium locus in the space of income distribution and the employment rate. In order to pin down equilibrium values, we can borrow from Goodwin (1967) and assume that real wages grow with the employment rate, say gw = m(e), m′ > 0, as a tighter labor market strengthens the bargaining power of workers. A constant wage share in the long run requires wages and labor productivity to grow at the same rate: thus, the condition m(ess) = h(ess) fixes the equilibrium employment rate and productivity growth, while the equilibrium wage share follows from (25). Employment and productivity are independent of the saving rate that, however, has a positive effect on the wage share similarly to the exogenous productivity growth case.
Although this model has not been studied in the literature, we can take the analysis one step further and introduce an explicit policy variable. Assume that real wage growth is also a function of labor market institutions z, for example, the degree of employment protection. If gw = m(e, z), labor market institutions affect the growth rate of labor productivity, as well as income distribution, through their effect on the equilibrium employment rate. Define z such that mz > 0.7 Then, the effect of a change in z on equilibrium employment and distribution depends on the sign of the partial derivative me(ess, z) − h′(ess). If the sign is positive, that is, if wages are more responsive than productivity to the employment rate, an increase in labor market protection lowers employment and productivity growth while raising the wage share. Vice versa, if the sign is negative, an increase in z has a positive effect on equilibrium employment but an adverse effect on the labor share. Either way, workers face a trade-off between employment and productivity on the one end, and the wage share on the other hand. Such trade-off is in contrast with the steady-state implications of the Goodwin (1967) model, where an increase in employment protection would reduce employment but would have no impact on income distribution.
4.3 The Induced Innovation Hypothesis
The pitfalls of the aggregate production function, as well as the dissatisfaction with the exogeneity of technical change in the neoclassical growth model, led some scholars to consider the microeconomic choice of factor-augmenting technologies made by profit-maximizing firms. In particular, while it became clear very soon that balanced growth requires technical change to take the pure labor-augmenting form, the economic rationale for such a biased pattern of technology was not as well understood.
Taking up an old insight by Hicks (1932), who argued that the quest for profit maximization would lead firms to augment the productivity of the factor of production whose share in total costs increases, Kennedy (1964) postulated the existence of an innovation possibility frontier (IPF). The IPF inversely relates the attainable growth rate of labor productivity to the growth rate of capital productivity: gB = ε(gA), ε′ < 0, ε′′ < 0. The strict concavity of the IPF captures a notion of increasing complexity in the trade-off between labor-augmenting and capital-augmenting blueprints. The induced innovation hypothesis is Kennedy's idea that firms choose, myopically, a profile of technical change (gA, gB) so as to maximize the rate of change in unit cost reduction ωgA + (1 − ω)gB under the constraint given by the IPF. The result of this program is that the growth rate of labor (capital) productivity becomes an increasing function of the wage (profit) share: gA = f(ω), f′ > 0. This expression is formally identical to equation (15), but it does not assume constant capital productivity. The microeconomic appeal of the induced innovation hypothesis has led to a renewed interest to this theory in recent years (Foley, 2003; Julius, 2005; Rada, 2012; Tavani, 2012, 2013; Zamparelli, 2015).
Once the induced innovation hypothesis is adopted, the relation between productivity growth and income distribution in the classical growth model with exogenous labor supply changes dramatically. In its simplest form, the steady state of such classical model consists of the following equations:
In balanced growth, the output/capital ratio B has to remain constant: therefore, gB = ε[f(ωss)] = 0, which solves for a unique long-run value of the labor share: ωss = f− 1[ε− 1(0)]. The corresponding growth rate of labor productivity is then determined through the IPF: gA = ε− 1(0). Finally, once the wage share is found, the balanced growth condition yields the long-run output/capital ratio as
Important features of the induced innovation model are that: (a) factor shares adjust over time in order to ensure a labor-augmenting profile of technical change in the long run, and (b) income distribution depends only on the shape of the IPF. These results are substantially different from the classical model with constant capital productivity, and from the Solow growth model. We have shown how the saving rate in the classical model with endogenous labor productivity growth is a crucial determinant of income distribution, and even of per capita growth under the specification (15) of technical change. We have also discussed in Section 2 the influence of the saving rate on income distribution in neoclassical theory. Under the induced innovation hypothesis, on the contrary, the saving rate has no influence on income distribution and growth; however, similarly to the neoclassical case, it does affect the long-run level of capital productivity. Consider, in fact, an increase in the saving rate in equation (27), which puts pressure on the accumulation in the left-hand side. However, the position and shape of the IPF have not changed: the labor share is fixed, and so is the labor force growth rate. Therefore, the increase in savings must be counteracted by a decrease in the output/capital ratio, as it is clear from equation (28). Notice finally that the independence of income distribution from savings makes this model similar to the neoclassical endogenous growth model with foregone output as an R&D input.8 Figure 1 displays Kennedy's IPF and the long-run profile of technical change in this model.
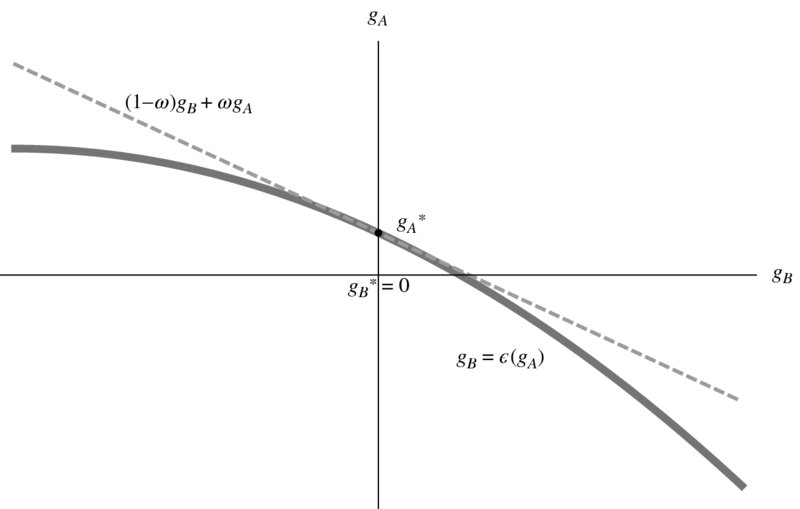
Figure 1. The Induced Innovation Hypothesis.
In a recent paper, Schlicht (2016) emphasizes the connections between the IPF and Kaldor's technical progress function; in fact, Kennedy (1964, p. 547n) already did notice that “if the technical progress function is known, the innovation possibility function can be derived from it.” However, while the two theories are isomorphic in terms of their representation of technology, they have different steady-state implications regarding income distribution, as a comparison of (23) and (26) shows.
The induced innovation hypothesis has also been implemented in the neoclassical framework beginning with Drandakis and Phelps (1965), Nordhaus (1967), Samuelson (1965), and von Weizsacker (1966) and more recently by Funk (2002). Even with a neoclassical production function, income shares in the long run depend on the IPF alone and not on the production technology and the saving rate, provided that the elasticity of substitution be less than 1 (Drandakis and Phelps, 1965). Strengths and weaknesses of these models are illustrated in Brugger and Geherke (2017).
4.3.1 Dynamics of Employment and the Output/Capital Ratio
Incorporating the induced innovation hypothesis in the classical Goodwin (1967) growth cycle model highlights the adjustment process toward a constant output/capital ratio, as well as constant income shares and employment rate, in the long run. The most important implication of this model is the disappearance of the perpetual Goodwin cycles as the economy actually reaches the steady state, instead of fluctuating permanently around it (Shah and Desai, 1981). However, the direction of adjustment is not monotonic: Goodwin cycles typically persist in the short-to-medium run under standard parameterizations. The model adds the employment rate e = BK/(AN) as a dynamic variable, and makes use as before of a real-wage Phillips curve so that an increase in employment feeds into higher real wage growth: gw = m(e) in its simplest form. The aggregate economy is described by three differential equations (Foley, 2003; Julius, 2005):
In steady state, setting as above gB = 0 solves for the long-run labor share ωss, once again determined by the IPF only.9 The long-run employment rate solves accordingly for ess = m− 1[f(ωss)]. Finally, because in steady state ε[f(ωss)] = 0, the long-run output/capital ratio is obtained as the solution to equation (28) above, which also follows by setting ge = 0 in (31). Importantly, the presence of induced innovation generates a negative feedback from the labor share to itself in equation (30): such feedback changes the dynamics of the growth cycle, turning the Goodwin steady state from a center into a stable spiral.
4.3.2 Assessment
The theory of induced technical change presented above is not immune to criticism: a first problem is that its logic involves a high level of abstraction, and it is not clear how to imagine an empirical counterpart to a strictly concave invention possibility frontier. Duménil and Levy (1995; 2010) have used a stochastic setting that better conforms with intuition, and delivers very similar implications for the choice of factor-augmenting technologies. A second, more important criticism is that the relationship between income distribution and factor productivities arises from the choice of a point along the IPF. But the position of the IPF is fully exogenous: the vertical intercept of the technical progress function in Figure 1—which determines the long-run growth rate of labor productivity—is a given of the theory. As such, the theory only explains the direction of technical change, that is, how changes in income distribution determine variations in labor productivity growth, as opposed to capital productivity growth: the theory is silent on the economic forces that give rise to a certain long-run growth rate, that is, the innovation intensity. In other words, labor-augmenting technical progress is basically available without costs to the economy, and the determination of income distribution is, in fact, driven by an exogenously given trade-off between factor-augmenting technologies (this point has been raised by Tobin, 1967, among others).
4.4 Unbalanced Growth: Marx-Biased Technical Change
Despite the balanced growth requirement that gB = 0, actual historical patterns have shown that the output-capital ratio may decrease for long periods of time. As an empirical illustration, Figure 2 plots Penn World Table series for the labor share, capital productivity, and the profit rate in United States, China, United Kingdom, and Japan over country-specific extended periods characterized by falling capital productivity (with trend lines for the US and the UK). The three variables are related through the basic long-run distributive curve (12), evaluated at full utilization:

Figure 2. Marx-Biased Technical Change for Selected Countries. Source: Penn World Tables 9.0 (Feenstra et al., 2015).
With a roughly trend-less labor share, decreasing capital productivity translates into a falling rate of profit of Marxian flavor. An almost constant labor share requires wages to grow in line with labor productivity: thus, the patterns displayed in Figure 2 are characterized by technical progress that is at the same time labor-augmenting (gA > 0) and capital-using (gB < 0) or, in the terminology by Foley and Michl (1999, chapter 7), Marx-biased technical change (MBTC). The analysis by Dumenil and Levy (2010) also refers to this pattern of technical change.
One question that arises when confronting falling profitability is why would firms adopt new production techniques that lower the profit rate: a basic criterion for the choice of technique (Okishio, 1961), in turn, similar to the quest for unit cost reduction that drives induced innovation, is to switch to a new technique if it does not decrease the profit rate at the current real wage. For simplicity, consider discrete time and two techniques characterized by productivity parameters (A, B) and ((1 + gA)A, (1 + gB)B), respectively. For a given real wage, the prospective profit rate associated with the new technique is
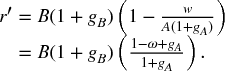
For the technique to be adopted, the prospective profit rate must be no less than the current profit rate. The required inequality can therefore be solved in order to identify a threshold value for the profit share ![]() such that if the actual share of profits does not exceed this value, the technique will be adopted. Such viability criterion is:
such that if the actual share of profits does not exceed this value, the technique will be adopted. Such viability criterion is:
Under MBTC, ![]() is always positive: thus, new techniques that increase labor productivity at the expenses of the output/capital ratio are viable. Notice that the higher the labor share, the easier it is to satisfy the viability condition. Therefore, a rising wage share makes the introduction of labor saving innovation more likely, which shows the resemblance of MBTC to theories of endogenous technical change captured in equation (15). What firms do not foresee when switching to the new technique, however, is that if real wages increase with labor productivity so as to maintain a constant wage share the profit rate falls following the decline in the output/capital ratio. Foley and Michl (1999, chapter 7) thus explain MBTC as analogous to a coordination failure: individually rational decision-making by firms results in a collectively self-defeating aggregate outcome. The historical patterns highlighted in Figure 2 leave little doubt about the relevance of MBTC.10 Notice also that MBTC is compatible with transitional dynamics in the NW quadrant of Figure 1.
is always positive: thus, new techniques that increase labor productivity at the expenses of the output/capital ratio are viable. Notice that the higher the labor share, the easier it is to satisfy the viability condition. Therefore, a rising wage share makes the introduction of labor saving innovation more likely, which shows the resemblance of MBTC to theories of endogenous technical change captured in equation (15). What firms do not foresee when switching to the new technique, however, is that if real wages increase with labor productivity so as to maintain a constant wage share the profit rate falls following the decline in the output/capital ratio. Foley and Michl (1999, chapter 7) thus explain MBTC as analogous to a coordination failure: individually rational decision-making by firms results in a collectively self-defeating aggregate outcome. The historical patterns highlighted in Figure 2 leave little doubt about the relevance of MBTC.10 Notice also that MBTC is compatible with transitional dynamics in the NW quadrant of Figure 1.
An important implication of MBTC is that subsequent labor-augmenting/capital-using innovations produce capital deepening that is “observationally equivalent” to the smooth capital-labor substitution in the Solow model. However, this process is driven by technical change, and not by factor substitution, as pointed out by Michl (1999): capital deepening leaves a trace that appears like a production function, but it is, in fact, just the fossil record of past technology. This observation has an obvious appeal for alternative economists: MBTC is immune from the logical flaws of the neoclassical aggregate production function highlighted by the Cambridge capital controversy of the 1960s, and therefore it provides a lens through which the process of capital deepening over time can be consistently accounted for.11
5. Post-Keynesian Closures
The rejection of Say's law is a cornerstone of Keynesian economics, and implies that output is demand-determined rather than constrained by supply factors. Post-Keynesian economists have incorporated Keynes' ideas into class-based models in order to emphasize the distributive implications of demand-driven growth. Here, we distinguish between a Kaleckian closure, where the rate of capacity utilization adjusts to ensure the equilibrium between the supply of savings and the demand for investment, and a Kaldorian closure, where the equilibrium in the goods market occurs through changes in income distribution. This sharp distinction is helpful from an expositional point of view, even though several contributions feature both adjustment mechanisms simultaneously (Palley, 1996; Cassetti, 2003; Sasaki, 2010; Taylor et al., 2016).
5.1 Kaleckian Closure
As seen above, a distinctive element of Kaleckian economics is the dependence of investment demand on income distribution. While the classical tradition only considers the supply of savings and therefore sees economic growth as ultimately profit-driven, the Kaleckian investment function opens up the possibility of a paradox of costs to arise, so that aggregate demand and growth can be wage-led, in the now standard terminology.
We will analyze the role of investment demand and its relation with income distribution in the context of endogenous technical change. The original Kaleckian model (Kalecki, 1971) adds effective demand to a classical-Marxian framework. If firms charge a constant markup μ over real unit labor costs, the labor share is anchored to the value of the markup and fully determined by the equation
which is formally equivalent to the classical closure (21). On the other hand, the short-run equilibrium between savings and investment is achieved through instantaneous adjustments in the utilization rate, which is a measure of aggregate demand. Using equations (17) and (19), and assuming in standard fashion that savings are more responsive than investment to changes in utilization, we can solve for the short-run equilibrium rate of capacity utilization and growth rate:
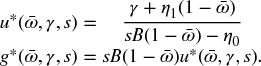
Since output is demand-determined, an increase in the saving rate lowers aggregate consumption and the level of economic activity: this effect is known as the paradox of thrift. Further, because u*ω > 0, the paradox of costs holds: an increase in the labor share pushes up consumption while it depresses investment. However, the former effect offsets the latter, and aggregate demand is wage-led. This mechanism highlights the fact that the paradox of costs is intimately connected to the paradox of saving: a redistribution that favors the class with the higher marginal propensity to consume has a boosting effect on aggregate demand.12 Finally, both utilization and growth respond positively to autonomous investment: more bullish sentiments by investors result in a higher level of economic activity and a higher growth rate in the short run. This is a version of the Keynesian metaphor of the “widow's cruse.”
In this model, growth can either be wage-led or profit-led. The simplest way to showcase the possibility of profit-led growth is to consider that if η0 = 0—that is, if there is no accelerator effect and investment only responds to profitability—then g*ω = −η1 < 0, so that growth is profit-led. Through a continuity argument, it can be shown that profit-led growth will prevail when the accelerator effect on investment demand is small (or negative, which would mean that there are self-stabilizing forces at work on aggregate demand, as opposed to self-reinforcing mechanisms), but the sensitivity of investment to profitability is strong. On the other hand, autonomous investment always has a positive effect on growth. Finally, the paradox of thrift holds for economic growth, too. In fact, differentiating with respect to the saving rate and recalling that s ∈ (0, 1), we find:
5.1.1 Constant Markup and Endogenous Labor Supply
Let us now introduce technological change using the two specifications of labor productivity growth (14) and (15), in turn, in the context of the distributive closure. With the Kaldor–Verdoorn law (14), gA = ![]() . In the short run, labor productivity growth is endogenous and reacts positively to demand shocks. Moreover, it maintains the wage-led or profit-led character of the short-run accumulation rate. When the economy approaches balanced growth in the long run, the endogenous labor supply and productivity growth both accommodate capital accumulation. In steady state, the equality
. In the short run, labor productivity growth is endogenous and reacts positively to demand shocks. Moreover, it maintains the wage-led or profit-led character of the short-run accumulation rate. When the economy approaches balanced growth in the long run, the endogenous labor supply and productivity growth both accommodate capital accumulation. In steady state, the equality ![]() yields gA = ϕ0/(1 − ϕ1) and
yields gA = ϕ0/(1 − ϕ1) and ![]() . While the accumulation rate is endogenous, labor productivity growth is semi-endogenous: the unlimited labor supply is the key adjusting variable that enables accumulation to progress unconstrained by supply factors. Hein and Tarassow (2010) provide a similar analysis, but with fully endogenous labor productivity growth.
. While the accumulation rate is endogenous, labor productivity growth is semi-endogenous: the unlimited labor supply is the key adjusting variable that enables accumulation to progress unconstrained by supply factors. Hein and Tarassow (2010) provide a similar analysis, but with fully endogenous labor productivity growth.
Alternatively, we can study the Kaleckian model where technical progress follows the classical-Marxian motive as in (15). Because distribution is exogenous, labor productivity growth is of the semi-endogenous variety, and does not add much to the analysis: ![]() . With unlimited labor supply, the growth rate of labor demand will again be the variable that adjusts in order to ensure balanced growth: it solves
. With unlimited labor supply, the growth rate of labor demand will again be the variable that adjusts in order to ensure balanced growth: it solves ![]() . Such an adjustment process emphasizes capital accumulation as the main driver of growth, similarly to the classical framework. However, differently from the classical case, a higher saving rate reduces growth: the paradox of thrift holds just like in the short run. Finally, autonomous investment is unconstrained in driving accumulation.
. Such an adjustment process emphasizes capital accumulation as the main driver of growth, similarly to the classical framework. However, differently from the classical case, a higher saving rate reduces growth: the paradox of thrift holds just like in the short run. Finally, autonomous investment is unconstrained in driving accumulation.
5.1.2 Exogenous Labor Supply and Endogenous Markup
We turn now to endogenous technical progress in the Kaleckian model in the context of exogenous labor supply growth. First notice that if we impose the Kaldor–Verdoorn law in per-worker terms, the balanced growth condition delivers a semi-endogenous growth rate:
Such a case is surprisingly similar to the corresponding classical model as per equation (23). For (35) to hold, however, we cannot assume that both the markup and investment are exogenous: if we retain the Keynesian assumption of autonomous investment, we need the labor share to adjust. Regarding the comparative statics, total differentiation of (35) shows dωss/dγ = −gγ/gω: an increase in autonomous investment will raise (lower) the wage share when growth is profit (wage)-led.
Second, we can let technical progress follow the classical-Marxian motive (15). In this case, the balanced growth condition is
With endogenous distribution, both accumulation and labor productivity growth are fully endogenous, and increase in the labor share. A shift in autonomous investment surely increases the share of labor when short-run growth is profit-led, since dω/dγ = gγ/(fω − gω) > 0. Under wage-led growth, instead, animal spirits and the wage share move together if the response of labor productivity growth to income distribution is stronger than the response of short-run accumulation, while they move in opposite directions if the converse is true. Exactly the opposite holds with regard to the effect of an increase in the saving rate on the wage share, given the paradox of thrift. In fact, dω/ds = gs/(fω − gω) is negative if growth is profit-led, and positive if gω > fω, that is, if accumulation is strongly wage-led. Thus, we see here a potential counterexample to the general case analyzed in this survey, namely, that savings and the share of labor always move together: the result is determined by the relative strength of the paradox of costs (gω) as opposed to the paradox of thrift (gs) on accumulation. Because labor productivity is endogenous, under profit-led growth, the paradox of thrift holds in the long run as dgA/ds = fωgs/(fω − gω) < 0; but the paradox of costs is not enough to offset it, and dω/ds < 0. If, on the other hand, the economy is strongly wage-led, the negative effect of the paradox of thrift on accumulation will be offset by the strength of the paradox of costs, and therefore the wage share will rise with the saving rate. Lima (2004) has generalized this case by assuming that f is a nonmonotonic function.
5.1.3 The Employment Rate as a Determinant of Technical Progress
As mentioned before, the dependence of labor productivity growth on employment as in (16) has been used extensively in the literature because it provides a solution to the first Harrodian problem with a Kaleckian closure and exogenous labor supply (Palley, 2012). The employment rate, in this case, adjusts to ensure that
Since h(e) is increasing, the steady-state employment rate retains the wage-led or profit-led character of the equilibrium growth rate, as well as the direct relationship with autonomous investment. Thus, even though utilization is always wage-led under the investment function (19), employment can be either wage-led or profit-led. Further, the “widow's cruse” argument also applies to the employment rate, as dess/dγ > 0. Third, the paradox of thrift holds, since dess/ds < 0. In this regard, notice the stark difference with the classical models, where employment and savings always go hand in hand. Finally, long-run productivity growth is fully endogenous, as it rises with the employment rate. Similar analyses can be found in Bhaduri (2006), Flaschel and Skott (2006), Lavoie (2006), and Sasaki (2010).
A related solution is the one proposed by Dutt (2006), with the important difference that distributive considerations are absent in his model. He postulates the specific functional form gA = h(e) = eθ, which implies ![]() . By construction, labor productivity growth in the long run reconciles actual and potential growth since gL − n = g − gA − n = 0. Dutt (2006) takes the argument one step further, and imposes slow adjustments in autonomous investment in response to the same forces (though working in the opposite direction). This generates indeterminacy and path dependence in the model. For instance, if a tighter labor market discourages investment growth, we can assume
. By construction, labor productivity growth in the long run reconciles actual and potential growth since gL − n = g − gA − n = 0. Dutt (2006) takes the argument one step further, and imposes slow adjustments in autonomous investment in response to the same forces (though working in the opposite direction). This generates indeterminacy and path dependence in the model. For instance, if a tighter labor market discourages investment growth, we can assume ![]() . The two equations that make up the corresponding dynamical system are linearly dependent on one another: the
. The two equations that make up the corresponding dynamical system are linearly dependent on one another: the ![]() and the
and the ![]() nullclines coincide, so that every point is an equilibrium point. Accordingly, the selection of equilibrium productivity and output growth depends on initial conditions and history. An extension of the model (Dutt, 2010) posits that changes in both labor productivity growth and autonomous investment respond positively to the difference between the employment rate (as opposed to its growth rate) and its “natural” level:
nullclines coincide, so that every point is an equilibrium point. Accordingly, the selection of equilibrium productivity and output growth depends on initial conditions and history. An extension of the model (Dutt, 2010) posits that changes in both labor productivity growth and autonomous investment respond positively to the difference between the employment rate (as opposed to its growth rate) and its “natural” level: ![]() . Contrary to the previous case, the steady-state level of employment is fixed at some exogenous equilibrium level, but indeterminacy still affects the growth rate of output and productivity growth due to the long-run endogenous rate of capacity utilization.
. Contrary to the previous case, the steady-state level of employment is fixed at some exogenous equilibrium level, but indeterminacy still affects the growth rate of output and productivity growth due to the long-run endogenous rate of capacity utilization.
5.2 Kaldorian Closure
As is well known, Kaldor (1972) rejected the notion of equilibrium analysis as irrelevant. In line with the Smithian tradition, but with a stronger emphasis on the demand side of the economy, he argued that the growth process is characterized by dynamic increasing returns, path dependence and cumulative causation between the size of the economy and technological progress. Macroeconomic theory therefore should be history-specific and hardly representable by equilibrium analysis. Still, beginning with Dixon and Thirlwall (1975), modern Kaldorian growth theory has produced equilibrium frameworks that convey analytically Kaldor's main insights on growth. It has been developed along three different, although intertwined, research agendas: balanced-of-payments-constrained growth, North-South growth, and export-led cumulative causation growth. Here, we focus on the last one as it features the most prominent role for technical change. Discussions and comparative surveys of the three approaches can be found in McCombie and Thirlwall (1994), King (2010), and Blecker (2013).
A standard representation of Kaldorian cumulative causation would follow Cornwall and Setterfield (2002) in combining a demand regime, such as the one captured by the investment function (20), with a productivity regime given by the Kaldor–Verdoorn law (see also Naastepad, 2006). We model productivity growth according to the Kaldor–Verdoorn law in absolute terms (13). Equating (20) and (13) gives
whereas with endogenous labor supply, employment growth can be found residually as ![]() . Both the equilibrium capital and labor productivity growth are increasing in autonomous investment. Quoting from Taylor et al. (2016), “demand drives growth all the way” and creates the necessary supply conditions. A similar point was raised earlier by Cornwall (1972): a “Say's law in reverse” is at work in the Kaldorian process of growth, in that aggregate demand creates its own supply and not vice versa.
. Both the equilibrium capital and labor productivity growth are increasing in autonomous investment. Quoting from Taylor et al. (2016), “demand drives growth all the way” and creates the necessary supply conditions. A similar point was raised earlier by Cornwall (1972): a “Say's law in reverse” is at work in the Kaldorian process of growth, in that aggregate demand creates its own supply and not vice versa.
Kaldor (1956, p. 94) also suggested that the Keynesian principle of the multiplier can be alternatively used to provide either a theory of the level of economic activity or of income distribution. Using (17) and (38), we have ![]() , which shows that in the short-run investment generates the necessary savings either through changes in utilization or the wage share. We already explored the Keynesian framework with adjustments in capacity utilization: here, we fix u = 1 and let income distribution be the accommodating variable. The long-run wage share can be found as solution to
, which shows that in the short-run investment generates the necessary savings either through changes in utilization or the wage share. We already explored the Keynesian framework with adjustments in capacity utilization: here, we fix u = 1 and let income distribution be the accommodating variable. The long-run wage share can be found as solution to
The adjustment of income distribution to changes in investment, the saving rate, or technology is based on the “forced saving” mechanism. If prices are more responsive than wages to excess demand, an increase in investment shifts the distribution of income in favor of the class with the higher propensity to save thus creating the additional savings necessary to accommodate higher growth. Conversely, the saving rate has an opposite effect on distribution: since higher savings reduce demand, if prices fall more rapidly than wages, the labor share rises and provides the increase in spending required to keep the macroeconomic balance. Finally, improvements in technology or trade conditions (φ0, φ1, λ) that increase equilibrium growth lower the wage share because, similarly to autonomous investment, they contribute to higher accumulation.
5.2.1 Exogenous Labor Supply and Long-Run Growth
The picture above changes drastically if we impose an exogenous growth rate of labor supply. The balanced growth condition becomes
There is only one value of γ compatible with balanced growth, and it is fully determined by the innovation technology and the structural conditions affecting foreign trade. Investment loses its autonomous nature and becomes endogenous; as a consequence, aggregate demand plays no role. Still, we are not quite back to semi-endogenous growth: if a country's propensity to import and, in turn, the foreign trade multiplier depend on trade policy, and policy makers can affect the value of λ. In this case, growth becomes fully endogenous. Notice that if we describe a closed economy by assuming λ = 0, the steady state in (40) becomes equivalent to the semi-endogenous case discussed in the classical model with exogenous labor supply, save for the different specification of the Kaldor–Verdoorn law. This explains why some authors working within the Kaldorian tradition (Skott, 1989, 2010; Ryoo, 2016) assume that growth in mature economies is constrained by the exogenous rate of population growth.
The irrelevance of aggregate demand in the long run clearly does not sit well with Kaldor's view of the growth process. One possibility to reestablish the demand-driven nature of Kaldorian growth is to assume that the structural parameters of the model react to disequilibrium in the labor market. Following Setterfield (2006; 2013a; 2013b), we can posit φ1 = φ1(e),φ′1 > 0. If a positive demand shock pushes growth above its natural rate (g* > gp), the employment rate rises because, given gL = g* − gA, labor demand grows faster than labor supply. If the slope of the technical progress function increases as a response, the natural growth rate gp rises and the initial demand shock has permanent growth effects. Palley (1996) has proposed a similar adjustment mechanism. He assumed that the innovation technology reacts to changes in capacity utilization rather than in the employment rate: since the equilibrium utilization rate is endogenous, this contribution combines the Kaleckian and the Kaldorian traditions.
The model is also capable of producing path dependence by imposing restrictions on its structural parameters. Under the restriction λφ1 = 1, the equilibrium growth rate is undefined as the demand schedule and productivity regime schedule have the same slope. If, in addition, we assume that the two curves coincide we find a continuum of equilibria, whose selection will be determined by initial conditions and will be sensitive to demand shocks: growth is fully path-dependent (Palley, 2003; Setterfield, 2013b).13 This conclusion, however, relies on the knife-edge condition.
5.2.2 Other Specifications of Technical Change
The Kaldor–Verdoorn relation is a core building block of Kaldorian growth. Nevertheless, it is interesting to explore the implications of other forms of technical change in a post-Keynesian environment characterized by full capacity utilization and endogenous income distribution. Assume first that labor productivity growth follows equation (15). In the short run, or in balanced growth with endogenous labor supply, the equilibrium is given by sB(1 − ω) = γ + λf(ω), which implicitly solves for the equilibrium wage share ω* = ω(s, γ). Just like in (39), the wage share is inversely related to autonomous investment while it increases with the saving rate. The short-run equilibrium growth rate is g* = γ + λf[ω(s, γ)], which highlights the ambiguous effect of autonomous investment. On the one hand, it directly increases the growth rate; on the other hand, however, its adverse distributional effect lowers the growth rate of labor productivity. Moreover, there is no paradox of saving: through its positive effect on the wage share, a higher saving rate increases labor productivity and output growth. Moving to the long run, balanced growth with exogenous labor supply requires
Once again, demand is irrelevant in the long run. Investment is not autonomous anymore, and it must adjust to satisfy supply constraints. Despite the fact that growth is supply-driven, the model is of the fully endogenous variety as the saving rate affects the equilibrium level of investment, income shares, and labor productivity growth. If λ ∈ (0, 1), that is if the foreign sector effect on investment is not too large, a higher saving rate determines an increase in investment as dγ/ds = (1 − λ)f[ωss(s, γ)]/[1 − (1 − λ)fωωγ] > 0; the effect on income distribution and growth, however, is ambiguous as dωss/ds = ∂ωss/∂s + (∂ωss/∂γ)dγ/ds≷0.
Finally, if we let labor productivity growth rise with the employment rate as assumed in (16), the short-run equilibrium condition is sB(1 − ω) = γ + λh(e). With full capacity utilization, the employment rate becomes a state variable in the model. Labor productivity growth is given in the short run and it does not affect the usual relation between income distribution, investment, and the saving rate: growth is demand-led, as investment creates the required savings through changes in income distribution. More interesting is the long-run equilibrium: the balanced growth condition is
Under this specification of technical change, demand matters even in the long-run. Autonomous investment increases capital accumulation, which determines a rise in the employment rate and, in turn, a higher natural growth rate. We are back to the “widow's cruse” result found in (37), with both steady-state employment and labor productivity growth increasing in response to stronger business confidence. However, the rise in the warranted growth rate necessary to keep the saving-investment balance occurs through a reduction in the wage share, rather than an increase in capacity utilization.
6. Costly Innovation
Until recently, researchers working within alternative frameworks have not considered the costly nature of the innovation process. Even though, to the best of our knowledge, there is no critical literature to draw from, one can think about a several explanations for this choice. First, in post-Keynesian economics, output and growth are demand-determined, supply only needs to accommodate demand conditions, and the assumption of a Kaldor–Verdoorn law such as (13) already well-captures the response of labor productivity growth to investment demand. Second, no matter whether one takes a classical or post-Keynesian viewpoint, inventive activity is highly uncertain, and does not lend itself to easy formalization as the output of a production process. Third, considering the costs incurred by firms when innovating requires to dive into the microeconomic allocation problem of choosing how to split resources between capital accumulation and inventive activity, which typically involves a profit-maximization problem. This may generate skepticism if profit maximization is identified with neoclassical marginal cost pricing.
And yet, in a world without a well-behaved production function but instead with labor and capital as perfect complements, firms have the ability to save on unit labor costs and increase profits through investment in labor-augmenting innovation. Since there is no question that the development of new technologies used for private production involves at least some expenditure, it is precisely the conflictual nature of the innovation process that calls for the inclusion of costly R&D into alternative models of growth and distribution. Here, we will distinguish between a series of recent contributions that focus on private R&D expenditure on the one hand, and public infrastructure spending on the other.
6.1 Private R&D
In recent contributions, Tavani and Zamparelli (2015) and Zamparelli (2015) study the problem of resource allocation on costly R&D by capitalist firms in the classical model with exogenous labor supply. We can follow the neoclassical endogenous growth theory in assuming that the flow of new ideas ![]() depends positively on R&D inputs on the one hand, and linearly on the existing level of technology itself on the other hand. As already noted, a linear spillover from past ideas is useful to generate sustained growth in the long run. Contrary to (4), however, it is forgone consumption rather than labor to be employed in the production process of new technology. Accordingly,
depends positively on R&D inputs on the one hand, and linearly on the existing level of technology itself on the other hand. As already noted, a linear spillover from past ideas is useful to generate sustained growth in the long run. Contrary to (4), however, it is forgone consumption rather than labor to be employed in the production process of new technology. Accordingly,
where R is the amount of R&D spending, homogeneous with output and capital stock, and ζ ∈ (0, 1) is the constant elasticity of innovation to R&D per unit of output. The normalization of R&D spending is necessary to avoid explosive growth: the growth rate of labor productivity would trend upward unless R&D investment is modeled as a share of output.
Once inventive activity becomes costly, capitalists have two alternative uses available for their saved profits: capital accumulation and innovation. Both types of investment raise total profits, but in different ways: innovation reduces unit labor costs in production, while capital accumulation increases the size of a firm's business. If we let δ be the share of saved profits invested in R&D, the growth rate of labor productivity is
while physical capital accumulation obeys:
The representative capitalist will choose δ to maximize some measure of profitability. The solution to the problem will be an allocation of investment as a (possibly implicit) function of all variables involved: saving preferences, technology, and unit labor cost δ* = δ(s, B, ζ, ω). Then, using the profit-maximizing allocation in the balanced growth condition, we can write:
In line with the standard results of the classical model with exogenous labor supply, equation (42) shows that steady-state income distribution is endogenous, although the effect of a change in the saving rate on the labor share cannot be established without further information on the shape of δ*. In equilibrium, labor productivity growth depends on the saving rate both directly and indirectly through its effect on the allocation of investment and on income distribution: g*A = [sδ(s, ωss)(1 − ωss)]ζ. Tavani and Zamparelli (2015) obtain the values of investment in both capital stock and R&D as the solution of intertemporal optimization by forward-looking capitalist households. The relation between saving preferences, income distribution, and growth is in principle ambiguous, but a numerical implementation of the model calibrated to match long-run US data shows that a higher saving rate increases labor productivity growth as well as the labor share.
Bridging the induced innovation hypothesis with endogenous growth considerations, Zamparelli (2015) assumes that the position of the innovation possibility frontier depends on the expenditure on R&D, so that firms choose capital accumulation as well as both the intensity and direction of technical change by solving a myopic profit maximization problem. In steady state, increases in the saving rate raise both long-run growth and the labor share.
In Section 4, we discussed the two possible outcomes of the classical growth framework: endogenous growth with exogenous distribution and endogenous distribution with exogenous (or semi-endogenous) growth. On the other hand, Section 4.3 has shown how the induced innovation hypothesis implies that both growth and income distribution are basically exogenous and determined solely by Kennedy's innovation possibility frontier. The introduction of costly innovation has therefore substantial implications for the classical model, in that it delivers the simultaneous endogeneity of growth and income distribution with or without the induced innovation hypothesis. Moreover, in contrast with the Romer (1990) contribution, this model delivers both a fully endogenous growth rate and labor share even with foregone consumption and not labor providing resources to the R&D process. The main element driving this result is that both the total amount of saving and its allocation between capital accumulation and R&D investment depend on income distribution, unlike in the Romer model.
6.2 Public Investment
The importance of the costly nature of technical change does not imply that subsequent increases in productivity are carried out and paid for by the private sector only. Public infrastructure spending that directly affects the production possibilities of an economy also has implications for long-run growth. In fact, taxes levied on private agents will divert resources from private capital accumulation; but tax receipts can be used toward accumulation of public capital. Hence, the introduction of public infrastructure and its financing into the picture has features that are very similar to the trade-offs that are at the heart of the costly innovation literature. Following the seminal paper by Barro (1990), neoclassical endogenous growth theory has extensively analyzed the importance of public investment in long-run growth (see Irmen and Kuehnel, 2009, for a survey). Non-neoclassical economists have recently picked up the topic: examples can be found in Dutt (2013b) and Tavani and Zamparelli (2016, 2017). Our exposition here presents slightly modified versions of these contributions that better fit the overall framework of this survey.
Assume that both public capital G and private capital K are essential in production, and that potential output is given by
where ν∈ (0, 1) is the elasticity of potential output to public capital, and χ ≡ X/K is the composition of aggregate capital stock. The interesting feature of this production function is that the productivity of private capital B = χν depends on how scarce public capital is relative to private capital, thus emphasizing the fundamental role of public infrastructure in the functioning of a market economy.
The government levies proportional taxes on profits at a rate τ ∈ (0, 1) in order to fund its infrastructure spending. Hence, ![]() , and gG = τ(1 − ω)u/χ1 − ν. The accumulation of private capital is affected by taxation, and obeys gK = s(1 − τ)(1 − ω)uχν. The law of motion of the composition of aggregate capital stock is thus:
, and gG = τ(1 − ω)u/χ1 − ν. The accumulation of private capital is affected by taxation, and obeys gK = s(1 − τ)(1 − ω)uχν. The law of motion of the composition of aggregate capital stock is thus:
Focusing on a balanced growth path where private and public capitals grow at the same rate yields the long-run value of capital composition as:
which highlights the role of taxation in determining the long-run productivity of private capital.
This result can be combined with both the classical and the post-Keynesian closures in order to analyze the impact of public investment on growth and technical change. Let us start with the classical framework with exogenous distribution discussed in Section 4.1 where u = 1 and ![]() . Using (44), the growth rate of the economy can be found as
. Using (44), the growth rate of the economy can be found as ![]() . It is endogenous and can be maximized by setting the tax rate equal to the output-elasticity of public capital: τ* = ν. If in addition we assume that productivity growth follows the Kaldor–Verdoorn law as in (13), its long-run growth rate is gA = φ0 + φ1gK(τ): technical change is fully endogenous, and can be maximized by levying a tax rate equal to τ*. Endogenous adjustments in labor supply will ensure that the long-run condition gK(τ) = φ0 + φ1gK(τ) + gL will be satisfied.
. It is endogenous and can be maximized by setting the tax rate equal to the output-elasticity of public capital: τ* = ν. If in addition we assume that productivity growth follows the Kaldor–Verdoorn law as in (13), its long-run growth rate is gA = φ0 + φ1gK(τ): technical change is fully endogenous, and can be maximized by levying a tax rate equal to τ*. Endogenous adjustments in labor supply will ensure that the long-run condition gK(τ) = φ0 + φ1gK(τ) + gL will be satisfied.
Consider instead the classical model with exogenous labor supply and endogenous distribution presented in Section 4.2, where u = 1 and gL = n. In the long run, we find [s(1 − τ)]1 − ντν(1 − ω) = gA + n. If labor productivity growth is exogenous, fiscal policy affects income distribution only, and τ* maximizes the labor share. If, conversely, we let productivity growth follow the Marxian motive (15), the balanced growth condition becomes [s(1 − τ)]1 − ντν(1 − ω) = f(ω) + n: both income distribution and productivity growth are endogenous and simultaneously maximized by levying a tax rate equal to τ*.
To study this model under the post-Keynesian closure, we need to introduce a role for investment demand. Tavani and Zamparelli (2017) adopt the early Kaleckian investment function ![]() ; the corresponding equilibrium capacity utilization rate is
; the corresponding equilibrium capacity utilization rate is
while the short-run growth rate is
If labor supply is endogenous and accommodates capital accumulation, the growth rate of the economy is fully endogenous in the long run and it increases in the tax rate (which constrains government spending) and autonomous investment. If, in addition, productivity growth follows the Kaldor–Verdoorn law, the endogeneity of the growth rate carries over to technical change: gA = φ0 + φ1gK(τ, γ). Under the exogenous labor supply closure, on the contrary, the Kaldor–Verdoorn assumption produces semi-endogenous results: from the balanced growth condition gK(τ, γ) = gA + n, we find
Growth and labor productivity growth are fixed by innovation technology and population growth. Fiscal policy only determines the composition of aggregate capital. In fact, when labor supply is exogenous, achieving a fully endogenous growth rate requires public investment to directly affect productivity growth. For example, Tavani and Zamparelli (2017) assume
with the underlying rationale that abundance of public capital produces more efficient infrastructures, which put private firms in a better position to innovate. An alternative route to full endogeneity of productivity growth can be found in Dutt (2013b). Elaborating on the framework developed in Dutt (2006) where productivity growth depends on the employment rate, he suggests that public investment may affect the elasticity of technical change to employment, that is:
Higher public investment raises the responsiveness of productivity growth to employment. In an economy characterized by indeterminacy such as the one at the end of Section 5.1, this assumption delivers higher output growth and productivity growth in the long run.
7. Conclusion
In this paper, we surveyed the non-neoclassical literature on endogenous technical change of the last 25 years. We identified three main views on the determinants of technical change one can find in the literature: (i) a Kaldorian hypothesis that sees labor productivity growth as a byproduct of capital accumulation, (ii) a classical-Marxian hypothesis that links factors productivity growth to income distribution, and (iii) a hypothesis made in recent post-Keynesian literature according to which the growth rate of labor productivity is related to labor market tightness as measured by the employment rate. These alternative viewpoints can be embedded into growth models classified by their different closures. We first investigated a supply-side classical-Marxian closure based on Say's law, and we distinguished between a labor-abundant and a labor-constrained version of the model. We then explored two post-Keynesian closures with independent investment functions: a Kaleckian closure in which quantity adjustments in the rate of capacity utilization achieve the equilibrium between savings and investment; and a Kaldorian closure where the equilibrium in the goods market is brought about by changes in income distribution. We studied these Keynesian cases both with and without labor constraints.
One element of novelty in our account of these contributions is the comparison with neoclassical exogenous and endogenous—as well as semi-endogenous—growth theories. We find the comparison illuminating along several dimensions, and we summarize here the main implications of classical supply-side models and demand-driven models, in turn, focusing on their respective steady states.
First, we showed that there are strong similarities between a classical-Marxian model with endogenous labor supply (Foley and Michl, 1999, chapter 6) and a version of the product-variety endogenous growth model where R&D is financed by foregone consumption, an example of which can be found in Aghion and Howitt (2010, chapter 3). In both frameworks, the labor share is exogenously given, but the growth rate is endogenous and increases in the saving rate: it can potentially be affected by policy action.
Second, we highlighted the analogy between a classical model with exogenous labor supply together with a Kaldorian technical progress function (Taylor, 2004, chapter 5) and the semi-endogenous neoclassical growth model by Jones (1995). In both cases, the long-run rate of growth of labor productivity is determined endogenously, but is independent of saving preferences and it is therefore policy-invariant. However, income distribution is fully endogenous, in that the labor share is an increasing function of the saving rate. The endogeneity of income distribution occurs even in the Solow model, where, however, labor productivity growth is unexplained.
Third, the classical model with induced technical change resembles the neoclassical exogenous growth model as it features an adjusting long-run output-capital ratio inversely related to the saving rate; however, contrary to the neoclassical model, income distribution is independent of saving preferences and fully determined by the shape of Kennedy's innovation possibility frontier.
Fourth, the Romer (1990) model with labor as R&D input determines both growth and the labor share endogenously as increasing functions of the saving rate, similarly to classical models with costly R&D (Tavani and Zamparelli, 2015; Zamparelli, 2015). The latter contributions, however, achieve the endogeneity of factor shares even with forgone output as an input to the R&D process: key to this result is that both capital accumulation and R&D investment depend on income distribution.
Fifth, in the sole-unbalanced growth case we described, there is a striking parallel to be drawn between the capital deepening arising from the capital-labor substitution that drives the transitional dynamics of the Solow model and a Marx-biased pattern of technical change.
Despite these remarkable similarities, the differences between classical and neoclassical models are profound. To begin with, none of the classical models presupposes full employment of labor, which is a crucial element of all their neoclassical counterparts. Second, the neoclassical models hinge mostly on a representative household, while the classical models are class-based. Third, the classical models are immune from the Cambridge critique of the neoclassical production function. Fourth, the classical models are in principle compatible with growth-distribution cycles around the steady state, while the convergence to the steady state is monotonic in both the Solow model and the Romer model (Arnold, 2000).14
Demand-driven models in the post-Keynesian tradition add the rejection of Say's law to the features that put classical models in contrast with neoclassical growth. Since saving and investment decisions do not coincide, it is autonomous investment that provides the key behavioral variable to investigate the relation between capital accumulation, technical change, and income distribution.
First, in the short run or if labor supply is endogenous, both Kaleckian and Kaldorian models feature a fully endogenous growth rate increasing in autonomous investment: the difference lays in what is the adjusting variable in the two models. Under the Kaldorian closure, it is income distribution to adjust, similarly to the classical model with exogenous population growth or the semi-endogenous neoclassical model: the labor share rises with the saving rate. In Kaleckian models, on the other hand, the saving-investment equilibrium is realized through quantity adjustments in capacity utilization. From this point of view, there is a similarity with the classical model with exogenous distribution where, following an increase in the saving rate, higher employment growth accommodates the increase in the growth rate.
Second, if labor supply is exogenous and productivity growth follows the Kaldor–Verdoorn law, Keynesian models lose their demand-led flavor in the long run: the balanced growth condition requires investment to adjust given population growth, the innovation technology, and (in the Kaldorian case) trade conditions. We thus explored multiple ways to achieve demand-determined endogenous growth with exogenous labor supply: (i) postulating that labor productivity growth depends on the level of endogenous variables such as the labor share or the employment rate; (ii) assuming that innovation technology reacts to differences between actual and potential output, and (iii) generating path-dependence by letting capital accumulation and labor productivity growth be defined by the same equation.
Overall, our account has shown that changes in capital accumulation, be they supply- or demand-driven, tend to have distributional rather than growth effects when the labor force grows at an exogenous rate. The analytical accomplishment of both neoclassical and alternative endogenous growth theories has consisted in devising specifications of technological change that make the natural growth rate sensitive to investment decisions, so that supply constraints do not prevent accumulation from affecting growth in the long run. In so doing, they all rely on knife-edge conditions: as noted by Solow (2007), endogenous growth requires a linear differential equation in the level of technology. However, a key difference is the emphasis on different factors that may be responsible for long-run growth. Neoclassical growth theorists have emphasized the role of intertemporal saving preferences and deviations from competitive markets; alternative theorists have focused on income distribution, the state of the labor market, and investors' behavior as key determinants of the pace of technical progress.
Acknowledgments
We thank Roberto Veneziani for his encouragement, Peter Skott, Heckhard Hein and Rajiv Sethi for helpful conversations about this topic, and two anonymous referees for their constructive comments. The usual disclaimer applies.
Notes
References
- Aghion, P. and Howitt, P. (1992) A model of growth through creative destruction. Econometrica 60: 323–351.
- Aghion, P. and Howitt, P. (2010) The Economics of Growth. Cambridge, MA: MIT Press.
- Arnold, L. (2000) Stability of the market equilibrium in Romer's model of endogenous technical change: A complete characterization. Journal of Macroeconomics 22(1): 69–84.
- Arrow, K.J. (1962) The economic implications of learning-by-doing. Review of Economic Studies 29: 55–173.
- Barro, R.J. (1990) Government spending in a simple model of endogenous growth. Quarterly Journal of Economics 98(5): S103–S125.
- Basu, D. (2010) Marx-biased technical change and the neoclassical view of income distribution. Metroeconomica 61(4): 593–620.
- Bhaduri, A. (2006) Endogenous economic growth: A new approach. Cambridge Journal of Economics 30(1): 69–83.
- Bhaduri, A. and Marglin, S. (1990) Unemployment and the real wage: The economic basis for contesting political ideologies. Cambridge Journal of Economics 14: 375–393.
- Black, J. (1962) The technical progress function and the production function. Economica 29(114): 166–170.
- Blecker, R. (2013) Long-run growth in open economies: Export-led cumulative causation or a balance-of-payments constraint? In G.C. Harcourt and P. Kriesler (eds.), The Oxford Handbook of Post-Keynesian Economics, Vol. I (pp. 390–414) Theory and Origins. Oxford, UK: Oxford University Press.
- Brugger, F. and Gehrke, C. (2017) The neoclassical approach to induced technical change: From Hicks to Acemoglu. Metroeconomica 68(4): 730–776.
- Cass, D. (1965) Optimum growth in an aggregative model of capital accumulation. Review of Economic Studies 32(3): 233–240.
- Cassetti, M. (2003) Bargaining power, effective demand and technical progress: A Kaleckian model of growth. Cambridge Journal of Economics 27(3): 449–464.
- Cornwall, J. (1972) Growth and Stability in a Mature Economy. London, UK: Martin Robertson.
- Cornwall, J. and Setterfield, M. (2002) A neo-Kaldorian perspective on the rise and decline of the golden age. In M. Setterfield (ed.), The Economics of Demand-Led Growth: Challenging the Supply Side Vision of the Long Run (pp. 67–86). Cheltenham, UK: Edward Elgar.
- Dixon, R. and Thirlwall, A.P. (1975) A model of regional growth-rate differences on Kaldorian lines. Oxford Economic Papers 27(2): 201–214.
- Drandakis, E.M. and Phelps, E.S. (1965) A model of induced invention, growth and distribution. Economic Journal 76(304): 823–840.
- Duménil, G. and Lévy, D. (1995) A stochastic model of technical change: An application to the US economy, 1869–1989. Metroeconomica 46: 213–245.
- Duménil, G. and Lévy, D. (2010) The classical-Marxian evolutionary model of technical change: Applications to historical tendencies. In M. Setterfield (ed.), Handbook of Alternative Theories of Economic Growth (pp. 243–273). Cheltenham, UK: Edward Elgar.
- Dutt, A.K. (2006) Aggregate demand, aggregate supply and economic growth. International Review of Applied Economics 20(3): 319–336.
- Dutt, A.K. (2010) Reconciling the growth of aggregate demand and aggregate supply. In M. Setterfield (ed.), Handbook of Alternative Theories of Economic Growth (pp. 220–240). London: Edward Elgar.
- Dutt, A.K. (2011) Alternative models of growth and distribution with a simple formulation of endogenous technical change. In C. Gehrke and N. Salvadori (eds.), Keynes, Sraffa, and the Criticism of Neoclassical Theory: Essays in Honor of Heinz Kurz (pp. 67–83). Routledge.
- Dutt, A.K. (2013a) Endogenous technological change in classical–Marxian models of growth and distribution. In T. Michl and A. Rezai (eds.), Social Fairness and Economics: Essays in the Spirit of Duncan Foley (pp. 264–285). New York, NY: Routledge.
- Dutt, A.K. (2013b) Government spending, aggregate demand, and economic growth. Review of Keynesian Economics 1(1): 105–119.
- Feenstra, R.C., Inklaar, R. and Timmer, M.P. (2015) The next generation of the Penn World Table. American Economic Review 105(10): 3150–3182. Available for download at https://doi.org/www.ggdc.net/pwt.
- Flaschel, P. and Skott, P. (2006) Steindlian models of growth and stagnation. Metroeconomica 57(3): 303–338.
- Foley, D.K. (2003) Endogenous technical change with externalities in a classical growth model. Journal of Economic Behavior and Organization 52(2): 167–189.
- Foley, D.K. and Michl, T.R. (1999) Growth and Distribution. Cambridge, MA: Harvard University Press.
- Funk, P. (2002) Induced innovation revisited. Economica 69: 155–171.
- Garegnani, P. (1970) Heterogeneous capital, the production function and the theory of distribution. Review of Economic Studies 37(3): 407–436.
- Goodwin, R. (1967) A growth cycle. In: C. Feinstein (ed.), Socialism, Capitalism, and Economic Growth (pp. 54–58). Cambridge, UK: Cambridge University Press.
- Grossman, M. and Helpman, E. (1991) Quality ladders in the theory of growth. Review of Economic Studies 58(1): 43–61.
- Harrod, R.F. (1939) An essay in dynamic theory. Economic Journal 49: 14–33.
- Hein, E. and Tarassow, A. (2010) Distribution, aggregate demand and productivity growth: Theory and empirical results for six OECD countries based on a post-Kaleckian model. Cambridge Journal of Economics 34(4): 727–754.
- Hicks, J.R. (1932[1960]) The Theory of Wages. London: Macmillan.
- Irmen, A. (2016) A generalized steady-state growth theorem. Macroeconomic Dynamics 1–26. First View, Published online: 27 June 2016.
- Irmen, A. and Kuehnel, J. (2009) Productive government expenditure and economic growth. Journal of Economic Surveys 23(4): 692–733.
- Jones, C. (1995) R&D-based models of economic growth. Journal of Political Economy 103(4): 759–784.
- Jones, C. and Romer, P. (2010) The new Kaldor facts: Ideas institutions, population, and human capital. American Economic Journal: Macroeconomics 2(1): 224–245.
- Jones, C. and Scrimgeour, D. (2008) A new proof of Uzawa's steady-state growth theorem. Review of Economics and Statistics 90(1): 180–182.
- Julius, A.J. (2005) Steady state growth and distribution with an endogenous direction of technical change. Metroeconomica 56(1): 101–125.
- Kaldor, N. (1956) Alternative theories of distribution. The Review of Economic Studies 23(2): 83–100.
- Kaldor, N. (1957) A model of economic growth. Economic Journal 67(268): 591–624.
- Kaldor, N. (1961) Capital accumulation and economic growth. In F.A. Lutz and D.C. Hague (eds.), The Theory of Capital (pp. 177–222). New York, NY: St. Martins Press.
- Kaldor, N. (1972) The irrelevance of equilibrium economics. The Economic Journal 82(328): 1237–1255.
- King, J.E. (2010) Kaldor and the Kaldorians. In M. Setterfield (ed.), Handbook of Alternative Theories of Economic Growth (pp. 157–186). Cheltenham, UK: Edward Elgar.
- Kalecki, M. (1971) Selected Essays on the Dynamics of the Capitalist Economy. Cambridge, UK: Cambridge University Press.
- Kennedy, C. (1964) Induced bias in innovation and the theory of distribution. Economic Journal 74(295): 541–547.
- Koopmans, T. (1965) On the concept of optimal economic growth. In J. Johansen (ed.), The Econometric Approach to Development Planning (pp. 225–287). Amsterdam: North-Holland.
- Kurz, H. and Salvadori, N. (1998) The ‘new’ growth theory: Old wine in new goatskins. In F. Coricelli, M. di Matteo and F. Hahn (eds.), New Theories in Growth and Development (pp. 63–94). Berlin: Springer.
- Lavoie, M. (2006) A post-Keynesian amendment to the new consensus on monetary policy. Metroeconomica 57(2): 165–192.
- Lewis, W.A. (1954) Economic development with unlimited supplies of labor. Manchester School of Economics and Social Studies 22: 139–191.
- Lima, G.T. (2004) Endogenous technological innovation, capital accumulation and distributional dynamics. Metroeconomica 55(4): 386–408.
- Marshall, A. (1920[1960]) Principles of Economics. C.W. Guillebaud (ed.), 9th edn. London: Macmillan.
- Marx, K. (1867 [1977]). Capital: A Critique of Political Economy, Vol. III. New York, NY: New York Books.
- McCombie, J. and Spreafico, M. (2016) Kaldor' s ‘technical progress function’ and Verdoorn' s law revisited. Cambridge Journal of Economics 40(4): 1117–1136
- McCombie, J. and Thirlwall, A.P. (1994) Economic Growth and the Balance-of-Payments Constraint. London, UK: Macmillan.
- Michl, T.R. (1999) Biased technical change and the aggregate production function. International Review of Applied Economics 13(2): 193–206.
- Michl, T.R. (2002) The fossil production function in a vintage model. Australian Economic Papers 41(1): 53–68.
- Michl, T.R. (2009) Capitalists, Workers, and Fiscal Policy. Cambridge, MA: Harvard University Press.
- Naastepad, C.W.M. (2006) Technology, demand and distribution: A cumulative growth model with an application to the Dutch productivity growth slowdown. Cambridge Journal of Economics 30: 403–434.
- Nordhaus, W. (1967) The optimal rate and direction of technical change. In K. Shell (ed.), Essays on the Theory of Optimal Economic Growth (pp. 53–66). Cambridge, MA: MIT Press.
- Okishio, N. (1961) Technical changes and the rate of profit. Kobe University Economic Review 7: 86–99.
- Palley, T.I. (1996) Growth theory in a Keynesian model. Journal of Post Keynesian Economics 19(1): 113–135.
- Palley, T.I. (2003) Pitfalls in the theory of growth: An application to the balance of payments-constrained growth model. Review of Political Economy 15(1): 75–84.
- Palley, T.I. (2012) Growth, unemployment and endogenous technical progress: A Hicksian resolution of Harrod's knife-edge. Metroeconomica 63(3): 512–541.
- Pasinetti, L.L. (1962) Rate of profit and income distribution in relation to the rate of economic growth. Review of Economics Studies 29(4): 267–279.
- Pasinetti, L.L. (1974) Growth and Income Distribution: Essays in Economic Theory. Cambridge, UK: Cambridge University Press.
- Rada, C. (2012) Social security tax and endogenous technical change in an economy with an aging population. Metroeconomica 63(4): 727–756.
- Ramsey, F.P. (1928) A mathematical theory of saving. Economic Journal 38(152): 543–559.
- Romer, P. (1990) Endogenous technological change. Journal of Political Economy 98(5): S71–S102.
- Ryoo, S. (2016) Demand-driven inequality, endogenous saving rate and macroeconomic instability. Cambridge Journal of Economics 40: 201–225.
- Samuelson, P.A. (1965) A theory of induced innovation along Kennedy-Weizsacker lines. The Review of Economics and Statistics 47(4): 343–356.
- Samuelson, P.A. (1966) A summing up. Quarterly Journal of Economics 80(4): 568–583.
- Sasaki, H. (2010) Endogenous technical change, income distribution and unemployment with inter-class conflict. Structural Change and Economic Dynamics 21: 123–134.
- Schlicht, E. (2006) A variant of Uzawa's theorem. Economics Bulletin 5(6): 1–5.
- Schlicht, E. (2016) Directed technical change and capital deepening: A reconsideration of Kaldor's technical progress function. Metroeconomica 67(1): 119–151.
- Schumpeter, J.A. (1942) Capitalism, Socialism, and Democracy. New York: Harper and Brothers.
- Setterfield, M. (2006) Thirlwall's law and Palley's pitfalls: A reconsideration. In P. Arestis, J. McCombie and R. Vickerman (eds.), Growth and Economic Development: Essays in Honour of A.P. Thirlwall (pp. 47–59). Cheltenham, UK: Edward Elgar.
- Setterfield, M. (2013a) Exploring the supply side of Kaldorian growth models. Review of Keynesian Economics 1(1): 22–36.
- Setterfield, M. (2013b) Endogenous growth: A Kaldorian approach. In G.C. Harcourt and P. Kriesler (eds.), The Oxford Handbook of Post-Keynesian Economics, vol. 1: Theory and Origins (pp. 231–256). Oxford, UK: Oxford University Press.
- Setterfield, M. (2014) Neoclassical growth theory and heterodox growth theory: Opportunities for (and obstacles to) greater engagement. Eastern Economic Journal 40(3): 365–386.
- Shah, A. and Desai, M. (1981) Growth cycles with induced technical change. The Economic Journal 91(364): 1006–1010.
- Skott, P. (1989) Conflict and Effective Demand in Economic Growth. Cambridge, UK: Cambridge University Press.
- Skott, P. (2010) Growth, instability and cycles: Harrodian and Kaleckian models of accumulation and income distribution. In M. Setterfield (ed.), Handbook of Alternative Theories of Economic Growth (pp. 108–131). Cheltenham, UK: Edward Elgar.
- Smith, A. (1776 [1981]) An Inquiry into the Nature and Causes of the Wealth of Nations, R.H. Campbell and A.S. Skinner (eds.). Indianapolis, IN: Liberty Fund.
- Solow, R. (1956) A contribution to the theory of economic growth. Quarterly Journal of Economics 70: 65–94.
- Solow, R. (1994) Perspectives on growth theory. Journal of Economic Perspectives 8(1): 45–54.
- Solow, R. (2007) The last 50 years in growth theory and the next 10. Oxford Review of Economic and Policy 23(1): 3–14.
- Tavani, D. (2012) Wage bargaining and induced technical change in a linear economy: Theory and application to the US (1963-2003). Structural Change and Economic Dynamics 23: 117–126.
- Tavani, D. (2013) Bargaining over productivity and wages when technical change is induced: Implications for growth, distribution, and employment. Journal of Economics 109: 207–244.
- Tavani, D. and Zamparelli, L. (2015) Endogenous technical change, employment and distribution in the Goodwin model of the growth cycle. Studies in Nonlinear Dynamics and Econometrics 19(2): 209–226.
- Tavani, D. and Zamparelli, L. (2016) Public capital, redistribution and growth in a two-class economy. Metroeconomica 67(2): 458–476.
- Tavani, D. and Zamparelli, L. (2017) Government spending composition, aggregate demand, growth, and distribution. Review of Keynesian Economics 5(2): 239–258.
- Taylor, L. (1985) A stagnationist model of economic growth. Cambridge Journal of Economics 9: 383–403.
- Taylor, L. (1991) Income Distribution, Inflation, and Growth. Cambridge, MA: MIT Press.
- Taylor, L. (2004) Reconstructing Macroeconomics. Cambridge, MA: Harvard University Press.
- Taylor, L., Foley, D.K., Rezai, A., Pires, L., Omer, O. and Scharfenaker, S. (2016) Demand drives growth all the way. Schwartz Center for Economic Policy Analysis and Department of Economics, The New School for Social Research, Working Paper Series 2016-4.
- Tobin, J. (1967) Comment to ‘Some recent developments in the theory of production’ by R.M. Solow. In M.B. Brown (ed.) The Theory and Empirical Analysis of Production (pp. 50–53). New York, NY: Columbia University Press.
- Uzawa, H. (1961) Neutral inventions and the stability of growth equilibrium. Review of Economic Studies 28: 117–124.
- Verdoorn, P.J. (1949) Fattori che regolano lo sviluppo della produttività del lavoro. L'Industria 1: 3–10.
- Young, A.A. (1928) Increasing returns and economic progress. Economic Journal 38: 527–542.
- von Weizsacker, C.C. (1966) Tentative notes on a two sector model with induced technical progress. Review of Economic Studies 33(3): 245–251.
- Zamparelli, L. (2015) Induced innovation, endogenous technical change and income distribution in a labor-constrained model of classical growth. Metroeconomica 66(2): 243–262.
