CHAPTER GOALS
To study several sorting and searching algorithms
To appreciate that algorithms for the same task can differ widely in performance
To understand the big-Oh notation
To learn how to estimate and compare the performance of algorithms
To learn how to measure the running time of a program
Sorting and searching are among the most common tasks in data processing. Of course, the Java library contains methods for carrying out these operations. Nevertheless, studying algorithms for sorting and searching is fruitful because you will learn how to analyze the performance of algorithms and how to choose the best algorithm for a particular task. Sorting and searching are an excellent entry point into the study of algorithm analysis because the tasks themselves are simple to understand. As you will see in this chapter, the most straightforward algorithms do not perform very well, and we can achieve dramatic improvements with more sophisticated algorithms.
In this section, we show you the first of several sorting algorithms. A sorting algorithm rearranges the elements of a collection so that they are stored in sorted order. To keep the examples simple, we will discuss how to sort an array of integers before going on to sorting strings or more complex data. Consider the following array a:
An obvious first step is to find the smallest element. In this case the smallest element is 5, stored in a[3]. We should move the 5 to the beginning of the array. Of course, there is already an element stored in a[0], namely 11. Therefore we cannot simply move a[3] into a[0] without moving the 11 somewhere else. We don't yet know where the 11 should end up, but we know for certain that it should not be in a[0]. We simply get it out of the way by swapping it with a[3].
Note
The selection sort algorithm sorts an array by repeatedly finding the smallest element of the unsorted tail region and moving it to the front.
Now the first element is in the correct place. In the foregoing figure, the darker color indicates the portion of the array that is already sorted.
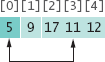
Next we take the minimum of the remaining entries a[1] ... a[4]. That minimum value, 9, is already in the correct place. We don't need to do anything in this case and can simply extend the sorted area by one to the right:
Repeat the process. The minimum value of the unsorted region is 11, which needs to be swapped with the first value of the unsorted region, 17:
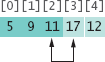
Now the unsorted region is only two elements long, but we keep to the same successful strategy. The minimum value is 12, and we swap it with the first value, 17.
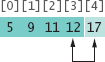
That leaves us with an unprocessed region of length 1, but of course a region of length 1 is always sorted. We are done.
Let's program this algorithm. For this program, as well as the other programs in this chapter, we will use a utility method to generate an array with random entries. We place it into a class ArrayUtil so that we don't have to repeat the code in every example. To show the array, we call the static toString method of the Arrays class in the Java library and print the resulting string.
This algorithm will sort any array of integers. If speed were not an issue, or if there simply were no better sorting method available, we could stop the discussion of sorting right here. As the next section shows, however, this algorithm, while entirely correct, shows disappointing performance when run on a large data set.
Special Topic 14.1 on page 604 discusses insertion sort, another simple sorting algorithm.
ch14/selsort/SelectionSorter.java
1/**2This class sorts an array, using the selection sort3algorithm.4*/5public class SelectionSorter6{7private int[] a;89/**10Constructs a selection sorter.11@param anArray the array to sort12*/13public SelectionSorter(int[] anArray)14{15a = anArray;16}1718/**19Sorts the array managed by this selection sorter.20*/21public void sort()22{
23for (int i = 0; i < a.length - 1; i++)24{25int minPos = minimumPosition(i);26swap(minPos, i);27}28}2930/**31Finds the smallest element in a tail range of the array.32@param from the first position in a to compare33@return the position of the smallest element in the34range a[from] ... a[a.length - 1]35*/36private int minimumPosition(int from)37{38int minPos = from;39for (int i = from + 1; i < a.length; i++)40if (a[i] < a[minPos]) minPos = i;41return minPos;42}4344/**45Swaps two entries of the array.46@param i the first position to swap47@param j the second position to swap48*/49private void swap(int i, int j)50{51int temp = a[i];52a[i] = a[j];53a[j] = temp;54}55}
ch14/selsort/SelectionSortDemo.java
1import java.util.Arrays;23/**4This program demonstrates the selection sort algorithm by5sorting an array that is filled with random numbers.6*/7public class SelectionSortDemo8{9public static void main(String[] args)10{11int[] a = ArrayUtil.randomIntArray(20, 100);12System.out.println(Arrays.toString(a));1314SelectionSorter sorter = new SelectionSorter(a);15sorter.sort();1617System.out.println(Arrays.toString(a));18}19}
1import java.util.Random;23/**4This class contains utility methods for array manipulation.5*/6public class ArrayUtil7{8private static Random generator = new Random();910/**11Creates an array filled with random values.12@param length the length of the array13@param n the number of possible random values14@return an array filled with length numbers between150 and n - 116*/17public static int[] randomIntArray(int length, int n)18{19int[] a = new int[length];20for (int i = 0; i < a.length; i++)21a[i] = generator.nextInt(n);2223return a;24}25}
Typical Output
[65, 46, 14, 52, 38, 2, 96, 39, 14, 33, 13, 4, 24, 99, 89, 77, 73, 87, 36, 81] [2, 4, 13, 14, 14, 24, 33, 36, 38, 39, 46, 52, 65, 73, 77, 81, 87, 89, 96, 99]

2. What steps does the selection sort algorithm go through to sort the sequence 6 5 4 3 2 1?
To measure the performance of a program, you could simply run it and use a stopwatch to measure how long it takes. However, most of our programs run very quickly, and it is not easy to time them accurately in this way. Furthermore, when a program takes a noticeable time to run, a certain amount of that time may simply be used for loading the program from disk into memory and displaying the result (for which we should not penalize it).
In order to measure the running time of an algorithm more accurately, we will create a StopWatch class. This class works like a real stopwatch. You can start it, stop it, and read out the elapsed time. The class uses the System.currentTimeMillis method, which returns the milliseconds that have elapsed since midnight at the start of January 1, 1970. Of course, you don't care about the absolute number of seconds since this historical moment, but the difference of two such counts gives us the number of milliseconds of a time interval.
Here is the code for the StopWatch class:
ch14/selsort/StopWatch.java
1/**2A stopwatch accumulates time when it is running. You can3repeatedly start and stop the stopwatch. You can use a4stopwatch to measure the running time of a program.5*/6public class StopWatch7{8private long elapsedTime;9private long startTime;10private boolean isRunning;1112/**13Constructs a stopwatch that is in the stopped state14and has no time accumulated.15*/16public StopWatch()17{18reset();19}2021/**22Starts the stopwatch. Time starts accumulating now.23*/24public void start()25{26if (isRunning) return;27isRunning = true;28startTime = System.currentTimeMillis();29}3031/**32Stops the stopwatch. Time stops accumulating and is33is added to the elapsed time.34*/35public void stop()36{37if (!isRunning) return;38isRunning = false;39long endTime = System.currentTimeMillis();40elapsedTime = elapsedTime + endTime - startTime;41}4243/**44Returns the total elapsed time.45@return the total elapsed time46*/47public long getElapsedTime()48{49if (isRunning)50{51long endTime = System.currentTimeMillis();52return elapsedTime + endTime - startTime;53}54else55return elapsedTime;
56}5758/**59Stops the watch and resets the elapsed time to 0.60*/61public void reset()62{63elapsedTime = 0;64isRunning = false;65}66}
Here is how we will use the stopwatch to measure the performance of the sorting algorithm:
ch14/selsort/SelectionSortTimer.java
1import java.util.Scanner;23/**4This program measures how long it takes to sort an5array of a user-specified size with the selection6sort algorithm.7*/8public class SelectionSortTimer9{10public static void main(String[] args)11{12Scanner in = new Scanner(System.in);13System.out.print("Enter array size: ");14int n = in.nextInt();1516// Construct random array1718int[] a = ArrayUtil.randomIntArray(n, 100);19SelectionSorter sorter = new SelectionSorter(a);2021// Use stopwatch to time selection sort2223StopWatch timer = new StopWatch();2425timer.start();26sorter.sort();27timer.stop();2829System.out.println("Elapsed time: "30+ timer.getElapsedTime() + " milliseconds");31}32}
Program Run
Enter array size: 100000 Elapsed time: 27880 milliseconds
By starting to measure the time just before sorting, and stopping the stopwatch just after, you get the time required for the sorting process, without counting the time for input and output.
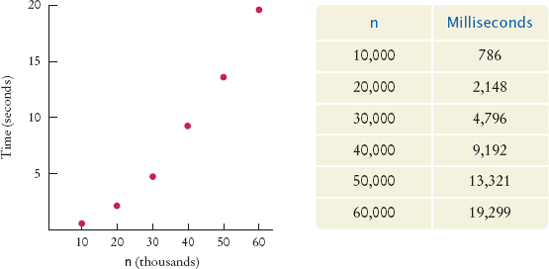
The table in Figure 1 shows the results of some sample runs. These measurements were obtained with a Intel processor with a clock speed of 2 GHz, running Java 6 on the Linux operating system. On another computer the actual numbers will look different, but the relationship between the numbers will be the same.
Note
To measure the running time of a method, get the current time immediately before and after the method call.
The graph in Figure 1 shows a plot of the measurements. As you can see, doubling the size of the data set more than doubles the time needed to sort it.

4. Look at the graph in Figure 1. What mathematical shape does it resemble?
Let us count the number of operations that the program must carry out to sort an array with the selection sort algorithm. We don't actually know how many machine operations are generated for each Java instruction, or which of those instructions are more time-consuming than others, but we can make a simplification. We will simply count how often an array element is visited. Each visit requires about the same amount of work by other operations, such as incrementing subscripts and comparing values.
Let n be the size of the array. First, we must find the smallest of n numbers. To achieve that, we must visit n array elements. Then we swap the elements, which takes two visits. (You may argue that there is a certain probability that we don't need to swap the values. That is true, and one can refine the computation to reflect that observation. As we will soon see, doing so would not affect the overall conclusion.) In the next step, we need to visit only n − 1 elements to find the minimum. In the following step, n − 2 elements are visited to find the minimum. The last step visits two elements to find the minimum. Each step requires two visits to swap the elements. Therefore, the total number of visits is
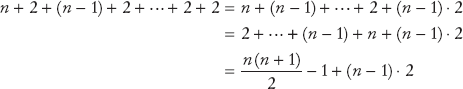
because
After multiplying out and collecting terms of n, we find that the number of visits is
We obtain a quadratic equation in n. That explains why the graph of Figure 1 looks approximately like a parabola.
Now simplify the analysis further. When you plug in a large value for n (for example, 1,000 or 2,000), then ½n2 is 500,000 or 2,000,000. The lower term, 5/2n – 3, doesn't contribute much at all; it is only 2,497 or 4,997, a drop in the bucket compared to the hundreds of thousands or even millions of comparisons specified by the ½n2 term. We will just ignore these lower-level terms. Next, we will ignore the constant factor ½. We are not interested in the actual count of visits for a single n. We want to compare the ratios of counts for different values of n. For example, we can say that sorting an array of 2,000 numbers requires four times as many visits as sorting an array of 1,000 numbers:
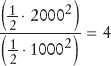
The factor ½ cancels out in comparisons of this kind. We will simply say, "The number of visits is of order n2". That way, we can easily see that the number of comparisons increases fourfold when the size of the array doubles: (2n)2 = 4n2.
To indicate that the number of visits is of order n2, computer scientists often use big-Oh notation: The number of visits is O(n2). This is a convenient shorthand.
In general, the expression f(n) = O(g(n)) means that f grows no faster than g, or, more formally, that for all n larger than some threshold, the ratio for some constant value C. The function g is usually chosen to be very simple, such as n2 in our example.
To turn an exact expression such as
into big-Oh notation, simply locate the fastest-growing term, n2, and ignore its constant coefficient, no matter how large or small it may be.
Note
Computer scientists use the big-Oh notation f(n) = O(g(n)) to express that the function fgrows no faster than the function g.
We observed before that the actual number of machine operations, and the actual amount of time that the computer spends on them, is approximately proportional to the number of element visits. Maybe there are about 10 machine operations (increments, comparisons, memory loads, and stores) for every element visit. The number of machine operations is then approximately 10 × ½n2. As before, we aren't interested in the coefficient, so we can say that the number of machine operations, and hence the time spent on the sorting, is of the order of n2 or O(n2).
The sad fact remains that doubling the size of the array causes a fourfold increase in the time required for sorting it with selection sort. When the size of the array increases by a factor of 100, the sorting time increases by a factor of 10,000. To sort an array of a million entries, (for example, to create a telephone directory) takes 10,000 times as long as sorting 10,000 entries. If 10,000 entries can be sorted in about 1/2 of a second (as in our example), then sorting one million entries requires well over an hour. We will see in the next section how one can dramatically improve the performance of the sorting process by choosing a more sophisticated algorithm.
Note
Selection sort is an O(n2) algorithm. Doubling the data set means a fourfold increase in processing time.

6. How large does n need to be so that ½n2 is bigger than 5/2 n – 3?
In this section, you will learn about the merge sort algorithm, a much more efficient algorithm than selection sort. The basic idea behind merge sort is very simple.
Suppose we have an array of 10 integers. Let us engage in a bit of wishful thinking and hope that the first half of the array is already perfectly sorted, and the second half is too, like this:
Now it is simple to merge the two sorted arrays into one sorted array, by taking a new element from either the first or the second subarray, and choosing the smaller of the elements each time:
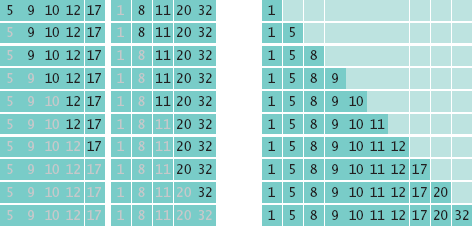
In fact, you may have performed this merging before if you and a friend had to sort a pile of papers. You and the friend split the pile in half, each of you sorted your half, and then you merged the results together.
That is all well and good, but it doesn't seem to solve the problem for the computer. It still must sort the first and second halves of the array, because it can't very well ask a few buddies to pitch in. As it turns out, though, if the computer keeps dividing the array into smaller and smaller subarrays, sorting each half and merging them back together, it carries out dramatically fewer steps than the selection sort requires.
Let's write a MergeSorter class that implements this idea. When the MergeSorter sorts an array, it makes two arrays, each half the size of the original, and sorts them recursively. Then it merges the two sorted arrays together:
public void sort()
{
if (a.length <= 1) return;
int[] first = new int[a.length / 2];
int[] second = new int[a.length - first.length];
// Copy the first half of a into first, the second half into second
...
MergeSorter firstSorter = new MergeSorter(first);
MergeSorter secondSorter = new MergeSorter(second);
firstSorter.sort();
secondSorter.sort();
merge(first, second);
}The merge method is tedious but quite straightforward. You will find it in the code that follows.
Note
The merge sort algorithm sorts an array by cutting the array in half, recursively sorting each half, and then merging the sorted halves.
ch14/mergesort/MergeSorter.java
1/**2This class sorts an array, using the merge sort algorithm.3*/4public class MergeSorter5{6private int[] a;78/**9Constructs a merge sorter.10@param anArray the array to sort11*/12public MergeSorter(int[] anArray)13{14a = anArray;15}1617/**18Sorts the array managed by this merge sorter.19*/20public void sort()21{22if (a.length <= 1) return;23int[] first = new int[a.length / 2];24int[] second = new int[a.length - first.length];25// Copy the first half of a into first, the second half into second26for (int i = 0; i < first.length; i++) { first[i] = a[i]; }27for (int i = 0; i < second.length; i++)28{29second[i] = a[first.length + i];30}
31MergeSorter firstSorter = new MergeSorter(first);32MergeSorter secondSorter = new MergeSorter(second);33firstSorter.sort();34secondSorter.sort();35merge(first, second);36}3738/**39Merges two sorted arrays into the array managed by this merge sorter.40@param first the first sorted array41@param second the second sorted array42*/43private void merge(int[] first, int[] second)44{45int iFirst = 0; // Next element to consider in the first array46int iSecond = 0; // Next element to consider in the second array47int j = 0; // Next open position in a4849// As long as neither iFirst nor iSecond past the end, move50// the smaller element into a51while (iFirst < first.length && iSecond < second.length)52{53if (first[iFirst] < second[iSecond])54{55a[j] = first[iFirst];56iFirst++;57}58else59{60a[j] = second[iSecond];61iSecond++;62}63j++;64}6566// Note that only one of the two loops below copies entries67// Copy any remaining entries of the first array68while (iFirst < first.length)69{70a[j] = first[iFirst];71iFirst++; j++;72}73// Copy any remaining entries of the second half74while (iSecond < second.length)75{76a[j] = second[iSecond];77iSecond++; j++;78}79}80}
ch14/mergesort/MergeSortDemo.java
1import java.util.Arrays;23/**4This program demonstrates the merge sort algorithm by5sorting an array that is filled with random numbers.6*/
7public class MergeSortDemo8{9public static void main(String[] args)10{11int[] a = ArrayUtil.randomIntArray(20, 100);12System.out.println(Arrays.toString(a));1314MergeSorter sorter = new MergeSorter(a);15sorter.sort();16System.out.println(Arrays.toString(a));17}18}
[8, 81, 48, 53, 46, 70, 98, 42, 27, 76, 33, 24, 2, 76, 62, 89, 90, 5, 13, 21] [2, 5, 8, 13, 21, 24, 27, 33, 42, 46, 48, 53, 62, 70, 76, 76, 81, 89, 90, 98]

8. Manually run the merge sort algorithm on the array 8 7 6 5 4 3 2 1.
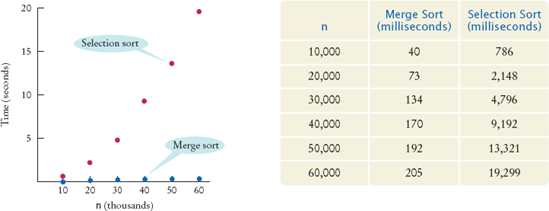
The merge sort algorithm looks a lot more complicated than the selection sort algorithm, and it appears that it may well take much longer to carry out these repeated subdivisions. However, the timing results for merge sort look much better than those for selection sort.
Figure 2 shows a table and a graph comparing both sets of performance data. As you can see, merge sort is a tremendous improvement. To understand why, let us estimate the number of array element visits that are required to sort an array with the merge sort algorithm. First, let us tackle the merge process that happens after the first and second halves have been sorted.
Each step in the merge process adds one more element to a. That element may come from first or second, and in most cases the elements from the two halves must be compared to see which one to take. We'll count that as 3 visits (one for a and one each for first and second) per element, or 3n visits total, where n denotes the length of a. Moreover, at the beginning, we had to copy from a to first and second, yielding another 2n visits, for a total of 5n.
If we let T(n) denote the number of visits required to sort a range of n elements through the merge sort process, then we obtain
because sorting each half takes T(n/2) visits. Actually, if n is not even, then we have one subarray of size (n − 1)/2 and one of size (n − 1)/2. Although it turns out that this detail does not affect the outcome of the computation, we will nevertheless assume for now that n is a power of 2, say n = 2m. That way, all subarrays can be evenly divided into two parts.
Unfortunately, the formula
does not clearly tell us the relationship between n and T(n). To understand the relationship, let us evaluate T(n/2), using the same formula:
Therefore
Let us do that again:
hence
This generalizes from 2, 4, 8, to arbitrary powers of 2:
Recall that we assume that n = 2m; hence, for k = m,
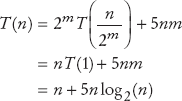
Because n = 2m, we have m = log2(n).
To establish the growth order, we drop the lower-order term n and are left with 5n log2(n). We drop the constant factor 5. It is also customary to drop the base of the logarithm, because all logarithms are related by a constant factor. For example,
Hence we say that merge sort is an O(n log(n)) algorithm.
Is the O(n log(n)) merge sort algorithm better than the O(n2) selection sort algorithm? You bet it is. Recall that it took 1002 = 10,000 times as long to sort a million records as it took to sort 10,000 records with the O(n2) algorithm. With the O( nlog(n)) algorithm, the ratio is
Note
Merge sort is an O(n log(n)) algorithm. The n log(n) function grows much more slowly than n2.
Suppose for the moment that merge sort takes the same time as selection sort to sort an array of 10,000 integers, that is, 3/4 of a second on the test machine. (Actually, it is much faster than that.) Then it would take about 0.75 × 150 seconds, or under 2 minutes, to sort a million integers. Contrast that with selection sort, which would take over 2 hours for the same task. As you can see, even if it takes you several hours to learn about a better algorithm, that can be time well spent.
In this chapter we have barely begun to scratch the surface of this interesting topic. There are many sorting algorithms, some with even better performance than merge sort, and the analysis of these algorithms can be quite challenging. These important issues are often revisited in later computer science courses.

10. If you double the size of an array, how much longer will the merge sort algorithm take to sort the new array?
Suppose you need to find your friend's telephone number. You look up the friend's name in the telephone book, and naturally you can find it quickly, because the telephone book is sorted alphabetically. Now suppose you have a telephone number and you must know to what party it belongs. You could of course call that number, but suppose nobody picks up on the other end. You could look through the telephone book, a number at a time, until you find the number. That would obviously be a tremendous amount of work, and you would have to be desperate to attempt it.
This thought experiment shows the difference between a search through an unsorted data set and a search through a sorted data set. The following two sections will analyze the difference formally.
If you want to find a number in a sequence of values that occur in arbitrary order, there is nothing you can do to speed up the search. You must simply look through all elements until you have found a match or until you reach the end. This is called a linear or sequential search.
Note
A linear search examines all values in an array until it finds a match or reaches the end.
How long does a linear search take? If we assume that the element v is present in the array a, then the average search visits n/2 elements, where n is the length of the array. If it is not present, then all n elements must be inspected to verify the absence. Either way, a linear search is an O(n) algorithm.
Note
A linear search locates a value in an array in O(n) steps.
Here is a class that performs linear searches through an array a of integers. When searching for the value v, the search method returns the first index of the match, or −1 if v does not occur in a.
ch14/linsearch/LinearSearcher.java
1/**2A class for executing linear searches through an array.3*/4public class LinearSearcher5{6private int[] a;78/**9Constructs the LinearSearcher .10@param anArray an array of integers11*/12public LinearSearcher(int[] anArray)13{14a = anArray;15}1617/**18Finds a value in an array, using the linear search19algorithm.20@param v the value to search21@return the index at which the value occurs, or −122if it does not occur in the array23*/24public int search(int v)25{26for (int i = 0; i < a.length; i++)27{28if (a[i] == v)29return i;30}31return −1;32}33}
ch14/linsearch/LinearSearchDemo.java
1import java.util.Arrays;2import java.util.Scanner;34/**5This program demonstrates the linear search algorithm.6*/7public class LinearSearchDemo8{9public static void main(String[] args)10{11int[] a = ArrayUtil.randomIntArray(20, 100);12System.out.println(Arrays.toString(a));13LinearSearcher searcher = new LinearSearcher(a);1415Scanner in = new Scanner(System.in);1617boolean done = false;18while (!done)19{20System.out.print("Enter number to search for, −1 to quit: ");21int n = in.nextInt();22if (n == −1)23done = true;24else25{26int pos = searcher.search(n);27System.out.println("Found in position " + pos);28}29}30}31}
Typical Output
[46, 99, 45, 57, 64, 95, 81, 69, 11, 97, 6, 85, 61, 88, 29, 65, 83, 88, 45, 88] Enter number to search for, −1 to quit: 11 Found in position 8

12. Why can't you use a "for each" loop for (int element : a) in the search method?
Now let us search for an item in a data sequence that has been previously sorted. Of course, we could still do a linear search, but it turns out we can do much better than that.
Consider the following sorted array a. The data set is:
We would like to see whether the value 15 is in the data set. Let's narrow our search by finding whether the value is in the first or second half of the array. The last point in the first half of the data set, a[3], is 9, which is smaller than the value we are looking for. Hence, we should look in the second half of the array for a match, that is, in the sequence:
Now the last value of the first half of this sequence is 17; hence, the value must be located in the sequence:
The last value of the first half of this very short sequence is 12, which is smaller than the value that we are searching, so we must look in the second half:
It is trivial to see that we don't have a match, because 15 ≠ 17. If we wanted to insert 15 into the sequence, we would need to insert it just before a[5].
This search process is called a binary search, because we cut the size of the search in half in each step. That cutting in half works only because we know that the sequence of values is sorted.
The following class implements binary searches in a sorted array of integers. The search method returns the position of the match if the search succeeds, or −1 if v is not found in a.
Note
A binary search locates a value in a sorted array by determining whether the value occurs in the first or second half, then repeating the search in one of the halves.
ch14/binsearch/BinarySearcher.java
1/**2A class for executing binary searches through an array.3*/4public class BinarySearcher5{6private int[] a;78/**9Constructs a BinarySearcher.10@param anArray a sorted array of integers11*/12public BinarySearcher(int[] anArray)13{14a = anArray;15}1617/**18Finds a value in a sorted array, using the binary19search algorithm.20@param v the value to search21@return the index at which the value occurs, or −122if it does not occur in the array23*/
24public int search(int v)25{26int low = 0;27int high = a.length - 1;28while (low <= high)29{30int mid = (low + high) / 2;31int diff = a[mid] - v;3233if (diff == 0) // a[mid] == v34return mid;35else if (diff < 0) // a[mid] < v36low = mid + 1;37else38high = mid - 1;39}40return −1;41}42}
Now let's determine the number of visits to array elements required to carry out a binary search. We can use the same technique as in the analysis of merge sort. Because we look at the middle element, which counts as one visit, and then search either the left or the right subarray, we have
Using the same equation,
By plugging this result into the original equation, we get
That generalizes to
As in the analysis of merge sort, we make the simplifying assumption that n is a power of 2, n = 2m, where m = log2(n). Then we obtain
| T(n) = 1 + log2(n) |
Therefore, binary search is an O(log(n)) algorithm.
That result makes intuitive sense. Suppose that n is 100. Then after each search, the size of the search range is cut in half, to 50, 25, 12, 6, 3, and 1. After seven comparisons we are done. This agrees with our formula, because log2(100) ≈ 6.64386, and indeed the next larger power of 2 is 27 = 128.
Because a binary search is so much faster than a linear search, is it worthwhile to sort an array first and then use a binary search? It depends. If you search the array only once, then it is more efficient to pay for an O(n) linear search than for an O(n log(n)) sort and an O(log(n)) binary search. But if you will be making many searches in the same array, then sorting it is definitely worthwhile.
Note
A binary search locates a value in a sorted array in O(log(n)) steps.
The Arrays class contains a static binarySearch method that implements the binary search algorithm, but with a useful enhancement. If a value is not found in the array, then the returned value is not −1, but −k − 1, where k is the position before which the element should be inserted. For example,
int[] a = { 1, 4, 9 };
int v = 7;
int pos = Arrays.binarySearch(a, v);
// Returns −3; v should be inserted before position 2
14. Why is it useful that the Arrays.binarySearch method indicates the position where a missing element should be inserted?
15. Why does Arrays.binarySearch return −k − 1 and not −k to indicate that a value is not present and should be inserted before position k?
When you write Java programs, you don't have to implement your own sorting algorithms. The Arrays class contains static sort methods to sort arrays of integers and floating-point numbers. For example, you can sort an array of integers simply as
int[] a = ...; Arrays.sort(a);
Note
The Arrays class implements a sorting method that you should use for your Java programs.
That sort method uses the quicksort algorithm—see Special Topic 14.3 on page 611 for more information about that algorithm.
Of course, in application programs, there is rarely a need to search through a collection of integers. However, it is easy to modify these techniques to search through real data.
The Arrays class also supplies a static sort method for sorting arrays of objects. However, the Arrays class cannot know how to compare arbitrary objects. Suppose, for example, that you have an array of Coin objects. It is not obvious how the coins should be sorted. You could sort them by their names, or by their values. The Arrays.sort method cannot make that decision for you. Instead, it requires that the objects belong to classes that implement the Comparable interface. That interface has a single method:
public interface Comparable
{
int compareTo(Object otherObject);
}Note
The sort method of the Arrays class sorts objects of classes that implement the Comparable interface.
The call
a.compareTo(b)
must return a negative number if a should come before b, 0 if a and b are the same, and a positive number otherwise.
Several classes in the standard Java library, such as the String and Date classes, implement the Comparable interface.
You can implement the Comparable interface for your own classes as well. For example, to sort a collection of coins, the Coin class would need to implement this interface and declare a compareTo method:
public class Coin implements Comparable
{
...
public int compareTo(Object otherObject)
{
Coin other = (Coin) otherObject;
if (value < other.value) return −1;
if (value == other.value) return 0;
return 1;
}
...
}When you implement the compareTo method of the Comparable interface, you must make sure that the method defines a total ordering relationship, with the following three properties:
Antisymmetric: If
a.compareTo(b)≤ 0, thenb.compareTo(a)≥ 0Reflexive:
a.compareTo(a)= 0Transitive: If
a.compareTo(b)≤ 0 andb.compareTo(c)≤ 0, thena.compareTo(c)≤ 0
Once your Coin class implements the Comparable interface, you can simply pass an array of coins to the Arrays.sort method:
Coin[] coins = new Coin[n]; // Add coins ... Arrays.sort(coins);
If the coins are stored in an ArrayList, use the Collections.sort method instead; it uses the merge sort algorithm:
ArrayList<Coin> coins = new ArrayList<Coin>(); // Add coins ... Collections.sort(coins);
As a practical matter, you should use the sorting and searching methods in the Arrays and Collections classes and not those that you write yourself. The library algorithms have been fully debugged and optimized. Thus, the primary purpose of this chapter was not to teach you how to implement practical sorting and searching algorithms. Instead, you have learned something more important, namely that different algorithms can vary widely in performance, and that it is worthwhile to learn more about the design and analysis of algorithms.
Note
The Collections class contains a sort method that can sort array lists.

17. What steps would you need to take to sort an array of BankAccount objects by increasing balance?
Describe the selection sort algorithm.
The selection sort algorithm sorts an array by repeatedly finding the smallest element of the unsorted tail region and moving it to the front.
Measure the running time of a method.
To measure the running time of a method, get the current time immediately before and after the method call.
Use the big-Oh notation to describe the running time of an algorithm.
Computer scientists use the big-Oh notation f(n) = O(g(n)) to express that the function f grows no faster than the function g.
Selection sort is an O(n2) algorithm. Doubling the data set means a fourfold increase in processing time.
Insertion sort is an O(n2) algorithm.
Describe the merge sort algorithm.
The merge sort algorithm sorts an array by cutting the array in half, recursively sorting each half, and then merging the sorted halves.
Contrast the running times of the merge sort and selection sort algorithms.
Merge sort is an O(n log(n)) algorithm. The n log(n) function grows much more slowly than n2.
Describe the linear search algorithm and its running time.
A linear search examines all values in an array until it finds a match or reaches the end.
A linear search locates a value in an array in O(n) steps.
Describe the binary search algorithm and its running time.
A binary search locates a value in a sorted array by determining whether the value occurs in the first or second half, then repeating the search in one of the halves.
A binary search locates a value in a sorted array in O(log(n)) steps.
Use the Java library methods for sorting data.
The
Arraysclass implements a sorting method that you should use for your Java programs.The
sortmethod of theArraysclass sorts objects of classes that implement theComparableinterface.The
Collectionsclass contains asortmethod that can sort array lists.
java.lang.Comparable<T> java.util.Collections
compareTo binarySearch
java.lang.System sort
currentTimeMillis java.util.Comparator<T>
java.util.Arrays compare
binarySearch
sort
toStringR14.1 What is the difference between searching and sorting?
R14.2 Checking against off-by-one errors. When writing the selection sort algorithm of Section 14.1, a programmer must make the usual choices of < against <=, a.length against a.length - 1, and from against from + 1. This is a fertile ground for off-by-one errors. Conduct code walkthroughs of the algorithm with arrays of length 0, 1, 2, and 3 and check carefully that all index values are correct.
R14.3 For the following expressions, what is the order of the growth of each?
n2 + 2n + 1
n10 + 9n9 + 20n8 + 145n7
(n + 1)4
(n2 + n)2
n + 0.001n3
n3 − 1000n2 + 109
n + log(n)
n2 + n log(n)
2n + n2
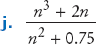
R14.4 We determined that the actual number of visits in the selection sort algorithm is
We characterized this method as having O(n2) growth. Compute the actual ratios
T(2.000)/T(1.000)
T(4.000)/T(1.000)
T(10.000)/T(1.000)
and compare them with
f(2.000)/f(1.000)
f(2.000)/f(1.000)
f(2.000)/f(1.000)
where f(n) = n2.
R14.5 Suppose algorithm A takes 5 seconds to handle a data set of 1,000 records. If the algorithm A is an O(n) algorithm, how long will it take to handle a data set of 2,000 records? Of 10,000 records?
R14.6 Suppose an algorithm takes 5 seconds to handle a data set of 1,000 records. Fill in the following table, which shows the approximate growth of the execution times depending on the complexity of the algorithm.
O(n) | O(n2) | O(n3) | O(nlog(n)) | O(2n) | |
|---|---|---|---|---|---|
1,000 | 5 | 5 | 5 | 5 | 5 |
2,000 | |||||
3,000 | 45 | ||||
10,000 |
For example, because 3,0002/1,0002 = 9, the algorithm would take 9 times as long, or 45 seconds, to handle a data set of 3,000 records.
R14.7 Sort the following growth rates from slowest to fastest growth.
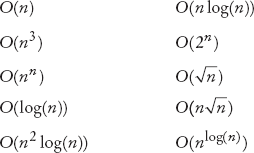
R14.8 What is the growth rate of the standard algorithm to find the minimum value of an array? Of finding both the minimum and the maximum?
R14.9 What is the growth rate of the following method?
public static int count(int[] a, int c)
{
int count = 0;
for (int i = 0; i < a.length; i++)
{
if (a[i] == c) count++;
}
return count;
}R14.10 Your task is to remove all duplicates from an array. For example, if the array has the values
| 4 7 11 4 9 5 11 7 3 5 |
then the array should be changed to
| 4 7 11 9 5 3 |
Here is a simple algorithm. Look at a[i]. Count how many times it occurs in a. If the count is larger than 1, remove it. What is the growth rate of the time required for this algorithm?
R14.11 Consider the following algorithm to remove all duplicates from an array. Sort the array. For each element in the array, look at its next neighbor to decide whether it is present more than once. If so, remove it. Is this a faster algorithm than the one in Exercise R14.10?
R14.12 Develop an O(nlog(n)) algorithm for removing duplicates from an array if the resulting array must have the same ordering as the original array.
R14.13 Why does insertion sort perform significantly better than selection sort if an array is already sorted?
R14.14 Consider the following speedup of the insertion sort algorithm of Special Topic 14.1 on page 604. For each element, use the enhanced binary search algorithm that yields the insertion position for missing elements. Does this speedup have a significant impact on the efficiency of the algorithm?
P14.1 Modify the selection sort algorithm to sort an array of integers in descending order.
P14.2 Modify the selection sort algorithm to sort an array of coins by their value.
P14.3 Write a program that generates the table of sample runs of the selection sort times automatically. The program should ask for the smallest and largest value of n and the number of measurements and then make all sample runs.
P14.4 Modify the merge sort algorithm to sort an array of strings in lexicographic order.
P14.5 Write a telephone lookup program. Read a data set of 1,000 names and telephone numbers from a file that contains the numbers in random order. Handle lookups by name and also reverse lookups by phone number. Use a binary search for both lookups.
P14.6 Implement a program that measures the performance of the insertion sort algorithm described in Special Topic 14.1 on page 604.
P14.7 Write a program that sorts an ArrayList<Coin> in decreasing order so that the most valuable coin is at the beginning of the array. Use a Comparator.
P14.8 Consider the binary search algorithm in Section 14.7. If no match is found, the search method returns −1. Modify the method so that if a is not found, the method returns −k − 1, where k is the position before which the element should be inserted. (This is the same behavior as Arrays.binarySearch.)
P14.9 Implement the sort method of the merge sort algorithm without recursion, where the length of the array is a power of 2. First merge adjacent regions of size 1, then adjacent regions of size 2, then adjacent regions of size 4, and so on.
P14.10 Implement the sort method of the merge sort algorithm without recursion, where the length of the array is an arbitrary number. Keep merging adjacent regions whose size is a power of 2, and pay special attention to the last area whose size is less.
P14.11 Use insertion sort and the binary search from Exercise P14.8 to sort an array as described in Exercise R14.14. Implement this algorithm and measure its performance.
P14.12 Supply a class Person that implements the Comparable interface. Compare persons by their names. Ask the user to input 10 names and generate 10 Person objects. Using the compareTo method, determine the first and last person among them and print them.
P14.13 Sort an array list of strings by increasing length. Hint: Supply a Comparator.
P14.14 Sort an array list of strings by increasing length, and so that strings of the same length are sorted lexicographically. Hint: Supply a Comparator.
Project 14.1 Write a program that keeps an appointment book. Make a class Appointment that stores a description of the appointment, the appointment day, the starting time, and the ending time. Your program should keep the appointments in a sorted array list. Users can add appointments and print out all appointments for a given day. When a new appointment is added, use binary search to find where it should be inserted in the array list. Do not add it if it conflicts with another appointment.
Project 14.2 Implement a graphical animation of sorting and searching algorithms. Fill an array with a set of random numbers between 1 and 100. Draw each array element as a bar, as in Figure 3. Whenever the algorithm changes the array, wait for the user to click the Step button, then call the repaint method. The Run button should run the animation until the animation has finished or the user clicks the Step button again.
Animate selection sort, merge sort, and binary search. In the binary search animation, highlight the currently inspected element and the current values of from and to.
Dropping the
tempvariable would not work. Thena[i]anda[j]would end up being the same value.1 | 5 4 3 2 6, 1 2 | 4 3 5 6, 1 2 3 4 5 6
Four times as long as 40,000 values, or about 50 seconds.
A parabola.
It takes about 100 times longer.
If n is 4, then is 8 and is 7.
When the preceding
whileloop ends, the loop condition must be false, that is,iFirst >= first.lengthoriSecond >= second.length(De Morgan's Law).First sort 8 7 6 5. Recursively, first sort 8 7. Recursively, first sort 8. It's sorted. Sort 7. It's sorted. Merge them: 7 8. Do the same with 6 5 to get 5 6. Merge them to 5 6 7 8. Do the same with 4 3 2 1: Sort 4 3 by sorting 4 and 3 and merging them to 3 4. Sort 2 1 by sorting 2 and 1 and merging them to 1 2. Merge 3 4 and 1 2 to 1 2 3 4. Finally, merge 5 6 7 8 and 1 2 3 4 to 1 2 3 4 5 6 7 8.
Approximately 100,000 · log(100,000) / 50,000 · log(50,000) = 2 · 5 / 4.7 = 2.13 times the time required for 50,000 values. That's 2.13 · 97 milliseconds or approximately 207 milliseconds.
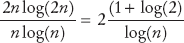
On average, you'd make 500,000 comparisons.
The
searchmethod returns the index at which the match occurs, not the data stored at that location.You would search about 20. (The binary log of 1,024 is 10.)
Then you know where to insert it so that the array stays sorted, and you can keep using binary search.
Otherwise, you would not know whether a value is present when the method returns 0.
The
Rectangleclass does not implement theComparableinterface.The
BankAccountclass would need to implement theComparableinterface. ItscompareTomethod must compare the bank balances.