Decimal notation represents numbers as powers of 10, for example
There is no particular reason for the choice of 10, except that several historical number systems were derived from people's counting with their fingers. Other number systems, using a base of 12, 20, or 60, have been used by various cultures throughout human history. However, computers use a number system with base 2 because it is far easier to build electronic components that work with two values, which can be represented by a current being either off or on, than it would be to represent 10 different values of electrical signals. A number written in base 2 is also called a binary number.
For example,
For digits after the "decimal" point, use negative powers of 2.
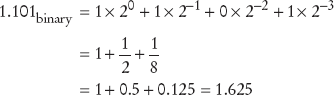
In general, to convert a binary number into its decimal equivalent, simply evaluate the powers of 2 corresponding to digits with value 1, and add them up. Table 1 shows the first powers of 2.
To convert a decimal integer into its binary equivalent, keep dividing the integer by 2, keeping track of the remainders. Stop when the number is 0. Then write the remainders as a binary number, starting with the last one.
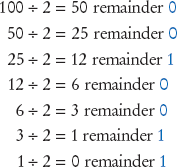
Therefore, 100decimal = 1100100binary.
Conversely, to convert a fractional number less than 1 to its binary format, keep multiplying by 2. If the result is greater than 1, subtract 1. Stop when the number is 0. Then use the digits before the decimal points as the binary digits of the fractional part, starting with the first one. For example,
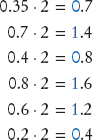
Here the pattern repeats. That is, the binary representation of 0.35 is 0.01 0110 0110 0110. . .
To convert any floating-point number into binary, convert the whole part and the fractional part separately.
To represent negative integers, there are two common representations, called "signed magnitude" and "two's complement". Signed magnitude notation is simple: use the leftmost bit for the sign (0 = positive, 1 = negative). For example, when using 8-bit numbers,
| − 13 = 10001101signed magnitude |
However, building circuitry for adding numbers gets a bit more complicated when one has to take a sign bit into account. The two's complement representation solves this problem.
To form the two's complement of a number,
Flip all bits.
Then add 1.
For example, to compute −13 as an 8-bit value, first flip all bits of 00001101 to get 11110010. Then add 1:
| − 13 = 11110011two's complement |
Now no special circuitry is required for adding two numbers. Simply follow the normal rule for addition, with a carry to the next position if the sum of the digits and the prior carry is 2 or 3. For example,

But only the last 8 bits count, so +13 and −13 add up to 0, as they should.
In particular, −1 has two's complement representation 1111 ... 1111, with all bits set.
The leftmost bit of a two's complement number is 0 if the number is positive or zero, 1 if it is negative.
Two's complement notation with a given number of bits can represent one more negative number than positive numbers. For example, the 8-bit two's complement numbers range from −128 to +127.
This phenomenon is an occasional cause for a programming error. For example, consider the following code:
byte b = ...; if (b < 0) b = (byte) -b;
This code does not guarantee that b is nonnegative afterwards. If b happens to be −128, then computing its negative again yields −128. (Try it out—take 10000000, flip all bits, and add 1.)
The Institute for Electrical and Electronics Engineering (IEEE) defines standards for floating-point representations in the IEEE-754 standard. Figure 1 shows how single-precision (float) and double-precision (double) values are decomposed into
A sign bit
An exponent
A mantissa
Floating-point numbers use scientific notation, in which a number is represented as
| b0·b1b2b3...2e |
In this representation, e is the exponent, and the digits b0·b1b2b3... form the mantissa. The normalized representation is the one where b0 ≠ 0. For example,
| 100decimal = 1100100binary = 1.100100binary × 26 |
Because in the binary number system the first bit of a normalized representation must be 1, it is not actually stored in the mantissa. Therefore, you always need to add it on to represent the actual value. For example, the mantissa 1.100100 is stored as 100100.
The exponent part of the IEEE representation uses neither signed magnitude nor two's complement representation. Instead, a bias is added to the actual exponent. The bias is 127 for single-precision numbers, 1023 for double-precision numbers. For example, the exponent e = 6 would be stored as 133 in a single-precision number.
Thus,
In addition, there are several special values. Among them are:
Zero: biased exponent = 0, mantissa = 0.
Infinity: biased exponent = 11...1, mantissa = ±0.
NaN (not a number): biased exponent = 11...1, mantissa ≠ ±0.
Because binary numbers can be hard to read for humans, programmers often use the hexadecimal number system, with base 16. The digits are denoted as 0, 1, ..., 9, A, B, C, D, E, F (see Table 2).
Four binary digits correspond to one hexadecimal digit. That makes it easy to convert between binary and hexadecimal values. For example,
In Java, hexadecimal numbers are used for Unicode character values, such as u03B1 (the Greek lowercase letter alpha). Hexadecimal integers are denoted with a 0x prefix, such as 0x3B1.

