Chapter 15
Mathematical Modeling of Mediated Amperometric Enzyme Sensors
A general discussion of enzyme sensor modeling has been presented in Chapter 04 where it has been assumed that the sensor response is proportional to the product concentration at the transducer surface. This condition can be fulfilled in the case of certain first-generation amperometric enzyme sensors. However, the mechanism of mediated amperometric enzyme sensors clearly deviates from the above assumption as the mediator is involved in a series of processes such as diffusion, reaction with the enzyme and the electrochemical reaction. That is why modeling of mediated amperometric enzyme sensors is a distinct problem, which is comprehensively reviewed in the literature [1–4].
This chapter introduces the principles of amperometric enzyme sensor modeling in two limiting cases depending on the location of the diffusion layer, namely the external diffusion and the internal diffusion cases.
In the external diffusion case, substrate diffusion is localized out of the sensing layer, within a membrane or within the diffusion layer formed in the solution when the solution is in direct contact with the enzyme layer. No diffusion processes occur within the enzyme layer.
The internal diffusion case is characterized by the fact that the enzyme reaction produces concentration gradients within the enzyme layer. Hence, diffusion occurs in parallel with the enzymatic reaction. This model assumes that no concentration gradients appear in the solution phase.
15.1 External Diffusion Conditions
This section addresses the modeling of mediated amperometric sensors under the assumption that the sensor functions under external diffusion control.
As discussed in Chapter 5, in the case of an enzyme sensor functioning under external diffusion conditions, the compounds present within the enzyme layer are uniformly distributed and no diffusion occurs within this film. A diffusion barrier is met out of the enzyme layer, within the external membrane or, when the membrane is absent, within the diffusion layer that develops in the solution phase near the sensing film. Such a situation arises when the thickness of the enzyme layer is sufficiently small and the substrate diffusion coefficient within this region is very high. These conditions are best fulfilled when the biocatalytic film consists of only one or a few molecular layers [5–7].
15.1.1 Model Formulation
The physical model used in the present approach is shown in Figure 15.1. The sensing element includes the enzyme and a mediator, both entrapped between an external membrane and the working electrode. The working electrode acts as electron collector and, in conjunction with a counterelectrode, it allows current to flow across the system.
Figure 15.1 Schematic presentation of the processes occurring in a mediated amperometric enzyme sensor under external diffusion conditions. Symbols in parentheses indicate concentrations of relevant species symbolized by capital letters.
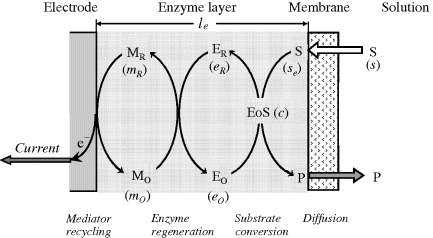
Reactions emphasized in Figure 15.1 can be formulated as follows:
(15.4) 
In this process, the substrate (S) is converted to the product P by an electron exchange involving the oxidized form of the enzyme (
) and going via the intermediate enzyme–substrate complex 
. As a result of this process, a substrate concentration gradient develops across the membrane and prompts the substrate to diffuse from the test solution. It will be assumed that the amount of substrate consumed during the measurement is very low and no noticeable alteration of the bulk concentration occurs. The reduced form of the enzyme (
) formed in reaction (15.2) is next recycled to the oxidized form by an electron-transfer reaction involving the oxidized form of the mediator, 
, (reaction (15.3)). Finally, the reduced mediator (
) produced in the above reaction is recycled by an electrochemical reaction at the electrode. This final reaction produces the current that serves as the sensor response. It will be assumed that the mediator is confined within the sensing layer and that no mediator exists in the test solution.
The overall process consists of an electron transfer from the substrate to the working electrode via two intermediate steps with the enzyme and the mediator acting as successive electron conveyors. Denoting the number of electrons by 
, the overall process can be represented as:
(15.5) 
Therefore, the response current, which is proportional to the absolute value of the substrate flux (J) and the sensor area (A) is given by the following equation:
where F is the Faraday constant.
The goal of the present approach is to derive an equation relating the current to the substrate concentration in solution. As is typical of electrochemical processes, the current is proportional to the overall reaction rate. Therefore, the rate of each step in the sensor process should be considered. The pertinent diffusion fluxes and reaction rates are summarized in Equations (15.7)–(15.10), in which 
is the mass-transfer coefficient of the substrate, 
and 
are the rate constants in reaction (15.1), 
is the rate constant of reaction (15.2), and 
is the rate constant of reaction (15.3). The meaning of concentration symbols is given in Figure 15.1.
In addition, the mass-balance equation (15.11) for the enzyme should be taken into account. In this equation, 
is the total concentration of the enzyme in the sensing layer.
Equations(15.8) and (15.9) are similar to those used in the Michaelis–Menten kinetic approach and need no comment. Conversely, Equation (15.10) deserves a preliminary discussion. This equation includes the concentration of the mediator in the oxidized state but this concentration depends on the electrode potential according to the Nernst equation:
where 
is the standard electrode potential of the mediator redox couple. Upon introducing the total mediator concentration 
, one can derive from Equation (15.12) the following equation relating the 
concentration to the total mediator concentration and the electrode potential:
Accordingly, 
represents the fraction of the total mediator concentration that is present in the oxidized form.
According to Equation (15.13), when the potential shifts from a very negative value with respect to E0 to a very positive one, 
varies from 0 to 1 and 
changes from 0 to 
. Keeping in mind this property, the rate Equation (15.10) can be reformulated as follows:
(15.14) 
As 
is a constant parameter, it is convenient to introduce the pseudofirst-order rate constant 
defined as:
(15.15) 
Upon substitution in Equation (15.10) the reaction rate of enzyme regeneration assumes the following form:
(15.16) 
The above equation shows that the reaction rate of enzyme regeneration is a function of electrode potential. This implies that the flux, and consequently the current, are also dependent on potential and can vary from zero to a limiting value as this parameter varies within a specific region around the standard potential. The best sensitivity is achieved when the reaction (15.3) occurs with maximum velocity and this condition is met if 
is sufficiently positive with respect to 
in order to render 
. Under these limiting conditions, the velocity of enzyme regeneration assumes the following limiting form:
(15.17) 
In the next section, the sensor response under limiting conditions is addressed.
15.1.2 Sensor Response: Limiting Cases
It will be assumed in this section that the electrode potential is sufficiently positive so as to render 
so that the substrate flux assumes its limiting value 
. As the current is proportional to the substrate flux, the next discussion focuses on the correlation between the flux and the substrate concentration. To this end, it will be assumed that the sensor functions under steady-state conditions, in which the flux equates the reaction rates transposed in a surface-normalized form. As indicated in Section 4.2.2, the surface-normalized reaction rate represents the reaction rate occurring at a sensor of unit surface area such that the reaction volume is numerically equal to the thickness of the enzyme layer, 
. Under these circumstances, the steady-state condition can be formulated as follows:
(15.18) 
By substituting appropriate expressions for each reaction rate term one obtains:
Equations(15.19), along with Equation (15.11) form a system of equations with 
, 
, 
and 
as unknowns. By solving for 
the following equation is obtained:
where 
is the Michaelis–Menten constant.
Among the terms in the right-hand side of Equation (15.20), only the first term depends on the diffusion rate via the substrate concentration, the remaining terms being dependent on rate constants only. It is possible therefore to reduce this equation to a simpler form, by assuming that the substrate concentration in the enzyme film is sufficiently low to make the second and third terms negligibly small with respect to the first term. This condition can be fulfilled by securing a very low substrate flux through the external membrane. Under these circumstances, the enzymatic reaction occurs under first-order kinetic conditions and Equation (15.20) turns into the following form, in which 
stands for the limiting flux under pseudofirst-order kinetics:
This equation includes the flux-dependent term 
that can be obtained from Equation (15.7) after substituting 
for 
:
From Equations (15.21) and (15.22) one obtains:
Accordingly, under first-order kinetics, the response is directly proportional to the substrate concentration in the solution phase (s), which is suitable for performing substrate determination. In addition, the response is in this case independent of the kinetics of the enzyme-regeneration (step (15.3)). If the sensor is designed so that 
, the first term in the right-hand side of Equation (15.23) can be disregarded, and the response function turns to the following simple form, where 
represents the limiting flux observed under first-order kinetics and external diffusion control:
is the maximum flux achievable at a given substrate concentration and for specific parameters of the external membrane such as permeability and thickness. In other words, the best sensitivity will be achieved when the enzyme concentration is so high that the response becomes independent of the enzyme loading and the kinetic constants. As these parameters may vary as an effect of pH change, action of activators or inhibitors, or enzyme denaturation, the above conditions make the sensor independent of such effects and bring about the best stability of the calibration parameters. On the other hand, Equation (15.24) demonstrates that the sensor sensitivity depends only on the mass-transfer coefficient of the substrate under the above-mentioned conditions.
It is of interest to examine also the opposite situation in which the sensor response is determined by kinetic factors only. Under these conditions, substrate consumption within the enzyme layer is a slow process as compared with diffusion. This could render 
sufficiently large to make the first term in the right-hand side of Equation (15.20) negligible with respect to the following terms and achieve the zero-order kinetics. Consequently, the limiting flux assumes the particular value 
that corresponds to the zero-order kinetics, and the response function becomes:
where 
is the quotient of 
and 
reaction rates:
In other words, 
represents the turnover number for the substrate conversion relative to that for the enzyme reoxidation. Clearly, under zero-order kinetics, the response is independent of substrate concentration in the solution phase. In turn, the response is directly proportional to the total enzyme concentration within the enzyme layer. This kind of response is useful when the enzyme is employed as a label tag for an electrochemically inactive analyte, such as an antibody. These conditions are also convenient when the sensor is designed for inhibitor determination. Equations (15.25) and (15.26) prove, at the same time, that the response is also depend on the mediator concentration that is included in the pseudofirst-order constant 
. However, if this concentration is sufficiently high to make 
, 
becomes negligible with respect to unity and then Equation (15.25) assumes the following limiting form:
(15.27) 
Therefore, at a sufficiently high mediator concentration, the response will not be affected by accidental changes in mediator concentration.
In conclusion, an enzyme amperometric sensor under external diffusion conditions can be designed to respond either to the substrate concentration (first-order kinetics) or the enzyme content within the sensing element (zero-order kinetics). In the second case, the response becomes independent of the mediator concentration if the pseudorate constant 
is much higher than the 
rate constant. This condition can be fulfilled by selecting a mediator characterized by a high 
constant and keeping as high as possible the total concentration of the mediator within the sensing layer.
15.1.3 The Dynamic Range and the Limit of Detection
The previous section proved that a shift from the proportional response range to substrate-independent response could, in principle, be achieved simply by increasing the substrate concentration with no alteration in sensor parameters. Consequently, the response is expected to display an approximately linear trend at low substrate concentrations but it will level off above an yet unspecified limit. As the extent of the proportional range is a very important figure of merit, the following discussion will deal with the effect of sensor design parameters (such as the enzyme loading and the mediator concentration) on the upper limit of the proportional response range. In order to solve this problem, it is necessary to derive a general response equation, with no restrictions in enzyme loading and other sensor characteristics. As in the previous section, this problem will be approached under the limiting condition in which all the mediator is present only in the oxidized form (
). The required equation can be obtained by substituting 
in Equation (15.20) by the following expression derived from Equation (15.7) with Jl instead of J:
(15.28) 
Upon making this substitution and solving for 
, one obtains:
It is easy to realize that the term 
in the above equation is the dimensionless substrate modulus for external diffusion (
), which was introduced in Section 4.2.4. As shown there, 
is the quotient of the rapidity of the enzyme reaction and the rapidity of substrate diffusion. The calculation can be simplified by introducing the dimensionless concentration of the substrate (S), defined as follows:
(15.30) 
Upon substitution of S and 
in Equation (15.29) the response equation becomes:
This is a rather intricate equation in 
but, for practical purposes, it can be simplified by assuming certain particular cases. Recalling the definition of 
, it is seen that the sensor will operate under diffusion control if this parameter is so great than the following condition is fulfilled:
Under such conditions, the flux assumes a limiting value that is first order in substrate concentration:
It is easy to prove that this equation is equivalent to the previously derived Equation (15.23). Equation (15.33) demonstrates that the diffusion-controlled flux, 
, defined in Equation (15.24), will be obtained when 
. So, in this particular case, the sensitivity reaches its maximum value that depends only on the diffusion coefficient and the thickness of the external membrane.
If 
, the response function turns into the limiting form (15.25) that is characteristic of enzyme saturation (zero-order kinetics).
Equation (15.32) yields a rough estimation of the limit of the linear range. More accurately, this limit can be defined as the substrate concentration yielding a response that is 95% of that expected in the case of a linear response. Using Equation (15.31) for the true response and Equation (15.33) for the linear one, it is found that the response is linear if:
(15.34) 
Hence, the limit of the linear range increases with 
but decreases with increasing the 
parameter. It is therefore suitable to design the sensor so that 
and 
. Under these circumstances, the limit of the linear range increases almost proportionally to 
.
The above treatment proves that, in addition to 
, 
plays an essential role in deciding the sensor characteristics.
The effect of sensor parameters on the response function is best illustrated by plotting the response as a function of substrate concentration. To this end, Equation (15.31) will be set in the following form:
where 
represents the particular value of 
for 
, that is:
As the current is proportional to the flux, Equation (15.35) leads to:
where 
is the actual limiting current and 
is the particular value of the limiting current recorded at 
and for 
, in accordance with Equation (15.36).
Equation (15.37) has been used to generate the response curve under selected conditions in order to show the effect of the dimensionless parameters 
and 
(Figure 15.2). Figure 15.2A displays the shape of the response function for various 
values at a very low 
value. It demonstrates that for any value of 
, the response is quasilinear at sufficiently low substrate concentrations, but the linear range expands considerably as the 
parameter increases.
Figure 15.2 (A) Effect of the substrate modulus (
) on the response function at a very low 
value. 
values are indicated on each curve. (B) Effect of the 
ratio on the response function at a constant substrate modulus (
) within the diffusion-control region. 
values are indicated on each curve.
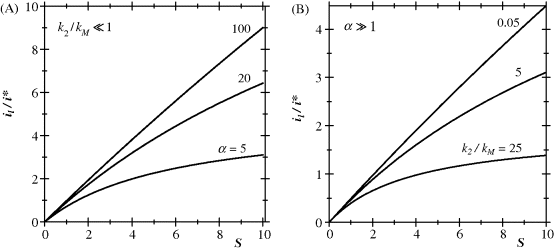
The effect of the 
parameter on the response function at a very high 
value is illustrated in Figure 15.2B. This figure proves that an appreciable increase in the span of the linear range can be obtained if 
is much larger than 
. Such favorable conditions can be achieved if the reoxidation of the enzyme (reaction (15.3)) is much faster that substrate oxidation (reaction (15.2)). Hence, the mediator concentration in the biocatalytic layer should be as high as possible. On the other hand, the proper selection of the mediator itself and its immobilization procedure can affect favorably the actual rate constant of the enzyme reoxidation (
) that is included in 
.
In summary, the best sensitivity and response function for the mediated sensor under external diffusion control is achieved when the sensor process occurs under full diffusion control, with no effect of kinetic parameters and enzyme loading. These conditions are met if the sensor is designed so as to secure a sufficiently high value of the substrate modulus 
and as low as possible a value of the 
ratio. In addition, under these conditions, the maximum stability of the calibration parameters is achieved, as any accidental change in enzyme activity or mediator concentration has no effect on the sensor response.
After discussing the criteria for adjusting the upper limit of the linear response range, it is useful to deal also with its lower limit, which is the limit of detection. To this end, it is worth recalling that the true signal is the electrolytic current, which is proportional to the substrate flux, according to Equation (15.6). In addition to the substrate-related current, a background current may arise as a result of secondary processes (such as electrochemical reactions involving concomitant compounds). In agreement with the general definition, the limit of detection is the concentration yielding a current equal to 3 times the standard deviation of the background fluctuations. It is therefore important to adjust the sensor design and the working conditions such that the background is much lower that the expected response current. This can be achieved by using a semipermeable external membrane that prevents diffusion of interferents.
A simpler method consists of including in the sensor structure a second working electrode coated with the same type of layer as that of the sensing electrode except for the fact that the enzyme is absent. If both electrodes are polarized at the same potential, the second electrode generates only the background current that can be subtracted from the current recorded at the sensing electrode.
15.1.4 Other Theoretical Models
The simple model above enables the derivation of the essential trends in the response dependence on various sensor parameters. A more refined model should consider the stepwise character of reaction (15.2). This reaction may consist of an internal electron transfer between enzyme and substrate within the complex, followed by splitting of the resulting product–enzyme complex to yield the final product and the free enzyme in the reduced form [4, 8]. The approach in [8] takes also into account the effect of enzyme inhibition by the product of the reaction. If the mediator is a soluble species that is present in the test solution, its diffusion to the enzyme layer should also be considered [9, 10].
A modeling of amperometric enzyme electrodes based on direct electron transfer from the enzyme to the electrode is presented in ref. [4].
The advent of nanomaterial application to enzyme sensor prompted the development of theoretical models of such systems. The problem of amperometric enzyme sensors including carbon nanotubes in the catalytic film is addressed in refs. [11, 12]
A fair alternative to the analytical approach to modeling is numerical simulation that can provide relevant information such as concentration profiles and the response value under selected conditions.
15.1.5 Outlook
An amperometric sensor functioning under external diffusion conditions can be built up by assembling a very thin biocatalytic layer including both the enzyme and a mediator. The key parameter of such a sensor is the external modulus factor 
, which represents the rapidity of the enzyme reaction relative to that of the diffusion process. In addition, the sensor behavior depends on 
, the relative turnover of the enzyme reaction with respect to the turnover of the enzyme regeneration. The overall reaction rate depends on the electrode potential, which controls the concentration of the oxidized mediator. In order to maximize sensitivity, the electrode potential should be selected so that the mediator is present only in the oxidized form, which causes the current to assume a limiting, potential-independent value. The limiting current represents the actual sensor response. The limiting current is proportional to the substrate concentration if 
is large enough and 
. If 
, the response becomes independent of the parameters of the biocatalytic layer and the current–concentration proportionality constant depends only on the diffusion coefficient within the external membrane and the thickness of this, both of them being included in the mass-transfer coefficient. This is the highest sensitivity that can be achieved. In addition, under these conditions the response is independent of the parameters of the biocatalytic layer, which imparts to the sensor a very good resilience.
approaches unity if 
V at 25 °C in the absence of any other chemical reaction.
modulus and discuss the effect of each of them on the sensor response under external diffusion control.
on sensitivity.
value effect on the long term stability of the calibration parameters.
. (b) Sensitivity 
is given by the product of two terms: 
and 
, where 
is the electrode surface area. For an activity of 500 μM/min ml, the sensitivity is 0.59 μA/mM. (c) The per cent variation in sensitivity is 
, where 
and 
stand for the initial and final sensitivities, respectively. (d) For an activity of 500 μM/min ml, the limit of detection is 0.05 mM.
or 20 and 
= 10 or 0.1. Calculate the limit of the linear range for each combination of 
and 
values and comment on the effect of these parameters on the extent of the linear response range.
ratio yields the ratio of the correct concentration to the concentration including an error due to the deviation from linearity. Derive an expression for the above flux ratio (answer, 
), equate it with 0.99 and solve for 
in order to find the concentration leading to a 1% deviation from the real one (answer: 
.15.2 Internal Diffusion Conditions
The internal diffusion functioning regime is characterized by the fact that no significant concentration gradients develop within the test solution as a result of the enzymatic reaction. Conversely, within the enzyme layer the concentration of the substrate is nonuniformly distributed, which also results in spatial variations in the velocity of the enzymatic reaction. Such circumstances arise when the enzyme layer is relatively thick and the diffusion coefficient of the substrate within this layer is very low (see Section 4.3 for details).
The approach in this section follows the general lines in refs. [1, 13].
15.2.1 Model Formulation
The structure of the sensor addressed in the present approach is shown in Figure 15.3. Accordingly, the sensor is a three-phase system that consists of a homogeneous biocatalytic layer confined between an electrode and the test solution. Both the enzyme and mediator are entrapped in the catalytic film, with the enzyme firmly bound to the matrix and not free to diffuse. If the mediator is not tightly bound to the matrix, it can travel freely and a true diffusion coefficient DM expresses its mobility. In this case, electrons are conveyed between the enzyme and electrode by free diffusion of the reduced mediator. However, if the mediator is covalently attached to the matrix (as in the case of redox hydrogel systems), the charge gradient induced by the enzymatic reactions causes electrons to move to the electrode surface by stepwise leaps from a reduced mediator molecule to a neighboring oxidized one. Under such circumstances, the diffusion coefficient corresponds to the pseudodiffusion of electrons through the matrix rather than to effective displacement of the mediator molecules.
Figure 15.3 Schematics of an amperometric mediated enzyme sensor with internal diffusion. The mediator is entrapped within the biocatalytic layer along with the enzyme. Thick arrows indicate diffusion. Symbols in parentheses indicate concentrations of relevant species symbolized by capital letters.
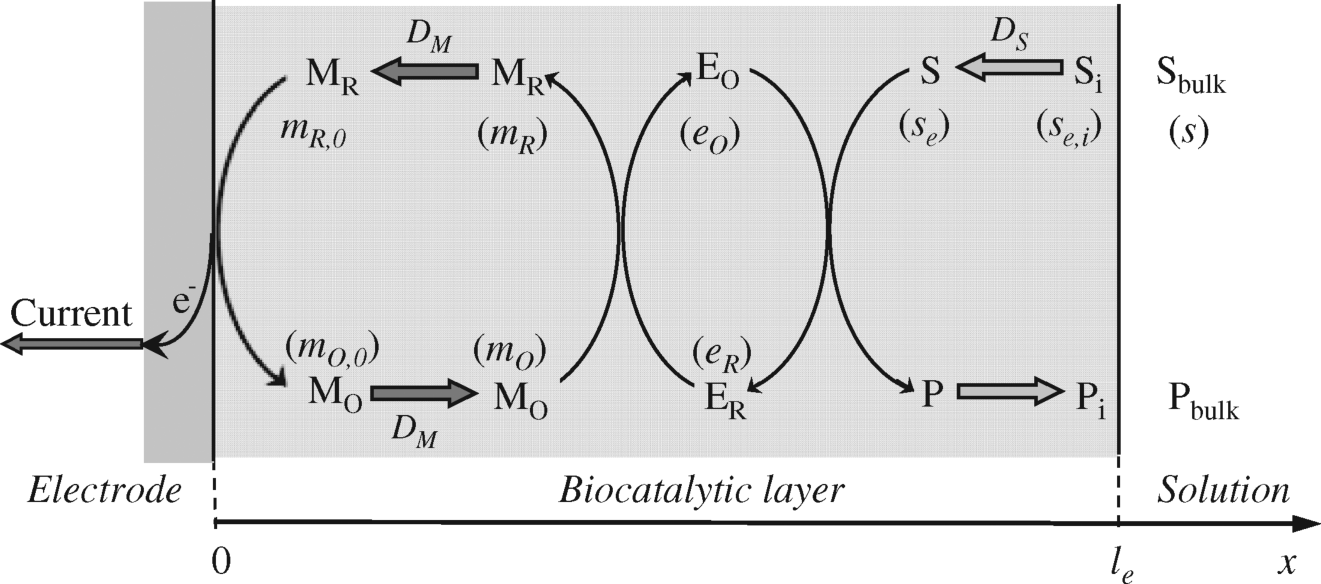
This model does not apply to the case of a conducting entrapment matrix, such as a carbon paste. In this case, electrons are transferred from mediator molecules to conducting particles in order to be further conveyed to the electrode. Such a reaction is heterogeneous in nature and the specific rate constant for mediator–conducting-particle electron transfer should also be introduced.
The chemical reaction sequence consists of substrate conversion followed by enzyme reoxidation according to the two states enzyme mechanism (the ping-pong mechanism):
The pseudorate constant for the reaction (15.38) is, according to the Michaelis–Menten kinetics:
(15.40) 
where 
is the Michaelis–Menten constant. This rate constant turns into the second-order rate constant 
if 
. It should be kept in mind that 
and 
represent here the apparent parameters of the immobilized enzyme that can be different from those characteristic of the enzyme in solution.
As a result of the above chemical reactions, electrons are transferred from the substrate to the mediator. In order to keep the process going, the mediator is reconverted to the active form after diffusing to the electrode surface where electron transfer takes place as follows:
This electrochemical reaction forms the transduction stage that provides the response signal as an electric current.
As this model refers to the case of internal diffusion, it is assumed that no noticeable concentration gradients occur in the solution phase owing to a very fast mass transfer. This condition can be met by vigorous stirring and/or by very low substrate diffusivity within the biocatalytic layer. Diffusion is coupled with chemical reactions; hence, a mathematical description of the process can be made by means of Fick's second equation including an additional term that accounts for reactant consumption. In the steady state, the pertinent equations are:
DS and DM are diffusion coefficients of the substrate and mediator, respectively. The meaning of the concentration symbols is given in Figure 15.3. Fick's equations (15.42) and (15.43) are mass-balance equations and indicate that the amount of diffusing component (left-hand term) equates to the amount of component converted by the enzymatic reaction (right-hand term).
The response current is proportional to the flux at the electrode surface (
) with the proportionality constant 
, so:
(15.44) 
where:
(15.45) 
Therefore, in order to derive the response current, an equation relating the flux to the substrate concentration in the test solution should be derived.
15.2.2 Dimensionless Parameters and Variables
In order to solve this modeling problem, it is necessary to introduce a series of dimensionless parameters and variables that allows the raw differential equations to be converted into more manageable forms. As is commonly the case, dimensionless parameters allow, in addition, the revealing of some important physical characteristics of the system and a better understanding of the behavior of the sensor in response to alterations in its design parameters and working conditions.
The reaction mechanism previously underlined points to two reacting species: the substrate and the mediator. It is important, therefore, to introduce for each reactant a parameter describing its chemical reactivity relative to its diffusivity. Such a parameter was already introduced for the substrate (Section 4.3.1) in the form of the substrate Thiele modulus 
, which, in this case is:
(15.46) 
stands here for the substrate Damköhler number. In other words, 
indicates the capacity of the enzyme to convert the substrate relative to the substrate replenishment capacity.
A similar parameter, 
should also be introduced for the mediator. If we assume that the 
concentration at 
equates to the total mediator concentration (
) and falls to zero at the limit of the film (
), the 
flux is, under the assumption of the Nernst diffusion layer, 
. At the same time, the rate of the reaction (15.39) attains a maximum value when all the enzyme is present in the reduced form (
) and all the mediator is in the oxidized form (
). Therefore, the maximum rate of the reaction (15.39) is:
(15.47) 
Note that this reaction rate is surface normalized. By definition, the Damköhler number for the mediator (
) is:
(15.48) 
Therefore, the mediator Thiele modulus is:
(15.49) 
If we keep in mind that the enzyme reoxidation consists of an electron transfer from the enzyme to the mediator and electrons are then conveyed by mediator diffusion, the physical meaning of 
can be formulated as follows:
(15.50) 
If one of the above 
coefficients is very high, it follows that the rate of the pertinent process (enzyme oxidation or substrate conversion) is diffusion controlled. In the opposite case, kinetic control occurs.
As substrate conversion and enzyme reoxidation occur in sequence, it is important to define a parameter that accounts for their relative rapidity. This is the 
parameter below:
(15.51) 
If we substitute 
for 
and 
for 
, we can realize that 
represents the quotient of the pseudofirst-order rate constant for reaction (15.39) and the pseudofirst order rate constant for reaction (15.38), corrected by the ratio of the diffusion coefficients. The meaning of 
can therefore be phrased as follows:
(15.52) 
The term “capacity” refers here to both the transport and chemical reaction processes that occur sequentially. Thus, the substrate conversion capacity can be limited by either substrate diffusion or the enzymatic conversion step.
The 
parameter compares the conversion and electron-conveying capacities in terms of both rate constants and diffusion coefficients. It disregards the effect of substrate and mediator concentrations that can affect essentially the velocity of chemical reactions. The interplay of these variables can be accounted for by the following dimensionless variable:
The numerator in Equation (15.53) is proportional to the limiting reoxidation rate 
that occurs when both the 
supply and substrate conversion are infinitely fast such that 
and 
, that is, 
. On the other hand, the denominator is proportional to the limiting conversion rate under first-order conditions, which is apparent when both substrate replenishment is infinitely fast (
) and enzyme reoxidation is extremely rapid (
). In this case, the rate of conversion is 
. Consequently:
(15.54) 
So, 
indicates the enzyme reoxidation capacity relative to the substrate conversion capacity in the absence of any diffusion limitation. It depends on experimental conditions via 
and on the sensor design characteristics, via 
.
It is evident that each of the dimensionless parameters introduced above compares the rapidity of two successive steps occurring in the overall sensor process. The applicability of the above-defined dimensionless parameters to various step combinations in the sensor process is demonstrated in Figure 15.4.
Figure 15.4 Applicability of dimensionless parameters to various step combinations in the overall sensor process.
15.2.3 Limiting Conditions
In order to solve the differential equations it is essential to define the limiting conditions, i.e. the physical state at the electrode interface (
) and at the external limit of the biocatalytic layer (
). So, at 
, the substrate is not yet converted and its concentration depends only on the partition coefficient (
) as 
. In the next treatment, the partition will be neglected for simplicity, hence 
.
At the opposite limit (
), reaction (15.41) takes place, allowing electrons to be transferred further to the external electronics to provide the response signal. It will be assumed that the electrochemical reaction proceeds reversibly and, consequently, the Nernst equation with respect to interface concentrations (
and 
) is obeyed:
(15.55) 
Therefore, the molar fraction of 
at the interface is:
(15.56) 
If the mass balance of the mediator is formulated as:
(15.57) 
then, the concentration of the oxidized mediator at the electrode surface is given by:
(15.58) 
The electrode potential is the driving force of the overall process. It determines the interface concentration of 
and, therefore, the rate of 
replenishment. The electrode, by means of the electrode potential, acts as a valve that controls the pace of the overall process between two limits: zero reaction rate if 
and the limiting reaction rate at 
. If the electrochemical reaction of the mediator is fast (reversible), the change between the above limits occurs over a potential span of several tens of millivolts.
15.2.4 Solving the Differential Equations. The Case Diagram
Upon substituting dimensionless parameters and variables in Equations (15.42) and (15.43) one obtains new differential equations that are more manageable as they put into evidence very clearly various approximate forms that can be solved analytically. Each approximate case is defined by some constraints imposed on relevant dimensionless parameters. Thus, the constraint 
implies that the enzyme reoxidation is very sluggish with respect to mediator diffusion and the overall reaction rate is determined by the backoxidation of the enzyme, that is, the process is mediator controlled. This situation occurs if substrate conversion is very rapid as compared with the enzyme reoxidation, which implies 
. The above restrictions identify therefore a kinetic regime in which the overall kinetics is mediator controlled, with no kinetic effects from enzyme reoxidation and substrate diffusion processes. However, if 
, the mediator diffusion is very sluggish with respect to enzyme reoxidation and acts as the rate-determining step if additional restrictions are fulfilled.
Various cases defined as above are displayed on the kinetic case diagram in Figure 15.5. Clearly, the kinetic regime depends on all dimensionless parameters involved in the mathematical model. In order to plot a handy, two-dimensional case diagram, two parameters are selected as variables and the remaining parameters are presumed to be constant. For example, Figure 15.5 was plotted under the assumption that 
and 
are variable whereas 
is constant and 
(in order to secure first-order kinetics for the substrate conversion). Similar diagrams can be plotted for various combinations of constant and variable parameters in order to explore the kinetic behavior of the sensor. As far as the diagram in Figure 15.5 is concerned, any change in either 
or 
affects both the position and extent of each region.
Figure 15.5 Two-dimensional case diagram for 
(equal conversion and reoxidation capacities), 
and 
(limiting response conditions). Adapted with permission from [13]. Copyright 1995 Elsevier.
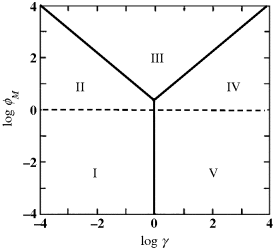
Among the five kinetic cases displayed in Figure 15.5 several selected cases of particular relevance to sensor applications will be discussed in the following sections.
15.2.5 Kinetic Currents
Cases I and V are clearly seen on the lower part of the case diagram in Figure 15.5, at very low values of both the mediator and substrate Thiele coefficients, i.e. 
and 
. Accordingly, diffusion of both mediator and substrate are very fast relative to the relevant chemical reaction. Taking into account the definition of the 
coefficients, it is obvious that these conditions are met if both the enzyme and the mediator loading are very low and the film is very thin. Under these conditions, fast diffusion allows concentrations of both substrate and oxidized mediator to achieve a uniform distribution throughout the film Therefore, 
and 
at any point within the sensing film. As a consequence, the overall reaction rate is dictated by chemical reaction steps and the process occurs under kinetic control. That is why the current generated under these conditions is a kinetic current. This case has been termed the thin-film approximation for internal diffusion because the distance a substrate molecule can travel before being converted is much greater than the film thickness. The same argument applies to the diffusion of charge. This case should not be confused with the thin-film model for external diffusion conditions, discussed above in Section 15.1.
15.2.6 Diffusion Currents
Diffusion control becomes evident when either 
or 
or both are much greater than unity, which implies slow diffusion of the substrate or the mediator or both. The last of the above three possibilities, which pertains to case III in Figure 15.5, proved to be the most convenient from the standpoint of sensor calibration and will be discussed in detail next.
Concentration profiles in case III are schematically drawn in Figure 15.6 where both the substrate and oxidized mediator (
) become depleted within specific boundary regions of the catalytic film. Of course, substrate conversion cannot proceed in such zones, where diffusion is the sole occurring process. Substrate conversion takes place only in the midreaction zone, where both reactants (that is, the substrate and the oxidized mediator) are present. Reactant concentrations can match each other in the middle of the reaction zone, but at the extremities, one of them falls to negligible values. The lowest-concentration reactant determines the kinetics in the pertinent segment. So, the process is mediator controlled (MC) at the right boundary of the reaction zone but proceeds under substrate control (SC) at the opposite side, whereas mixed control occurs within the midpart of the reaction zone.
Figure 15.6 Schematics of concentration profiles for substrate (solid line) and mediator (broken line) through the biocatalytic film in case III, for 
, 
and limiting current conditions (
). Relative concentrations: 
; 
(partition neglected). SC = substrate controlled kinetics; MC = mediator-controlled kinetics. Arrows indicate the shift of the reaction zone in response to 
or 
modification.
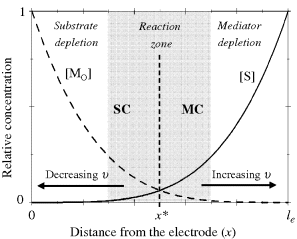
Concentration profiles in Figure 15.6 are symmetrical in this particular case in which it is assumed that both 
and 
are unity. This implies that substrate and mediator flux balance each other (i.e., 
). At the same time substrate conversion and enzyme reoxidation balance each other as 
. In general, the position of the reaction zone is determined by the replenishment factor defined as:
(15.59) 
Accordingly, the replenishment factor represents the promptness of substrate supply to the reaction zone, relative to the rapidity of the mediator supply.
As demonstrated in [13], the position of the reaction zone (indicated by x* in Figure 15.4) is determined by the supply factor according to:
(15.60) 
This equation demonstrates that the reaction zone shifts to the limits of the enzyme layer when 
deviates from unity. If the relative substrate supply is sluggish (
), the reaction will occur at the external periphery (
), whereas the remaining part of the catalytic slab can act as a replacement reserve to compensate for gradual decay of the exposed enzyme. However, too sluggish substrate supply causes the kinetics to shift to case IV in Figure 15.5, where the reaction is substrate controlled all across the catalytic layer.
Conversely, with a fast substrate supply (
), the reaction will occur near the electrode surface and, at very high 
, the process becomes mediator controlled all through the film (case II in Figure 15.5). Note that the supply factor depends not only on the 
ratio but also on the electrode potential, via the 
term. The actual kinetics under limiting-current conditions can be inferred by setting 
.
The diffusion current (
) recorded under case III conditions is a linear function of the substrate concentration, as follows [1]:
(15.61) 
So, the sensitivity is inversely proportional to the thickness of the biocatalytic slab and is independent of the rate constants and the enzyme or mediator concentrations. This is especially convenient when performing substrate determinations. However, the response includes also a substrate-independent term that is proportional to the mediator concentration. Therefore, the response is dependent on two calibration parameters. Stringent limits of applicability of this response function are imposed by the conditions determining the occurrence of case III, namely, the supply factor should be located somewhere between 0.1 and 10 in order to avoid the kinetics from shifting the system to cases II or IV. Optimization of the response range depends on the interplay of substrate and mediator concentrations.
If partition cannot be neglected, 
in the response function should by corrected by the partition coefficient which means that the sensitivity is affected by partition.
In short, case III is characterized by a convenient response function, but care should be exercised in order to prevent the kinetics from shifting to cases II or IV. In each of these cases, the response is a function of 
and depends in addition on rate constants and both enzyme and mediator loading [1]. The main optimization parameters are the substrate and mediator concentrations that should be selected so as to render the supply factor close to unity. Consequently, the linear response range cannot be expected to exceed one order of magnitude.
15.2.7 Outlook
This section gave an insight into the inherent complexity of the processes occurring in a mediated amperometric enzyme sensor. Despite this intricacy, theory provides useful guidelines for selecting design parameters and working conditions that secure a convenient response function. Such conditions can be met by operating the sensor under kinetic control, (case V) and nonsaturated enzyme kinetics. The sensitivity in this case can be adjusted by means of the enzyme loading but, at the same time, the response will be affected by enzyme decay or inhibition. A diffusion-limited current (case III) is obtained at high enzyme and mediator loadings, with the additional condition of a supply factor close to unity. The sensitivity depends in this case on the substrate diffusion coefficient and the thickness of the enzyme layer but is free of effects from kinetic parameters and enzyme or mediator concentrations. Consequently, this regime allows the sensor to be almost insensitive to small temperature or pH fluctuations and also not to be affected by partial enzyme inactivation.
Following the treatment in [13], it was assumed here that a mediator molecule can accept two electrons. The case of a single-electron mediator was considered in [14]. On the other hand, it was assumed in this section that the enzyme–mediator reaction is a single-step process. A further refinement can be introduced by assuming that the enzyme–mediator reaction proceeds according to the Michaelis–Menten kinetics as was assumed in ref. [15] for the case for a solution-dissolved mediator.
Although the immobilized mediator design is the most convenient format, the case of the solution-dissolved mediator is also of interest for both mechanistic investigation and for some practical applications. Sensor modeling under these conditions has been reviewed in refs. [16, 17] (which also includes sections profiled on immobilized mediator sensors).
1. Bartlett, P.N., Toh, C.S., Calvo, E.J. et al. (2008) Modelling biosensor response, in Bioelectrochemistry: Fundamentals, Experimental Techniques and Applications (ed. P.N. Bartlett), John Wiley & Sons, Chichester, pp. 267–325.
2. Eddowes, M.J. (1990) Theoretical methods for analysing biosensor performance, in Biosensors: A Practical Approach (ed. A.E.G. Cass), IRL Press, Oxford, pp. 211–263.
3. Bartlett, P.N., Tebbutt, P., and Whitaker, R.G. (1991) Kinetic aspects of the use of modified electrodes and mediators in bioelectrochemistry, in Progress in Reaction Kinetics (ed. G. Porter), Pergamon Press, London, pp. 55–155.
4. Albery, W.J. and Craston, D.H. (1987) Amperometric enzyme electrodes: theory and experiment, in Biosensors: Fundamentals and Applications (eds I. Karube, G.S. Wilson, and A.P.F. Turner), Oxford University Press, Oxford, pp. 180–210.
5. Gooding, J.J., Hall, E.A.H., and Hibbert, D.B. (1998) From thick films to monolayer recognition layers in amperometric enzyme electrodes. Electroanalysis., 10, 1130–1136.
6. Gooding, J.J. and Hibbert, D.B. (1999) The application of alkanethiol self-assembled monolayers to enzyme electrodes. TrAC-Trends Anal. Chem., 18, 525–533.
7. Willner, I. and Katz, E. (2000) Integration of layered redox proteins and conductive supports for bioelectronic applications. Angew. Chem. Int. Ed., 39, 1180–1218.
8. Albery, W.J. and Bartlett, P.N. (1985) Amperometric enzyme electrodes. 1. Theory. J. Electroanal. Chem., 194, 211–222.
9. Lyons, M.E.G. (2003) Mediated electron transfer at redox active monolayers. Part 4: Kinetics of redox enzymes coupled with electron mediators. Sensors, 3, 19–42.
10. Baronas, R. and Kulys, J. (2008) Modelling amperometric biosensors based on chemically modified electrodes. Sensors, 8, 4800–4820.
11. Lyons, M.E.G. (2009) Transport and kinetics at carbon nanotube - redox enzyme composite modified electrode biosensors. Int. J. Electrochem. Sci., 4, 77–103.
12. Lyons, M.E.G. (2009) Transport and kinetics at carbon nanotube -redox enzyme composite modified electrode biosensors Part 2. Redox enzyme dispersed in nanotube mesh of finite thickness. Int. J. Electrochem. Sci., 4, 1196–1236.
13. Bartlett, P.N. and Pratt, K.F.E. (1995) Theoretical treatment of diffusion and kinetics in amperometric immobilized enzyme electrodes.1. Redox mediator entrapped within the film. J. Electroanal. Chem., 397, 61–78.
14. delle Noci, S., Frasconi, M., Favero, G. et al. (2008) Electrochemical kinetic characterization of redox mediated glucose oxidase reactions: A simplified approach. Electroanalysis., 20, 163–169.
15. Limoges, B., Moiroux, J., and Saveant, J.M. (2002) Kinetic control by the substrate and/or the cosubstrate in electrochemically monitored redox enzymatic homogeneous systems. Catalytic responses in cyclic voltammetry. J. Electroanal. Chem., 521, 1–7.
16. Bourdillon, C., Demaille, C., Moiroux, J. et al. (1996) From homogeneous electroenzymatic kinetics to antigen-antibody construction and characterization of spatially ordered catalytic enzyme assemblies on electrodes. Accounts Chem. Res., 29, 529–535.
17. Savéant, J.M. (2006) Enzymatic catalysis of electrochemical reactions, in Elements of Molecular and Biomolecular Electrochemistry, Wiley-Interscience, Hoboken, N.J., pp. 298–347.