Chapter 3: Knowing as Little as Possible about Math

In This Chapter

Getting to know other number systems

Figuring out the differences between bits and bytes

Converting values between number systems

You might be wondering, “Why do I need to read about numbers? I learned them from zero to ten in kindergarten, so what more do I need to know?” Well, mathematicians might just disagree with you. But in this case, you encounter many types of numbers while working with computers and network devices. In this chapter, I give you a primer on those numbers.

You are probably used to the Base 10 (decimal) number system, which has the ten numerals you are familiar with in it (0–9). This chapter introduces you to the limited Base 2 (binary), the Base 8 (octal), and the larger Base 16 (hexadecimal). With the familiar Base 10 number system having 10 numerals, you may already be thinking that the Base 2 number system only has two numerals; if that is the case, then you are correct. The two numerals in the Base 2 system are zero and one; while the eight numerals in the Base 8 system are zero to seven and the Base 16 number system has sixteen numerals. Wait, how do you get sixteen numerals? With the Base 16 number system, the first ten are your familiar zero to nine, and then you use A, B, C, D, E, and F.

After you complete this chapter, you will have a firm grasp of converting numbers between the different number systems (Base 2, Base 8, Base 10, and Base 16) that are commonly used with computing devices (in fact, those values in the Windows Registry might even make a little more sense). With this knowledge, you will not be quite so confused when you get deeper into routing, switching, and firewall security rules, or subnetting and the device configuration register as you read through this book.

Why These Number Systems Are Important

The main number system in our world is Base 10. I often wonder if we had six fingers whether society would have adopted a Base 6 number system. Although the Base 10 system works great with our body construction and we have become very used to working with it, it does not work equally well with all other things in our environment. Therefore, I discuss the other number systems that you encounter in your work with digital equipment. If you continue to look around computing devices, you start to notice how these values and number systems keep popping up.

Bit is short for binary digit. Binary is another name for the Base 2 number system. Binary, with its two digit values, nicely matches the two electrical states that exist — on and off, or current or no current. All electrical devices, including routers and switches, rely heavily on these two states. All core decisions that a computing device makes come down to true or false decisions, which means these decisions can be manipulated with electrical current.

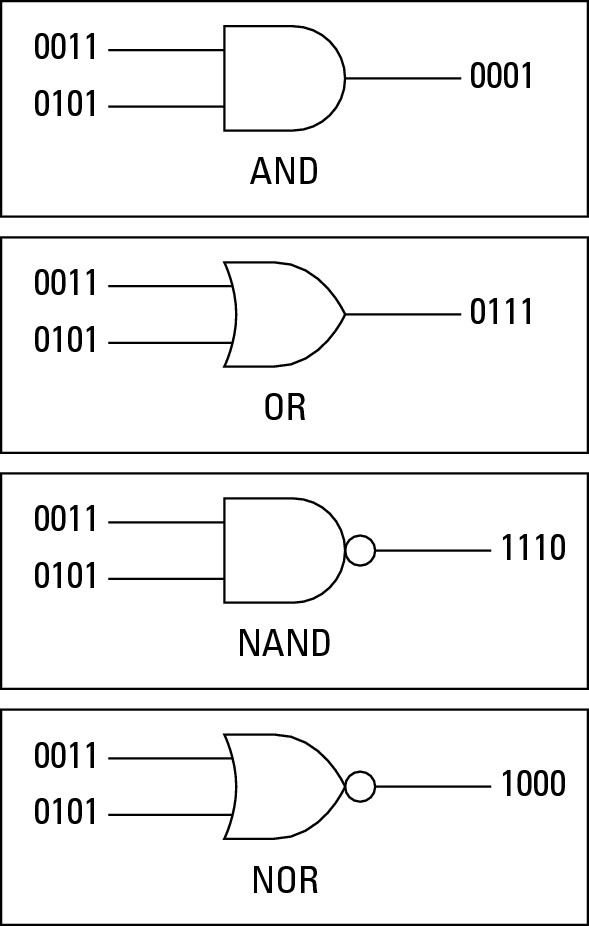
When you look at the logic decision making process, some basic structures are used. These structures are logic gates, which include the following and are shown in Figure 3-1:

• AND: Bits are allowed through the output if both inputs are present. In Figure 3-1, two ones on the two input streams on the left of the gate resulted in a one on the right. The following two sets of digits were both composed of a one and a zero also both resulted in a zero on the right side of the gate for each pair of numbers. With the final set of input values, when there were two zeros in the input streams, the result on the right side of the gate was also a zero.

• OR: Bits are allowed through the output if either input is present. In Figure 3-1, two ones on the two input streams on the left of the gate resulted in a one on the right. The following two sets of digits were both composed of a one and a zero also both resulted in a one on the right side of the gate for each pair of numbers. Only when there were two zeros in the input streams did the result on the right have a zero.

• NAND: Standing for NOT AND, bit results are reversed of the AND. The initial processing of these calculations is identical to the AND processing, but prior to sending the value out of the gate, the value is reversed. So to examine each bit being processed in Figure 3-1, the two ones at the start of the input stream would AND to a result of one; but because this a NOT AND, the value is reversed to a zero in the resultant stream on the right of the gate. Similarly, the next three sets of input values all have at least one zero, which would AND to zero; but because this is a NOT AND, the result is reversed and the resultant stream ends up with three zeros.

• NOR: Standing for NOT OR, bit results are reversed of the OR. To visit Figure 3-1 one last time, this is similar to the NOT AND, in the case that all of the normal results will be reversed. So for the first three pairs of numbers from the two source data streams, there is a one in each pair, so the normal OR process would result in a stream of three ones. Because this is a NOT OR, each of these values is reverse before existing the gate, resulting in a stream of three zeros. The final pair of values in the input streams are two zeros, which would result in an OR of one zero; but because this is a NOT OR, the final result would be a one.

These logic gates are used in computer programming decision-making, but they have been used for basic electrical systems for generations. Writing an entire computer program with just manipulating electrical states to on and off would be confusing and long. Picture Bart Simpson writing lines of ones and zeroes on the chalkboard and then multiply that by a million, and you have some idea how ridiculous that would be.

To complicate things further, all programmers use high-level languages that take away from the zeros and ones so they can work with word length values to tell the computer what to do. A word is a group of bits that are moved as a unit; typically they would be from 8 to 64 bits in length, depending on the operating system. For example, you will often see DWords in the Microsoft Windows registry, which are 32 bit numbers, representing a Double Word length value. This can mean that you are now dealing with a lot more bits. To deal with numbers that take a long time to write, you can convert to different numbering systems. For example, eight binary digits could look like 11111111, but you could convert that into the following number systems:

• Base 8: 377

• Base 10: 255

• Base 16: FF

So using other number formats can save your hand from cramping, especially when writing a 128-bit IPv6 address such as 10010100101001001110011110101000001111111100101010011000111000000011101010100111100001111000011110000000011111011010001111011011. I show you how to convert these numbers in the later sections of this chapter using the base 10 number 215.

You may notice from the previous example that Base 16 looks kind of easy to deal with — you have to write only two characters. For example, 00111111 in Base 2 is 77 in Base 8, or 63 in Base 10. Eight ones give a nice, easy to write and remember Base 16 number FF (two digits with the highest digit values in the Base 16 number system), and six ones gives a nice, easy to write and remember Base 8 number 77 (two digits with the highest digit values in the Base 8 number system). In either case though, the Base 10 number is nothing particularly graceful or spectacular, being 255 in the first example and 63 in the second example. After you get beyond one in Base 10, a lot of numbers are simultaneously memorable in both the Base 2 and Base 10 number systems.

Working with Bits and Bytes

While I said earlier that a binary digit (or bit) is the smallest unit you can work with, it is by far not the most the common. In Table 3-1, I detail the number of binary digits, the number of combinations from that digit, and the value of the last highest-order digit.

Grouping together eight of these bits, which creates a byte, is very common. When converting from binary to decimal, a byte gives you up to 256 possible values ranging from 0 to 255.

If you have been working with computers or Cisco devices, you may notice that many of these numbers seem familiar because many appear as limitations, such as storage limitations based on bit or byte values, within electronic devices. For example, if you create a database, you need to define a storage space that holds a numeral value and is eight bits large, allowing you to store a number from 0 to 255. You see these limitations again and again when working with electronic devices. When working with computers and other electronic devices, you regularly encounter the same numbers as limitations. I dub these numbers naturally occurring binary numbers. Well, they are not truly naturally occurring because a programmer somewhere decided to use that value. Typically, limitations are based on conserving space or memory. As the amounts of memory in devices increases as quickly as it does today, though, memory becomes less of a concern.

Typically when storing data in a computing device, every attempt is made to store data in uniform-sized blocks. Because memory is a binary storage media, you start with a large block, such as 1KB or 1,024 bytes (in computers, you always use binary based numbers, so 1MB is a million or actually 1,048,576 bytes). If you break that 1KB block into even chunks by dividing it by another binary number, then you always end up with another binary number. In some cases, when this does not seem to match, you have some overhead, such as storing delimiter characters, which means a 16-byte storage space may allow you to store a 14–15 character word. That means that the 15-character word still makes sense in a binary storage world.

Take a bit of time and look at your electronics and Table 3-1. You may be surprised how many times these numbers appear.

Pondering the Significance of the Significant Bit

If you have followed along so far, you have read about bits and the maximum number of combinations from a binary number of a certain number of digits. In this section, I take that just a bit further and discuss the significant bit. If you see a binary number, such as 10010011, and you are asked which digit has the greatest value, you would likely say that it is the leftmost digit because people tend to read from left to right. However, in the computing devices world, two systems are in use: The most-used system for networking protocols is big-endian, which treats the leftmost digit as the most significant digit or high-ordered bit; most computer operating systems running x86 and x64 processors use little-endian, which treats the rightmost digit as the high-order bit.

For the purposes of this book, when I discuss the high-order bit or most significant digit, I mean the leftmost digit. When I discuss the low-order bit or least significant digit, I mean the rightmost digit.

Making Conversions

In the “Working with Bits and Bytes” section, earlier in this chapter, I discuss the difference between bits and bytes. Within standard computing systems, a byte is often enough to store data, which is less than eight bits. In cases where the data is greater than a byte, then multiple bytes are required to be used. When working with multi-byte values, in the computing world, the term word is used. As you move from one operating system (OS) to another OS, you will learn that the length of a word is not the same for all operating systems but words are typically 16-bits (2 bytes), 32-bits (4 bytes), or 64-bits (8 bytes) in length. This simply makes defined storage blocks easier to deal with in those operating systems. So in addition to bytes, words also define standard units of binary storage.

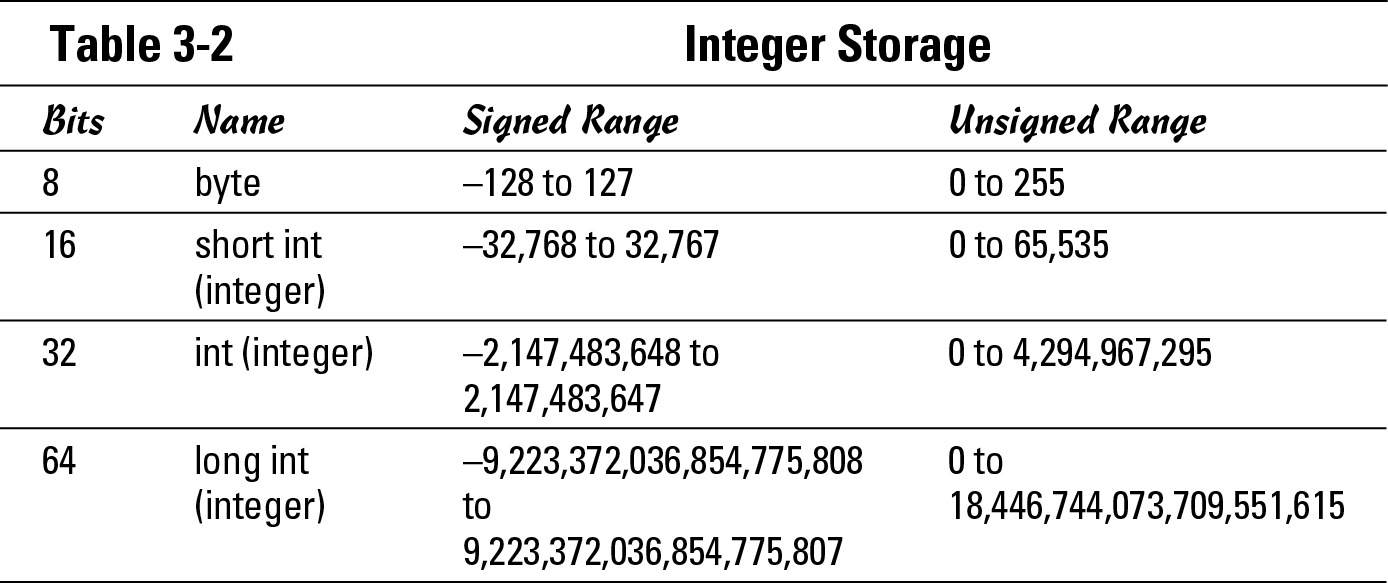
You may be wondering what you can store in these binary storage structures (bits, bytes, and words). A byte is 8 bits in length and can store up to 256 combinations or numbers from 0 to 255. To match this, the American Standard Code for Information Interchange (ASCII) defines a character set, which represents the standard characters or letters that you could type on a keyboard. The ASCII character set has only 256 unique characters or letters, numbered from 0 to 255. Therefore, with a byte being a standard unit of data, it can also represent a single character from the ASCII character set. If you attempt to store a different type of data, you use different amounts of storage. For example, to store a Boolean value, you need only one bit, which would be a zero or a one; whereas to store an integer, you need more space (see Table 3-2).

Converting Base 2 (binary) to Base 10 (decimal)

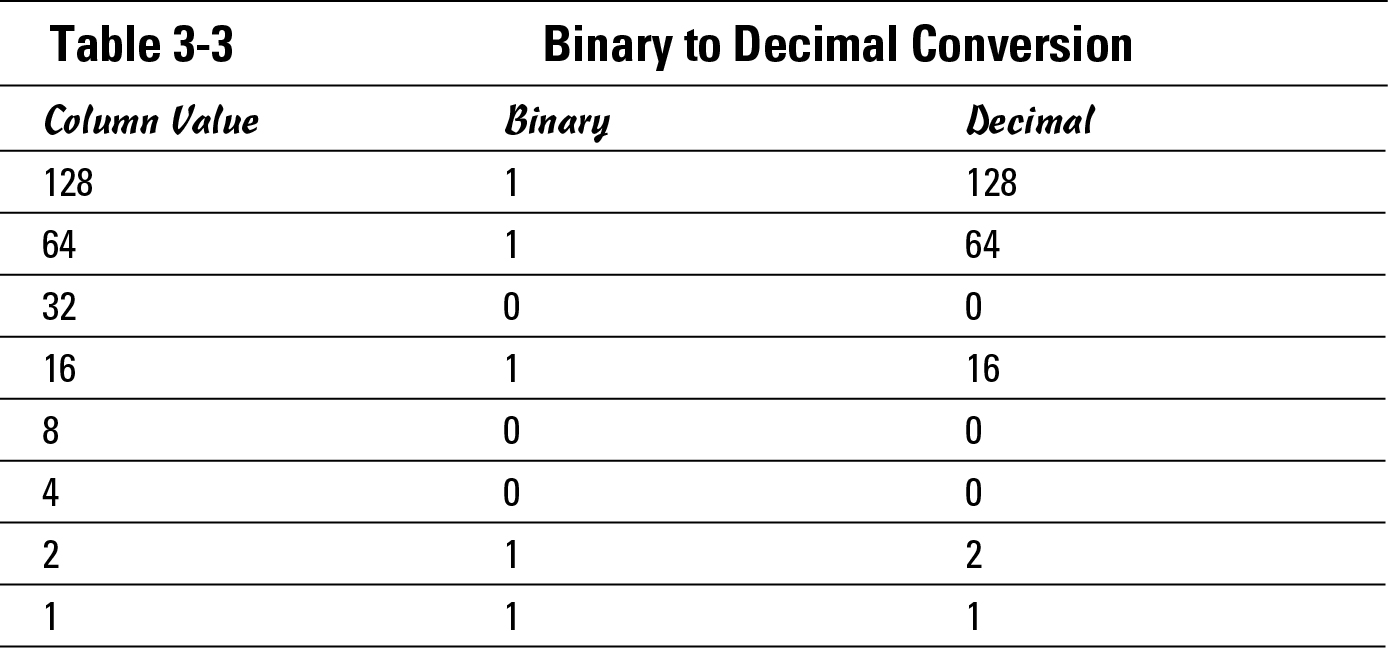
Even though you might not think so, binary to decimal conversions are quite easy. Because many of the binary numbers you work with are in byte (8 bit) length, I work those in the example. A binary number like 10010011 is just like the Base 10 number system, except that each number represents a different column, not 1, 10, 100, 1,000, and so on. These binary numbers represent 1, 2, 4, 8, 16, 32, 64, and 128. Unlike the decimal system in which you have values from zero to nine in each column, with binary, you have only a zero or one in each column. If I start with a one in binary, it will be in first column; if I add another one to that value, I would add one to the first column. Because that exceeds the highest value for the one’s column, I put a zero in the one’s column and carry a one over to the second column (or the two’s column). So in binary, 1+1=10, just like the joke, “There are 10 types of people in the world, those that understand binary and those that do not.”

In Table 3-3, I show you the conversions. If you look at the decimal values, you simply need to total them to get the decimal value of 11010011, or 128 + 64 + 16 + 2 + 1, or 211. See, I told you it was going to be simple. You may become good enough to do that in your head.

The tough part (for me, at least) is going the other way. As a decimal, 215, think of the binary conversion this way: Table 3-4 shows how to convert a base 10 number to a binary number; for simplicity, I have chosen a number that will result in an answer of eight bits or less.

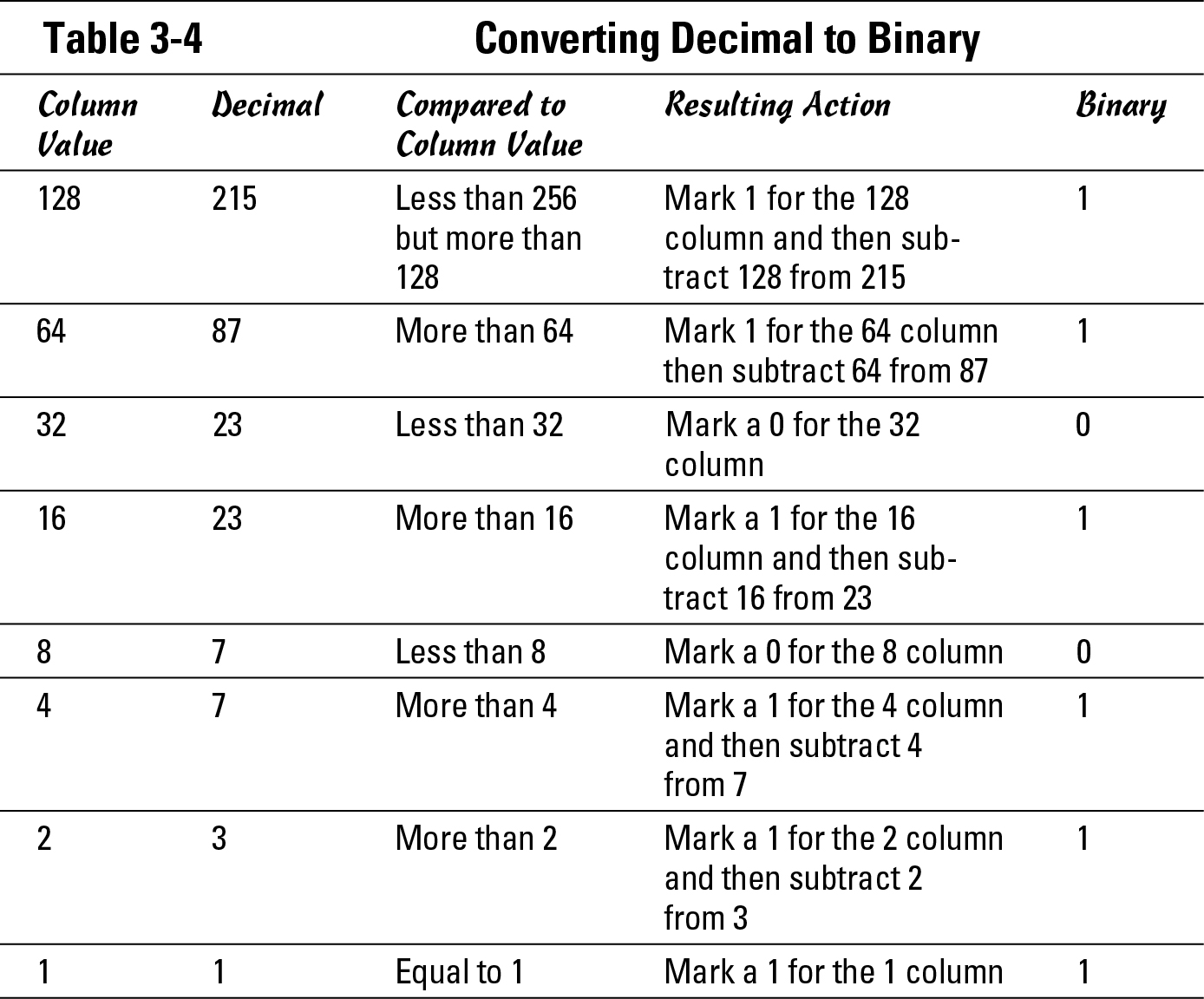
By going through the zeros and ones from top to bottom, the final binary number is 11010111. A zero is given to any position where that number is not present. Not quite as easy as the other way, but still not terribly complicated. If you work through a few numbers, you may find that it does not take long to figure out.

If you want some practice doing binary/decimal conversions quickly and in your head, give some of the Cisco training games a shot, which are available at https://learningnetwork.cisco.com/community/connections/games. One game that is good for binary to decimal conversion (and vice versa) is the Binary Game. This game is a Tetris-like game, as shown in Figure 3-2, in which you need to fill in the missing numbers to clear a row off-screen. When the screen is full, you lose, so work quickly.

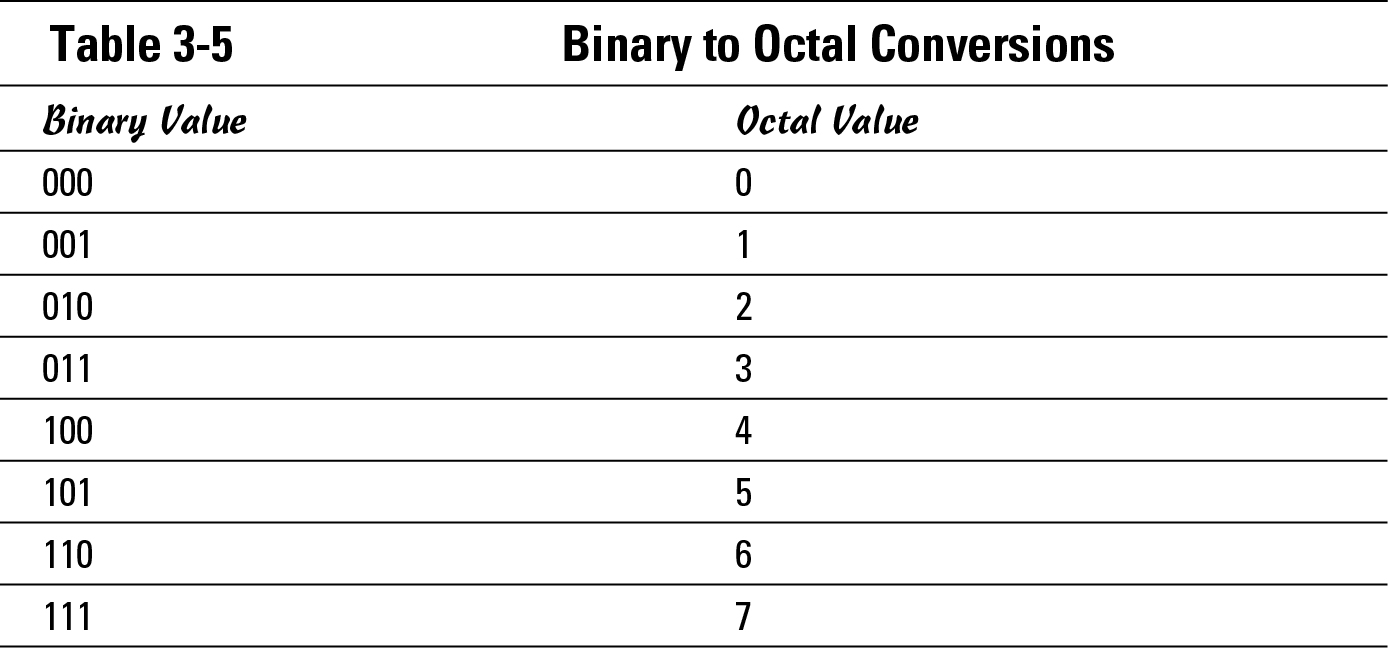
Converting binary to Base 8 (octal)

After you get the hang of binary to decimal conversions (see the preceding section), try converting from binary to octal. Binary to octal conversions are actually even easier. This is due to the fact that octal numbers can be managed by simply grouping your binary numbers in sets of three. For example, start with the binary number, 11010011, from the preceding section, which resulted from the conversion from the decimal number of 215. Because 11010111 is only eight digits, add a leading zero to make this easier: 011010111. By breaking this number into groups of three bits, you get 011, 010, and 111. Each of these three-bit binary numbers can now be converted into a number between zero and seven depending on the positions of the bits (see Table 3-5). After you convert these three groups of bits, your results should be 3 (from 011), 2 (from 010), and 7 (from 111), so the octal number is 327.

If you have been trying the binary to decimal conversions, converting binary numbers to octal, which are only three bits long, is easier.

Converting from octal to binary is not really any more difficult because each octal digit simply expands to three binary digits. For example, if you are given an octal number like 247, break it apart to 2, 4, and 7. Then convert each digit to 010, 100, and 111, giving you a total of 010100111. (Again, I added the leading zero to make life easier.) The byte length value (minus the zero, that is) would be 10100111.

You may be thinking that this was fairly easy; however, it was easy only because binary matches up nicely with octal (Base 8) and hexadecimal (Base 16), as you will see in the next section, but not decimal (Base 10). Remember, 10 works well for humans (maybe because we have ten fingers and toes?), but 10 is not a natural binary number, whereas 4, 8, 16, and 32 are.

Converting binary to Base 16 (hexadecimal)

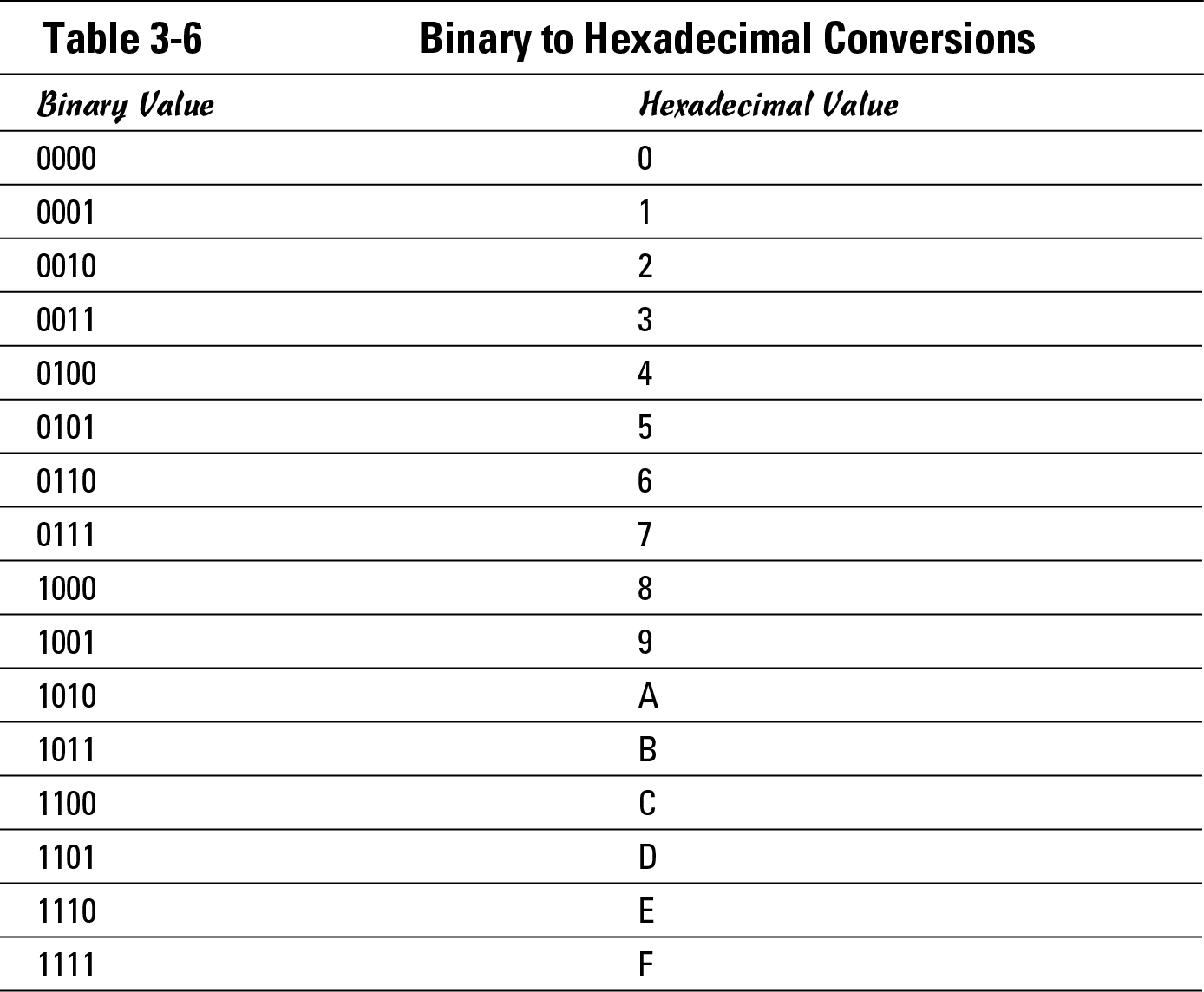
No sense in putting off the last conversion in this chapter — binary to Base 16 (hexadecimal). This conversion is easier than the binary to decimal conversion. The strangest thing about hexadecimal is that there are more than just ten numbers (zero to nine), so you need to use the following extra characters: A (10), B (11), C (12), D (13), E (14), and F (15) with each sequentially representing the extra values.

The easiest way to do the conversion is to again break the binary number in groups. Use the same binary number from earlier sections, 11010011; however, this time, break it into groups of four digits: 1001 and 0011. Each group easily converts into a hexadecimal number between 0 and 15, or 0 and F. Your results should be 13 (from 1001) and 3 (from 0011), so the hexadecimal number is D3. Table 3-6 helps you with these hexadecimal conversions.

Hexadecimal to binary migration is fairly simple. Convert each digit to binary and then concatenate (or join then sequentially end-to-end) the numbers (remember to include all leading zeros). For example, break 9C into 9 and C, and then convert each to binary, yielding 1001 and 1100. The binary number is then 10011100.

The Windows Calculator is capable of making all these conversions for you. To launch the Windows Calculator in Scientific view:

1. Choose Start⇒All Programs⇒Accessories⇒Calculator.

The Calculator opens.

2. Choose View⇒Scientific (or View⇒Programmer if you are using Windows 7).

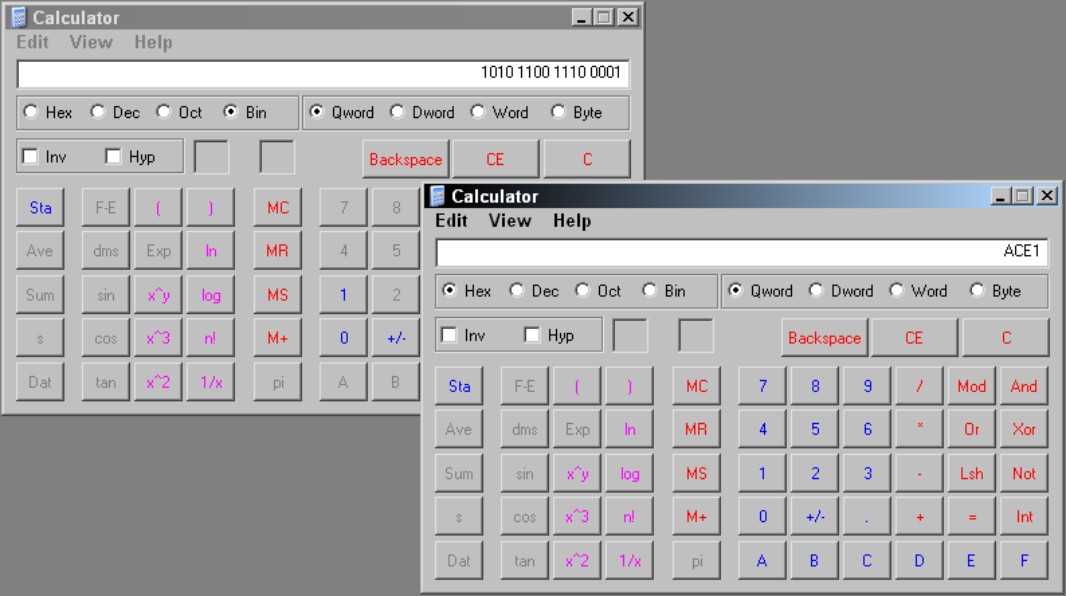
You can also enable Digit Grouping from the View menu to make reading values easier. Figure 3-3 shows a conversion from hexadecimal to binary.

3. To convert from one number system to another, select the Hex, Dec, Oct, or Bin radio button.

For example, to enter a hexadecimal number and convert it to binary, select the Hex radio button. The hexadecimal keys at the bottom of the keyboard are enabled.

4. Type a number and select the Hex, Dec, Oct, or Bin radio button to see the equivalent value.