The easiest way to parallelize data is to take a loop that you already have and handle each item in it in a thread.
This is essentially what pmap does. If you replace a call to map with pmap, it takes each call to the function's argument and executes it in a thread pool. pmap is not completely lazy, but it's not completely strict either. Instead, it stays just ahead of the output consumed. So, if the output is never used, it won't be fully realized.
For this recipe, we'll calculate the Mandelbrot set. Each point in the output takes enough time that this is a good candidate to parallelize. We can just swap map for pmap and immediately see a speedup.
The Mandelbrot set can be found by feeding a point into a function and then feeding the results of this back into the function. The point will either settle on a value or it will take off. The Mandelbrot set contains the points that don't settle that is, points whose values explode after repeatedly being feed into the function.
- We need a function that takes a point and the maximum number of iterations in order to return the iteration it escapes on. This just means that the value goes above four:
(defn get-escape-point [scaled-x scaled-y max-iterations] (loop [x 0, y 0, iteration 0] (let [x2 (* x x) y2 (* y y)] (if (and (< (+ x2 y2) 4) (< iteration max-iterations)) (recur (+ (- x2 y2) scaled-x) (+ (* 2 x y) scaled-y) (inc iteration)) iteration)))) - The scaled points are the pixel points in the output. These are scaled to relative positions in the Mandelbrot set. Here are the functions that handle the scaling. Along with a particular x-y coordinate in the output, they're given the range of the set and the number of pixels in each direction:
(defn scale-to [pixel maximum [lower upper]] (+ (* (/ pixel maximum) (Math/abs (- upper lower))) lower)) (defn scale-point [pixel-x pixel-y max-x max-y set-range] [(scale-to pixel-x max-x (:x set-range)) (scale-to pixel-y max-y (:y set-range))]) - The
output-pointsfunction returns a sequence ofX,Yvalues for each of the pixels in the final output:(defn output-points [max-x max-y] (let [range-y (range max-y)] (mapcat (fn [x] (map #(vector x %) range-y)) (range max-x)))) - For each output pixel, we need to scale it to a location in the range of the Mandelbrot set and then get the escape point for this location:
(defn mandelbrot-pixel ([max-x max-y max-iterations set-range] (partial mandelbrot-pixel max-x max-y max-iterations set-range)) ([max-x max-y max-iterations set-range [pixel-x pixel-y]] (let [[x y] (scale-point pixel-x pixel-y max-x max-y set-range)] (get-escape-point x y max-iterations)))) - At this point, we can simply map
mandelbrot-pixelover the results ofoutput-points. We'll also pass in the function to be used (maporpmap):(defn mandelbrot [mapper max-iterations max-x max-y set-range] (doall (mapper (mandelbrot-pixel max-x max-y max-iterations set-range) (output-points max-x max-y)))) - Finally, we have to define the range that the Mandelbrot set covers:
(def mandelbrot-range {:x [-2.5, 1.0], :y [-1.0, 1.0]})
How does running this with map and pmap compare? A lot depends on the other parameters we pass them. (For more precise and robust times, we use Criterium. See the Benchmarking with Criterium recipe for more information on this library and how to use it.) The following is an example output from timing map using Criterium:
user=> (quick-bench (mandelbrot map 500 1000 1000 mandelbrot-range)) WARNING: Final GC required 1.788622983983204 % of runtime Evaluation count : 6 in 6 samples of 1 calls. Execution time mean : 20.993891 sec Execution time std-deviation : 38.107942 ms Execution time lower quantile : 20.971178 sec ( 2.5%) Execution time upper quantile : 21.059463 sec (97.5%) Overhead used : 1.817165 ns Found 1 outliers in 6 samples (16.6667 %) low-severe 1 (16.6667 %) Variance from outliers : 13.8889 % Variance is moderately inflated by outliers
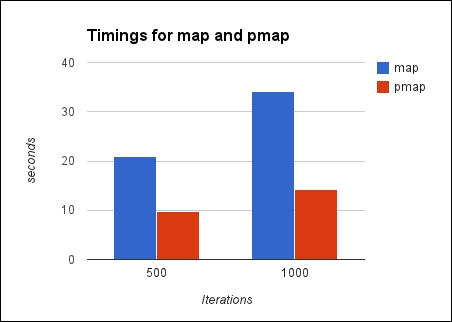
In both the cases, pmap is more than twice as fast when running it on a machine with eight cores.
Parallelization is a balancing act. If each separate work item is small, the overhead of creating threads, coordinating between them, and passing data back and forth takes more time than doing the work itself. However, when each thread has enough to do, we can get nice speedups just by using pmap.
Behind the scenes, pmap takes each item and uses future to run it in a thread pool. It forces only a couple of more items than the number of processors, so it keeps your machine busy without generating more work or data than you need.
For an in-depth, excellent discussion on the nuts and bolts of pmap, along with pointers about things to watch out for, check out David Liebke's talk, From Concurrency to Parallelism (http://youtu.be/ZampUP6PdQA).
