Computer Arithmetic 59
4.2 ADDITION AND SUBTRACTION
In Chapter 3, we have illustrated how a full-adder (Section 3.5.2) may be used for adding two bits. This
full-adder is capable of performing the addition with or without carry, and would generate an eventual
carry if demanded by the result. Four basic variations of 1-bit addition using binary numbers are pre-
sented in Figure 4.1 (a), without considering the carry-in (i.e., carry = 0). If carry is taken into account,
the result would be as shown in Figure 4.1 (b). In several cases, as indicated in the diagram, the result
would also generate a carry, which is designated as carry-out. For multiple-bit additions, this carry-out
would be treated as carry-in for the next (at its immediate left) bit.
++ + + + + + +
Carry Carry
Carry
Carry Carry Carry
Carry Carry
Figure 4.1 Variations of binary addition (a) without carry and (b) with carry
4.2.1 Two’s Complement Representation
In Chapter 3, we have designed a simple ALU (solved Example 3.3) capable of adding and subtracting
two 4-bit binary numbers, apart from performing a few more simple functions. In that example, it was
explained how the subtraction operation may be performed through addition, using two’s complement form
of binary numbers. As described in that section, two’s complement of any binary number is generated
from its one’s complement (explained below) and then by adding 1 to it. Any eventual carry, generated
by adding 1, is neglected or discarded (not taken into consideration). To generate one’s complement, each
binary digit (or each bit) need to be complemented, i.e., any 1 to be changed to 0 and any 0 to be changed
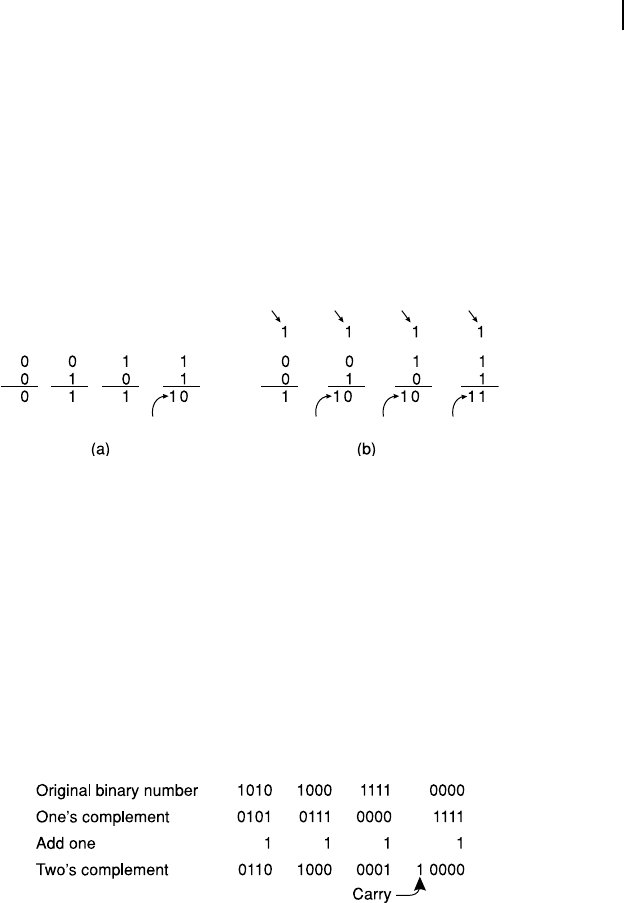
to 1. Four such examples of two’s complement calculation are presented in Figure 4.2 .
Figure 4.2 Examples of two’s complement calculation
In the rst case, the original binary number, 1010, is complemented to get 0101, with which 1 is added
to produce 0110. The second case is a very special case. Here, the original binary number, 1000, is
complemented to get 0111, which is then incremented by 1. The result becomes 1000, which is the same
as the original number. In the third case, we take the maximum binary number within 4-bit representa-
tion, i.e., 1111 and complement it to get 0000, with which 1 is added to produce 0001. In the last case,
the smallest binary number 0000 is considered. Complementing it, we get 1111 and by adding 1 with it,
we get 0000, if we discard the carry. Note that in this case also the original number remains unchanged.
M04_GHOS1557_01_SE_C04.indd 59M04_GHOS1557_01_SE_C04.indd 59 4/29/11 5:03 PM4/29/11 5:03 PM
60 Computer Architecture and Organization
In these examples, we have considered a 4-bit representation. However, the same rule is applicable for
8-bit or 16-bit representation and the result may be interpreted in the same way.
4.2.2 Purpose of Two’s Complement
However, at this stage, the reader may ask about the meaning of two’s complement representation. As a
matter of fact it simply changes the sign of a given number. If we take +3 (0011 in binary) and calculate
its two’s complement, it would give us −3 (1101 in binary). Similarly, if we take −5 (1011 in binary) and
calculate its two’s complement, it would generate +5 (0101 in binary). The reader may take any integer
in binary form, positive or negative and prove it by longhand calculations using 4-bit or 8-bit format
(or any n -bit format). Just remember that any eventual carry, generated after adding 1 has to be dis-
carded and the n -bit format has to be maintained throughout.
The purpose of two’s complement representation is to make the subtraction process easier, as an
addition of any number in its two’s complement is actually its subtraction. We can easily understand
that, addition or subtraction is a matter of the sign involved. Otherwise they may be considered as
identical (refer our algebra course in schools). Therefore, we shall now discuss about sign representa-
tion in Section 4.2.3.
4.2.3 Sign Representation
If we have to perform the arithmetic operations, we cannot avoid the signs involved with numbers.
Of course, we do not consider the imaginary numbers but only the positive and negative numbers.
In this section, we shall consider only integers and in a later section we shall discuss about the sign
convention adopted for real numbers. Out of several available methods (at least four), two methods
of sign representation are widely adopted. In the rst method, known as signed-magnitude method,
the most signi cant bit of binary representation is reserved as the sign bit, which should contain 0 to
indicate positive and 1 to represent negative integers. The remaining bits of the location are to repre-
sent the magnitude of the number, i.e., its absolute value. Therefore, if we consider 8-bit representa-
tion of integers, using this method, 00000001 would represent +1 and 10000001 would represent −1.
In Table 4.1, considering 4-bit representation, signed decimal integers from +7 to −7 are shown in its
second column, using signed-magnitude representation scheme. Another widely adopted method for
sign representation is the two’s complement method, which we have discussed above. Using 4-bit
representation, two’s complement values for the decimal range between +7 and −7 are presented in the
third column of Table 4.1.
One of the major disadvantages of signed-magnitude method of sign representation is the duplication
of the value of zero (0). As we may observe, in 4-bit representation, the most signi cant bit would indi-
cate the sign and remaining three bits are left to represent the number. To represent zero, all these three
bits would be 0, i.e., 000. The most signi cant bit may contain either 0 or 1 indicating the value as +0 or
−0. However, the advantage of this method is that the absolute value of the integer (value irrespective of
its sign) may easily be obtained by discarding its sign bit, which is an easy process in Boolean operation.
In two’s complement method, this duplicate representation of zero is avoided, as we may observe
from Table 4.1. Moreover, the sign of the integer may be readily available through its most signi cant
bit, similar to the signed-magnitude representation. In other words, in two’s complement representation,
if the most signi cant bit is 0, then the number is positive, and if it is 1, then the number is negative.
However, unlike the signed-magnitude method, the range of integers is not identical for positive and
negative numbers, in this representation.
M04_GHOS1557_01_SE_C04.indd 60M04_GHOS1557_01_SE_C04.indd 60 4/29/11 5:03 PM4/29/11 5:03 PM

Computer Arithmetic 61
The allowable range in two’s complement representation depends upon the number of available bits.
In 4-bit representation, this range would vary from +7 to −8 (the last entry is not shown in Table 4.1). In
8-bit representation this range would be spread from +127 to −128. Ranges of integers with respect to
available bits (for 4-bit, 8-bit and 16-bit cases) are presented in Table 4.2. In Table 4.1, we may observe
that the 4-bit binary representation 1000 is missing from the two’s complement’s column (right-most
column). Referring Figure 4.2 , we may observe that two’s complement of 1000 is also 1000. Consider-
ing the decimal value, it may be taken as either +8 or −8. As we cannot represent two different numbers
by the same value, in practice, it is considered as a negative integer, i.e., −8, in 4-bit representation.
However, in case of 8-bit representation, 00001000 is considered as +8.
Signed-decimal
number
Signed-magnitude
representation
Two’s complement
representation
+7 0111 0111
+6 0110 0110
+5 0101 0101
+4 0100 0100
+3 0011 0011
+2 0010 0010
+1 0001 0001
+0 0000 0000
−0 1000 0000
−1 1001 1111
−2 1010 1110
−3 1011 1101
−4 1100 1100
−5 1101 1011
−6 1110 1010
−7 1111 1001
Table 4.1 Signed-magnitude and two’s complement representation of decimal
numbers (within the range of +7 to −7, using 4-bit representation)
As a matter of fact, 1000 is not the only case of anomaly. Consider any binary number start-
ing with 1 followed by 0s and the same situation would be faced. The reader may consider
binary numbers like: 10, 100, 10000, etc., and check their cases of two’s complement rep-
resentation. However, 4-bit, 8-bit, 16-bit, 32-bit and 64-bit representations are common and
widely used. Therefore, binary numbers like 10000000, etc., must be carefully considered.
F
O
O
D
F
O
R
T
H
O
U
G
H
T
M04_GHOS1557_01_SE_C04.indd 61M04_GHOS1557_01_SE_C04.indd 61 4/29/11 5:03 PM4/29/11 5:03 PM
62 Computer Architecture and Organization
Available bits
Unsigned
integer
Signed bit
representation Two’s complement
4 0 to 15 −7 to +7 −8 to +7
8 0 to 255 −127 to +127 −128 to +127
16 0 to 65535 −32767 to
+32767
−32768 to +32767
Table 4.2 Integer ranges for available bits
4.2.4 Signed Addition and Subtraction
In case of signed-magnitude representation scheme, addition and subtraction operations are performed
by initially discarding their sign values (represented through the most signi cant bit). After completion
of the operation (addition or subtraction), the sign value of the nal result is to be separately computed
and placed before the nal result. However, as a normal practice, two’s complement representation is
preferred for performing addition and subtraction, in the case of computers.
If two’s complement scheme of sign representation is used, then addition may be performed with the
available forms of the involved numbers, without any pre-processing. The result would be correct with
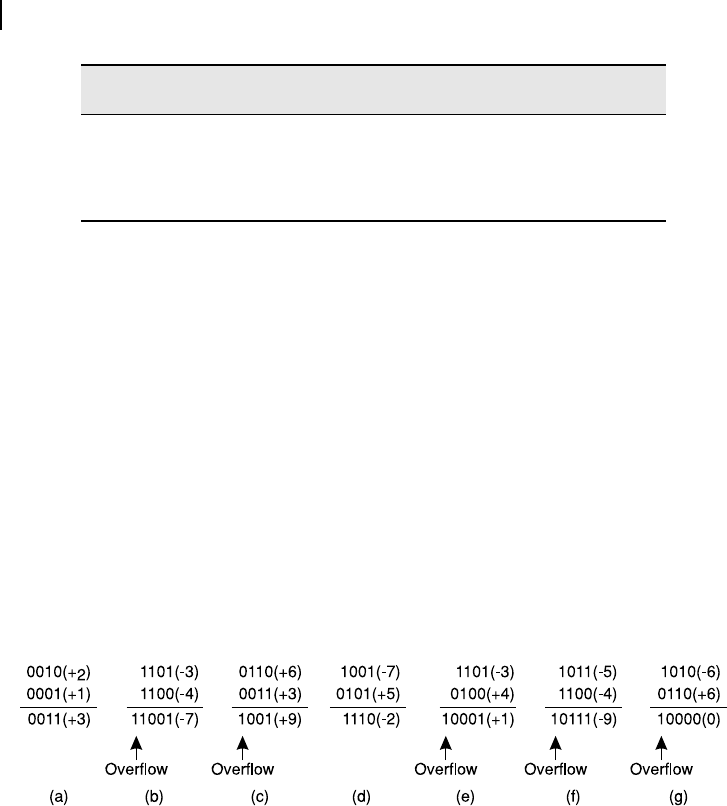
a correct sign, unless some over ow has occurred. We present a few illustrative examples of addition
of two binary numbers ranging between +7 and −7, expressed in two’s complement form. In decimal
form, these examples may be represented as 2 + 1, (−3) + (−4), 6 + 3, (−7) + 5, (−3) + 4, (−5) + (−4) and
(−6) + 6. Decimal equivalent of all these binary numbers are presented at their right side within paren-
thesis for quick reference. Over ows after addition are indicated at the appropriate places, below the
results. Table 4.1 may be used for cross-veri cation of the binary representations.
Figure 4.3 Examples of addition in two’s complement form
Certain interesting aspects of a few additions may be highlighted here. Figure 4.3 (a) and (d) do not
need any comments. In Figure 4.3 (b), (e), (f) and (g), over ow from bit 3 (bit 0 being least signi cant
bit) may be observed. Referring Table 4.1, we nd that in cases of additions represented in Figure 4.3 (c)
and (f) the result exceeded the allowable range of 4-bit. If we discard these two out-of-the-range cases
and discard the over ows out of bit 3, then results may be taken as correct.
To perform subtraction in two’s complement representation, the binary number to be subtracted
should be converted to its two’s complement form and then added with other number to generate the
correct result. In this case also, an over ow from the most signi cant bit needs to be discarded, and the
range has to be checked. Considering the range between +7 and −7 of our 4-bit representation, let us
investigate a few cases of subtraction by calculating the results for 7 − 1, 2 − 3, (−3) − 4, 5 − 0, 0 − 6,
4 − 4 and 1 − 7. These calculations are presented in Figure 4.4 . Note that in the second row, two’s
complement forms are shown.
M04_GHOS1557_01_SE_C04.indd 62M04_GHOS1557_01_SE_C04.indd 62 4/29/11 5:03 PM4/29/11 5:03 PM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
