Describing a Single Set of Data

Through a combination of word of mouth and luck, DataSciencester has grown to dozens of members, and the VP of Fundraising asks you for some sort of description of how many friends your members have that he can include in his elevator pitches.

Using techniques from Chapter 1, you are easily able to produce this data. But now you are faced with the problem of how to describe it.

One obvious description of any dataset is simply the data itself:

num_friends = [100, 49, 41, 40, 25,
               # ... and lots more
              ]

For a small enough dataset, this might even be the best description. But for a larger dataset, this is unwieldy and probably opaque. (Imagine staring at a list of 1 million numbers.) For that reason, we use statistics to distill and communicate relevant features of our data.

As a first approach, you put the friend counts into a histogram using Counter and plt.bar (Figure 5-1):

from collections import Counter
import matplotlib.pyplot as plt

friend_counts = Counter(num_friends)
xs = range(101)                         # largest value is 100
ys = [friend_counts[x] for x in xs]     # height is just # of friends
plt.bar(xs, ys)
plt.axis([0, 101, 0, 25])
plt.title("Histogram of Friend Counts")
plt.xlabel("# of friends")
plt.ylabel("# of people")
plt.show()

Figure 5-1. A histogram of friend counts

Unfortunately, this chart is still too difficult to slip into conversations. So you start generating some statistics. Probably the simplest statistic is the number of data points:

num_points = len(num_friends)               # 204

You’re probably also interested in the largest and smallest values:

largest_value = max(num_friends)            # 100
smallest_value = min(num_friends)           # 1

which are just special cases of wanting to know the values in specific positions:

sorted_values = sorted(num_friends)
smallest_value = sorted_values[0]           # 1
second_smallest_value = sorted_values[1]    # 1
second_largest_value = sorted_values[-2]    # 49

But we’re only getting started.

def mean(xs: List[float]) -> float:
    return sum(xs) / len(xs)

mean(num_friends)   # 7.333333

# The underscores indicate that these are "private" functions, as they're
# intended to be called by our median function but not by other people
# using our statistics library.
def _median_odd(xs: List[float]) -> float:
    """If len(xs) is odd, the median is the middle element"""
    return sorted(xs)[len(xs) // 2]

def _median_even(xs: List[float]) -> float:
    """If len(xs) is even, it's the average of the middle two elements"""
    sorted_xs = sorted(xs)
    hi_midpoint = len(xs) // 2  # e.g. length 4 => hi_midpoint 2
    return (sorted_xs[hi_midpoint - 1] + sorted_xs[hi_midpoint]) / 2

def median(v: List[float]) -> float:
    """Finds the 'middle-most' value of v"""
    return _median_even(v) if len(v) % 2 == 0 else _median_odd(v)

assert median([1, 10, 2, 9, 5]) == 5
assert median([1, 9, 2, 10]) == (2 + 9) / 2

print(median(num_friends))  # 6

def quantile(xs: List[float], p: float) -> float:
    """Returns the pth-percentile value in x"""
    p_index = int(p * len(xs))
    return sorted(xs)[p_index]

assert quantile(num_friends, 0.10) == 1
assert quantile(num_friends, 0.25) == 3
assert quantile(num_friends, 0.75) == 9
assert quantile(num_friends, 0.90) == 13

def mode(x: List[float]) -> List[float]:
    """Returns a list, since there might be more than one mode"""
    counts = Counter(x)
    max_count = max(counts.values())
    return [x_i for x_i, count in counts.items()
            if count == max_count]

assert set(mode(num_friends)) == {1, 6}

# "range" already means something in Python, so we'll use a different name
def data_range(xs: List[float]) -> float:
    return max(xs) - min(xs)

assert data_range(num_friends) == 99

from scratch.linear_algebra import sum_of_squares

def de_mean(xs: List[float]) -> List[float]:
    """Translate xs by subtracting its mean (so the result has mean 0)"""
    x_bar = mean(xs)
    return [x - x_bar for x in xs]

def variance(xs: List[float]) -> float:
    """Almost the average squared deviation from the mean"""
    assert len(xs) >= 2, "variance requires at least two elements"

    n = len(xs)
    deviations = de_mean(xs)
    return sum_of_squares(deviations) / (n - 1)

assert 81.54 < variance(num_friends) < 81.55

import math

def standard_deviation(xs: List[float]) -> float:
    """The standard deviation is the square root of the variance"""
    return math.sqrt(variance(xs))

assert 9.02 < standard_deviation(num_friends) < 9.04

def interquartile_range(xs: List[float]) -> float:
    """Returns the difference between the 75%-ile and the 25%-ile"""
    return quantile(xs, 0.75) - quantile(xs, 0.25)

assert interquartile_range(num_friends) == 6

Correlation

DataSciencester’s VP of Growth has a theory that the amount of time people spend on the site is related to the number of friends they have on the site (she’s not a VP for nothing), and she’s asked you to verify this.

After digging through traffic logs, you’ve come up with a list called daily_minutes that shows how many minutes per day each user spends on DataSciencester, and you’ve ordered it so that its elements correspond to the elements of our previous num_friends list. We’d like to investigate the relationship between these two metrics.

We’ll first look at covariance, the paired analogue of variance. Whereas variance measures how a single variable deviates from its mean, covariance measures how two variables vary in tandem from their means:

from scratch.linear_algebra import dot

def covariance(xs: List[float], ys: List[float]) -> float:
    assert len(xs) == len(ys), "xs and ys must have same number of elements"

    return dot(de_mean(xs), de_mean(ys)) / (len(xs) - 1)

assert 22.42 < covariance(num_friends, daily_minutes) < 22.43
assert 22.42 / 60 < covariance(num_friends, daily_hours) < 22.43 / 60

Recall that dot sums up the products of corresponding pairs of elements. When corresponding elements of x and y are either both above their means or both below their means, a positive number enters the sum. When one is above its mean and the other below, a negative number enters the sum. Accordingly, a “large” positive covariance means that x tends to be large when y is large and small when y is small. A “large” negative covariance means the opposite—that x tends to be small when y is large and vice versa. A covariance close to zero means that no such relationship exists.

Nonetheless, this number can be hard to interpret, for a couple of reasons:

• Its units are the product of the inputs’ units (e.g., friend-minutes-per-day), which can be hard to make sense of. (What’s a “friend-minute-per-day”?)

• If each user had twice as many friends (but the same number of minutes), the covariance would be twice as large. But in a sense, the variables would be just as interrelated. Said differently, it’s hard to say what counts as a “large” covariance.

For this reason, it’s more common to look at the correlation, which divides out the standard deviations of both variables:

def correlation(xs: List[float], ys: List[float]) -> float:
    """Measures how much xs and ys vary in tandem about their means"""
    stdev_x = standard_deviation(xs)
    stdev_y = standard_deviation(ys)
    if stdev_x > 0 and stdev_y > 0:
        return covariance(xs, ys) / stdev_x / stdev_y
    else:
        return 0    # if no variation, correlation is zero

assert 0.24 < correlation(num_friends, daily_minutes) < 0.25
assert 0.24 < correlation(num_friends, daily_hours) < 0.25

The correlation is unitless and always lies between –1 (perfect anticorrelation) and 1 (perfect correlation). A number like 0.25 represents a relatively weak positive correlation.

However, one thing we neglected to do was examine our data. Check out Figure 5-2.

Figure 5-2. Correlation with an outlier

The person with 100 friends (who spends only 1 minute per day on the site) is a huge outlier, and correlation can be very sensitive to outliers. What happens if we ignore him?

outlier = num_friends.index(100)    # index of outlier

num_friends_good = [x
                    for i, x in enumerate(num_friends)
                    if i != outlier]

daily_minutes_good = [x
                      for i, x in enumerate(daily_minutes)
                      if i != outlier]

daily_hours_good = [dm / 60 for dm in daily_minutes_good]

assert 0.57 < correlation(num_friends_good, daily_minutes_good) < 0.58
assert 0.57 < correlation(num_friends_good, daily_hours_good) < 0.58

Without the outlier, there is a much stronger correlation (Figure 5-3).

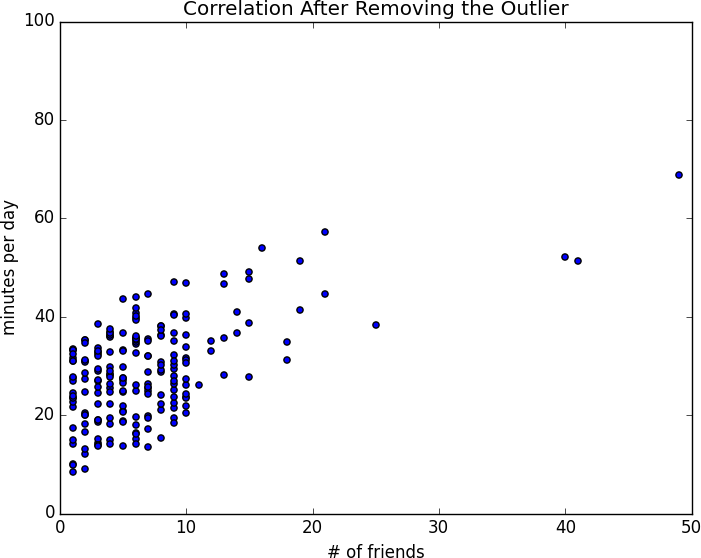
Figure 5-3. Correlation after removing the outlier

You investigate further and discover that the outlier was actually an internal test account that no one ever bothered to remove. So you feel justified in excluding it.

Simpson’s Paradox

One not uncommon surprise when analyzing data is Simpson’s paradox, in which correlations can be misleading when confounding variables are ignored.

For example, imagine that you can identify all of your members as either East Coast data scientists or West Coast data scientists. You decide to examine which coast’s data scientists are friendlier:

It certainly looks like the West Coast data scientists are friendlier than the East Coast data scientists. Your coworkers advance all sorts of theories as to why this might be: maybe it’s the sun, or the coffee, or the organic produce, or the laid-back Pacific vibe?

But when playing with the data, you discover something very strange. If you look only at people with PhDs, the East Coast data scientists have more friends on average. And if you look only at people without PhDs, the East Coast data scientists also have more friends on average!

Once you account for the users’ degrees, the correlation goes in the opposite direction! Bucketing the data as East Coast/West Coast disguised the fact that the East Coast data scientists skew much more heavily toward PhD types.

This phenomenon crops up in the real world with some regularity. The key issue is that correlation is measuring the relationship between your two variables all else being equal. If your dataclasses are assigned at random, as they might be in a well-designed experiment, “all else being equal” might not be a terrible assumption. But when there is a deeper pattern to class assignments, “all else being equal” can be an awful assumption.

The only real way to avoid this is by knowing your data and by doing what you can to make sure you’ve checked for possible confounding factors. Obviously, this is not always possible. If you didn’t have data on the educational attainment of these 200 data scientists, you might simply conclude that there was something inherently more sociable about the West Coast.

Some Other Correlational Caveats

A correlation of zero indicates that there is no linear relationship between the two variables. However, there may be other sorts of relationships. For example, if:

x = [-2, -1, 0, 1, 2]
y = [ 2,  1, 0, 1, 2]

then x and y have zero correlation. But they certainly have a relationship—each element of y equals the absolute value of the corresponding element of x. What they don’t have is a relationship in which knowing how x_i compares to mean(x) gives us information about how y_i compares to mean(y). That is the sort of relationship that correlation looks for.

In addition, correlation tells you nothing about how large the relationship is. The variables:

x = [-2, -1, 0, 1, 2]
y = [99.98, 99.99, 100, 100.01, 100.02]

are perfectly correlated, but (depending on what you’re measuring) it’s quite possible that this relationship isn’t all that interesting.

Correlation and Causation

You have probably heard at some point that “correlation is not causation,” most likely from someone looking at data that posed a challenge to parts of his worldview that he was reluctant to question. Nonetheless, this is an important point—if x and y are strongly correlated, that might mean that x causes y, that y causes x, that each causes the other, that some third factor causes both, or nothing at all.

Consider the relationship between num_friends and daily_minutes. It’s possible that having more friends on the site causes DataSciencester users to spend more time on the site. This might be the case if each friend posts a certain amount of content each day, which means that the more friends you have, the more time it takes to stay current with their updates.

However, it’s also possible that the more time users spend arguing in the DataSciencester forums, the more they encounter and befriend like-minded people. That is, spending more time on the site causes users to have more friends.

A third possibility is that the users who are most passionate about data science spend more time on the site (because they find it more interesting) and more actively collect data science friends (because they don’t want to associate with anyone else).

One way to feel more confident about causality is by conducting randomized trials. If you can randomly split your users into two groups with similar demographics and give one of the groups a slightly different experience, then you can often feel pretty good that the different experiences are causing the different outcomes.

For instance, if you don’t mind being angrily accused of https://www.nytimes.com/2014/06/30/technology/facebook-tinkers-with-users-emotions-in-news-feed-experiment-stirring-outcry.html?r=0[experimenting on your users], you could randomly choose a subset of your users and show them content from only a fraction of their friends. If this subset subsequently spent less time on the site, this would give you some confidence that having more friends _causes more time to be spent on the site.

For Further Exploration

• SciPy, pandas, and StatsModels all come with a wide variety of statistical functions.

• Statistics is important. (Or maybe statistics are important?) If you want to be a better data scientist, it would be a good idea to read a statistics textbook. Many are freely available online, including:

  • Introductory Statistics, by Douglas Shafer and Zhiyi Zhang (Saylor Foundation)

  • OnlineStatBook, by David Lane (Rice University)

  • Introductory Statistics, by OpenStax (OpenStax College)