7
RECURSION
Recursive algorithms are especially useful in manipulating data structures that are themselves defined recursively. Whenever a data object is defined recursively, it is often easy to describe algorithms that work on these objects recursively. Though all the languages, such as BASIC, COBOL, and the like, do not have the recursive facility, however, all new programming languages use recursion as their primary iterative control structures. If our programming language does not allow recursion, that should not matter because we can always translate a recursive programme into a nonrecursive version. C language has an inherent property to use recursion. We will show the readers how the recursion can be implemented through C language. So a discussion on recursion will be helpful to our readers for proper understanding of the use of recursion in data structures.
In this chapter we introduce recursion, a problem-solving technique often used in computer science. The basic objective is to provide a variety of examples alongwith explanation to design and understand recursion. We will confine ourself to the basic concept of recursive algorithms and the way they can be implemented using C language.
7.1 BASIC CONCEPTS OF RECURSION
Recursion is a function invoking an instance of itself, either directly or indirectly. In C, all library functions can be used recursively. Recursion is a programming technique and some programming tasks are naturally solved with the use of recursion, which can be considered an advanced form of flow of control. Recursion is an alternate to iteration . Recursion defines a problem in terms of itself. A recursive solution repeatedly divides a problem into smaller subproblems until a directly solvable subproblem is reached. Once we obtain the solution of to solvable subproblem, we feed it back into the next larger subproblem for its solution. This process continues until we solve the original problem. Let us clarify the basic idea of recursion.
Let the original problem be P. P is redefined in terms of subproblem P1 and P1 is again redefined in terms of P2 and so on. Let the last subproblem be Pn. If the subproblem Pn can be solved without further subdivision, then the solution of Pn can be used to solve the subproblem Pn–1. This solution is fed back into Pn–2,…, P2, P1 until we finally have solved our original problem P.
As an example, we will now introduce some fundamental concepts of recursive programming. The most common is a factorial in which n! = n (n–l)(n–2)…2*l= n(n–l) is calculated.
Here we obtain the value of n! by taking the number n and multiplying it by (n–1)!. To obtain the value of (n–1)!, we use the following by substituting (n–1) for n, that is, (n–1)! = (n–l)(n–2)!.
Suppose we want to compute 3! . From the above discussion, we obtain the following result
3! = 3* (3–1)!
=3*2!
=3*2* (2–1)!
=3*2*1!
=3*2*1* (1–1)!
=3*2*1*0!
=3*2*1*0*(0–1)!
=3*2*1*0*(–1)!
=…
Note that the symbol asterisk (*) represents multiplication. The above example, that is, calculation of factorials, identifies two major problems — (i) termination of recursion was not provided and (ii) n! will always evaluate to zero for n>0.
To solve the problems, we need to divide the recursive definition into two cases: a base case and a general case.
0!=1 /* The base case */
n!=n * (n–1)!, n > 0 /* The general case */
The base case is the non-recursive definition that terminates the recursion. On the other hand, the general case is the recursive part of the solution definition.
We now implement the recursive version of factorial program using C language. For the case of understanding the factorial program, we first illustrate the non-recursive version of factorial program.
Example 7.1
/* Non-recursive version of Factorial program */
#include <stdio.h>
main( )
{
int Number;
printf{“
Give the number :”);
scanf(“%d”, &Number);
printf(“
Factorial of Number %d is %d
”, Number
Factorial(Number)),
}
Factorial(Number)
int Number;
{
int Fact = 1;
int i;
for(i=1; i<=Number; i++)
Fact*=i;
return(Fact);
}
Example 7.2
/* Recursive version of Factorial N */
/* Recursive function */
Factorial _ Recursion (N)
int N;
{
if (N<0)
{ printf(“
Negative number is entered
”);
return ;
}
if (N)
return(l); /* Base case */
else
return(n * Factorial _Recursion (n–1));
/* General case */
}
To understand how recursion works, let us take the value of N as 3. We have labelled two cases by two comment statements. We assume the first call to the function Factorial_Recursion ( ) as being at level 1. The next recursive call will be at level 2 and so on. To calculate the factorial of 3, we proceed as follows.
Level 1: Factorial_Recursion(3)
return(3 * Factorial_Recursion(2))
[from General case]
Level 2: Factorial_Recursion(2)
return(2 * Factorial_Recursion(1))
[from General case]
Level 3: Factorial_Recursion(1)
return(1* Factorial_Recursion(0))
[from General case]
Level 4: Factorial_Recursion (0)
return(1)
[from Base case]
We now compute the factorial of 3 since we have reached the base case. We move in the reverse order (i.e., from the order in which they are generated). The output of level 4 is 1, level 3 produces 1, level 2 computes 2, and finally level 1 calculates 6.
We now take some more examples to illustrate the idea of recursion.
Example 7.3
/*Recursive version to calculate xn, n>0, n is positive */
/* integer*/
POWER(x,n)
int x,n;
{
/* x is the number and n is power */
if(n == 1)
return(x);
return(x * POWER(x,n–1));
}
Let us look at another example. This programme counts to the desired number, but also displays information that help us to see what happens in recursive calls.
Example 7.4
/* Program to count recursively and also to write */
/* information about current level of recursion */
#include <stdio.h>
int level;
void count(int val)
{
printf(“
Starting count at level % 2d : val
= %2d
”, ++level, val);
if (val>l)
count(val-1);
printf(“Displaying val ; %2d
”, val);
printf (“Leaving count at level %2d : val = %2d
” Level --, val);
}
/*Main program */
main ( )
{
void count(int);
int val;
printf(“Count to what value?”);
scanf(“%d”, &val);
level =0;
count(val);
}
Let us see how the recursion process works.
The program begins executing in main function. Let this function call count ( ) with an argument of 4 (i.e., the value of val is 4). The function count (4) begins its execution while the main function is on hold. This function displays level information about level of recursion. Since the value of val, that is, argument of count (now it is 4) is greater than 1, the function calls count ( ) with an argument of 3. Count ( 3 ) displays information about the level of recursion. Since the parameter has a value greater than 1, the function calls count ( ) with an argument 2.
At this point, main ( ), count (4), and count (3) are on hold, and count (2) begins its execution. Just as the two previous calls to count ( ) did, count (2) displays information about the level of recursion. The function now checks whether its argument value is greater than 1. Since the condition is true, main ( ), count (4), count (3), and count (2) are on hold, and count (1) starts its execution. Count (1) displays its information about recursion level. Now the best condition for the if statement fails. Control thus transfers to the next statement in the same function which turns out to be the call to printf( ) for displaying the value of val. Note that the last version of count( ) function called was the first version to do any work. One feature of recursive function calls is that the last version called is the first one to do work. The last one called is also the first one to finish its work. We can also see this in the output as given below.
Count to what value? 4
Starting count at level 1: val =4
Starting count at level 2: val =3
Starting count at level 3: val =2
Starting count at level 4: val =1
Leaving count at level 4: val =1
Leaving count at level 3: val =2
Leaving count at level 2: val =3
Leaving count at level 1: val =4
A recursive function must always test whether it can stop before calling another version of itself. If a recursive call is made, the parameters in some calls should eventually have values that will make further recursive calls unnecessary.
Suppose we want to calculate a recursive algorithm to implement the routine power (x,y), that is, it raises the value contained in x to the yth power. For example, if we need to calculate the value of 5 raised to the power of 4, power (5.4), we are really solving for 5* power (5.3). Likewise, power (5,3) is equivalent to 5* (5,2) when in the power the value is raised to be equal to 0, the ending value, the value 1, is returned to the calling function.
If power ( ) function is called with power(5, 2), the following processing is performed:
power (5, 2) return
5* power (5, 2–1)
power (5, 1) return
5* power (5, 1–1)
power (5, 0)
return 1 by definition
5 ------------ result of power(5, l)
25 ------------ result of power (5, 2)
We will now present the recursive routine for the power function.
Example 7.5
/* Power function */
/* Returns the result of value raised to the */
/* power contained in the variable raised */
/* to, or -1 if the value in raised to is negative */
float power(x,y)
float x;
float y;
{
if (y<0)
return(-1, 0);
else
if(y ==0) /* Any value raised to zero is one */
return(1, 0);
else
return(x* power(x,y -1);
}
7.2 RECURSION IMPLEMENTATION
Recursive algorithms are frequently quite short and elegant but they may not always be the quickest in terms of execution time and of memory space. We can calculate a factorial in iterative way in a more efficient way than the recursive method. In this section we will see how recursion is implemented and why it is sometimes inefficient.
Whenever a function is called, the run-time system dynamically allocates memory spaces for storing parameters of that function and other variables and constants that are declared within it. Also it is required to store return address. Since it is difficult to know in advance about the memory spaces which will be reserved for the recursive call, the stack will store the necessary information. The stack holds all the information of every function that has been invoked but not yet completed. Let us consider a simple program to illustrate the use of the stack.
Example 7.6
/* Recursive call */
# include <stdio.h>
main( )
{
static int x=0;
x++;
x<7 ? main( ) :x++;
printf(“%2d”, x);
}
Output: The output of the programme will be:8888888
In the above program main( ) calls itself, though it is not common to the programmer. The integer variable, x, is defined as storage class, static. Thus, it stores the changed value of x after initialization. So the value of x is zero for the first time and at the time of next call it stores the incremented value of x. Each time main( ) function is called, the printf(. ) statementis stored in the stack. This statement remains on the stack until the function is completed. The condition x<7 imposes that there are six calls to main( ) function and naturally six printf( ) statements are stored on the stack. Since functions are always excited in a reverse order from the order in which they are invoked, these informations are stored in a stack due to the nature of the stack (last-in-first-out). Finally, when the condition x<7 fails, the value of x is incremented again (i.e., x=7+l =8). Now the informations from the stack are popped off and execute the printf( ) statement with the latest value of x. We will show the process in Fig. 7.1.
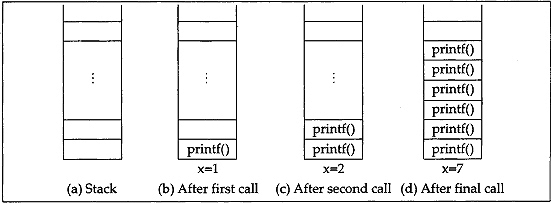
Fig. 7.1 Run-time stack structure
It is always possible to exhaust the space allocated to the run-time stack and get a stack overflow error condition. Besides this there is also the issue of time required to store the remaining statements on the stack when a function is invoked and return the space when it is completed. Function invocation involves a great deal of overhead, and it can be a time-consuming operation. Therefore, recursive algorithms that invoke a great deal of function linkage can sometimes run more slowly than interactive programs that solve the same problem.
We will now present another recursive function which is often used in string manipulation.
The following routine counts the number of characters contained in a string via a recursive process.
string-length (String )
char *String;
{
if(*String == NULL) /* End of the string */
return(0);
else
return(l + String-length (++String ));
/* Recursive call */
}
The routine examines the value referenced by *String to see if it is NULL (the ending condition). If the *String does not contain NULL the value returned is return (1+String_length (++ String));
If *String is NULL, it will return zero. If the routine is invoked with the string “Hello”, the following processing will take place:
String _ length (String); /* Return 1 */
1st time: *String points to ‘H’
return( 1+String_length (++String ));
2nd time: String_length(String); /* Return 1+1 =2 */
*String points to ‘e’
return(1+String_length (++String ));
5th time: String_length (String) ;
*String points to “o” /*return 4+1=5 */
return (1+String_length (++String));
6th time: if(*String == NULL) is true,
so it returns(0), that is, 5+0 =5
7.3 THE TOWER OF HANOI
The traditional game Tower of Hanoi is also an example of recursion. The game involves three pegs: peg1, peg2, and peg3. Suppose there are N discs on peg1. It is required to move N discs from peg1 (source) to peg3 (destination). The relative ordering of the discs on peg1 has to be maintained as they are moved to peg3. The discs are to be stacked from the largest to smallest beginning from the bottom.
While moving the discs from peg1 to peg3, the following rules are to be observed.
(i) Only one disc can be moved at a time.
(ii) No large disc can be placed over the top of a smaller disc.
(iii) An auxiliary peg, that is, peg2 can be used to act as an intermediate to store one or more discs while they are being moved from their source, (peg peg1) to their destination peg (peg3).
Let us illustrate the changeover process considering the value of N as 1, 2, and 3. Finally, we will conclude the problem in general. Suppose there is only one disc, that is, N=l. The solution is very simple, that is, merely move the disc from peg1 to peg3, as shown in Figs. 7.2(a) and 7.2(b).
If there are two discs on peg1, move the top disc from peg1 to peg2 and then move the second disc from peg1 to peg3. Finally, move the top (first) disc from peg2 to peg3. The transfer procedure is shown in Figs. 7.3(a) – 7.3(d).
The problem of transferring discs from peg1 to peg3 is somewhat complex in case when the value of N is 3. In this case, move the first two discs from peg1 to peg2 using peg3 as an intermediate. Then move the third disc from peg1 to peg3. Next, move two discs from peg2 to peg3 using peg1 as an intermediate. The entire procedure is shown in Fig. 7.4. Fig. 7.5 illustrates the same problem when N contains four discs.
For general N, use the technique already established for transferring three discs. First, move (N–1) discs from peg1 to peg2 using peg3 as an intermediate. Then move top disc from peg1 to peg3. Then again apply the same technique to move (N–1) discs from peg2 to peg3 using peg1 as an intermediate.
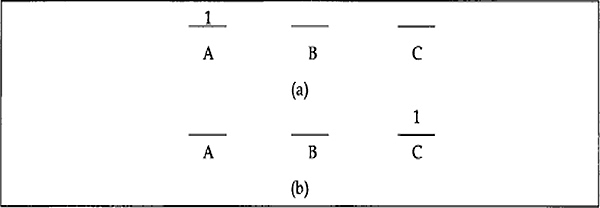
Fig. 7.2 (a) Initial configuration when N=1 (b) Final configuration when N=1
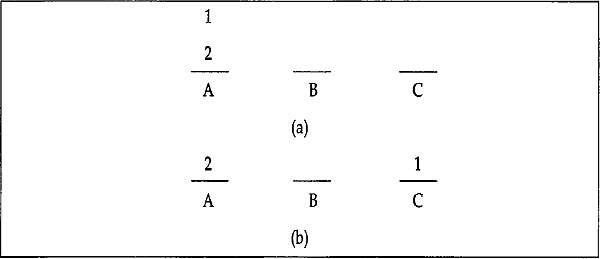
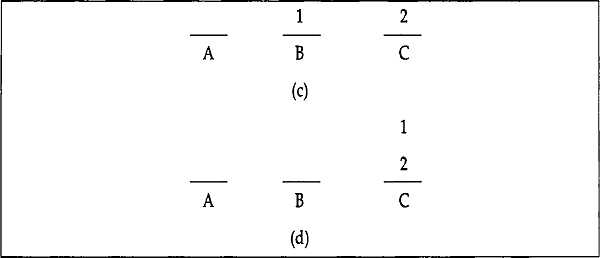
Fig. 7.3 (a) — (d) Initial configuration to final configuration for N = 2


Fig. 7.4 (a) – (h) Initial to final configuration when number of discs is 3




Fig. 7.5 (a) – (p) Initial to final configuration when number of discs is 4
7.4 TIME AND SPACE REQUIREMENTS
Recursion is a powerful tool when used properly, but there are trade-offs. Recursion can simplify difficult programming tasks, such as the Tower of Hanoi. It is doubtful whether a programmer could have developed the non-recursive solution to the Tower of Hanoi problem directly from the problem statement. A non-recursive solution involving stacks is more difficult to realize and more prone to error when a stack cannot be eliminated from the nonrecursive version of a program and when its counterpart recursive version can be as fast or faster than the non-recursive version under a standard complier.
In general, a nonrecursive version of a program will execute more efficiently in terms of time and space than a recursive version. This is because the overhead involved in entering and exiting a block is not required in the recursive routine. In a non-recursive program, the stack activity can be eliminated. However, it may sometimes be possible to convert a recursive function to a non-recursive function and vice versa. The cost involved for this conversion may depend entirely on the knowledge of the programmer. Finally, even C language supports recursion, a recursive solution to a problem is often more expensive than a non-recursive solution, both in terms of time and space. Frequently this expense is a small price to pay for the simplicity and self-documentation of the recursive solution. We now present the program for the Tower of Hanoi problem.
Example 7.7
#include <stdio.h>
/* Recursive routine for Tower of Hanoi */
/* It performs to move N-number of discs */
/* from source to destination using*/
/* auxiliary N given as input */
Tower_of_Hanoi ( N, peg1, peg2, peg3)
int N;
char peg1, peg2, peg3;
{
if (N<1)
printf(“
No disc is present on peg1
”);
else if (N ==1)
printf(“Move disc from %c to %c
”, pegl, peg2);
else
{
Tower_of_Hanio (N-1, peg1, peg3, peg2);
printf(“Move disc from %C to %C
”, peg1, peg3);
Tower _of_Hanoi(n-1, peg2, peg1, peg3);
}
}
/*Main program */
main( )
{
int N ; /* Number of discs to be moved */
char pegl, peg2, peg3 ;
peg1= ‘A’;
peg2= ‘B’;
peg3= ‘C’;
printf (“
Enter the number of discs to be moved:”);
scanf(“%d”, &N);
Tower_of_Hanoi(N, peg1, peg2, peg3);
}
Output:
Sample run is given below:
Enter the number of discs to be move: 3
Move disc from A to C
Move disc from A to B
Move disc from C to B
Move disc from A to C
Move disc from B to A
Move disc from B to C
Move disc from A to C
In the above program, we call Tower_of_Hanoi function within the function Tower_of_Hanoi. This represents a recursive call. Although such a function may be easily written but it is somewhat difficult to understand thoroughly. While describing the process of recursive call, it will be evident that the use of a stack is essential for implementing the recursive call.
7.5 RECURSION VS ITERATION
Recursion is an extremely powerful problem-solving technique. For certain classes of problems (specially those involving recursively defined data structures), it allows us to create highly elegant and compact solutions to complex problems. Generally there are essentially two types of recursion. The first type concerns recursively defined functions, such as factorial function whereas the second type is the recursive use of non-primitive recursion. A typical example of this type is the Tower of Hanoi problem. It is always possible to transform mechanically any primitive recursive function into an equivalent iterative process. However, this is not the case for nonprimitive recursive function. Although there exists an iterative solution for the Tower of Hanoi problem, in general, there are many problems of that form for which iterative solutions either do not exist or are not easily found. Certain inherently recursive processes can be solved in programming languages where such facilities do not exist. For example, a factorial program can be easily solved iteratively as compared to the recursive method. It is also true that even when there is no inherent recursive structure, the recursive solution may be much simpler.
By setting up an external stack, we can transform any recursive program into its iterative form. However, it is often complicated and harder to understand. Therefore we should always evaluate whether an iterative solution may be superior to recursion in a particular case.
The key to understanding the function is to be aware about the process when the recursive call is made. The difficulty with handling recursion lies in the process that a function is called from within that function. Eventually, a return will be made to the last calling function. Since the call also involves changing the values of the function's parameters, the old values will be destroyed unless they were stored in the stack along with their return address. Thus, a recursive call involves a stack to store not only the return address but also the values of all parameters essential to the current state of the function. To illustrate this, we will trace the actions taken when a call of the form Tower_of_Hanoi (3, ‘A’, ‘B’, ‘C’) is initiated.

7.6 EXAMPLES
In this section we present more examples to illustrate the design, development, and implementation of recursive functions. In the subsequent chapters, we will come across examples that are more easily solved by recursion. We will present here only programs and recursive routines without describing the construction of programs. The reader will understand the actual process through the output which will be given after each program.
Example 7.1: The Fibonacci sequence is the sequence of integers
0, 1, 1, 2, 3, 5, 8, 13, 21, ............................
Each element in the sequence is the sum of the two preceding elements. We can define the sequence by the following recursive expressions:
fibo(n) = n if n = 0 or 1
fibo(n) = fibo (n–2) + fibo (n–1) if n> = 2
We will now present the recursive version of the above sequence.
Example 7.8
/* main */
#include <stdio.h>
main( )
{
int n ; /* No. of terms */
printf(“
Enter the value of n:”);
scanf(“%d”, &n);
fibo(n);
}
/* Recursive function for Fibonacci sequence */
fibo(n)
int n;
{
if ((n== 0)||(n== l))
return(n);
else
return(fibo(n–2)+fibo(n–1));
}
The next example is to write a recursive function convert (number, base) to convert a given positive integer(number) to its equivalent number in another base and return it as a string.
Example 7.9
#include(stdio.h>
char A[16];
int i =0;
main( )
{
int number, base, l, p, q, t;
printf(“
Enter number and base:”);
scanf(“%d, %d”, &number, &base);
l=strlen(A);
Convert(number,base);
for(p=0, q=l-l; p<q, p++, q--)
{
t=A[p];
A[p]=A[q]; /* Swap A [p] and A[q] */
A[q]= T;
}
printf(“
%S”, A);
return ;
}
/* Recursive function convert( ) */
Convert(number,base)
int number, base ;
{
if( number==0)
return;
else
{
if(number % base <10)
A[i++] = number % base +‘0’;
else
A[i++]= number % base + 55;
/* For hexadecimal number
‘A' to'F' */
Convert(number/base, base); /* Recursive call */
}
}
We are now presenting a set of inputs and the corresponding outputs.
(i) Input:
Enter number and base: 10, 2
Output:
1010
(ii) Input:
Enter number and base: 255, 16
Output:
FF
Example 7.10
#include <stdio.h>
bitcount(word)
unsigned int word ;
{
/* This function returns the number of bits in a word */
/* which are 1 */
if(word == 0)
return(0);
else
return(1+bitcount(word&(word-1)));
}
/* Main program */
main( )
{
unsigned int word ;
printf(“
Enter an unsigned word:”);
scanf(“%n”, &word);
/* Call the bit count function */
printf(“
Number of l's in the word = %d”, bitcount(word));
}
Input:
Enter an unsigned word: 15
Output:
Number of l's in the word =4
Example 7.11: The following example illustrates a function that returns an integer value to its ASCII representation.
/* This function returns an integer value */
/* to its ASCII representation */
To_ascii(value, S, index)
int value;
char S[ ];
int index;
{
int sign = value;
S[index ++] = Absolute (value) % 10 + ‘O’;
value = value/10;
if (Absolute (value)>0)
To_ascii (Value,S,index);
else
{
if (sign<0)
S [index ++] = ‘-’;
S [index]= NULL;
Reverse(S,0, index-1);
}
}
/* Returns the absolute value of the value */
/* Contained in the variable, value*/
Absolute(value)
int value;
{
if (value>0)
return(value);
else
return(-value);
}
/* This function reverses the characters in a string*/
/* or substring contained in the string */
Reverse(S, start, end)
char S[ ];
int start, end;
{
int length;
char temp;
length = strlen(S); /* String length function */
if(start>= length)
return(-1);
else
if (end>= length)
end = length -1;
if (start >= end)
return;
else
{
temp = S [start];
S[start]= S[end];
S[end]=temp;
Reverse (S, ++ start, -- end);
}
}
It is also possible to write a reverse function in different ways. Program 7.12 is another way of representing this.
Example 7.12
#include <stdio.h>
/* Function to print the contents of the character string */
/* in reverse order, e.g., “This* will be printed as “sihT” */
print_reverse(S);
char *S;
{
if (*S ! = NULL)
{
print_reverse(++S);
putchar(* ( -- S));
}
}
/* Main program */
main( )
{
char S[80] ;
printf(“M Enter a string:
”);
gets(S); /* Read a string */
print-reverse (S);
}
Input:
Enter a string
This is a String
Output:
g n i r t S a Si sihT
7.7 COST OF RECURSION
Recursive functions can make code much more compact and easy to read, but not necessarily always more efficient. In fact, sometimes recursive versions of a function can be very inefficient. In this section, we will look briefly at an example of a recursive function that becomes more inefficient as the values used increase. The main point here is to understand the idea of how the number of recursive calls can grow. This example also shows that the recursive function of the Fibonacci numbers is far more expensive than the iterative function.
Fibonacci numbers are elements in a mathematical series that occur in many situations. The definition of a Fibonacci number is simple but recursive. The first two Fibonacci numbers, fibo(l) and fibo(2), are defined as 1. Subsequent numbers are formed by adding the preceding two Fibonacci numbers.
To understand the cost of recursion, we again rewrite the Fibonacci program (with a minor modification) to compute the desired Fibonacci number. The program is inefficient after about the twentieth Fibonacci number.
Example 7.13
/* Program to compute Fibonacci numbers */
#include <stdio.h>
#include <math.h>
long No_of_calls =0 ;
long fibo(int n);
{
No_of_calls ++;
if (n>2)
return(fibo (n–l) + fibo (n–2));
else
return(1);
}
main( )
{
long fibo( int), fibo_number;
int seed ;
printf(“
Number?”);
scanf (“%d”, &seed);
fibo_number= fibo(seed);
printf (“fibo (%2d) = %ld”, seed, fibo_number);
printf(“%7ld calls to fibo( )
”, no_of_calls );
}
At the beginning of the recursive call, the function tests when it can stop. If it so happens, it will return a specific value 1 and the function returns control to the calling function. The Fibonacci number fibo (4) is the sum of fibo (2) and fibo (3) and fibo (3) is the sum of fibo (2) and fibo (1). Let us look at the following outputs for selected Fibonacci numbers.
Number?fibo (10) = 55, 109 calls to fibo ( )
Number? fibo (20) = 6765, 13529 calls to fibo ( )
Number? fibo (30) = 832040, 1664079 calls to fibo ( )
In the above it is seen that the number of calls is unacceptably high even for a relatively small value of seed. It is much simpler and more straightforward to use the iterative method for evaluation of the Fibonacci function, that is, fibo ( ).
It is always possible to accomplish a task in a nonrecursive way. The trade-offs are efficiency of coding and efficiency of execution. For example, the following program will compute Fibonacci numbers nonrecursively with a higher efficiency than its iterative counterpart.
/* Non-recursive version of Fibonacci function */
long fibo(int x)
{
long fl = 1, /* fibo (n–1) */
f2 = 1, /* fibo (n–2) */
curr_fibo; /* Current value of fibo( )*/
int i;
if (x>2)
{
/* Case 1 and case 2 are handled by */
/* the else part */
for( i=3; i<=x; i++)
{
curr_fibo = fl+f2;
f2 = f1;
fl=curr_fibo;
}
return(curr_fibo);
)
else
return(1);
}
In this section, we illustrate how the cost of recursion increases exponentially when the depth of recursion increases. The depth of recursion is proportional to the number of times the function is called recursively in the process of evaluating a given argument or arguments. We will see more examples in subsequent chapters where the recursive method is more effective than the iterative method. This chapter has introduced the basic concept of recursion. The central point to remember is the fundamental difference between iteration and recursion. We described the merits and demerits of recursion in comparison with iteration. Examples are given to illustrate the idea of recursion.
E![]() X
X![]() E
E![]() R
R![]() C
C![]() I
I![]() S
S![]() E
E![]() S
S
1. Write a non-recursive routine to calculate x*y by using addition only. Assume that both x and y are non-negetive integers.
2. Write a recursive function to evaluate
s(n)=2+4+6+…+n
3. The greatest common divisor (GCD) of two integers A and B is defined as
gcd(A, B) = gcd(B, A) if A<B
A if B=0
gcd(B, A%B) if A>=B
The expression A%B yields the remainder of A upon division by B. Write a recursive routine to compute gcd(A, B). Find also a non-recursive method for computing this function.
4. The Ackeman's function is defined as follows
ack(m, n) = n+1 if m=0
ack(m-l, 1) if m!≠0 and n=0
ack(m-l, ack(m, n-1)) if m!= 0, n!= 0
Write an iterative routine to compute Ackeman's function.
5. Write a recursive function to compute the number of sequences of n binary digits that do not contain two 1s in a row.
6. We can recursively define sorting an array A as finding the biggest element in A, placing it at the beginning of A, and concatenating to it the result of sorting the remaining n–1 items in the arrey. Write a recursive routine to sort elements of an array A.
7. Write a recursive function that counts the number of times a particular key occurs in a linked list L.
8. Write a recursive C program to compute a+b using postincrement (x++) operation. Assume that a and b are non-negetive integers.
9. Write an iterative routine to implement Tower of Hanoi problem.
10. Develop a recursive function to compute the number of different ways in which an integer X can be written as a sum, each of whose operands is less than n.
