Chapter 15
Advanced relationships
At this point in the book, there are no more DAX secrets to share. In previous chapters we covered all there is to know about the syntax and the functionalities of DAX. Still, there is a long way to go. There are another two chapters dedicated to DAX, and then we will talk about optimization. The next chapter is dedicated to advanced DAX calculations. In this chapter we describe how to leverage DAX to create advanced types of relationships. These include calculated physical relationships and virtual relationships. Then, while on the topic of relationships, we want to share a few considerations about different types of physical relationships: one-to-one, one-to-many, and many-to-many. Each of these types of relationships is worth describing in its peculiarities. Moreover, a topic that still needs some attention is ambiguity. A DAX model can be—or become—ambiguous; this is a serious problem you need to be aware of, in order to handle it well.
At the end of this chapter we cover a topic that is more relevant to data modeling than to DAX, which is relationships with different granularity. When a developer needs to analyze budget and sales, they are likely working with multiple tables with different granularity. Knowing how to manage them properly is a useful skill for DAX developers.
Implementing calculated physical relationships
The first set of relationships we describe is calculated physical relationships. In scenarios where the relationship cannot be set because a key is missing, or when one needs to compute the key with complex formulas, a good option is to leverage calculated columns to set the relationship. The result is still a physical relationship; the only difference with a standard relationship is that the relationship key is a calculated column instead of being a column from the data source.
Computing multiple-column relationships
A Tabular model allows the creation of relationships based on a single column only. It does not support relationships based on multiple columns. Nevertheless, relationships based on multiple columns are useful when they appear in data models that cannot be changed. Here are two methods to work with relationships based on multiple columns:
Define a calculated column containing the composition of the keys; then use it as the new key for the relationship.
Denormalize the columns of the target table—the one-side in a one-to-many relationship—using the LOOKUPVALUE function.
As an example, consider the case of Contoso offering a “Products of the Day” promotion. On certain days, a discount is offered on a set of products. The model is visible in Figure 15-1.

The Discounts table contains three columns: Date, ProductKey, and Discount. If a developer needs this information in order to compute the amount of the discount, they are faced with a problem: for any given sale, the discount depends on ProductKey and Order Date. Thus, it is not possible to create the relationship between Sales and Discounts; it would involve two columns, and DAX only supports relationships based on a single column.
The first option is to create a new column in both Discount and Sales, containing the combination of the two columns:
Sales[DiscountKey] =
COMBINEVALUES (
"-",
Sales[Order Date],
Sales[ProductKey]
)
Discounts[DiscountKey] =
COMBINEVALUES(
"-",
Discounts[Date],
Discounts[ProductKey]
)The calculated columns use the COMBINEVALUES function. COMBINEVALUES requires a separator and a set of expressions that are concatenated as strings, separated by the separator provided. One could obtain the same result in terms of column values by using a simpler string concatenation, but COMBINEVALUES offers a few advantages. Indeed, COMBINEVALUES is particularly useful when creating relationships based on calculated columns if the model uses DirectQuery. COMBINEVALUES assumes—but does not validate—that when the input values are different, the output strings are also different. Based on this assumption, when COMBINEVALUES is used to create calculated columns to build a relationship that joins multiple columns from two DirectQuery tables, an optimized join condition is generated at query time.
![]() Note
Note
More details about optimizations obtained by using COMBINEVALUES with Direct-Query are available at https://www.sqlbi.com/articles/using-combinevalues-to-optimizedirectquery-performance/.
Once the two columns are in place, one can finally create the relationship between the two tables. Indeed, a relationship can be safely created on top of calculated columns.
This solution is straightforward and works well. Yet there are scenarios where this is not the best option because it requires the creation of two calculated columns with potentially many different values. As you learn in later chapters about optimization, this might have a negative impact on both model size and query speed.
The second option is to use the LOOKUPVALUE function. Using LOOKUPVALUE, one can denormalize the discount in the Sales table by defining a new calculated column containing the discount:
Sales[Discount] =
LOOKUPVALUE (
Discounts[Discount],
Discounts[ProductKey], Sales[ProductKey],
Discounts[Date], Sales[Order Date]
)Following this second pattern, no relationship is created. Instead, the Discount value is denormalized in the Sales table by performing a lookup.
Both options work well, and picking the right one depends on several factors. If Discount is the only column needed, then denormalization is the best option because it makes the code simple to author, and it reduces memory usage. Indeed, it requires a single calculated column with fewer distinct values compared to the two calculated columns required for a relationship.
On the other hand, if the Discounts table contains many columns needed in the code, then each of them should be denormalized in the Sales table. This results in a waste of memory and possibly in decreased processing performance. In that case, the calculated column with the new composite key might be preferable.
This simple first example is important because it demonstrates a common and important feature of DAX: the ability to create relationships based on calculated columns. This demonstrates that a user can create a new relationship, provided that they can compute and materialize the key in a calculated column. The next example demonstrates how to create relationships based on static ranges. By extending the concept, it is possible to create several kinds of relationships.
Implementing relationships based on ranges
In order to show why calculated physical relationships are a useful tool, we examine a scenario where one needs to perform a static segmentation of products based on their list price. The price of a product has many different values and performing an analysis slicing by price does not provide useful insights. In that case, a common technique is to partition the different prices into separate buckets, using a configuration table like the one in Figure 15-2.
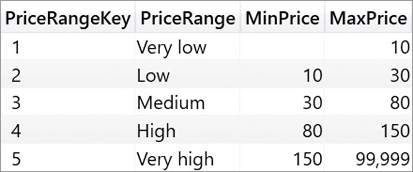
As was the case in the previous example, it is not possible to create a direct relationship between the Sales table and the Configuration table. The reason is that the key in the configuration table depends on a relationship based on a range of values (also known as a between condition), which is not supported by DAX. We could compute a key in the Sales table by using nested IF statements; however, this would require including the values of the configuration table in the formula like in the following example, which is not the suggested solution:
Sales[PriceRangeKey] =
SWITCH (
TRUE (),
Sales[Net Price] <= 10, 1,
Sales[Net Price] <= 30, 2,
Sales[Net Price] <= 80, 3,
Sales[Net Price] <= 150, 4,
5
)A good solution should not include the boundaries in the formula. Instead, the code should be designed to adapt to the contents of the table, so that updating the configuration table updates the whole model.
In this case a better solution is to denormalize the price range directly in the Sales table by using a calculated column. The pattern of the code is quite similar to the previous one—the main difference being the formula, which, this time, cannot be a simple LOOKUPVALUE:
Sales[PriceRange] =
VAR FilterPriceRanges =
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
VAR Result =
CALCULATE (
VALUES ( PriceRanges[PriceRange] ),
FilterPriceRanges
)
RETURN
ResultIt is interesting to note the usage of VALUES to retrieve a single value: VALUES returns a table, not a value. However, as explained in Chapter 3, “Using basic table functions,” whenever a table contains a single row and a single column, the table is automatically converted into a scalar value if required by the expression.
Because of the way FILTER computes its result, it always returns a single row from the configuration table. Therefore, VALUES is guaranteed to always return a single row; the result of CALCULATE is thus the description of the price range containing the net price of the current row in the Sales table. This expression works well if the configuration table is well designed. But if the ranges contain holes or overlaps in range of values, then VALUES might return multiple rows, and the expression might result in an error.
The previous technique denormalizes values in the Sales table. Going one step further means denormalizing the key instead of the description and then building a physical relationship based on the new calculated column. This additional step requires some level of attention in the definition of the calculated column. A simple modification of the PriceRange column is enough to retrieve the key, but it is still not enough to create the relationship. The following is the code required to retrieve the key and blank the result in case of errors:
Sales[PriceRangeKey] =
VAR FilterPriceRanges =
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
VAR Result =
CALCULATE (
IFERROR (
VALUES ( PriceRanges[PriceRangeKey] ),
BLANK ()
),
FilterPriceRanges
)
RETURN
ResultThe column computes the correct value. Unfortunately, trying to build the relationship between PriceRanges and Sales based on the newly created PriceRangeKey column results in an error because of a circular dependency. Circular dependencies frequently occur when creating relationships based on calculated columns or calculated tables.
In this example, the fix is indeed simple: you need to use DISTINCT instead of VALUES in the highlighted row of the formula. Once DISTINCT is in place, the relationship can be created. The result is visible in Figure 15-3.
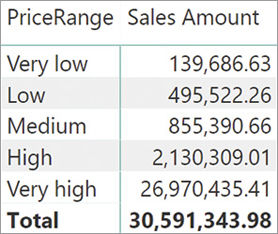
Prior to using DISTINCT, the presence of VALUES would generate a circular dependency. Replacing VALUES with DISTINCT works like magic. The underlying mechanisms are quite intricate. The next section provides a complete explanation of circular dependencies that might appear because of relationships with calculated columns or calculated tables, along with a complete explanation of why DISTINCT removes the problem.
Understanding circular dependency in calculated physical relationships
In the previous example, we created a calculated column and then used it in a relationship. This resulted in a circular dependency error. As soon as you start working with calculated physical relationships, this error can appear quite often. Therefore, it is useful to spend some time understanding exactly the source of the error. This way, you will also learn how to avoid it.
Let us recall the code of the calculated column in its shorter form:
Sales[PriceRangeKey] =
CALCULATE (
VALUES ( PriceRanges[PriceRangeKey] ),
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
)The PriceRangeKey column depends on the PriceRanges table. If a change is detected in the PriceRanges table, then Sales[PriceRangeKey] must be recalculated. Because the formula contains several references to the PriceRanges table, the dependency is clear. What is less obvious is that creating a relationship between this column and the PriceRanges table creates a dependency the other way around.
In Chapter 3 we mentioned that the DAX engine creates a blank row on the one-side of a relationship if the relationship is invalid. Thus, when a table is on the one-side of a relationship, its content depends on the validity of the relationship. In turn, the validity of the relationship depends on the content of the column used to set the relationship.
In our scenario, if one could create a relationship between Sales and PriceRanges based on Sales[PriceRangeKey], then PriceRanges might have a blank row or not, depending on the value of Sales[PriceRangeKey]. In other words, when the value of Sales[PriceRangeKey] changes, the content of the PriceRanges table might also change. But in turn, if the value of PriceRanges changes, then Sales[PriceRangeKey] might require an update—even though the added blank row should never be used. This is the reason why the engine detects a circular dependency. It is hard to spot for a human, but the DAX algorithm finds it immediately.
If the engineers who created DAX had not worked on the problem, it would have been impossible to create relationships based on calculated columns. Instead, they added some logic in DAX specifically to handle scenarios like this.
Instead of having only one kind of dependency, in DAX there are two types of dependencies: formula dependency and blank row dependency. In our example, this is the situation:
Sales[PriceRangeKey] depends on PriceRanges both because of the formula (it references the PriceRanges table) and because of the blank row (it uses the VALUES function, which might return the additional blank row).
PriceRanges depends on Sales[PriceRangeKey] only because of the blank row. A change in the value of Sales[PriceRangeKey] does not change the content of PriceRanges. It only affects the presence of the blank row.
To break the chain of the circular dependency, it is enough to break the dependency of Sales[PriceRangeKey] from the presence of the blank row in PriceRanges. This can be obtained by making sure that all the functions used in the formula do not depend on the blank row. VALUES includes the additional blank row if present. Therefore, VALUES depends on the blank row. DISTINCT, on the other hand, always has the same value, regardless of the presence of the additional blank row. Consequently, DISTINCT does not depend on the blank row.
If you use DISTINCT instead of VALUES, then Sales[PriceRangeKey] no longer depends on the blank row. The net effect is that the two entities—the table and the column—still depend on each other, but for different reasons. PriceRanges depends on Sales[PriceRangeKey] for the blank row, whereas Sales[PriceRangeKey] depends on Sales because of the formula. Being two unrelated dependencies, the circular dependency disappears and it is possible to create the relationship.
Whenever creating columns that might later be used to set relationships, you need to pay special attention to the following details:
Using DISTINCT instead of VALUES.
Using ALLNOBLANKROW instead of ALL.
Beware of CALCULATE with filters using the compact syntax.
The first two points are quite clear. The following elaborates on the last point—paying attention to CALCULATE. For example, consider the following expression:
=
CALCULATE (
MAX ( Customer[YearlyIncome] ),
Customer[Education] = "High school"
)At first sight, it looks like this formula does not depend on the blank row in Customer. But in fact, it does. The reason is that DAX expands the syntax of CALCULATE with the compact syntax of a filter argument, into a complete filter over a table corresponding to the following code:
=
CALCULATE (
MAX ( Customer[YearlyIncome] ),
FILTER (
ALL ( Customer[Education] ),
Customer[Education] = "High school"
)
)The highlighted row containing the ALL function creates a dependency on the blank row. In general, blank row dependencies might be hard to spot. But once you understand the basic principle of circular dependencies, they are not complex to remove. The previous example can easily be rewritten this way:
=
CALCULATE (
MAX ( Customer[YearlyIncome] ),
FILTER (
ALLNOBLANKROW ( Customer[Education] ),
Customer[Education] = "High school"
)
)By using ALLNOBLANKROW instead of ALL, the dependency on the additional blank row in Customer table disappears.
It is important to note that often, the presence of functions that rely on the blank row is hidden within the code. As an example, consider the code used in the previous section where we created the calculated physical relationship based on the price range. Here is the original code:
Sales[PriceRangeKey] =
CALCULATE (
VALUES ( PriceRanges[PriceRangeKey] ),
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
)In the previous formula, the presence of VALUES is very clear. Yet, a different way to author the same code without using VALUES is to rely on SELECTEDVALUE, which does not return an error in case multiple rows are visible:
Sales[PriceRangeKey] =
VAR FilterPriceRanges =
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
VAR Result =
CALCULATE (
SELECTEDVALUE ( PriceRanges[PriceRangeKey] ),
FilterPriceRanges
)
RETURN ResultUnfortunately, as soon as you try to create the relationship, this code raises a circular dependency error too, although it looks like VALUES is not present. Indeed, though hidden, VALUES is present. The reason is that SELECTEDVALUE internally implements the following logic:
Sales[PriceRangeKey] =
VAR FilterPriceRanges =
FILTER (
PriceRanges,
AND (
PriceRanges[MinPrice] <= Sales[Net Price],
PriceRanges[MaxPrice] > Sales[Net Price]
)
)
VAR Result =
CALCULATE (
IF (
HASONEVALUE ( PriceRanges[PriceRangeKey] ),
VALUES ( PriceRanges[PriceRangeKey] ),
BLANK ()
),
FilterPriceRanges
)
RETURN
ResultBy expanding the code of SELECTEDVALUES, now the presence of VALUES is more evident. Hence, so is the dependency on the blank row that generates the circular dependency.
Implementing virtual relationships
In the previous sections we discussed how to leverage calculated columns to create physical relationships. However, there are scenarios where a physical relationship is not the right solution and virtual relationships are a better approach. A virtual relationship mimics a real relationship. From a user point of view, a virtual relationship looks like a real relationship although there is no relationship in the physical model. Because there is no relationship, you need to author DAX code to transfer a filter from one table to another.
Transferring filters in DAX
One of the most powerful features of DAX is its ability to move a filter from one table to another by following relationships. Yet, there are scenarios where it is hard—if not impossible—to create a physical relationship between two entities. A DAX expression can mimic the relationship in multiple ways. This section shows a few techniques by using a somewhat elaborate scenario.
Contoso advertises in local newspapers and on the web, choosing one or more brands to promote each month. This information is stored in a table named Advertised Brands that contains the year, the month, and the brand—if any—on sale. You can see an excerpt of the table in Figure 15-4.
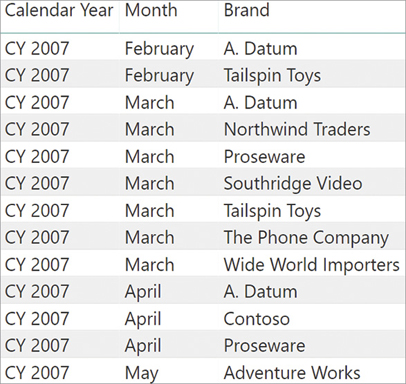
It is important to note that there is no unique column in the table. Although all the rows are unique, each column has many duplicates. Therefore, the table cannot be on the one-side of a relationship. This fact becomes of higher importance as soon as we further outline the requirements.
The requirement is to create a measure that computes the sales amount of the products, only within the time period when they were being advertised. In order to solve that scenario, it is necessary to determine whether a brand is being advertised or not in a given month. If it were possible to create a relationship between Sales and the Advertised Brands table, the code would be simple to author. Unfortunately, the relationship is not easy to create (and this is by design for the purpose of this teaching).
One possible solution is to create a new calculated column in both tables containing the concatenation of year, month, and brand. This follows the technique outlined earlier in this chapter, to create a relationship between two tables based on multiple columns. Nevertheless, in this scenario there are other interesting alternatives worth exploring that avoid the creation of new calculated columns.
A first yet suboptimal solution is to rely on iterations. One could iterate the Sales table row by row, and on each row check if the brand of the product being sold was being advertised in that month. Thus, the following measure solves the scenario, but it is not the best solution:
Advertised Brand Sales :=
SUMX (
FILTER (
Sales,
CONTAINS (
'Advertised Brands',
'Advertised Brands'[Brand], RELATED ( 'Product'[Brand] ),
'Advertised Brands'[Calendar Year], RELATED ( 'Date'[Calendar Year] ),
'Advertised Brands'[Month], RELATED ( 'Date'[Month] )
)
),
Sales[Quantity] * Sales[Net Price]
)The measure uses the CONTAINS function, which searches for the presence of a row in a table. CONTAINS accepts the table to search in as its first parameter. Following are pairs of parameters: the first one being a column in the table to search and the second one being the value to search. In the example, CONTAINS returns True if in Advertised Brands there is at least one row where the brand is the current brand, the year is the current year, and the month is the current month—where “current” means the Sales row currently iterated by FILTER.
The measure computes a correct result, as shown in Figure 15-5, but there are several issues.

Here are the two most problematic issues of the previous code:
FILTER iterates over Sales—which is a large table—and for each row it calls the CONTAINS function. Even though CONTAINS is a fast function, calling it millions of times results in poor performance.
The measure does not take advantage of the presence of the Sales Amount measure, which already computes the sales amount. In this case the duplicated code is a simple multiplication, but if the measure to compute were more complex, this approach would not be the best. Indeed, it requires duplicating the expression to compute within the iteration.
A much better option to solve the scenario is to use CALCULATE to transfer the filter from the Advertised Brands table both to the Product table (using the brand as a filter) and to the Date table (using the year and the month). This can be accomplished in several ways, as shown in the next sections.
Transferring a filter using TREATAS
The first and best option is using TREATAS to move the filter from the Advertised Brands over to the other tables. As explained in Chapters 10, “Working with the filter context,” 12, “Working with tables,” and 13, “Authoring queries,” TREATAS changes the data lineage of a table so that its content can be used as a filter on specific columns of the data model.
Advertised Brands has no relationships with any other table in the model. Thus, normally its content cannot be used as a filter. By using TREATAS, one can change the data lineage of Advertised Brands so that it can be used as a filter argument of CALCULATE and propagate its filter to the entire model. The following measure performs exactly this operation:
Advertised Brand Sales TreatAs :=
VAR AdvertisedBrands =
SUMMARIZE (
'Advertised Brands',
'Advertised Brands'[Brand],
'Advertised Brands'[Calendar Year],
'Advertised Brands'[Month]
)
VAR FilterAdvertisedBrands =
TREATAS (
AdvertisedBrands,
'Product'[Brand],
'Date'[Calendar Year],
'Date'[Month]
)
VAR Result =
CALCULATE ( [Sales Amount], KEEPFILTERS ( FilterAdvertisedBrands ) )
RETURN
ResultSUMMARIZE retrieves the brand, year, and month advertised. TREATAS receives this table and changes its lineage, so that it will filter the product brand and the year and month in Date. The resulting table in FilterAdvertisedBrands has the correct data lineage. Therefore, it filters the model showing only the brands in the year and month when they are being advertised.
It is important to note that KEEPFILTERS is required. Indeed, forgetting it means that CALCULATE will override the filter context on the brand, year, and month—and this is unwanted. The Sales table needs to receive both the filter coming from the visual (which might be filtering only one year or one brand) and the filter coming from the Advertised Brands table. Therefore, KEEPFILTERS is mandatory to obtain a correct result.
This version of the code is much better than the one using the iteration. It uses the Sales Amount measure, thus avoiding the need to rewrite its code, and it does not iterate over the Sales table to perform the lookup. This code only scans the Advertised Brands table, which is expected to be on the smaller side; it then applies the filter to the model prior to calling the Sales Amount measure. Even though this version might be less intuitive, it performs much better than the example based on CONTAINS shown in the previous section.
Transferring a filter using INTERSECT
Another option to obtain the same result is to use the INTERSECT function. Compared to the previous example using TREATAS, the logic is similar; performance-wise there is a small difference in favor of the TREATAS version, which is still the best option. The following code implements the technique based on INTERSECT:
Advertised Brand Sales Intersect :=
VAR SelectedBrands =
SUMMARIZE (
Sales,
'Product'[Brand],
'Date'[Calendar Year],
'Date'[Month]
)
VAR AdvertisedBrands =
SUMMARIZE (
'Advertised Brands',
'Advertised Brands'[Brand],
'Advertised Brands'[Calendar Year],
'Advertised Brands'[Month]
)
VAR Result =
CALCULATE (
[Sales Amount],
INTERSECT (
SelectedBrands,
AdvertisedBrands
)
)
RETURN
ResultINTERSECT retains the data lineage of the first table it receives. Therefore, the resulting table is still a table that can filter Product and Date. This time, KEEPFILTERS is not needed because the first SUMMARIZE already only contains the visible brands and months; INTERSECT only removes from this list the ones that are not being advertised.
From a performance point of view, this code requires a scan of the Sales table to produce the list of existing brands and months, plus another scan to compute the sales amount. Therefore, it is slower than the version using TREATAS. But it is worth learning this technique because it might be useful in other scenarios involving other set functions, like UNION and EXCEPT. The set functions in DAX can be combined to create filters, authoring powerful measures in a relatively simple way.
Transferring a filter using FILTER
A third alternative is available to the DAX developer: using FILTER and CONTAINS. The code is similar to the first version with SUMX—the main differences being that it uses CALCULATE instead of SUMX, and it avoids iterating over the Sales table. The following code implements this alternative:
Advertised Brand Sales Contains :=
VAR SelectedBrands =
SUMMARIZE (
Sales,
'Product'[Brand],
'Date'[Calendar Year],
'Date'[Month]
)
VAR FilterAdvertisedBrands =
FILTER (
SelectedBrands,
CONTAINS (
'Advertised Brands',
'Advertised Brands'[Brand], 'Product'[Brand],
'Advertised Brands'[Calendar Year], 'Date'[Calendar Year],
'Advertised Brands'[Month], 'Date'[Month]
)
)
VAR Result =
CALCULATE (
[Sales Amount],
FilterAdvertisedBrands
)
RETURN
ResultThe FILTER function used as a filter argument to CALCULATE uses the same CONTAINS technique used in the first example. This time, instead of iterating Sales, it iterates over the result of SUMMARIZE. As explained in Chapter 14, “Advanced DAX concepts,” using the Sales table as a filter argument in CALCULATE would be wrong because of the expanded table. Therefore, filtering only three columns is a better approach. The result of SUMMARIZE already has the correct data lineage; moreover, KEEPFILTERS is not required because SUMMARIZE already only retains the existing values for brand, year, and month.
Performance-wise this is the worst solution among the last three, even though it is faster than the original code based on SUMX. Moreover, all the solutions based on CALCULATE share the significant advantage that they do not need to duplicate the business logic of the calculation included in the Sales Amount measure, as our first trial with SUMX did.
Implementing dynamic segmentation using virtual relationships
In all the variations demonstrated earlier, we used DAX code to compute values and transfer a filter in absence of a relationship, though it would have been possible to create a physical relationship modifying the data model. However, there are scenarios where the relationship cannot be created in any way, like the one described in this section.
The virtual relationship solves a variation of the static segmentation learned earlier in this chapter. In the static segmentation, we assigned each sale to a specific segment using a calculated column. In dynamic segmentation, the assignment occurs dynamically; also, it is not based on a column like the net price but rather on a calculation like the sales amount. The dynamic segmentation must have a filter target: In this example, the segmentation filters customers based on the Sales Amount measure.
The configuration table contains the segment names and their boundaries, as shown in Figure 15-6.

If a customer spends between 75 and 100 USD in one sale, then they are assigned to the Low segment as per the configuration table. One important detail about dynamic segmentation is that the value of the measure depends on the user selection in the report. For example, if a user selects one color, then the assignment of a customer to a segment must be executed only considering the sales of products of that given color. Because of this dynamic calculation, using a relationship is not an option. Consider the following report in Figure 15-7 that shows how many customers belong to each segment every year, only filtering a selection of categories.
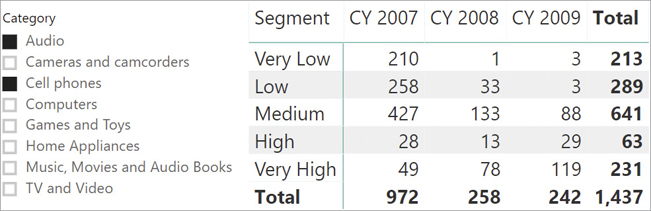
One customer might belong to different segments over the years. One customer can be in the Very Low segment in 2008 and then move to the Medium segment the next year. Moreover, by changing the selection on the categories, all the numbers must be updated accordingly.
In other words, a user browsing the model has the perception that a relationship is indeed present, meaning that each customer is uniquely assigned to one segment. However, this assignment cannot be made by using a physical relationship. The reason is that the same customer can be assigned to different segments in different cells of the report. In this scenario, DAX is the only way to solve the problem.
The measure to compute is the number of customers belonging to a specific segment. In other words, the measure counts how many customers belong to a segment considering all the filters in the current filter context. The formula looks simple, and yet its behavior requires a little clarification:
CustInSegment :=
SUMX (
Segments,
COUNTROWS (
FILTER (
Customer,
VAR SalesOfCustomer = [Sales Amount]
VAR IsCustomerInSegment =
AND (
SalesOfCustomer > Segments[MinSale],
SalesOfCustomer <= Segments[MaxSale]
)
RETURN
IsCustomerInSegment
)
)
)Apart from the grand total, every row of the report in Figure 15-7 has a filter context filtering one segment only. Thus, SUMX iterates only one row. SUMX is useful to make it easy to retrieve the segment boundaries (MinSale and MaxSale) and to correctly compute the total in the presence of filters. Inside SUMX, COUNTROWS counts the number of customers whose sales (saved in the SalesOfCustomer variable for performance reasons) fall between the boundaries of the current segment.
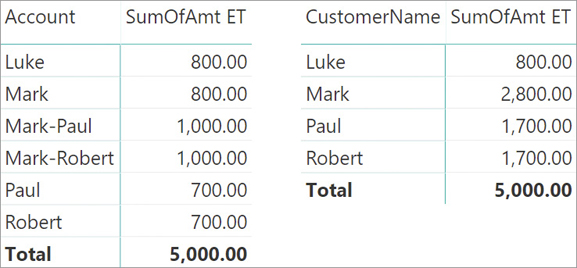
The resulting measure is additive against segments and customers, and nonadditive against all other filters. You can note that in the first row of the report, the Total result 213 is lower than the sum of the three years, which is 214. The reason is that at the Total level, the formula counts the number of customers that are in the Very Low segment over the three years. It appears that one of those customers bought enough products in three years to be moved to the next segment at the total level.
Though it is somewhat counterintuitive, the nonadditive behavior over time is a good feature. Indeed, to make it additive over the years, one would need to update the formula to include the time as part of the calculation. For instance, the following version of the code is additive over time. Yet, it is less powerful because one can no longer produce meaningful results if the year is not part of the report:
CustInSegment Additive :=
SUMX (
VALUES ( 'Date'[Calendar Year] ),
SUMX (
Segments,
COUNTROWS (
FILTER (
Customer,
VAR SalesOfCustomer = [Sales Amount]
VAR IsCustomerInSegment =
AND (
SalesOfCustomer > Segments[MinSale],
SalesOfCustomer <= Segments[MaxSale]
)
RETURN
IsCustomerInSegment
)
)
)
)As shown in Figure 15-8, the rows now sum up correctly in the Total column, even though the Grand Total—that is, the total of all years and segments—might be inaccurate.
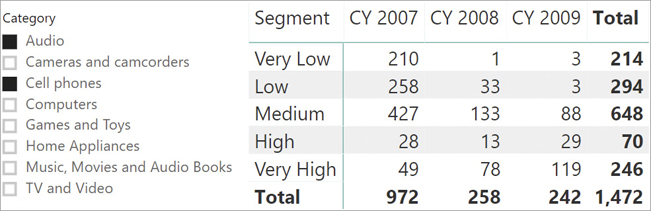
The problem is that by obtaining the correct sum for one segment, one needs to sacrifice the grand total cumulating multiple segments and years. For example, one customer might be in the Very Low cluster in 2009 and in the Very High cluster in 2008; therefore, in the Grand Total they would be counted twice. The Grand Total shown in Figure 15-8 is 1,472, whereas the total number of customers is 1,437 as reported accurately in Figure 15-7.
Unfortunately with these kinds of calculations, additivity is more of a problem than a feature. By nature these calculations are nonadditive. Trying to make them additive might be appealing at first sight, but it is likely to produce misleading results. Therefore, it is always important to pay attention to these details, and our suggestion is to not force a measure to be additive without carefully considering the implications of that choice.
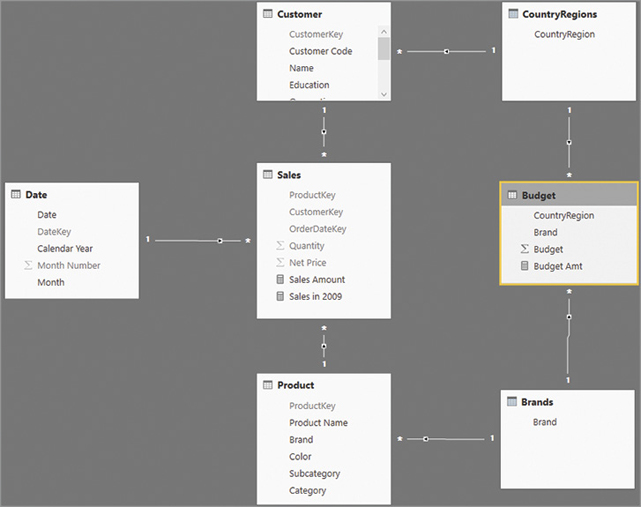
Understanding physical relationships in DAX
A relationship can be strong or weak. In a strong relationship the engine knows that the one-side of the relationship contains unique values. If the engine cannot check that the one-side of the relationship contains unique values for the key, then the relationship is weak. A relationship can be weak because either the engine cannot ensure the uniqueness of the constraint, due to technical reasons we outline later in this section, or the developer defined it as such. A weak relationship is not used as part of table expansion described in Chapter 14.
Starting from 2018, Power BI allows composite models. In a composite model it is possible to create tables in a model containing data in both VertiPaq mode (a copy of data from the data source is preloaded and cached in memory) and in DirectQuery mode (the data source is accessed only at query time). DirectQuery and VertiPaq engines are explained in Chapter 17, “The DAX engines.”
A single data model can contain some tables stored in VertiPaq and some others stored in DirectQuery. Moreover, tables in DirectQuery can originate from different data sources, generating several DirectQuery data islands.
In order to differentiate between data in VertiPaq and data in DirectQuery, we talk about data in the continent (VertiPaq) or in the islands (DirectQuery data sources), as depicted in Figure 15-9.
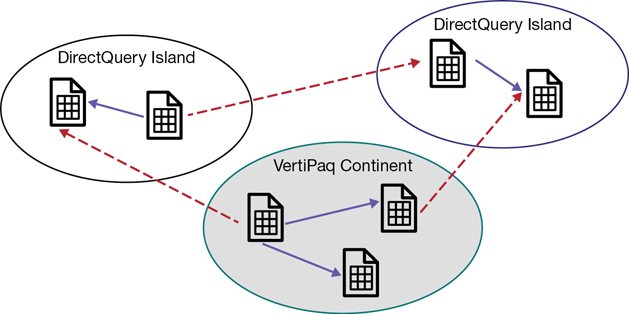
The VertiPaq store is nothing but another data island. We call it the continent only because it is the most frequently used data island.
A relationship links two tables. If both tables belong to the same island, then the relationship is an intra-island relationship. If the two tables belong to different islands, then it is a cross-island relationship. Cross-island relationships are always weak relationships. Therefore, table expansion never crosses islands.
Relationships have a cardinality, of which there are three types. The difference between them is both technical and semantical. Here we do not cover the reasoning behind those relationships because it would involve many data modeling digressions that are outside of the scope of the book. Instead, we need to cover the technical details of physical relationships and the impact they have on the DAX code.
These are the three types of relationship cardinality available:
One-to-many relationships: This is the most common type of relationship cardinality. On the one-side of the relationship the column must have unique values; on the many-side the value can (and usually does) contain duplicates. Some client tools differentiate between one-to-many relationships and many-to-one relationships. Still, they are the same type of relationship. It all depends on the order of the tables: a one-to-many relationship between Product and Sales is the same as a many-to-one relationship between Sales and Product.
One-to-one relationships: This is a rather uncommon type of relationship cardinality. On both sides of the relationship the columns need to have unique values. A more accurate name would be “zero-or-one”-to-“zero-or-one” relationship because the presence of a row in one table does not imply the presence of a corresponding row in the other table.
Many-to-many relationships: On both sides of the relationship the columns can have duplicates. This feature was introduced in 2018, and unfortunately its name is somewhat confusing. Indeed, in common data modeling language “many-to-many” refers to a different kind of implementation, created by using pairs of one-to-many and many-to-one relationships. It is important to understand that in this scenario many-to-many does not refer to the many-to-many relationship but, instead, to the many-to-many cardinality of the relationship.
In order to avoid ambiguity between the canonical terminology, which uses many-to-many for a different kind of implementation, we use acronyms to describe the cardinality of a relationship:
One-to-many relationship: We call them SMR, which stands for Single-Many-Relationship.
One-to-one relationship : We use the acronym SSR, which stands for Single-Single-Relationship.
Many-to-many relationship: We call them MMR, which stands for Many-Many-Relationship.
Another important detail is that an MMR relationship is always weak, regardless of whether the two tables belong to the same island or not. If the developer defines both sides of the relationship as the many-side, then the relationship is automatically treated as a weak relationship, with no table expansion happening.
In addition, each relationship has a cross-filter direction. The cross-filter direction is the direction used by the filter context to propagate its effect. The cross-filter can be set to one of two values:
Single: The filter context is always propagated in one direction of the relationship and not the other way around. In a one-to-many relationship, the direction is always from the one-side of the relationship to the many-side. This is the standard and most desirable behavior.
Both: The filter context is propagated in both directions of the relationship. This is also called a bidirectional cross-filter and sometimes just a bidirectional relationship. In a one-to-many relationship, the filter context still retains its feature of propagating from the one-side to the many-side, but it also propagates from the many-side to the one-side.
The cross-filter directions available depend on the type of relationship.
In an SMR relationship one can always choose single or bidirectional.
An SSR relationship always uses bidirectional filtering. Because both sides of the relationship are the one-side and there is no many-side, bidirectional filtering is the only option available.
In an MMR relationship both sides are the many-side. This scenario is the opposite of the SSR relationship: Both sides can be the source and the target of a filter context propagation. Thus, one can choose the cross-filter direction to be bidirectional, in which case the propagation always goes both ways. Or if the developer chooses single propagation, they also must choose which table to start the filter propagation from. As with all other relationships, single propagation is the best practice. Later in this chapter we expand on this topic.
Table 15-1 summarizes the different types of relationships with the available cross-filter directions, their effect on the filter context propagation, and the options for weak/strong relationship.
Table 15-1 Different types of relationships
Type of Relationship |
Cross-filter Direction |
Filter Context Propagation |
Weak / Strong Type |
|---|---|---|---|
SMR |
Single |
From the one side to the many side |
Weak if cross-island, strong otherwise |
SMR |
Both |
Bidirectional |
Weak if cross-island, strong otherwise |
SSR |
Both |
Bidirectional |
Weak if cross-island, strong otherwise |
MMR |
Single |
Must choose the source table |
Always weak |
MMR |
Both |
Bidirectional |
Always weak |
When two tables are linked through a strong relationship, the table on the one-side might contain the additional blank row in case the relationship is invalid. Thus, if the many-side of a strong relationship contains values not present in the table on the one-side, then a blank row is appended to the one-side table. This was further explained in Chapter 3. The additional blank row is never added to a weak relationship.
As explained earlier, we are not going to discuss why one would choose one type of relationship over another. The choice between different types of relationships and filter propagation is in the hands of the data modeler; their decision flows from a deep reasoning on the semantics of the model itself. However, from a DAX point of view each relationship behaves differently, and it is important to understand the differences among the relationships and the impact they have on DAX code.
The next sections provide useful information about the differences between these types of relationships and several tips on which relationship to use in your models.
Using bidirectional cross-filters
Bidirectional cross-filters can be enabled in two ways: in the data model or by using the CROSSFILTER modifier in a CALCULATE function, as explained in Chapter 5, “Understanding CALCULATE and CALCULATETABLE.” As a rule, a bidirectional cross-filter should not be enabled in the data model unless strictly needed. The reason is that bidirectional cross-filters quickly increase the complexity of the filter context propagation, up to a point where it is hard to predict and control how the filter context will propagate.
Nevertheless, there are scenarios where bidirectional cross-filtering is a useful feature. For example, look at the report in Figure 15-10; it is built on top of the usual Contoso model with all relationships set to single cross-filter propagation.
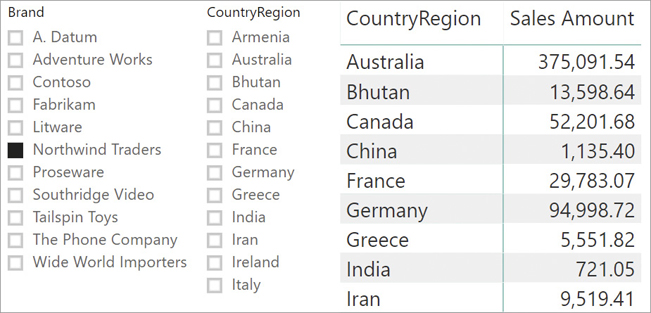
There are two slicers: Brand, which filters the Product[Brand] column; and CountryRegion, which filters the Customer[CountryRegion] column. Even though there are no sales for Northwind Traders in Armenia, the CountryRegion slicer shows Armenia as valid options to select.
The reason for this is that the filter context on Product[Brand] affects Sales because of the one-to-many relationship between Product and Brand. But then from Sales, the filter does not move to Customer because Customer is on the one-side of the one-to-many relationship between Customer and Sales. Therefore, the slicer shows all the possible values of CountryRegion. In other words, the two slicers are not in sync. The matrix does not show Armenia because the value of Sales Amount is a blank for this country, and by default a matrix does not show rows containing blank values from measures.
If slicer syncing is important, then it is possible to enable the bidirectional cross-filter between Customer and Sales, generating a model like the one in Figure 15-11.
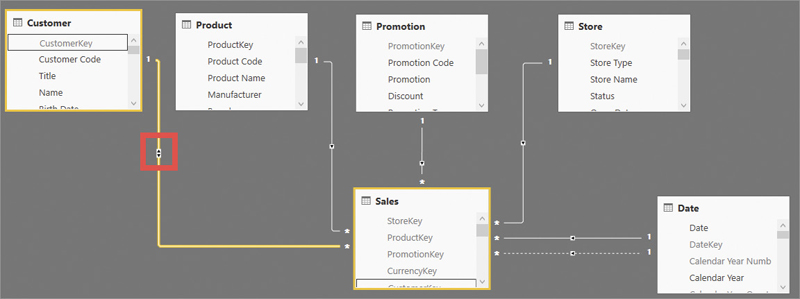
Setting the cross-filter direction of the relationship to bidirectional ensures that the CountryRegion slicer only shows the rows that are referenced by Sales. Figure 15-12 shows that the slicers are now synced, improving user experience.

Bidirectional filtering is convenient, but it comes at a price. First, from a performance point of view, the bidirectional cross-filter slows down the model because the filter context must be propagated to both sides of the relationship. It is much faster to filter the many-side starting from the one-side rather than going in the opposite direction. Thus, with the goal of optimal performance in mind, bidirectional cross-filtering is one of the features to avoid. Moreover, bidirectional cross-filters increase chances to generate ambiguous data models. We discuss ambiguity later in this chapter.
![]() Note
Note
Using visual level filters, it is possible to reduce the members visible in a Power BI visual without using the bidirectional filter in a relationship. Unfortunately, visual level filters are not supported for slicers in Power BI as of April 2019. Once visual level filters will also be available for slicers, using bidirectional filters will be no longer necessary to reduce the members visible in a slicer.
Understanding one-to-many relationships
One-to-many relationships are the most common and desirable type of relationships in a data model. For example, a one-to-many relationship relates Product with Sales. Given one product there can be many sales related to it, whereas for one given sale there is only one product. Consequently, Product is on the one-side and Sales is on the many-side.
Moreover, when analyzing data, users expect to be able to slice by a product attribute and compute values from Sales. Therefore, the default behavior is that a filter on Product (one-side) is propagated to Sales (many-side). If needed, one can change this behavior by enabling a bidirectional cross-filter in the relationship.
With strong one-to-many relationships, table expansion always goes towards the one-side. Moreover, in case the relationship is invalid, the table sitting on the one-side of the relationship might receive the blank row. Semantically, weak one-to-many relationships behave the same, except from the blank row. Performance-wise, weak one-to-many relationships generally generate slower queries.
Understanding one-to-one relationships
One-to-one relationships are quite uncommon in data models. Two tables linked through a one-to-one relationship are really just the same table split into two. In a well-designed model, these two tables would have been joined together before being loaded into the data model.
Therefore, the best way to handle one-to-one relationships is to avoid them by merging the two tables into a single table. One exception to this best practice is when data is going into one same business entity from different data sources that must be refreshed independently. In those cases, one might prefer to import two separate tables into the data model, avoiding complex and expensive transformations during the refresh operation. In any case, when handling one-to-one relationships, users need to pay attention to the following details:
The cross-filter direction is always bidirectional. One cannot set the cross-filter direction to single on a one-to-one relationship. Thus, a filter on one of the two tables is always propagated to the other table, unless the relationship is deactivated—either by using CROSSFILTER or in the model.
From a table expansion point of view, as described in Chapter 14 in a strong one-to-one relationship each table expands the other table that is part of that relationship. In other words, a strong one-to-one relationship produces two identical expanded tables.
Because both sides of the relationship are on the one-side, if the relationship is both strong and invalid—that is, there are values for the key in one table that are not matched in the other—then both tables might contain the blank row. Moreover, the values of the column used for the relationship need to be unique in both tables.
Understanding many-to-many relationships
Many-to-many relationships are an extremely powerful modeling tool, and they appear much more often than one-to-one relationships. Handling them correctly is not trivial, yet it is useful to master them because of their analytical power.
A many-to-many relationship is present in a model whenever two entities cannot be related through a simple one-to-many relationship. There are two different types of many-to-many relationships, and several ways to solve the two scenarios. The next sections present several techniques to manage many-to-many relationships.
Implementing many-to-many using a bridge table
The following example comes from a banking scenario. The bank stores accounts in one table and customers in a different table. One account can be owned by multiple customers, while one customer may own multiple accounts. Therefore, it is not possible to store the customer name in the account, and at the same time it is not possible to store the account number in the customer table. This scenario cannot be modeled by using regular relationships between accounts and customers.
The canonical solution to this scenario is to build a table to store the relationship between customers and accounts. This is called a bridge table, and is shown in the model in Figure 15-13.
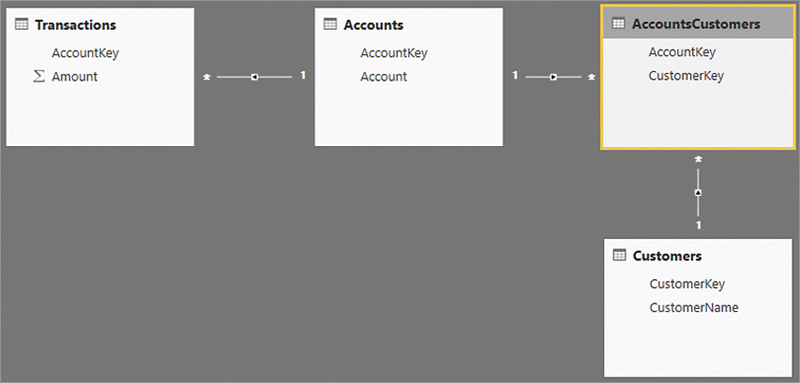
In this model, the many-to-many relationship between Account and Customers is implemented through the bridge table called AccountsCustomers. A row in the bridge table indicates that one account is owned by one customer.
As it is now, the model is not working yet. Indeed, a report slicing by Account works well because Accounts filters Transactions, Accounts being on the one-side of a one-to-many relationship. On the other hand, slicing by Customers does not work because Customers filters AccountsCustomers, but then AccountsCustomers does not propagate the filter to Accounts because the cross-filter goes in the other direction. Moreover, this last relationship must have its one-side on the Accounts table because AccountKey has unique values in Accounts and contains duplicates in AccountsCustomers.
Figure 15-14 shows that the CustomerName values do not apply any kind of filter to the sum of Amount displayed in the matrix.

This scenario can be solved by enabling the bidirectional cross-filter in the relationship between AccountsCustomers and Accounts; this is achieved either by updating the data model or by using CROSSFILTER as in the following measure:
-- Version using CROSSFILTER
SumOfAmt CF :=
CALCULATE (
SUM ( Transactions[Amount] ),
CROSSFILTER (
AccountsCustomers[AccountKey],
Accounts[AccountKey],
BOTH
)
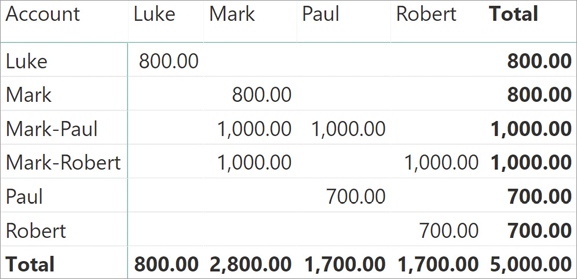
)Either way, the formula will now produce the expected result, as shown in Figure 15-15.
Setting the bidirectional cross-filter in the data model has the advantage of ensuring that it is automatically applied to any calculation—also working on implicit measures generated by client tools such as Excel or Power BI. However, the presence of bidirectional cross-filters in a data model increases the complexity of the filter propagation and might have a negative impact on the performance of measures that should not be affected by said filter. Moreover, if new tables are later added to the data model, the presence of the bidirectional cross-filter might generate ambiguities that require a change in the cross-filter. This could potentially break other, pre-existing reports. For these reasons, before enabling bidirectional cross-filters on a relationship, one should think twice and carefully check that the model is still sound.
You are of course free to use bidirectional cross-filter in your models. But for all the reasons described in the book, our personal attitude is to never enable bidirectional cross-filter on a relationship. Because we love simplicity and sound models, we strongly prefer the CROSSFILTER solution applied to every measure. Performance-wise, enabling the bidirectional cross-filter in the data model or using CROSSFILTER in DAX is identical.
Another way of achieving our goal is by using more complex DAX code. Despite its complexity, that code also brings an increased level of flexibility. One option to author the SumOfAmt measure without using CROSSFILTER is to rely on SUMMARIZE and use it as a CALCULATE filter argument:
-- Version using SUMMARIZE
SumOfAmt SU :=
CALCULATE (
SUM ( Transactions[Amount] ),
SUMMARIZE (
AccountsCustomers,
Accounts[AccountKey]
)
)SUMMARIZE returns a column with the data lineage of Accounts[AccountKey], actively filtering the Accounts and then the Transactions table. Another way of obtaining a similar result is by using TREATAS:
-- Version using TREATAS
SumOfAmt TA :=
CALCULATE (
SUM ( Transactions[Amount] ),
TREATAS (
VALUES ( AccountsCustomers[AccountKey] ),
Accounts[AccountKey]
)
)Also in this case, VALUES returns the values of AccountsCustomers[AccountKey] filtered by the Customers table, and TREATAS changes the data lineage to make it filter the Accounts and then the Transactions table.
Lastly, an even simpler formulation of the same expression is to use table expansion. Noting that the bridge table expands to both the Customers and the Accounts tables, the following code produces almost the same result as the previous ones. It is, however, noticeably shorter:
-- Version using Expanded Table
SumOfAmt ET :=
CALCULATE (
SUM ( Transactions[Amount] ),
AccountsCustomers
)Despite the many variations, all these solutions can be grouped into two options:
Using the bidirectional cross-filter feature of DAX.
Using a table as a filter argument in CALCULATE.
These two groups behave differently if the relationship between Transactions and Accounts is invalid. Indeed, if a relationship is invalid, the table on the one-side of the relationship contains an additional blank row. In case the Transactions table relates to accounts that are not available in the Accounts table, the relationship between Transactions and Accounts is invalid and the blank row is added to the Accounts table. This effect does not propagate to Customers. Therefore, in this case the Customers table has no blank row, and only the Accounts table has one blank row.
Consequently, slicing Transactions by Account shows the blank row, whereas slicing Transactions by CustomerName does not show transactions linked to the blank row. This behavior might be confusing; to demonstrate the behavior, we added a row to the Transactions table with an invalid AccountKey and a value of 10,000.00. The different results are visible in Figure 15-16, where the matrix on the left slices by Account and the matrix on the right slices by CustomerName. The measure shown is the one using CROSSFILTER.
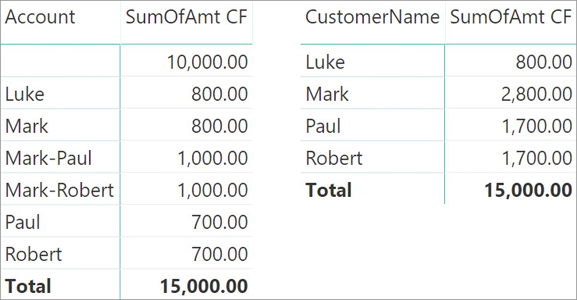
When the matrix is slicing by Account, the blank row is present and the value of 10,000.00 is visible. When the matrix is slicing by CustomerName, there is no blank row to show. The filter starts from the CustomerName column in the Customers table, but there are no values in AccountsCustomers that can include in the filter the blank row in Accounts. The value related to the blank row is only visible at the grand total because the filter on CustomerName is no longer present there. Consequently, at the grand total level the Accounts table is no longer cross-filtered; all the rows of Accounts become active, including the blank row, and 15,000.00 is displayed as a result.
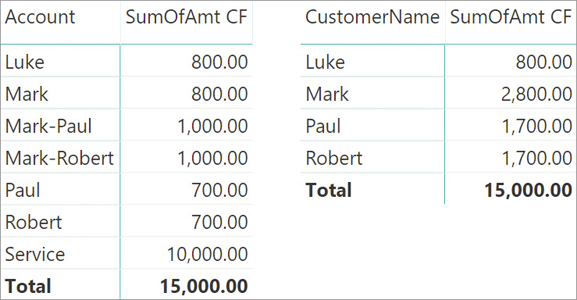
Be mindful that we are using the blank row as an example, but the same scenario would happen whenever there are accounts that are not linked to any customer. Starting the filter from the customer, their value will not show up other than on the grand total. The reason is that the filter on the customer removes accounts not linked to any customer from any row. This consideration is important because the behavior observed in Figure 15-16 is not necessarily related to the presence of an invalid relationship. For example, if the transaction with the value of 10,000.00 were related to a Service account defined in the Accounts table but not related to any Customer, the Account name would be visible in the report—despite the fact that this value still would not be related to any single customer. This is shown in Figure 15-17.
![]() Note
Note
The scenario depicted in Figure 15-17 does not violate any referential integrity constraints in a relational database, as was the case in Figure 15-16. Thus, validating data making sure that this condition is not present requires additional validation logic in the relational database.
If, instead of using the CROSSFILTER technique, we rely on table filtering in CALCULATE, then the behavior is different. The rows that are not reachable from the bridge table are always filtered out. Because the filter is always forced by CALCULATE, they will not show even at the grand total level. In other words, the filter is always forced to be active. You can look at the result in Figure 15-18.
Not only does the total now show a lower value; this time, even slicing by Account does not show the blank row anymore. The reason is that the blank row is filtered out by the table filter applied by CALCULATE.
Neither of these values is totally correct or totally wrong. Moreover, if the bridge table references all the rows in Transactions starting from Customers, then the two measures behave the same way. Developers should choose the technique that better fit their needs, paying attention to details and making sense of unexpected values, if any.
![]() Note
Note
Performance-wise, the solutions based on using a table as a filter argument in CALCULATE always involve paying the price of scanning the bridge table (AccountsCustomers). This means that any report using the measure without a filter over Customers will pay the highest possible price, which is useless in case every account has at least one customer. Therefore, the solutions based on the bidirectional cross-filter should be the default choice whenever the data consistency guarantees the same result with both techniques. Moreover, remember that any solution involving table expansion works only with strong relationships. Therefore, the presence of weak relationships might force the solution in favor of the bidirectional cross-filter. More details about these considerations are available in the article at https://www.sqlbi.com/articles/many-to-many-relationships-in-power-bi-and-excel-2016/.
Implementing many-to-many using a common dimension
There is another scenario where many-to-many is a useful tool, even though from a technical point of view it is not a many-to-many relationship. This scenario defines a relationship between two entities at a granularity different from the primary key.
The example comes from a budgeting scenario, where the budget information is stored in a table containing the country, the brand, and the budget for the one year. The model is visible in Figure 15-19.
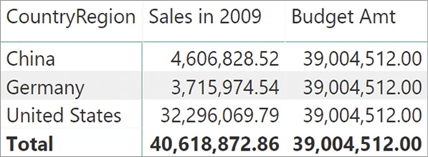
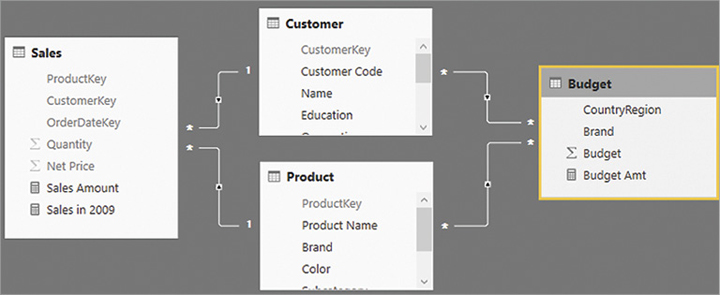
If the requirement is to produce a report that shows the sales and the budget values side-by-side, then it is necessary to filter both the Budget table and the Sales table at the same time. The Budget table contains CountryRegion, which is also a column in Customer. However, the CountryRegion column is not unique—neither in the Customer table nor in the Budget table. Similarly, Brand is a column in Product, but it is also not unique in either table. One could author a Budget Amt measure that simply sums the Budget column of the Budget table.
Budget Amt := SUM ( Budget[Budget] )
A matrix slicing by Customer[CountryRegion] with this data model produces the result visible in Figure 15-20. The Budget Amt measure always shows the same value, corresponding to the sum of all the rows in the Budget table.
There are several solutions to this scenario. One involves implementing a virtual relationship using one of the techniques previously shown in this chapter, moving the filter from one table to another. For example, by using TREATAS, one could move the filter from both the Customer and Product tables to the Budget table using this code:
Budget Amt :=
CALCULATE (
SUM ( Budget[Budget] ),
TREATAS (
VALUES ( Customer[CountryRegion] ),
Budget[CountryRegion]
),
TREATAS (
VALUES ( 'Product'[Brand] ),
Budget[Brand]
)
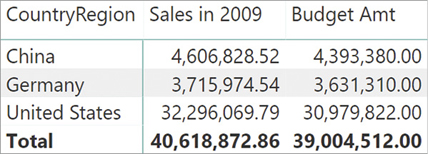
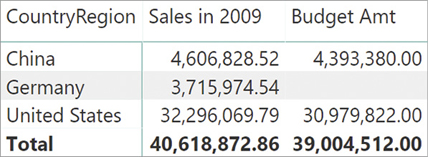
)The Budget Amt measure now uses the filter coming from Customer and/or from Product properly, producing the correct result shown in Figure 15-21.
This solution presents a couple of limitations:
If a new brand exists in the Budget table and it is not present in the Product table, its value will always be filtered out. As a result, the figures of the budget will be inaccurate.
Instead of using the most efficient technique of relying on physical relationships, the code is using DAX to move the filter. On large models, this might lead to bad performance.
A better solution to this scenario is to slightly change the data model, adding a new table that acts as a filter on both the Budget and the Customer tables. This can be easily accomplished with a DAX calculated table:
CountryRegions =
DISTINCT (
UNION (
DISTINCT ( Budget[CountryRegion] ),
DISTINCT ( Customer[CountryRegion] )
)
)This formula retrieves all the values of CountryRegion from both Customer and Budget, then it merges them into a single table that contains duplicates. Finally, the formula removes duplicates from the table. As a result, this new table contains all the values of CountryRegion, whether they come from Budget or from Customer. In a similar way, a table that links to Product and Budget is needed, following the same process for Product[Brand] and for Budget[Brand].
Brands =
DISTINCT (
UNION (
DISTINCT ( 'Product'[Brand] ),
DISTINCT ( Budget[Brand] )
)
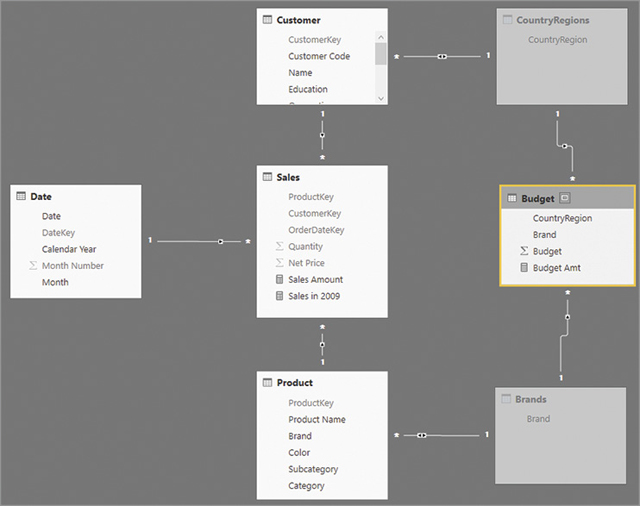
)Once the table is in the data model, one then needs to create the proper set of relationships. The resulting model is visible in Figure 15-22.
With the new model in place, the Brands table filters both Product and Budget, whereas the new CountryRegions table filters both Customer and Budget. Thus, there is no need to use the TREATAS pattern shown in the previous example. A simple SUM computes the correct value from both Budget and Sales as shown in the following version of the Budget Amt measure. This does require using the columns from the CountryRegions and Brands tables in the report, which will appear as in Figure 15-21.
Budget Amt := SUM ( Budget[Budget] )
By leveraging the bidirectional cross-filter between Customer and CountryRegions and between Product and Brands, it is possible to hide the CountryRegions and Brands tables in report view, moving the filter from Customer and Product to Budget without writing any additional DAX code. The resulting model shown in Figure 15-23 creates a logical relationship between Customer and Budget at the granularity of the CountryRegion column. The same happens between Product and Budget at the granularity of the Brand column.
The result of the report produced by this model is identical to Figure 15-21. The relationship between Customer and Budget is a sequence of a many-to-one and a one-to-many relationship. The bidirectional cross-filter between Customer and CountryRegions ultimately transfers the filter from Customer to Budget and not the other way around. If the bidirectional filter were also active between CountryRegions and Budget, the model would have involved some level of ambiguity that would stop the creation of a similar pattern between Product and Budget.
![]() Note
Note
The model in Figure 15-23 suffers from the same limitations as the model in Figure 15-19: If there are brands or countries in the budget that are not defined in the Customer and Product tables, that budget value might disappear in the report. This problem is described in more detail in the next section.
Be mindful that technically, this is not a many-to-many pattern. In this model we are linking Product to Budget (same for Customer) using a granularity that is not the individual product. Instead, we are linking the two tables at the granularity level of Brand. The same operation can be achieved in a simpler—though less effective—way by using weak relationships, as described in the next section. Moreover, linking tables at different granularity conceals several complex aspects that are discussed later in this chapter.
Implementing many-to-many using MMR weak relationships
In the previous example we linked Products to Budget by using an intermediate—ad hoc—table. DAX versions from after October 2018 introduced the feature of weak relationships, which addresses the same scenario in a more automated way.
One can create an MMR weak relationship between two tables in case the two columns involved in the relationship have duplicates in both tables. In other words, the same model shown in Figure 15-23 can be created by directly linking Budget to Product using the Product[Brand] column, avoiding the creation of the intermediate Brands table used in the previous section. The resulting model is visible in Figure 15-24.

When creating an MMR weak relationship, one has the option of choosing the direction of the filter context propagation. It can be bidirectional or single, as is the case with a regular one-to-many relationship. The choice for this example is necessarily the single direction from Customer to Budget and from Product to Budget. Setting a bidirectional filter in both relationships would create a model ambiguity.
In MMR relationships, both sides of the relationship are the many-side. Therefore, the columns can contain duplicates in both tables. This model works exactly like the model shown in Figure 15-23, and it computes the correct values without the need for additional DAX code in measures or calculated tables.
Nevertheless, a trap lies in this model that our reader must be aware of. Because the relationship is weak, neither of the two tables will contain the blank row in case the relationship is invalid. In other words, if Budget contains a country or a brand that is not present in Customer or in Product, then its values will be hidden, as is the case for the model in Figure 15-24.
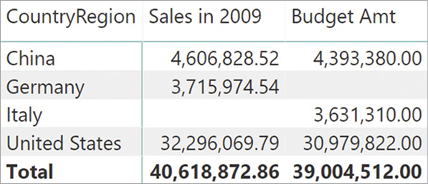
To demonstrate this behavior, we changed the content of the Budget table, replacing Germany with Italy. There are no customers whose country is Italy in the model used for this example. The result of this change is somewhat surprising, as shown in Figure 15-25.
The row with Germany is empty. This is correct, because we moved the entire budget of Germany to Italy. But you should notice two details:
There is no row showing the budget for Italy.
The grand total of the budget is larger than the sum of the two visible rows.
When there is a filter on Customer[CountryRegion], the filter is moved to the Budget table through the weak relationship. As a consequence, the Budget table only shows the values of the given country. Because Italy does not exist in Customer[CountryRegion], no value is shown. That said, when there is no filter on Customer[CountryRegion], Budget does not receive any filter. As such, it shows its grand total, which also includes Italy.
The result of Budget Amt thus depends on the presence of a filter on Customer[CountryRegion]; in the presence of invalid relationships, the numbers produced might be surprising.
Weak MMR relationships represent a powerful tool that greatly simplifies the creation of data models because it reduces the need to create additional tables. Nevertheless, the fact that no blank row is ever added to the tables might produce unexpected results if the feature is not used properly. We showed the more complex technique of creating additional tables before showing weak relationships because they are basically the same thing: The difference is that creating additional tables makes visible the values that exist in just one of the two related tables—something that is not possible using weak MMR relationships, but that might be required in particular scenarios.
Indeed, if we perform the same substitution of Germany with Italy in the data model with the Brands and CountryRegions table (Figure 15-23), the result is much clearer, as shown in Figure 15-26.
Choosing the right type of relationships
Complex relationships are a powerful way to generate advanced models. Working with complex scenarios, you face the choice between building a physical (maybe calculated) relationship and building a virtual relationship.
Physical and virtual relationships are similar because they fulfill the same goal: transferring a filter from one table to another. However, they have different performance and different implications at the data model level.
A physical relationship is defined in the data model; a virtual relationship only exists in DAX code. The diagram view of a data model clearly shows the relationships between tables. Yet virtual relationships are not visible in the diagram view; locating them requires a detailed review of the DAX expression used in measures, calculated columns, and calculated tables. If a logical relationship is used in several measures, its code must be duplicated in every measure requiring it, unless the logical relationship is implemented in a calculation item of a calculation group. Physical relationships are easier to manage and less error-prone than virtual relationships.
A physical relationship defines a constraint on the one-side table of the relationship. One-to-many and one-to-one relationships require that the column used on the one-side of a relationship have unique nonblank values. The refresh operation of a data model fails in case the new data would violate this constraint. From this point of view, there is a huge difference with the foreign key constraint defined in a relational database. A foreign key relationship defines a constraint on the many-side of a relationship, whose values can only be values that exist in the other table. A relationship in a Tabular model never enforces a foreign key constraint.
A physical relationship is faster than a virtual relationship. The physical relationship defines an additional structure that accelerates the query execution, enabling the storage engine to execute part of the query involving two or more queries. A virtual relationship always requires additional work from the formula engine, which is slower than the storage engine. Differences between formula engine and storage engine are discussed in Chapter 17.
Generally, physical relationships are a better option. In terms of query performance there is no difference between a standard relationship (based on a column coming from the data source) and a calculated physical relationship (based on a calculated column). The engine computes calculated columns at process time (when data is refreshed), so it does not really matter how complex the expression is; the relationship is a physical relationship and the engine can take full advantage of it.
A virtual relationship is just an abstract concept. Technically, every time one transfers a filter from one table to another using DAX code, they are implementing a virtual relationship. Virtual relationships are resolved at query time, and the engine does not have the additional structures created for physical relationships to optimize the query execution. Thus, whenever you have the option of doing that, you should prefer a physical relationship to a virtual relationship.
The many-to-many relationships are in an intermediate position between physical and virtual relationships. One can define many-to-many relationships in the model by leveraging bidirectional relationships or table expansion. In general, the presence of a relationship is better than an approach based on table expansion because the engine has more chances to optimize the query plan by removing unnecessary filter propagations. Even so, table expansion and bidirectional cross-filters have a similar cost when a filter is active, even though technically they execute two different query plans with a similar cost.
Performance-wise the priority in relationships choice should be the following:
Physical one-to-many relationships to get best performance and the best use of the VertiPaq engine. Calculated physical relationships have the same query performance as relationships on native columns.
Bidirectional cross-filter relationships, many-to-many with table expansion, and weak relationships are a second option. They provide good performance and a good use of the engine, although not the best.
Virtual relationships are the last choice because of the risk of bad performance. Note that being at risk does not mean you will experience performance issues, but only that you need to care about different aspects of the query, which you will learn in the next chapters about optimization.
Managing granularities
As described in earlier sections, by using intermediate tables or MMR weak relationships, one can link two tables using a relationship at a granularity level lower than the primary key of a table. In a previous example, we linked the Budget table to both Product and Customer. The relationship with Product is at the Brand level, whereas the relationship with Customer is at the CountryRegion level.
If a data model contains relationships at a lower granularity, special care needs to be taken whenever authoring measures that use that relationship. As an example, Figure 15-27 shows the starting model with two MMR weak relationships between Customer, Product, and Budget.
A weak relationship transfers the filter from one table to another following the granularity of the column. This statement is true for any relationship. Indeed, the relationship between Customer and Sales also transfers the filter at the granularity of the column involved in the relationship. Nevertheless, if the column used to create the relationship is the key of the table, the behavior is intuitive. When the relationship is set at a lower granularity—as in the case of weak relationships—it is all too easy to produce calculations that might be hard to understand.
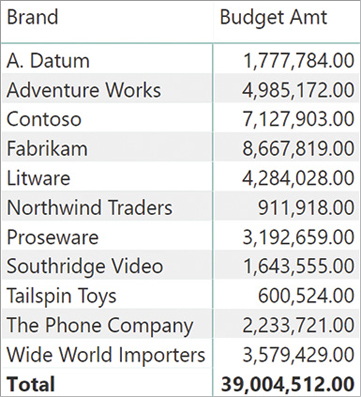
For example, consider the Product table. The relationship with Budget is set at the Brand level. Thus, one can create a matrix that slices Budget Amt by Brand and obtain an accurate result, as shown in Figure 15-28.
Things suddenly become much more intricate if other columns from the Product table are involved in the analysis. In Figure 15-29 we added a slicer to filter a few colors, and we added the color on the columns of the matrix. The result is confusing.

Please note that given a Brand, its value—if present—is always the same, regardless of the filter on the color. The total of each color is different, but the grand total is clearly not the sum of individual colors.
To make sense of these numbers, we use a simplified version of the matrix where the brand is not present. In Figure 15-30, Budget Amt is sliced only by Product[Color].
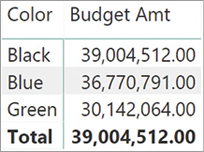
Look at the Blue budget amount in Figure 15-30. When the evaluation starts, the filter context filters the Product table only showing blue products. Not all the brands produce blue products. For instance, The Phone Company does not have any product that is blue, as shown in Figure 15-29. Thus, the Product[Brand] column is cross-filtered by Product[Color], and it shows all the brands except for The Phone Company. When the filter context is moved to the Budget table, the operation occurs at the Brand granularity. Consequently, the Budget table is filtered showing all brands but The Blue Company.
The value shown is the sum of all brands except for The Blue Company. While traversing the relationship, the information about the color has been lost. The relationship between Color and Brand is used when cross-filtering Brand by Color, but then, the filter on Budget is based on Brand alone. In other words, every cell shows the sum of all brands that have at least one product of the given color. This behavior is seldom desirable. There are few scenarios where this is exactly the calculation required; most of the times the numbers are just wrong.
The problem appears whenever a user browses an aggregation of values at a granularity that is not supported by the relationship. A good practice consists of hiding the value if the browsing granularity is not supported. This raises the problem of detecting when the report is or is not analyzing data at the correct granularity. To solve the problem, we create more measures.
We start with a matrix containing the brand (correct granularity) and the color (wrong granularity). In the report, we also added a new measure, NumOfProducts that just counts the number of rows in the Product table:
NumOfProducts := COUNTROWS ( 'Product' )
You can see the resulting report in Figure 15-31.
The key to solve the scenario is the NumOfProducts measure. When the A. Datum brand is selected, there are 132 products visible, which are all A. Datum products. If the user further filters with the color (or any other column), the number of visible products is reduced. The values from Budget make sense if all 132 products are visible. They lose meaning if fewer products are selected. Thus, we hide the value of the Budget Amt measure when the number of visible products is not exactly the number of all the products within the selected brand.
A measure that computes the number of products at the brand granularity is the following:
NumOfProducts Budget Grain :=
CALCULATE (
[NumOfProducts],
ALL ( 'Product' ),
VALUES ( 'Product'[Brand] )
)In this case ALL / VALUES must be used instead of ALLEXCEPT; the reader can find more details about their differences in Chapter 10. With this new measure, it is now enough to use a simple IF statement to check if the two numbers are identical to show the Budget Amt measure; otherwise, a blank is returned and the row will be hidden in the report. The Corrected Budget measure implements this logic:
Corrected Budget :=
IF (
[NumOfProducts] = [NumOfProducts Budget Grain],
[Budget Amt]
)Figure 15-32 shows the entire report with the newly introduced measures. The Corrected Budget value is hidden when the granularity of the report is not compatible with the granularity of the Budget table.
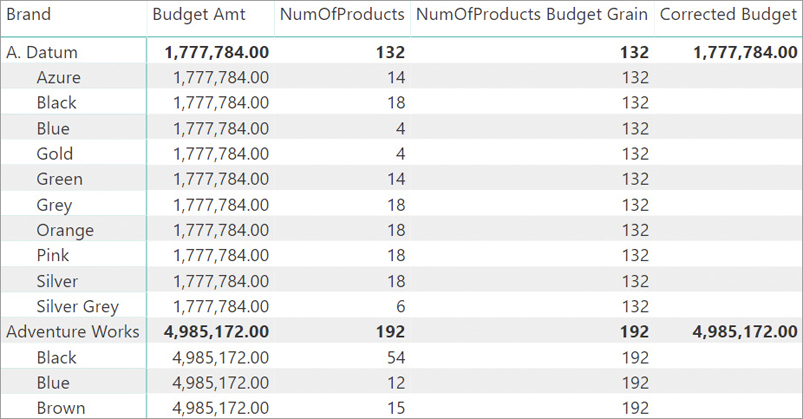
The same pattern must be applied to the Customer table too, where the granularity is set at the CountryRegion level. If needed, more information about this pattern is available at https://www.daxpatterns.com/budget-patterns/.
In general, whenever using relationships at a granularity different than the key of a table, one should always check the calculations and make sure any value is hidden if the granularity is not supported. Using MMR weak relationships always requires attention to these details.
Managing ambiguity in relationships
When we think about relationships, another important topic is ambiguity. Ambiguity might appear in a model if there are multiple paths linking two tables, and unfortunately, ambiguity could be hard to spot in a complex data model.
The simplest kind of ambiguity that one can introduce in a model is by creating two or more relationships between two tables. For example, the Sales table contains both the order date and the delivery date. When you try to create two relationships between Date and Sales based on the two columns, the second one is disabled. For example, Figure 15-33 shows that one of the two relationship between Date and Sales is represented by a dashed line because it is not active.
If both relationships were active at the same time, then the model would be ambiguous. The engine would not know which path to follow to transfer a filter from Date to Sales.
Understanding ambiguity when working with two tables is easy. But as the number of tables increases, ambiguity is much harder to spot. The engine automatically detects ambiguity in a model and prevents developers from creating ambiguous models. However, the engine uses an algorithm that is complex, following rules that are not easy to grasp for humans. As a result, sometimes it does not consider as ambiguous a model that, in reality, contains ambiguity.
For example, consider the model in Figure 15-34. Before moving further, focus on the figure and answer this simple question: Is the model ambiguous?
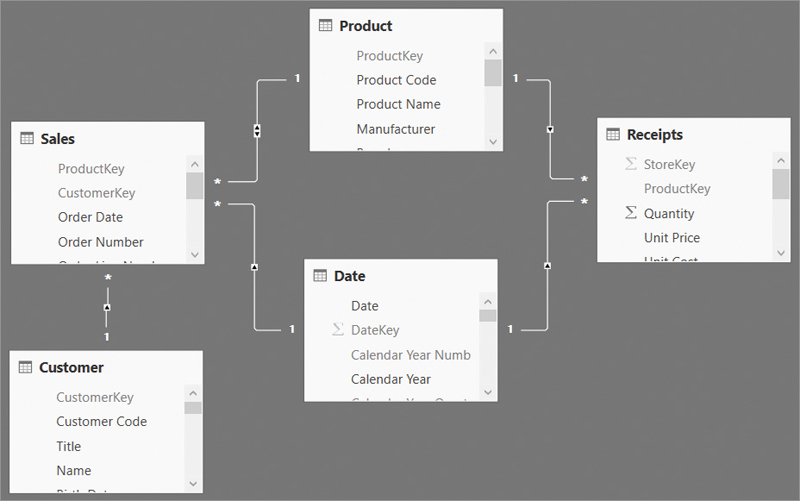
The answer to the question itself is ambiguous: The model is ambiguous for a human, but it is not ambiguous for DAX. Still, it is a bad data model because it is extremely complex to analyze. First, we analyze where the ambiguity is.
There is a bidirectional cross-filter in the relationship between Product and Sales, meaning that the filter context from Sales flows to Product and then to Receipts. Now, focus on Date. Starting from Date, the filter can go to Sales, then to Product, and finally to Receipts, following a legitimate path. At the same time, the filter could flow from Date to Receipts, simply using the relationship between the two tables. Thus, the model is ambiguous because there are multiple paths to propagate the filter from Date to Receipts.
Nevertheless, it is possible to create and use such models because the DAX engine implements special rules to reduce the number of ambiguous models detected. In this case, the rule is that only the shortest path propagates the filter. Therefore, the model is allowed, even though it is ambiguous. This is not to say that working with such models is a good idea in any way. Instead, it is a bad idea, and we strongly suggest our readers avoid ambiguity at all in their models.
Moreover, things are more intricate than this. Ambiguity can appear in a model because of the way relationships are designed. Ambiguity might also appear during the execution of DAX code because a DAX developer can change the relationship architecture using CALCULATE modifiers like USERELATIONSHIP and CROSSFILTER. For example, you write a measure that works perfectly fine, then you call the measure from inside another measure that uses CROSSFILTER to enable a relationship, and your measure starts computing wrong values because of ambiguity introduced in the model by CROSSFILTER. We do not want to scare our readers; we want them to be aware of the complexity that can arise in a model as soon as ambiguity comes into play.
Understanding ambiguity in active relationships
The first example is based on the model shown in Figure 15-34. The report projects Sales Amount and Receipts Amount (simple SUMX over the two tables) in a matrix that slices by year. The result is visible in Figure 15-35.
The filter from Date can reach Receipts through two paths:
A direct path (Date to Receipts).
A path traversing Date to Sales, then Sales to Product, and finally Product to Receipts.
The model is not considered ambiguous because the DAX engine chooses the shortest path between the two tables. Having the ability to move the filter from Date to Receipts directly, it ignores any other path. If the shortest path is not available, then the engine uses the longer one. Look at what happens by creating a new measure that calls Receipts Amt after having disabled the relationship between Date and Receipts:
Rec Amt Longer Path :=
CALCULATE (
[Receipts Amt],
CROSSFILTER ( 'Date'[Date], Receipts[Sale Date], NONE )
)The Rec Amt Longer Path measure disables the relationship between Date and Receipts, so the engine must follow the longer path. The result is visible in Figure 15-36.

At this point, one interesting exercise for the reader is to describe exactly what the numbers reported by Rec Amt Longer Path mean. We encourage this effort be made before reading further, as the answer follows in the next paragraphs.
The filter starts from Date; then it reaches Sales. From Sales, it proceeds to Product. The products filtered are the ones that were sold in one of the selected dates. In other words, when the filter is 2007, Product only shows the products sold in 2007. Then, the filter moves one step forward and it reaches Receipts. In other words, the number is the total of Receipts for all the products sold in one given year. Not an intuitive value at all.
The most complex detail about the formula is that it uses CROSSFILTER NONE. Thus, a developer would tend to think that the code only deactivates a relationship. In reality, deactivating one path makes another path active. Thus, the measure does not really remove a relationship, it activates another one that is not cited anywhere in the code.
In this scenario, ambiguity is introduced by the bidirectional cross-filter between Product and Sales. A bidirectional cross-filter is a very dangerous feature because it might introduce ambiguities that are resolved by the engine but hard for a developer to find. After many years using DAX, we concluded that the bidirectional cross-filter should be avoided if not strictly necessary. Moreover, in the few scenarios where it makes sense to use a bidirectional cross-filter, one should double-check the whole model and then double-check it again to make sure no ambiguity is present. Obviously, as soon as another table or relationship is added to the model, the full checking process should start again. Doing this exercise on a model with 50 tables is a tedious exercise that can be easily avoided by staying away from bidirectional cross-filters defined in the data model.
Solving ambiguity in non-active relationships
Though bidirectional cross-filters are likely the most offending feature that generates ambiguity, they are not the only reason behind the appearance of ambiguity. Indeed, a developer could create a perfectly legitimate model, with no ambiguity, and still face the problem of ambiguity at query time.
As an example, look at the model in Figure 15-37. It is not ambiguous.
Focus on the Date table. Date filters Sales through the only active relationship (Date[Date] to Sales[Date]). There are two relationships between Date and Sales. One of them is inactive to avoid ambiguity. There is also a relationship between Date and Customer, based on Customer[FirstSale] that must be inactive. If this latter relationship were activated, then the filter from Date could reach Sales following two paths, making the model ambiguous. Thus, this model works just fine because it only uses the active relationships.
Now what happens if one activates one or more of the inactive relationships inside a CALCULATE? The model would suddenly become ambiguous. For example, the following measure activates the relationship between Date and Customer:
First Date Sales :=
CALCULATE (
[Sales Amount],
USERELATIONSHIP ( Customer[FirstSale], 'Date'[Date] )
)Because USERELATIONSHIP makes the relationship active, inside CALCULATE the model becomes ambiguous. The engine cannot work on an ambiguous model, so it needs to deactivate other relationships. In this case, it does not use the shortest path. Indeed, the shortest path between Date and Sales is the direct relationship. A reasonable conclusion could be that—to disambiguate the model—the engine uses the direct relationship, as it did in the previous example. But because the developer explicitly asked to activate the relationship between Customer and Date by using USERELATIONSHIP, the engine decides to disable the relationship between Date and Sale instead.
As a result, because of USERELATIONSHIP, the filter will not propagate from Date to Sales using the direct relationship. Instead, it propagates the filter from Date to Customer and then from Customer to Sales. Therefore, given a customer and a date, the measure shows all the sales of that customer but only at the date of that customer’s first purchase. You can see this behavior in Figure 15-38.

The First Date Sales measure always shows the total of the Sales of each customer, showing blank values on dates that do not correspond to the first date of purchase. From a business point of view, this measure shows the future value of a customer projected on the date when that customer was acquired. While this description makes sense, the chances that it be a real requirement are very low.
As it happened earlier, the goal here is not to understand exactly how the engine resolved the ambiguity. The disambiguation rules have never been documented; thus, they might change at some point. The real problem of such models is that ambiguity might appear in a valid model because of an inactive relationship being activated. Understanding which of the multiple paths the engine will follow to solve ambiguities is more of a guess than science.
With ambiguity and relationships, the golden rule is to just keep it simple. DAX might have some disambiguation algorithm that is powerful and can disambiguate nearly every model. Indeed, to raise an ambiguity error at runtime, one needs to use a set of USERELATIONSHIP functions that forces the model to be ambiguous. Only in such cases does the engine raise an error. For example, the following measure requests a clearly ambiguous model:
First Date Sales ERROR :=
CALCULATE (
[Sales Amount],
USERELATIONSHIP ( Customer[FirstSale], 'Date'[Date] ),
USERELATIONSHIP ( 'Date'[Date], Sales[Date] )
)At this point, DAX is not able to disambiguate a model with both relationships active, and it raises an error. Regardless, the measure can be defined in the data model without raising any exception; the error only appears when the measure is executed and filtered by date.
The goal of this section was not to describe the modeling options in Tabular. Instead, we wanted to bring your attention to issues that might happen when the data model is not correctly built. Building the correct model to perform an analysis is a complex task. Using bidirectional cross-filters and inactive relationships without a deep understanding of their implications is perhaps the quickest way to produce an unpredictable model.
Conclusions
Relationships are an important part of any data model. The Tabular mode offers different types of relationships, like one-to-many (SMR), one-to-one (SSR), and MMR weak relationships. MMR relationships are also called many-to-many relationships in some user interfaces, which is a misleading name that can be confused with a different data modeling concept. Every relationship can propagate the filter either in a single direction or bidirectionally, with the only exception of one-to-one relationships that are always bidirectional.
The available tools can be extended in a logical data model by implementing calculated physical relationships, or virtual relationships by using TREATAS, SUMMARIZE, or table expansion. The many-to-many relationships between business entities can be implemented with a bridge table and rely on bidirectional cross-filters applied to the relationships in the chain.
All these features are extremely powerful, and being powerful they can be dangerous. Relationships must be handled with care. A developer should always double-check the models for ambiguity, also verifying that ambiguity will not be introduced by using USERELATIONSHIP or CROSSFILTER.
The larger the model, the higher the chances of making mistakes. If a model contains any inactive relationship, check the reason why the relationship is inactive and what would happen if it were activated. Remember that investing the time to properly design your model is foundational to successful DAX calculations, whereas a poorly designed model will usually give developers many headaches down the road.
