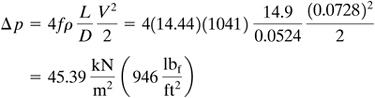3.5. NON-NEWTONIAN FLUIDS
3.5A. Types of Non-Newtonian Fluids
As discussed in Section 2.4, Newtonian fluids are those which follow Newton's law, Eq. (3.5-1):
Equation 3.5-1

where μ is the viscosity and is a constant independent of shear rate. In Fig. 3.5-1 a plot is shown of shear stress τ versus shear rate −dv/dr. The line for a Newtonian fluid is straight, the slope being μ.
Figure 3.5-1. Shear diagram for Newtonian and time-independent non-Newtonian fluids.

If a fluid does not follow Eq. (3.5-1), it is a non-Newtonian fluid. Then a plot of τ versus −dν/dr is not linear through the origin for these fluids. Non-Newtonian fluids can be divided into two broad categories on the basis of their shear-stress/shear-rate behavior: those whose shear stress is independent of time or duration of shear (time-independent) and those whose shear stress is dependent on time or duration of shear (time-dependent). In addition to unusual shear-stress behavior, some non-Newtonian fluids also exhibit elastic (rubberlike) behavior, which is a function of time and results in their being called viscoelastic fluids. These fluids exhibit normal stresses perpendicular to the direction of flow in addition to the usual tangential stresses. Most of the emphasis here will be put on the time-independent class, which includes the majority of non-Newtonian fluids.
3.5B. Time-Independent Fluids
1. Bingham plastic fluids
These are the simplest because, as shown in Fig. 3.5-1, they differ from Newtonian only in that the linear relationship does not go through the origin. A finite shear stress τC (called yield stress) in N/m2 is needed to initiate flow. Some fluids have a finite yield (shear) stress τO, but the plot of τ versus -dvldr is curved upward or downward. However, this departure from exact Bingham plasticity is often small. Examples of fluids with a yield stress are drilling muds, peat slurries, margarine, chocolate mixtures, greases, soap, grain-water suspensions, toothpaste, paper pulp, and sewage sludge.
2. Pseudoplastic fluids
The majority of non-Newtonian fluids are in this category and include polymer solutions or melts, greases, starch suspensions, mayonnaise, biological fluids, detergent slurries, dispersion media in certain pharmaceuticals, and paints. The shape of the flow curve is shown in Fig. 3.5-1, and it generally can be represented by a power-law equation (sometimes called the Ostwald-de Waele equation):
Equation 3.5-2

where K is consistency index in N · sn/m2 or lbf · snft2, and n is the flow behavior index, dimensionless. The apparent viscosity μa in Eq. (3.5-3) is obtained from Eqs. (3.5-1) and (3.5-2) and decreases with increasing shear rate:
Equation 3.5-3

3. Dilatant fluids
These fluids are far less common than pseudoplastic fluids, and their flow behavior (Fig. 3.5-1) shows an increase in apparent viscosity with increasing shear rate. The power-law equation (3.5-2) is often applicable, but with n > 1:
Equation 3.5-4

For a Newtonian fluid, n = 1. Solutions showing dilatancy are some corn flour-sugar solutions, wet beach sand, starch in water, potassium silicate in water, and some solutions containing high concentrations of powder in water.
3.5C. Time-Dependent Fluids
1. Thixotropic fluids
These fluids exhibit a reversible decrease in shear stress with time at a constant rate of shear. This shear stress approaches a limiting value that depends on the shear rate. Examples include some polymer solutions, shortening, some food materials, and paints. At present the theory for time-dependent fluids is still not completely developed.
2. Rheopectic fluids
These fluids are quite rare in occurrence and exhibit a reversible increase in shear stress with time at a constant rate of shear. Examples are bentonite clay suspensions, certain sols, and gypsum suspensions. In design procedures for thixotropic and rheopectic fluids for steady flow in pipes, the limiting flow-property values at a constant rate of shear are sometimes used (S2, W3).
3.5D. Viscoelastic Fluids
Viscoelastic fluids exhibit elastic recovery from the deformations that occur during flow. They show both viscous and elastic properties. Part of the deformation is recovered upon removal of the stress. Examples are flour dough, napalm, polymer melts, and bitumens.
3.5E. Laminar Flow of Time-Independent Non-Newtonian Fluids
1. Flow properties of a fluid
In determining the flow properties of a time-independent non-Newtonian fluid, a capillary-tube viscometer is often used. The pressure drop ΔP N/m2 for a given flow rate q m3/s is measured in a straight tube of length L m and diameter D m. This is repeated for different flow rates or average velocities V m/s. If the fluid is time-independent, these flow data can be used to predict the flow in any other pipe size.
A plot of D Δp/4L, which is τw, the shear stress at the wall in N/m2, versus 8V/D, which is proportional to the shear rate at the wall, is shown in Fig. 3.5-2 for a power-law fluid following Eq. (3.5-5):
Equation 3.5-5
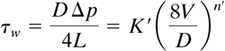
Figure 3.5-2. General flow curve for a power-law fluid in laminar flow in a tube.

where n' is the slope of the line when the data are plotted on logarithmic coordinates and K' has units of N · sn'/m2. For n' = 1, the fluid is Newtonian; for n' < 1, pseudoplastic, or Bingham plastic if the curve does not go through the origin; and for n' > 1, dilatant. The K', the consistency index in Eq. (3.5-5), is the value of D Δp/4L for 8V/D = 1. The shear rate at the wall, (-dv/dr)w, is
Equation 3.5-6

Also, K' = μ for Newtonian fluids.
Equation (3.5-5) is simply another statement of the power-law model of Eq. (3.5-2) applied to flow in round tubes, and is more convenient to use for pipe-flow situations (D2). Hence, Eq. (3.5-5) defines the flow characteristics just as completely as Eq. (3.5-2). It has been found experimentally (M3) that for most fluids K' and n' are constant over wide ranges of 8V/D or D Δp/4L. For some fluids this is not the case, and K' and n' vary. Then the particular values of K' and n' used must be valid for the actual 8V/D or D Δp/4L with which one is dealing in a design problem. This method using flow in a pipe or tube is often used to determine the flow properties of a non-Newtonian fluid.
In many cases the flow properties of a fluid are determined using a rotational viscometer. The flow properties K and n in Eq. (3.5-2) are determined in this manner. A discussion of the rotational viscometer is given in Section 3.5I.
When the flow properties are constant over a range of shear stresses that occurs for many fluids, the following equations hold (M3):
Equation 3.5-7
![]()
Equation 3.5-8
![]()
Often a generalized viscosity coefficient γ is defined as
Equation 3.5-9

where γ has units of N · sn'/m2 or lbm/ft · s2-n'
Typical flow-property constants (rheological constants) for some fluids are given in Table 3.5-1. Some data give γ values instead of K' values, but Eq. (3.5-9) can be used to convert these values if necessary. In some cases in the literature, K or K' values are given as dyn · sn'/cm2 or lbf · sn'/ft2. From Appendix A.1, the conversion factors are

| Flow-Property Constants | ||||
|---|---|---|---|---|
| Fluid | n' |  |  | Ref. |
| 1.5% carboxymethylcellulose in water | 0.554 | 1.369 | (S1) | |
| 3.0% CMC in water | 0.566 | 4.17 | (S1) | |
| 4% paper pulp in water | 0.575 | 9.12 | (A1) | |
| 14.3% clay in water | 0.350 | 0.0512 | (W2) | |
| 10% napalm in kerosene | 0.520 | 1.756 | (S1) | |
| 25% clay in water | 0.185 | 0.3036 | (W2) | |
| Applesauce, brand A (297 K), density = 1.10 g/cm3 | 0.645 | 0.500 | (C1) | |
| Banana purée, brand A (297 K), density = 0.977 g/cm3 | 0.458 | 6.51 | (C1) | |
| Honey (297 K) | 1.00 | 5.61 | (C1) | |
| Cream, 30% fat (276 K) | 1.0 | 0.01379 | (M4) | |
| Tomato concentrate, 5.8% total solids (305 K) | 0.59 | 0.2226 | (H1) | |
2. Equations for flow in a tube
In order to predict the frictional pressure drop Δp in laminar flow in a tube, Eq. (3.5-5) is solved for Δp (p0 - pL):
Equation 3.5-10
![]()
If the average velocity is desired, Eq. (3.5-5) can be rearranged to give
Equation 3.5-11

If the equations are desired in terms of K instead of K', Eqs. (3.5-7) and (3.5-8) can be substituted into (3.5-10) and (3.5-11). Substituting Eqs. (3.5-7) and (3.5-8) into Eq. (3.5-11) and noting that V = vx av,
Equation 3.5-12

The flow must be laminar. The generalized Reynolds number has been defined as
Equation 3.5-13

3. Friction factor method
Alternatively, using the Fanning friction factor method given in Eqs. (2.10-5)–(2.10-7) for Newtonian fluids, but using the generalized Reynolds numbers,
Equation 3.5-14

Equation 3.5-15
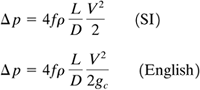
EXAMPLE 3.5-1. Pressure Drop of Power-Law Fluid in Laminar FlowA power-law fluid having a density of 1041 kg/m3 is flowing through 14.9 m of a tubing having an inside diameter of 0.0524 m at an average velocity of 0.0728 m/s. The rheological or flow properties of the fluid are K' = 15.23 N · sn'/m2 (0.318 lbf · sn'/ft2) and n' = 0.40.
Solution: The known data are as follows: K' = 15.23, n' = 0.40, D = 0.0524 m, V = 0.0728 m/s, L = 14.9 m, and ρ = 1041 kg/m3. For part (a), using Eq. (3.5-10),
Also, to calculate the friction loss,
Using Eq. (3.5-13),
Hence, the flow is laminar. For part (b), using Eq. (3.5-14)
Substituting into Eq. (3.5-15),
|
3.5F. Friction Losses in Contractions, Expansions, and Fittings in Laminar Flow
Since non-Newtonian power-law fluids flowing in conduits are often in laminar flow because of their usually high effective viscosity, losses in sudden changes of velocity and fittings are important in laminar flow.
1. Kinetic energy in laminar flow
In application of the total mechanical-energy balance in Eq. (2.7-28), the average kinetic energy per unit mass of fluid is needed. For fluids, this is (S2)
Equation 3.5-16
![]()
For Newtonian fluids, α =
![]() for laminar flow. For power-law non-Newtonian fluids,
for laminar flow. For power-law non-Newtonian fluids,
Equation 3.5-17
![]()
For example, if n = 0.50, α = 0.585. If n = 1.00, α =
![]() . For turbulent flow for Newtonian and non-Newtonian flow, α = 1.0(D1).
. For turbulent flow for Newtonian and non-Newtonian flow, α = 1.0(D1).
2. Losses in contractions and fittings
Skelland (S2) and Dodge and Metzner (D2) state that when a fluid leaves a tank and flows through a sudden contraction to a pipe of diameter D2 or flows from a pipe of diameter D1 through a sudden contraction to a pipe of D2, a vena contracta is usually formed downstream from the contraction. General indications are that the frictional pressure losses for pseudoplastic and Bingham plastic fluids are very similar to those for Newtonian fluids at the same generalized Reynolds numbers in laminar and turbulent flow for contractions as well as for fittings and valves.
For contraction losses, Eq. (2.10-16) can be used, where α = 1.0 for turbulent flow; and for laminar flow Eq. (3.5-17) can be used to determine α, since n is not 1.00.
For fittings and valves, friction losses should be determined using Eq. (2.10-17) and values from Table 2.10-1.
3. Losses in sudden expansion
For the friction loss for a non-Newtonian fluid in laminar flow through a sudden expansion from D1 to D2 diameter, Skelland (S2) gives
Equation 3.5-18
![]()
where hex is the friction loss in J/kg. In English units Eq. (3.5-18) is divided by gc and hex is in ft · lbf/lbm.
Equation (2.10-15) for laminar flow with α =
![]() for a Newtonian fluid gives values reasonably close to those of Eq. (3.5-18) for n = 1 (Newtonian fluid). For turbulent flow the friction loss can be approximated by Eq. (2.10-15), with α = 1.0 for non-Newtonian fluids (S2).
for a Newtonian fluid gives values reasonably close to those of Eq. (3.5-18) for n = 1 (Newtonian fluid). For turbulent flow the friction loss can be approximated by Eq. (2.10-15), with α = 1.0 for non-Newtonian fluids (S2).
3.5G. Turbulent Flow and Generalized Friction Factors
In turbulent flow of time-independent fluids the Reynolds number at which turbulent flow occurs varies with the flow properties of the non-Newtonian fluid. In a comprehensive study Dodge and Metzner (D2) derived a theoretical equation for turbulent flow of non-Newtonian fluids through smooth, round tubes. The final equation is plotted in Fig. 3.5-3, where the Fanning friction factor is plotted versus the generalized Reynolds number, NRe,gen, given in Eq. (3.5-13). Power-law fluids with flow-behavior indexes n' between 0.36 and 1.0 were experimentally studied at Reynolds numbers up to 3.5 × 104 and the derivation was confirmed.
Figure 3.5-3. Fanning friction factor versus generalized Reynolds number for time-independent non-Newtonian and Newtonian fluids flowing in smooth tubes. [From D. W. Dodge and A. B. Metzner, A.I.Ch.E. J., 5, 189 (1959). With permission.]

The curves for different n' values break off from the laminar line at different Reynolds numbers to enter the transition region. For n' = 1.0 (Newtonian), the transition region starts at NRe,gen = 2100. Since many non-Newtonian power-law fluids have high effective viscosities, they are often in laminar flow. The correlation for a smooth tube also holds for a rough pipe in laminar flow.
For rough commercial pipes with various values of roughness ε/D, Fig. 3.5-3 cannot be used for turbulent flow, since it is derived for smooth tubes. The functional dependence of the roughness values ε/D on n' requires experimental data which are not yet available. Metzner and Reed (M3, S3) recommend use of the existing relationship, Fig. 2.10-3, for Newtonian fluids in rough tubes using the generalized Reynolds number NRe,gen. This is somewhat conservative, since preliminary data indicate that friction factors for pseudoplastic fluids may be slightly smaller than for Newtonian fluids. This is also consistent with Fig. 3.5-3 for smooth tubes, which indicates lower f values for fluids with n' below 1.0 (S2).
EXAMPLE 3.5-2. Turbulent Flow of Power-Law FluidA pseudoplastic fluid that follows the power law, having a density of 961 kg/m3, is flowing through a smooth, circular tube having an inside diameter of 0.0508 m at an average velocity of 6.10 m/s. The flow properties of the fluid are n' = 0.30 and K' = 2.744 N · sn'/m2. Calculate the frictional pressure drop for a tubing 30.5 m long. Solution: The data are as follows: K' = 2.744, n' = 0.30, D = 0.0508 m, V = 6.10 m/s, ρ = 961 kg/m3, and L = 30.5 m. Using the general Reynolds-number equation (3.5-13),
Hence, the flow is turbulent. Using Fig. 3.5-3 for NRe,gen = 1.328 × 104 and n' = 0.30, f = 0.0032. Substituting into Eq. (3.5-15),
|
3.5H. Velocity Profiles for Non-Newtonian Fluids
1. Pseudoplastic and dilatant fluids
For pipe flow, Eq. (3.5-2) can be written as
Equation 3.5-19
![]()
Equation (2.9-6) holds for all fluids:
Equation 2.9-6
![]()
which relates τrx with the radial distance r from the center. Equating the above two equations and integrating between r = r and r = R0 where vx = 0,
Equation 3.5-20

At r = 0, vx = vx max and Eq. (3.5-20) becomes
Equation 3.5-21

The average velocity vx av is given by Eq. (3.5-12):
Equation 3.5-12
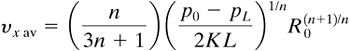
Dividing Eq. (3.5-20) by (3.5-12),
Equation 3.5-22

Using Eq. (3.5-22), the velocity profile can be calculated for laminar flow of a Newtonian fluid for n = 1 to show the parabolic profile in Fig. 3.5-4. The velocity profiles for pseudoplastic fluids (n < 1) show a flatter profile compared to the velocity profile for a Newtonian fluid. For extreme pseudoplastic behavior for n = 0, plug flow is obtained across the entire pipe. For dilatant behavior (n > 1) the velocity profile is more pointed and narrower. For extreme dilatant fluids (n = ∞) the velocity profile is a linear function of the radius.
Figure 3.5-4. Dimensionless velocity profile vx/vx av for power-law non-Newtonian fluids.

2. Bingham plastic fluids
For Bingham plastic fluids a finite yield stress τ0 in N/m2 is needed to initiate flow, as given in Eq. (3.5-23):
Equation 3.5-23
![]()
The velocity profile for this fluid is more complex than that for non-Newtonian fluids. This velocity profile for Bingham plastic fluids is shown in Fig. 3.5-5. Note the plug-flow region r = 0 to r = r0. In this region dvx/dr = 0 because the momentum flux or shear stress τrx is less than the yield value τ0.
Figure 3.5-5. Velocity profile and shear diagram for flow of a Bingham plastic fluid in a pipe.

In Table 3.5-2 some typical values for the rheological constants for Bingham plastic fluids are given.
| Fluid | τ0, N/m2 | μ, Pa · s | Ref. |
|---|---|---|---|
| Coal slurry (ρ = 1500 kg/m3) | 2.0 | 0.03 | (D4) |
| Molten chocolate (100°F) | 20 | 2.0 | (D4) |
| Printing pigment in varnish (10% by wt) | 0.4 | 0.25 | (C5) |
To derive the equation for pipe flow, note that Eq. (2.9-6) holds for all fluids:
Equation 2.9-6
![]()
Substituting Eq. (2.9-6) into (3.5-23),
Equation 3.5-24
![]()
Rearranging and integrating, where νx = νx at r = r and νx = 0 at r = R,
Equation 3.5-25
![]()
The equation holds for the region where r > r0 and up to r = R. For the plug-flow region r ≤ r0, dvx/dr = 0. In this region, using Eq. (2.9-6) and setting τrx = τ0 at r0,
Equation 3.5-26
![]()
Substituting Eq. (3.5-26) into (3.5-25) for r = r0, where plug flow occurs,
Equation 3.5-27
![]()
To obtain the flow rate Q in m3/s, the following integral must be evaluated:
Equation 3.5-28

Substituting Eq. (3.5-27) into the first part of Eq. (3.5-28) and (3.5-25) into the last part and integrating,
Equation 3.5-29

where τR = (p0 - pL)R/2L, the momentum flux at the wall. This is the Buckingham-Reiner equation.
When τ0 is zero, Eq. (3.5-29) reduces to the Hagen-Poiseuille Eq. (2.9-11) for Newtonian fluids.
EXAMPLE 3.5-3. Flow Rate of a Bingham Plastic FluidA printing-pigment solution with properties similar to those in Table 3.5-2 is flowing in a 1.0-cm-diameter pipe which is 10.2 m long. A pressure driving force of 4.35 kN/m2 is being used. Calculate the flow rate Q in m3/s. Solution: From Table 3.5-2, τ0 = 0.4 N/m2 and μ = 0.25 Pa · s. Also, (p0 - p) = 4.35 kN/m2 = 4350 N/m2, L = 10.2 m, R = 1.0/2 cm = 0.005 m. Substituting into Eq. (3.5-26),
Solving,
Substituting into the following for τR,
Finally, substituting into Eq. (3.5-29),
|
3.5I. Determination of Flow Properties of Non-Newtonian Fluids Using Rotational Viscometer
The flow-property or rheological constants of non-Newtonian fluids can be measured using pipe flow, as discussed in Section 3.5E. Another, more important method for measuring flow properties is by using a rotating concentric-cylinder viscometer, first described by Couette in 1890. In this device a concentric rotating cylinder (spindle) spins at a constant rotational speed inside another cylinder. Generally, there is a very small gap between the walls. This annulus is filled with the fluid. The torque needed to maintain this constant rotation rate of the inner spindle is measured by means of a torsion wire from which the spindle is suspended. A typical commercial instrument of this type is the Brookfield viscometer. Some types rotate the outer cylinder.
The shear stress at the wall of the bob or spindle is given by
Equation 3.5-30
![]()
where τw is the shear stress at the wall, N/m2 or kg/s2 · m; T is the measured torque, kg · m2/s2; Rb is the radius of the spindle, m; and L is the effective length of the spindle, m. Note that Eq. (3.5-30) holds for Newtonian and non-Newtonian fluids.
The shear rate at the surface of the spindle for non-Newtonian fluids is as follows (M6) for 0.5 < Rb/Rc < 0.99:
Equation 3.5-31

where Rc is the radius of the outer cylinder or container, m; and ω is the angular velocity of the spindle, rad/s. Also, ω = 2πN/60, when N is the RPM. Results calculated using Eq. (3.5-31) give values very close to those using the more complicated equation of Krieger and Maron (K2), also given in (P4, S2).
The power-law equation is given as
Equation 3.5-2
![]()
where K = N · sn/m2, kg · sn-2/m. Substituting Eqs. (3.5-30) and (3.5-31) into (3.5-2) gives
Equation 3.5-32

or,
Equation 3.5-33
![]()
Equation 3.5-34
![]()
Experimental data are obtained by measuring the torque T at different values of ω for a given fluid. The flow-property constants may be evaluated by plotting log T versus log ω. The parameter n is the slope of the straight line and the intercept is log A. The consistency factor K is now easily evaluated from Eq. (3.5-34).
Various special cases can be derived for Eq. (3.5-31):
1. Newtonian fluid. (n = 1)
Equation 3.5-35

2. Very large gap (Rb/Rc < 0.1)
This is the case of a spindle immersed in a large beaker of test fluid. Equation (3.5-31) becomes
Equation 3.5-36
![]()
Substituting Eqs. (3.5-30) and (3.5-36) into (3.5-2),
Equation 3.5-37
![]()
Again, as before, the flow-property constants can be evaluated by plotting log T versus log ω.
3. Very narrow gap (Rb/Rc > 0.99)
This is similar to flow between parallel plates. Taking the shear rate at radius (Rb + Rc)/2,
Equation 3.5-38
![]()
This equation, then, is the same as Eq. (3.5-35).
3.5J. Power Requirements in Agitation and Mixing of Non-Newtonian Fluids
For correlating the power requirements in agitation and mixing of non-Newtonian fluids, the power number NP is defined by Eq. (3.4-2), which is also the equation used for Newtonian fluids. However, the definition of the Reynolds number is much more complicated than for Newtonian fluids, since the apparent viscosity is not constant for non-Newtonian fluids but varies with the shear rates or velocity gradients in the vessel. Several investigators (G1, M1) have used an average apparent viscosity μa, which is used in the Reynolds number as follows:
Equation 3.5-39

The average apparent viscosity can be related to the average shear rate or average velocity gradient by the following method. For a power-law fluid,
Equation 3.5-40
![]()
For a Newtonian fluid,
Equation 3.5-41

Combining Eqs. (3.5-40) and (3.5-41),
Equation 3.5-42
![]()
Metzner and others (G1, M1) found experimentally that the average shear rate (dv/dy)av for pseudoplastic liquids (n < 1) varies approximately as follows with the rotational speed:
Equation 3.5-43
![]()
Hence, combining Eqs. (3.5-42) and (3.5-43),
Equation 3.5-44
![]()
Substituting into Eq. (3.5-39),
Equation 3.5-45

Equation (3.5-45) has been used to correlate data for a flat six-blade turbine with disk in pseudoplastic liquids, and the dashed curve in Fig. 3.5-6 shows the correlation (M1). The solid curve applies to Newtonian fluids (R1). Both sets of data were obtained for four baffles with Dt/J = 10, Da/W = 5, and ![]() . However, since it has been shown that the difference in results for Dt/J = 10 and Dt/J = 12 is very slight (R1), this Newtonian line can be considered the same as curve 1 in Fig. 3.4-5. The curves in Fig. 3.5-6 show that the results are identical for the Reynolds number range 1–2000, except that they differ only in the Reynolds number range 10–100, where the pseudoplastic fluids use less power than the Newtonian fluids. The flow patterns for the pseudoplastic fluids show much greater velocity-gradient changes than do the Newtonian fluids in the agitator. The fluid far from the impeller may be moving in slow laminar flow with a high apparent viscosity. Data for fan turbines and propellers are also available (M1).
. However, since it has been shown that the difference in results for Dt/J = 10 and Dt/J = 12 is very slight (R1), this Newtonian line can be considered the same as curve 1 in Fig. 3.4-5. The curves in Fig. 3.5-6 show that the results are identical for the Reynolds number range 1–2000, except that they differ only in the Reynolds number range 10–100, where the pseudoplastic fluids use less power than the Newtonian fluids. The flow patterns for the pseudoplastic fluids show much greater velocity-gradient changes than do the Newtonian fluids in the agitator. The fluid far from the impeller may be moving in slow laminar flow with a high apparent viscosity. Data for fan turbines and propellers are also available (M1).
Figure 3.5-6. Power correlation in agitation for a flat, six-blade turbine with disk in pseudoplastic non-Newtonian and Newtonian fluids (G1, M1, R1): Da/W = 5, L/W = 5/4, Dt/J = 10.