3.7. DIFFERENTIAL EQUATIONS OF MOMENTUM TRANSFER OR MOTION
3.7A. Derivation of Equations of Momentum Transfer
The equation of motion is really the conservation-of-momentum equation (2.8-3), which we can write as
Equation 3.7-1
We will make a balance on an element as in Fig. 3.6-2. First we shall consider only the x component of each term in Eq. (3.6-30). The y and z components can be described in an analogous manner.
The rate at which the x component of momentum enters the face at x in the x direction by convection is (ρνxνx)x Δy Δz, and the rate at which it leaves at x + Δx is (ρνxνx)x+Δx Δy Δz. The quantity (ρvx) is the concentration in momentum/m3 or (kg · m/s)/m3, and it is multiplied by νx to give the momentum flux as momentum/s · m2.
The x component of momentum entering the face at y is (ρνyνx)y Δx Δz, and leaving at y + Δy it is (ρνyνx)y+Δy Δx Δz. For the face at z we have (ρνzνx)z Δx Δy entering, and at z + Δz we have (ρνzνx)z+Δz Δx Δy leaving. Hence, the net convective x momentum flow into the volume element Δx Δy Δz is
Equation 3.7-2
Momentum flows in and out of the volume element by the mechanisms of convection or bulk flow as given in Eq. (3.7-2) and also by molecular transfer (by virtue of the velocity gradients in laminar flow). The rate at which the x component of momentum enters the face at x by molecular transfer is (τxx)x Δy Δz, and the rate at which it leaves the surface at x + Ax is (τxx)x+Δx Δy Δz. The rate at which it enters the face at y is (τyx)y Δx Δz, and it leaves at y + Δy at a rate of (τyx)y+Δy Δx Δz. Note that τyx is the flux of x momentum through the face perpendicular to the y axis. Writing a similar equation for the remaining faces, the net x component of momentum by molecular transfer is
Equation 3.7-3
These molecular fluxes of momentum may be considered as shear stresses and normal stresses. Hence, τyx is the x-direction shear stress on the y face and τzx the shear stress on the z face. Also, τxx is the normal stress on the x face.
The net fluid-pressure force acting on the element in the x direction is the difference between the forces acting at x and x + Δx:
Equation 3.7-4
The gravitational force gx acting on a unit mass in the x direction is multiplied by the mass of the element to give
Equation 3.7-5
where gx is the x component of the gravitational vector g.
The rate of accumulation of x momentum in the element is
Equation 3.7-6
Substituting Eqs. (3.7-2)-(3.7-6) into (3.7-1), dividing by Δx Δy Δz, and taking the limit as Δx, Δy, and Δz approach zero, we obtain the x component of the differential equation of motion:
Equation 3.7-7
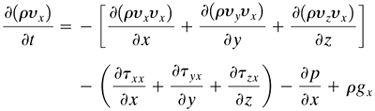
The y and z components of the differential equation of motion are, respectively,
Equation 3.7-8
Equation 3.7-9
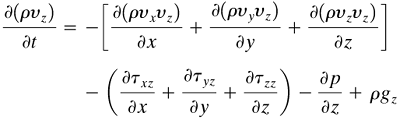
We can use Eq. (3.6-20), which is the continuity equation, and Eq. (3.7-7) to obtain an equation of motion for the x component and also do the same for the y and z components as follows:
Equation 3.7-10
Equation 3.7-11
Equation 3.7-12
Adding vectorially, we obtain an equation of motion for a pure fluid:
Equation 3.7-13
We should note that Eqs. (3.7-7)-(3.7-13) are valid for any continuous medium.
3.7B. Equations of Motion for Newtonian Fluids with Varying Density and Viscosity
In order to use Eqs. (3.7-7)-(3.7-13) to determine velocity distributions, expressions must be used for the various stresses in terms of velocity gradients and fluid properties. For Newtonian fluids the expressions for the stresses τxx, τyx, τzx, and so on, have been related to the velocity gradients and the fluid viscosity μ (B1, B2, D1) and are as follows:
1. Shear-stress components for Newtonian fluids in rectangular coordinates
Equation 3.7-14
Equation 3.7-15
Equation 3.7-16
Equation 3.7-17
Equation 3.7-18
Equation 3.7-19
Equation 3.7-20
2. Shear-stress components for Newtonian fluids in cylindrical coordinates
Equation 3.7-21
Equation 3.7-22
Equation 3.7-23
Equation 3.7-24
Equation 3.7-25
Equation 3.7-26
Equation 3.7-27
3. Shear-stress components for Newtonian fluids in spherical coordinates
Equation 3.7-28
Equation 3.7-29
Equation 3.7-30
Equation 3.7-31
Equation 3.7-32
Equation 3.7-33
Equation 3.7-34
4. Equation of motion for Newtonian fluids with varying density and viscosity
After Eqs. (3.7-14)-(3.7-20) for shear-stress components are substituted into Eq. (3.7-10) for the x component of momentum, we obtain the general equation of motion for a Newtonian fluid with varying density and viscosity:
Equation 3.7-35
Similar equations are obtained for the y and z components of momentum.
3.7C. Equations of Motion for Newtonian Fluids with Constant Density and Viscosity
The equations above are seldom used in their complete forms. When the density ρ and the viscosity μ are constant where (∇ · ν) = 0, the equations are simplified and we obtain the equations of motion for Newtonian fluids. These equations are also called the Navier-Stokes equations.
1. Equation of motion in rectangular coordinates
For Newtonian fluids for constant ρ and μ for the x component, y component, and z component we obtain, respectively,
Equation 3.7-36
Equation 3.7-37
Equation 3.7-38
Combining the three equations for the three components, we obtain
Equation 3.7-39
2. Equation of motion in cylindrical coordinates
These equations are as follows for Newtonian fluids for constant ρ and μ for the r, θ, and z components, respectively:
Equation 3.7-40
Equation 3.7-41
Equation 3.7-42
3. Equation of motion in spherical coordinates
The equations for Newtonian fluids are given below for constant ρ and μ for the r, θ, and ϕ components, respectively:
Equation 3.7-43
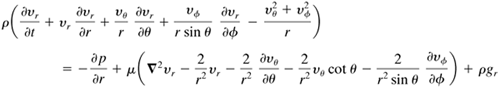
Equation 3.7-44
Equation 3.7-45
where in the three equations above,
Equation 3.7-46
Significant advantages and uses arise in the transformation from rectangular coordinates to cylindrical coordinates. For example, in Eq. (3.7-40) the term 
is the centrifugal force. This gives the force in the r direction (radial) resulting from the motion of the fluid in the θ direction. Note that this term is obtained automatically from the transformation from rectangular to cylindrical coordinates. It does not have to be added to the equation on physical grounds.
The Coriolis force ρνrνθ/r also arises automatically in the transformation of coordinates in Eq. (3.7-41). It is the effective force in the θ direction when there is flow in both the r and the θ directions, as in the case of flow near a rotating disk.