4.2. CONDUCTION HEAT TRANSFER

4.2A. Conduction Through a Flat Slab or Wall

In this section Fourier's equation (4.1-2) will be used to obtain equations for one-dimensional steady-state conduction of heat through some simple geometries. For a flat slab or wall where the cross-sectional area A and k in Eq. (4.1-2) are constant, we obtained Eq. (4.1-10), which we rewrite as

Equation 4.2-1

This is shown in Fig. 4.2-1, where Δx = x₂ - x₁. Equation (4.2-1) indicates that if T is substituted for T₂ and x for X₂, the temperature varies linearly with distance, as shown in Fig. 4.2-1b.

If the thermal conductivity is not constant but varies linearly with temperature, then substituting Eq. (4.1-11) into Eq. (4.1-2) and integrating,

Equation 4.2-2

where

Equation 4.2-3

This means that the mean value of k (i.e., k_m) to use in Eq. (4.2-2) is the value of k evaluated at the linear average of T₁ and T₂.

As stated in the introduction to transport processes in Eq. (2.3-1), the rate of a transfer process equals the driving force over the resistance. Equation (4.2-1) can be rewritten in that form:

Equation 4.2-4

where R = Δx/kA and is the resistance in K/W or h · °F/btu.

4.2B. Conduction Through a Hollow Cylinder

In many instances in the process industries, heat is being transferred through the walls of a thick-walled cylinder, such as a pipe that may or may not be insulated. Consider the hollow cylinder in Fig. 4.2-2 with an inside radius of r_1, where the temperature is T₁, an outside radius of r₂ having a temperature of T₂, and a length of L m. Heat is flowing radially from the inside surface to the outside. Rewriting Fourier's law, Eq. (4.1-2), with distance dr instead of dx,

Equation 4.2-5

The cross-sectional area normal to the heat flow is

Equation 4.2-6

Substituting Eq. (4.2-6) into (4.2-5), rearranging, and integrating,

Equation 4.2-7

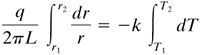
Equation 4.2-8

Multiplying numerator and denominator by (r₂ - r₁),

Equation 4.2-9

where

Equation 4.2-10

Equation 4.2-11

The log mean area is A_lm. In engineering practice, if A₂/A₁ < 1.5/1, the linear mean area of (A₁ + A₂)/2 is within 1.5% of the log mean area. From Eq. (4.2-8), if r is substituted for r₂ and T for T₂, the temperature is seen to be a linear function of In r instead of r as in the case of a flat wall. If the thermal conductivity varies with temperature as in Eq. (4.1-10), it can be shown that the mean value to use in a cylinder is still k_m of Eq. (4.2-3).

EXAMPLE 4.2-1. Length of Tubing for Cooling Coil A thick-walled cylindrical tubing of hard rubber having an inside radius of 5 mm and an outside radius of 20 mm is being used as a temporary cooling coil in a bath. Ice water is flowing rapidly inside, and the inside wall temperature is 274.9 K. The outside surface temperature is 297.1 K. A total of 14.65 W must be removed from the bath by the cooling coil. How many m of tubing are needed? Solution: From Appendix A.3, the thermal conductivity at 0°C (273 K) is k = 0.151 W/m · K. Since data at other temperatures are not available, this value will be used for the range of 274.9 to 297.1 K. The calculation will be done first for a length of 1.0 m of tubing. Solving for the areas A1, A2, and Alm in Eq. (4.2-10), Substituting into Eq. (4.2-9) and solving, The negative sign indicates that the heat flow is from r2 on the outside to r1 on the inside. Since 15.2 W is removed for a 1-m length, the needed length is

Note that the thermal conductivity of rubber is quite small. Generally, metal cooling coils are used, since the thermal conductivity of metals is quite high. The liquid film resistances in this case are quite small and are neglected.

4.2C. Conduction Through a Hollow Sphere

Heat conduction through a hollow sphere is another case of one-dimensional conduction. Using Fourier's law for constant thermal conductivity with distance dr, where r is the radius of the sphere,

Equation 4.2-5

The cross-sectional area normal to the heat flow is

Equation 4.2-12

Substituting Eq. (4.2-12) into (4.2-5), rearranging, and integrating,

Equation 4.2-13

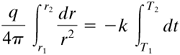
Equation 4.2-14

It can easily be shown that the temperature varies hyperbolically with the radius. (See Problem 4.2-5.)