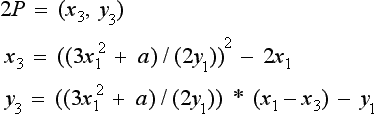Public Key Algorithms
![]() . What Is Public Key Cryptography?
. What Is Public Key Cryptography?
![]() . Goals of Public Key Cryptography
. Goals of Public Key Cryptography
Introduction
So far, we have been discussing symmetric key algorithms such as AES, HMAC, CMAC, GCM, and CCM. These algorithms are known as symmetric (or shared secret) algorithms, since all parties share the same key values. Revealing this key would compromise the security of the system. This means we have been assuming that we somehow shared a key, and now we are going to answer the how part.
Public key algorithms, also known as asymmetric key algorithms, are used (primarily) to solve two problems that symmetric key algorithms cannot: key distribution and nonrepudiation. The first helps solve privacy problems, and the latter helps solve authenticity problems.
Public key algorithms accomplish these goals by operating asymmetrically; that is, a key is split into two corresponding parts, a public key and a private key. The public key is so named as it is secure to give out publicly to all those who ask for it. The public key enables people to encrypt messages and verify signatures. The private key is so named as it must remain private and cannot be given out. The private key is typically owned by a single person or device in most circumstances, but could technically be shared among a trusted set of parties. The private key allows for decrypting messages and the generation of signatures.
The first publicly disclosed public key algorithm was the Diffie-Hellman key exchange, which allowed, at least initially, only for key distribution between known parties. It was extended by ElGamal to a full encrypt and signature public key scheme, and is used for ECC encryption, as we will see shortly. Shortly after Diffie-Hellman was published, another algorithm known as RSA (Rivest Shamir Adleman) was publicly presented. RSA allowed for both encryption and signatures while using half of the bandwidth as ElGamal. Subsequently, RSA became standardized in various forms.
Later, in the 1980s, elliptic curves were proposed as an abelian group over which ElGamal encryption and DSA (variant of ElGamal) could be performed, and throughout the 1990s and 2000s, various algorithms were proposed that make elliptic curve cryptography an attractive alternative to RSA and ElGamal.
For the purposes of this text, we will discuss PKCS #1 standard RSA and ANSI standard ECC cryptography. They represent two of the three standard algorithms specified by NIST for public key cryptography, and in general are representative of the commercial sector demands.
Goals of Public Key Cryptography
Public key cryptography is used to solve various problems that symmetric key algorithms cannot. In particular, it can be used to provide privacy, and nonrepudiation. Privacy is usually provided through key distribution, and a symmetric key cipher. This is known as hybrid encryption. Nonrepudiation is usually provided through digital signatures, and a hash function.
Privacy
Privacy is accomplished with public key algorithms in one of two fashions. The first method is to only use the public key algorithm to encode plaintext into ciphertext (Figure 9.1). For example, RSA can accept a short plaintext and encrypt it directly. This is useful if the application must only encrypt short messages. However, this convenience comes at a price of speed. As we will see shortly, public key operations are much slower than their symmetric key counterparts.
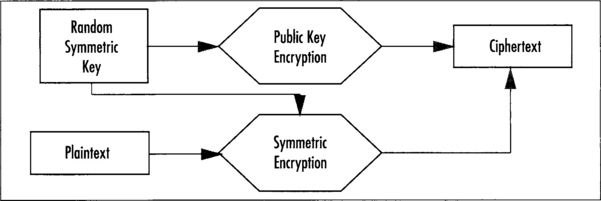
The second useful way of accomplishing privacy is in a mode known as hybrid-encryption (Figure 9.2). This mode leverages the key distribution benefits of public key encryption, and the speed benefits of symmetric algorithms. In this mode, each encrypted message is processed by first choosing a random symmetric key, encrypting it with the public key algorithm, and finally encrypting the message with the random symmetric key. The ciphertext is then the combination of the random public key and random symmetric key ciphertexts.
Nonrepudiation and Authenticity
Nonrepudiation is the quality of being unable to deny or refuse commitment to an agreement. In the paper world, this is accomplished with hand signatures on contracts. They have the quality that in practice they are nontrivial to forge, at least by a layperson. In the digital world, they are produced with public key signatures using a private key. The corresponding public key can verify the signature. Signatures are also used to test the authenticity of a message by verifying a signature from a trusted party.
In the Public Key Infrastructure (PKI) commonly deployed in the form of X.509 certificates (SSL, TLS), and PGP keys, a public key can be signed by an authority common to all users as a means of guaranteeing identity. For example, VeriSign is one of many root certificate authorities in the SSL and TLS domains. Applications that use SSL typically have the public key from VeriSign installed locally so they can verify other public keys VeriSign has vouched for.
Regardless of the purpose of the signature, they are all generated in a common fashion. The message being authenticated is first hashed with a secure cryptographic hash function, and the message digest is then sent through the public key signature algorithm (Figure 9.3).
This construction of public key signatures requires the hash function be collision resistant. If it were easy to find collisions, signatures could be forged by simply producing documents that have the same hash. For this reason, we usually match the hash size and strength with the strength of the underlying public key algorithm. There is, for instance, no point in using a public key algorithm that takes only 264 operations to break with SHA-256. An attacker could just break the public key and produce signatures without finding collisions.
RSA Public Key Cryptography
RSA public key cryptography is based on the problem of taking e’th roots modulo a composite. If you do not know what that means, that is ok; it will be explained shortly. RSA is unique among public key algorithms in that the message (or message digest in the case of signatures) is transformed directly by the public key primitive. As difficult as inverting this transform is (this is known as the trapdoor), it cannot be used directly in a secure fashion.
To solve this problem, RSA Security (the company) invented a standard known as Public Key Cryptographic Standards (PKCS), and their very first standard #1 details how to use RSA. The standard includes how to pad data such that you can apply the RSA transform in a secure fashion. There are two popular versions of this standard: vl.5 and the current v2.1. The older version is technically still secure in most circumstances, but is less favorable as the newer version addresses a couple of cases where vl.5 is not secure. For this reason, it is not recommended to implement vl.5 in new systems. Sadly, this is not always the case. SSL still uses vl.5 padding, as do a variety of PKI based applications.
RSA used to fall under a U.S. patent, which has since expired. The original RSA, including the PKCS #1 padding, are now entirely patent free. There are patents on variants of RSA such as multiprime RSA; however, these are not as popularly deployed and often are avoided for various security concerns.
RSA in a Nutshell
We will now briefly discuss the mathematics behind RSA so the rest of this chapter makes proper sense.
Key Generation
Key generation for RSA is conceptually a simple process. It is not trivial in practice, especially for implementations seeking speed (Figure 9.4).
The e exponent must be odd, as p – 1 and q – 1 will both have factors of two in them. Typically, e is equal to 3, 17, or 65537, which are all efficient to use as a power for exponentiation. The value of d is such that for any m that does not divide n, we will have the property that (mc)d is congruent to m mod n; similarly, (md)c is also congruent to the same value.
The pair e and n form the public key, while the pair d and n form the private key. A party given e and n cannot trivially compute d, nor trivially reverse the computation c = me mod n.
For details on how to choose primes, one could consider reading various sources such as BigNum Math, (Tom St Denis, Greg Rose, BigNum Math—Implementing Cryptographic Multiple Precision Arithmetic, Syngress, 2006), which discuss the matters in depth. That text also discusses other facets required for fast RSA operations such as fast modular exponentiation. The reader could also consider The Art Of Computer Programming” (Donald Knuth, The Art of Computer Programming, Volume 2, third edition, Addison Wesley) as another reference on the subject matter. The latter text treats the arithmetic from a very academic view point and is useful for teaching students the finer points of efficient multiple precision arithmetic.
RSA Transform
The RSA transform is performed by converting a message (interpreted as an array of octets) to an integer, exponentiating it with one of the exponents, and finally converting the integer back to an array of octets. The private transform is performed using the d exponent and is used to decrypt and sign messages. The public transform is performed using the e exponent and is used to encrypt and verify messages.
PKCS #1
PKCS #1 is an RSA standard’ that specifies how to correctly encrypt and sign messages using the RSA transform as a trapdoor primitive (PKCS #1 is available at www.rsasecurity.com/rsalabs/node.asp?id=2125). The padding applied as part of PKCS #1 addresses various vulnerabilities that raw RSA applications would suffer.
The PKCS #1 standard is broken into four parts. First, the data conversion algorithms are specified that allow for the conversion from message to integer, and back again. Next are the cryptographic primitives, which are based on the RSA transform, and provide the trapdoor aspect to the public key standard. Finally, it specifies a section for a proper encryption scheme, and another for a proper signature scheme.
PKCS #1 makes very light use of ASN.1 primitives and requires a cryptographic hash function (even for encryption). It is easy to implement without a full cryptographic library underneath, which makes it suitable for platforms with limited code space.
PKCS #1 Data Conversion
PKCS #1 specifies two functions, OS2IP and I2OSP, which perform octet string and integer conversion, respectively. They are used to describe how a string of octets (bytes) is transformed into an integer for processing through the RSA transform.
The OS2IP function maps an octet string to an integer by loading the octets in big endian fashion. That is, the first byte is the most significant. The I2OSP functions perform the opposite without padding. That is, if the input octet string had leading zero octets, the I2OSP output will not reflect this. We will see shortly how the PKCS standard addresses this.
PKCS #1 Cryptographic Primitives
The PKCS #1 standard specifies four cryptographic primitives, but technically, there are only two unique primitives. The RSAEP primitive performs the public key RSA transform by raising the integer to e modulo n.
The RSADP primitive performs a similar operation, except it uses the d exponent instead. With the exception of leading zeros and inputs that divide the modulus n, the RSADP function is the inverse of RSAEP. The standard specifies how RSADP can be performed with the Chinese Remainder Theorem (CRT) to speed up the operation. This is not technically required for numerical accuracy, but is generally a good idea.
The standard also specifies RSASP1 and RSAVP1, which are equivalent to RSADP and RSAEP, respectively. These primitives are used in the signature algorithms, but are otherwise not that special to know about.
PKCS #1 Encryption Scheme
The RSA recommended encryption scheme is known as RSAES-OAEP, which is simply the combination of OAEP padding and the RSAEP primitive. The OAEP padding is what provides the scheme with security against a variety of active adversarial attacks. The decryption is performed by first applying RSADP followed by the inverse OAEP padding (Figure 9.5).
The hash function is not specified in the standard, and users are free to choose one. The MGF function is specified as in Figure 9.6.
RSA decryption is performed by first applying RSADP, and then the inverse of the OAEP padding scheme. Decryptions must be rejected if they are missing any of the constant bytes, the PS string, or the lHash string.
PKCS #1 Signature Scheme
Like the encryption scheme, the signature scheme employs a padding algorithm before using the RSA primitive. In the case of signatures, this padding algorithm is known as PSS, and the scheme as EMSA-PSS.
The EMSA-PSS signature algorithm is specified as shown in Figure 9.7.
The signature is verified by first applying RSAVP1 to the signature, which returns the value of EM. We then look for the 0xBC octet and check if the upper 8 *emLen – emBits bits of the leftmost octet are zero. If either test fails, the signature is invalid. At this point, we extract maskedDB and H from EM, re-compute dbMask, and decode maskedDB to DB. DB should then contain the original PS zero octets (all emLen – sLen – hLen – 2 of them), the 0x01 octet, and the salt. From the salt, we can re-compute H and compare it against the H we extracted from EM. If they match, the signature is valid; otherwise, it is not.
PKCS #1 Key Format
PKCS #1 specifies two key formats for RSA keys; one is meant for public keys, and the other is meant for private keys. The public key format is the following.

While the private key format is the following.

The private key stores the CRT information used to speed up private key operations. It is not optional that it be stored in the SEQUENCE, but it is optional that you use it. The format also allows for what is known as multi-prime RSA by specifying a Version of 1 and providing OtherPrimelnfos. This is optional to support and generally is a good idea to ignore, as it is covered by a patent owned by HP.
RSA Security
The security of RSA depends mostly on the inability to factor the modulus into the two primes it is made of. If an attacker could factor the modulus, he could compute the private exponent and abuse the system. To this end, extensive research has been undertaken in the field of algebraic number theory to discover factoring algorithms. The first useful algorithm was the quadratic sieve invented in 1981 by Carl Pomerance.
The quadratic sieve had a running time of O(exp(sqrt(log n log log n))) for an integer n. For example, to factor a 1024-bit number, the expected average runtime would be on the order of 298 operations. The quadratic sieve works by gathering relations of the form X2 = Y (mod n) and then factoring Y using a small set of primes known as a factor bound. These relations are gathered and analyzed by looking for combinations of relations such that their product forms a square on both sides; for instance, if X12 * X22 = Y1Y2 (mod n) and Y1Y2 is a square, then the pair can be used to attempt a factorization. If we let P = X12 * X22 and Q = Y1Y2, then if x1 * x2 is not congruent to sqrt(Q) modulo n, we can factor n. If P = Q (mod n), then P – Q = 0 (mod n), and since P and Q are squares, it may be possible to factor n with a difference of squares.
A newer factoring algorithm known as the Number Field Sieve attempts to construct the same relations but in a much different fashion. It was originally meant for numbers of a specific (non-RSA) form, and was later improved to become the generalized number field sieve. It has a running time of O(exp(64/9 * log(n))2/3 * log(log(n))2/3)). For example, to factor a 1024-bit number the expected average runtime would be on the order of 286 operations (Table 9.1).
Table 9.1
| RSA Modulus Size (bits) | Security from Factoring (bits) |
| 1024 | 86 |
| 1536 | 103 |
| 1792 | 110 |
| 2048 | 116 |
| 2560 | 128 |
| 3072 | 138 |
| 4096 | 156 |
This implies if you want your attacker to expend at least 2112 work breaking your key, you must use at least a 2048-bit RSA modulus. In practice, once you pass the 2048-bit mark the algorithm becomes very inefficient, often impossible to implement in embedded systems. There is also no practical RSA key size that will match AES-256 or SHA-512 in terms of bit strength. To obtain 256 bits of security from RSA, you would require a 13,500-bit RSA modulus, which would tax even the fastest desktop processor. One of the big obstacles in making factoring more practical is the size requirements. In general, the number field sieve requires the square root of the work effort in storage to work. For example, a table with 243 elements would be required to factor a 1024-bit composite. If every element were a single bit, that would be a terabyte of storage, which may not seem like a lot until you realize that for this algorithm to work efficiently, it would have to be in random access memory, not fixed disk storage.
In practice, RSA-1024 is still safe to use today, but new applications should really be looking at using at least RSA-1536 or higher—especially where a key may be used for several years to come. Many in the industry simply set the minimum to 2048-bit keys as a way to avoid eventual upgrades in the near future.
RSA References
There are many methods to make the modular exponentiation step faster. The first thing the reader will want to seek out is the use of the Chinese Remainder Theorem (CRT), which allows the private key operation to be split into two half-size modular exponentiations. The PKCS #1 standard explains how to achieve CRT exponentiation with the RSADP and RSAVP1 primitives.
After that optimization, the next optimization is to choose a suitable exponentiation algorithm. The most basic of all is the square and multiply (Figure 9.1, page 192 of BigNum Math), which uses the least amount of memory but takes nearly the maximum amount of time. Technically, square and multiply is vulnerable to timing attacks, as it only multiplies when there is a matching bit in the exponent. A Montgomery Powering Ladder approach can remove that vulnerability, but is also the slowest possible exponentiation algorithm (Marc Joye and Sung-MingYen, “The Montgomery Powering Ladder,” Hardware and Embedded Systems, CHES 2002, vol. 2523 of Lecture Notes in Computer Science, pp. 291–302, Springer-Verlag, 2003). Unlike blinded exponentiation techniques, the Montgomery powering ladder is fully deterministic and does not require entropy at runtime to perform the operation. The ladder is given by the algorithm in Figure 9.8.
This algorithm performs the same operations, at least at the high level, regardless of the bits of the exponent—which can be essential for various threat models given adversaries who can gather side channel information. It can be sped up by realizing that the two operations per iteration can be performed in parallel. This allows hardware implementations to reclaim some speed at a significant cost in area. This observation pays off better with elliptic curve algorithms, as we will see shortly, as the numbers are smaller, and as a consequence, the hardware can be smaller as well.
A simple blinding technique is to pre-compute gr for a random r, and compute gk as gk+r * gr. As long as you never re-use r, it is random, and it is the same length as k the technique blinds timing information that would have been leaked by k.
If memory is abundant, windowed exponentiation is a possible alternative (Figure 7.4, page 196 of BigNum Math). It allows the combination of several multiplications into one step at an expense of pre-compute time and storage. It can also be made to run in fixed time by careful placement of dummy operations.
Elliptic Curve Cryptography
Over the last two decades, a different form of public key cryptography has been gaining ground—elliptic curve cryptography, or ECC. ECC encompasses an often hard to comprehend set of algebraic operations to perform cryptography that is faster than RSA, and more secure.
ECC makes use of the mathematical construct known as an elliptic curve to construct a trapdoor in a manner not vulnerable to sub-exponential attacks (as of yet). This means that every bit used for ECC goes toward the end security of the primitives more than it would with RSA. For this reason, the numbers (or polynomials) used in ECC are smaller than those in RSA. This in turn allows the integer operations to be faster and use less memory.
For the purposes of this text, we will discuss what are known as the prime field ECC curves as specified by NIST and used in the NSA Suite B protocol. NIST also specifies a set of binary field ECC curves, but are less attractive for software. In either case, an excellent resource on the matter is the text Guide to Elliptic Curve Cryptography (Darrel Hankerson, Alfred Menezes, Scott Vanstone, Guide to Elliptic Curve Cryptography, Springer, 2004). That text covers the software implementation of ECC math for both binary and prime field curves in great depth. Readers are strongly encouraged to seek out that text if they are interested in implementing ECC, as it will give them pointers not included here toward high optimization and implementation ease.
What Are Elliptic Curves?
An elliptic curve is typically a two-space graph defined by the square roots of a cubic equation. For instance, y2 = x3 – x is an elliptic curve over the set of real numbers. Elliptic curves can also be defined over other fields such as the field of integers modulo a prime, denoted as GF(p), and over the extension field of various bases, such as GF(2k) (this is known as binary field ECC).
Given an elliptic curve such as Ep : y2 = x3 – 3x + b (typical prime field definition) defined in a finite field modulo p, we can compute points on the curve. A point is simply a pair (x, y) that satisfies the equation of the curve. Since there is a finite number of units in the field, there must be a finite number of unique points on the curve. This number is known as the order of the curve. For various cryptographic reasons, we desire that the order be a large prime, or have a large prime as one of its factors.
In the case of the NIST curves, they specify five elliptic curves with fields of sizes 192, 224, 256, 384, and 521 bits in length. All five of the curves have orders that are themselves large primes. They all follow the definition of Ep listed earlier, except they have unique b values. The fact that they have the same form of equation for the curve is important, as it allows us to use the same basic mathematics to work with all the curves. The only difference is that the modulus and the size of the numbers change (it turns out that you do not need b to perform ECC operations).
From our elliptic curve, we can construct an algebra with operations known as point addition, point doubling, and point multiplication. These operations allow us to then create a trapdoor function useful for both DSA signatures and Diffie-Hellman-based encryption.
Elliptic Curve Algebra
Elliptic curves possess an algebra that allows the manipulation of points along the curve in controlled manners. Point addition takes two points on the curve and constructs another. If we subtract one of the original points from the sum, we will have computed the other original point. Point doubling takes a single point and computes what would amount to the addition of the point to itself. Finally, point multiplication combines the first two operations and allows us to multiply a scalar integer against a point. This last operation is what creates the trapdoor, as we shall see.
Point Addition
Point addition is defined as computing the slope through two points and finding where it strikes the curve when starting from either point. This third point is negated by negating the y portion of the point to compute the addition. Given P = (x1, y1) and Q = (x2, y2), two different points on the curve, we can compute the point addition with the following.
All of these operations are performed in the finite field; that is, modulo some prime. The equations are only defined for the case where P and Q do not lie at the same x co-ordinate.
Point Doubling
Point doubling is defined as computing the tangent of a point on the curve and finding where it strikes the curve. There should be only one unique answer, and it is the double of the point. Point doubling can be thought of as adding a point to itself. By using the tangent instead of the slope, we can obtain well-defined behavior. Given P = (x1, y1), the point double is computed as follows.
Again, all of these operations are performed in a finite field. The a value comes from the definition of the curve, and in the case of the NIST curves is equal to −3.
Point Multiplication
Point multiplication is defined as adding a point to itself a set number of times, typically denoted as kP where k is the scalar number of times we wish to add P to itself. For instance, if we wrote 3P, that literally is equivalent to P + P + P, or specifically, a point double and addition.
The order of the curve plays an important role in the use of point multiplication. The order specifies the maximum number of unique points that are possible given an ideal fixed point G on the curve. That is, if we cycle through all possible values of k, we will hit all of the points. In the case of the NIST curves, the order is prime; this has a neat side effect that all points on the curve have maximal order.
Elliptic Curve Cryptosystems
To construct a public key cryptosystem from elliptic curves, we need a manner of creating a public and private key. For this, we use the point multiplier and a standards specified base point that lies on the curve and is shared among all users. NIST has provided one base point for each of the five different curves they support (on the prime field side of ECC).
Elliptic Curve Parameters
NIST specifies five prime field curves for use with encryption and signature algorithms. A PDF copy of the standard is available through NIST and is very handy to have around (NIST recommended curves: http://csrc.nist.gov/CryptoToolkit/dss/ecdsa/NISTReCur.pdf).
NIST specifies five curves with the sizes 192, 224, 256, 384, and 521 bits, respectively. When we say size, we really mean the order of the curve. For instance, with the 192-bit curve (also known as P-192), the order is a 192-bit number. For any curve over the prime fields, four parameters describe the curve. First is the modulus, p, which defines the field in which the curve lies. Next is the b parameter, which defines the curve in the finite field. Finally is the order of the curve n and the base point, G, on the curve with the specified order. The tuple of (p, n, b, G) is all a developer requires to implement an elliptic curve cryptosystem.
For completeness, following is the P-192 curve settings so you can see what they look like. We will not list all five of them, since printing a page full of random-looking numbers is not useful. Instead, consider reading the PDF that NIST provides, or look at LibTomCrypt in the file src/pk/ecc/ecc.c. That file has all five curves in an easy to steal format to include in other applications (LibTomCrypt is public domain). The following is a snippet from that file.

The first line of the structure describes the field size in octets. The second line is a nice string literal name of the curve (for diagnostic support). Next are p, b, r, and finally the base point (x, y). All the numbers are stored in hexadecimal format.
Key Generation
The algorithm in Figure 9.9 describes the key generation process.
We can now give out Y to anyone we want, and the recipient can use this to encrypt messages for us, or verify messages we sign. The format—that is, byte format of how we store this public key—is specified as part of ANSI X9.63 (Section 4.3.6); however, there are better formats. For the benefit of the reader, we will show the ANSI method.
ANSI X9.63 Key Storage
An elliptic curve point can be represented in one of three forms in the ANSI standard.
When storing P = (x, y), first convert x to an octet string X. In the case of prime curves, this means store the number as a big endian array of octets.
1. If using the compressed form, then
The compression function is computing which of the square roots y is. Taking from ANSI X9.63 (Section 4.2.1), we can compress a point (x, y) by taking the rightmost bit of y and returning that as the output. Decompressing the point is fairly simple, given x and the compressed bit t, the decompression is:
If the rightmost bit of a is equal to t, then return a; otherwise, return p – a
Generally, ECC keys are so small that point compression is not required. However, if you still want to compress your points, there is a clever trick you can use that seems to avoid the Certicom patent (Figure 9.10).
This method of key generation is roughly twice as slow as the normal key generation, but generates public keys you can compress and avoids the Certicom patent. Since the compressed bit will always be 0, there is no requirement to transmit it. The user only has to give out his x co-ordinate of his public key and he is set. What is more, this key generation produces keys compatible with other algorithms such as EC-DH and EC-DSA.
Elliptic Curve Encryption
Encryption with elliptic curves uses a variation of the ElGamal algorithm, as specified in section 5.8 of ANSI X9.63. The algorithm is as shown in Figure 9.11).
ANSI allows for additional shared data in the encryption, and it is optional. The key derivation function is, without this optional shared data, equivalent to the recommended mask generation function (MGF) from the PKCS #1 standard. The MAC required (step 6) must be an ANSI approved MAC with a security level of at least 80 bits. They recommend X9.71, which is the ANSI standard for HMAC. HMAC-SHA1 would provide the minimum security required for X9.63.
Decryption is performed by computing z as the x co-ordinate of k(xq, yq), where k is the recipient’s private key. From z, the recipient can generate the encryption and MAC keys, verify the MAC, and decrypt the ciphertext.
Elliptic Curve Signatures
Elliptic curve signatures use an algorithm known as EC-DSA, which is derived from the NIST standard digital signature algorithm (DSA, FIPS-186-2), and from ElGamal. Signatures are in section 7.3 of ANSI X9.62 (Figure 9.12).
The signature is actually two integers of the size of the order. For instance, with P–192, the signature would be roughly 384 bits in size. ANSI X9.62 specifies that the signatures be stored with the following ASN. 1 SEQUENCE when transporting them (Section E.8):
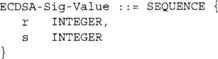
which is a welcome change from the X9.63 key storage format given that it is uniquely decodable. Verification is given as shown in Figure 9.13 (ANSI X9.62 Section 7.4).
For clarification, step 7 performs a point addition of the two point multiplications.
Elliptic Curve Performance
So far, we have been only looking at the very basics of elliptic curve operations such as point addition and doubling using affine co-ordinates. If we implemented a cryptosystem using the functions as so far described, we would have a very slow cryptosystem. The reason being that modular inversions—that is, computing 1/x modulo a prime—is a very slow operation, often comparable to dozens of field multiplications.
To solve this problem, various projective systems have been described that map the two-space operations to three-space or more. The goal is to trade off the inversions with field multiplications. Ideally, if you minimize the field multiplications, you can break even and achieve the point addition and doubling faster. In turn, this makes point multiplication faster, and finally the dependent operations such as encryption and signatures.
Another important optimization is how we perform the point multiplication itself. If we simply added the point to itself the requisite number of times, it would take forever to perform a point multiplication. There are various windowed and fixed point algorithms useful for this as well.
Jacobian Projective Points
In the Jacobian projective co-ordinate system, we represent a standard point with three variables. The mapping is fairly simple going into projective format. The forward mapping turns (x, y) into (x, y, z), with z = 1 to start with. To map back from projective, we compute (x/z2, y/z3, 1), where the division is performed in the finite field. Typically, one would compute 1/z first, and from this derive 1/z2 and l/z3 using only one inversion.
For example, point doubling then becomes the algorithm in Figure 9.14 (taken from page 91, “Guide to Elliptic Curve Cryptography,” algorithm 3.21). Point addition is on the same page, and listed as algorithm 3.22.
The division by two require the value to be even; otherwise, you must first add the modulus (forcing it to be even) and then perform the division (usually by performing the right shift). As we can see, this doubling has a fair bit more steps than the original point double algorithm. In fact, there are more field multiplications as well. However, there are no inversions, and most of the operations are trivial additions or subtractions.
The point addition algorithm assumes the second input is in affine co-ordinates (z = 1). This is important to keep in mind when performing the point multiplication. If you would rather not map to affine, you can use the algorithm from section 4.2 of the “A Practical Implementation of Elliptic Curve Cryptosystems over GF(p) on a 16-bit Microprocessor,” by T. Hasegawa, J. Nakajima, and M. Matsui. It describes both the Jacobian-Jacobian and the Jacobian-affine addition techniques. Mixed additions are slightly faster and consume less memory (as your 2nd operand only needs two co-ordinates of storage), but cost more to set up initially.
Point Multiplication Algorithms
There are a variety of useful manners in which one could accomplish point multiplication, the most basic being the double and add method. It is essentially the square and multiply technique for exponentiation converted to point multiplication (Algorithm 3.27 of the Guide, page 97).
That method works, but is not typically used because it is too slow. Instead, most developers opt instead for a sliding window approach (Algorithm 3.38 of the Guide, page 101). It has fewer point additions and consumes little memory. This algorithm is similar to the exponentiation trick listed in Figure 7.7, page 198 of BigNum Math.
Another approach for when the point is known (or fixed) is the fixed point technique. A variation of this algorithm is described as algorithm 3.41 on page 104 of the Guide. It was also recently added to LibTomCrypt, but as a slightly different variation. This technique leads to very fast point multiplication but at a cost in memory. It is also only useful for encryption, signature generation, and verification. It cannot be used for decryption, as the points are always random. It is therefore important to always have a fast random point multiplier (when decryption is required) before spending resources on a fast fixed point multiplier.
The Guide describes various methods based on nonadjacent forms (NAF) encodings (Algorithm 3.31, page 99), which seem ideal for limited memory platforms. In practice, they often are not faster than the normal windowed approach. It is worth the investigation, though, if memory is a problem.
Putting It All Together
There are two competent public key algorithms in the standards bodies: RSA, which is older and more traditionally used throughout the industry, and ECC, which is slightly newer, more efficient, and making quite a few new appearances in the wild.
The choice between RSA or ECC is often easy given no logistical restrictions such as standards compliance.
ECC versus RSA
ECC with Jacobian co-ordinates and a proper point multiplier leads to much faster private key operations when compared to RSA. The fact that RSA uses larger integers and must perform a slow modular exponentiation make any private key operation very slow. ECC, by using smaller integers, can perform its primitive operations such as field multiplications much faster.
Where RSA wins over ECC is with public key operations (such as encryption and verification). Since the public exponent, e, is typically small, the modular exponentiation can be computed very efficiently. For instance, with e = 65537, only 16 field squarings and 1 field multiplication are required to compute the power. Granted, the field is larger, but it still wins out.
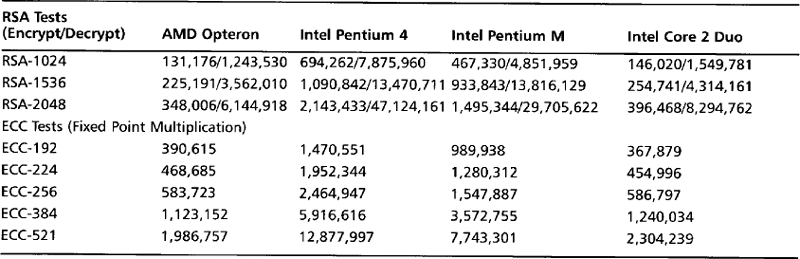
In Table 9.2, we see that RSA-1024 encryption on the AMD Opteron requires 131,176 cycles, while encryption with ECC-192 (the closest ECC match in terms of bit strength) requires two point multiplications and would consume at least 780,000 cycles. On the other hand, signature generation would require at least 1.2 million cycles with RSA-1024, and only 390,000 cycles with ECC-192.
Size
ECC uses smaller numbers (the reason for which will become apparent shortly), which allows it to use less memory and storage when transmitting data.
For example, while aiming for 80 bits of security, ECC would only have to use a 160bit curve, whereas RSA would have to use a 1024-bit modulus. This means our ECC public key is only 320 bits in size. It also means our EC-DSA signature is only 320 bits, compared to the 1024 bits required for RSA-PSS.
It also pays off during the implementation phase. In the same space required for a single RSA sized integer, one could store roughly eight or more ECC sized parameters. We saw from the Jacobian point doubling algorithm that we require 11 integers (one for the modulus, one for overflow, three for the input, three for the output, and three temporaries). This would mean that for ECC-192, we would require 264 bytes of storage for that operation, and 360 for point addition. RSA-1024 with a simple square and multiply would require at least four integers, requiring 512 bytes of storage. (In practice, to get any sort of speed out of RSA, you would require a few more integers. The size estimates are just that—estimates.)
Security
The security of RSA for the most part rests on the difficulty of factoring. While this is not entirely true, it is the current only line of attack against RSA public keys that works. On the other hand, ECC is not vulnerable to factoring or other attacks in the sub-exponential range.
The only known attack against the current elliptic curves chosen by NIST is a exponential cycle finding attack known as Pollard-Rho; that is, assuming the order of the curve is prime. If the order of a curve is n, then it would require roughly O(n1/2) operations to break the ECC public key and find the secret key. For example, with P-192, an attacker would have to expend roughly 296 time breaking the key on average. This means that P-192 is actually about 1024 times harder to break than RSA-1024 when mounting offline attacks on the public key. In practice, RSA-1024 pairs with ECC P-192, RSA-2048 with ECC P-224, and RSA-3072 with ECC P-256.
This is where ECC really shines. At the 112 bits of security level (RSA-2048), the ECC operations are not much harder than from P-192. On the other hand, RSA-2048 is much harder to work with. The field operations are four times slower and there are twice as many of them. On the AMD Opteron when moving from RSA-1024 to RSA-2048, the private key operations become roughly 600-percent slower, whereas when moving from ECC P-192 to P-224, the point multiplication only becomes 20-percent slower.
Standards
Both IEEE and ANSI specify standards for elliptic curve cryptography. The IEEE P1363a is the current IEEE standard, while X9.62 and X9.63 are the current ANSI standards. NIST specifies the use of the ANSI X9.62 EC-DSA as part of the digital signature standard (DSS, FIPS 180-2).
While ANSI specifies RSA standards (X9.31), the PKCS #1 standard is the reference most other standards default to. In particular, quite a few older systems use vl.5 of PKCS #1, which should be avoided. This is not because vl.5 of PKCS #1 is entirely insecure; it is simply less optimal from a security standpoint than v2.1. New applications should avoid both X9.31 (which is very similar to vl.5 of PKCS #1) and vl.5 of PKCS #1 in favor of v2.1.
References
When implementing RSA, the PKCS #1 standard (v2.1) is by far the most important resource. It describes the OAEP and PSS padding techniques, CRT exponentiation, and the ASN. 1 definitions required for interoperability.
For FIPS 180-2 DSS compliance, the ANSI X9.31 standard must be used.
When implementing ECC, the ANSI X9.62 standard specifies EC-DSA and is used by FIPS 180-2 DSS. The ANSI X9.63 standard specifies ECC encryption, key storage, and a few authentication schemes (a couple of which have patents). Currently, NIST is working on SP800-56A, which specifies ANSI X9.42 using discrete logarithm systems (like ElGamal), and X9.63 using ECC. An additional specification SP800-56B specifies ANSI X9.44 (RSA encryption). It is more likely that SP800-56A will become more popular in the future, as it uses ECC as oppose to RSA.
A good reference for the large integer operations is BigNum Math (Tom St Denis, Greg Rose, BigNum Math: Implementing Cryptographic Multiple Precision Arithmetic, Syngress, 2006, ISBN 1-59749-112-8), which discusses the creation of a portable and efficient multiple precision large integer operations. That book uses both pseudo code and real production C source code to demonstrate the math to the reader. It is by no means a hard read and is well suited for the target audience of this text.
For implementing ECC math, the reader is strongly encouraged to obtain a copy of the Guide to Elliptic Curve Cryptography (D. Hankerson, A. Menezes, S. Vanstone, Guide to Elliptic Curve Cryptography, Springer, 2004, ISBN 0-387-95273-X). That text discusses both binary and prime field ECC operations, and detailed explanations of point operations and multiplication. It spends less time on the field operations (such as integer multiplication), but a good deal of time on the binary field operations (which are typically harder to understand at first for most). It is an invaluable resource on point multiplication techniques.
Source Code References
The LibTomCrypt package provides PKCS #1 compliant RSA and ANSI X9.62 compliant EC-DSA. It uses a modified key derivation function and key storage that is incompatible with X9.63. LibTomCrypt employs the use of CRT exponentiation for RSA. It uses Jacobian-affine co-ordinates for the ECC math. It provides both a sliding window random point multiplier and a fixed point multiplier. Since the code is well commented and public domain, it is a valuable source of implementation insight.
The Crypto++ package also provides PKCS #1, and ANSI X9.62 and X9.63 support. Its code base is larger than LibTomCrypt and is not public domain. It includes a variety of patented algorithms as well, such as EC-MQV. The reader should be careful when exploring this code base, as it is not all free and clear to use.
The following Frequently Asked Questions, answered by the authors of this book, are designed to both measure your understanding of the concepts presented in this chapter and to assist you with real-life implementation of these concepts. To have your questions about this chapter answered by the author, browse to www.syngress.com/solutioris and click on the “Ask the Author” form.
Q: What are public key algorithms?
A: Public key algorithms are algorithms where a key can be split into a public and private portion. This then allows the holder of the private key to perform operations that are not possible with the public key. For example, the private key can sign messages while the public key can only verify them.
Q: What else are they good for?
A: Public key cryptographmolves, or at least, offers a solution to, the key distribution problem that plagues syeLacyj algorithms. For example, one may encrypt a message with a public key, and only the private key can decrypt it. In this way, without first securing a shared secret, we can still transmit encrypted data.
Q: What public key algorithms are alt there?
A: There are many, from Diffie-Hellman, ElGamal, RSA, ECC, and NTRU. Most standards focus on RSA, and recently more often on ECC. ElGamal is Bill considered secure; it is merely too inefficient to contend with RSA (which is now patent free).
Q: What standards are out there?
A: ANSI X9.62 specifies ECC signatures, while ANSI X9.63 specifies ECC encryption. PKCS #1 specifies RSA encryption and signatures. ANSI X9.31 specifies RSA signatures, and X9.42 specifies RSA encryption. The FIPS 180-2 specifies X9.62 for ECC and X9.31 for RSA, along with its own DSA (over integers).
Q: What is good/bad about RSA?
A: Conceptually, RSA is very simple. It is fairly easy to develop against, and PKCS #1 is not too painful to digest. RSA public key operations (encrypt and verify) are typically very fast. On the other hand, RSA private key operations are very slow. RSA also requires large keys for typically demanded bit security. For example, for 112 bits of security, one must use a 2048-bit RSA key. This can make RSA very inefficient very quickly.
Q: What is good/bad about ECC?
A: The security of ECC is much better than that of RSA. With smaller parameters, ECC provides more security than RSA. This means that ECC math can be both memory efficient and fast. ECC public key operations are slower than their private key counterparts, but are still typically faster than RSA at the nontrivial bit security levels. ECC is also more complicated than RSA to implement and more prone to implementation errors. It’s conceptually hard to get going very fast and requires more time to complete than RSA.
Q: Are there libraries I can look at?
A: Both LibTomCrypt and Crypto ++ implement public key algorithms. The latter implements many more algorithms than just RSA and ECC. LibTomCrypt does not fully adhere to the X9.63 standard, as it deviates to solve a few problems X9.63 has. It does, however, implement X9.62, and PKCS #1 for RSA.
Q: Why should I buy Guide to Elliptic Curve Cryptography, if I just bought this book?
A: The Guide was written by some of the best minds in cryptography, from Certicom, and are essentially the professionals in elliptic curve mathematics. The book also fully covers the NIST suite of ECC curves with algorithms that are efficient, patent free, and easy to implement. Duplicating the content of that book here seems like a waste of time and does not serve the audience well. Trust us, it’s worth the purchase.