CHAPTER
SIXTY-TWO
INTEREST-RATE SWAPS AND SWAPTIONS
FRANK J. FABOZZI, PH.D., CFA, CPA
Professor of Finance
EDHEC Business School
STEVEN V. MANN, PH.D.
Professor of Finance
Moore School of Business
University of South Carolina
MOORAD CHOUDHRY, PH.D.
MD, Head of Business Treasury, Global Banking & Markets
Royal Bank of Scotland
Swaps and swaptions are also used extensively by market participants to control interest-rate risk. The most prevalent swap contract is an interest-rate swap. An interest-rate swap contract provides a vehicle for market participants to transform the nature of cash-flows and the interest-rate exposure of a portfolio or balance sheet. In this chapter we explain how to analyze interest-rate swaps. We will describe a generic interest-rate swap, the parties to a swap, the risk and return of a swap, and the economic interpretation of a swap. Then we look at how to compute the floating-rate payments and calculate the present value of these payments. Next, we will see how to calculate the fixed-rate payments given the swap rate. Before we look at how to calculate the value of a swap, we will see how to calculate the swap rate. Given the swap rate, we will then see how the value of a swap is determined after the inception of a swap. We also will discuss other types of swaps as well as options on swaps called swaptions. Swaptions are used ever more frequently as a tool for investors to control their interest-rate risk. These instruments are described in the latter part of the chapter and their valuation is described in Chapter 63.
DESCRIPTION OF AN INTEREST-RATE SWAP
In an interest-rate swap, two parties (called counterparties) agree to exchange periodic interest payments. The dollar amount of the interest payments exchanged is based on some predetermined dollar principal, which is called the notional amount. The dollar amount each counterparty pays to the other is the agreed-on periodic interest rate times the notional amount. The only dollars that are exchanged between the parties are the interest payments, not the notional amount. Accordingly, the notional principal serves only as a scale factor to translate an interest rate into a cash flow. In the most common type of swap, one party agrees to pay the other party fixed interest payments at designated dates for the life of the contract. This party is referred to as the fixed-rate payer. The other party, who agrees to make interest-rate payments that float with some reference rate, is referred to as the floating-rate payer.
The reference rates that have been used for the floating-rate in an interest-rate swap are various money market rates: Treasury bill rate, the London Interbank Offered Rate (LIBOR), commercial paper rate, bankers acceptances rate, certificates of deposit rate, the federal funds rate, and the prime rate. The most common is the LIBOR. LIBOR is the rate at which prime banks offer to pay on Eurodollar deposits available to other prime banks for a given maturity. There is not just one rate but a rate for different maturities. For example, there is a one-month LIBOR, three-month LIBOR, and six-month LIBOR.
To illustrate an interest-rate swap, suppose that for the next five years party X agrees to pay party Y 10% per year, while party Y agrees to pay party X six-month LIBOR (the reference rate). Party X is a fixed-rate payer/floating-rate receiver, while party Y is a floating-rate payer/fixed-rate receiver. Assume that the notional amount is $50 million and that payments are exchanged every six months for the next five years. This means that every six months, party X (the fixed-rate payer/floating-rate receiver) will pay party Y $2.5 million (10% times $50 million divided by 2). The amount that party Y (the floating-rate payer/fixed-rate receiver) will pay party X will be six-month LIBOR times $50 million divided by 2. If six-month LIBOR is 7%, party Y will pay party X $1.75 million (7% times $50 million divided by 2). Note that we divide by 2 because one-half year’s interest is being paid.
Interest-rate swaps are over-the-counter (OTC) instruments. This means that swaps are not traded on an exchange. An institutional investor wishing to enter into a swap transaction can do so through either a securities firm or a commercial bank that transacts in swaps. These entities can do one of the following. First, they can arrange or broker a swap between two parties that want to enter into an interest-rate swap. In this case, the securities firm or commercial bank is acting in a brokerage capacity.
The second way in which a securities firm or commercial bank can get an institutional investor into a swap position is by taking the other side of the swap. This means that the securities firm or the commercial bank is a dealer rather than a broker in the transaction. Acting as a dealer, the securities firm or the commercial bank must hedge its swap position in the same way that it hedges its position in other securities. Also, it means that the swap dealer is the counterparty to the transaction.
The risks that the two parties take on when they enter into a swap is that the other party will fail to fulfill its obligations as set forth in the swap agreement. That is, each party faces default risk. The default risk in a swap agreement is called counterparty risk. In any agreement between two parties that must perform according to the terms of a contract, counterparty risk is the risk that the other party will default. With futures and exchange-traded options, the counterparty risk is the risk that the clearinghouse will default. Market participants view this risk as small. In contrast, counterparty risk in a swap can be significant.
Because of counterparty risk, not all securities firms and commercial banks can be swap dealers. Several securities firms have established subsidiaries that are separately capitalized so that they have a high credit rating that permits them to enter into swap transactions as a dealer.
Thus it is imperative to keep in mind that any party who enters into a swap is subject to counterparty risk.
INTERPRETING A SWAP POSITION
There are two ways that a swap position can be interpreted: (1) a package of forward/futures contracts and (2) a package of cash-flows from buying and selling cash market instruments.
Package of Forward Contracts
Consider the hypothetical interest-rate swap used earlier to illustrate a swap. Let’s look at party X’s position. Party X has agreed to pay 10% and receive six-month LIBOR. More specifically, assuming a $50 million notional amount, X has agreed to buy a commodity called “six-month LIBOR” for $2.5 million. This is effectively a six-month forward contract where X agrees to pay $2.5 million in exchange for delivery of six-month LIBOR. The fixed-rate payer is effectively long a six-month forward contract on six-month LIBOR. The floating-rate payer is effectively short a six-month forward contract on six-month LIBOR. There is therefore an implicit forward contract corresponding to each exchange date.
Consequently, interest-rate swaps can be viewed as a package of more basic interest-rate derivative instruments—forwards. The pricing of an interest-rate swap then will depend on the price of a package of forward contracts with the same settlement dates in which the underlying for the forward contract is the same reference rate.
While an interest-rate swap may be nothing more than a package of forward contracts, it is not a redundant contract for several reasons. First, maturities for forward or futures contracts do not extend out as far as those of an interest-rate swap; an interest-rate swap with a term of 15 years or longer can be obtained. Second, an interest-rate swap is a more transactionally efficient instrument. By this we mean that in one transaction an entity can effectively establish a payoff equivalent to a package of forward contracts. The forward contracts would each have to be negotiated separately. Third, the interest-rate swap market has grown in liquidity since its establishment in 1981; interest-rate swaps now provide more liquidity than forward contracts, particularly long-dated (i.e., long-term) forward contracts.
Package of Cash-Market Instruments
To understand why a swap also can be interpreted as a package of cash-market instruments, consider an investor who enters into the transaction below:
• Buy $50 million par value of a five-year floating-rate bond that pays six-month LIBOR every six months
• Finance the purchase by borrowing $50 million for five years at a 10% annual interest rate paid every six months.
The cash-flows for this transaction are set forth in Exhibit 62–1. The second column of the exhibit shows the cash-flows from purchasing the five-year floating-rate bond. There is a $50 million cash outlay and then 10 cash inflows. The amount of the cash inflows is uncertain because they depend on future levels of six-month LIBOR. The next column shows the cash-flows from borrowing $50 million on a fixed-rate basis. The last column shows the net cash-flows from the entire transaction. As the last column indicates, there is no initial cash-flow (the cash inflow and cash outlay offset each other). In all 10 six-month periods, the net position results in a cash inflow of LIBOR and a cash outlay of $2.5 million. This net position, however, is identical to the position of a fixed-rate payer/floating-rate receiver.
EXHIBIT 62–1
Cash-Flows for the Purchase of a Five-Year Floating-Rate Bond Financed by Borrowing on a Fixed-Rate Basis
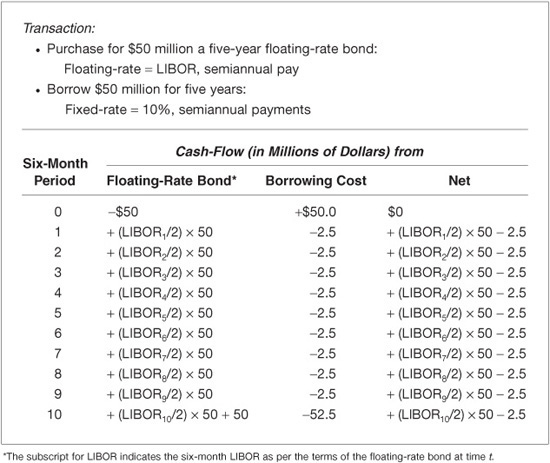
It can be seen from the net cash-flow in Exhibit 62–1 that a fixed-rate payer has a cash market position that is equivalent to a long position in a floating-rate bond and a short position in a fixed-rate bond—the short position being the equivalent of borrowing by issuing a fixed-rate bond.
What about the position of a floating-rate payer? It can be easily demonstrated that the position of a floating-rate payer is equivalent to purchasing a fixed-rate bond and financing that purchase at a floating-rate, where the floating-rate is the reference rate for the swap. That is, the position of a floating-rate payer is equivalent to a long position in a fixed-rate bond and a short position in a floating-rate bond.
TERMINOLOGY, CONVENTIONS, AND MARKET QUOTES
Here we review some of the terminology used in the swaps market and explain how swaps are quoted. The trade date for a swap is the date on which the swap is transacted. The terms of the trade include the fixed interest rate, the maturity, the notional amount of the swap, and the payment bases of both legs of the swap. The date from which floating interest payments are determined is the reset or setting date, which also may be the trade date. In the same way as for FRAs (discussed in Chapter 59), the rate is fixed two business days before the interest period begins. The second (and subsequent) reset date will be two business days before the beginning of the second (and subsequent) swap periods. The effective date is the date from which interest on the swap is calculated, and this is typically two business days after the trade date. In a forward-start swap, the effective date will be at some point in the future, specified in the swap terms. The floating interest rate for each period is fixed at the start of the period, so the interest payment amount is known in advance by both parties (the fixed-rate is known, of course, throughout the swap by both parties).
While our illustrations assume that the timing of the cash-flows for both the fixed-rate payer and floating-rate payer will be the same, this is rarely the case in a swap. An agreement may call for the fixed-rate payer to make payments annually but the floating-rate payer to make payments more frequently (semiannually or quarterly). Also, the way in which interest accrues on each leg of the transaction differs. Normally, the fixed interest payments are paid on the basis of a 30/360 day count. Floating-rate payments for dollar and euro-denominated swaps use an actual/360-day count similar to other money market instruments in those currencies. Sterling-denominated swaps use an actual/365-day count.
Accordingly, the fixed interest payments will differ slightly owing to the differences in the lengths of successive coupon periods. The floating payments will differ owing to day counts as well as movements in the reference rate.
The terminology used to describe the position of a party in the swap markets combines cash-market jargon and futures-market jargon, given that a swap position can be interpreted either as a position in a package of cash-market instruments or a package of futures/forward positions. As we have said, the counterparty to an interest-rate swap is either a fixed-rate payer or floating-rate payer.
The fixed-rate payer receives floating-rate interest and is said to be “long” or to have “bought” the swap. The long side has conceptually purchased a floating-rate note (because it receives floating-rate interest) and issued a fixed-coupon bond (because it pays out fixed interest at periodic intervals). In essence, the fixed-rate payer is borrowing at fixed-rate and investing in a floating-rate asset. The floating-rate payer is said to be “short” or to have “sold” the swap. The short side has conceptually purchased a coupon bond (because it receives fixed-rate interest) and issued a floating-rate note (because it pays floating-rate interest). A floating-rate payer is borrowing at floating-rate and investing in a fixed-rate asset.
The convention that has evolved for quoting swaps levels is that a swap dealer sets the floating-rate equal to the reference rate and then quotes the fixed-rate that will apply. To illustrate this convention, consider the following 10-year swap terms available from a dealer:
• Floating-rate payer: Pay floating-rate of three-month LIBOR quarterly. Receive fixed-rate of 8.75% semiannually.
• Fixed-rate payer: Pay fixed-rate of 8.85% semiannually. Receive floating-rate of three-month LIBOR quarterly.
The offer price that the dealer would quote the fixed-rate payer would be to pay 8.85% and receive LIBOR “flat.” (The word flat means with no spread.) The bid price that the dealer would quote the floating-rate payer would be to pay LIBOR flat and receive 8.75%. The bid-offer spread is 10 basis points.
In order to solidify our intuition, it is useful to think of the swap market as a market where two counterparties trade the floating reference rate in a series of exchanges for a fixed price. In effect, the swap market is a market to buy and sell LIBOR. Thus, buying a swap (pay fixed/receive floating) can be thought of as buying LIBOR on each reset date for the fixed-rate agreed to on the trade date. Conversely, selling a swap (receive fixed/pay floating) is effectively selling LIBOR on each reset date for a fixed-rate agreed to on the trade date. In this framework, a dealer’s bid-offer spread can be easily interpreted. Using the numbers presented earlier, the bid price of 8.75% is the price the dealer will pay to the counterparty to receive three-month LIBOR. In other words, buy LIBOR at the bid. Similarly, the offer price of 8.85% is the price the dealer receives from the counterparty in exchange for three-month LIBOR. In other words, sell LIBOR at the offer.
The fixed-rate is some spread above the Treasury yield-curve with the same term-to-maturity as the swap. In our illustration, suppose that the 10-year Treasury yield is 8.35%. Then the offer price that the dealer would quote to the fixed-rate payer is the 10-year Treasury rate plus 50 basis points versus receiving LIBOR flat. For the floating-rate payer, the bid price quoted would be LIBOR flat versus the 10-year Treasury rate plus 40 basis points. The dealer would quote such a swap as 40-50, meaning that the dealer is willing to enter into a swap to receive LIBOR and pay a fixed-rate equal to the 10-year Treasury rate plus 40 basis points, and he would be willing to enter into a swap to pay LIBOR and receive a fixed-rate equal to the 10-year Treasury rate plus 50 basis points.
VALUING INTEREST-RATE SWAPS
In an interest-rate swap, the counterparties agree to exchange periodic interest payments. The dollar amount of the interest payments exchanged is based on the notional principal. In the most common type of swap, there is a fixed-rate payer and a fixed-rate receiver. The convention for quoting swap rates is that a swap dealer sets the floating-rate equal to the reference rate and then quotes the fixed-rate that will apply.
Computing the Payments for a Swap
In the preceding section we described in general terms the payments by the fixed-rate payer and fixed-rate receiver, but we did not give any details. That is, we explained that if the swap rate is 6% and the notional amount is $100 million, then the fixed-rate payment will be $6 million for the year, and the payment is then adjusted based on the frequency of settlement. Thus, if settlement is semiannual, the payment is $3 million. If it is quarterly, it is $1.5 million. Similarly, the floating-rate payment would be found by multiplying the reference rate by the notional amount and then scaling based on the frequency of settlement.
It was useful to illustrate the basic features of an interest-rate swap with simple calculations for the payments such as described earlier and then explain how the parties to a swap either benefit or hurt when interest rates change. However, we will show how to value a swap in this section. To value a swap, it is necessary to determine both the present value of the fixed-rate payments and the present value of the floating-rate payments. The difference between these two present values is the value of a swap. As will be explained below, whether the value is positive (i.e., an asset) or negative (i.e., a liability) will depend on the party.
At the inception of the swap, the terms of the swap will be such that the present value of the floating-rate payments is equal to the present value of the fixed-rate payments. That is, the value of the swap is equal to zero at its inception. This is the fundamental principle in determining the swap rate (i.e., the fixed-rate that the fixed-rate payer will make).
Here is a roadmap of the presentation. First, we will look at how to compute the floating-rate payments. We will see how the future values of the reference rate are determined to obtain the floating-rate for the period. From the future values of the reference rate we will then see how to compute the floating-rate payments, taking into account the number of days in the payment period. Next, we will see how to calculate the fixed-rate payments given the swap rate. Before we look at how to calculate the value of a swap, we will see how to calculate the swap rate. This will require an explanation of how the present value of any cashflow in an interest-rate swap is computed. Given the floating-rate payments and the present value of the floating-rate payments, the swap rate can be determined by using the principle that the swap rate is the fixed-rate that will make the present value of the fixed-rate payments equal to the present value of the floating-rate payments. Finally, we will see how the value of swap is determined after the inception of a swap.
Calculating the Floating-Rate Payments
For the first floating-rate payment, the amount is known. For all subsequent payments, the floating-rate payment depends on the value of the reference rate when the floating-rate is determined. To illustrate the issues associated with calculating the floating-rate payment, we will assume that
• A swap starts today, January 1 of year 1 (swap settlement date).
• The floating-rate payments are made quarterly based on “actual/360.”
• The reference rate is three-month LIBOR.
• The notional amount of the swap is $100 million.
• The term of the swap is three years.
The quarterly floating-rate payments are based on an actual/360-day count convention. Recall that this convention means that 360 days are assumed in a year and that in computing the interest for the quarter, the actual number of days in the quarter is used. The floating-rate payment is set at the beginning of the quarter but paid at the end of the quarter—that is, the floating-rate payments are made in arrears.
Suppose that today three-month LIBOR is 4.05%. Let’s look at what the fixed-rate payer will receive on March 31 of year 1—the date when the first quarterly swap payment is made. There is no uncertainty about what the floating-rate payment will be. In general, the floating-rate payment is determined as follows:
![]()
In our illustration, assuming a nonleap year, the number of days from January 1 of year 1 to March 31 of year 1 (the first quarter) is 90. If three-month LIBOR is 4.05%, then the fixed-rate payer will receive a floating-rate payment on March 31 of year 1 equal to
![]()
Now the difficulty is in determining the floating-rate payment after the first quarterly payment. That is, for the three-year swap, there will be 12 quarterly floating-rate payments. Thus, while the first quarterly payment is known, the next 11 are not. However, there is a way to hedge the next 11 floating-rate payments by using a futures contract. Specifically, the futures contract used to hedge the future floating-rate payments in a swap whose reference rate is three-month LIBOR is the Eurodollar futures contract.
Determining Future Floating-Rate Payments
Now let’s determine the future floating-rate payments. These payments can be locked in over the life of the swap using the Eurodollar futures contract. We will show how these floating-rate payments are computed using this contract.
We will begin with the next quarterly payment—from April 1 of year 1 to June 30 of year 1. This quarter has 91 days. The floating-rate payment will be determined by three-month LIBOR on April 1 of year 1 and paid on June 30 of year 1. Where might the fixed-rate payer look today (January 1 of year 1) to project what three-month LIBOR will be on April 1 of year 1? One possibility is the Eurodollar futures market. There is a three-month Eurodollar futures contract for settlement on June 30 of year 1. That futures contract will express the market’s expectation of three-month LIBOR on April 1 of year 1. For example, if the futures price for the three-month Eurodollar futures contract that settles on June 30 of year 1 is 95.85, then as explained earlier, the three-month Eurodollar futures rate is 4.15%. We will refer to that rate for three-month LIBOR as the “forward rate.” Therefore, if the fixed-rate payer bought 100 of these three-month Eurodollar futures contracts on January 1 of year 1 (the inception of the swap) that settle on June 30 of year 1, then the payment that will be locked in for the quarter (April 1 to June 30 of year 1) is
![]()
Note that each futures contract is for $1 million, and hence 100 contracts have a notional amount of $100 million.
Similarly, the Eurodollar futures contract can be used to lock in a floating-rate payment for each of the next 10 quarters. Once again, it is important to emphasize that the reference rate at the beginning of period t determines the floating-rate that will be paid for the period. However, the floating-rate payment is not made until the end of period t.
Exhibit 62–2 shows this for the three-year swap. Shown in column (1) is when the quarter begins and in column (2) when the quarter ends. The payment will be received at the end of the first quarter (March 31 of year 1) and is $1,012,500. This is the known floating-rate payment, as explained earlier. It is the only payment that is known. The information used to compute the first payment is in column (4), which shows the current three-month LIBOR (4.05%). The payment is shown in the last column, column (8).
EXHIBIT 62–2
Floating-Rate Payments Based on Initial LIBOR and Eurodollar Futures

Notice that column (7) numbers the quarters from 1 through 12. Look at the heading for column (7). It identifies each quarter in terms of the end of the quarter. This is important because we will eventually be discounting the payments (cashflows). We must take care to understand when each payment is to be exchanged in order to properly discount. Thus, for the first payment of $1,012,500, it is going to be received at the end of quarter 1. When we refer to the time period for any payment, the reference is to the end of quarter. Thus the fifth payment of $1,225,000 would be identified as the payment for period 5, where period 5 means that it will be exchanged at the end of the fifth quarter.
Calculating the Fixed-Rate Payments
The swap will specify the frequency of settlement for the fixed-rate payments. The frequency need not be the same as the floating-rate payments. For example, in the three-year swap we have been using to illustrate the calculation of the floating-rate payments, the frequency is quarterly. The frequency of the fixed-rate payments could be semiannual rather than quarterly.
In our illustration we will assume that the frequency of settlement is quarterly for the fixed-rate payments, the same as with the floating-rate payments. The day-count convention is the same as for the floating-rate payment, actual/360. The equation for determining the dollar amount of the fixed-rate payment for the period is
![]()
It is the same equation as for determining the floating-rate payment except that the swap rate is used instead of the reference rate (three-month LIBOR in our illustration).
For example, suppose that the swap rate is 4.98% and the quarter has 90 days. Then the fixed-rate payment for the quarter is
![]()
If there are 92 days in a quarter, the fixed-rate payment for the quarter is
![]()
Note that the rate is fixed for each quarter, but the dollar amount of the payment depends on the number of days in the period.
Exhibit 62–3 shows the fixed-rate payments based on different assumed values for the swap rate. The first three columns of the exhibit show the same information as in Exhibit 62–2—the beginning and end of the quarter and the number of days in the quarter. Column (4) simply uses the notation for the period.
EXHIBIT 62–3
Fixed-Rate Payments for Several Assumed Swap Rates
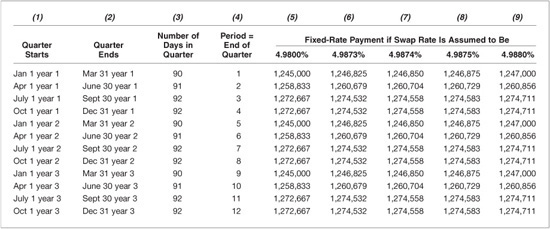
That is, period 1 means the end of the first quarter, period 2 means the end of the second quarter, and so on. The other columns of the exhibit show the payments for each assumed swap rate.
Calculation of the Swap Rate
Now that we know how to calculate the payments for the fixed-rate and floating-rate sides of a swap where the reference rate is three-month LIBOR given (1) the current value for three-month LIBOR, (2) the expected three-month LIBOR from the Eurodollar futures contract, and (3) the assumed swap rate, we can demonstrate how to compute the swap rate.
At the initiation of an interest-rate swap, the counterparties are agreeing to exchange future payments, and no upfront payments are made by either party. This means that the swap terms must be such that the present value of the payments to be made by the counterparties must be at least equal to the present value of the payments that will be received. In fact, to eliminate arbitrage opportunities, the present value of the payments made by a party will be equal to the present value of the payments received by that same party. The equivalence (or no arbitrage) of the present value of the payments is the key principle in calculating the swap rate.
Since we will have to calculate the present value of the payments, let’s show how this is done.
Calculating the Present Value of the Floating-Rate Payments
As explained earlier, we must be careful about how we compute the present value of payments. In particular, we must carefully specify (1) the timing of the payment and (2) the interest rates that should be used to discount the payments. We have already addressed the first issue. In constructing the exhibit for the payments, we indicated that the payments are at the end of the quarter. Thus we denoted the time periods with respect to the end of the quarter.
Now let’s turn to the interest rates that should be used for discounting. First, every cash-flow should be discounted at its own discount rate using a spot rate. Thus, if we discounted a cash-flow of $1 using the spot rate for period t, the present value would be
![]()
Second, forward rates are derived from spot rates, so if we discounted a cash-flow using forward rates rather than spot rates, we would come up with the same value. That is, the present value of $1 to be received in period t can be rewritten as
Present value of $1 to be received in period t discounted with forward rates
We will call the present value of $1 to be received in period t as the forward discount factor. In our calculations involving swaps, we will compute the forward discount factor for a period using the forward rates. These are the same forward rates that are used to compute the floating-rate payments—those obtained from the Eurodollar futures contract. We must make just one more adjustment. We must adjust the forward rates used in the formula for the number of days in the period (i.e., the quarter in our illustrations) in the same way that we made this adjustment to obtain the payments. Specifically, the forward rate for a period, which we will call the period forward rate, is computed using the following equation:
![]()
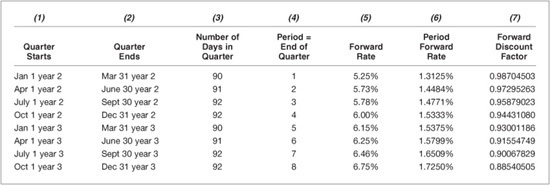
For example, look at Exhibit 62–2. The annual forward rate for period 4 is 4.72%. The period forward rate for period 4 is
![]()
Column (5) in Exhibit 62–4 shows the annual forward rate for all 12 periods (reproduced from Exhibit 62–3), and column (6) shows the period forward rate for all 12 periods. Note that the period forward rate for period 1 is 4.05%, the known rate for three-month LIBOR.
Also shown in Exhibit 62–4 is the forward discount factor for all 12 periods. These values are shown in the last column. Let’s show how the forward discount factor is computed for periods 1, 2, and 3. For period 1, the forward discount factor is
![]()
For period 2,
![]()
For period 3,
![]()
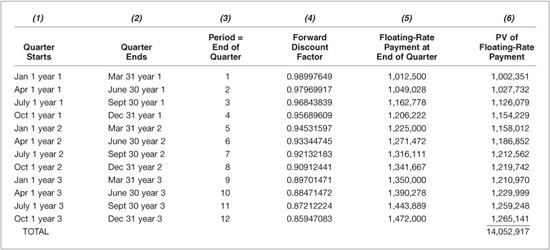
Given the floating-rate payment for a period and the forward discount factor for the period, the present value of the payment can be computed. For example, from Exhibit 62–2 we see that the floating-rate payment for period 4 is $1,206,222. From Exhibit 62–4, the forward discount factor for period 4 is 0.95689609. Therefore, the present value of the payment is
Present value of period 4 payment = $1,206,222 × 0.95689609
= $1,154,229
EXHIBIT 62–4
Calculating the Forward Discount Factor

Exhibit 62–5 shows the present value for each payment. The total present value of the 12 floating-rate payments is $14,052,917 Thus the present value of the payments that the fixed-rate payer will receive is $14,052,917, and the present value of the payments that the fixed-rate receiver will make is $14,052,917.
EXHIBIT 62–5
Present Value of the Floating-Rate Payments
Determination of the Swap Rate
The fixed-rate payer will require that the present value of the fixed-rate payments that must be made based on the swap rate not exceed the $14,052,917 payments to be received from the floating-rate payments. The fixed-rate receiver will require that the present value of the fixed-rate payments to be received is at least as great as the $14,052,917 that must be paid. This means that both parties will require a present value for the fixed-rate payments to be $14,052,917. If this is the case, the present value of the fixed-rate payments is equal to the present value of the floating-rate payments, and therefore, the value of the swap is zero for both parties at the inception of the swap. The interest rates that should be used to compute the present value of the fixed-rate payments are the same interest rates as those used to discount the floating-rate payments.
To show how to compute the swap rate, we begin with the basic relationship for no arbitrage to exist:
PV of floating-rate payments = PV of fixed-rate payments
We know the value for the left-hand side of the equation.
If we let
SR = swap rate
and
Dayst = number of days in the payment period t
then the fixed-rate payment for period t is equal to
![]()
The present value of the fixed-rate payment for period t is found by multiplying the previous expression by the forward discount factor. If we let FDFt denote the forward discount factor for period t, then the present value of the fixed-rate payment for period t is equal to
![]()
We can now sum up the present value of the fixed-rate payment for each period to get the present value of the floating-rate payments. Using the Greek symbol sigma (Σ) to denote summation, and letting N be the number of periods in the swap, then the present value of the fixed-rate payments can be expressed as
This also can be expressed as
![]()
The condition for no arbitrage is that the present value of the fixed-rate payments as given by the preceding expression is equal to the present value of the floating-rate payments. That is,
![]()
Solving for the swap rate,

All the values needed to compute the swap rate are known.
Let’s apply the formula to determine the swap rate for our three-year swap. Exhibit 62–6 shows the calculation of the denominator of the formula. The forward discount factor for each period shown in column (5) is obtained from column (4) of Exhibit 62–5. The sum of the last column in Exhibit 62–6 shows that the denominator of the swap-rate formula is $281,764,282. We know from Exhibit 62–5 that the present value of the floating-rate payments is $14,052,917. Therefore, the swap rate is
EXHIBIT 62–6
Calculating the Denominator for the Swap-Rate Formula

![]()
Given the swap rate, the swap spread can be determined. For example, since this is a three-year swap, the convention is to use the three-year on-the-run Treasury rate as the benchmark. If the yield on that issue is 4.5875%, the swap spread is 40 basis points (4.9875% – 4.5875%).
The calculation of the swap rate for all swaps follows the same principle: equating the present value of the fixed-rate payments to that of the floating-rate payments.
Valuing a Swap
Once the swap transaction is completed, changes in market interest rates will change the payments of the floating-rate side of the swap. The value of an interest-rate swap is the difference between the present value of the payments of the two sides of the swap. The three-month LIBOR forward rates from the current Eurodollar futures contracts are used to (1) calculate the floating-rate payments and (2) determine the discount factors at which to calculate the present value of the payments.
To illustrate this, consider the three-year swap used to demonstrate how to calculate the swap rate. Suppose that one year later, interest rates change as shown in columns (4) and (6) in Exhibit 62–7. Column (4) shows the current three-month LIBOR. In column (5) are the Eurodollar futures price for each period. These rates are used to compute the forward rates in column (6). Note that the interest rates have increased one year later because the rates in Exhibit 62–7 are greater than those in Exhibit 62–2. As in Exhibit 62–2, the current three-month LIBOR and the forward rates are used to compute the floating-rate payments. These payments are shown in column (8) of Exhibit 62–7.
EXHIBIT 62–7
Rates and Floating-Rate Payments One Year Later if Rates Increase

In Exhibit 62–8, the forward discount factor is computed for each period. The calculation is the same as in Exhibit 62–4 to obtain the forward discount factor for each period. The forward discount factor for each period is shown in the last column of Exhibit 62–8.
EXHIBIT 62–8
Period Forward Rates and Forward Discount Factors One Year Later if Rates Increase
In Exhibit 62–9, the forward discount factor (from Exhibit 62–8) and the floating-rate payments (from Exhibit 62–7) are shown. The fixed-rate payments need not be recomputed. They are the payments shown in column (8) of Exhibit 62–3. These are fixed-rate payments for the swap rate of 4.9875% and are reproduced in Exhibit 62–9. Now the two payment streams must be discounted using the new forward discount factors. As shown at the bottom of Exhibit 62–9, the two present values are as follows:
EXHIBIT 62–9
Valuing the Swap One Year Later if Rates Increase

Present value of floating-rate payments $11,459,495
Present value of fixed-rate payments $9,473,390
The two present values are not equal, and therefore, for one party, the value of the swap increased, and for the other party, the value of the swap decreased. Let’s look at which party gained and which party lost.
The fixed-rate payer will receive the floating-rate payments. And these payments have a present value of $11,459,495. The present value of the payments that must be made by the fixed-rate payer is $9,473,390. Thus the swap has a positive value for the fixed-rate payer equal to the difference in the two present values of $1,986,105. This is the value of the swap to the fixed-rate payer. Notice, consistent with what we said earlier, that when interest rates increase (as they did in our illustration), the fixed-rate payer benefits because the value of the swap increases.
In contrast, the fixed-rate receiver must make payments with a present value of $11,459,495 but will only receive fixed-rate payments with a present value equal to $9,473,390. Thus the value of the swap for the fixed-rate receiver is −$1,986,105. Again, as explained earlier, the fixed-rate receiver is adversely affected by a rise in interest rates because it results in a decline in the value of a swap.
The same valuation principle applies to more complicated swaps. For example, there are swaps whose notional amount changes in a predetermined way over the life of the swap. These include amortizing swaps, accreting swaps, and roller-coaster swaps. Once the payments are specified, the present value is calculated as described earlier simply by adjusting the payment amounts by the changing notional amounts—the methodology does not change.
PRIMARY DETERMINANTS OF SWAP SPREADS
The swap spread is determined by the same factors that drive the spread over Treasuries on instruments that replicate a swap’s cash-flows, i.e., produce a similar return or funding profile. As discussed below, the swap spread’s key determinant for swaps with tenors (i.e., maturities) of five years or less is the cost of hedging in the Eurodollar futures market. Although listed contracts exist with delivery dates out to 10 years, the liquidity of the Eurodollar futures market diminishes considerably after about five years. For longer tenor swaps, the swap spread is largely driven by credit-spreads in the corporate bond market. Specifically, longer-dated swaps are priced relative to rates paid by investment-grade credits in traditional fixed- and floating-rate markets.
Given that a swap is a package of futures/forward contracts, the shorter-term swap spreads respond directly to fluctuations in Eurodollar futures prices. As noted, there is a liquid market for Eurodollar futures contracts with maturities every three months for approximately five years. A market participant can create a synthetic fixed-rate security or a fixed-rate funding vehicle by taking a position in a bundle of Eurodollar futures contracts (i.e., a position in every three-month Eurodollar futures contract up to the desired maturity date).
For example, consider a financial institution that has fixed-rate assets and floating-rate liabilities. Both the assets and liabilities have a maturity of three years. The interest rate on the liabilities resets every three months based on three-month LIBOR. This financial institution can hedge this mismatched asset/liability position by buying a three-year bundle of Eurodollar futures contracts. By doing so, the financial institution is receiving LIBOR over the three-year period and paying a fixed dollar amount (i.e., the futures price). The financial institution is now hedged because the assets are fixed-rate, and the bundle of long Eurodollar futures synthetically creates a fixed-rate funding arrangement. From the fixed dollar amount over the three years, an effective fixed-rate that the financial institution pays can be computed. Alternatively, the financial institution can synthetically create a fixed-rate funding arrangement by entering into a three-year swap in which it pays fixed and receives three-month LIBOR. Other things equal, the financial institution will use the vehicle that delivers the lowest cost of hedging the mismatched position. That is, the financial institution will compare the synthetic fixed-rate (expressed as a percentage over U.S. Treasuries) to the three-year swap spread. The difference between the synthetic spread and the swap spread should be within a few basis points under normal circumstances.
For swaps with tenors greater than five years, we cannot rely on the Eurodollar futures owing to diminishing liquidity of such contracts. Instead, longer-dated swaps are priced using rates available for investment-grade corporate borrowers in fixed-rate and floating-rate debt markets. Since a swap can be interpreted as a package of long and short positions in a fixed-rate bond and a floating-rate bond, it is the credit-spreads in those two market sectors that will be the primary determinant of the swap spread. Empirically, the swap curve lies above the U.S. Treasury yield-curve and below the on-the-run yield-curve for AA-rated banks.1 Swap fixed-rates are lower than AA-rated bond yields due to their lower credit risk due to netting and offsetting of swap positions.
In addition, there are a number of other technical factors that influence the level of swap spreads.2 While the impact of some these factors is ephemeral, their influence can be considerable in the short run. Included among these factors are (1) the level and shape of the Treasury yield-curve, (2) the relative supply of fixed- and floating-rate payers in the interest-rate swap market, (3) the technical factors that affect swap dealers, and (4) the level of asset-based swap activity.
The level, slope, and curvature of the U.S. Treasury yield-curve are important influences on swap spreads at various maturities. The reason is that embedded in the yield-curve are the market’s expectations of the direction of future interest rates. While these expectations are sometimes challenging to extract, the decision to borrow at a fixed-rate or a floating-rate will be based, in part, on these expectations. The relative supply of fixed- and floating-rate payers in the interest-rate swap market also should be influenced by these expectations. For example, many corporate issuers—financial institutions and federal agencies in particular—swap their newly issued fixed-rate debt into floating using the swap market. Consequently, swap spreads will be affected by the corporate debt issuance calendar. In addition, swap spreads, like credit-spreads, also tend to increase with the swap’s tenor or maturity.
Swap spreads are also affected by the hedging costs faced by swap dealers. Dealers hedge the interest-rate risk of long (short) swap positions by taking a long (short) position in a Treasury security with the same maturity as the swap’s tenor and borrowing funds (lending funds) in the repo market. As a result, the spread between LIBOR and the appropriate repo rate will be a critical determinant of the hedging costs. When on-the-run Treasuries go “on special,” it is correspondingly more expensive to use these Treasuries as a hedge. This increase in hedging costs results in wider swap spreads.3
Another influence on the level of swap spreads is the volume of asset-based swap transactions. An asset-based swap transaction involves the creation of a synthetic security via the purchase of an existing security and the simultaneous execution of a swap. For example, after the Russian debt default and devaluation in August 1998, risk-averse investors sold corporate bonds and fled to the relative safety of U.S. Treasuries. Credit-spreads widened considerably and liquidity diminished. A contrary-minded floating-rate investor (like a financial institution) could have taken advantage of these circumstances by buying newly issued investment-grade corporate bonds with relatively attractive coupon rates and simultaneously taking a long position in an interest-rate swap (pay fixed/receive floating). Accordingly, the financial institution ends up with a synthetic floating-rate asset with a spread above LIBOR.
By similar reasoning, investors can use swaps to create a synthetic fixed-rate security. For example, during the mid-1980s, many banks issued perpetual floating-rate notes in the Eurobond market. A perpetual floating-rate note is a security that delivers floating-rate cash-flows forever. The coupon is reset and paid usually every three months with a coupon formula equal to the reference rate (e.g., three-month LIBOR) plus a spread. When the perpetual floating-rate note market collapsed in late 1986, the contagion spread into other sectors of the floaters market.4 Many floaters cheapened considerably. As before, contrary-minded fixed-rate investors could exploit this situation through the purchase of a relatively cheap (from the investor’s perspective) floater while simultaneously taking a short position in an interest-rate swap (pay floating/receive fixed) thereby creating a synthetic fixed-rate investment. The investor makes floating-rate payments (say, based on LIBOR) to the counterparty and receives fixed-rate payments equal to the Treasury yield plus the swap spread. Accordingly, the fixed-rate on this synthetic security is equal to the sum of the following: (1) the Treasury bond yield that matches the swap’s tenor, (2) the swap spread, and (3) the floater’s index spread.
NONGENERIC INTEREST-RATE SWAPS
The swap market is very flexible, and instruments can be tailor-made to fit the requirements of individual customers. A wide variety of swap contracts are traded in the market. Although the most common reference rate for the floating leg of a swap is six-month LIBOR for a semiannual-paying floating leg, other reference rates that have been used include three-month LIBOR, the prime rate (for dollar swaps), the one-month commercial paper rate, the Treasury bill rate, and the municipal bond rate.
The term of a swap need not be fixed; swaps may be extendible or putable. In an extendible swap, one of the parties has the right but not the obligation to extend the life of the swap beyond the fixed maturity date, whereas in a putable swap one party has the right to terminate the swap prior to the specified maturity date.
It is also possible to transact options on swaps, known as swaptions. A swaption is the right to enter into a swap agreement at some point in the future during the life of the option. Essentially a swaption is an option to exchange a fixed-rate bond cash-flow for a floating-rate bond cash-flow structure. Swaptions will be described in more detail later. Other swaps are described below.
Constant-Maturity Swap
In a constant-maturity swap, the parties exchange a LIBOR rate for a fixed swap rate. For example, the terms of the swap might state that six-month LIBOR is exchanged for the five-year swap rate on a semiannual basis for the next five years or for the five-year government bond rate. In the U.S. market, the second type of constant-maturity swap is known as a constant-maturity Treasury swap.
Accreting and Amortizing Swaps
In a plain-vanilla swap, the notional principal remains unchanged during the life of the swap. However it is possible to trade a swap where the notional principal varies during its life. An accreting (or step-up) swap is one in which the principal starts off at one level and then increases in amount over time. The opposite, an amortizing swap, is one in which the notional reduces in size over time. An accreting swap would be useful where, for instance, a funding liability that is being hedged increases over time. The amortizing swap might be employed by a borrower hedging a bond issue that featured sinking-fund payments, where a part of the notional amount outstanding is paid off at set points during the life of the bond. If the principal fluctuates in amount, for example, increasing in one year and then reducing in another, the swap is known as a roller-coaster swap. Another application of an amortizing swap is as a hedge for a loan that is itself an amortizing one. Frequently this is combined with a forward-start swap to tie in with the cash-flows payable on the loan. The pricing and valuation of an amortizing swap are no different in principle to a vanilla interest-rate swap; a single swap rate is calculated using the relevant discount factors, and at this rate the net present value of the swap cash-flows will equal zero at the start of the swap.
Basis Swap
In a conventional swap, one leg comprises fixed-rate payments and the other floating-rate payments. In a basis swap, both legs are floating-rate but linked to different money market indexes. One leg is normally linked to LIBOR, while the other might be linked to the CD rate or the commercial paper rate. This type of swap would be used by a bank in the United States that had made loans that paid at the prime rate and funded its loans at LIBOR. A basis swap would eliminate the basis risk between the bank’s income and interest expense. Other basis swaps are traded in which both legs are linked to LIBOR, but at different maturities; for instance, one leg might be at three-month LIBOR and the other at six-month LIBOR. In such a swap, the basis is different as is the payment frequency: One leg pays out semiannually, while the other would be paying on a quarterly basis.
Off-Market Swap
When a swap is transacted, its fixed-rate is quoted at the current market rate for that maturity. When the fixed-rate is different from the market rate, this type of swap is an off-market swap, and a compensating payment is made by one party to the other. An off-market rate may be used for particular hedging requirements, for example, or when a bond issuer wishes to use the swap to hedge the bond as well as to cover the bond’s issue costs.
Forward-Start Swap
A forward-start swap is an obligation where two counterparties agree to enter into a swap contract at some future date under terms negotiated today.5 Accordingly, the swap’s effective (i.e., start) date is not the usual one or two days after the trade date but some time afterwards, say, six months after the trade date: for example, an interest-rate swap with a tenor of three years that has an effective date one year from today. Once the effective date is reached, a forward-start swap is identical to a normal interest-rate swap. Earlier in the chapter we noted that it is useful to think of the generic interest-rate swap market as one where two counterparties trade the floating reference rate in a series of exchanges for a fixed price. Extending this intuition, the forward-start interest-rate swap market is a forward market for trading the floating reference rate as opposed to the spot market.
A forward-start swap contract will specify the swap’s fixed-rate at which the two counterparties agree to exchange cash-flows during the swap’s life which begins on some future effective date. This rate is referred to as the forward swap fixed-rate.
Overnight Interest-Rate Swaps and Eonia/SONIA Swaps
Overnight-index swaps (OIS) are interest-rate swaps that are traded in the money markets because of their short-term maturity but are generically identically to interest-rate swaps and so also may be considered a capital market instrument.
We saw earlier in this chapter that an interest-rate swap contract, which is generally regarded as a capital market instrument, is an agreement between two counterparties to exchange a fixed-interest-rate payment in return for a floating-interest-rate payment, calculated on a notional swap amount, at regular intervals during the life of the swap. A swap may be viewed as being equivalent to a series of successive forward contracts, with each forward contract starting as the previous one matures. The basis of the floating interest rate is agreed as part of the contract terms at the inception of the trade. Conventional swaps index the floating interest rate to LIBOR; however an exciting recent development in the money markets has been the OIS. In the sterling market they are known as sterling overnight interest rate average swaps, or SONIA, while Eurocurrency OIS are known as Eonia. In this section we review OIS swaps, which are used extensively by commercial and investment banks.
SONIA is the average interest rate of interbank (unsecured) overnight sterling deposit trades undertaken before 15:30 hours each day between members of the London Wholesale Money Brokers’ Association. Recorded interest rates are weighted by volume. A SONIA swap is a swap contract that exchanges a fixed interest rate (the swap rate) against the geometric average of the overnight interest rates that have been recorded during the life of the contract. Exchange of interest takes place on maturity of the swap. SONIA swaps are used to speculate on or to hedge against interest rates at the very short end of the sterling yield-curve; in other words, they can be used to hedge an exposure to overnight interest rates.6 The swaps themselves are traded in maturities of one week to one year, although two-year SONIA swaps have also been traded.
Conventional swap rates are calculated off the government bond yield-curve and represent the credit premium over government yields of interbank default risk. Essentially, they represent an average of the forward rates derived from the government spot (zero-coupon) yield-curve. The fixed-rate quoted on a SONIA swap represents the average level of the overnight interest rates expected by market participants over the life of the swap. In practice, the rate is calculated as a function of the Bank of England’s repo rate. This is the two-week rate at which the Bank conducts reverse repo trades with banking counterparties as part of its open market operations. In other words, this is the Bank’s base rate. In theory, one would expect the SONIA rate to follow the repo rate fairly closely, since the credit risk on an overnight deposit is low. However, in practice, the spread between the SONIA rate and the Bank repo rate is very volatile, and for this reason, the swaps are used to hedge overnight exposures.
Overnight-index swaps dealt in U.S. dollars are linked to the federal funds rate. Since this rate is considerably below the overnight LIBOR rate, it means that the swap is not always used by banks to hedge overnight interest rate liability exposure, especially when the latter is linked to LIBOR.
CANCELING A SWAP
When financial institutions enter into a swap contract in order to hedge interest-rate liabilities, the swap will be kept in place until its expiration. However, circumstances may change, or a financial institution may alter its view on interest rates, and so circumstances may arise such that it may be necessary to terminate the swap. The most straightforward option is for the corporation to take out a second contract that negates the first. This allows the first swap to remain in place, but there may be residual cash-flows unless the two swaps cancel each other out precisely. The terms for the second swap, being nonstandard (and unlikely to be exactly whole years to maturity, unless traded on the anniversary of the first), also may result in it being more expensive than a vanilla swap. Since it is unlikely that the second swap will have the same rate, the two fixed legs will not net to zero. And if the second swap is not traded on an anniversary, payment dates will not match.
For these reasons, an entity may wish to cancel the swap entirely. To do this, it will ask a swap market maker for a quotation on a cancellation fee. The bank will determine the cancellation fee by calculating the net present value of the remaining cash-flows in the swap using the relevant discount factor for each future cash-flow. In practice just the fixed leg will be present valued and then netted with LIBOR. The net present value of all the cash-flows is the fair price for canceling the swap. The valuation principles we established earlier will apply; that is, if the fixed-rate payer is asking to cancel the swap when interest rates have fallen, he will pay the cancellation fee, and vice versa if rates have risen.
CREDIT RISK
The rate quoted for swaps in the interbank market assumes that the counterparty to the transaction has a lending line with the swap bank, so the swap rate therefore reflects the credit risk associated with an interbank quality counterparty. This credit risk is reflected in the spread between the swap rate and the equivalent-maturity government bond, although, as noted, the spread also reflects other considerations such as liquidity and supply and demand. The credit risk of a swap is separate from its interest-rate risk or market risk, and arises from the possibility of the counterparty to the swap defaulting on its obligations. If the present value of the swap at the time of default is net positive, then a bank is at risk of loss of this amount. While market risk can be hedged, it is more problematic to hedge credit risk. The common measures taken include limits on lending lines, collateral, and diversification across counterparty sectors, as well as a form of credit value-at-risk to monitor credit exposures.
A bank therefore is at risk of loss due to counterparty default for all its swap transactions. If at the time of default, the net present value of the swap is positive, this amount is potentially at risk and will probably be written off. If the value of the swap is negative at the time of default, in theory this amount is a potential gain to the bank, although in practice the counterparty’s administrators will try to recover the value for their client. In this case, then, there is no net gain or loss to the swap bank. The credit risk management department of a bank will therefore often assess the ongoing credit quality of counterparties with whom the swap transactions are currently positive in value.
SWAPTIONS
We conclude this chapter with a discussion of swaptions. A swaption is an option to establish a position in an interest-rate swap at some future date. The swaption contract specifies the swaption’s expiration date, as well as the fixed-rate and tenor of the underlying swap. The swap’s fixed-rate is called the swaption’s strike rate. There are two types of swaptions—pay fixed or receive fixed. A pay (receive) fixed swaption gives the buyer the right to establish a position in an interest-rate swap where she will pay (receive) the fixed-rate cash-flows and receive (pay) the floating-rate cash-flows.
Let’s illustrate a hypothetical swaption with a one-year swaption on a five-year generic interest-rate swap with a $10 million notional principal in which the buyer will receive fixed cash inflows and pay floating-rate cash-flows. Assume the swaption is European and is therefore exercisable only at expiration. Further assume the swap’s fixed-rate is 3.35188% while the floating-rate is three-month LIBOR flat. If the swaption is exercised on its expiration date say, January 1, 2012, the five-year swap begins on January 1, 2012 at a fixed-rate of 3.35188% in exchange for floating cash flows and ends on January 1, 2017 (“maturity”).
When valuing interest-rate derivatives or bonds with embedded options, it is essential to model expected future interest-rate volatility. Accordingly, the lattice approach discussed in Chapter 40 is a commonly used method to value swaptions. A swaption’s value will depend on a few critical parameters that include market inputs (e.g., the current yield-curve) as well as terms of the swaption contract (e.g., time to expiration). To solidify our intuition about how swaptions work, we examine how changes in key factors affect swaption values. In particular, we will consider changes in the following: yield-curve (level and slope), volatility, strike rate, and time to expiration.
Changes in the Yield-Curve
As with conventional call and put options, pay-fixed or receive-fixed swaptions tend to react in an opposite manner to changes in the underlying parameters. For example, a pay-fixed swaption increases in value with an upward parallel shift in the yield-curve, and a receive-fixed swaption becomes more valuable with a downward parallel shift in the yield-curve. To see this, consider a one-year European pay-fixed swaption on a five-year generic interest-rate swap. The notional principal is $10 million, and the strike rate is 6%. On the expiration date, the buyer will either exercise it (i.e., enter into the five-year swap to pay 6% fixed-rate cash-flows and receive floating-rate cash-flows) or let the swaption expire. If the five-year swap rate is above 6% on the expiration date, the buyer of this pay-fixed swaption will exercise it. Conversely, if the five-year swap rate is below 6%, the pay-fixed swaption will expire worthless. The principle is the same for a receive swaption, only in reverse.
Next, we consider the impact of a change in the yield-curve’s shape on swaption values. In particular, we will discuss the impact of a steepening and an inverting yield-curve. If the yield-curve steepens, the value of a pay-fixed swaption increases, and the value of a receive-fixed swaption decreases. The intuition is straightforward. A steepening yield-curve indicates that the implied forward rates are increasing at a faster rate than suggested by the initial yield-curve. The higher rates indicate that the floating-rate cash-flows of the underlying swap contract are going to be higher than previously expected. This effect works to the advantage of the pay-fixed swaption buyer because she will receive higher floating-rate cash-flows if the swaption is exercised. The opposite is true for a receive-fixed swaption buyer. By analogous reasoning, an inverted yield-curve indicates that the implied forward rates are decreasing. If this occurs, the value of a pay-fixed swaption decreases, and the value of a receive-fixed swaption increases.
Volatility
There is a positive relationship between swaption values and the assumed interest-rate volatility. If interest volatility increases, all else held constant, chances are greater that underlying swap’s value will move in a favorable direction (i.e., higher floating-rate cash-flows for the pay-fixed swaption and higher fixed-rate cash-flows for the receive-fixed swaption). Vega measures the impact of a change in interest-rate volatility on an option’s value. For a swaption, vega tells us the sensitivity of the swaption’s value (in basis points) to a 1% change in the assumed interest-rate volatility.
A market convention for calculating implied volatility is to use the Black pricing model for options on commodity futures for translating the price of option-type interest rate derivatives into implied volatility. Most market participants use implied volatility of swaption contracts as their estimate of interest-rate volatility. What is the meaning of an “implied yield volatility of, say, 25%?” To interpret this number, one needs to be cognizant that it is derived from the observed option price based on the Black model. As a result, the meaning of it not only depends on the assumption that the market correctly prices the option, but also the fact that the market prices the option in accordance with the Black model. Given these assumptions, one may interpret that the option market expects a constant annualized yield volatility of 25% for the underlying instrument to the maturity date of the option.
Two major assumptions of the Black model are problematic. First, interest rates are assumed to be constant. Yet, the assumption is used to derive the pricing formula for the option, which derives its payoff precisely from the fact that future interest rates (forward rates) are stochastic. The Black model implies a time evolution path for the term structure that leads to the presence of arbitrage opportunities. In other words, the model itself implicitly violates the no-arbitrage spirit in derivatives pricing.
Second, volatilities of futures prices, or forward interest rates, are assumed to be constant over the life of the contract. This assumption runs counter to the empirical record as well as intuition. For example, a forward contract with one month to maturity is more sensitive to changes in the current term structure than a forward contract with one year to maturity. Accordingly, the volatility of the forward rate is inversely related to the time to maturity.
Strike Rate
The value of a swaption is essentially the difference between the strike rate and prevailing swap rate at the time it is being valued. At expiration, a pay-fixed swaption is only exercised when the swap rate is higher than the strike rate. Conversely, at expiration, a receive-fixed swaption is only exercised when the swap rate is lower than the strike rate. Given this backdrop, it is apparent that as the strike rate changes, a pay-fixed swaption and a receive-fixed swaption will behave in an opposite manner. An increase in the strike rate, all else equal, will decrease the value of a pay-fixed swaption and increase the value of a receive-fixed swaption. The reasoning is as follows: As the strike rate increases, the pay-fixed swaption buyer will pay higher fixed-rate cash-flows over the swap’s life if the swaption is exercised. This is obviously less valuable than paying a lower fixed-rate for the same floating-rate cash-flows in return. For the receive-fixed swaption buyer, an increase in the strike rate means that the receive-fixed swaption buyer will receive higher fixed-rate cash-flows over the swap’s life if the swaption is exercised. For decreases in the strike rate, the effects are reversed.
Time to Expiration
For most options (calls and puts) traded in the financial markets, increasing the option’s time to expiration makes it more valuable. This is not the case for swaptions. Increasing a swaption’s time to expiration can either increase or decrease its value. This ambiguity is due to the interaction of increasing the time to expiration and the other variables that drive a swaption’s value—the current yield-curve, volatility, and the strike rate.
KEY POINTS
• An interest-rate swap is an agreement between two parties to exchange interest payments at designated times in the future based on a notional principal amount.
• In a generic interest-rate swap, one party agrees to make fixed-rate payments and receive floating-rate payments while the counterparty agrees to make floating-rate payments and receive fixed-rate payments.
• The most common reference rate for the floating-rate payments is LIBOR.
• Interest-rate swaps are over-the-counter instruments.
• The default risk in a swap agreement is called counterparty risk.
• A swap position can be interpreted as either a package of forward contracts or a package of cash-flows from buying and selling cash market instruments.
• The convention for quoting swap levels is that a swap dealer sets the floating-rate equal to the reference rate and then quotes the fixed-rate that will apply.
• The swap rate is determined by finding the rate that will make the present value of the cash-flow of both sides of the swap equal.
• In a LIBOR-based swap, the cash-flow of the floating-rate side is determined from the Eurodollar futures contract.
• The discount rates used to calculate the present value of the cash-flows in a swap are forward rates.
• The value of an existing swap is equal to the difference in the present value of the two payments.
• The swap spread is the spread over the Treasury par curve specified at the initiation of the swap that the fixed-rate payer must pay.
• Non-generic swaps include constant maturity, accreting/amortizing, zero-coupon, LIBOR-in-arrears, basis, margin, off-market, differential, and forward-start swaps.
• The net present value of all cash-flows is the fair price for canceling a swap.
• Swaption are options to establish a position in an interest-rate swap at some future date.
• The key factors that impact a swaption’s value are the yield-curve, volatility, strike rate, and time to expiration.
