Chapter 14. GPU Accelerated RNA Folding Algorithm
*
*
Work performed while the first author was visiting Colorado State University and supported in part by NSF grant CCF-0917319, “Simplifying Reductions,” and in part by French ANR BioWIC: ANR-08-SEGI-005.
Guillaume Rizk, Dominique Lavenier and Sanjay Rajopadhye
In this chapter, we present an implementation of the main kernel in the widely used RNA folding package Unafold. Its key computation is a dynamic programming algorithm with complex dependency patterns, making it an a priori bad match for GPU computing. This study, however, shows that reordering computations in such a way to enable tiled computations and good data reuse can significantly improve GPU performance and yields good speedup compared with optimized CPU implementation that also uses the same approach to tile and vectorize the code.
14.1. Problem Statement
RNA, or ribonucleic acid, is a single-stranded chain of nucleotide units. There are four different nucleotides, also called
bases
: adenine (A), cytosine (C), guanine (G), and uracil (U). Two nucleotides can form a bond, thus forming a
base pair
, according to the Watson-Crick complementarity: A with U, G with C; but also the less stable combination G with U, called wobble base pair. Because RNA is single stranded, it does not have the double-helix structure of DNA. Rather, all the base pairs of a sequence force the nucleotide chain to fold in “on itself” into a system of different recognizable domains like hairpin loops, bulges, interior loops, or stacked regions.
This 2-D space conformation of RNA sequences is called the secondary structure, and many bioinformatics studies require detailed knowledge of this.
Algorithms computing this 2-D folding runs in
 complexity, which means computation time quickly becomes prohibitive when dealing with large datasets of long sequences. The first such algorithm was introduced in 1978 by Nussinov, which finds the structure with the largest number of base pairs
[1]
. In 1981 Zuker and Stiegler proposed an algorithm with a more realistic energy model than simply the count of the number of pairs
[2]
. It is still widely used today and is available in two packages, ViennaRNA
[3]
and Unafold
[4]
. Our goal is to write a GPU efficient algorithm with the same usage and results as the one in the Unafold implementation.
complexity, which means computation time quickly becomes prohibitive when dealing with large datasets of long sequences. The first such algorithm was introduced in 1978 by Nussinov, which finds the structure with the largest number of base pairs
[1]
. In 1981 Zuker and Stiegler proposed an algorithm with a more realistic energy model than simply the count of the number of pairs
[2]
. It is still widely used today and is available in two packages, ViennaRNA
[3]
and Unafold
[4]
. Our goal is to write a GPU efficient algorithm with the same usage and results as the one in the Unafold implementation.
RNA folding algorithms compute the most stable structure of an RNA sequence; that is, the structure maximizing a given scoring system, or rather, minimizing the total free energy of the RNA molecule.
Although this may seem like a daunting task because there is an exponential number of different possible structures, a key observation makes it computationally feasible in reasonable time: the optimal score of the whole sequence can be defined in terms of optimal scores of smaller subsequences, leading to a simple dynamic programming formulation.
Let us look at the optimal score
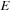 of the whole sequence. As shown in recursion
Figure 14.1(a)
, there are two possible ways it can be constructed: the last base
of the whole sequence. As shown in recursion
Figure 14.1(a)
, there are two possible ways it can be constructed: the last base
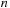 is either paired or unpaired. If it is unpaired, the scoring system implies that
is either paired or unpaired. If it is unpaired, the scoring system implies that
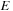 can be directly derived from the score of sequence
can be directly derived from the score of sequence
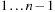 . In the second case, it is paired with some base
. In the second case, it is paired with some base
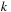 , thus breaking the sequence in two parts: subsequences
, thus breaking the sequence in two parts: subsequences
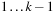 and
and
 , with
, with
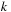 ,
,
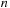 forming a base pair. The scoring system implies that
forming a base pair. The scoring system implies that
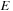 is the sum of the score of these two constituent parts. Now, if determining optimal scores of both parts are self-contained subproblems, meaning they are independent of the rest of the sequence, then they need to be computed only once, and then stored and reused wherever the subsequence occurs again. This opens the path to dynamic programming;
is the sum of the score of these two constituent parts. Now, if determining optimal scores of both parts are self-contained subproblems, meaning they are independent of the rest of the sequence, then they need to be computed only once, and then stored and reused wherever the subsequence occurs again. This opens the path to dynamic programming;
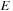 is computed as the optimal way to construct it recursively with the equation:
is computed as the optimal way to construct it recursively with the equation:
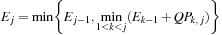 with
with
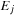 the optimal score of subsequence
the optimal score of subsequence
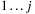 and
and
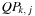 the optimal score of subsequence
the optimal score of subsequence
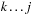 when
when
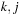 form a base pair. The assumption that subproblems are self-contained implies that there cannot exist a base pair
form a base pair. The assumption that subproblems are self-contained implies that there cannot exist a base pair
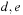 with
with
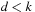 and
and
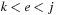 , i.e., something that would make their scores dependent on exterior elements. Such forbidden base pairs are called pseudoknots.
, i.e., something that would make their scores dependent on exterior elements. Such forbidden base pairs are called pseudoknots.
(14.1)
 |
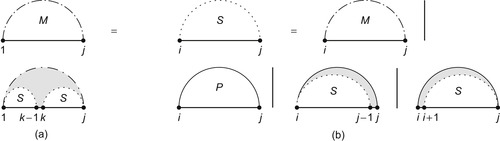
| Figure 14.1
Recursion diagrams
[5]
represent the recursive equations of the dynamic programming algorithm. The flat line represents the backbone of an RNA sequence. A base pair is indicated by a solid curved line, and a dashed curved line represents a subsequence with terminal bases that may be paired or unpaired. Shaded regions are parts of the structure fixed by the recursion, while white regions denote substructures whose scores have already been computed and stored in previous steps of the recursion. (a) Recursion of subsequence
|
Quantity
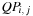 is also broken down in smaller subproblems, as shown in recursion
Figure 14.1(b)
. Either subsequence
is also broken down in smaller subproblems, as shown in recursion
Figure 14.1(b)
. Either subsequence
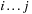 contains no other base pairs —
contains no other base pairs —
 ,
,
 is then called a
hairpin loop
— or there exists one internal base pair
is then called a
hairpin loop
— or there exists one internal base pair
 forming the
interior loop
forming the
interior loop
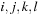 , or there are at least two interior base pairs, forming a
multiloop
. The recursion can then be conceptually written in the simplified form:
, or there are at least two interior base pairs, forming a
multiloop
. The recursion can then be conceptually written in the simplified form:
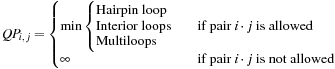
(14.2)
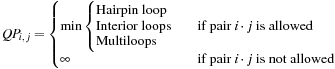
14.2. Core Method
The main computation is a dynamic programming algorithm, the majority of whose time is spent in a triply nested loop with complex, affine dependency patterns. Despite the complexity, dependency patterns nevertheless allow a parallelization scheme with one of the triply nested loops parallelized, and another expressing a reduction operation. However, with this parallelization, the threads work on different data, preventing us from using shared memory. This lack of a good memory access scheme
leads to a low ratio between computation and memory loads and thus mediocre performance. It is illegal to tile the loops as written in this direct implementation.
Our main idea is to exploit associativity to change the algorithm. We reorder the accumulations in such a way to make it legal to tile the code. This new tiled approach exhibits a lot of data reuse between threads. This technique therefore allows us to move from a memory-bound algorithm to a compute-bound kernel, thus fully unleashing raw GPU power. We note that our algorithmic modification also enables tiling and subsequent vectorization of the standard CPU implementation. This will allow us to a do a fair apples-to-apples comparison of the CPU and GPU implementations in
Section 14.4.2
and avoid the hype surrounding GPGPU.
14.3. Algorithms, Implementations, and Evaluations
14.3.1. Recurrence Equations
We first describe with more details the principles of the folding algorithm as implemented in the Unafold package in the function
hybrid-ss-min
[4]
. Recurrence equations of the RNA folding algorithm are well known in the bioinformatic community
[2]
and
[3]
; we describe them here to make our paper self-contained. Recurrence
Eq. 14.1
shows that finding the most stable structure of an RNA sequence involves computing table
 , itself constructed in three possible ways, as shown in
Eq. 14.2
. The first possibility is a hairpin loop, whose score is given by a function
, itself constructed in three possible ways, as shown in
Eq. 14.2
. The first possibility is a hairpin loop, whose score is given by a function
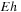 mainly depending on loop length. The second possibility is interior loops, containing the special case where
mainly depending on loop length. The second possibility is interior loops, containing the special case where
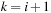 and
and
 corresponding to a stacked base pair. Functions
corresponding to a stacked base pair. Functions
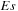 and
and
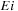 give, respectively, the scores of stacked pairs and interior loops. The last possibility is when subsequence
give, respectively, the scores of stacked pairs and interior loops. The last possibility is when subsequence
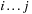 contains at least two internal base pairs, forming a multiloop. Another quantity,
contains at least two internal base pairs, forming a multiloop. Another quantity,
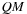 , is introduced, representing the score of a subsequence assuming it is forming a multiloop. Recursive
Eq. 14.2
can then be detailed as:
, is introduced, representing the score of a subsequence assuming it is forming a multiloop. Recursive
Eq. 14.2
can then be detailed as:
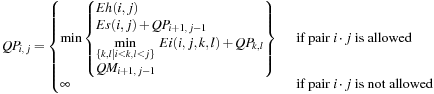
(14.3)
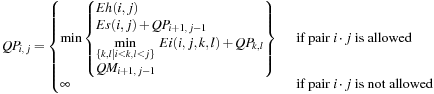
The value
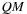 represents the score of a subsequence with at least two internal base pairs. It is simply broken down as two subsequences
represents the score of a subsequence with at least two internal base pairs. It is simply broken down as two subsequences
 and
and
 containing both at least one internal base pair. A third value,
containing both at least one internal base pair. A third value,
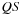 , is introduced to represent the score of such subsequences.
, is introduced to represent the score of such subsequences.
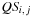 decomposition is then straightforward: either a pair is on
decomposition is then straightforward: either a pair is on
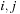 giving
giving
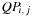 , or there are several pairs giving
, or there are several pairs giving
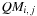 , or
, or
 or
or
 are unpaired, giving
are unpaired, giving
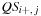 or
or
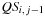 .
.
Recursion
Figures 14.2(a)
and (b) show their decomposition patterns. Their recurrence equations are written as:
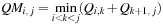
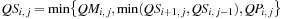
(14.4)
(14.5)
 |
| Figure 14.2
(a) Recursion of subsequence
|
The third term of
Eq. 14.3
is computed over the four variables
 ,
,
 ,
,
 ,
,
 , hence implying a complexity of
, hence implying a complexity of
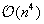 . However, a common approximation is to limit internal loop sizes to
. However, a common approximation is to limit internal loop sizes to
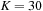 , thus reducing complexity to
, thus reducing complexity to
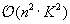 .
Equation 14.4
is in
.
Equation 14.4
is in
 , leading to an overall
, leading to an overall
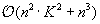 complexity. The corresponding secondary structure is then obtained by a traceback procedure, which will not be parallelized on the GPU since its computing time is negligible for large sequences.
complexity. The corresponding secondary structure is then obtained by a traceback procedure, which will not be parallelized on the GPU since its computing time is negligible for large sequences.
GTfold is a multicore implementation conducted with OpenMP and reports a
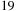 x speedup on a 16 dual-core 1.9 GHz server over the sequential CPU code for a sequence of 9781 nucleotides
[6]
. Jacob
et al.
report a
x speedup on a 16 dual-core 1.9 GHz server over the sequential CPU code for a sequence of 9781 nucleotides
[6]
. Jacob
et al.
report a
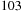 x speedup with an FPGA implementation over a single core of a 3.0GHz Core 2 duo, but their implementation is limited to 273-nucleotide-long sequences
[7]
. Other previous efforts were aimed toward parallelization over multiple computers via MPI
[8]
and
[9]
.
x speedup with an FPGA implementation over a single core of a 3.0GHz Core 2 duo, but their implementation is limited to 273-nucleotide-long sequences
[7]
. Other previous efforts were aimed toward parallelization over multiple computers via MPI
[8]
and
[9]
.
14.3.3. General Parallelization Scheme
Figure 14.3
shows the data dependencies coming from the recursion
Eqs. 14.3
to
14.5
. They imply that, once all previous diagonals are available, all cells of a diagonal can be processed independently. Three kernels are designed for the computation of
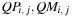 , and
, and
 , corresponding to
Eqs. 14.3
to
14.5
. Each one computes one full diagonal. The whole matrix is then processed sequentially through a loop over the diagonals. The next step corresponding to
Eq. 14.1
is a combination of reductions (search of the minimum of an array) which is parallelized in another kernel. The pseudo code for the host side of this parallelization scheme is given in
Algorithm 1
.
, corresponding to
Eqs. 14.3
to
14.5
. Each one computes one full diagonal. The whole matrix is then processed sequentially through a loop over the diagonals. The next step corresponding to
Eq. 14.1
is a combination of reductions (search of the minimum of an array) which is parallelized in another kernel. The pseudo code for the host side of this parallelization scheme is given in
Algorithm 1
.
 |
| Figure 14.3
Left: Data dependency relationship.
Each cell of the matrix contains the three values:
|
14.3.4.
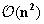 Part: Internal Loops
Part: Internal Loops
The third term of
Eq. 14.3
corresponds to the computation of internal loops. Their size is usually limited to
 , which means the minimization is conducted over the domain defined by
, which means the minimization is conducted over the domain defined by
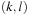 with
with
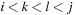 and
and
 . This domain is represented by the dashed triangle in
Figure 14.3
. This term is therefore responsible in total for
. This domain is represented by the dashed triangle in
Figure 14.3
. This term is therefore responsible in total for
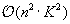 computations. The kernel
computations. The kernel
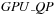 is designed to compute all cells
is designed to compute all cells
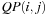 over a diagonal
over a diagonal
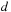 .
.
One major issue with this kernel is the divergence caused by the two branches in
Eq. 14.3
: if pair
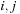 is not allowed, then
is not allowed, then
 is assigned the score
is assigned the score
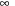 and no computations are required. Different cells of the diagonal are following different code paths, causing a huge loss in performance. To tackle this problem we compute on the CPU an index of all diagonal cells
and no computations are required. Different cells of the diagonal are following different code paths, causing a huge loss in performance. To tackle this problem we compute on the CPU an index of all diagonal cells
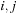 where the base pair
where the base pair
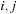 is allowed. The kernel computation domain is then the set of cells pointed by this index.
is allowed. The kernel computation domain is then the set of cells pointed by this index.
14.3.5.
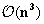 Part: Multiloops
Part: Multiloops
Equation 14.4
computes the most stable multiloop formed by subsequence
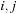 , and requires
, and requires
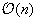 computations per cell, thus
computations per cell, thus
 overall for the
overall for the
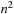 cells of the matrix. It requires the knowledge of the
line and column represented by dotted lines in
Figure 14.3
and is simply computed by finding the minimum of
cells of the matrix. It requires the knowledge of the
line and column represented by dotted lines in
Figure 14.3
and is simply computed by finding the minimum of
 over
over
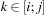 . Although it is a simple computation, it is the only
. Although it is a simple computation, it is the only
 part of the algorithm and as such the most important one for large sequences.
part of the algorithm and as such the most important one for large sequences.
First Implementation
The obvious way to implement the multiloop computation is to compute cells of a diagonal in parallel, with the reduction computation of each cell being itself parallelized over several threads. This way is implemented in kernel
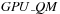 , shown in
Algorithm 2
and used in our first implementation. The scheme is simple:
, shown in
Algorithm 2
and used in our first implementation. The scheme is simple:
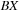 threads cooperate to compute the reduction, with each thread sequentially accessing memory locations
threads cooperate to compute the reduction, with each thread sequentially accessing memory locations
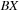 cells apart so that the memory accesses to
cells apart so that the memory accesses to
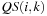 are coalesced among threads. The code shows that each thread does two operations for every two global memory elements accessed, on line 7. This is a very poor ratio, worsened by the fact that accesses
are coalesced among threads. The code shows that each thread does two operations for every two global memory elements accessed, on line 7. This is a very poor ratio, worsened by the fact that accesses
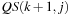 are not coalesced. Performance for this piece of code is measured at only 4.5 GOPS (giga operations per second) and a bandwidth usage of 17 GB/s for a 10 Kb sequence. It is obviously severely bandwidth limited. It may be possible to improve and coalesce the second reference in the loop body by storing
QS
and its transpose in global memory, but we did not pursue this approach because tiling leads to significantly higher performance as we shall see next.
are not coalesced. Performance for this piece of code is measured at only 4.5 GOPS (giga operations per second) and a bandwidth usage of 17 GB/s for a 10 Kb sequence. It is obviously severely bandwidth limited. It may be possible to improve and coalesce the second reference in the loop body by storing
QS
and its transpose in global memory, but we did not pursue this approach because tiling leads to significantly higher performance as we shall see next.
Reduction Split and Reordering
The main issue with our first implementation is that it requires a lot of memory bandwidth, as each cell of the diagonal requires
 data, and there is no reuse of data between the computation of different cells. Theoretically, there is a lot of data reuse, as a single value
data, and there is no reuse of data between the computation of different cells. Theoretically, there is a lot of data reuse, as a single value
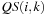 will be used for the computation of all cells
will be used for the computation of all cells
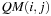 with
with
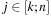 . Unfortunately, the dependency pattern makes it a priori impossible to take advantage of this, as the set of cells
. Unfortunately, the dependency pattern makes it a priori impossible to take advantage of this, as the set of cells
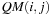
 are located on different diagonals and thus computed in separate kernel calls.
are located on different diagonals and thus computed in separate kernel calls.
In our “tiled implementation,” we designed a way to exploit this data reuse. The key observation is that the computation of a single cell is a minimization over
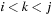 , which can be split into several parts. Our approach is inspired by the systolic array implementation of the optimum string parenthesization problem by Guibas-Kung-Thompson
[10]
and
[11]
, which completely splits reductions in order to have a parallelization scheme working for an array of
, which can be split into several parts. Our approach is inspired by the systolic array implementation of the optimum string parenthesization problem by Guibas-Kung-Thompson
[10]
and
[11]
, which completely splits reductions in order to have a parallelization scheme working for an array of
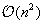 processors. Although our approach does not go this far, it exploits the same idea: we split and reorder the reductions, in order to obtain a parallelization scheme better suited for a GPU.
processors. Although our approach does not go this far, it exploits the same idea: we split and reorder the reductions, in order to obtain a parallelization scheme better suited for a GPU.
Let's say we have already computed all cells up to a given diagonal
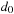 , meaning that all cells
, meaning that all cells
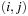 such that
such that
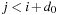 are known. For a given
are known. For a given
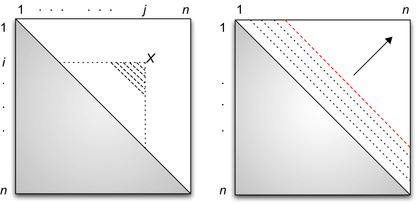
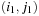 outside of the known area (marked with an x in
Figure 14.4
) with
outside of the known area (marked with an x in
Figure 14.4
) with
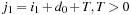 , the whole computation
, the whole computation
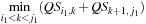 is not possible as many
is not possible as many
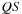 values are still unknown.
values are still unknown.
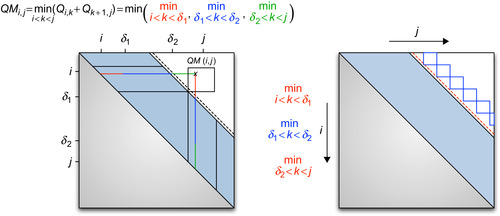 |
| Figure 14.4
Left: Reduction split.
All shaded cells in the upper part of the matrix are already available. For a point
|
Nevertheless, we can compute a
part
of the minimization for which
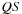 values are already known: for
values are already known: for
 with
with
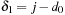 and
and
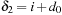 . Similar “portions” of the accumulations of all the points in the tile can be computed in parallel. This means that by taking apart the range that violates the dependency pattern, we can compute in parallel a tile of cells and thus benefit from a good memory reuse scheme.
Figure 14.4
shows such a tile and how the minimization is split.
. Similar “portions” of the accumulations of all the points in the tile can be computed in parallel. This means that by taking apart the range that violates the dependency pattern, we can compute in parallel a tile of cells and thus benefit from a good memory reuse scheme.
Figure 14.4
shows such a tile and how the minimization is split.
Tiling Scheme
We still move sequentially diagonal after diagonal, but we compute “in advance” the middle part of the minimization of
Eq. 14.4
in tiles. This tiled computation is implemented in the kernel
 , and called every
, and called every
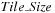 diagonal. The remaining part of the minimization is done in kernel
diagonal. The remaining part of the minimization is done in kernel
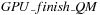 and called every diagonal, as shown in
Algorithm 3
and depicted in the right part of
Figure 14.4
.
and called every diagonal, as shown in
Algorithm 3
and depicted in the right part of
Figure 14.4
.
GPU Implementation
The tiled implementation allows for a very efficient GPU program: each tile is computed by a thread block, which can sequentially load into shared memory blocks of lines and columns, similar to a standard tiled matrix-matrix multiplication. Kernel code of
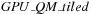 is shown in
Algorithm 4
.
is shown in
Algorithm 4
.
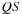 values are stored in shared memory lines 9,10 and reused
values are stored in shared memory lines 9,10 and reused
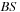 times each, on line 13. Bandwidth
requirement is therefore reduced by a factor of
times each, on line 13. Bandwidth
requirement is therefore reduced by a factor of
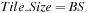 compared with the first implementation. Performance of this kernel is now 90 GOPS with a bandwidth usage of 23 GB/s.
compared with the first implementation. Performance of this kernel is now 90 GOPS with a bandwidth usage of 23 GB/s.
14.3.6. Related Algorithms
We also applied the technique presented here to the computation of suboptimal foldings and the partition function of a sequence, whose algorithms are similar to the one presented here. Suboptimal foldings and partition function are very useful to give a more accurate view of a sequence ensemble of possible foldings, because the unique “optimal” folding is not necessarily always representative of biological reality.
1:
BlockSize
: Two dimension
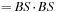
2:
Block Assignment
: Computation of “middle part” of
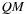 for a tile of
for a tile of
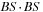 cells, with upper left corner
cells, with upper left corner
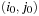
3:
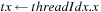 ,
,

4:
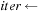 beginning of “middle part”
beginning of “middle part”
5:
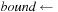 end of “middle part”
end of “middle part”
6:
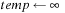
7:
while
 do
do
8:
Load blocks in shared memory:
9:
Shared_L [tx][ty]
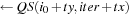
10:
Shared_C [tx][ty]
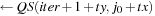
11:
Syncthreads
12:
for
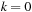 ,
,
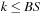 ,
,
 do
do
13:
temp
 min(temp,Shared_L [ty][k]
min(temp,Shared_L [ty][k]
 Shared_C [k][tx])
Shared_C [k][tx])
14:
end for
15:
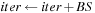
16:
end while
17:
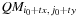
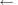 temp
temp
14.4.1. Results
Our GPU implementation uses exactly the same thermodynamic rules as Unafold, thus the results and accuracy obtained on a GPU are exactly the same as for the standard CPU Unafold function. We therefore compare only the execution time between programs, including the host-to-device transfer for the GPU implementation. Our tests are run on a Xeon E5450 @ 3.0GHz and a Tesla C1060. CPU code is running on Fedora 9, compiled with the GCC 4.3.0 compiler with -O3 optimization level.
14.4.2. Tiled Implementation
Figure 14.5(a)
shows the speedup obtained by the tiled implementation on a Tesla C1060 over the standard Unafold algorithm running on one core of a Xeon E5450 for randomly generated sequences of different lengths. Tests are run with a large enough number of sequences, ensuring that GPU starting costs are amortized. The speedup starts at around
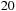 x for short sequences and goes up to
x for short sequences and goes up to
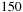 x for large sequences. For small sequences, the
x for large sequences. For small sequences, the
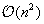 part of the algorithm is preponderant, so the overall speedup is roughly that of the kernel computing internal loops, called
part of the algorithm is preponderant, so the overall speedup is roughly that of the kernel computing internal loops, called
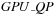 and explained in
Section 14.3.4
. As sequence size increases, the
and explained in
Section 14.3.4
. As sequence size increases, the
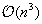 multiloop computation becomes more important, so the speedup approaches that of kernel
multiloop computation becomes more important, so the speedup approaches that of kernel
 , which is very efficient thanks to our tiled code.
, which is very efficient thanks to our tiled code.
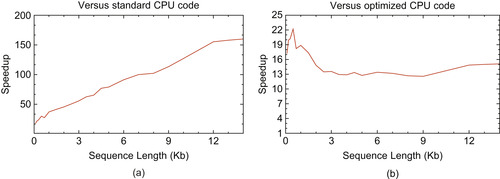 |
| Figure 14.5
Tesla C1060 speedup against one core of Xeon E5450 @ 3.0GHz for various sequence lengths. (a) Speedup against standard Unafold code. (b) Speedup against tiled and vectorized CPU code.
|
In order to do a fair, “apples-to-apples” comparison, we applied our tiling technique on the CPU and used SSE vectorized instructions to get the full potential of CPU performance. Execution speed of the vectorized part of the code is 5.4 GOPS for a 10 Kb sequence, which is quite high considering first GPU implementation speed was only 4.5 GOPS. Speedup obtained by the second GPU implementation
against this optimized code is presented
Figure 14.5(b)
. Here speedup is more stable across sequence lengths because like the GPU, CPU tiled code is very efficient. GPU speedup of the
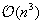 part of the code compared with CPU code using the same tiling technique and vectorized code is 90 GOPS / 5.4 GOPS = 16.6 x. This is therefore the theoretical maximum speedup that can be achieved when running on very large sequences when the
part of the code compared with CPU code using the same tiling technique and vectorized code is 90 GOPS / 5.4 GOPS = 16.6 x. This is therefore the theoretical maximum speedup that can be achieved when running on very large sequences when the
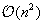 part — exhibiting different speedup — becomes negligible.
part — exhibiting different speedup — becomes negligible.
14.4.3. Overall Comparison
Figure 14.6
compares performance on a 9781-nucleotide-long virus sequence on a larger set of programs: on the first untiled GPU implementation, the tiled one, the standard Unafold CPU code
[4]
, the GTfold algorithm
[6]
running on eight CPU cores, and the new SSE-optimized CPU code running on one or eight threads.
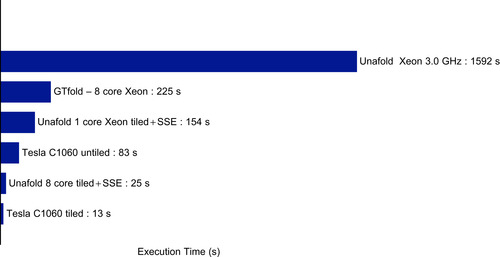 |
| Figure 14.6
Execution time on a 9781-nucleotide-long virus sequence.
|
We can see that our new CPU code is running
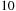 times faster than the regular Unafold code, thanks to both SSE and better memory locality of the tiled code. Even against this fast CPU code, the Tesla C1060 is still more than
times faster than the regular Unafold code, thanks to both SSE and better memory locality of the tiled code. Even against this fast CPU code, the Tesla C1060 is still more than
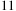 times faster than the Xeon. It is also worth noting the
times faster than the Xeon. It is also worth noting the
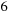 x speedup obtained between the GPU tiled and untiled code. For the CPU tiled and vectorized, however, going from one to eight threads yielded a
x speedup obtained between the GPU tiled and untiled code. For the CPU tiled and vectorized, however, going from one to eight threads yielded a
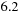 x speedup. We measured memory bandwidth usage of the tiled part of the code at
x speedup. We measured memory bandwidth usage of the tiled part of the code at
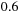 GB/s when running on one CPU core; therefore, running eight cores at full potential would require
GB/s when running on one CPU core; therefore, running eight cores at full potential would require
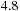 GB/s, exceeding the memory bandwidth limit of the Xeon E5450. As a result, the single GPU tested is approximately two times faster than this eight-CPU system. This may seem a low speedup, especially to those used to seeing hyped-up GPU performance gains. However, this is a more reasonable expectation — for example, the commercially released CULA package for linear algebra is “only” about three to five times faster than a vectorized and optimized linear algebra library on a four-core CPU. Also, note that GPU computing provides significant advantages for dealing with huge numbers of sequences; a single system fitted with several GPUs rivals with a small cluster at a fraction of the cost.
GB/s, exceeding the memory bandwidth limit of the Xeon E5450. As a result, the single GPU tested is approximately two times faster than this eight-CPU system. This may seem a low speedup, especially to those used to seeing hyped-up GPU performance gains. However, this is a more reasonable expectation — for example, the commercially released CULA package for linear algebra is “only” about three to five times faster than a vectorized and optimized linear algebra library on a four-core CPU. Also, note that GPU computing provides significant advantages for dealing with huge numbers of sequences; a single system fitted with several GPUs rivals with a small cluster at a fraction of the cost.
For the
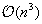 part of the code, it seems difficult to get much better performance than our tiled approach. Some work could in theory be done to get a little closer to the peak 312 GOPS of the Tesla. However, code profiling shows that now that this part is well optimized, it has become a non-preponderant part of total time even for large 10 Kb sequences. Therefore, future optimizations should focus on the
part of the code, it seems difficult to get much better performance than our tiled approach. Some work could in theory be done to get a little closer to the peak 312 GOPS of the Tesla. However, code profiling shows that now that this part is well optimized, it has become a non-preponderant part of total time even for large 10 Kb sequences. Therefore, future optimizations should focus on the
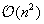 part computing interior loops, which is bandwidth limited with a complex memory access pattern.
part computing interior loops, which is bandwidth limited with a complex memory access pattern.
References
[1]
R. Nussinov, G. Pieczenik, J. Griggs, D. Kleitman,
Algorithms for loop matchings
,
SIAM, J. Appl. Math.
35
(1
) (1978
)
68
–
82
.
[2]
M. Zuker, P. Stiegler,
Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information
,
Nucleic Acids Res.
9
(1
) (1981
)
133
–
148
.
[3]
I.L. Hofacker, W. Fontana, P.F. Stadler, L.S. Bonhoeffer, M. Tacker, P. Schuster,
Fast folding and comparison of RNA secondary structures
,
Monatsh. Chem.
125
(1994
)
167
–
188
.
[4]
N. Markham, M. Zuker,
DINAMelt web server for nucleic acid melting prediction
,
Nucleic Acids Res.
33
(2005
)
W577
–
W581
.
[5]
E. Rivas, S. Eddy,
A dynamic programming algorithm for RNA structure prediction including pseudoknots1
,
J. Mol. Biol.
285
(5
) (1999
)
2053
–
2068
.
[6]
A. Mathuriya, D. Bader, C. Heitsch, S. Harvey,
GTfold: a scalable multicore code for RNA secondary structure prediction
,
In:
Proceedings of the 2009 ACM Symposium on Applied Computing, Honolulu, Hawaii, March 2009
(2009
)
ACM
,
New York
, pp.
981
–
988
.
[7]
A. Jacob, J. Buhler, R. Chamberlain,
Rapid RNA folding: analysis and acceleration of the Zuker recurrence
,
In:
Proceedings of the 2010 IEEE Symposium on Field-Programmable Custom Computing Machines, IEE, New York, May 2010, Charlotte NC
(2010
), pp.
87
–
94
.
[8]
I. Hofacker, M. Huynen, P. Stadler, P. Stolorz, RNA folding on parallel computers: the minimum free energy structures of complete HIV genomes, Working Papers, Santa Fe Institute Tech Report, 95-10-089, 1995.
[9]
F. Almeida, R. Andonov, D. Gonzalez, L. Moreno, V. Poirriez, C. Rodriguez,
Optimal tiling for the RNA base pairing problem
,
In:
Proceedings of the Fourteenth Annual August 2002, Winnipeg, Manitoba
(2002
)
Canada ACM Symposium on Parallel Algorithms and Architectures
,
New York
, p.
182
.
[10]
L. Guibas, H. Kung, C. Thompson,
Direct VLSI implementation of combinatorial algorithms
,
In:
Proceedings of the Caltech Conference on Very Large Scale Integration, January 22–24, California Institute of Technology, Caltech Computer Science Dept.
(1979
), p.
509
.
[11]
S.V. Rajopadhye,
Synthesizing systolic arrays with control signals from recurrence equations
,
Distrib. Comput.
3
(1989
)
88
–
105
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
