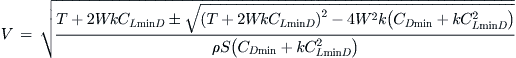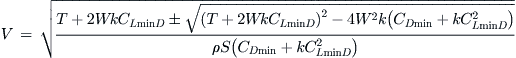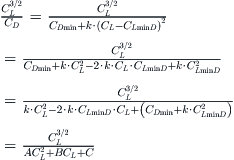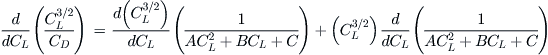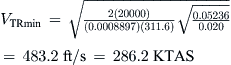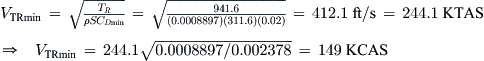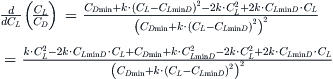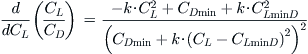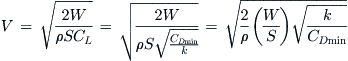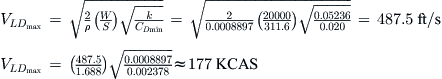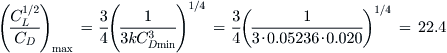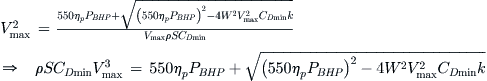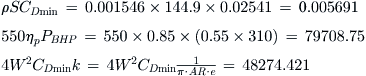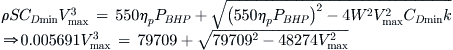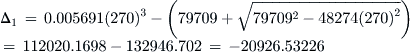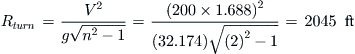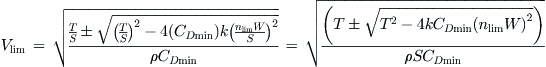Performance – Cruise
Abstract
A large number of steady level and accelerated cruise methods are presented in the chapter. First, the equation of motion is adapted to unaccelerated level flight. The resulting formulation is used to develop many classical analysis methods to determine a number of important steady level cruise performance, including the most important types of cruising speeds encountered in the operation of aircraft. Formulation is provided that extends the theory associated with the simplified drag model to that of the adjusted drag model (both are presented in Chapter 15, Aircraft Drag Analysis). Creation of the the flight envelope is presented, as well as computer programs used to determine the maximum airspeed for a propeller aircraft, as this requires an iterative approach. This is followed by a presentation of a number of classical analysis methods for accelerated flight. This includes maneuvers such as a general constant velocity turns and energy state calculations.
Keywords
Free-body; equation of motion; drag polar; lift-induced drag; minimum drag; required thrust; available thrust; required power; available power; speed stability; post-stall region; simplified drag; adjusted drag; minimum airspeed; stalling speed; load factor; thrust effect; flap effect; CG effect; banking; maximum endurance; maximum range; best rate-of-climb; best glide speed; maximum L/D ratio; maximum airspeed; dive speed; flight envelope; coffin corner; accelerated flight; level constant velocity turn; bank angle; maximum sustainable bank angle; turning radius; maximum sustainable turning radius; energy height; specific energy; specific excess power; specific excess power contour plot; zooming
Outline
19.1.1 The Content of this Chapter
19.1.2 General Free-body Diagram for Steady Level Flight
19.1.3 Planar Equations of Motion (Assumes No Rotation About y-axis)
19.1.4 Important Airspeeds for Propeller Aircraft
19.1.5 Important Airspeeds for Subsonic Jet Aircraft
19.2 General Cruise Analysis Methods for Steady Flight
19.2.1 Plotting the Drag Polar
19.2.3 Required Versus Available Thrust
Introducing the Effect of Thrust and Power
19.2.4 Airspeed in Terms of Thrust
Level Stalling Speed with a Load Factor n
Level Stalling Speed with Thrust, Flap, and CG Effects
Derivation of Equations (19-7), (19-8), and (19-9)
Derivation of Equation (19-10)
19.2.7 Airspeed of Minimum Power Required, VPRmin
Requirement for Max Endurance for a Propeller-powered Airplane
Derivation of Equation (19-11) and (19-12)
Derivation of Equation (19-13)
Maximum Endurance Airspeed for a Propeller-powered Aircraft, VEmax
Best Rate-of-climb Airspeed for a Propeller-powered Aircraft, VY
Derivation of Equation (19-14)
Comparison to the Best Glide Speed
19.2.8 Airspeed of Minimum Thrust Required, VTRmin, or Best Glide Speed, VBG, VLDmax
Derivation of Equation (19-15)
Derivation of Equation (19-16)
Derivation of Equation (19-18)
Derivation of Equation (19-19)
Airspeed for Maximum L/D Ratio
Derivation of Equation (19-20)
Derivation of Equation (19-21)
19.2.9 Best Range Airspeed for a Jet, VRmax
Requirement for Maximum Range for a Jet-powered Airplane
Derivation of Equation (19-22)
Derivation of Equation (19-23)
Comparison to the Best Glide Speed
Derivation of Equation (19-24)
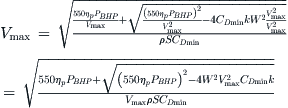
19.2.10 Maximum Level Airspeed, Vmax
Special Case: Propeller Aircraft
Derivation of Equations (19-25) and (19-26)
Derivation of Equation (19-27)
Derivation of Equation (19-30)
19.2.13 Power Available for a Piston-powered Aircraft
19.2.14 Computer code: Determining Maximum Level Airspeed, Vmax, for a Propeller Aircraft
19.2.15 Computer code: Determining Maximum Level Airspeed, Vmax, for a Jet
19.3 General Analysis Methods for Accelerated Flight
19.3.1 Analysis of a General Level Constant-velocity Turn
Derivation of Equation (19-35)
Derivation of Equation (19-36)
Derivation of Equation (19-37)
Derivation of Equation (19-38)
Derivation of Equation (19-39)
Derivation of Equation (19-40)
Derivation of Equation (19-41)
19.3.2 Extremes of Constant-velocity Turns
Maximum Sustainable Load Factor, nmax
Maximum Sustainable Turn Rate, ψ˙max
Minimum Sustainable Turning Radius
Airspeed for Maximum Bank Angle
Derivation of Equation (19-47)
Specific Energy and Energy Height
Derivation of Equation (19-52)
19.1 Introduction
The cruise maneuver is what the typical aircraft is designed to perform. That should highlight its importance. While fundamentally a simple maneuver, the goal of the designer is to ensure the airplane accomplishes this efficiently. In this sense, the term “efficiently” means the highest possible airspeed for a given fuel consumption. Figure 19-1 shows an organizational map displaying the cruise among other members of the performance theory.

FIGURE 19-1 An organizational map placing performance theory among the disciplines of dynamics of flight, and highlighting the focus of this chapter: cruise performance analysis.
Cruise can be defined as a straight and level flight at constant airspeed. Straight means the absence of a roll, which would result in a heading change, and level means no change in altitude. In the interests of accuracy, it would be more appropriate to say mostly straight and level flight at a mostly constant airspeed, as there exist cruise methods that require a slow change in both altitude and airspeed, and a change in heading is often required to fly to a destination. Such cruise methods are presented in Chapter 20, Performance – range analysis (although heading changes are not accounted for). However, these changes are so slow and gradual that the flight itself can be treated as if these were constant. The cruise maneuver in this chapter entails all variations of this type of flying, ranging from a very slow airspeed to the highest airspeed the airplane can achieve in level flight. As usual, the simplified drag model is used to develop expressions that highlight the various characteristics of cruise, such as best range or endurance, to name a few.
In general, the methods presented in here are the “industry standard” and mirror those presented by a variety of authors, e.g. Perkins and Hage [1], Torenbeek [2], Nicolai [3], Roskam [4], Hale [5], Anderson [6] and many, many others.
19.1.1 The Content of this Chapter
• Section 19.2 presents classic analysis methods to determine a number of important steady level cruise performance characteristics. Among those are the most important types of cruising speeds encountered in the operation of aircraft.
• Section 19.3 presents classic analysis methods to determine a number of important performance parameters for accelerated flight.
19.1.2 General Free-body Diagram for Steady Level Flight
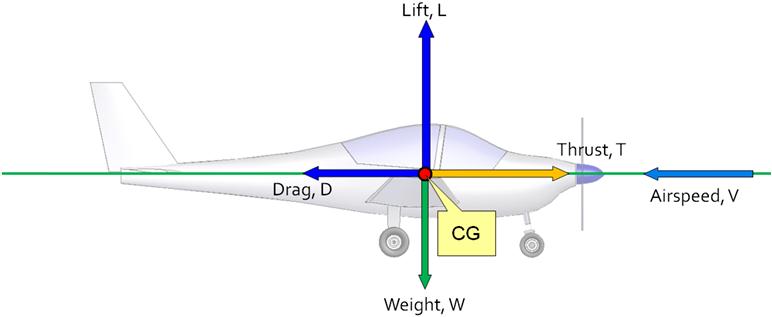
A general free-body diagram for steady level flight is presented in Figure 19-2. It is based on the dynamic diagram of Section 18.2.1, General two-dimensional free-body diagram for an aircraft, and Equations (18-1) and (18-2). However, it has been modified to represent level flight, yielding a form familiar to many pilots, in which L = W and T = D. However, as shown in Chapters 18 and 21, this is the only instance during the flight of the airplane where this simplification is applicable. The free body assumes all forces are applied at the center of gravity (CG) and all moments are balanced. It assumes a steady motion, that the climb angle, θ, is 0°, the angle-of-attack, α, is small, and the thrust angle, ε, is 0°.
19.1.3 Planar Equations of Motion (Assumes No Rotation About y-axis)
Using the assumptions in the image above, Equations (18-1) and (18-2) can be simplified as shown below (steady motion means dV/dt = 0):
![]() (19-1)
(19-1)
![]() (19-2)
(19-2)
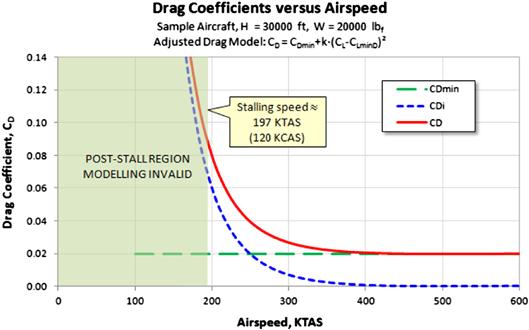
The solution of the equations of motion for level flight reveals a large number of very important characteristics of the airplane. Among those are the minimum and maximum airspeed the aircraft can (theoretically) achieve, as well as the minimum airspeed the airplane can maintain in level flight (stall). Additionally, there are a number of airspeeds that represent selected optimum conditions, such as best endurance, best range, and the so-called Carson’s airspeed, to name a few. Figures 19-3 and 19-4 show a number of important airspeeds for a typical aircraft. The formulas shown, excluding the one for the stalling speed, VS, are all based on the simplified drag model. The sections in the chapter are ordered from the lowest to the highest with respect to Figures 19-3 and 19-4.
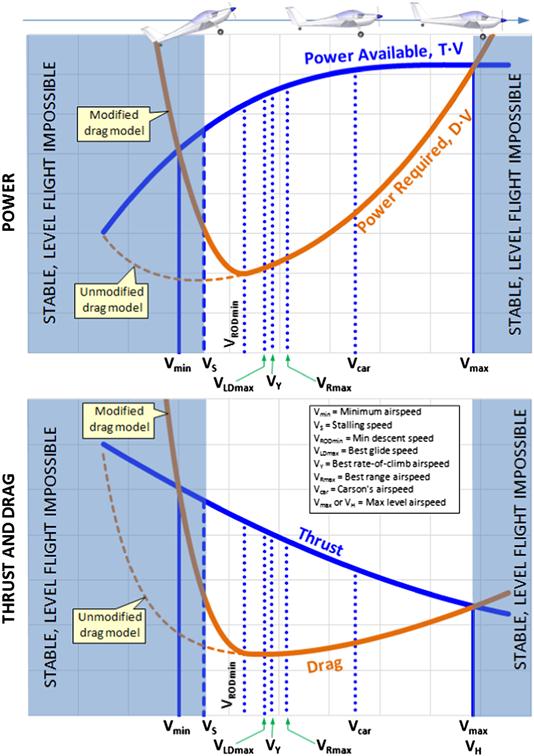
FIGURE 19-3 Important airspeeds for a propeller aircraft in cruising flight. Note that the modified drag model uses the method of Section 15.2.3, Approximating the drag coefficient at high lift coefficients.

FIGURE 19-4 Important airspeeds for a jet aircraft in cruising flight. Note that the modified drag model uses the method of Section 15.2.3, Approximating the drag coefficient at high lift coefficients.
Note that in this chapter, formulation for unsteady flight is also developed.
19.1.5 Important Airspeeds for Subsonic Jet Aircraft
19.2 General Cruise Analysis Methods for Steady Flight
In this chapter we will introduce a number of common cruise analysis methods for un-accelerated flight. All depend on our knowledge of drag as well as thrust. The reader should keep in mind that, generally, three different drag models are used for this purpose: (1) the simplified, (2) adjusted, and (3) all others. The latter could be a situation that involves a sailplane with a well-defined drag bucket that calls for the use of a spline or a lookup table. Performance characteristics can be evaluated using closed-form solutions as long as the drag model is well defined using smooth and continuous mathematical expressions. As such, only the simplified and adjusted drag models allow general closed-form solutions to be developed. In this chapter, analysis methods are developed that utilize those two models, although most are based on the simplified drag model. The reader should recognize that these closed-form solutions can only be used for the said drag models. Using them with other representations will yield erroneous results.
It should be stated that modern-day performance analyses shy away from using the simplified drag model, as its results are suspect for the aircraft that features cambered airfoils. Additionally, it is a good practice to prepare the methods in a spreadsheet. The spreadsheet has become one of the most powerful tools at the disposal of the aerospace engineer. It allows the designer to set up numerical solutions that are highly non-linear and, when properly formulated, allow very complicated problems to be analyzed. Such methodologies are essential when analyzing the performance of very sleek aircraft, such as powered sailplanes and other aircraft that operate outside normal quadratic drag behavior. Regardless, the strength of the simplified model is – well – its simplicity. This allows various hard-to-grasp concepts to be explained and presented in a clear manner using closed-form analytical solutions.
19.2.1 Plotting the Drag Polar
The drag polar presents the drag coefficient, CD, as a function of the lift coefficient, CL. The generation of the drag polar is discussed in detail in Chapter 15, Aircraft drag analysis. Figure 19-6 shows the subsonic drag polar for the Learjet 45XR, separating the contribution of induced drag, CDi, from the minimum drag, CDmin.
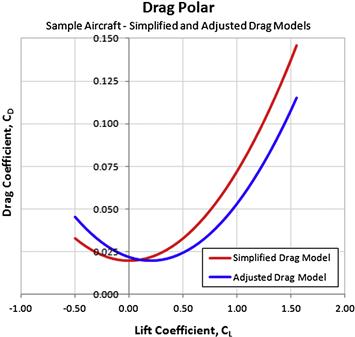
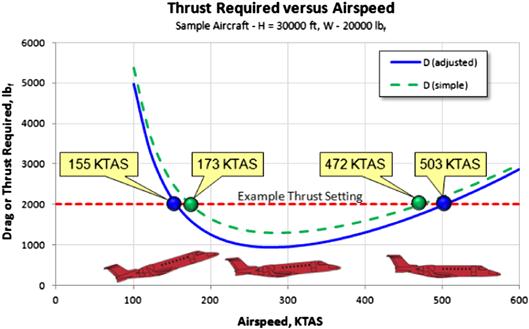
Figure 19-5 compares the constituent components of the drag model. The reader must be mindful that both models, the simplified and adjusted, represent the simplest “reasonable” forms of the drag polar. For instance, in the figure, the effect of increased flow separation will force CDmin upward at low and high lift coefficients; it would not be a horizontal line. This would make the total drag coefficient rise substantially, well beyond what is represented in the figure and more like that of the modified drag model of Figures 19-3 and 19-4.
Figure 19-6 compares the simplified and adjusted drag models. The offset of the adjusted drag model will have significant effects on very important performance parameters, such as airspeed for minimum power required; best glide speed, and others. Airplanes that feature cambered airfoils almost always have a CLminD > 0 and, thus, require the adjusted model.
Another lesson the reader must be mindful of when comparing the two drag models is that it would appear the adjusted drag model leads to much higher L/D ratio on other performance parameters. This is primarily caused by the assumption here that the CDmin for both models is equal. However, this in not always true in practice.
19.2.2 Drag Breakdown
Chapter 15, Aircraft drag analysis, describes the generation of drag and its constituent components. It can be very useful to break the total drag into these components and consider their magnitudes as functions of airspeed. For instance, consider the hypothetical installation of a winglet on an existing airplane. A winglet is a device that reduces the induced drag of the aircraft. However, it adds to the wetted area of the aircraft, increasing CDmin by a magnitude of ΔCDmin. Its installation will thus only be beneficial at airspeeds where (and if) the decrease in induced drag, ΔCDi, is greater than the increase ΔCDmin. In order to find out the total drag must be broken down into its constituent components. The following example shows how this is done for the Learjet 45XR.
19.2.3 Required Versus Available Thrust
As shown in Section 18.2.6, Vertical airspeed in terms of thrust or power, an airplane can only increase its altitude if it is equipped with an engine capable of delivering more power than required to maintain level flight. It was shown at the beginning of this section that the thrust required for level flight equals the drag of the airplane. While the requirement holds for any airplane, the analysis method for airplanes with piston engines differs in the sense that power is used rather than force. However, the general philosophy of analysis remains the same for both.
Consider the Learjet 45XR as it cruises at 30,000 ft and at a weight of 20,000 lbf. The thrust required to cruise at 400 KTAS can be obtained from Equation (17-11) through (17-13).
From Equation (17-12) using the simplified drag model:
![]()
From Equation (17-13) using the adjusted drag model:
![]()
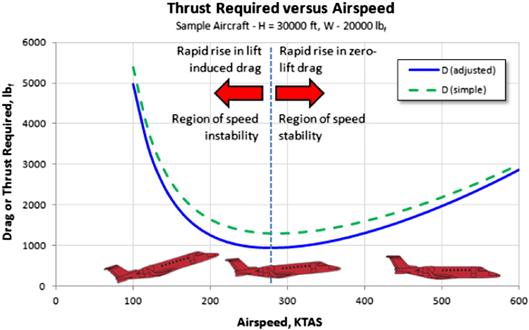
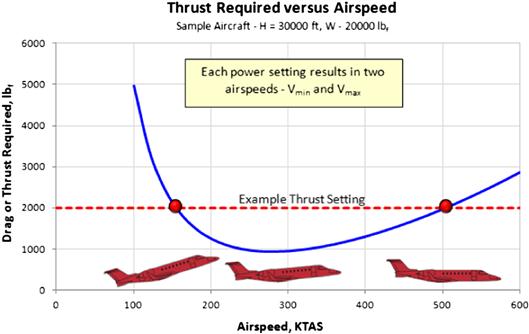
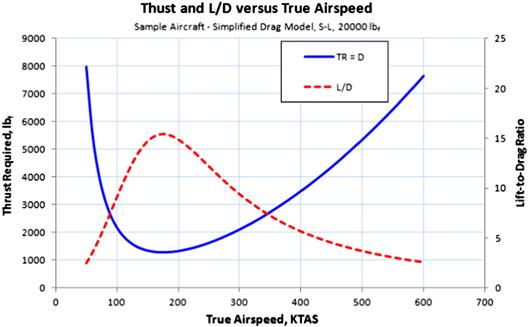
There are two important points to be made regarding the required thrust, TR. The first point is the difference in the magnitude of the drag force between the simple and adjusted drag models (see the curves in Figure 19-10). Two regions of importance are shown and of which the designer must be aware. These are referred to as the regions of speed stability and instability. The second point is shown in Figure 19-11; it shows that each power setting (here displayed as 2000 lbf of thrust) results in two distinct airspeeds.
Region of Speed Stability
Consider Figure 19-10. Assume the airplane is flying at 400 KTAS when a sudden gust or change in its attitude reduces the speed of the airplane. As a consequence, its drag decreases but this increases the airspeed, eventually bringing it back to 400 KTAS (since the thrust setting has not been changed). By the same token, should the airplane experience a speed increase, its drag now increases, reducing the airspeed and eventually bringing it back to the original airspeed (as the thrust has not been changed). This phenomenon is recognized by pilots as speed stability.
Region of Speed Instability
Again consider Figure 19-10. Assume we are flying at 200 KTAS when a sudden gust or change in airplane attitude reduces the speed of the airplane. As this happens, its drag increases, which reduces the speed further. By the same token, should the airplane experience a speed increase, its drag now reduces, increasing the airspeed further. This phenomenon is recognized by pilots as speed instability. Speed instability is also known by pilots as flying “on the back side of the power curve.” Speed instability can be helpful during landing, as it helps the pilot slow down the airplane during flare.
Figure 19-11 shows an important property when comparing available to required thrust: each power setting results in two possible equilibrium airspeeds, one low and one high. The lower the available thrust, the closer will these speeds be to each other. One and only one airspeed will result in a condition at which the two acquire the same value; this is the airspeed of minimum thrust required.
Introducing the Effect of Thrust and Power
The preceding graphs have all demonstrated how the drag of the airplane changes with airspeed. The effects of thrust and power have not yet been presented. It is conventional to superimpose those on the same graph, as this will give important clues to the capability of the aircraft. Figure 19-12 shows a typical such representation, here based on the Learjet 45XR and depicting both the “standard” representation of thrust and power (linear) and one that is more realistic (curved). Both graphs show that where the thrust intersects the drag curve, or the power available intersects the power required curve, it holds that T = D. In other words, it is a point of equilibrium. There are two such points on each graph: the minimum and maximum airspeed. Of course there is a serious shortcoming to the lower airspeed – it is usually less than the stalling speed, which is then the true minimum speed of the aircraft. Also, the drag at this point is higher than shown – a limitation of the simplified drag model being used.
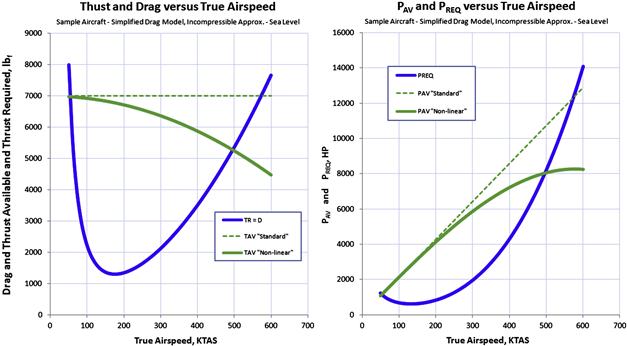
FIGURE 19-12 Required and available thrust and required and available power based on Figure 19-12 The “Standard” is an idealized turbojet, whereas “Non-linear” resembles a more realistic turbofan engine.
19.2.4 Airspeed in Terms of Thrust
Based on Figure 19-11 it is possible to determine two equilibrium airspeeds associated with any arbitrary power setting. Thus, one could predict the airspeeds associated with, say, 50% or 75% thrust settings, or for that matter any other setting of interest. If the thrust (T), weight (W), and drag characteristics of the aircraft are known, the two airspeeds can be estimated as follows, based on the two drag models:
Note that if CLminD = 0 then, as expected, the ratio under the radical reduces to the simplified CDi:
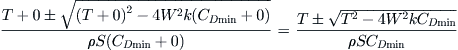
Derivation of Equation (19-3)
First, write the thrust in terms of the drag model:
![]()
Then, try to eliminate the term 1/q:
![]()
This is a quadratic equation in terms of q:
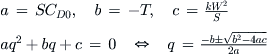
Solving the quadratic equation:
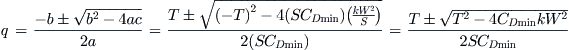
Writing q explicitly leads to:
![]()
QED
Derivation of Equation (19-4)
First, write the thrust in terms of the drag model:
![]()
Therefore;
![]()
![]()
Simplifying further:
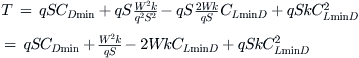
Then, try to eliminate the term 1/q:
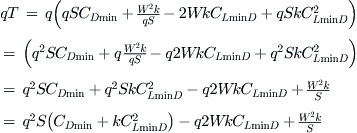
![]()
![]()
This is a quadratic equation in terms of q:
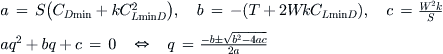
Finally, solve the quadratic equation:
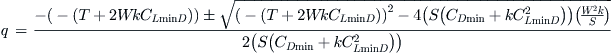
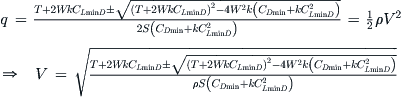
QED
19.2.5 Minimum Airspeed, Vmin
The minimum level airspeed is the lower of the two airspeeds at which the power required and power available are equal (see Section 19.2.4, Airspeed in terms of thrust). The absolute theoretical minimum airspeed will be achieved at the maximum thrust. When estimated using the simplified or adjusted drag models, this airspeed is often lower than the stalling speed and, thus, really meaningless. As stated before, this is caused by inaccuracies in the simplified and adjusted drag models at high lift coefficients (refer to Section 15.2.3 for a remedy). Furthermore, the following estimation of the minimum level airspeed assumes (1) the simplified drag model and (2) thrust does not contribute to vertical force (lift).
![]() (19-5)
(19-5)
Note that if the minimum speed is smaller than the stalling speed of the aircraft, then the stalling speed becomes the Vmin.
For the adjusted drag model use:
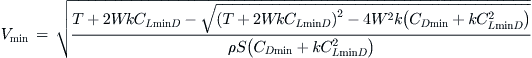 (19-6)
(19-6)
19.2.6 Stalling Speed, VS
The stalling speed, VS, is the minimum speed at which an airplane can maintain altitude. If the airspeed is slowed a hair below the stalling speed this will cause a well-designed airplane to drop its nose uncontrollably, while maintaining wings level. This nose drop, in turn, will increase the airspeed of the airplane so it becomes airborne again. Due to stability and control issues, some aircraft do not achieve a stall break, but rather descend at some AOA below their stall AOA. The resulting airspeed is considered the minimum airspeed by the aviation authorities, although it is higher than the true stalling speed of such aircraft. A determination of the stalling speed during the design phase requires the engineer to estimate the maximum lift coefficient and then calculate it as follows:
Figure 19-14 shows how the stalling speed changes with altitude, while the calibrated airspeed remains unchanged for aircraft with a low subsonic stalling speed. On the other hand, the true airspeed increases with altitude, something the designer must keep in mind as it affects impact loads in emergency landings and durability of brakes for airplanes consistently operated from high-altitude airports.
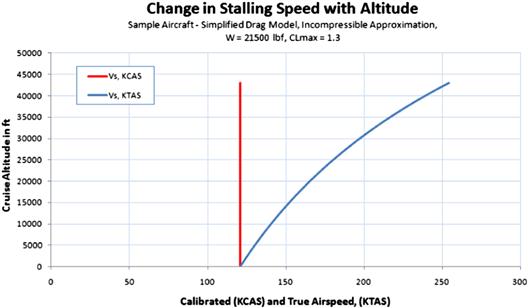
FIGURE 19-14 Stalling speed in terms of calibrated (KCAS) and true (KTAS) airspeed as a function of altitude.
Level Stalling Speed with a Load Factor n
If the airplane is performing some specific wings-level maneuver, for instance a loop, it will experience a change in the load factor. If the total load factor is denoted by n (note n = 1 for level flight), the stalling speed will change and can be calculated by making the following modification to Equation (19-7):
Stalling Speed During Banking
When an airplane banks at an angle ϕ while maintaining altitude (level constant-speed turn), the load factor acting on it increases. This is identical to carrying greater weight; its stalling speed increases. Using the preceding formulation, this stalling speed at any given angle of bank ϕ can be estimated using the following expression:
Stalling speed at angle of bank ϕ:
![]() (19-9)
(19-9)
where VSlevel is the stalling speed with wings level. Note that 14 CFR Part 23 denotes the stalling speed of an airplane in the landing configuration using the term VS0. This implies flaps are fully deflected and retractable landing gear is deployed. Similarly, the term VS1 refers to the stalling speed of the airplane in the take-off configuration. This implies flaps are in a take-off position and retractable landing gear is deployed.
Level Stalling Speed with Thrust, Flap, and CG Effects
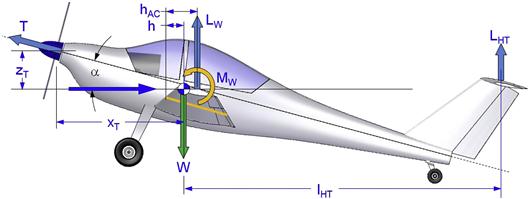
In practice, the stalling speed is affected by engine thrust, flap deflection, and the CG location. Thrust and deployed flaps will reduce the stalling speed, while a forward location of the CG increases it. The forward CG requires higher download to be generated by the HT for trim. This load must be added to the weight of the aircraft, which means the wing must generate lift greater than the weight of the airplane and therefore, its stalling speed is higher than indicated by the above methods. The same stabilizing effect due to flaps will also render the stall speed reduction smaller than in its absence. To include these effects, the stalling speed must be calculated as shown below:
![]() (19-10)
(19-10)
where
Refer to Figure 19-15 for the dimensions h, hAC, xT, zT, and lHT.
Note that this expression is suitable for conventional tail-aft configurations only. Strictly speaking it requires an iterative procedure to solve, because both MW and T depend on airspeed. If the expected stalling speed is known, it can be used to calculate both MW and T, which can then be used as constants in the formulation with acceptable accuracy. However, implementing the calculations in a spreadsheet will make it easy to solve iteratively. Note that the effects of flaps are accounted for in the variable MW. Example 19-4 demonstrates the use of this equation and evaluates its accuracy.
Derivation of Equations (19-7), (19-8), and (19-9)
Formulation is obtained from Equation (9-47), by solving for V and applies to all three equations:
![]()
QED
Derivation of Equation (19-10)
Referring to Figure 19-15, statics requires the following to hold in steady level flight, where at the point of stall, the lift of the wing, LW, will depend on the maximum lift coefficient of the wing.
Referring to Figure 19-15, statics requires the following to hold in steady level flight:
![]()
Following a similar process as for the derivation of Equation (15-81), the moment equation can be solved for the balancing force the HT must generate:
![]()
Inserting this result into the force equation and simplifying leads to the expression below:
![]()
Yielding the following relation holds between the wing lift and the other contributors:
![]()
At stall, LW = ½ρVS2·S·CLmax, so solving for VS yields:
![]()
QED
19.2.7 Airspeed of Minimum Power Required, VPRmin
The upper graph in Figure 19-3 shows there is a distinct minimum in the power require curve. For propeller-powered aircraft this implies that the engine can be operated at a minimum power and, thus, with minimum consumption of fuel. For this reason, this airspeed is of great importance to the aircraft designer as it will allow the aircraft to stay aloft the longest. This airspeed is also called the maximum endurance speed, VEmax, for the propeller aircraft. Additionally, as shown in 18.3.9, Airspeed for best ROC for a propeller-powered airplane, this airspeed is also the best rate of climb speed, VY, for a propeller-powered aircraft.
Requirement for Max Endurance for a Propeller-powered Airplane
Equation (20-21) of Section 20.4.2, Endurance profile 2: constant attitude/altitude cruise, as well as 19.2.12, Power required, show that the maximum endurance of a propeller-powered airplane depends on the maximum of the ratio CL1.5/CD, and this maximum can be found from the following expression:
 (19-11)
(19-11)
The lift coefficient of this condition can be determined using the relations below:
Derivation of Equation (19-11) and (19-12)
Start by writing the expression for L/D:
![]() (i)
(i)
Differentiate with respect to CL:

![]()
![]()
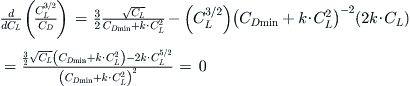
The maximum can be found when the numerator equals zero, or;
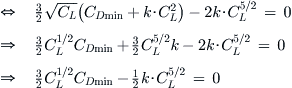
![]() (ii)
(ii)
Insert this result into the original expression and manipulate:
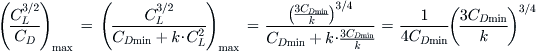 (iii)
(iii)
QED
Derivation of Equation (19-13)
Expanding;
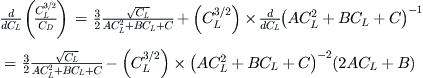
Manipulate algebraically;
![]()
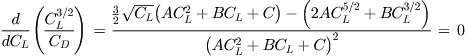
The maximum can be found when the numerator equals zero, or;

We have quadratic formulation that can be solved using Equation (E-12), here repeated for convenience:
![]()
Therefore:

By observation we also note that only when CL > 0 does the solution make physical sense (because the airplane needs a positive CL to maintain altitude). Therefore, we must select the plus sign in front of the radical.
![]() (iv)
(iv)
As expected, we can see that if CLminD = 0 we get the same expression as that of the simplified drag model. Insert this result into Equation (iii) to determine the ratio.
QED
Maximum Endurance Airspeed for a Propeller-powered Aircraft, VEmax
Since a condition for maximum endurance of a propeller-powered airplane has been identified, it becomes imperative to determine the airspeed at which this occurs. This will allow the Pilot’s Operating Handbook (POH) to specify a specific airspeed for loitering or remaining in holding flight due to air traffic control requirements (although airspeeds greater than this can certainly be expected). Also refer to 19.2.8, Airspeed of minimum thrust required, for a similar airspeed for jets. This expression is only valid for the simplified drag model.
Best Rate-of-climb Airspeed for a Propeller-powered Aircraft, VY
Equation (19-14) is also derived in Section 18.3.9, Airspeed for best ROC for a propeller-powered airplane, as Equation (18-27), where it is used to determine the best ROC for a propeller aircraft.
Derivation of Equation (19-14)
We demonstrated that CL for PRmin was given by: ![]() (see Equation (19-12))
(see Equation (19-12))
Insert this into the lift equation and solve for V:
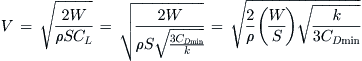
QED
Comparison to the Best Glide Speed
Using the specific results based on the simplified drag model, it is of interest to compare Equation (19-14) to Equation (19-20), repeated below for convenience:
![]()
Dividing the former by the latter reveals the following difference between the two:
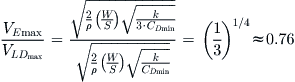
In other words, the best endurance speed is about 76% of the speed for best L/D.
19.2.8 Airspeed of Minimum Thrust Required, VTRmin, or Best Glide Speed, VBG, VLDmax
This airspeed is also the best glide speed, VBG or VLDmax, for both a jet and propeller-powered aircraft. Furthermore, it is the maximum endurance airspeed, VEmax, for a jet and the best range airspeed, VRmax, for a propeller-powered aircraft.
It is vitally important for the operation of jets that the designer (and operator) can determine the airspeed that requires the least amount of thrust. It is logical to assume that this airspeed must also be that which requires the least amount of fuel to be consumed. The airspeed of minimum thrust required is particularly important for airplanes whose mission may demand prolonged periods of loitering. Examples of such aircraft are reconnaissance aircraft and even fighter aircraft. Their missions often require them to stay for a prolonged period of time in a specific geographic location. However, the high fuel consumption of jet engines in general renders this airspeed imperative for all jets, regardless of mission. Albeit rare, situations may arise that require the pilot to slow down to the airspeed of minimum thrust required, VTRmin, which is calculated from:
When using the adjusted drag model, the primary trick is to first determine the two roots from Equation (19-17) and then select proper thrust (T) from the two (the one with the positive sign). This is then used with Equation (19-16) to calculate the airspeed.
Derivation of Equation (19-15)
Airspeed as a function of thrust was determined from Equation (19-3):
![]()
When the quantity under the radical is zero there is only one solution: the airspeed at which the required thrust is minimum. The thrust for this condition can be found from:
![]()
When the quantity under the radical is zero the minimum required thrust can be written as follows:
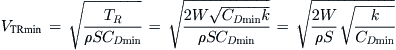
QED
Derivation of Equation (19-16)
Airspeed as a function of thrust was found from Equation (19-4):
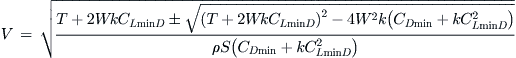
As before, when the quantity under the radical is zero there is only one solution: the airspeed at which required thrust is minimum.
![]()
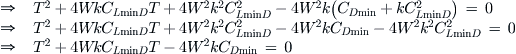
Therefore, the solution to the quadratic formulation is:
![]()

Therefore,

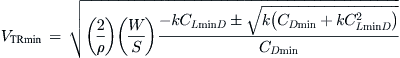
QED
Maximum L/D Ratio
One of the most important performance parameters of an aircraft is its maximum lift-to-drag ratio, LDmax. This ratio indicates not only how far an airplane will glide from a given altitude (see Section 21.3.8, Glide Distance), but also, in the case of a propeller aircraft, how far it can fly and, in the case of a jet, how long it can stay aloft. Table 15-18 shows typical values for the maximum L/D ratio for several classes of aircraft.
The ratio is also known as the best glide ratio and, less commonly, minimum-thrust-required-to-weight-ratio. Here, two methods to calculate the best glide ratio are presented: one using the simplified and the other the adjusted drag models. When using the simplified drag model, the LDmax can be calculated from:
![]() (19-18)
(19-18)
The expression shows that the magnitude of the LDmax is independent of altitude. Figure 19-17 and Figure 19-18 show that the airspeed of LDmax changes with altitude in terms of KTAS, but not KCAS. This is important and helpful to the pilot, who only has to remember one number; the KCAS value, as he operates the airplane using KCAS. For the adjusted drag model, the LDmax is determined using the following expression:
 (19-19)
(19-19)

FIGURE 19-18 Change in L/D with calibrated airspeed, using the simplified drag model. Note that all the curves are superimposed on top of each other and, thus, will appear independent of altitude to the pilot. This is very fortunate for the pilot, who must remember only one number as the best glide speed.
Derivation of Equation (19-18)
Start by writing the expression for L/D:
![]()
Differentiate with respect to CL:
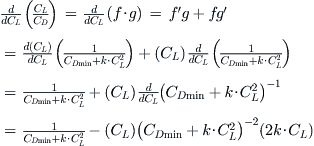
![]()
![]()
Insert this into the original expression to get:
![]()
QED
Derivation of Equation (19-19)
Start by writing the expression for L/D:
![]()
Differentiate with respect to CL:

Completing the differentiation:
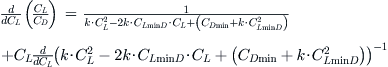
Complete differentiation and expand further to get:
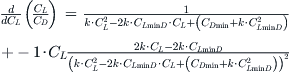
Therefore, the maximum can be found for CL when the numerator equals zero, or:
![]()
Using this expression, the value of CL reduces to (note that it reduces to the result for the simplified model when CLminD = 0):
![]()
Insert this into the original expression to get:
![]()
For clarity let’s treat the denominator separately:

Noting that (CL/CD)max = (CD/CL)min we get:

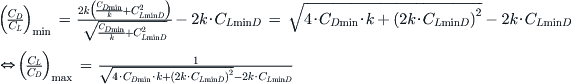
QED
Airspeed for Maximum L/D Ratio
Knowing the airspeed at which the maximum L/D ratio is achieved is imperative, not only from a standpoint of safety but also as it is the airspeed of minimum thrust required (see 19.2.8, Airspeed of minimum thrust required). Pilots of single-engine aircraft are trained to establish this airspeed as soon as possible in the case of engine failure as it will result in a maximum glide distance, therefore improving survivability. It is also known as the airspeed for minimum thrust required. Using the simplified drag model, the airspeed for maximum L/D ratio is:
![]() (19-20)
(19-20)
Not that this result is the same as Equation (19-15) of 19.2.8, Airspeed of minimum thrust required. Using the adjusted drag model, it is given by:
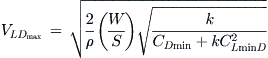 (19-21)
(19-21)
Derivation of Equation (19-21)
The CL for LDmax using the adjusted drag model is:
![]()
Insert this into the lift equation and solve for V:

QED
Various Lift-to-drag Ratios
As is evident from several of the analysis methodologies presented thus far, a number of important optimum properties of the airplane can be extracted once the drag polar has been defined. In particular, three cruising speeds based on the optimization on the various products and ratios of lift, L, drag, D, and airspeed, V, are of interest to the designer. The first is that of optimum range (maximum L/D), endurance (minimum D·V), and cruise efficiency (minimum D/V).
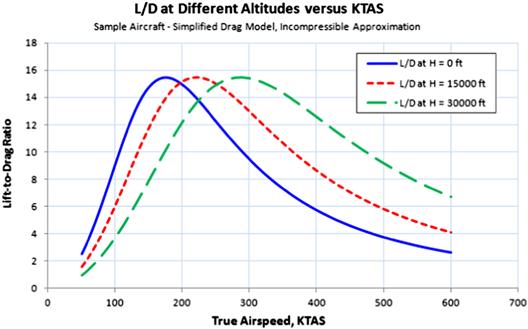
Figure 19-20 shows three types of lift-to-drag ratios and their corresponding optimums. Note that the ratio CL1.5/CD pertains to propeller aircraft, which renders it moot for the Learjet 45XR. However, it is included for completeness. Figure 19-21 shows the L/D and thrust required for the Learjet 45XR sample aircraft plotted at three altitudes (S-L, 15,000 ft, and 30,000 ft). The graph shows well how the thrust required changes with altitude and how high airspeed is more easily achieved at altitude. The simplified drag model used for this demonstration does not account for compressibility, so the high-speed range (450+ KTAS) is erroneous.
19.2.9 Best Range Airspeed for a Jet, VRmax
This airspeed is also the so-called Carson’s speed, VCAR, for both a jet and a propeller aircraft.
Requirement for Maximum Range for a Jet-powered Airplane
It can be seen from Equation (20-11) that the maximum range for a jet-powered airplane depends on the maximum of the ratio CL0.5/CD. This maximum can be determined from the following expression, which is only valid for the simplified drag model:
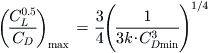 (19-22)
(19-22)
This assumes that the TSFC is constant with power setting, but this ensures the minimum thrust for level flight results in minimum fuel consumption. Note that this may not be the case for real engines equipped with the Full Authority Digital Engine Control system (FADEC).
Derivation of Equation (19-22)
Start by writing the expression for L/D:
![]()
Differentiate with respect to CL:
![]()
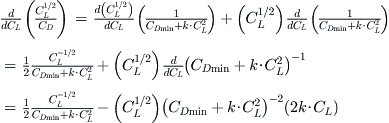
Further manipulation leads to:
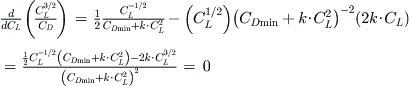
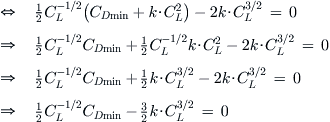
![]()
Insert this result into the original expression and manipulate:
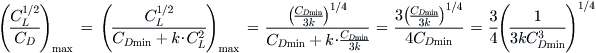
QED
Best Range Airspeed for a Jet
The airspeed that yields the maximum range of a jet is clearly an important parameter. The following expression, which is only valid for the simplified drag model, can be used to calculate this airspeed. It should be added that this airspeed is almost always too low to be practical for passenger transportation. As usual, the units for the airspeed are ft/s in the UK system and m/s in the SI system.
![]() (19-23)
(19-23)
Derivation of Equation (19-23)
We showed that CL for CL0.5/CD was given by:
![]()
Insert this into the lift equation and solve for V:
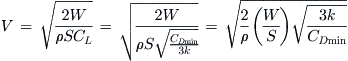
QED
Comparison to the Best Glide Speed
Similar to an earlier comparison that used the specific results based on the simplified drag model, it is of interest to compare Equation (19-23) to Equation (19-20), repeated below for convenience:
![]()
We observe the following difference between the two:

In other words, the best range speed is about 32% greater than the speed for best L/D.
Carson’s Airspeed
In a paper titled Fuel Efficiency of Small Aircraft [7], B. H. Carson discusses the mismatch between the amounts of power required for climb and cruise in small propeller-driven aircraft. In the paper Carson demonstrates that this excess power can be used more efficiently by bringing it closer to the so-called Gabrielli-Von Kárman [8] limit for vehicle performance. In the paper Carson states that (1) aircraft fuel economy is directly proportional to the L/D ratio, and the optimum is usually realized only at unacceptably low airspeeds. (2) Power required for climb results in aircraft airspeeds well beyond this optimum. (3) This results in greater fuel penalties than otherwise. In short, Carson suggests that flying at a speed faster than the airspeed for LDmax is more advantageous, as the flying public generally value a shorter time en route more than fuel efficiency. From a certain point of view, Carson’s airspeed can be considered the “fastest efficient airspeed” to fly.
The most frequently cited measure of efficiency is the so-called transport efficiency, defined as WV/P, where W is the vehicle weight, V its speed of travel, and P is the installed power. Expanding on this idea, Carson derives a relation for a specific airspeed that is about 32% higher than the best glide airspeed (see Equation (19-20)). This speed is now recognized as Carson’s airspeed.
19.2.10 Maximum Level Airspeed, Vmax
This airspeed is also denoted by the variable VH in 14 CFR Part 23.
The maximum level airspeed is of great interest in the marketing, certification, and operation of the aircraft. High maximum airspeed has a great marketing appeal, especially when compared to slower rival aircraft. From the standpoint of certification it is indicative not only of the magnitude of the maximum loads the airframe must react but also of the required aeroelastic resistance. Its impact on operation is reflected in its efficiency and this directly affects fuel consumption and, therefore, how it will be used. The maximum level airspeed is obtained as the positive value of the radical of Equation (19-3). It leads to the following expression, which is only valid for the simplified drag model:
![]() (19-25)
(19-25)
For the adjusted drag model use:
 (19-26)
(19-26)
The following observations can be made: (1) Vmax increases with Tmax; (2) Vmax increases with W/S; (3) Vmax increases if CDmin and/or k decreases (AR increases).
Special Case: Propeller Aircraft
It is unlikely that the thrust for a propeller-powered aircraft will be known at Vmax, as it is a function of the airspeed itself. For this reason, the airspeed must be determined by iteratively solving the equation below.
![]() (19-27)
(19-27)
Equation (19-27) can be solved using a multitude of methods, for instance the bisection method, regula falsi, or others. These functions require a single function to be solved, in which case the equation can be rewritten as the function f(Vmax):
![]() (19-28)
(19-28)
A possible initial condition would then be written for Vmax = 0:
![]()
Note that for other values of Equation (19-27), terms under the radical require the following to hold:
![]()
Both methods are implemented in the computer codes in Sections 19.2.14 and 19.2.15.
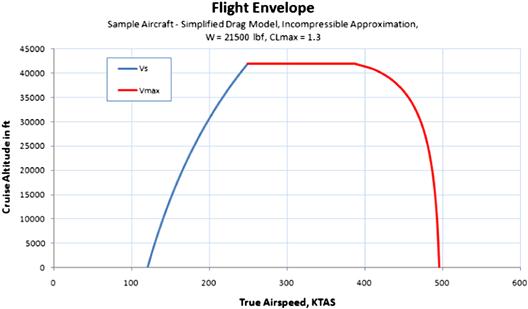
19.2.11 Flight Envelope
The flight envelope is one of several ways to demonstrate the capability of the aircraft in terms of its minimum and maximum airspeed with altitude. The preceding analyses make it possible to begin building such a diagram by plotting the stalling speed and maximum airspeed with altitude. The flight envelope is based on the fact that the performance of the airplane is a function of altitude. An example of this is shown in Figure 19-23 for the Learjet 45XR. It shows how altitude affects the drag and thrust of the airplane and modifies where the two curves intersect, where the maximum difference between the two occurs, and so on. A different presentation of this information is shown in Figure 19-24. It plots the maximum and minimum airspeed for the 45XR, assuming a maximum “clean configuration” lift coefficient of 1.3.
The flight envelope has very specific utility for the aircraft designer. First, it shows the capability of the aircraft over its entire altitude range. The graph is fundamentally simple and can thus be helpful to management and customers and is relatively simple even for laypeople to understand. It is appropriate to also superimpose VX and VY on the graph to further indicate the airplane’s performance relative to its low- and high-speed limitations. Second, it should be used to create a set of airspeeds and altitudes at which the dynamic stability characteristics and aeroelastic test matrix for the aircraft can be established. For instance, the designer should map a matrix of points (e.g. minimum, maximum, and the average of the two) at selected altitudes (e.g. 0, 5000, 10,000 ft, etc.) and evaluate phugoid and dutch roll damping at those points. It is possible the flight envelope has to be limited further if points of instability are discovered. Third, a similar matrix should be prepared for aeroelastic evaluation of the structure. This allows the flight test team to plan where structural shakers should be activated during flutter testing.
Coffin Corner
The maximum airspeed of high-flying jet aircraft is called the MMO, or the maximum operating Mach number. Soon after exceeding this value, local airspeeds over the airplane begin to exceed Mach 1 and a weak shock begins to form. This will cause several anomalies: first, there is a sharp rise in drag. Second, there is a change in pitching moment as the center of lift on the lifting surfaces begins to move to a different location, eventually moving as far aft as 50% of the MGC. This greatly increases the distance between the CG and the center of lift, leading to the phenomenon called Mach tuck. A Mach tuck is essentially a powerful nose pitch-down moment that is uncontrollable for aircraft not designed to handle it. Therefore, the airplane will dive, increasing its speed further, and this may lead to structural failure during recovery, and certain demise if recovery is not possible. The side effects are more complicated than that, as the shock formation may also lead to abnormal shaking and un-commanded wing rocking. Third, compounding the problem, the formation of shockwaves on the lifting surfaces leads to a shock-stall (see Figure 8-43). This means that the control surfaces are now operating in separated wake, rendering them far less effective.
As shown above, as the airplane increases its altitude, the stalling speed in terms of true airspeed increases as well, while its calibrated airspeed remains the same. Consider the graph of Figure 19-25, which shows Mach isobars extending from S-L to 80,000 ft plotted against the airspeed in KCAS. The graph allows the altitude at which a given airspeed reaches a set Mach number to be determined. For instance, 200 KCAS becomes Mach 0.7 at approximately 40,000 ft. Now consider a high-flying aircraft whose MMO is 0.80 and stalling speed, VS, is 150 KCAS. This is represented as the thick solid and dotted curves in the figure.
As the aircraft continues to climb, and assuming a constant airspeed in KCAS, its Mach number increases. Eventually, the aircraft will near its MMO and the indicated airspeed (or KCAS assuming an ideal airspeed indication system) will have to be reduced. For instance, if the indicated airspeed during climb is 200 KCAS it can be seen that once the airplane approaches 45,000 ft, the pilot will have to reduce the airspeed to avoid reaching the MMO. Then, if the climb is continued, at approximately 57,000 ft a new dilemma appears: the required indicated airspeed is now nearing the stalling speed. Thus, if the pilot slows down further, the plane will stall and stalling at this condition may easily result in a dive that takes the airplane beyond MMO. If the airplane accelerates, the plane will hit MMO. This peculiar situation is called the coffin corner because any change in airspeed can potentially lead to a very dangerous situation. Flying near the coffin corner requires the pilot to be alert and precise, because it only takes flying into a mass of air whose temperature changes rapidly or encountering a clear air turbulence (CAT) to upset the equilibrium.
Reality is a tad more complicated than reflected here, as a typical airplane would reduce its weight as it climbs and for that reason the vertical stall speed line in Figure 19-25 would be slanted to the left. However, since the stalling speed is really a function of the equivalent airspeed the effect would slant it to the right. The resulting stall speed line would thus depend on the compressibility and the weight. However, in spite of that, the effects are reasonably represented for demonstration purposes in this graph.
In order to create the graph of Figure 19-25 the calibrated airspeed is determined for a given Mach number and altitude. For instance, the true airspeed in knots corresponding to M = 0.1 at S-L is 0.1×(1116 ft/s)/(1.688 ft/s per knot) or 66.1 KTAS. To convert this to KCAS use Equation (16-33). Do this for a range of altitudes and Mach numbers ranging from 0.1 to 0.9 as shown.
19.2.12 Power Required
If we know the lift and drag coefficient associated with a specific flight condition, then it is possible to calculate the power required for level flight at that condition. This can be determined using the expression below:
![]() (19-29)
(19-29)
In the UK system, the resulting value can be converted to BHP by a division by 550. In the SI system the units are in watts or joules/second. Note that by inspection it can be seen that the power required to propel the aircraft at a given flight condition (specified through CL and CD) is:
![]() (19-30)
(19-30)
So the smaller this ratio, the less is the power required to maintain level flight. When this ratio becomes a minimum the airspeed of minimum power required has been achieved, but this is also the maximum of the ratio ![]() . This can be calculated from Equation (19-11) and explains why this represents the condition for minimum power required or max endurance for a propeller-powered airplane.
. This can be calculated from Equation (19-11) and explains why this represents the condition for minimum power required or max endurance for a propeller-powered airplane.
19.2.13 Power Available for a Piston-powered Aircraft
If the power generated by piston engine and propeller efficiency is known, the power available for propulsion is defined using the expression below:
![]() (19-31)
(19-31)
Note that ηp is the propeller efficiency and it is a function of the airspeed, RPM, and propeller geometry. Refer to Chapter 14, The anatomy of the propeller, for more information.
19.2.14 Computer code: Determining Maximum Level Airspeed, Vmax, for a Propeller Aircraft
The following Visual Basic for Applications functions are used to determine Vmax for a propeller-powered aircraft by solving Equation (19-27) using the bisection method (see Article E.6.20 STEP-BY-STEP: Finding roots using the bisection method). Both functions must be used, as the first one calls the second one. Note that as long as the value under the radical of Equation (19-27) is greater than zero, a solution is possible. The arguments are explained in the comment section of the code. Also note that the routine calculates the density (rho) by calling the routine AtmosProperty (see Article A.2.10, Computer code A-1: Atmospheric modeling) using the argument H. This line can easily be replaced with Equation (16-18).
19.2.15 Computer code: Determining Maximum Level Airspeed, Vmax, for a Jet
The following Visual Basic for Applications routine can be used to determine Vmax based on Equation (19-25).
19.3 General Analysis Methods for Accelerated Flight
The previous section developed analysis methods for aircraft in steady level flight. In this section we will introduce a number of common analysis methods intended to evaluate a number of maneuvers that involve accelerated flight. Such maneuvers include turning flight, pull-up (loop), and accelerated rate-of-climb. All utilize the simplified drag model.
19.3.1 Analysis of a General Level Constant-velocity Turn
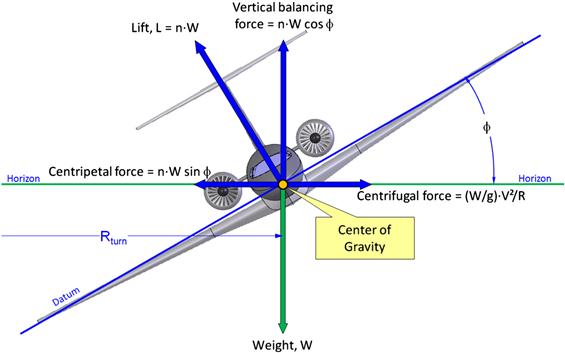
Consider the aircraft in Figure 19-26, which is banking at an angle ϕ. In order for the airplane to maintain altitude (no slipping or skidding) its lift must balance the weight while generating a centripetal force component that balances the centrifugal force component. The resulting motion renders a steady heading change. This requires the magnitude of the lift to be larger than the weight of the aircraft (otherwise the airplane will lose altitude). Consequently, the airframe is loaded up beyond what would happen in level flight and this additional loading is represented in the load factor, defined as n = L/W. The set of equations describing the motion of the airplane in this condition is written as follows:
The level constant velocity turn can be analyzed using the following set of equations:
The load factor that can be sustained at a given thrust, T, and airspeed, V, can be obtained as shown below. Note that inserting the maximum thrust will yield the maximum load factor at a given airspeed:
![]() (19-41)
(19-41)
This expression is used to plot a part of the banking constraint diagram of Figure 19-27.

FIGURE 19-27 A banking constraint diagram for the SR22. The maximum stall load factor is calculated by solving Equation (19-8) for the load factor. The maximum banking load factor is calculated using Equation (19-41).
A common way to present the turn performance of an aircraft can be seen in the banking constraint diagram of Figure 19-27 and the turn performance map of Figure 19-28. Both present a convenient way to show the banking capability of an aircraft. First, consider the banking constraint diagram of Figure 19-27, here based on the SR22 sample aircraft. The straight dashed horizontal line shows the limit load factor of 3.8g. The two vertical dashed lines show the clean stalling speed at normal 1g loading (VS, to the left) and the normal operating speed (VNO, to the right). These two lines effectively enclose the normal speed range of the aircraft. The solid curve, labeled “Max stall load factor,” shows the stalling speed of the aircraft at various load factors. Thus, it can be seen that at a load factor of 3g, the airplane will stall at about 120 KCAS. This curve is a part of the standard V-n diagram. The dotted curve, labeled “Max banking load factor,” shows the maximum gs the aircraft can bank at while maintaining altitude. It can be seen that between VS and 120 KCAS, the airplane will simply stall before achieving its maximum “theoretical” banking load factor. Thus, at 100 KCAS, if the airplane didn’t stall first (at n ≈ 2.1g) it could achieve n = 2.1g before it would begin to lose altitude. At airspeeds beyond 120 KCAS, the airplane cannot achieve 3.8g (its limit load factor) while maintaining altitude. This means that when flight testing the aircraft for structural flight tests (e.g. per 14 CFR 23.307, Proof of structure), means other than constant-altitude banking may have to be considered. Conversely, for some other aircraft, it might reveal the aircraft can indeed exceed the limit load factor in some airspeed range.
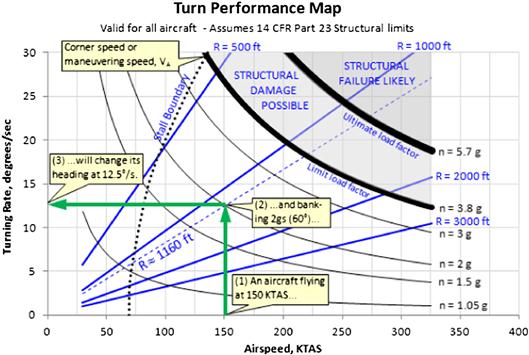
FIGURE 19-28 A turn performance map is constructed using Equation (19-39).
The turn performance map of Figure 19-28 is a cross-plot of Equation (19-39). It is generated by plotting curves for constant turn radius (the straight lines) and then for constant load factors (the curves). Since the equation does not involve any variables dependent on particular aircraft geometry, it is valid for all aircraft, although Figure 19-28 has been drawn up for aircraft that comply with 14 CFR Part 23 (and the stall boundary varies from airplane to airplane). The map shows how rapidly an aircraft can maneuver at specific airspeeds. The maneuvering speed is where the stall boundary intersects the curve for the limit load factor. It is also called the corner speed and is the lowest airspeed where the airplane achieves its maximum bank angle, most rapid heading change, and minimum turning radius.
Derivation of Equation (19-35)
Load factor n is defined as n = L/W. From Figure 19-26 we readily see that:
![]()
QED
Derivation of Equation (19-37)
Centrifugal force corresponding to the force diagram in Figure 19-26 can be found from the standard curvilinear relation mV2/R:
![]()
Manipulating algebraically leads to:
![]()
QED
Derivation of Equation (19-38)
The distance the airplane covers in the turn at an airspeed V in time tψ is equal to the standard arc length of a circle of radius Rturn through the angle ψ. In other words:
![]()
By solving for tψ in the above expression and noting the angle to be used must be in radians (note the conversion factor π/180) we get the expression for the time to turn.
QED
Derivation of Equation (19-39)
Turn rate is the change in heading with respect to time and can be written as follows:
![]()
QED
Derivation of Equation (19-40)
The level constant-velocity turn requires thrust to equal the drag of the airplane in the turn, in other words (assuming the simplified drag model):
![]()
Since elevator is required to trim the airplane in the turn, the increase in trim (trim drag) should be considered if it is significant. This term, Dtrim, is shown in Equation (19-40).
QED
Derivation of Equation (19-41)
First note that, typically, Dtrim is around 1–2% of the total drag of the airplane and, thus, ignoring it will yield acceptable accuracy. Use Equation (19-40), assuming Dtrim = 0 and solve for the load factor, n.
![]()
Then, assuming a given thrust, T, the maximum load factor can be determined.
QED
19.3.2 Extremes of Constant-velocity Turns
Maximum Sustainable Load Factor, nmax
The maximum load factor that the aircraft can sustain without stalling is obtained from Equation (19-36) when the thrust-to-weight and lift-to-drag ratios are at their maximum values:
Maximum Sustainable Turn Rate, ψ˙max
The maximum turn rate is a very important indicator of an airplane’s maneuverability. A large T/W and AR·e combined with a low W/S and altitude yield the smallest turning radius. This is the fastest heading change the airplane can perform and is given by the following relation:
![]() (19-44)
(19-44)
where ![]() = fastest turn velocity, given by Equation (19-15), repeated below for convenience.
= fastest turn velocity, given by Equation (19-15), repeated below for convenience.
![]() (19-15)
(19-15)
A derivation of this result is given by Asselin [10].
Minimum Sustainable Turning Radius
The minimum sustainable turning radius is another important indicator of an airplane’s maneuverability. A large T/W and AR·e combined with a low W/S and altitude yield the smallest turning radius. It can be calculated from the following relation:
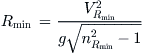 (19-45)
(19-45)
where ![]() = load factor for minimum turning radius
= load factor for minimum turning radius
A derivation of this result is given by Asselin [10].
Maximum Bank Angle
This is the maximum angle the aircraft can bank while maintaining altitude (provided it has enough power or thrust) and sustain the limit load factor it has been designed to. It can simply be determined using Equation (19-35) with nlim being the limit load factor:
Airspeed for Maximum Bank Angle
Using the simplified drag model, the airspeed required to reach the limit load factor for a given thrust setting is given by the following expression:
 (19-47)
(19-47)
The expression will return two airspeeds, one for each sign. These represent low- and high-speed conditions.
19.3.3 Energy State
Energy Height
The total energy of the airplane whose mass and weight are given by m and W, respectively, flying at an altitude h and airspeed V is a linear combination of its potential and kinetic energy and can be computed from:
![]() (19-48)
(19-48)
Specific Energy and Energy Height
The specific energy is defined as the total energy per unit weight and can be computed as follows:
![]() (19-49)
(19-49)
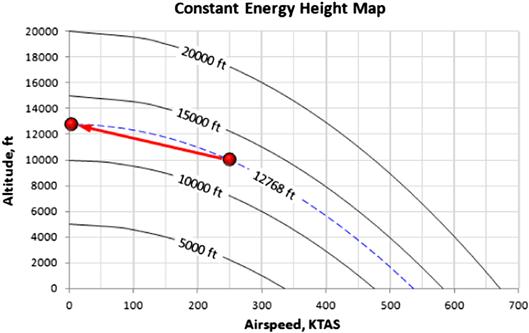
Since the units of specific energy are that of height (ft or m) it is also called energy height. This concept highlights that the maneuvering of an airplane can be considered an exchange of potential and kinetic energy. To explain what this means, consider an airplane cruising at an altitude of 10,000 ft at airspeed of 236 KTAS (400 ft/s) as shown in Figure 19-29. Its specific energy is then 10,000+4002/(2·32.174) = 12,768 ft. This means that if the pilot exchanged all the kinetic energy into potential energy, by raising the nose of the aircraft and allowing it to climb until the airspeed drains to zero (this is a maneuver called zooming), the airplane would reach an altitude of 12,768 ft.
The graph of Figure 19-29 is called a constant energy height map. It consists of isobars of constant energy height that extend from the vertical to the horizontal axis. The airspeed at any altitude can be calculated for a given energy height by solving for the airspeed in Equation (19-49) as follows:
![]() (19-50)
(19-50)
Equation (19-50) was used to create the constant energy height map of Figure 19-29. The figure shows isobars for energy heights (HE) of 5000, 10,000, 15,000, and 20,000 ft, with the one of 12,768 ft shown as a dashed line. Furthermore, the exchange from the initial altitude of 10,000 ft and 250 KTAS to 12768 and 0 KTAS is shown as well. The plot applies to all aircraft, regardless of weight. A more type-dependent representation is obtained by determining and plotting the specific excess power contour plots (see below).
Specific Excess Power
Just as the specific energy was defined as the total energy per unit weight, we also define specific excess power as the excess power (per Equation (18-15)):
![]() (19-51)
(19-51)
The specific excess power can also be written as follows:
![]() (19-52)
(19-52)
The expression shows that the specific excess power of an airplane is the combination of its rate-of-climb (dh/dt) and forward acceleration (V/g·dV/dt). Thus, if dV/dt = 0 (steady state), the specific excess power is simply the ROC of the airplane. Likewise, if dh/dt = 0, the specific excess power is simply its acceleration. An inspection of Equation (19-49) reveals its time derivative equals the specific excess power, that is:
![]() (19-53)
(19-53)
In short, the specific excess power is the time rate of change of the energy height.
![]() (19-54)
(19-54)
Derivation of Equation (19-52)
Begin with the dynamic version of the equations of motion, i.e. Equation (18-2), repeated here for convenience (assuming the thrust angle ε = 0):
![]() (18-2)
(18-2)
Noticing that Vsinθ = rate-of-climb = dh/dt we can rewrite Equation (ii) as follows:
![]() (19-52)
(19-52)
QED
Constructing a Specific Excess Power Contour Plot
A specific excess power contour plot is used to demonstrate the maneuvering capability of the aircraft throughout its operational airspeed and altitude range. An example of such a contour plot is shown as the lower graph of Figure 19-30. It is typically constructed using the plot of rate-of-climb for a range of altitudes, as shown in the upper graph of Figure 19-30. Thus, the PS contour for zero ROC (PS = 0 ft/s, which represents the minimum and maximum airspeed) is constructed by transferring the points labeled a through i to the lower graph. The PS contour for the PS = 10 ft/s (an ROC of 600 fpm) is constructed in a similar manner, by transferring the points along the line A–A to the lower graph. And the PS contour for the PS = 20 ft/s (an ROC of 1200 fpm) is constructed by transferring the points along the line B–B to the lower graph.
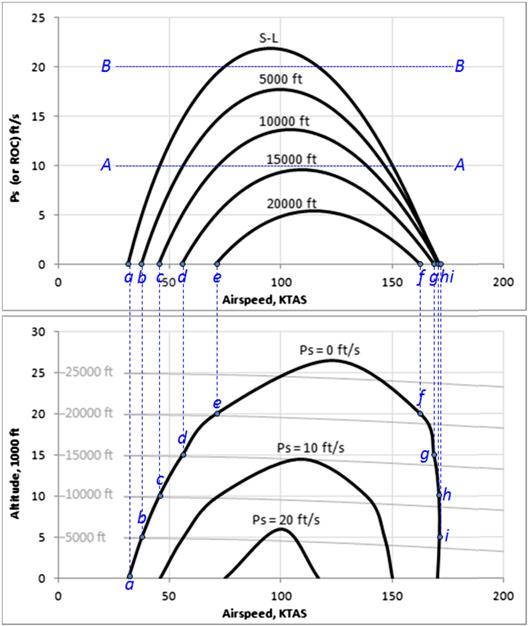
FIGURE 19-30 Constructing a specific excess power contour plot for an SR22 class aircraft. The light-colored curves (labeled 5000 ft through 25000 ft) are the constant energy height isobars plotted in Figure 19-29.
References
1. Perkins CD, Hage RE. Airplane Performance, Stability, and Control. John Wiley & Sons 1949.
2. Torenbeek E. Synthesis of Subsonic Aircraft Design. 3rd edn Delft University Press 1986.
3. Nicolai L. Fundamentals of Aircraft Design. 2nd edn 1984.
4. Roskam J, Lan Chuan-Tau Edward. Airplane Aerodynamics and Performance. DARcorporation 1997.
5. Hale FJ. Aircraft Performance, Selection, and Design. John Wiley & Sons 1984; 137–138.
6. Anderson Jr JD. Aircraft Performance & Design. 1st edn McGraw-Hill 1998.
7. AIAA-80-1847. Fuel Efficiency of Small Aircraft. Carson, B.H., AIAA 1980.
8. Gabrielli G, von Kármán T. What price speed? Specific power required for propulsion of vehicles. Mechanical Engineering. 1950;72(10):775–781.
9. Smith, H.C. An Application of the Carson Cruise Optimum Airspeed – A Compromise Between Speed and Efficiency. SAE SP-621, Paper 850867, p. 95.
10. Asselin M. An Introduction to Aircraft Performance. AIAA Education Series 1997.