2.1 Time

Reasoning about concurrent computation is mostly reasoning about time. Sometimes we want things to happen simultaneously, and sometimes we want them to happen at different times. We need to reason about complicated conditions involving how multiple time intervals can overlap, or, sometimes, how they cannot. We need a simple but unambiguous language to talk about events and durations in time. Everyday English is too ambiguous and imprecise. Instead, we introduce a simple vocabulary and notation to describe how concurrent threads behave in time.

In 1689, Isaac Newton stated “absolute, true and mathematical time, of itself and from its own nature, flows equably without relation to anything external.” We endorse his notion of time, if not his prose style. Threads share a common time (though not necessarily a common clock). A thread is a state machine, and its state transitions are called events.

Events are instantaneous: they occur at a single instant of time. It is convenient to require that events are never simultaneous: distinct events occur at distinct times. (As a practical matter, if we are unsure about the order of two events that happen very close in time, then any order will do.) A thread A produces a sequence of events a₀, a₁, … Threads typically contain loops, so a single program statement can produce many events. We denote the j-th occurrence of an event a_i by . One event a precedes another event b, written a → b, if a occurs at an earlier time. The precedence relation “→” is a total order on events.

Let a₀ and a₁ be events such that a₀ → a₁. An interval (a₀, a₁) is the duration between a₀ and a₁. Interval I_A = (a₀, a₁) precedes I_B = (b₀, b₁), written I_A → I_B, if a₁ → b₀ (that is, if the final event of I_A precedes the starting event of I_B). More succinctly, the → relation is a partial order on intervals. Intervals that are unrelated by → are said to be concurrent. By analogy with events, we denote the j-th execution of interval I_A by .

2.2 Critical Sections

In an earlier chapter, we discussed the Counter class implementation shown in Fig. 2.1. We observed that this implementation is correct in a single-thread system, but misbehaves when used by two or more threads. The problem occurs if both threads read the value field at the line marked “start of danger zone,” and then both update that field at the line marked “end of danger zone.”

Figure 2.1 The Counter class.

We can avoid this problem if we transform these two lines into a critical section: a block of code that can be executed by only one thread at a time. We call this property mutual exclusion. The standard way to approach mutual exclusion is through a Lock object satisfying the interface shown in Fig. 2.2.

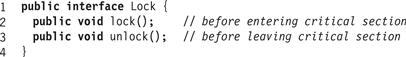
Figure 2.2 The Lock interface.

For brevity, we say a thread acquires (alternately locks) a lock when it executes a lock() method call, and releases (alternately unlocks) the lock when it executes an unlock() method call. Fig. 2.3 shows how to use a Lock field to add mutual exclusion to a shared counter implementation. Threads using the lock() and unlock() methods must follow a specific format. A thread is well formed if:

Figure 2.3 Using a lock object.

We now formalize the properties that a good Lock algorithm should satisfy. Let be the interval during which A executes the critical section for the j-th time. Let us assume, for simplicity, that each thread repeatedly acquires and releases the lock, with other work taking place in the meantime.

Note that starvation freedom implies deadlock freedom.

The mutual exclusion property is clearly essential. Without this property, we cannot guarantee that a computation’s results are correct. In the terminology of Chapter 1, mutual exclusion is a safety property. The deadlock-freedom property is important. It implies that the system never “freezes.” Individual threads may be stuck forever (called starvation), but some thread makes progress. In the terminology of Chapter 1, deadlock-freedom is a liveness property. Note that a program can still deadlock even if each of the locks it uses satisfies the deadlock-freedom property. For example, consider threads A and B that share locks ₀ and ₁. First, A acquires ₀ and B acquires ₁. Next, A tries to acquire ₁ and B tries to acquire ₀. The threads deadlock because each one waits for the other to release its lock.

The starvation-freedom property, while clearly desirable, is the least compelling of the three. Later on, we will see practical mutual exclusion algorithms that fail to be starvation-free. These algorithms are typically deployed in circumstances where starvation is a theoretical possibility, but is unlikely to occur in practice. Nevertheless, the ability to reason about starvation is essential for understanding whether it is a realistic threat.

The starvation-freedom property is also weak in the sense that there is no guarantee for how long a thread waits before it enters the critical section. Later on, we will look at algorithms that place bounds on how long a thread can wait.

2.3 2-Thread Solutions

We begin with two inadequate but interesting Lock algorithms.

2.4 The Filter Lock

We now consider two mutual exclusion protocols that work for n threads, where n is greater than 2. The first solution, the Filter lock, is a direct generalization of the Peterson lock to multiple threads. The second solution, the Bakery lock, is perhaps the simplest and best known n-thread solution.

The Filter lock, shown in Fig. 2.7, creates n − 1 “waiting rooms,” called levels, that a thread must traverse before acquiring the lock. The levels are depicted in Fig. 2.8. Levels satisfy two important properties:

Figure 2.7 The Filter lock algorithm.

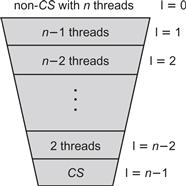
Figure 2.8 There are n − 1 levels threads pass through, the last of which is the critical section. There are at most n threads that pass concurrently into level 0, n − 1 into level 1 (a thread in level 1 is already in level 0), n − 2 into level 2 and so on, so that only one enters the critical section at level n − 1.

The Peterson lock uses a two-element boolean flag array to indicate whether a thread is trying to enter the critical section. The Filter lock generalizes this notion with an n-element integer level[] array, where the value of level[A] indicates the highest level that thread A is trying to enter. Each thread must pass through n − 1 levels of “exclusion” to enter its critical section. Each level has a distinct victim[] field used to “filter out” one thread, excluding it from the next level.

Initially a thread A is at level 0. We say that A is at level j for j > 0, when it last completes the waiting loop in Line 17 with level[A] ≥ j. (So a thread at level j is also at level j − 1, and so on.)

Entering the critical section is equivalent to entering level n − 1.

2.5 Fairness

The starvation-freedom property guarantees that every thread that calls lock() eventually enters the critical section, but it makes no guarantees about how long this may take. Ideally (and very informally) if A calls lock() before B, then A should enter the critical section before B. Unfortunately, using the tools at hand we cannot determine which thread called lock() first. Instead, we split the lock() method into two sections of code (with corresponding execution intervals):

The requirement that the doorway section always finish in a bounded number of steps is a strong requirement. We will call this requirement the bounded wait-free progress property. We discuss systematic ways of providing this property in later chapters.

Here is how we define fairness.

2.6 Lamport’s Bakery Algorithm

The Bakery lock algorithm appears in Fig. 2.9. It maintains the first-come-first-served property by using a distributed version of the number-dispensing machines often found in bakeries: each thread takes a number in the doorway, and then waits until no thread with an earlier number is trying to enter it.

Figure 2.9 The Bakery lock algorithm.

In the Bakery lock, flag[A] is a Boolean flag indicating whether A wants to enter the critical section, and label[A] is an integer that indicates the thread’s relative order when entering the bakery, for each thread A.

Each time a thread acquires a lock, it generates a new label[] in two steps. First, it reads all the other threads' labels in any order. Second, it reads all the other threads' labels one after the other (this can be done in some arbitrary order) and generates a label greater by one than the maximal label it read. We call the code from the raising of the flag (Line 13) to the writing of the new label[] (Line 14) the doorway. It establishes that thread’s order with respect to the other threads trying to acquire the lock. If two threads execute their doorways concurrently, they may read the same maximal label and pick the same new label. To break this symmetry, the algorithm uses a lexicographical ordering << on pairs of label[] and thread ids:

(2.6.13)

In the waiting part of the Bakery algorithm (Line 15), a thread repeatedly rereads the labels one after the other in some arbitrary order until it determines that no thread with a raised flag has a lexicographically smaller label/id pair.

Since releasing a lock does not reset the label[], it is easy to see that each thread’s labels are strictly increasing. Interestingly, in both the doorway and waiting sections, threads read the labels asynchronously and in an arbitrary order, so that the set of labels seen prior to picking a new one may have never existed in memory at the same time. Nevertheless, the algorithm works.

Note that any algorithm that is both deadlock-free and first-come-first-served is also starvation-free.

2.7 Bounded Timestamps

Notice that the labels of the Bakery lock grow without bound, so in a long-lived system we may have to worry about overflow. If a thread’s label field silently rolls over from a large number to zero, then the first-come-first-served property no longer holds.

Later on, we will see constructions where counters are used to order threads, or even to produce unique identifiers. How important is the overflow problem in the real world? It is difficult to generalize. Sometimes it matters a great deal. The celebrated “Y2K” bug that captivated the media in the last years of the twentieth century is an example of a genuine overflow problem, even if the consequences were not as dire as predicted. On January 18, 2038, the Unix time_t data structure will overflow when the number of seconds since January 1, 1970 exceeds 2³². No one knows whether it will matter. Sometimes, of course, counter overflow is a nonissue. Most applications that use, say, a 64-bit counter are unlikely to last long enough for roll-over to occur. (Let the grandchildren worry!)

In the Bakery lock, labels act as timestamps: they establish an order among the contending threads. Informally, we need to ensure that if one thread takes a label after another, then the latter has the larger label. Inspecting the code for the Bakery lock, we see that a thread needs two abilities:

A Java interface to such a timestamping system appears in Fig. 2.10. Since our principal application for a bounded timestamping system is to implement the doorway section of the Lock class, the timestamping system must be wait-free. It is possible to construct such a wait-free concurrent timestamping system (see the chapter notes), but the construction is long and rather technical. Instead, we focus on a simpler problem, interesting in its own right: constructing a sequential timestamping system, in which threads perform scan-and-label operations one completely after the other, that is, as if each were performed using mutual exclusion. In other words, consider only executions in which a thread can perform a scan of the other threads' labels, or a scan, and then an assignment of a new label, where each such sequence is a single atomic step. The principles underlying a concurrent and sequential timestamping systems are essentially the same, but they differ substantially in detail.

Figure 2.10 A timestamping system interface.

Think of the range of possible timestamps as nodes of a directed graph (called a precedence graph). An edge from node a to node b means that a is a later time-stamp than b. The timestamp order is irreflexive: there is no edge from any node a to itself. The order is also antisymmetric: if there is an edge from a to b, then there is no edge from b to a. Notice that we do not require that the order be transitive: there can be an edge from a to b and from b to c, without necessarily implying there is an edge from a to c.

Think of assigning a timestamp to a thread as placing that thread’s token on that timestamp’s node. A thread performs a scan by locating the other threads' tokens, and it assigns itself a new timestamp by moving its own token to a node a such that there is an edge from a to every other thread’s node.

Pragmatically, we would implement such a system as an array of single-writer multi-reader fields, where array element A represents the graph node where thread A most recently placed its token. The scan() method takes a “snapshot” of the array, and the label() method for thread A updates the A-th array element.

Fig. 2.11 illustrates the precedence graph for the unbounded timestamp system used in the Bakery lock. Not surprisingly, the graph is infinite: there is one node for each natural number, with a directed edge from node a to node b whenever a > b.

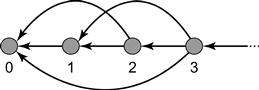
Figure 2.11 The precedence graph for an unbounded timestamping system. The nodes represent the set of all natural numbers and the edges represent the total order among them.

Consider the precedence graph T² shown in Fig. 2.12. This graph has three nodes, labeled 0, 1, and 2, and its edges define an ordering relation on the nodes in which 0 is less than 1, 1 is less than 2, and 2 is less than 0. If there are only two threads, then we can use this graph to define a bounded (sequential) timestamping system. The system satisfies the following invariant: the two threads always have tokens located on adjacent nodes, with the direction of the edge indicating their relative order. Suppose A’s token is on Node 0, and B’s token on Node 1 (so B has the later timestamp). For B, the label() method is trivial: it already has the latest timestamp, so it does nothing. For A, the label() method “leapfrogs” B’s node by jumping from 0 to 2.

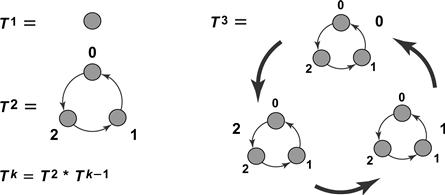
Figure 2.12 The precedence graph for a bounded timestamping system. Consider an initial situation in which there is a token A on Node 12 (Node 2 in subgraph 1) and tokens B and C on Nodes 21 and 22 (Nodes 1 and 2 in subgraph 2) respectively. Token B will move to 20 to dominate the others. Token C will then move to 21 to dominate the others, and B and C can continue to cycle in the T² subgraph 2 forever. If A is to move to dominate B and C, it cannot pick a node in subgraph 2 since it is full (any T^k subgraph can accommodate at most k tokens). Instead, token A moves to Node 00. If B now moves, it will choose Node 01, C will choose 10 and so on.

Recall that a cycle¹ in a directed graph is a set of nodes n₀, n₁, …, n_k such that there is an edge from n₀ to n₁, from n₁ to n₂, and eventually from n_{k − 1} to n_k, and back from n_k to n₀.

The only cycle in the graph T² has length three, and there are only two threads, so the order among the threads is never ambiguous. To go beyond two threads, we need additional conceptual tools. Let G be a precedence graph, and A and B subgraphs of G (possibly single nodes). We say that A dominates B in G if every node of A has edges directed to every node of B. Let graph multiplication be the following noncommutative composition operator for graphs (denoted G H):

Replace every node v of G by a copy of H (denoted H_v), and let H_v dominate H_u in G H if v dominates u in G.

Define the graph T^k inductively to be:

For example, the graph T³ is illustrated in Fig. 2.12.

The precedence graph Tⁿ is the basis for an n-thread bounded sequential timestamping system. We can “address” any node in the Tⁿ graph with n − 1 digits, using ternary notation. For example, the nodes in graph T² are addressed by 0, 1, and 2. The nodes in graph T³ are denoted by 00, 01, …, 22, where the high-order digit indicates one of the three subgraphs, and the low-order digit indicates one node within that subgraph.

The key to understanding the n-thread labeling algorithm is that the nodes covered by tokens can never form a cycle. As mentioned, two threads can never form a cycle on T², because the shortest cycle in T² requires three nodes.

How does the label() method work for three threads? When A calls label(), if both the other threads have tokens on the same T² subgraph, then move to a node on the next highest T² subgraph, the one whose nodes dominate that T² subgraph. For example, consider the graph T³ as illustrated in Fig. 2.12. We assume an initial acyclic situation in which there is a token A on Node 12 (Node 2 in subgraph 1) and tokens B and C, respectively, on Nodes 21 and 22 (Nodes 1 and 2 in subgraph 2). Token B will move to 20 to dominate all others. Token C will then move to 21 to dominate all others, and B and C can continue to cycle in the T² subgraph 2 forever. If A is to move to dominate B and C, it cannot pick a node in subgraph 2 since it is full (any T^k subgraph can accommodate at most k tokens). Token A thus moves to Node 00. If B now moves, it will choose Node 01, C will choose 10 and so on.

2.8 Lower Bounds on the Number of Locations

The Bakery lock is succinct, elegant, and fair. So why is it not considered practical? The principal drawback is the need to read and write n distinct locations, where n (which may be very large) is the maximum number of concurrent threads.

Is there a clever Lock algorithm based on reading and writing memory that avoids this overhead? We now demonstrate that the answer is no. Any deadlock-free Lock algorithm requires allocating and then reading or writing at least n distinct locations in the worst case. This result is crucially important, because it motivates us to add to our multiprocessor machines, synchronization operations stronger than read-write, and use them as the basis of our mutual exclusion algorithms.

In this section, we observe why this linear bound is inherent before we discuss practical mutual exclusion algorithms in later chapters. We will observe the following important limitation of memory locations accessed solely by read or write instructions (in practice these are called loads and stores): any information written by a thread to a given location could be overwritten (stored-to) without any other thread ever seeing it.

Our proof requires us to argue about the state of all memory used by a given multithreaded program. An object’s state is just the state of its fields. A thread’s local state is the state of its program counters and local variables. A global state or system state is the state of all objects, plus the local states of the threads.

Any Lock algorithm that solves deadlock-free mutual exclusion must have n distinct locations. Here, we consider only the 3-thread case, showing that a deadlock-free Lock algorithm accessed by three threads must use three distinct locations.

In a covering state, we say that each thread covers the location it is about to write.

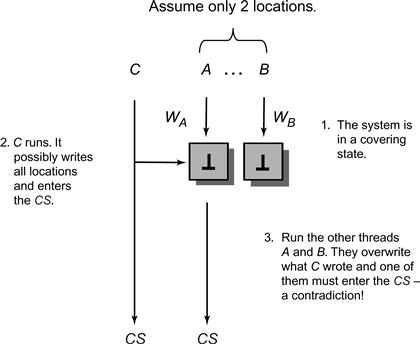
Figure 2.13 Contradiction using a covering state for two locations. Initially both locations have the empty value ⊥.

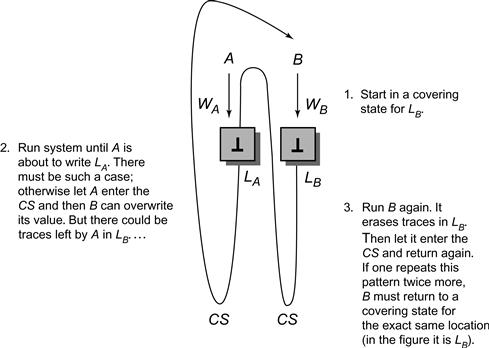
Figure 2.14 Reaching a covering state. In the initial covering state for L_B both locations have the empty value ⊥.

The same line of argument can be extended to show that n-thread deadlock-free mutual exclusion requires n distinct locations. The Peterson and Bakery locks are thus optimal (within a constant factor). However, as we note, the need to allocate n locations per Lock makes them impractical.

This proof shows the inherent limitation of read and write operations: information written by a thread may be overwritten without any other thread ever reading it. We will remember this limitation when we move on to design other algorithms.

In later chapters, we will see that modern machine architectures provide specialized instructions that overcome the “overwriting” limitation of read and write instructions, allowing n-thread Lock implementations that use only a constant number of memory locations. We will also see that making effective use of these instructions to solve mutual exclusion is far from trivial.

2.9 Chapter Notes

Isaac Newton’s ideas about the flow of time appear in his famous Principia [121]. The “→” formalism is due to Leslie Lamport [89]. The first three algorithms in this chapter are due to Gary Peterson, who published them in a two-page paper in 1981 [124]. The Bakery lock presented here is a simplification of the original Bakery Algorithm due to Leslie Lamport [88]. The sequential time-stamp algorithm is due to Amos Israeli and Ming Li [77], who invented the notion of a bounded timestamping system. Danny Dolev and Nir Shavit [34] invented the first bounded concurrent timestamping system. Other bounded timestamping schemes include Sibsankar Haldar and Paul Vitányi [51], and Cynthia Dwork and Orli Waarts [37]. The lower bound on the number of lock fields is due to Jim Burns and Nancy Lynch [23]. Their proof technique, called a covering argument, has since been widely used to prove lower bounds in distributed computing. Readers interested in further reading can find a historical survey of mutual exclusion algorithms in a classic book by Michel Raynal [131].