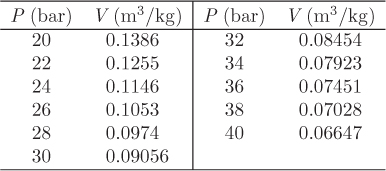
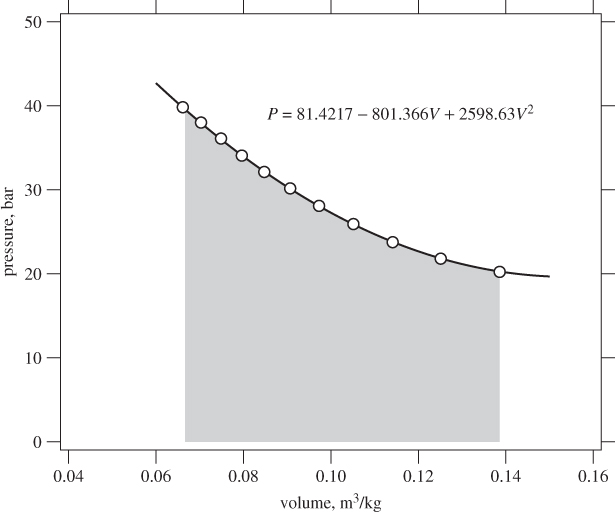
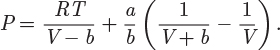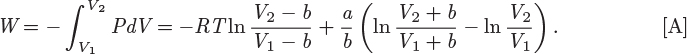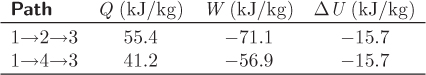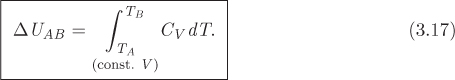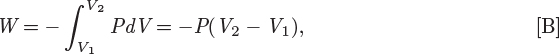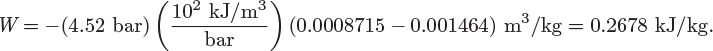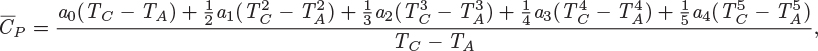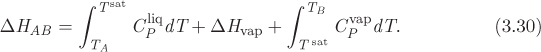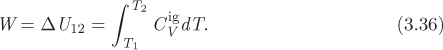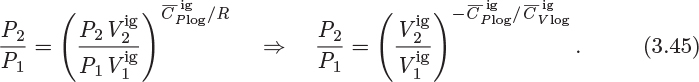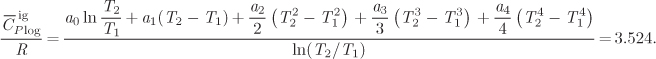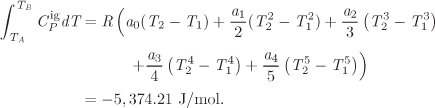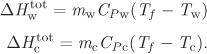Chapter 3. Energy and the First Law
A classical mechanical system is characterized by a set of mechanical state variables: velocity, elevation in a gravitational field, electrical charges, and so forth. If these variables are given and the external fields are known, the system is fully specified and its behavior at any instant of time, past or future, can be calculated. Thermodynamic systems are characterized by an additional state variable: temperature. Unlike mechanical variables, which describe external interactions, temperature characterizes the internal state of macroscopic matter. Temperature is a measure of the energy stored inside matter in various forms, which we collectively call internal energy. Temperature gives rise to another type of energy exchange that is not encountered among purely mechanical systems, heat: when two systems, each at its own temperature, are put into thermal contact, energy in the form of heat flows from the higher temperature to the lower temperature. For the complete energy balance, heat and internal energy must both be accounted for.
The incorporation of heat effects into the energy balance constitutes one of the fundamental principles of thermodynamics known as the first law. This chapter is devoted to the mathematical formulation of the first law and in the definition of two thermodynamic properties, internal energy and enthalpy, both of which are important in the calculation of energy balances.
Instructional Objectives In this chapter we will formulate the mathematical statement of the first law for a closed system and will learn how to:
1. Do energy balances in closed systems.
2. Distinguish between path and state functions.
3. Use the steam tables to calculate internal energy and enthalpy.
4. Use heat capacities to calculate changes in internal energy and enthalpy.
5. Apply the energy balance to systems undergoing vaporization or condensation.
6. Perform calculations of internal energy and enthalpy in the ideal-gas state.
3.1 Energy and Mechanical Work
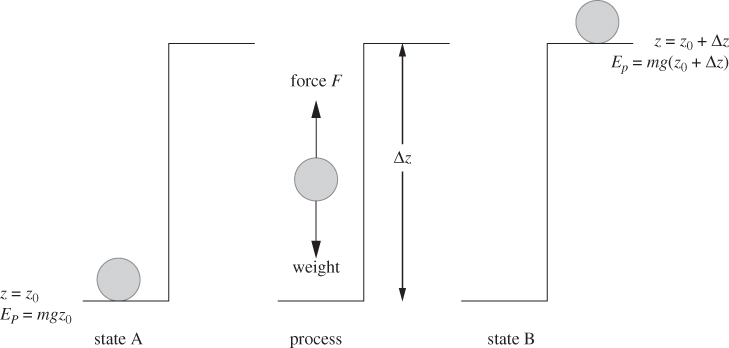
Heat, work and energy are measured in the same units but they represent different physical entities. We begin with work and energy, which are familiar concepts from mechanics. Energy is the ability of a system to produce work, namely, ability to cause the displacement of a force. Consider an object with mass m resting on the floor (Figure 3-1). To lift it to the top of the table at height Δz above ground, we must supply an amount of work equal to W = mgΔz. When the mass is resting on the desk, its potential energy has increased by ΔEp = mgΔz, and the work done to lift the object is now part of the energy of the body and is stored as potential energy. The energy added to the system will stay with it for as long it remains at rest on the table. This could be hours, days, or millennia: potential energy is preserved for as long as the state of the system, in this case elevation, is preserved. The more general conclusion to be drawn from this analysis is that energy is a property of the state and as such, a storable quantity. We can recover it by letting the mass drop to the floor and use its kinetic energy to, say, catapult a small projectile into the air, or to load a spring, or to push a nail into the floor.
Figure 3-1: Potential energy and mechanical work. From state A to state B the potential energy increases by the amount of work needed to lift the weight. This work must be supplied from the surroundings, that is, from a force external to the system.
Let us focus on work now. Work takes place when a force is displaced. If we lift the weight ourselves, this work is supplied through the action of our muscle. Once the object is placed on the table, there is no more displacement, thus no more work: work is exchanged during a process. It characterizes, not the state of the system, but the transition of the system between states (from the floor to the top of the desk). In thermodynamic terms, the picture illustrated in Figure 3-1 would be described as follows: A system initially in equilibrium state A undergoes a process that brings it to final state B; during this process the system exchanges work with the surroundings so that the energy change of the system is equal to the amount of work exchanged:
This equation reads, “as a result of the process, the energy of the system in state B has increased relative to A by the amount of work added.” Also notice that work represents energy that passes from one system into another. In this example, our muscle (chemical energy) transfers work to the lifted object, where it is converted into potential energy. As a transfer quantity, work is characterized by a direction, “from” (the muscle) “to” (the system). Finally, when work passes into a new system, it is converted into some form of energy (in our example, potential), which now is property of the state. Let us summarize:
• Energy is storable; it remains in the system for as long as the state of the system is preserved. It is a state function.
• Work is energy in transit: it appears when energy is passed from one system into another.
• Work is not a storable quantity as such.1 Work that enters a system must be stored in some form of energy.
1. By this we mean that it is incorrect to say that a system “stores work”; the proper statement is, the system “stores energy.”
• Work is associated with a direction “from” one system in which it originates, “to” another, where it is transferred to.
To indicate the direction of the transfer we adopt a sign convention:
When the surroundings do the work, the work is positive because it is absorbed by the system. When the work is negative, it is done by the system and absorbed by the surroundings. Clearly, the sign depends on the definition of the system since work that enters one system (the “system”) exits the other (the “surroundings”) and vice versa. To avoid ambiguity, the definition of the system must be made clear when we report positive or negative values of work.
Forms of Energy
As a matter of classification, energy comes in two basic forms, kinetic, and potential. Kinetic is energy stored in the motion of a moving object. Potential energy is a more general category and encompasses several forms that arise from various conservative forces, such as gravitational fields, electric charges, spring forces, and others. All forms of potential energy have the common characteristic that they are described by a potential function Φ(x, y, z) that depends on the space coordinates, x, y, z, and has the property that the force in a given direction is equal to the negative derivative of the potential with respect to the corresponding coordinate:
As an example, in the gravitational potential Φ(x, y, z) = mgz, the force (weight) in the z direction is
with the negative sign indicating that the weight points downwards. The forces in the x and y direction are both zero. The intermolecular potential introduced in Section 1.1 is another example of potential energy.
3.2 Shaft Work and PV Work
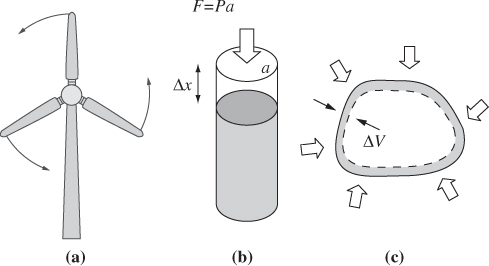
A direct method by which to exchange work with a fluid is through the use of a mechanical device. When wind blows through a turbine, it produces work that is manifested in the rotational motion of the turbine. A centrifugal pump imparts work to a fluid through the rotation of an impeller. This type of work is called shaft work. It will generally be recognizable through the presence of a rotating or reciprocating shaft that absorbs work from a fluid or imparts work to it.
Another more subtle form of work is associated with movement of the system boundaries. Thermodynamic systems make mechanical contact through the pressure that is exerted on the boundaries that separate them. At equilibrium, this pressure is equal on both sides of the boundary. If a pressure imbalance arises between the system and its surroundings, the boundaries of the system must move in response to the mechanical force. Such imbalance may arise from the application of a mechanical force that acts to compress or expand the system, or through the application of heat, which causes the volume to expand or contract. The movement of boundaries involves the exchange of work, which we call PV work.
To obtain an equation for the PV work, consider the compression of a gas in a cylinder fitted with a piston whose area is a (Fig. 3-2b). Compression is done through the application of an external pressure Pex, which produces a force on the piston, F = Pexa, and causes the piston to move by dx. The amount of work associated with this process is equal to the force on the piston, Pexa, multiplied by the displacement dx. Noting that the product adx is equal to the change of volume, −dV, the amount of work is
Figure 3-2: Examples of work: (a) shaft work (wind turbine); (b) PV work for compression/ expansion of a gas in a cylinder; (c) PV work associated with volume changes.
The negative sign is consistent with the convention adopted for work: in compression, dV is negative and the work is positive (it is added to the system); in expansion, dV is positive and the work is negative (work is transferred from the system to the surroundings).
Equation (3.2) gives the work in terms of the external pressure that causes the change. It is more convenient, however, to relate the work to the pressure of the system. For compression, the external pressure must be higher than the pressure of the system, P, which means, Pex = P + δP, where δP is a positive increment; for expansion, δP is negative. If the process is conducted in a quasi-static manner, then δP → 0 and Pex → P. Such process is called mechanically reversible and in this case the PV work is
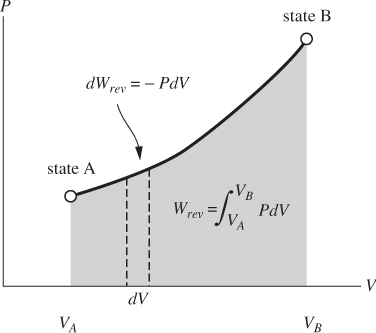
This is the differential amount of work along a small step of a process that causes a volume change. The total amount of work involved in taking the system from an initial state A to final state B along a reversible path is obtained by integration:
Figure 3-3: Graphical interpretation of reversible PV work.
This result is general and not limited to gases, nor to objects of cylindrical shape. It applies to any system, gas, liquid, or solid, whose volume changes by compression or expansion, under or against the opposing pressure of the surroundings. The only requirement is that the process must be mechanically reversible.
Reversible PV work has a simple graphical interpretation on the PV graph: it is equal in absolute value to the area under the path of the process when this is plotted on the PV graph (Figure 3-3). The sign indicates whether the work is added to or removed from the system. For a path that moves in the direction of increasing V, the area is by convention positive and the work is negative: the system expands and does work against the surroundings. For a process that moves in the direction of decreasing V (compression), the area is negative and the work is positive.
An important conclusion is that PV work depends on the entire path that connects the two states. Different paths between the same two states generally correspond to different areas, and thus different amounts of work. Therefore, the PV work is a path function whose value depends not only on the initial and final states, but on the entire path. This is in contrast to thermodynamic properties (state functions) whose value depends on the state alone.
3.3 Internal Energy and Heat
Molecules possess energy of various forms. All molecules possess kinetic energy due to the motion of the center of mass in space (translational kinetic energy). In addition to translational kinetic energy, polyatomic molecules possess rotational kinetic energy, manifested as motion relative to the center of mass, and vibrational energy, as motion of the constituent atoms relative to the equilibrium length of their chemical bonds. Molecules also possess potential energy as a result of interactions between different molecules as well as between atoms of the same molecule. These interactions can be loosely visualized as springs whose compression or extension requires energy.2 For our purposes it is not necessary to consider these molecular modes of energy storage in any detail. It suffices to say that matter, regardless of chemical composition or phase, is capable of storing energy internally. We refer to these combined storage modes as internal energy and we will use the symbol U. Like all forms of energy, internal energy is a state function and for a pure substance, it is a function of pressure and temperature.
2. To apply the spring analogy to intermolecular interactions we imagine the spring constant to be variable with distance: the intermolecular spring stiffens when highly compressed but becomes very soft when it is overextended.
The molecular nature of matter gives rise to a different type of energy transfer, heat. The mean kinetic energy of molecules in a hot substance is higher than that in a cold substance. The nature of molecular collisions is such, that when molecules with low kinetic energy are mixed with molecules of higher energy, energy is exchanged in a way that gives all molecules the same energy on average. The effect of collisions then is to spread the energy among molecules, much like the cue ball distributes its energy among all balls on a pool table. This process amounts to transferring energy from “hot” molecules to “cold” ones. Collisional transfer of energy does not require intimate mixing and it can take place when two solids are placed into contact, or when two fluids come into contact with a common solid wall. Molecules in the solid phase, though restricted in the range of their motion, move vigorously about their equilibrium position and collide with their neighbors, thus absorbing energy from higher-energy molecules and transferring it to those with lower energy. The rate of this transfer varies among materials, but this affects only how long it takes to reach equilibrium, not the final equilibrium itself. A thermal insulator, we may note here, is a material that offers a resistance to heat transfer so that the amount transferred over the duration of a typical application is negligibly small. Over time, however, heat will escape, even through an insulator, and thermal equilibrium will be established across all systems that are in contact with each other.
Heat shares some important characteristics with work:
1. It is a transient form of energy that is observed during a change of state (process); once the system is in equilibrium with its surroundings there is no net heat transfer because both system and surroundings are at the same temperature.3
3. On an instantaneous basis, individual collisions may transfer energy in either direction, from the system to the bath or the other way around, even at equilibrium. Overall, however, there is no net transfer between system and surroundings if the conditions of thermal equilibrium are met.
2. As a transient form, heat is not a storable mode of energy: once it enters a system, it is stored as internal energy. It is incorrect to say that a system “contains heat,” or to speak of energy that “is converted into heat.”
3. It has a direction, from the system to the surroundings, or vice versa.
4. It is a path function whose value is determined by the entire path of the process. This property of heat is not obvious at the moment but will become so in the next section.
3.4 First Law for a Closed System
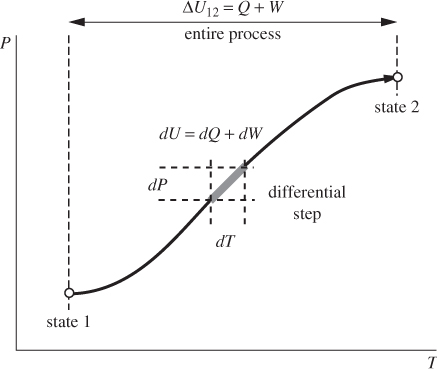
All material systems possess internal energy. They may possess various other forms of energy as well. In systems of interest to chemical engineers the most relevant forms are kinetic energy due to bulk motion (for example, a moving fluid in a pipe) and potential energy, due to changes in elevation (for example, a piping network that spans various elevations). Consider a closed system, originally at state A, undergoing a change of state to final state B, as shown in Figure 3-5. Changes of state invariably require the exchange of energy between the system and the surroundings. Such exchanges must be in the form of work (PV, shaft, or both) and/or heat. Suppose that the net amount of work that is exchanged during this process is W, and the net amount of heat is Q. The work W is the combined amount of PV and shaft work involved in the process. As a result of the transfer of work and heat, the energy content of the system changes during a process. By energy conservation, the energy content in the final state (EB) is increased relative to that at the initial state (EA) by the amount of work and heat added to the system:
This we can write in the equivalent form,
Figure 3-5: Schematic illustration of the differential and integral expressions of the first law.
where ΔEAB = EB − EA is the difference in the energy between the initial and final states. The terms EA and EB refer to the total energy stored in the system in all possible forms. In general, this includes internal (U), kinetic (Ek), and potential (Ep) energy:4
4. If other forms of energy are relevant, they should be included on the right-hand side as needed.
Equation (3.6) may now be written as
It will often be the case that kinetic and potential energy are either not present or their contribution to the energy balance is negligible. Whenever these conditions are met, these energy terms may be dropped and the first law takes the simpler form,
with the subscript AB dropped from ΔU for simplicity. This equation is the mathematical statement of the first law for a closed system. It extends the familiar energy balance to include heat and internal energy, two terms that arise from molecular phenomena. The significance of the first law is that it relates internal energy, an “invisible” form of energy, to heat and work, both of which are directly measurable. If eq. (3.9) is applied to a differential step along the process for a small change of state from (P, T) to (P + dP, T + dT), we obtain
This equation is the differential of eq. (3.9). Conversely, eq. (3.9) is the integrated form of this differential between two states.
Note
The Operator Δ(...)
The operator Δ is introduced as shorthand notation for a change of a property between two states. Given a property X and a change of state from A to B, ΔXAB is defined as
ΔXAB = XB − XA.
If no subscripts are given, the difference will be understood to be (final) − (initial):
ΔX = Xfinal − Xinitial.
Here, X stands for any state function. It is incorrect to write ΔW or ΔQ: neither work nor heat are state functions; therefore, they cannot be represented by a difference Δ. A differential amount of work or heat is written as dW, or dQ; for the integrated quantity we will write W and Q, without a Δ in front. The notation δQ and δW will be used in numerical calculations to denote finite approximations of dQ, dW, respectively.
Note
A Brief History of the First Law
Throughout history humans have valued mechanical work more than heat. Work makes cars move, airplanes fly, electrons perform binary computations. However, sources of raw work in nature, while plentiful, are often in forms that are not immediately usable without considerable engineering ingenuity: waterfalls, wind, ocean currents, avalanches. Heat, on the other hand, is plentiful and easily available by burning wood, coal, or oil. By converting heat into work we obtain a valuable form of energy from a plentiful form of energy. The technological development that made such conversion possible on a grand scale was the steam engine: heat is used to produce high-pressure steam, which is then used to push a piston and produce shaft work. This engineering development attracted interest in the theoretical problems raised by these new machines, in particular, how to maximize the amount of work that can be extracted from a given amount of heat. The answer to this problem was made difficult by the confusion surrounding the nature of heat. A popular scientific theory that persisted during the 18th and 19th centuries was the “caloric” theory of heat, which believed heat to be an invisible fluid contained inside matter. Heat was given its own units (calorie, Btu), which survive to date, and which are based on the temperature rise that follows the addition of heat.5 James Prescott Joule demonstrated that mechanical work raises temperature by a specific amount per unit of work, thus establishing the equivalence between heat and work. The microscopic explanation for heat would come with the development of statistical thermodynamics, through the works of William Thomson (Lord Kelvin), Boltzmann, Clausius, and Maxwell.
5. The calorie is the amount of heat that raises the temperature of 1 g of water by 1 °C. The Btu is the amount of heat that raises the temperature of 1 lb of water by 1 °F.
Between 1845 and 1850, Joule performed several of his now famous experiments that established the equivalence between heat and work. The highlight of the experiments was the measurement of the temperature rise in a system (water) resulting from the application of mechanical work. That work can cause temperature to increase was hardly a new discovery, as anyone who has rubbed their hands on a cold day knows. Joule’s breakthrough was to demonstrate that the temperature increase is proportional to the amount of work, thus proving that the unit of heat (calorie) is proportional to the unit for work—now named after Joule himself. He performed his experiment in a paddle-wheel apparatus consisting of a stirrer in the form of paddles. To rotate the stirrer, Joule used the motion of falling weights via pulleys and strings attached to the shaft of the stirrer. This arrangement allowed Joule to calculate precisely the amount of work applied. By making the stirrer in the shape of a paddle instead of a more streamlined shape, the rotational kinetic energy of the stirrer is more efficiently transferred into the fluid via viscous force. From the proportionality between the applied work and the resulting temperature rise, Joule was able to obtain a fairly accurate numerical value for the work equivalent of heat. He found that one degree Fahrenheit is equivalent to 890 pounds falling from the altitude of one foot.
3.5 Elementary Paths
Constant-Volume Heating
Consider the process in which a closed system is heated under constant volume. There is no PV work because the volume of the system is fixed. We assume there is no shaft work either. Then, the first law gives,
Therefore, the amount of heat that is exchanged under constant volume is equal to the change of internal energy, provided that no shaft work is present. Recall that shaft work, if present, will be made obvious through the presence of mechanical devices such as impellers, pumps, compressors, turbines, and the like. If a problem makes no mention of any such devices, it will be assumed that no shaft work is involved, without explicitly stating this assumption each time.
Constant-Pressure Heating
A common way to exchange heat is under constant pressure. The expansion/ contraction of volume that accompanies heating/cooling involves the exchange of PV work with the surroundings, and this must be accounted for in the energy balance. We assume that the PV work is exchanged reversibly. Experimentally, this means that heat must be added or removed at a gentle rate to allow temperature to equilibrate and the expansion or contraction to take place in an controlled manner. Applying eq. (3.4) and noting that pressure is constant, the work is
with subscripts A and B referring to the initial and final state, respectively. Substituting this result in eq. (3.9) and solving for the heat, we find,
ΔUAB = Q − P(VB − VA) ⇒ Q = (UB + PVB) − (UA + PVA).
In the last result, the right-hand side is the difference of the term U + PV evaluated at the final state B, and the same term evaluated at the initial state A (recall that PB = PA = P for this process). This grouping of state functions is itself a state function. This motivates the definition of a new thermodynamic property, enthalpy:
Using this definition, the heat in constant-pressure process is
Therefore, in constant-pressure heating of a closed system, the amount of heat that is exchanged is equal to the change in enthalpy. Enthalpy is a state function and has the same units as internal energy (kJ/kg or J/mol). It is the relevant thermodynamic in the energy balance of open systems, as we will see in Chapter 6. As the large majority of chemical processes involves open systems, such as units with multiple inlet and outlet flow streams, enthalpy is used far more than internal energy and is tabulated more extensively. In fact, tabulations of internal energy are uncommon because it can be calculated from tabulations of enthalpy and volume.
Constant-Temperature Process
An isothermal process is one conducted at constant temperature and its path is represented by an isotherm. Experimentally, it is conducted by placing the system inside a heat bath. A typical example of an isothermal process would be compression or expansion. In general, this process involves the simultaneous exchange of both work and heat, as demonstrated with an example.
3.6 Sensible Heat—Heat Capacities
In the absence of phase transitions, the exchange of heat is accompanied with a temperature change. Such heat is called sensible because it can be sensed with a thermometer. The amount of heat needed to produce a given temperature change varies from one substance to another and is quantified by the heat capacity, defined as the ratio of the amount of heat exchanged to the temperature change observed:
The amount of heat depends on the path of the heating process. We have encountered two simple paths, the constant-volume and the constant-pressure path. Each is characterized by its own heat capacity.
Constant-Volume Heat Capacity
In constant-volume heating, eq. (3.11) gives dQ = dU. Applying this result to eq. (3.14) we obtain the constant-volume heat capacity:
Thus, even though the definition of the heat capacity was motivated by heat, the heat capacity is a partial derivative of a state function (internal energy), and itself a state function. The above can also be expressed in the differential form,
This equation gives the change in internal energy during a small step along a path of constant volume. It can be integrated between two states to give the change in internal energy between these states:
The condition “constant V” specifies the integration path, that is, the initial state, final state, and all states between are at the same volume.
Derivatives and Integrals With Functions of Multiple Variables
In dealing with functions of multiple variables we encounter various partial derivatives. For a function of two variables, F(x, y), the partial derivative
is the usual derivative of F with respect to x, while keeping y constant. In thermodynamics we are free to choose the set of variables that we take to be independent. Although we prefer to express properties as a function of P and T, we will often use other combinations of variables. To make clear which are the independent variables, a partial derivative must indicate all of them. This is done by adopting the notation
with the differentiation variable appearing in the denominator, as usual, and the remaining variables (in this case, y) appearing as subscripts outside the derivative. Notice that the following two derivatives below are not the same:
The left-hand side is a partial derivative of the function U(T, V) whereas the right-hand side is a derivative of the function U(T, P); these are two different mathematical functions.
A partial derivative can be broken up to form a differential, which can then be integrated:
Integration between two states A and B produces the change of F between the two states:
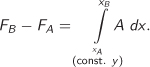
Upon separating the derivative into a differential, the specification “const. y,” which originated as a subscript in the partial derivative, must be explicitly written down. When the differential is integrated, the condition “const. y” becomes the specification of the integration path, namely, a line on the xy plane along which we evaluate the integral. Integration paths are necessary when working with functions of multiple variables: When we integrate with respect to one variable, the path specifies what to do with the remaining variables.
Proper notation is important for consistency but also serves the practical purpose of facilitating learning by organizing mathematical thought: It is not necessary to memorize the fact that eq. (3.17) applies only to constant volume processes, as long as one can recall the standard mathematical steps that connect this result to the basic definition in eq. (3.15).
Constant-Pressure Heat Capacity
For constant-pressure process, dQ = dH, from eq. (3.13). Applying this result to eq. (3.14) we obtain the constant-pressure-heat capacity:
As an immediate consequence, the enthalpy change along a path of constant pressure is given by the integral,
Both CP and CV have dimensions of energy per mass per temperature. In the SI system, their values are usually reported in J/mol K, or kJ/kg K. The term specific heat is sometimes used when the heat capacity is reported on a per-mass basis. Equation (3.19) may be written in simpler terms by making use of the mean heat capacity, ![]() , which we define as
, which we define as
Using this definition, eq. (3.19) becomes
The use of the mean heat capacity does not eliminate the need for the integration because ![]() depends on the end temperatures, TA and TB, and must be recalculated each time the interval changes. Written in the above form, however, eq. (3.21) suggests that if the heat capacity does not change much with temperature in the interval TA to TB, it may be taken to be constant and equal to its value at TA or at TB. This approximation should be made only for quick estimates, when high accuracy is not critical.
depends on the end temperatures, TA and TB, and must be recalculated each time the interval changes. Written in the above form, however, eq. (3.21) suggests that if the heat capacity does not change much with temperature in the interval TA to TB, it may be taken to be constant and equal to its value at TA or at TB. This approximation should be made only for quick estimates, when high accuracy is not critical.
Why Are CV and CP Different?
The mathematical answer is that they represent different partial derivatives. The thermodynamic answer is that each is associated with heating along different paths. We may also provide a third explanation based on physical arguments. Consider the following two experiments, shown schematically in Figure 3-7: in the first one, a closed system is heated under constant volume until its temperature increases by ΔT. In the second experiment, an identical system at the same initial state is heated under constant pressure until its temperature increases by the same amount ΔT. Let QV and QP be the amounts of heat for the constant- V and the constant-P experiments, respectively. How do these amounts compare? In constant-volume heating, the amount QV is used to increase the temperature by ΔT. In constant-pressure heating the amount QP is used to increase temperature by the same amount and to expand the volume against the surroundings. This argument suggests that QP > QV, which further implies that CP > CV. We also expect the difference between CP and CV to be larger for gases, because of the large volume expansion, and smaller for liquids and solids, whose volume expands much less. These qualitative conclusions are indeed true.
Figure 3-7: Constant-volume and constant-pressure heating: to achieve the same temperature increase, constant-pressure heating must provide more heat because of the work needed to expand the volume against the surroundings.
The practical utility of the heat capacities is twofold. First, they allow us to calculate heat in constant-volume and constant-pressure processes. This is useful in energy balances. Second, they allow us to calculate changes in internal energy and enthalpy. This allows us to calculate these properties using equations rather than tables, or to obtain their values in states that are not found in tables. There is a limitation, however. Equation (3.17) may be used only between two states of the same volume, and eq. (3.19) only between two states of the same pressure. The general calculation of properties between any two states will be discussed in Chapter 5.
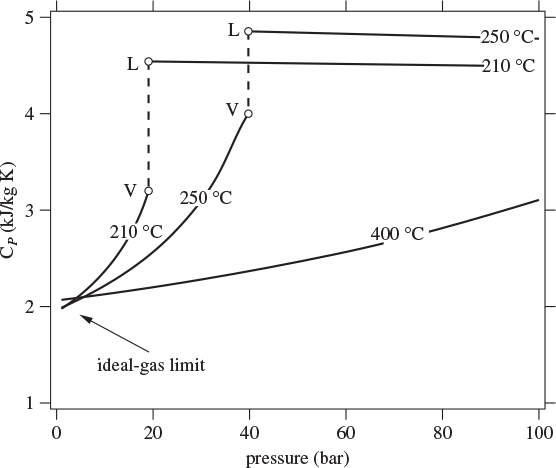
Effect of Pressure and Temperature on Heat Capacity
As state functions, CV and CP depend on pressure and temperature. This dependence is illustrated for CP in Figure 3-8, which shows the constant-pressure heat capacity of water as a function of pressure at selected temperatures. In general, the heat capacity of the liquid is higher than that of the vapor; heat capacity is a strong function of pressure in the vapor phase but almost independent of pressure in the liquid. In both phases, CP is fairly sensitive on temperature. Following an isotherm to zero pressure we reach the ideal-gas limit and the corresponding value is the ideal-gas heat capacity, ![]() . In the ideal-gas state the heat capacity is independent of pressure but it remains a function of temperature (notice that the isotherms in Figure 3-8 do not converge to a single value at P = 0).
. In the ideal-gas state the heat capacity is independent of pressure but it remains a function of temperature (notice that the isotherms in Figure 3-8 do not converge to a single value at P = 0).
Figure 3-8: CP of steam as a function of pressure and temperature. Points V, L, mark the saturated vapor and saturated liquid, respectively.
Ideal-Gas Heat Capacity
Ideal-gas heat capacities have been compiled for a large number of pure components and the data are usually presented in the form of empirical correlations that give ![]() as a function of temperature. One common representation is in the form of a polynomial in temperature:
as a function of temperature. One common representation is in the form of a polynomial in temperature:
where R is the ideal-gas constant, T is temperature, and ai, i = 1, ..., 4, are parameters specific to the fluid. This equation gives the ratio of the ideal-gas heat capacity to the ideal-gas constant and the heat capacity is obtained by multiplying the right-hand side by R. One must be careful about the proper units of T. These units cannot be inferred from the equation and must be specified explicitly (this information should be obtained from the source that specifies the equation and the parameters). Parameters of this equation for a large number of substances are given in The Properties of Gases and Liquids (5th ed., 2007).
Liquid Heat Capacities
The heat capacity in the liquid phase is nearly independent of pressure for the same reasons discussed for other liquid properties (see Section 1.1). The liquid heat capacity is expressed as a function of temperature by empirical equations, often polynomial in T.
Properties of Compressed Liquid
At temperatures well below the critical, enthalpy (and internal energy) is approximately independent of pressure. Under this approximation, eq. (3.21) can be used to calculate the enthalpy difference between two states in the compressed liquid region, not necessarily at the same pressure. Alternatively, the enthalpy of compressed liquid may be approximated by the enthalpy of the saturated liquid at the same temperature.
3.7 Heat of Vaporization
To convert the saturated liquid into vapor of the same pressure and temperature, we must provide the energy required to free molecules from the attractive forces that hold the liquid together. This energy is called heat of vaporization and since this process is at constant pressure, it is equal to the difference of the enthalpy of the saturated liquid and saturated vapor:
This amount of energy is also called latent heat of vaporization, to indicate that it is not accompanied by any temperature change. Writing H = U + PV for the enthalpy, the enthalpy of vaporization can also be expressed as
Here, ΔUvap is the internal energy of vaporization, ΔVvap is the change in volume from the saturated liquid to the saturated vapor, and Psat is the saturation pressure. The heat of vaporization can be calculated from tabulated properties of the saturated liquid and saturated vapor.
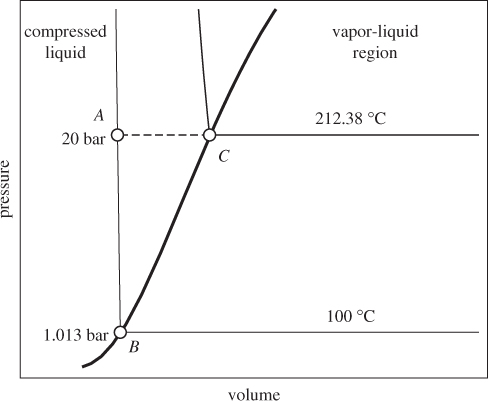
A state that lies in the vapor-liquid region (point C in Figure 3-10) consists of a mixture of saturated vapor and saturated liquid. If the mass fraction of liquid is xL and the mass fraction of vapor is xV, the specific enthalpy of the two-phase system is
Figure 3-10: Liquid-vapor transition at constant pressure.
Using xL + xV = 1, the above relationship can be solved for the mass fractions:
Equations (3.25) and (3.26) are expressions of the lever rule for enthalpy. It will be left as an exercise to show that internal energy also satisfies the lever rule. An alternative form of the two expressions in eq. (3.26) is obtained by solving each expression for the enthalpy of the two-phase system. Noting that the denominator in both expressions is the enthalpy of vaporization, the result is
This equation has a simple interpretation that can be useful in calculations: If we start with the saturated vapor and remove an amount of heat that is equal to fraction a of the heat of vaporization (0 < a < 1), the fraction of the vapor that condenses is xL = a. Similarly, if we start with saturated liquid and add an amount of heat equal to fraction a of the heat of vaporization, the fraction of the liquid that vaporizes is xV = a. This relationship is helpful when the amount of heat is not enough to carry the system entirely through the vapor-liquid region.
Note
Lever Rule
The lever rule applies to the molar or specific version of any extensive property. So far we have encountered three such properties: volume, enthalpy, internal energy.
Pitzer Correlation for ΔHvap
The heat of vaporization can be obtained from various sources. It can often be found in tables directly, or calculated from tabulated values of the enthalpy of the saturated vapor and liquid. Several empirical equations have been developed for the heat of vaporization, and these are reviewed in The Properties of Gases and Liquids by Polling, Prausnitz, and O’Connell (5th ed., 2007). Here we mention one that is based on Pitzer’s method:
where Tc is the critical temperature, Tr is the reduced temperature, and ω is the acentric factor. This should be treated as an approximation, to be used if more reliable data are not available. As with all correlations based on corresponding states, this equation should be applied to normal fluids.
Consider the constant-pressure path AB in Figure 3-10: The initial state is compressed liquid and the final state is superheated vapor. The enthalpy change between initial and final state is
If HA and HB are available from tables, this difference can be immediately determined. An alternative calculation is to break the path into three parts: AL, LV, and VB. The first part involves constant-pressure heating of a liquid (sensible heat only). The enthalpy change for this part is
where ![]() is the constant-pressure heat capacity of the liquid, and Tsat is the saturation pressure at the pressure of the process. The enthalpy change between L and V is the equal to the enthalpy of vaporization:
is the constant-pressure heat capacity of the liquid, and Tsat is the saturation pressure at the pressure of the process. The enthalpy change between L and V is the equal to the enthalpy of vaporization:
ΔHLV = ΔHvap.
In the last part, VB, the vapor is heated under constant pressure. The enthalpy change for this part is
The enthalpy change for the complete path ALVB is the sum of the parts:
In this form, the parts of the path that involve sensible heat are expressed as integrals of CPdT, using the heat capacity of the appropriate phase. Equations (3.29) and (3.30) are equivalent and either one can be used. The choice between the two will depend on the type of information that is available.
3.8 Ideal-Gas State
The properties of the ideal-gas state will be discussed in detail in Chapter 5, but some important results will be introduced here on the basis of qualitative molecular arguments. In the ideal-gas state, intermolecular interactions are unimportant because distances between molecules are large, beyond the range of such interactions. If the volume of the system is increased at constant temperature, there should be no change in internal energy: since temperature remains constant, the kinetic energy of the molecules (including translational, rotational, vibrational, etc.) is the same before and after the expansion; and since there is no interaction between molecules, there is no other mode of energy storage available to the system. Therefore, internal energy remains constant as long as temperature is not changed. In other words, the internal energy in the ideal-gas state is a function of temperature only:
The enthalpy of the ideal gas is Hig = Uig + PVig = Uig + RT. The right-hand side is a function of temperature only. Therefore, enthalpy in the ideal-gas state is also independent of pressure and a function of temperature only:
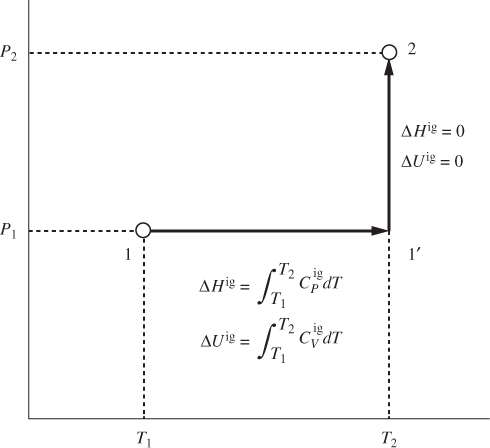
These results greatly simplify the calculation of internal energy and enthalpy in the ideal-gas state. Consider two states (P1, T1) and (P2, T2) on the PT plane (Figure 3-11). To calculate the enthalpy difference between these states we construct
Figure 3-11: Path for the calculation of ΔH and ΔU between any two states in the ideal-gas state.
the composite path 11′2, which consists of a constant-pressure segment (11′) and a constant-temperature segment (1′2). Along the constant-pressure part, the enthalpy is given by eq. (3.19):
In the second segment, temperature is constant. Since enthalpy in the ideal-gas state depends only on temperature, there is no enthalpy change along this part:
The enthalpy change for the combined path is the sum of the parts:
This result gives the enthalpy change between any two states in the ideal-gas limit. Since enthalpy is a state function, the result is the same for any integration path between the two states, therefore, eq. (3.33) has general validity. A similar analysis on the VT plane leads to the following result for the internal energy:
Another useful result is obtained by expressing the relationship between enthalpy and internal energy in the ideal-gas state. Starting with eq. (3.12) and using Vig = RT/P, we have
Hig = Uig + PVig = Uig + RT.
Differentiation with respect to T at constant P gives
Since Uig is a function of temperature only (i.e., independent of P and V), the following two partial derivatives of internal energy are equal
The same is true for enthalpy.6 Thus we conclude that
This relationship allows us to calculate the constant-volume heat capacity in the ideal-gas state from tabulations of the constant-pressure heat capacity. For this reason, ![]() is not tabulated separately.
is not tabulated separately.
6. For enthalpy we have,
Since Hig is also a function of T only, it is independent of P or V.
Reversible Adiabatic Process
This is a special process in which the system exchanges reversible work with the surroundings but no heat. Experimentally, this can be accomplished by thermally insulating the system and conducting the process in a quasi-static manner. Such system can either be compressed or expanded. The conditions “reversible” and “adiabatic” fully specify the path, as we will see below. The process is not specific to ideal-gases, but the calculation of this path for a general fluid will be delayed until Chapter 4.
For an adiabatic process, dQ = 0, and application the first law gives
To calculate this work we must know the initial and final temperatures. In typical problems, we usually know the initial state (pressure and temperature) and one property (pressure, temperature, or volume) in the final state. To fully specify the final state we must fix one more intensive property and this is done through the equation that describes the path. The path of the process is expressed as a relationship between any two variables, either P and T, P and V, or T and V. If the path is obtained in terms of one of these pairs, all the others can be obtained by using the ideal-gas law to eliminate one variable in terms of another. This procedure is developed below.
We begin by applying the differential form of the first law, eq. (3.10), along a small step of the process. For adiabatic process, dQ = 0, and for reversible work, dW = −PdV. Then, the first law gives
dUig = dW = − PdVig.
If the heat capacity is constant (independent of temperature), the log-x is equal to the heat capacity ![]() . This suggests that if the heat capacity does not change much over the temperature interval of the problem it can be approximately taken to be constant,
. This suggests that if the heat capacity does not change much over the temperature interval of the problem it can be approximately taken to be constant, ![]() . Then, the reversible adiabatic path is simplified and becomes,
. Then, the reversible adiabatic path is simplified and becomes,
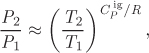
where ![]() . This eliminates the need for the calculation of the log-x heat capacity. This approximation is acceptable if the heat capacity is an insensitive function of temperature, or if the temperature interval is too small to make much of a difference in the heat capacity.
. This eliminates the need for the calculation of the log-x heat capacity. This approximation is acceptable if the heat capacity is an insensitive function of temperature, or if the temperature interval is too small to make much of a difference in the heat capacity.
Note
Log-x Mean
Equation (3.47) and eq. (3.40) involve integrals of the form
This is a weighted integral of f (x) with weights 1/x. If function f (x) is replaced by a constant value, ![]() , the integral becomes
, the integral becomes
The two integrals are equal if ![]() has the value
has the value
This defines the mean log-x value of f in the interval (x1, x2). This value is a weighted mean of f that gives the same result as f when integrated in the interval x1 to x2 with weights 1/x. With the substitution y = ln x, eq. (3.47) becomes
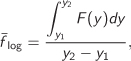
where F(y) is f expressed as a function of y = ln x. Therefore, the log-x mean is the usual arithmetic mean with respect to ln x. The subscript log will be used to distinguish this from the arithmetic mean of f. The value of the log-T mean depends on x1 and x2; therefore, the mean must be recalculated if the interval changes. The use of the log x in equations like eq. (3.44) does not eliminate the need for integrations, it just simplifies the notation. However, if f (x) does not vary much between x1 and x2, it may be replaced by a constant value, which may be approximated as ![]() , or
, or ![]() , or
, or ![]() . Treating f as constant is acceptable if the range (x1, x2) is narrow or if f is not a sensitive function of x.
. Treating f as constant is acceptable if the range (x1, x2) is narrow or if f is not a sensitive function of x.
3.9 Energy Balances and Irreversible Processes
As a statement of energy conservation, the first law is applicable to any process, whether it is reversible or not. The change of internal energy, ΔU, between the initial and final state is fixed by the initial and final state and independent of the path used to connect them. This difference gives the net amount of energy that the system must exchange with its surroundings in order for this change to take place. The exchange is generally a combination of heat and work, but the individual amounts of heat and work depend on the specific path. For mechanically reversible paths, the work is calculated by eq. (3.3). If the process is irreversible and involves work, one must be careful because eq. (3.3) is not applicable. If the process does not involve work, the calculation is done in the usual way. Implicit in all of these calculations is the assumption that the system is internally uniform so that its state can be described by a uniform pressure and temperature.
3.10 Summary
The first law extends the energy balance to include heat, and in doing so it introduces internal energy as a state function. Internal energy represents the collective ways in which matter is capable of storing energy. During a process, changes in internal energy can be tracked through the exchange of heat and work that take place between the system and its surroundings. Enthalpy,
is a state function with units of energy. Both internal energy and enthalpy are important in energy balances. As state functions, internal energy and enthalpy can be obtained from tables, if available, or they can be calculated using suitable methodologies. So far we have formulated equations for the calculation of internal energy and enthalpy in two special cases:
• Internal energy in constant-volume path:
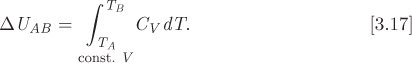
• Enthalpy in constant pressure path:


It is a recurring theme in thermodynamics that calculations in the ideal-gas state are simpler than in any other state. However, the ideal-gas equations should never be used without adequate justification, and even then, only as an approximation!
As a statement of energy conservation, the first law is the starting point for all energy balances in a closed system. Problems of this type typically require the calculation of heat and work. The amount of heat that is exchanged can, under special conditions, be related to internal energy or enthalpy:
In the calculation of work we must distinguish between shaft work and PV work. There is no special formula for shaft work in a closed system; this type of work, if present, will be calculated from mechanical considerations of device that is used to produce or absorb this type of work. The PV work is of fundamental importance in thermodynamics and it arises whenever the boundaries of a system move in the presence of a forcing or opposing external pressure. In the special case that the exchange of work is conducted in mechanically reversible manner, the PV work is
Care must be taken when applying energy balances to mechanically irreversible processes because in such cases the work cannot be calculated using eq. (3.4).
3.11 Problems
Problem 3.1: A gas is confined in a cylinder sealed by a piston 20 cm in diameter whose mass is 30 kg. The pressure in the room is 1 bar.
a) What is the pressure inside the cylinder?
b) Heat is added to the cylinder causing the gas to expand. The piston rises and finally rests at 50 cm above its initial level. How much work was done during this process?
c) What is the pressure inside the cylinder at the end of part (b)?
Problem 3.2: The PVT behavior of a certain gas is described by the equation P (V − b) = RT where b is a constant.
a) Show that when P → 0, this gas becomes ideal.
b) Calculate the work done by this gas when it expands reversibly under constant temperature from initial volume VA to final volume VB.
c) Obtain the second and the third virial coefficients.
Problem 3.3: a) At 0 °C, 1 atm, the density of liquid water is 1 g/cm3 and that of ice is 0.917 g/cm3. Calculate the amount of work (in joule) that is exchanged when 1 liter of liquid water freezes to produce ice at 0 °C and 1 atm. Use the proper sign convention!
b) If this work could be converted into kinetic energy of this quantity of water, what would be the speed? Give your answer in m/s and in mph.
c) If the work of part (a) were used to raise this quantity of water by a distance h, what would be that distance? Report the result in m and in ft.
Problem 3.4: a) Calculate the amount of work necessary for the reversible expansion of 1 kg of steam from 3 bar to 7 bar. The compression is to take place in a cylinder fitted with a weightless piston at the constant temperature of 250 °C.
b) Calculate the amount of heat, if any, associated with this process.
Problem 3.5: a) Calculate the amount of work necessary for the reversible expansion of 1 kg of steam from 10 bar to 5 bar. The expansion is to take place in a cylinder fitted with a weightless piston at the constant temperature of 400 °C.
b) Calculate the amount of heat associated with this process.
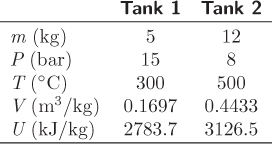
Problem 3.6: A sealed tank contains saturated steam at 5 bar. The volume of the tank is1m3.
a) Heat is added until the pressure in the tank doubles. What is the final temperature?
b) Calculate the necessary amount of heat.
Problem 3.7: A closed rigid tank contains saturated water vapor at 100 °C. The tank has a safety relief valve that will go off at 2.5 bar. How much heat can be added to the steam before the valve goes off?
Problem 3.8: A sealed pressure cooker contains steam at 5 bar and 200 °C. Subsequently, the cooker is cooled until the contents become saturated vapor.
a) What is the final temperature?
b) How much heat is removed during the cooling step?
Problem 3.9: A sealed rigid tank is filled with 1 kg of steam at 200 °C and 10 bar.
a) What is the volume of the tank?
b) 0.5 kg of steam are removed from the tank. If the temperature remains at 200 °C, what is the new pressure in the tank?
c) What is the state of the steam at the end of part b (e.g., liquid, vapor, saturated, superheated)?
d) How much heat must be added to bring the pressure back to 10 bar?
e) What is the temperature at the end of step (d)?
Problem 3.10: A closed and sealed rigid tank contains 11 kg of liquid water at equilibrium with 1.17 kg of vapor at a pressure of 2 bar. The tank is equipped with two alarms: a pressure alarm that will sound if the pressure exceeds 10 bar; and a temperature alarm that will sound if the temperature exceeds 200 °C.
a) What is the volume of the tank?
b) Calculate the internal energy of the liquid-vapor mixture in the tank.
c) If we add heat to the tank continuously, which alarm will sound first?
d) We stop the heating when the contents are saturated vapor. How much heat has been added?
e) Which alarm(s), if any, will be sounding at the end of step (d)?
f) Draw a qualitative PV graph and sketch the path of the processes involved. Mark all the relevant isotherms and pressures.
Problem 3.11: a) A closed tank contains steam with 20% moisture at 3 bar. Heat is added until one of the two phases disappears. Which phase disappears and what is the final pressure and temperature?
b) Another closed tank contains steam with 99.9 % moisture at 3 bar. Heat is added until one of the two phases disappears. Which phase disappears and what is the final pressure and temperature?
c) A third closed tank contains a vapor-liquid mixture of toluene at 1 atm. Ninety-eight percent of the toluene (by mole) is in the liquid phase. Heat is added until one of the two phases disappears. Which phase disappears? The normal boiling point of toluene is 384 K.
Problem 3.12: A sealed rigid tank of 1 m3 capacity contains 1.2 kg of water at 1 bar and 99.63 °C. To this tank we add heat until the pressure increases to 3 bar.
a) What is the temperature at the end of the heating?
b) Calculate the amount of vapor before and after the heating.
c) Calculate the amount of heat added.
Problem 3.13: A sealed rigid tank contains 1 kg of wet steam at 300 °C. The fraction of the liquid in the tank is not known. Upon adding heat to the tank it is observed that the vapor condenses. The heating stops when the system becomes saturated liquid. At that point the pressure in the tank is 148 bar.
a) What fraction of the water is initially liquid?
b) How much heat was added?
c) What is the minimum amount of liquid that must be present in the tank initially, in order to observe condensation upon heating?
d) What would be observed upon heating, if the initial amount of liquid was less than the minimum value calculated in part (c)?
e) How do you explain the fact that heating can result in condensation of the vapor?
Problem 3.14: A 0.5m3 sealed rigid vessel contains 15 kg of water (phase unknown) at 120 °C. Heat is added or removed, as needed, until the steam becomes a single saturated phase.
a) Determine the state of water before heating.
b) Determine the pressure and temperature at the end of heating.
c) Determine the amount of heat.
Problem 3.15: A3m3 tank is divided into two parts via a thermally insulated wall. One part has a volume of 2 m3 and contains a vapor-liquid mixture of steam, 7% liquid, at 5 bar. The other part contains steam at 10 bar, 500 °C. A valve is opened and allows the two parts to thoroughly mix.
a) Determine the final pressure and temperature in the tank assuming no losses to the surroundings.
b) Determine the amount of heating or cooling that must be supplied in order to make the final pressure 5 bar.
Problem 3.16: A closed tank, 1 m3 in volume is filled with water at 1 bar 80 °C.
A second identical tank contains 20 kg of steam at 20 bar.
a) What is the mass of water in tank 1?
b) What is the temperature and phase in tank 2?
c) The contents of the two tanks are mixed together in a third closed tank whose volume is 2 m3. Heat is added or removed, as needed, to bring the final temperature to 175 °C. What is the final pressure?
Problem 3.17: An insulated cylinder is divided into two parts: one part has a volume of 5 L and contains steam at 1 bar, 200 °C; the other part has a volume of 2 L and contains steam at 2 bar, 400 °C. The partition that divides the cylinder is removed and the contents are allowed to reach equilibrium without heat losses to the surroundings.
a) Determine the pressure and temperature in the final state assuming steam to be an ideal-gas. Is ideality an acceptable assumption?
b) Repeat using the steam tables.
Problem 3.18: Wet steam with quality 63.1% exchanges heat in a closed system under constant pressure P = 6 bar. Determine the final temperature and the amount of PV work in each of the following cases:
a) The system is cooled by removing 1500 kJ/kg of heat.
b) The system is heated by adding 1500 kJ/kg of heat. Report the work using the proper sign convention.
Problem 3.19: a) 200 kJ of heat is added under constant pressure to 1 kg of steam initially at 30 bar, 400 °C. What is the final temperature?
b) What is the change in internal energy during this process?
Problem 3.20: Steam at 200 °C and 10 bar is cooled under constant pressure until it becomes saturated liquid.
a) What is the final temperature?
b) How much heat is removed from the steam?
c) Calculate the work involved in this process, if any.
Problem 3.21: a) Water at 1 bar, 20 °C is heated at const P to produce steam with quality 95%. What is the amount of heat?
b) What is the final state if the amount of heat is 2100 kJ/kg?
Problem 3.22: 1 mol of liquid octane is heated in a closed system at constant pressure of 11 bar from 8 °C until it becomes saturated liquid (Tsat = 240 °C). Calculate:
a) The amount of heat.
b) The amount of work.
c) The enthalpy at the initial state.
d) The internal energy at the initial state.
Additional data: The enthalpy of the saturated liquid at 1.1 bar is 38.592 kJ/mol. The heat capacity of the liquid is
CP/R = 27.0423 −0.0224477 T + 0.000115337 T2
with T in kelvin. For the liquid volume, use the Rackett equation. You may assume that the liquid is incompressible.
Problem 3.23: Steam is heated in closed system from 20 bar, 300 °C to 450 °C. Determine the amount of heat and work in the following cases:
a) Heating is conducted at constant pressure.
b) Heating is conducted at constant volume. What is the final pressure?
c) Use these results to estimate the CP and CV of steam. The process may be assumed to be mechanically reversible.
Problem 3.24: Wet steam at 200 °C with 80% moisture is cooled by removing 600 kJ/kg of heat.
a) Determine the final state (pressure and temperature and quality, if a two-phase system) if cooling is at constant pressure.
b) Determine the final state if cooling is at constant volume.
Problem 3.25: Use the steam tables to calculate the CV and CP of water at the following states:
a) 25 °C, 1 bar.
b) 50 bar, 400 °C.
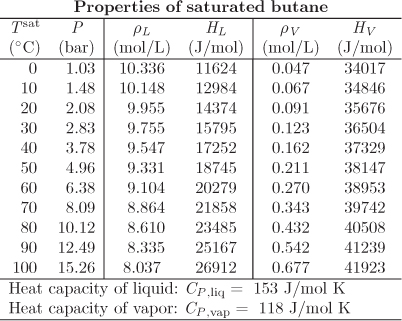
Problem 3.26: a) A cylinder with a volume of 3 L contains 2.031 mol of butane at 50 °C. Determine the enthalpy and internal energy of the contents in the tank (report in J/mol).
b) How much heat must be emoved from the system in part (a) under constant volume to turn the contents into saturated vapor? What is the temperature?
c) How much heat must be added to the system in part (a) under constant pressure to bring the temperature to 0 °C?
d) State your assumptions clearly.
The following data are available:
Problem 3.27: Ammonia is heated under constant pressure of 5 bar, from 0 °C to 200 °C. Determine the amount of heat. Additional information is given below:

Problem 3.28: Ammonia vapor is cooled under a constant pressure of 5 bar. The initial temperature is 120 °C and the amount of heat that is removed is 10 kJ/mol. Determine the final temperature. If the system is a vapor-liquid mixture, determine the mass fractions in each phase. Use the data given in problem 3.27.
Problem 3.29: 1 mol of liquid hexane at 10 bar, 50 °C, is mixed with 2 mol of hexane vapor at 250 °C, 10 bar. The process takes place adiabatically in a closed system at constant pressure. Determine the final temperature and if the system is a vapor-liquid mixture report the mass fraction in each phase.
Additional data:
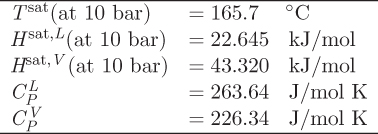
Problem 3.30: 1 mol of liquid hexane at 10 bar, 25 °C, is mixed adiabatically and under constant pressure with hexane vapor at 180 °C. Determine the moles of the vapor that must be mixed with the liquid in order to produce a final state that consists of a vapor-liquid mixture with 75% (by mass) liquid. You may use the data given in problem 3.29.
Problem 3.31: Methanol at 25 °C, 8 bar is heated under constant P in closed system.
a) Determine the amount of heat to produce 95% vapor
b) Determine the final state if Q = 32000 J/mol
c) Determine the final state if Q = 52000 J/mol
Additional data:

Problem 3.32: 1 kg of liquid water, initially at 40 °C, 2 bar, is heated under constant pressure. If the amount of heat added is 1200 kJ, determine the final temperature and the phase of the system in the final state (if vapor-liquid mixture, report the mass fraction of each phase).
Problem 3.33: a) Obtain the heat of vaporization of steam at 30 bar.
b) Saturated liquid water at 30 bar is heated until the quality is 75%. What is the amount of heat?
c) Saturated liquid water at 30 bar is heated by adding 750 kJ/kg of heat at constant pressure. What is the final state?
d) What is the final state if the amount of heat that is added to the saturated liquid is 1950 kJ/kg?
Problem 3.34: a) Water at 1 bar, 20 °C is heated at const P to produce steam with quality 95%. What is the amount of heat?
b) Steam at 1 bar 400 °C is cooled by removing 300 kJ/kg of heat at constant pressure. What is the final temperature? If the state is a vapor-liquid mixture, report the mass fraction in each phase.
Problem 3.35: Water at 20 °C 30 bar is heated in a closed system under constant pressure.
a) If the quality in the final state is 75%, what is the amount of heat?
b) If the amount of heat is 2000 kJ/kg, what is the final temperature?
c) If the amount of heat is 3000 kJ/kg, what is the final temperature?
Problem 3.36: An insulated tank is divided into two equal parts. Both halves contain the same ideal gas but one is at 300 K and 2 bar while the other one is at 400 K and 1 bar. The partition is suddenly removed and the system is allowed to reach equilibrium. What is the temperature and pressure when equilibrium has been established?
Additional data: The heat capacities of this ideal gas may be assumed to be constant in the temperature range of this problem.
Problem 3.37: At 120 °C the saturation pressure of ethanol is 4.3 bar.
a) What is the state of ethanol at 120 °C and 10 bar (i.e., compressed liquid, saturated liquid/vapor, superheated vapor)? At 140 °Cand 1bar?
b) Can we assume that ethanol vapor at 1800 °C and 20 bar behaves as an ideal gas?
c) A rigid vessel contains 1 mol of ethanol at 1800 °C and 20 bar. How much heat must be removed in order for the pressure to drop to 10 bar?
Additional data: The CP of ethanol is 173 J/mol/K.
Problem 3.38: Oxygen in a closed system is compressed adiabatically from 25 °C and 1 bar to a final temperature of 450 °C. Then it is cooled under constant pressure until the temperature falls to 5 °C. Assuming oxygen to be an ideal-gas:
a) Draw a PV graph on the computer and show the path of the process.
b) Calculate the final pressure.
c) Calculate ΔU, ΔH, Q, and W for the entire process.
d) Is it correct to assume that oxygen is an ideal gas under the conditions of this problem? You may use ![]() J/molK.
J/molK.
Problem 3.39: Saturated steam at 1 bar is heated at constant pressure to a final temperature of 500 °C in a closed system. Treating steam as an ideal gas, determine the amount of heat and work, and the change in enthalpy and internal energy. Compare with the steam tables and discuss. The ideal-gas heat capacity of steam is given by
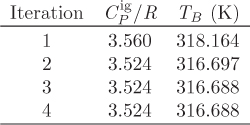
with T in kelvin.
Problem 3.40: Steam undergoes reversible adiabatic expansion from 500 °C, 10 bar. Assuming ideal-gas state, answer the following:
a) What is the pressure if the final temperature is 350 °C?
b) What is the temperature if the final pressure is 7 bar?
Additional data: The ideal-gas heat capacity of steam is
with T in kelvin.