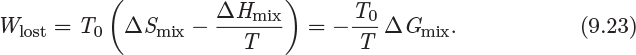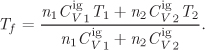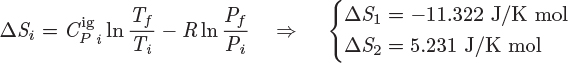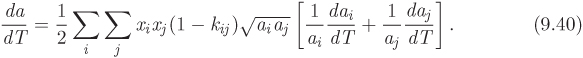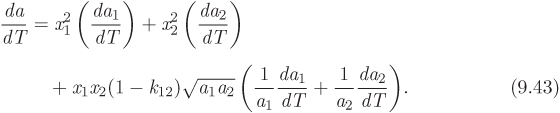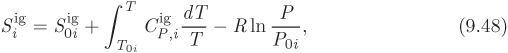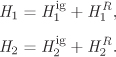Chapter 9. Properties of Mixtures

In the first part of this book we developed the principles (laws) of the thermodynamics and applied them to pure fluids. We now we want to extend their application to multicomponent systems. The thermodynamics laws themselves are general and apply to all systems, whether pure or multicomponent. Their mathematical expressions were developed in Chapter 6 and are summarized below:

These equations require the enthalpy and entropy of the system and its various streams. The problem, then is how to calculate the properties of mixture. The properties of pure substance are functions of pressure and temperature. For mixtures, in addition to pressure and temperature we must consider composition. The goal in this chapter is to formulate equations for the properties of mixtures as a function of pressure, temperature and composition. Essentially, the task will be to incorporate composition as a new independent variable. We will express composition in terms of moles of each component,¹ therefore, when we refer to composition as an independent variable we will understand not a single variable but a set of variables. First we will develop formal mathematical expressions for properties, their differentials and their partial derivatives in terms of the independent variables, temperature, pressure and moles of component i. Next we will show how we can use equations of state to calculate the volume, enthalpy and entropy of mixtures. The mathematical formulation is based on the material developed in Chapter 5. A review of that chapter is recommended, as we will make frequent references to results obtained there.

1. We will also use other measures of composition, for example, mass or mass fractions, various forms of concentration (molarity, molality), but for the most part we will express composition in terms of moles and mole fractions.

The learning objectives in this chapter are to:

1. Formulate the differential of mixture properties with temperature, pressure and composition as the independent variables,

2. Apply equations of state to mixtures,

3. Calculate the properties of mixtures from a cubic equation of state.

9.1 Composition

Let us form a mixture of N components that contains n_i mol of component i, i = 1, ..., N. The total number of moles is

We understand summations like this to run over all components and for simplicity the limits will be omitted. The mol fraction of component i is defined

The mol fractions in a mixture satisfy the normalization condition,

Mathematically, this means that of the N mol fractions only N − 1 are independent. All extensive properties of mixtures are mathematical functions of pressure, temperature, and the number of moles of all components. Using the enthalpy as an example, we write

This makes H^tot a function of N + 2 independent variables. The molar form of an extensive property is obtained by dividing the extensive property by the number of moles, for example,

H = H^tot/n.

The molar properties of a mixture are mathematical functions of pressure, temperature and mole fractions:

Since mol fractions are not independent but must satisfy the normalization condition in eq. (9.1), the above is a function of N + 1 independent variables. To avoid mathematical inconveniences from the fact that the mole fractions are not all independent, we will formulate the basic theory for the extensive form of a property. Once we have expressions for the extensive property, we can obtain the molar property through division by the total number of moles.

The mass of the mixture is the sum of the masses of its constituents:

where m is the mass of the mixture and m_i is the mass of component i. The mass (or weight) fraction, w_i, of component i is

The mass fractions also satisfy the normalization condition:

The mass and number of moles are related as follows

where is the mean molar mass of the mixture and is weighted average of the molar masses M_mi of all components:

The mean molar mass of mixture plays the same role as the molar mass of pure component and may be used to convert the mass of mixture into moles, and vice versa.

9.2 Mathematical Treatment of Mixtures

Now we consider the mathematical problem of how to express properties as functions of pressure, temperature, and composition. We will develop equations for the generic extensive property F^tot, which will stand in for enthalpy, entropy, volume, and the like. This is a mathematical function of T, P, and the moles of all components:

F^tot = F^tot(T, P, n₁, n₂, ...).

By standard calculus the differential of this expression is

This expression contains the partial derivatives with respect to every variable and each derivative is multiplied by the differential of the corresponding variable. In these derivatives, all variables except one are held constant. In the derivatives with respect to T or P, all n_i are held constant. This is indicated by the subscript n_i. In derivatives with respect to n_i, pressure, temperature, and all other moles (n_j ≠ n_i) are held constant. This is indicated by the subscript n_j that appears in the derivative. We define the partial molar property, , as

With this definition, the differential of an extensive property is written in the more compact form,

This differential expresses the change in property F^tot upon a change of state by (dT, dP, dn₁, ...).

The Partial Molar Property

Partial molar properties are defined for any property that has an extensive form for example, volume, enthalpy, etc. They are intensive properties and as such, they are functions of pressure, temperature, and mol fractions. To see how partial molar properties can be useful, consider the following thought experiment: a vessel A that contains a mixture (for example, a solution of several components) is poured into another vessel B. We will calculate the enthalpy in vessel B as it builds up during this process. The differential of H^tot is given by eq. (9.8); the process obviously takes place under constant pressure and constant temperature, therefore, dT = 0 and dP = 0. This simplifies the differential to the form,

During transfer from one vessel to another, pressure, temperature, and mole fractions are constant. Accordingly, all molar and partial molar properties also remain constant. Under these conditions, integration of the differential dH^tot with respect to n_i is trivial and the result is

This result gives the enthalpy of the mixture in vessel B as a function of the amounts n_i of all components. This enthalpy is of course the same as in vessel A. In other words, eq. (9.9) is a general relationship between an extensive property and the corresponding partial molar properties. It states that

a partial molar property is the contribution (per mole) of a component to the total property of the mixture

This remarkably simple relationship applies to any property; therefore, we can generalize the result by writing

Partial molar properties obey the same equations as regular properties. For example, the partial molar internal energy, enthalpy, and volume are related through the equation,

in complete analogy to the relationship H = U + PV.

Gibbs-Duhem Equation

Equations (9.10) and (9.11) express a simple but important relationship between partial molar properties and the corresponding property, total or molar, of the mixture. Another relationship can be derived for the differential of the partial molar property. We begin by taking the differential of eq. (9.10) keeping in mind that pressure and temperature are held constant:

The same differential is now calculated from eq. (9.8) by holding P and T constant:

Comparing the last two results we conclude that

After dividing both sides by the total number of moles, this result is expressed in terms of mol fractions as

This result states that variations of the partial molar properties with composition at constant temperature and pressure are not independent but satisfy a zero-sum condition: if all variations are multiplied by the corresponding mole fraction, their sum must be zero.⁴ This is known as the Gibbs-Duhem equation and applies to any molar property. In the special case of a two-component mixture, eq. (9.12) gives

4. We are referring to small variations that can be treated as differentials.

Dividing both sides by dx₁ this can be written in the form

Here, the variations of the partial molar property are seen explicitly to depend on variations of the mol fractions. If the partial molar property of one component is known as a function of the mole fraction, the partial molar property of the other component can be evaluated by integration of this equation. Alternatively, if both partial molar properties are known (experimentally, for example), eq. (9.13) represents a test of thermodynamic consistency: if the measured values do not satisfy this condition, we would have reason to suspect that the data are not reliable.

Special Case: Systems of Constant Composition

The properties of mixtures depend on temperature, pressure and composition but some processes leave the composition unchanged while having an effect only on pressure or temperature. Typical examples are compression, expansion, heating or cooling, as long as there is only one phase present.⁵ For such process, dn_i = 0 for all components and the differential of extensive property F^tot simplifies to

5. As we saw in Chapter 8, when a mixture is brought into the two-phase region there is an effect on composition since each phase has its own composition.

The corresponding expression for the differential of the molar property:⁶

6. To obtain this result we write dF^tot/n = d(F^tot/n), and treat n as constant, since the moles of all components are constant.

Here, the subscript x in the partial derivatives indicates that all mole fractions are held constant, since molar properties depend on the mol fractions, not the number of moles. This equation is identical to that for pure component. In fact, a mixture of constant composition behaves just as a pure component, except when phase change is involved.⁷ This conclusion has important practical implications: It means that all of the relationships developed in Chapter 5 for pure components also apply to mixtures of constant composition. For example, by analogy to eq. (5.17), the differential of the molar Gibbs energy of mixture is

7. When phase change occurs, the system splits into phases of different compositions. This requires special treatment and will be discussed in Chapter 10.

where S and V is the molar entropy and molar volume of the mixture. Since n is constant, we also have

which is the same relationship between the total properties of the mixture.

9.3 Properties of Mixing

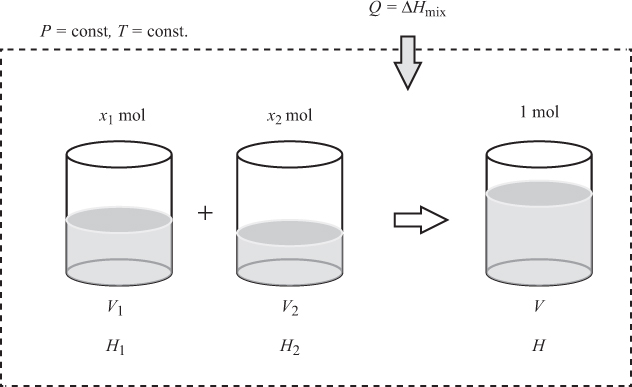
It is generally desirable to relate the properties of a mixture to those of the pure components, since pure-component properties are easier to calculate. To study this relationship, we form 1 mol of mixture by mixing its components under constant temperature and pressure, as shown in Figure 9-1. If the desired mol fractions are x_i, then we must mix x_i mol of component i. Before mixing, the total volume occupied by the pure components is

where V_i is the molar volume of component i; after mixing, the mixture occupies volume V, the molar volume of the mixture. The change in volume is

This is called volume of mixing and it may be positive (volume expansion upon mixing), negative (contraction) or zero (no change). Similar expressions can be written for all extensive properties.⁸ An important property is the enthalpy of mixing,

8. For any extensive property, its combined value over all pure components before mixing is after mixing it is F (on the basis of 1 mol of mixture). The change, therefore, is

Figure 9-1: Formation of mixture from the pure components at constant pressure and temperature.

Since the mixing process is at constant pressure, the enthalpy of mixing represents the amount of heat that must exchanged in order to conduct the process isothermally. If ΔH_mix < 0, the enthalpy of the solution is lower that of the pure components and the difference appears as heat transferred to the surroundings. Such process is called exothermic. If ΔH_mix > 0, the mixture has higher enthalpy than the pure components. In this case the difference must be supplied from the surroundings and the process is called endothermic. If ΔH_mix = 0, no heat is exchanged and the process is called athermal. Experimentally, the enthalpy of mixing may be determined from the heat that must be exchanged in order to mix the components isothermally, or from the resulting temperature change, if components are mixed adiabatically.

Other properties of mixing are defined in the same way. The entropy of mixing, in particular, is

Similar expressions can be written for the internal energy, Gibbs free energy and Helmholtz free energy. The various properties of mixing are related among themselves through relationships analogous to those of the regular properties. For example,

and so on. Because of these relationships, if the primary properties ΔV_mix, ΔH_mix and ΔS_mix are known, either by measurement or by calculation, all others can be obtained from their relationship to them.

9.4 Mixing and Separation

Mixing is a spontaneous process: if pure components are brought into contact, for example, oxygen and nitrogen in a closed vessel, sugar and water in a coffee pot, components mix to form a mixture. Even in systems that are partially or even sparingly miscible, such as water and oil, some mixing does take place until the solubility limit is reached. This process occurs through molecular motion, and while its rate is enhanced through the application of work (e.g., stirring), such interference is not necessary for the process to take place. As a spontaneous process, the mixing of pure components under constant temperature and pressure produces a mixture whose Gibbs free energy is lower than that of the pure components:

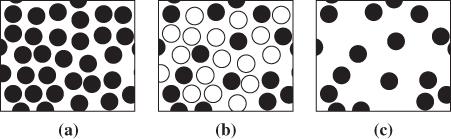
From eq. (9.21) we see that there are two contributions to the Gibbs free energy of mixing: one comes from the entropy of mixing ΔS_mix, and the other from the enthalpy of mixing ΔH_mix. Molecules in a mixture can assume more microscopic states compared to the pure components because they can be surrounded by various combinations of like and unlike species (see Figure 9-2). In molecular language, this means that the entropy of the mixture is higher than the entropy of the pure components combined, that is, ΔS_mix> 0. The enthalpy of mixing may be positive, negative, or zero. If it is negative (mixing is exothermic), it contributes to the decrease of ΔG_mix and acts as a further driving force for mixing. If it is positive (mixing is endothermic), it increases the value of ΔG_mix and opposes mixing. If it is zero it makes no contribution to the Gibbs free energy of mixing and the process is driven entirely by entropy. Exothermic mixing indicates favorable interaction between unlike components, which makes the separation of the mixture more difficult. Endothermic mixing indicates the opposite: interaction between unlike components is energetically unfavorable (energy must be supplied to form the mixture) and the mixture they form is easier to separate. The work required for the separation of the components is equal to the lost work of mixing because, as we recall, lost work refers to the work needed to reverse a process (in this case, to separate the components). From eq. (6.34), this work is

Figure 9-2: Molecular view of mixing: (a) pure component; (b) component in mixture; (c) component in mixture with the other components made invisible. In the mixed state a component has undergone isothermal “expansion” relative to the pure state. This gives rise to the entropy of mixing.

W_lost = T₀S_gen.

The entropy generation consists of the entropy change of the system, ΔS_mix, and the entropy change of the surroundings, −ΔH_mix/T:⁹

9. For constant-pressure mixing, the amount of heat exchanged with the surroundings is Q = ΔH_mix; accordingly, the entropy change of the surroundings at temperature T is

Combining these results the lost work is,

In the special case that the heat bath is at the temperature of the system (T₀ = T), the lost work simplifies to

W_lost = −ΔG_mix.

As we recall, the lost work is also equal to the minimum amount of work that must be done to reverse the process, in this case, to separate the components. Since the Gibbs free energy of mixing is always negative, the work for separation is positive. The more important conclusion is that the Gibbs free energy of mixing is a direct measure of the energy released when the mixture is formed, also equal (in absolute value) to the amount of energy that must be consumed to separate the mixture.

9.5 Mixtures in the Ideal-Gas State

The ideal-gas state for a mixture is reached by reducing pressure at constant temperature and constant composition. When this state is reached, molecules behave as point masses that exert no interactions. Neither the chemical nature of the gas, nor its composition (if mixture) has any effect on its volumetric properties. Therefore, the equation of state of the ideal-gas mixture is the same as for a pure fluid in the ideal-gas state:

Here the superscript ^igm is used to indicate ideal-gas mixture. It follows from this equation that when we form an ideal-gas mixture by mixing the pure components in the ideal-gas state at constant temperature and pressure, the volume of the mixture formed is equal to the volume of the pure components before mixing:¹⁰

10. The proof is straightforward: multiply eq. (9.24) by n = n₁ + n₂ + ..., to obtain

On the left-hand side we have the total volume of the mixture, and on the right-hand side we have the sum of the volumes of the pure components.

The enthalpy and entropy of the ideal-gas mixture are¹¹

11. We use the superscript ^igm rather than ^ig to remember that we are dealing with a mixture, not a pure component.

These results are given without proof (for the qualitative arguments that support these results, see the note later in this section). Accordingly, volume and enthalpy of mixing in the ideal-gas state are both zero:

ΔV_mix = 0, ΔH_mix = 0.

The entropy of mixing is not zero but is given by

This is always a positive quantity because the logarithm of all mole fractions is negative (x_i < 1) and the minus sign makes the right-hand side positive. According to this result, the mixing of components in the ideal-gas state is a spontaneous process and leads to entropy generation. The reverse process, separation, is not spontaneous and requires work.

From the above relationships we may easily identify the partial molar properties of mixture. Recall the basic relationship between molar and partial molar properties:

Comparing this with eqs. (9.25), (9.26), and (9.27) for the volume, enthalpy and entropy of the ideal mixture we identify the respective partial molar properties as

The partial molar volume and partial molar enthalpy are equal to the corresponding properties of the pure component. The partial molar entropy is higher than the entropy of the pure component by −R ln x_i: a component in the mixture contribute more entropy per mole than the original entropy of the pure component before mixing. The properties of the ideal-gas state are summarized in Table 9-1.

Table 9-1: Properties of mixture in the ideal-gas state. All properties (mixture or pure component) are understood to be in the ideal-gas state. The superscripts ^ig and ^igm have been omitted for simplicity.

Other Properties

Other properties of the ideal-gas mixture can be obtained easily. For example, for the internal energy we write

where we used eqs. (9.26) and (9.25) for the enthalpy and volume of the ideal-gas mixture. The quantity in parenthesis on the right-hand side in the above equation is the ideal-gas internal energy. Therefore, the final result for internal energy is

From this result it also follows that the internal energy of mixing is zero, and the partial molar internal energy is equal to the internal energy of the pure component:

The corresponding results for the Gibbs free energy are

These are obtained from the relationship between G, H, and S and their derivation is left as an exercise.

9.6 Equations of State for Mixtures

As with pure substances, the properties of mixtures can be tabulated for future reference. However, such tabulations quickly become impractical as the number of components increase. It is therefore of great practical value to be able to obtain the properties of mixture by calculation from an equation of state, as done for pure fluids. In general, equations of state developed for pure fluids may be extended to mixtures provided that composition is properly accounted for. Cubic equations such as the Soave-Redlich-Kwong and the Peng-Robinson equation require two parameters, a and b (see Chapter 2). For mixtures, these parameters are typically calculated from the corresponding parameters of the individual components. In this approach, the effect of composition is reflected in the mixture parameters a and b. Once these parameters have been determined, the calculation is identical to that for pure components. This includes the calculation of the compressibility factor, molar volume, residual enthalpy, and residual entropy.

Equations that prescribe how to obtain the mixture parameters a and b from those of the pure components are known as mixing rules. The following mixing rules are commonly used with cubic equations of state:

with the summations going over all components of the mixture. Here a_i and b_i, are the parameters of the pure component i, x_i, i = 1, ..., N are the mole fractions of the components, and k_ij is symmetric function of i and j with the properties,

k_ij = k_ji, k_ii = 0.

This parameter reflects interactions between components but it should be treated as an adjustable parameter whose purpose is to improve the accuracy of the calculation.

Residual Properties

The residual properties of mixture are given by the same equations as for pure components (see Table 5-3). The calculation also requires the derivative of the mixture parameter a with respect to temperature. This is obtained by differentiation of the mixing rule in eq. (9.39) and is given by

where da_i/dT is the derivative of the parameter a_i of the pure component i.

Binary Mixture

The equations given here apply to mixtures with any number of components. For a binary mixture in particular, they reduce to the following form:

The calculation of the mixture parameters adds one layer of computations to the overall calculation. Once the mixture values of a, b, and da/dT have been determined, the calculation of the compressibility factor, residual enthalpy, and residual entropy, proceeds in exactly the same way as for pure components. The procedure goes like this:

1. Calculate the pure component parameters a_i, b_i, and da_i/dT using the critical constants and acentric factor of the pure components. These equations were given in Chapter 2 and depend on the equation of state.

2. Calculate the mixture parameters using the mixing rules.

3. Calculate the dimensionless parameters Aʹ and Bʹ, of the polynomial equation for Z:

4. Solve the cubic polynomial for the compressibility factor. If there are more than one positive roots, choose according to the phase of the mixture:¹² for a liquid mixture choose the smallest root; for gas mixture, choose the largest.

12. The phase must be known ahead of time. We will learn in Chapter 10 that it is possible to determine the phase from the equation of state itself.

5. Use the compressibility factor to calculate the residual enthalpy and entropy according to the equations in Table 5-3.

In working with eqs. (9.38)–(9.43) we follow the convention: a single subscript refers to pure component, whereas no subscript refers to mixture.

9.7 Mixture Properties from Equations of State

Residual properties are defined in the same manner as for pure components:

where F is the molar property of the mixture at a given state, F^igm is the same property in the hypothetical ideal-gas state, and F^R is the residual property. All terms in eq. (9.44) are at the same pressure, temperature, and composition. For the enthalpy of the mixture, this equation becomes

Here we have substituted for H^igm the expression from eq. (9.26), which gives the ideal-gas enthalpy of the mixture in terms of the ideal-gas enthalpy of the pure components. For entropy we obtain a similar result,

Here, the ideal-gas entropy of mixture is given by eq. (9.27) and includes the ideal entropy of mixing. Equations (9.45) and (9.46) reduce the calculation of mixture properties into a two-step calculation, one for the ideal-gas contributions, and one for the residual corrections.

To calculate the absolute enthalpy and entropy of mixture we need the absolute properties of the pure components, and . These must be calculated based on a reference state. We must specify one reference state for each component, not necessarily the same for all components, though this choice is convenient. If the reference state for component i is at temperature T_{0 i} and pressure P_{0 i}, its ideal-gas properties at temperature T and pressure P are

where and are the ideal-gas enthalpy and entropy, respectively, of the component at its reference state. The value of these constants depends on the reference state adopted:

• Actual enthalpy and entropy at P₀, T₀, are set to zero. For this reference state we use,

where and are the residual properties of pure component at its reference state.¹³

13. Using you should be able to confirm that this above reference state leads to H₀ = 0 and S₀ = 0.

• Ideal-gas enthalpy and entropy at P₀, T₀, are set to zero. In this case,

Once the reference state for each component is selected, and become numerical constants and the calculation proceeds as usual. Table 9-2 summarizes all the equations needed for the calculation of the enthalpy and entropy of a binary mixture based on the Soave-Redlich-Kwong equation of state. The calculation is somewhat involved but completely straightforward. Except for the calculation of the ideal-gas integrals, everything else involves serial algebraic calculations. The entire procedure can be coded easily for computer calculation. The required inputs are the critical properties, the ideal-gas heat capacities as functions of temperature, and the numerical values of the reference state values of all components. The calculation should then be set up so that enthalpy and entropy are calculated for any user input of temperature, pressure, mol fractions and phase of the mixture. The phase is needed in order to select the proper root of the compressibility equation, if more than one real root is found.

Table 9-2: Properties of binary mixture using the Soave-Redlich-Kwong equation of state. Subscript _i refers to pure component 1 or 2; the values of and are fixed by the reference state.

9.8 Summary

In dealing with multicomponent systems, the new element is composition, which is expressed through the number of moles (or mass) of each component. If composition remains constant during a process, a multicomponent mixture behaves as a pure fluid in all respects except when multiple phases are present. This observation makes the extension of the theoretical relationships from pure components to mixtures straightforward, though algebraically more involved. Of practical importance is the application of cubic equations to mixtures, which makes possible the calculation of volume, enthalpy and entropy of systems with several components. The new element is the introduction of mixing rules, which are recipes for the calculation of the parameters of the mixture EOS from those of the pure components. Like the equations themselves, mixing rules are empirical. The mathematical form of mixing rules is guided by theoretical considerations but ultimately these equations are based on trial and error.

Equations of state such as the Soave-Redlich-Kwong and the Peng-Robinson, are appropriate for like, nonpolar components. Components that interact strongly cannot be represented accurately by these equations. It is important then to establish whether a given equation of state is appropriate for the system of interest through validation of the results against known data. If the answer is yes, then the calculation of mixture properties follows the same procedure as for pure components.

9.9 Problems

Problem 9.1: A stream that contains a mixture of methane (25% by mol) and carbon monoxide is compressed from 1 bar, 35 °C to 12 bar. The compressor efficiency is 90%. Treating the mixture as an ideal gas, calculate the required work.

Additional data: C_PA = 40.8 J/mol K, C_PB = 29.4 J/mol K (A = CH₄, B = CO).

Problem 9.2: Air is compressed from 1 bar, 25 °C to 50 bar, and subsequently is cooled to 300 K using cooling water. Assuming air to be an ideal-gas mixture and the compressor to be 100% efficient, calculate the work in the compressor and the heat removed in the heat exchanger per mol of air. Assume air to be ideal-gas mixture (79% N₂, 21% O₂) and use the heat capacities given in Perry’s Handbook.

Problem 9.3: Streams A and B are mixed adiabatically to produce stream C. Stream A is at 1 bar, 50 °C, it contains pure methane and its flow rate is 0.2 mol/min. Stream B is at 1 bar, 100 °C, contains a methane-ethane mixture 50% in methane (by mol) and its flow rate is 0.8 mol/min. Stream C exits at 1 bar.

a) What is the composition in the final mixture?

b) What is the temperature and pressure at the end of the process?

c) Calculate the entropy generation.

d) What is the change in the total Gibbs energy of the system?

e) How much work is needed to separate the final stream into the two streams we had before mixing, at their respective temperature and pressure? Assume that the temperature of the surroundings is 20 °C.

f) What is the irreversible feature of this process?

Additional data: The ideal-gas C_P’s of the pure components are: ethane: 10.3 R; methane: 6.2R; where R is the ideal-gas constant.

Problem 9.4: An insulated cylinder is divided by a partition into two compartments. Compartment A contains 0.2 mol of pure methane at 50 °C, 1 bar. Compartment B contains 0.8 mol of a methane-ethane mixture at 100 °C, 1 bar with y_methane = 0.5. The partition is removed and the system reaches equilibrium.

a) What is the composition of the final mixture?

b) What is the temperature and pressure at the end of the process?

c) Calculate the entropy generation.

d) What is the change in the total Gibbs energy of the system?

e) How much work is needed to separate the final mixture into A and B at the conditions before mixing? Assume that the temperature of the surroundings is 20 °C.

f) Which of the above answer would change (and by how much), if both compartments contained methane? All other conditions are the same.

Additional data: The ideal-gas C_P’s of the pure components are: ethane: 10.3 R; methane: 6.2R; where R is the ideal-gas constant.

Problem 9.5: In Figure 9-3, all streams are mixtures of methane/carbon monoxide with molar compositions indicated on the flow chart. Calculate the material and energy balances and perform an entropy analysis of the mixing point, the heat exchanger, and of the entire process. The heat capacities of methane and carbon monoxide are C_PA = 40.8 J/mol K, and C_PB = 29.4 J/mol K, respectively.

Figure 9-3: Flow chart for Problem 9.5.

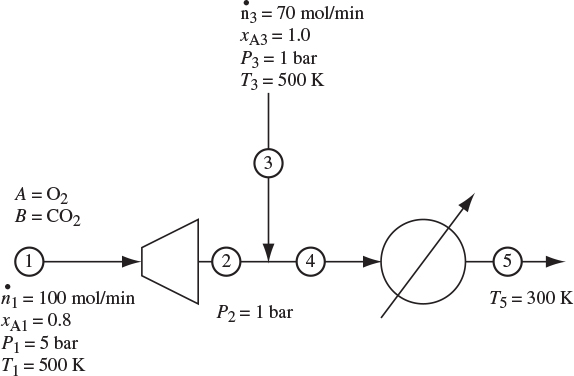
Problem 9.6: A mixture of O₂/CO₂ (stream 1) expands in turbine (see Figure 9-4). The outlet (stream 2) is mixed with a stream of pure oxygen and the new stream (number 4) passes through a heat exchanger and exits as stream 5. The efficiency of the turbine is 80%. There are no heat losses and pressure drops in pipes and in the heat exchanger can be ignored.

Figure 9-4: Flow chart for Problem 9.6.

a) Calculate the enthalpy and entropy of all streams. For the enthalpy and entropy of the pure components the reference state is at 5 bar, 500 K.

b) Calculate the work in the turbine, and the heat load in the heat exchanger.

c) Calculate the entropy generation.

d) Calculate the ideal work and the lost work for the process.

Additional data: Assume the components of their mixtures to be at the ideal-gas state at all pressures and temperatures of this problem with ideal-heat capacities, C_PA = 44.7 J/mol K, C_PB = 31.1 J/mol K.

Problem 9.7: A reservoir contains natural gas at a pressure of 5000 psig and a temperature of 180 °F. The composition of the gas is 80% methane, 15% ethane, and 5% CO₂ (all fractions are by mole). Estimate the temperature of the gas when it emerges at the surface under the following alternative assumptions:

a) The flow to the surface is assumed to be reversible adiabatic expansion.

b) The flow to the surface is assumed to be a throttling process.

Take the natural gas to be an ideal-gas mixture with temperature-dependent heat capacities for each component given in Perry’s Handbook. Is the ideal-gas assumption reasonable?

Problem 9.8: A flow process receives two streams (A and B) that contain mixtures of methane and propane and produce a stream of pure methane (C) and a stream of pure propane (D). All streams may be considered ideal-gas mixtures with heat capacities, 35 and 53 J/mol K, for methane and ethane, respectively. Information about the system is given in the table below.

a) Fill out the missing entries on this table. For the enthalpy and entropy, use as reference state the pure components in the ideal-gas state at 1 bar, 300 K.

b) Calculate the ideal work for this process.

Problem 9.9: A process stream contains a mixture of argon (1) and ethane (2) with the following properties: P = 50 bar, T = −123 °C, x₁ = 0.75 (by mole). Under these conditions the residual properties of the stream are, H^R = −7211 J/mol, S^R = −36 J/mol K.

a) Calculate the enthalpy of the mixture.

b) Calculate the entropy of the mixture.

c) This stream is to be separated into its pure components in a flow process from which the two pure streams exit at 1 bar, 25 °C. Assuming the surroundings to be at 25 °C, what is the ideal work for this process? Is this work produced or absorbed by the process?

Additional information: The reference state for both components is the ideal-gas state at P_ref = 1 bar, T_ref = −123 °C. The ideal-gas heat capacities of the pure components are , (where R is the ideal-gas constant) and may be assumed independent of temperature. At 25 °C, 1 bar, argon, and ethane may be assumed to be in the ideal-gas state.

Problem 9.10: A flow process is used to split a mixture of carbon monoxide (1) and ethane (2) (stream A) into two streams, B and C. Information about the inlet and outlet streams is shown in the table below.

a) Fill out the table.

b) Calculate the entropy change for this process.

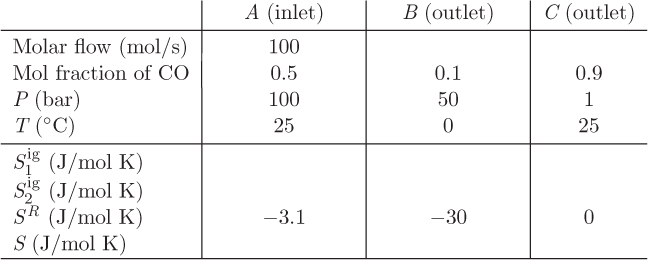
Reference states for both components: ideal-gas state at 50 bar, 25 °C. Ideal-gas heat capacities: ; .

Problem 9.11: A batch of natural gas contains 93% by mol methane with the rest being mostly ethane. Use the SRK equation to estimate the volume of tank needed to store 100 kg of this natural gas in liquid form at 1 bar, at −165 °C.

Problem 9.12: a) Use the SRK equation to calculate the residual properties of a N₂(1)/CH₄(2) mixture at 120 K, 10 bar, with x₁ = 0.5. Under the conditions, the mixture is in the liquid phase.

b) Calculate the enthalpy and entropy of the mixture in the previous part using as reference for both components the ideal-gas state at 25 °C, 1 bar. The ideal-gas heat capacities of the two components are:

C_P1 = 29 + 0.0005768T, C_P2 = 24 + 0.03926T

with T in K and C_P in J/mol/K.

Problem 9.13: In an air-liquefaction process, air is compressed from 1 bar, 25 °C, to 180 bar. To avoid overheating, compression is done in stages so that the exit temperature does not exceed 200 °C. The stream exiting a stage is cooled to 25 °C before it is led to the next stage. If the efficiency of each stage is 80%, determine the number of stages, and the total amount of compression work.

Problem 9.14: Use the SRK equation to do the following calculations:

a) The enthalpy (J/mol) of a vapor mixture at 1.2 bar, 130 °C, that contains 25% (by mol) n-hexane in n-octane.

b) The enthalpy of a liquid solution at 1.2 bar 90 °C that contains 25% (by mol) n-hexane in n-octane.

c) A mixture of n-hexane (25% by mole) in n-octane, initially at 1.2 bar, 130 °C, passes through a heat exchanger and exits as liquid at 90 °C. Assuming no pressure drop in the heat exchanger, calculate the amount of heat removed.

Additional data: Assume for simplicity that the ideal-gas heat capacities are constant: n-hexane = 176 J/mol K; n-octane = 247 J/mol K.

The reference state for both pure components is the ideal-gas state at 1 bar, 300 K.