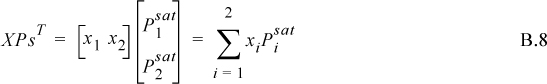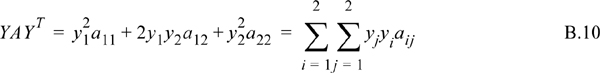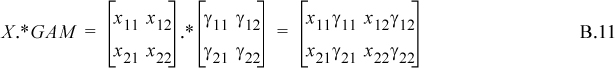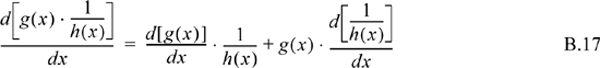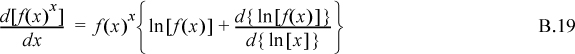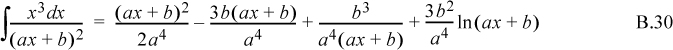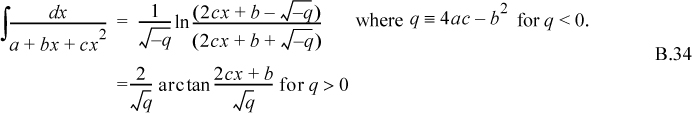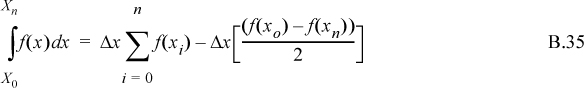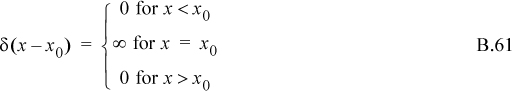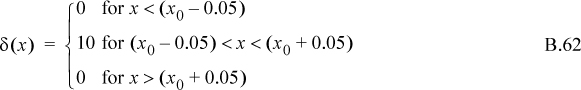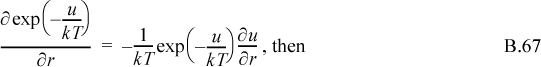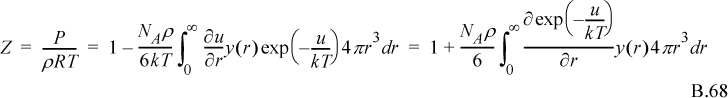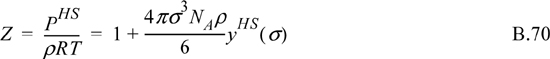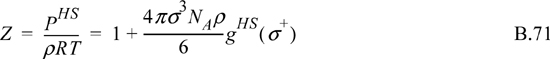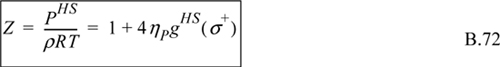Appendix B. Mathematics
B.1. Important Relations
Algebra
Some functions like logarithms and exponentials appear so often in thermodynamics that it makes sense to summarize some of them here. Also, integrations and differentiations are frequently performed, so a few important formulae are presented.
The quadratic formula provides roots to the equation ax2 + bx + c = 0:
Cubic equations are discussed in Section B.2.
Beginning in Chapter 10, summation notation is used extensively. Many of the formulas are easily programmed using matrices and linear algebra. A matrix is a rectangular representation of the elements of an array. The elements of an array are identified by subscripts. For example:
X = [0.4, 0.6], x1 = 0.4, x2 = 0.6
For a multidimensional array, the first element subscript represents the row and the second element subscript identifies the column, for example:

The transpose of a matrix is obtained by exchanging aij with aji. In shorthand notation, the transpose is represented by a superscript T. The number of rows and columns interchange after the transpose operation:
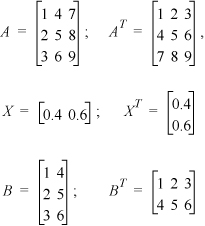
Matrices can be multiplied. The product of array1 and array2 becomes array3 and:
a. The number of columns in array1 must equal the number of rows in array2.
b. array3 has the same number of rows as array1 and the same number of columns as array2.
c. Element ij of array3 is obtained by multiplying the elements in the ith row of array1 by the elements in the jth column of array2 and summing the products.
For one-dimensional arrays,
which is the linear mixing rule, Eqn. 15.8. Suppose ![]() and
and ![]() , then
, then
which is a bubble formula for Raoult’s Law. A set of compositions can be stored in a matrix. For example, using two sets of compositions,
where the first subscript in designation for X indicates the data set, and the subscripts on Pbub indicate the corresponding bubble pressure for that composition.
An example of a one- and two-dimensional array is:

Multiplying the result by YT,
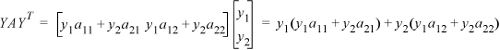
when aij = aji, we may write
which is the quadratic mixing rule, Eqn. 15.8. For an example using two multidimensional arrays:
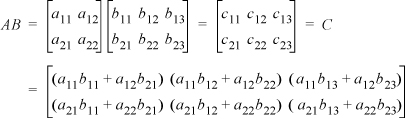
MATLAB offers element-by-element algebra for vectors and matrices. If two matrices have the same dimensions, they may be dot multiplied. For example:
Therefore, modified Raoult’s law can be programmed for bubble-pressure calculations as
For an overview of programming arrays in Excel, see Appendix A.
Calculus
Differentiation:
General differentiation of composite functions:
(Product rule)
Integration:
Integration by parts ![]() .
.
Numerical integration by trapezoidal rule:
where Δx is a constant step size between discrete values of f(x).
See also Chapter 6 for additional mathematical relationships.
B.2. Solutions to Cubic Equations
A cubic equation of state may be solved by trial and error or analytically,
where the a2, a1, and a0 are constants for the purposes of solving the cubic.
Iterative Method
The Newton-Raphson method uses an initial guess along with the derivative value to rapidly converge on the solution. This discussion focuses on an example solution for the following equation:
We seek the value of Z where F = 0. Suppose we have made an initial guess Zold which gives a value Fold, as shown in the upper-left graph in Fig. 7.6 on page 265. We are seeking a value of Z that results in F = 0. If Fold is the current value, and if we use the derivative of F as a linear approximation of the function behavior, then 0 = m · Znew + b, (where the slope m can be calculated analytically from Eqn. B.37 as dF/dZ = (3Z2 – 2(1 – B)Z + (A – 3B2 – 2B)). Since the current point is on the same line, we may also write Fold = m · Zold + b. Taking the difference we get 0 – Fold = m · (Znew–Zold) + (b–b) or rearranging, –Fold/m + Zold = Znew. Since m = (dF/dZ), we have Znew = Zold – F/(dF/dZ). The procedure can be repeated until the answer is obtained. A summary of steps is:
1. Guess Zold = 1 or Zold = 0 and compute Fold(Zold).
2. Compute dF/dZ.
3. Compute Znew = Zold – F/(dF/dZ).
4. If |ΔZ/Znow| < 1.E – 5, print the value of Znow and stop.
5. Compute Fnew(Znew) and use this as Fold. Return to step 3 until step 4 terminates.
Note that an initial guess of Z = 0 converges on the smallest real root. An initial guess of Z = 1 almost always converges on the largest real root. At very high reduced pressures, an initial guess greater than one is sometimes required since the compressibility factor can exceed one (see Fig. 7.4 on page 257).
Analytical Method
Below are summaries of two methods for solving analytically. These techniques are implemented for the Peng-Robinson equation in the spreadsheet Preos.xlsx. Eqn. B.36 can be reduced to the form
by substituting for Z the value
The values of p and q for Eqn. B.38 will then be
If a2, a1, and a0 are real (which they are for an EOS), then defining
results in one real root and two conjugate roots if R > 0;
results in three real roots, of which two are equal if R = 0;
results in three real and unequal roots if R < 0.
Solution Method I: Algebraic Solution
Let
The values of x are given by using Eqns. B.40, B.41, and B.42:
Values of Z are then found with Eqn. B.39.
Solution Method II: Trigonometric Solution
Let x = m cos θ; then
therefore,
which leads to
therefore,
where θ1 is in radians. By the functionality of the cosine function, two other solutions will be
The values of x are given by using Eqns. B.40 and B.48:
Values of Z are found with Eqn. B.39.
Sorting Roots
Meaningful roots for the Peng-Robinson and many other common EOSs are of the form
P = Prep + Patt
where ![]() . To ensure that Prep > 0, we must have Z > B, where B = bP/(RT).
. To ensure that Prep > 0, we must have Z > B, where B = bP/(RT).
When three real, positive roots exist, the meaningful roots must satisfy ![]() , that is, the isothermal compressibility must be positive. The value of κT may also be used to determine whether a root is vapor or liquid in cases where only one root is found by identifying the phase with the larger isothermal compressibility as the vapor phase. κT is always greater for a vapor root than for a liquid root except at the critical point.1
, that is, the isothermal compressibility must be positive. The value of κT may also be used to determine whether a root is vapor or liquid in cases where only one root is found by identifying the phase with the larger isothermal compressibility as the vapor phase. κT is always greater for a vapor root than for a liquid root except at the critical point.1
Determination of Equation of State Constants from the Critical Point
Determination of equation of state constants from the critical conditions has been the prevalent method of characterizing fluids. When a cubic equation of state is fit to the critical point, the parameters may be determined in a couple of ways. First, we can evaluate the derivatives,
applied at Tc. By differentiating the equation of state, the resultant equations can be simultaneously solved to find two equation of state constants. A simpler approach using significantly less calculus and algebra is to write out (Z – Zc)3, which goes to zero at the critical point.
If we compare Eqn. B.51 with Eqn. B.36 at the critical point, we find
For the van der Waals equation, comparing Eqns. B.51 and B.52 with Example 7.7 on page 271,
where the superscript EOS has been added to explicitly show that this is the value predicted by the equation of state. Plugging Eqn. B.54 into Eqn. B.55, we find
Plugging into Eqn. B.53,
Thus, the van der Waals equation predicts a universal value of Zc = 0.375. Plugging this into Eqn. B.56, we find
and into Eqn. B.54,
B.3. The Dirac Delta Function
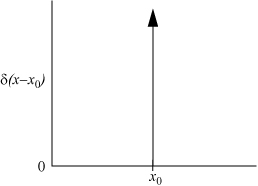
Understanding many of the terms appearing in thermodynamic functions like the repulsive contribution to the equation of state requires an understanding of a somewhat peculiar mathematical function known as the Dirac delta function. This function has the property of “filtering” the value of a function being integrated and focusing attention on the function value at a particular value of the independent variable. That is, over the interval x1 < x0 < x2,
where δ is the Dirac delta function defined by
and shown in the figure below. The following discussion should clarify the function.
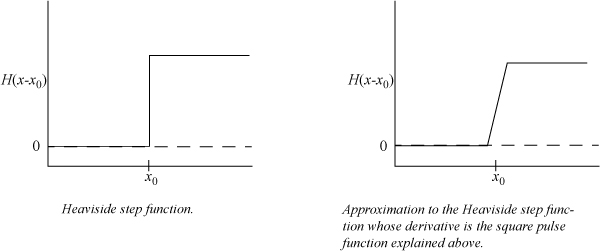
The Dirac delta function
Suppose for the moment that we approximate the delta function as a square pulse function, such that,
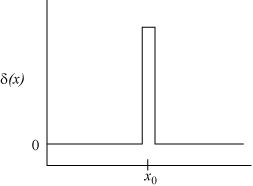
Approximation of the Dirac delta function as a square pulse function.
Then when we evaluate the integral,
a reasonable approximation would be that F(x) = F(x0) over the relatively short interval where δ holds a nonzero value. Since F (x0) is approximately constant over the short interval, it may be factored out of the integral, giving,
The next step is obvious. Let δ be zero except for an interval of ±0.005 around x0. Within the interval, set δ = 100. Then our approximation of F(x) = F(x0) throughout the interval is even more reasonable. Proceeding in this fashion leads to an interval that is differentially deviating from x0 with δ approaching infinity.
This seems like a crazy thing to do, since we have now defined the function value to be itself times an integral that must be unity. But note that our ultimate goal is to leave the function inside and we will show how this helps us momentarily. Looking at this final result, we see that the function δ has filtered out the value of F(x) at a single value of x.
Despite its peculiarity, the δ function is a well-defined function and therefore integrable. To understand the importance of the δ function, consider taking the derivative of a step function, H(x – x0), shown below. The derivative of H(x – x0) is positively infinite at x0 but zero on either side of x0. It may help you to imagine slanting the corners of the step function and plotting the derivative first and then making the corners systematically more square. If you plot this derivative function, you will see that it is the square pulse function and becomes the Dirac delta function in the limit of the Heaviside step function. Therefore, the Dirac delta function is the derivative of a Heaviside step function. And the integral of the Dirac delta function is equal to the Heaviside step function. It is really this last observation that permits us to derive important results for the integrals of discontinuous functions.
Example B.1. The hard-sphere equation of state
A significant application of the Dirac delta function is suggested by the pressure equation developed for hard-sphere fluids. The discussion in Unit II indicates that, at low density, the radial distribution function (rdf) is given by a simple Boltzmann weighting probability:
g(r) ~ exp(–u/kT)
Note that for hard-sphere fluids, this function is discontinuous and behaves as the Heaviside step function at r = σ.
The pressure equation is:
If we were to substitute the hard-sphere potential and a discontinuous rdf like the low-density one into the pressure equation, we would have a combination of discontinuities that we could not resolve. Note what happens if we postulate a function y(r) such that
Clearly, y(r) would be continuous at low density and approaches a value of one. Furthermore, it turns out that y(r) can be rigorously proven to be continuous for all densities and all potentials.1 Apply these insights to develop the equation of state for a hard-sphere fluid in terms of its rdf value at r = σ.
Solution
Substituting g(r) = y(r)exp(–u/kT) and recognizing
If you plot the function exp(–u/kT) versus r for the hard-sphere potential, you will see that it is a Heaviside step function. This means that its derivative is a Dirac delta. So the pressure equation becomes,
Applying Eqn. B.60,
Although it may seem that we don’t know y(σ), recall that it is a continuous function. Therefore the value of y(σ) will be approximated by y(σ+). Further, recognizing that uHS(σ+) = 0, therefore exp(uHS(σ+)/kT) = 1 in Eqn. B.66, and therefore yHS(σ+) = gHS(σ+).
Defining ![]()
The relationship between ZHS and gHS(σ+) is used often. It provides the functional form for building Zrep in the equation of state. It also provides a basis for converting our approximate equation of state for Zrep back into a quantitative estimate of gHS(σ). Recognize that Eqn. B.72 is a virial equation for hard spheres, Z = 1 + Bρ. At low density, gHS(σ+) = exp(–uHS(σ+)/kT) = 1, resulting in Boltzmann’s value for the second virial coefficient for hard spheres.
Example B.2. The square-well equation of state
The preceding example illustrates the use of all the tools necessary to develop any equation of state, but one more illustration may help to clarify the way that the tools can be used in combination to derive a wide variety of results. The problem statement is as follows: Develop a formula for deriving the equation of state for any fluid described by the square-well potential (λ = 1.5), given an estimate for the radial distribution function (rdf). Apply this formula to obtain the equation of state from the following approximation for the rdf,
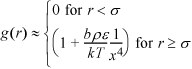
where x = r/σ, and b = πNAσ3/6. Before looking at the solution, think for yourself. Can you conceive of how to solve the problem without any help?
Solution
The trick is to realize that the exponential of the square-well potential is composed of two step functions, each of a different height. The step up is of height, exp(ε/kT) whereas the step down is of height, exp(ε/kT) –1.
exp(–u/kT) = exp(ε/kT) H(r – σ) – [exp(ε/kT) –1]·H(r – λσ)
Taking the derivative of the Heaviside function gives the Dirac Delta in two places:
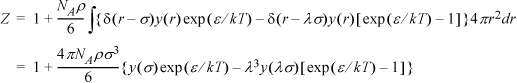
Noting that y(r) = g(r)exp(u/kT) and that exp(u/kT) is best evaluated inside the well:
This is valid for the square-well fluid with any g(r).
For the above expression for λ = 1.5: g(σ+) = 1 + bρε/kT and g(λσ–) = g(1.5σ–)= 1 + 0.198 bρε/kT
At the given conditions: Z = 1 + 4(0.2){1 + 0.2 – 2.1333(1.0396)} = 0.1858
It would be straightforward at this point to develop the entire phase diagram for this new equation of state. The result would yield expressions for ε/k and b in terms of Tc and Pc. The value for the acentric factor would be a fixed value since there is no third parameter to affect it. Its numerical value could be determined in the same way that the value was determined for the van der Waals equation in Chapter 8.
At first glance, one may wonder why we have expended so much effort to represent this problem in terms of the rdf when we must approximate it anyway. It may seem fruitless to have translated our ignorance of the equation of state into ignorance of the radial distribution function. It turns out that the thermodynamic properties are fairly insensitive to details of the rdf. If you doubt this, reflect on what van der Waals achieved by effectively assuming that g (r) = 1 for all temperatures and densities. Furthermore, if you refer to the discussion of local composition theory in Chapter 13, you will see that the fundamental basis for virtually all of the activity coefficient models currently in use is: gij(r)/gjj(r) = exp[(εij – εjj)/kT)]. As a slightly oversimplified summary of modern research in equilibrium thermodynamics, one could say that it is a search for better approximations of the radial distribution function. The thermodynamics of hydrogen bonding can be related to the rdf as discussed in Chapter 19. The thermodynamics of polymers and folding of proteins simply require generalization in terms of an intramolecular rdf known as the conformation. Electrolyte and solution thermodynamics are given very directly in terms of the rdf as discussed in Chapter 13. Adsorption and slit thermodynamics can be expressed in terms of the rdf between the fluid molecules and the adsorbent surface. Clearly, even rough approximations can be very useful when developed at the level of the rdf and carried to their logical conclusion. It may not be worth the effort for every chemical engineer, but it should not be beyond the grasp of many engineering students who sincerely want to understand the method behind the madness of fugacity estimation.