Appendix B. The Naylor-Shine Table for Determining the Increase in Mean Criterion Score Obtained by Using a Selection Device
Using the Table
The following definitions are used in the table:
And the table is based upon the following equation:
![]()
Note: The use of the table may differ slightly in the case where rxy is really a multiple regression coefficient. The major difference occurs in the Zxi column. With a single predictor, there is no difficulty in expressing a cutoff score in terms of a particular value of X, the predictor variable (thus, we use Zxi). However, in the case of multiple predictors, it is no longer feasible to do so because there are several X variables. The easiest procedure, therefore, is to reduce conceptually the multivariate case to the bivariate case by treating the multiple correlation coefficient as the correlation coefficient between the observed criterion scores (Zy) and the predicted criterion scores (Z’y). Thus, it becomes possible to talk about cutoff values for the multiple predictor case, but these cutoff scores are expressed in terms of Z’yi values rather than Zxi values. The only difficulty this creates is that s2z’y ≠ 1, but will always be equal to R2xy, the squared multiple correlation coefficient. Thus, to use the tables when rxy is actually a multiple correlation coefficient, it is necessary to transform Z’yi values by the following:
![]()
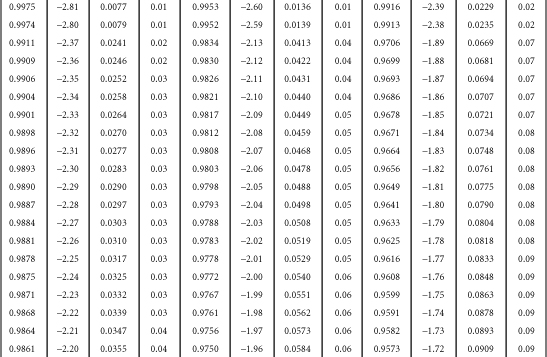
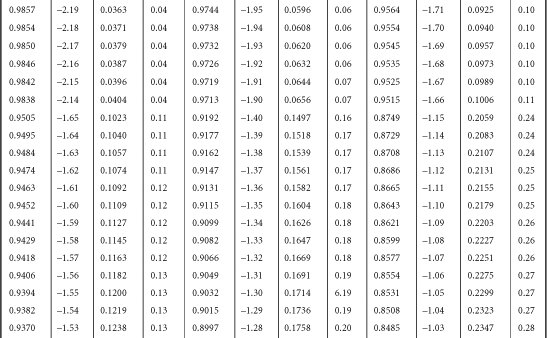
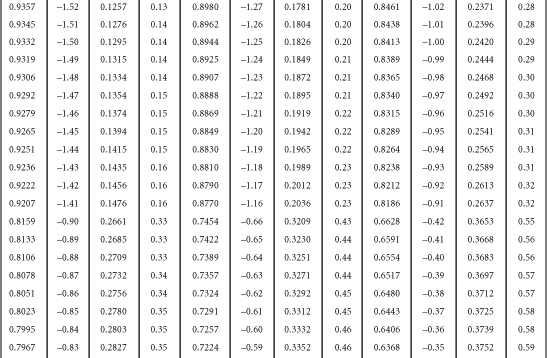
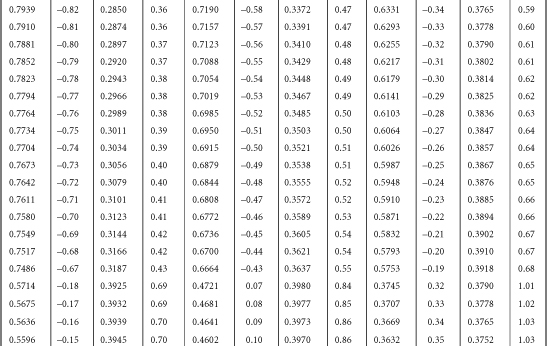
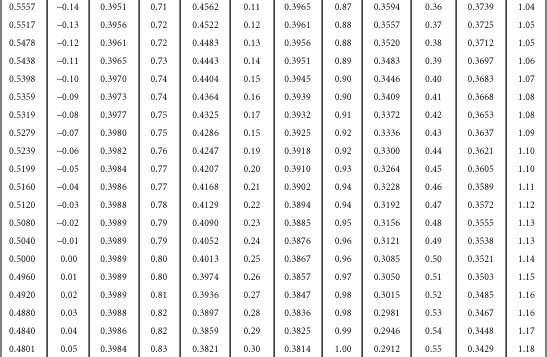
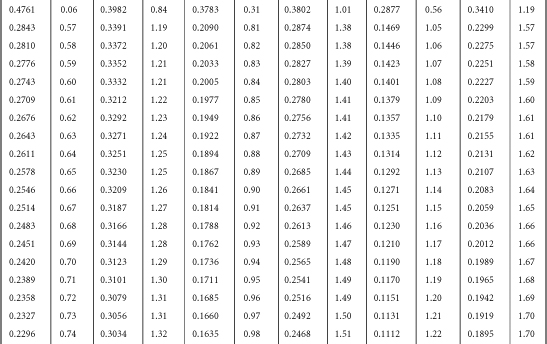
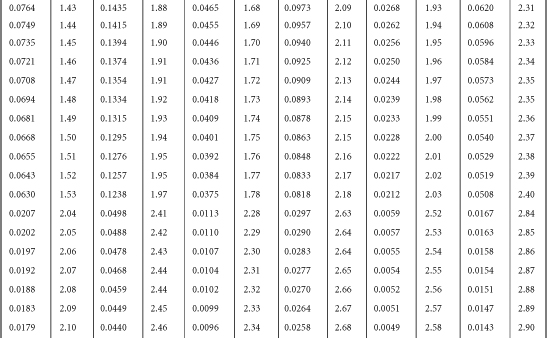
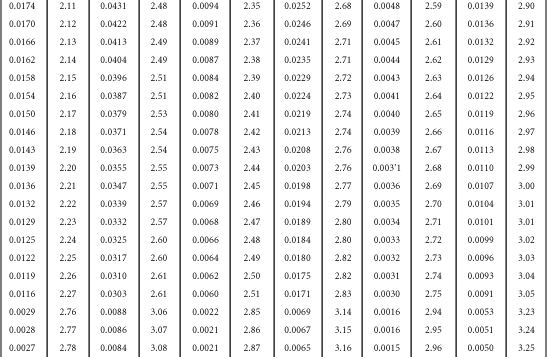
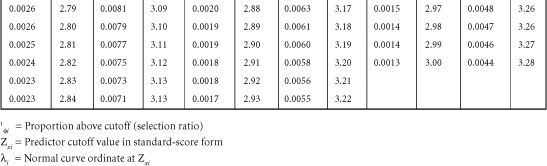
Table B-1. A Table for Computing the Mean Criterion Score (Zyi) for the Group Falling above Some Cutoff Score (Zxi)
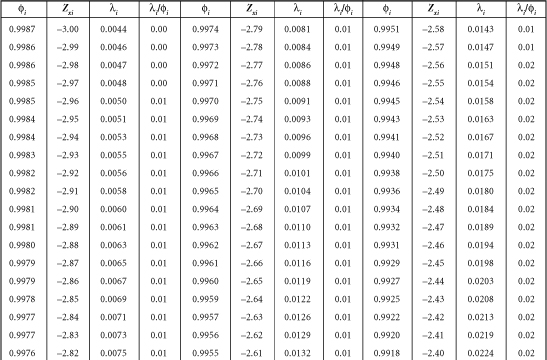
Source: J.C. Naylor and L.C. Shine, “A Table for Determining the Increase in Mean Criterion Score Obtained by Using a Selection Device.” Journal of Industrial Psychology, 3, 1965, 33-42. Used by permission.