2.3 Recursion
The idea of calling one function from another immediately suggests the possibility of a function calling itself. The function-call mechanism in Java and most modern programming languages supports this possibility, which is known as recursion. In this section, we will study examples of elegant and efficient recursive solutions to a variety of problems. Recursion is a powerful programming technique that we use often in this book. Recursive programs are often more compact and easier to understand than their nonrecursive counterparts. Few programmers become sufficiently comfortable with recursion to use it in everyday code, but solving a problem with an elegantly crafted recursive program is a satisfying experience that is certainly accessible to every programmer (even you!).
Recursion is much more than a programming technique. In many settings, it is a useful way to describe the natural world. For example, the recursive tree (to the left) resembles a real tree, and has a natural recursive description. Many, many phenomena are well explained by recursive models. In particular, recursion plays a central role in computer science. It provides a simple computational model that embraces everything that can be computed with any computer; it helps us to organize and to analyze programs; and it is the key to numerous critically important computational applications, ranging from combinatorial search to tree data structures that support information processing to the fast Fourier transform for signal processing.

One important reason to embrace recursion is that it provides a straightforward way to build simple mathematical models that we can use to prove important facts about our programs. The proof technique that we use to do so is known as mathematical induction. Generally, we avoid going into the details of mathematical proofs in this book, but you will see in this section that it is worthwhile to understand that point of view and make the effort to convince yourself that recursive programs have the intended effect.

Your first recursive program
The “Hello, World” for recursion is the factorial function, defined for positive integers n by the equation
n ! = n × (n–1) × (n–2) × ... × 2 × 1
In other words, n! is the product of the positive integers less than or equal to n. Now, n! is easy to compute with a for loop, but an even easier method is to use the following recursive function:
public static long factorial(int n)
{
if (n == 1) return 1;
return n * factorial(n-1);
}
This function calls itself. The implementation clearly produces the desired effect. You can persuade yourself that it does so by noting that factorial() returns 1 = 1! when n is 1 and that if it properly computes the value
(n–1) ! = (n–1) × (n–2) × ... × 2 × 1
then it properly computes the value
n ! = n × (n–1)!
= n × (n–1) × (n–2) × ... × 2 × 1
To compute factorial(5), the recursive function multiplies 5 by factorial(4); to compute factorial(4), it multiplies 4 by factorial(3); and so forth. This process is repeated until calling factorial(1), which directly returns the value 1. We can trace this computation in precisely the same way that we trace any sequence of function calls. Since we treat all of the calls as being independent copies of the code, the fact that they are recursive is immaterial.
factorial(5)
factorial(4)
factorial(3)
factorial(2)
factorial(1)
return 1
return 2*1 = 2
return 3*2 = 6
return 4*6 = 24
return 5*24 = 120
Function-call trace for factorial(5)
Our factorial() implementation exhibits the two main components that are required for every recursive function. First, the base case returns a value without making any subsequent recursive calls. It does this for one or more special input values for which the function can be evaluated without recursion. For factorial(), the base case is n = 1. Second, the reduction step is the central part of a recursive function. It relates the value of the function at one (or more) arguments to the value of function at one (or more) other arguments. For factorial(), the reduction step is n * factorial(n-1). All recursive functions must have these two components. Furthermore, the sequence of argument values must converge to the base case. For factorial(), the value of n decreases by 1 for each call, so the sequence of argument values converges to the base case n = 1.
1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800 12 479001600 13 6227020800 14 87178291200 15 1307674368000 16 20922789888000 17 355687428096000 18 6402373705728000 19 121645100408832000 20 2432902008176640000
Values of n! in long
Tiny programs such as factorial() perhaps become slightly clearer if we put the reduction step in an else clause. However, adopting this convention for every recursive program would unnecessarily complicate larger programs because it would involve putting most of the code (for the reduction step) within curly braces after the else. Instead, we adopt the convention of always putting the base case as the first statement, ending with a return, and then devoting the rest of the code to the reduction step.
The factorial() implementation itself is not particularly useful in practice because n! grows so quickly that the multiplication will overflow a long and produce incorrect answers for n > 20. But the same technique is effective for computing all sorts of functions. For example, the recursive function
public static double harmonic(int n)
{
if (n == 1) return 1.0;
return harmonic(n-1) + 1.0/n;
}
computes the nth harmonic numbers (see PROGRAM 1.3.5) when n is small, based on the following equations:
Hn = 1 + 1/2 + ... + 1/n
= (1 + 1/2 + ... + 1/(n–1)) + 1/n
= Hn–1 + 1/n
Indeed, this same approach is effective for computing, with only a few lines of code, the value of any finite sum (or product) for which you have a compact formula. Recursive functions like these are just loops in disguise, but recursion can help us better understand the underlying computation.
Mathematical induction
Recursive programming is directly related to mathematical induction, a technique that is widely used for proving facts about the natural numbers.
Proving that a statement involving an integer n is true for infinitely many values of n by mathematical induction involves the following two steps:
• The base case: prove the statement true for some specific value or values of n (usually 0 or 1).
• The induction step (the central part of the proof): assume the statement to be true for all positive integers less than n, then use that fact to prove it true for n.
Such a proof suffices to show that the statement is true for infinitely many values of n: we can start at the base case, and use our proof to establish that the statement is true for each larger value of n, one by one.
Everyone’s first induction proof is to demonstrate that the sum of the positive integers less than or equal to n is given by the formula n (n + 1) / 2. That is, we wish to prove that the following equation is valid for all n ≥ 1:
1 + 2 + 3 ... + (n–1) + n = n (n + 1) / 2
The equation is certainly true for n = 1 (base case) because 1 = 1(1 + 1) / 2. If we assume it to be true for all positive integers less than n, then, in particular, it is true for n–1, so
1 + 2 + 3 ... + (n–1) = (n–1) n / 2
and we can add n to both sides of this equation and simplify to get the desired equation (induction step).
Every time we write a recursive program, we need mathematical induction to be convinced that the program has the desired effect. The correspondence between induction and recursion is self-evident. The difference in nomenclature indicates a difference in outlook: in a recursive program, our outlook is to get a computation done by reducing to a smaller problem, so we use the term reduction step; in an induction proof, our outlook is to establish the truth of the statement for larger problems, so we use the term induction step.
When we write recursive programs we usually do not write down a full formal proof that they produce the desired result, but we are always dependent upon the existence of such a proof. We often appeal to an informal induction proof to convince ourselves that a recursive program operates as expected. For example, we just discussed an informal proof to become convinced that factorial() computes the product of the positive integers less than or equal to n.
Program 2.3.1 Euclid’s algorithm
public class Euclid
{
public static int gcd(int p, int q)
{
if (q == 0) return p;
return gcd(q, p % q);
}
public static void main(String[] args)
{
int p = Integer.parseInt(args[0]);
int q = Integer.parseInt(args[1]);
int divisor = gcd(p, q);
StdOut.println(divisor);
}
}
p, q | arguments divisor | greatest common divisor
% java Euclid 1440 408 24 % java Euclid 314159 271828 1
This program prints the greatest common divisor of its two command-line arguments, using a recursive implementation of Euclid’s algorithm.
Euclid’s algorithm
The greatest common divisor (gcd) of two positive integers is the largest integer that divides evenly into both of them. For example, the greatest common divisor of 102 and 68 is 34 since both 102 and 68 are multiples of 34, but no integer larger than 34 divides evenly into 102 and 68. You may recall learning about the greatest common divisor when you learned to reduce fractions. For example, we can simplify 68/102 to 2/3 by dividing both numerator and denominator by 34, their gcd. Finding the gcd of huge numbers is an important problem that arises in many commercial applications, including the famous RSA cryptosystem.
We can efficiently compute the gcd using the following property, which holds for positive integers p and q:
If p > q, the gcd of p and q is the same as the gcd of q and p % q.
To convince yourself of this fact, first note that the gcd of p and q is the same as the gcd of q and p–q, because a number divides both p and q if and only if it divides both q and p–q. By the same argument, q and p–2q, q and p–3q, and so forth have the same gcd, and one way to compute p % q is to subtract q from p until getting a number less than q.
The static method gcd() in Euclid (PROGRAM 2.3.1) is a compact recursive function whose reduction step is based on this property. The base case is when q is 0, with gcd(p, 0) = p. To see that the reduction step converges to the base case, observe that the second argument value strictly decreases in each recursive call since p % q < q. If p < q, the first recursive call effectively switches the order of the two arguments. In fact, the second argument value decreases by at least a factor of 2 for every second recursive call, so the sequence of argument values quickly converges to the base case (see EXERCISE 2.3.11). This recursive solution to the problem of computing the greatest common divisor is known as Euclid’s algorithm and is one of the oldest known algorithms—it is more than 2,000 years old.
gcd(1440, 408)
gcd(408, 216)
gcd(216, 192)
gcd(192, 24)
gcd(24, 0)
return 24
return 24
return 24
return 24
return 24
Function-call trace for gcd()
Towers of Hanoi
No discussion of recursion would be complete without the ancient towers of Hanoi problem. In this problem, we have three poles and n discs that fit onto the poles. The discs differ in size and are initially stacked on one of the poles, in order from largest (disc n) at the bottom to smallest (disc 1) at the top. The task is to move all n discs to another pole, while obeying the following rules:
• Move only one disc at a time.
• Never place a larger disc on a smaller one.
One legend says that the world will end when a certain group of monks accomplishes this task in a temple with 64 golden discs on three diamond needles. But how can the monks accomplish the task at all, playing by the rules?
To solve the problem, our goal is to issue a sequence of instructions for moving the discs. We assume that the poles are arranged in a row, and that each instruction to move a disc specifies its number and whether to move it left or right. If a disc is on the left pole, an instruction to move left means to wrap to the right pole; if a disc is on the right pole, an instruction to move right means to wrap to the left pole. When the discs are all on one pole, there are two possible moves (move the smallest disc left or right); otherwise, there are three possible moves (move the smallest disc left or right, or make the one legal move involving the other two poles). Choosing among these possibilities on each move to achieve the goal is a challenge that requires a plan. Recursion provides just the plan that we need, based on the following idea: first we move the top n–1 discs to an empty pole, then we move the largest disc to the other empty pole (where it does not interfere with the smaller ones), and then we complete the job by moving the n–1 discs onto the largest disc.
TowersOfHanoi (PROGRAM 2.3.2) is a direct implementation of this recursive strategy. It takes a command-line argument n and prints the solution to the towers of Hanoi problem on n discs. The recursive function moves() prints the sequence of moves to move the stack of discs to the left (if the argument left is true) or to the right (if left is false). It does so exactly according to the plan just described.
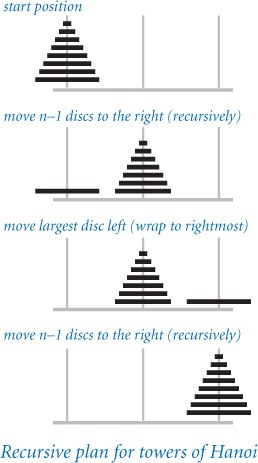
Function-call trees
To better understand the behavior of modular programs that have multiple recursive calls (such as TowersOfHanoi), we use a visual representation known as a function-call tree. Specifically, we represent each method call as a tree node, depicted as a circle labeled with the values of the arguments for that call. Below each tree node, we draw the tree nodes corresponding to each call in that use of the method (in order from left to right) and lines connecting to them. This diagram contains all the information we need to understand the behavior of the program. It contains a tree node for each function call.
We can use function-call trees to understand the behavior of any modular program, but they are particularly useful in exposing the behavior of recursive programs. For example, the tree corresponding to a call to move() in TowersOfHanoi is easy to construct. Start by drawing a tree node labeled with the values of the command-line arguments. The first argument is the number of discs in the pile to be moved (and the label of the disc to actually be moved); the second is the direction to move the disc. For clarity, we depict the direction (a boolean value) as an arrow that points left or right, since that is our interpretation of the value—the direction to move the piece. Then draw two tree nodes below with the number of discs decremented by 1 and the direction switched, and continue doing so until only nodes with labels corresponding to a first argument value 1 have no nodes below them. These nodes correspond to calls on moves() that do not lead to further recursive calls.

public class TowersOfHanoi
{
public static void moves(int n, boolean left)
{
if (n == 0) return;
moves(n-1, !left);
if (left) StdOut.println(n + " left");
else StdOut.println(n + " right");
moves(n-1, !left);
}
public static void main(String[] args)
{ // Read n, print moves to move n discs left.
int n = Integer.parseInt(args[0]);
moves(n, true);
}
}
n | number of discs left | direction to move pile
The recursive method moves() prints the moves needed to move n discs to the left (if left is true) or to the right (if left is false).
% java TowersOfHanoi 1 1 left % java TowersOfHanoi 2 1 right 2 left 1 right % java TowersOfHanoi 3 1 left 2 right 1 left 3 left 1 left 2 right 1 left
% java TowersOfHanoi 4
1 right
2 left
1 right
3 right
1 right
2 left
1 right
4 left
1 right
2 left
1 right
3 right
1 right
2 left
1 right
Take a moment to study the function-call tree depicted earlier in this section and to compare it with the corresponding function-call trace depicted at right. When you do so, you will see that the recursion tree is just a compact representation of the trace. In particular, reading the node labels from left to right gives the moves needed to solve the problem.
Moreover, when you study the tree, you probably notice several patterns, including the following two:
• Alternate moves involve the smallest disc.
• That disc always moves in the same direction.
These observations are relevant because they give a solution to the problem that does not require recursion (or even a computer): every other move involves the smallest disc (including the first and last), and each intervening move is the only legal move at the time not involving the smallest disc. We can prove that this approach produces the same outcome as the recursive program, using induction. Having started centuries ago without the benefit of a computer, perhaps our monks are using this approach.

Trees are relevant and important in understanding recursion because the tree is a quintessential recursive object. As an abstract mathematical model, trees play an essential role in many applications, and in CHAPTER 4, we will consider the use of trees as a computational model to structure data for efficient processing.
Exponential time
One advantage of using recursion is that often we can develop mathematical models that allow us to prove important facts about the behavior of recursive programs. For the towers of Hanoi problem, we can estimate the amount of time until the end of the world (assuming that the legend is true). This exercise is important not just because it tells us that the end of the world is quite far off (even if the legend is true), but also because it provides insight that can help us avoid writing programs that will not finish until then.
The mathematical model for the towers of Hanoi problem is simple: if we define the function T(n) to be the number of discs moved by TowersOfHanoi to solve an n-disc problem, then the recursive code implies that T(n) must satisfy the following equation:
T(n) = 2 T(n–1) + 1 for n > 1, with T(1) = 1
Such an equation is known in discrete mathematics as a recurrence relation. Recurrence relations naturally arise in the study of recursive programs. We can often use them to derive a closed-form expression for the quantity of interest. For T(n), you may have already guessed from the initial values T(1) = 1, T(2) = 3, T(3), = 7, and T(4) = 15 that T(n) = 2 n – 1. The recurrence relation provides a way to prove this to be true, by mathematical induction:
• Base case: T(1) = 2n – 1 = 1
• Induction step: if T(n–1)= 2n–1 – 1, T(n) = 2 (2n–1 – 1) + 1 = 2n – 1
Therefore, by induction, T(n) = 2n – 1 for all n > 0. The minimum possible number of moves also satisfies the same recurrence (see EXERCISE 2.3.11).
Knowing the value of T(n), we can estimate the amount of time required to perform all the moves. If the monks move discs at the rate of one per second, it would take more than one week for them to finish a 20-disc problem, more than 34 years to finish a 30-disc problem, and more than 348 centuries for them to finish a 40-disc problem (assuming that they do not make a mistake). The 64-disc problem would take more than 5.8 billion centuries. The end of the world is likely to be even further off than that because those monks presumably never have had the benefit of using PROGRAM 2.3.2, and might not be able to move the discs so rapidly or to figure out so quickly which disc to move next.

Even computers are no match for exponential growth. A computer that can do a billion operations per second will still take centuries to do 264 operations, and no computer will ever do 21,000 operations, say. The lesson is profound: with recursion, you can easily write simple short programs that take exponential time, but they simply will not run to completion when you try to run them for large n. Novices are often skeptical of this basic fact, so it is worth your while to pause now to think about it. To convince yourself that it is true, take the print statements out of TowersOfHanoi and run it for increasing values of n starting at 20. You can easily verify that each time you increase the value of n by 1, the running time doubles, and you will quickly lose patience waiting for it to finish. If you wait for an hour for some value of n, you will wait more than a day for n + 5, more than a month for n + 10, and more than a century for n + 20 (no one has that much patience). Your computer is just not fast enough to run every short Java program that you write, no matter how simple the program might seem! Beware of programs that might require exponential time.
We are often interested in predicting the running time of our programs. In SECTION 4.1, we will discuss the use of the same process that we just used to help estimate the running time of other programs.
Gray codes
The towers of Hanoi problem is no toy. It is intimately related to basic algorithms for manipulating numbers and discrete objects. As an example, we consider Gray codes, a mathematical abstraction with numerous applications.
The playwright Samuel Beckett, perhaps best known for Waiting for Godot, wrote a play called Quad that had the following property: starting with an empty stage, characters enter and exit one at a time so that each subset of characters on the stage appears exactly once. How did Beckett generate the stage directions for this play?
code |
subset |
move |
|
empty |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gray code representations |
||
One way to represent a subset of n discrete objects is to use a string of n bits. For Beckett’s problem, we use a 4-bit string, with bits numbered from right to left and a bit value of 1 indicating the character onstage. For example, the string 0 1 0 1 corresponds to the scene with characters 3 and 1 onstage. This representation gives a quick proof of a basic fact: the number different subsets of n objects is exactly 2 n. Quad has four characters, so there are 24 = 16 different scenes. Our task is to generate the stage directions.
An n-bit Gray code is a list of the 2n different n-bit binary numbers such that each element in the list differs in precisely one bit from its predecessor. Gray codes directly apply to Beckett’s problem because changing the value of a bit from 0 to 1 corresponds to a character entering the subset onstage; changing a bit from 1 to 0 corresponds to a character exiting the subset.
How do we generate a Gray code? A recursive plan that is very similar to the one that we used for the towers of Hanoi problem is effective. The n-bit binary-reflected Gray code is defined recursively as follows:
• The (n–1) bit code, with 0 prepended to each word, followed by
• The (n–1) bit code in reverse order, with 1 prepended to each word
The 0-bit code is defined to be empty, so the 1-bit code is 0 followed by 1. From this recursive definition, we can verify by induction that the n-bit binary reflected Gray code has the required property: adjacent codewords differ in one bit position. It is true by the inductive hypothesis, except possibly for the last codeword in the first half and the first codeword in the second half: this pair differs only in their first bit.
The recursive definition leads, after some careful thought, to the implementation in Beckett (PROGRAM 2.3.3) for printing Beckett’s stage directions. This program is remarkably similar to TowersOfHanoi. Indeed, except for nomenclature, the only difference is in the values of the second arguments in the recursive calls!

As with the directions in TowersOfHanoi, the enter and exit directions are redundant in Beckett, since exit is issued only when an actor is onstage, and enter is issued only when an actor is not onstage. Indeed, both Beckett and TowersOfHanoi directly involve the ruler function that we considered in one of our first programs (PROGRAM 1.2.1). Without the printing instructions, they both implement a simple recursive function that could allow Ruler to print the values of the ruler function for any value given as a command-line argument.
Gray codes have many applications, ranging from analog-to-digital converters to experimental design. They have been used in pulse code communication, the minimization of logic circuits, and hypercube architectures, and were even proposed to organize books on library shelves.
public class Beckett
{
public static void moves(int n, boolean enter)
{
if (n == 0) return;
moves(n-1, true);
if (enter) StdOut.println("enter " + n);
else StdOut.println("exit " + n);
moves(n-1, false);
}
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
moves(n, true);
}
}
n | number of actors enter | stage direction
This recursive program gives Beckett’s stage instructions (the bit positions that change in a binary-reflected Gray code). The bit position that changes is precisely described by the ruler function, and (of course) each actor alternately enters and exits.
% java Beckett 1 enter 1 % java Beckett 2 enter 1 enter 2 exit 1 % java Beckett 3 enter 1 enter 2 exit 1 enter 3 enter 1 exit 2 exit 1
% java Beckett 4
enter 1
enter 2
exit 1
enter 3
enter 1
exit 2
exit 1
enter 4
enter 1
enter 2
exit 1
exit 3
enter 1
exit 2
exit 1
Recursive graphics
Simple recursive drawing schemes can lead to pictures that are remarkably intricate. Recursive drawings not only relate to numerous applications, but also provide an appealing platform for developing a better understanding of properties of recursive functions, because we can watch the process of a recursive figure taking shape.
As a first simple example, consider Htree (PROGRAM 2.3.4), which, given a command-line argument n, draws an H-tree of order n, defined as follows: The base case is to draw nothing for n = 0. The reduction step is to draw, within the unit square
• three lines in the shape of the letter H
• four H-trees of order n–1, one centered at each tip of the H with the additional proviso that the H-trees of order n–1 are halved in size.
Drawings like these have many practical applications. For example, consider a cable company that needs to run cable to all of the homes distributed throughout its region. A reasonable strategy is to use an H-tree to get the signal to a suitable number of centers distributed throughout the region, then run cables connecting each home to the nearest center. The same problem is faced by computer designers who want to distribute power or signal throughout an integrated circuit chip.

Though every drawing is in a fixed-size window, H-trees certainly exhibit exponential growth. An H-tree of order n connects 4n centers, so you would be trying to plot more than a million lines with n = 10, and more than a billion with n = 15. The program will certainly not finish the drawing with n = 30.
If you take a moment to run Htree on your computer for a drawing that takes a minute or so to complete, you will, just by watching the drawing progress, have the opportunity to gain substantial insight into the nature of recursive programs, because you can see the order in which the H figures appear and how they form into H-trees. An even more instructive exercise, which derives from the fact that the same drawing results no matter in which order the recursive draw() calls and the StdDraw.line() calls appear, is to observe the effect of rearranging the order of these calls on the order in which the lines appear in the emerging drawing (see EXERCISE 2.3.14).
Program 2.3.4 Recursive graphics
public class Htree
{
public static void draw(int n, double size, double x, double y)
{ // Draw an H-tree centered at x, y
// of depth n and given size.
if (n == 0) return;
double x0 = x - size/2, x1 = x + size/2;
double y0 = y - size/2, y1 = y + size/2;
StdDraw.line(x0, y, x1, y);
StdDraw.line(x0, y0, x0, y1);
StdDraw.line(x1, y0, x1, y1);
draw(n-1, size/2, x0, y0);
draw(n-1, size/2, x0, y1);
draw(n-1, size/2, x1, y0);
draw(n-1, size/2, x1, y1);
}
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
draw(n, 0.5, 0.5, 0.5);
}
}
n | depth size | line length x, y | center

The function draw() draws three lines, each of length size, in the shape of the letter H, centered at (x, y). Then, it calls itself recursively for each of the four tips, halving the size argument in each call and using an integer argument n to control the depth of the recursion.



Brownian bridge
An H-tree is a simple example of a fractal: a geometric shape that can be divided into parts, each of which is (approximately) a reduced-size copy of the original. Fractals are easy to produce with recursive programs, although scientists, mathematicians, and programmers study them from many different points of view. We have already encountered fractals several times in this book—for example, IFS (PROGRAM 2.2.3).
The study of fractals plays an important and lasting role in artistic expression, economic analysis, and scientific discovery. Artists and scientists use fractals to build compact models of complex shapes that arise in nature and resist description using conventional geometry, such as clouds, plants, mountains, riverbeds, human skin, and many others. Economists use fractals to model function graphs of economic indicators.
Fractional Brownian motion is a mathematical model for creating realistic fractal models for many naturally rugged shapes. It is used in computational finance and in the study of many natural phenomena, including ocean flows and nerve membranes. Computing the exact fractals specified by the model can be a difficult challenge, but it is not difficult to compute approximations with recursive programs.
Brownian (PROGRAM 2.3.5) produces a function graph that approximates a simple example of fractional Brownian motion known as a Brownian bridge and closely related functions. You can think of this graph as a random walk that connects the two points (x0, y0) and (x1, y1), controlled by a few parameters. The implementation is based on the midpoint displacement method, which is a recursive plan for drawing the plot within the x-interval [x0, x1]. The base case (when the length of the interval is smaller than a given tolerance) is to draw a straight line connecting the two endpoints. The reduction case is to divide the interval into two halves, proceeding as follows:
• Compute the midpoint (xm, ym) of the interval.
• Add to the y-coordinate ym of the midpoint a random value δ, drawn from the Gaussian distribution with mean 0 and a given variance.
• Recur on the subintervals, dividing the variance by a given scaling factor s.

The shape of the curve is controlled by two parameters: the volatility (initial value of the variance) controls the distance the function graph strays from the straight line connecting the points, and the Hurst exponent controls the smoothness of the curve. We denote the Hurst exponent by H and divide the variance by 22H at each recursive level. When H is 1/2 (halved at each level), the curve is a Brownian bridge—a continuous version of the gambler’s ruin problem (see PROGRAM 1.3.8). When 0 < H < 1/2, the displacements tend to increase, resulting in a rougher curve. Finally, when 2 > H > 1/2, the displacements tend to decrease, resulting in a smoother curve. The value 2 –H is known as the fractal dimension of the curve.
public class Brownian
{
public static void curve(double x0, double y0,
double x1, double y1,
double var, double s)
{
if (x1 - x0 < 0.01)
{
StdDraw.line(x0, y0, x1, y1);
return;
}
double xm = (x0 + x1) / 2;
double ym = (y0 + y1) / 2;
double delta = StdRandom.gaussian(0, Math.sqrt(var));
curve(x0, y0, xm, ym + delta, var/s, s);
curve(xm, ym+delta, x1, y1, var/s, s);
}
public static void main(String[] args)
{
double hurst = Double.parseDouble(args[0]);
double s = Math.pow(2, 2*hurst);
curve(0, 0.5, 1.0, 0.5, 0.01, s);
}
}
x0, y0 | left endpoint x1, y1 | right endpoint xm, ym | middle delta | displacement var | variance hurst | Hurst exponent
By adding a small, random Gaussian to a recursive program that would otherwise plot a straight line, we get fractal curves. The command-line argument hurst, known as the Hurst exponent, controls the smoothness of the curves.



The volatility and initial endpoints of the interval have to do with scale and positioning. The main() test client in Brownian allows you to experiment with the Hurst exponent. With values larger than 1/2, you get plots that look something like the horizon in a mountainous landscape; with values smaller than 1/2, you get plots similar to those you might see for the value of a stock index.
Extending the midpoint displacement method to two dimensions yields fractals known as plasma clouds. To draw a rectangular plasma cloud, we use a recursive plan where the base case is to draw a rectangle of a given color and the reduction step is to draw a plasma cloud in each of the four quadrants with colors that are perturbed from the average with a random Gaussian. Using the same volatility and smoothness controls as in Brownian, we can produce synthetic clouds that are remarkably realistic. We can use the same code to produce synthetic terrain, by interpreting the color value as the altitude. Variants of this scheme are widely used in the entertainment industry to generate background scenery for movies and games.

Pitfalls of recursion
By now, you are perhaps persuaded that recursion can help you to write compact and elegant programs. As you begin to craft your own recursive programs, you need to be aware of several common pitfalls that can arise. We have already discussed one of them in some detail (the running time of your program might grow exponentially). Once identified, these problems are generally not difficult to overcome, but you will learn to be very careful to avoid them when writing recursive programs.
Missing base case
Consider the following recursive function, which is supposed to compute harmonic numbers, but is missing a base case:
public static double harmonic(int n)
{
return harmonic(n-1) + 1.0/n;
}
If you run a client that calls this function, it will repeatedly call itself and never return, so your program will never terminate. You probably already have encountered infinite loops, where you invoke your program and nothing happens (or perhaps you get an unending sequence of printed output). With infinite recursion, however, the result is different because the system keeps track of each recursive call (using a mechanism that we will discuss in SECTION 4.3, based on a data structure known as a stack) and eventually runs out of memory trying to do so. Eventually, Java reports a StackOverflowError at run time. When you write a recursive program, you should always try to convince yourself that it has the desired effect by an informal argument based on mathematical induction. Doing so might uncover a missing base case.
No guarantee of convergence
Another common problem is to include within a recursive function a recursive call to solve a subproblem that is not smaller than the original problem. For example, the following method goes into an infinite recursive loop for any value of its argument (except 1) because the sequence of argument values does not converge to the base case:
public static double harmonic(int n)
{
if (n == 1) return 1.0;
return harmonic(n) + 1.0/n;
}
Bugs like this one are easy to spot, but subtle versions of the same problem can be harder to identify. You may find several examples in the exercises at the end of this section.
Excessive memory requirements
If a function calls itself recursively an excessive number of times before returning, the memory required by Java to keep track of the recursive calls may be prohibitive, resulting in a StackOverflowError. To get an idea of how much memory is involved, run a small set of experiments using our recursive function for computing the harmonic numbers for increasing values of n:
public static double harmonic(int n)
{
if (n == 1) return 1.0;
return harmonic(n-1) + 1.0/n;
}
The point at which you get StackOverflowError will give you some idea of how much memory Java uses to implement recursion. By contrast, you can run PROGRAM 1.3.5 to compute Hn for huge n using only a tiny bit of memory.
Excessive recomputation
The temptation to write a simple recursive function to solve a problem must always be tempered by the understanding that a function might take exponential time (unnecessarily) due to excessive recomputation. This effect is possible even in the simplest recursive functions, and you certainly need to learn to avoid it. For example, the Fibonacci sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
is defined by the recurrence Fn = Fn–1 + Fn–2 for n ≥ 2 with F0 = 0 and F1 = 1. The Fibonacci sequence has many interesting properties and arise in numerous applications. A novice programmer might implement this recursive function to compute numbers in the Fibonacci sequence:
// Warning: this function is spectacularly inefficient.
public static long fibonacci(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
fibonacci(8)
fibonacci(7)
fibonacci(6)
fibonacci(5)
fibonacci(4)
fibonacci(3)
fibonacci(2)
fibonacci(1)
return 1
fibonacci(0)
return 0
return 1
fibonacci(1)
return 1
return 2
fibonacci(2)
fibonacci(1)
return 1
fibonacci(0)
return 0
return 1
return 3
fibonacci(3)
fibonacci(2)
fibonacci(1)
return 1
fibonacci(0)
return 0
return 1
fibonacci(1)
return 1
return 2
return 5
fibonacci(4)
fibonacci(3)
fibonacci(2)
.
.
.
Wrong way to compute Fibonacci numbers
However, this function is spectacularly inefficient! Novice programmers often refuse to believe this fact, and run code like this expecting that the computer is certainly fast enough to crank out an answer. Go ahead; see if your computer is fast enough to use this function to compute fibonacci(50). To see why it is futile to do so, consider what the function does to compute fibonacci(8) = 21. It first computes fibonacci(7) = 13 and fibonacci(6) = 8. To compute fibonacci(7), it recursively computes fibonacci(6) = 8 again and fibonacci(5) = 5. Things rapidly get worse because both times it computes fibonacci(6), it ignores the fact that it already computed fibonacci(5), and so forth. In fact, the number of times this program computes fibonacci(1) when computing fibonacci(n) is precisely Fn (see EXERCISE 2.3.12). The mistake of recomputation is compounded exponentially. As an example, fibonacci(200) makes F200 > 1043 recursive calls to fibonacci(1)! No imaginable computer will ever be able to do this many calculations. Beware of programs that might require exponential time. Many calculations that arise and find natural expression as recursive functions fall into this category. Do not fall into the trap of implementing and trying to run them.
Next, we consider a systematic technique known as dynamic programming, an elegant technique for avoiding such problems. The idea is to avoid the excessive recomputation inherent in some recursive functions by saving away the previously computed values for later reuse, instead of constantly recomputing them.
Dynamic programming
A general approach to implementing recursive programs, known as dynamic programming, provides effective and elegant solutions to a wide class of problems. The basic idea is to recursively divide a complex problem into a number of simpler subproblems; store the answer to each of these subproblems; and, ultimately, use the stored answers to solve the original problem. By solving each subproblem only once (instead of over and over), this technique avoids a potential exponential blow-up in the running time.
For example, if our original problem is to compute the nth Fibonacci number, then it is natural to define n + 1 subproblems, where subproblem i is to compute the ith Fibonacci number for each 0 ≤ i ≤ n. We can solve subproblem i easily if we already know the solutions to smaller subproblems—specifically, subproblems i–1 and i–2. Moreover, the solution to our original problem is simply the solution to one of the subproblems—subproblem n.
Top-down dynamic programming
In top-down dynamic programming, we store or cache the result of each subproblem that we solve, so that the next time we need to solve the same subproblem, we can use the cached values instead of solving the subproblem from scratch. For our Fibonacci example, we use an array f[] to store the Fibonacci numbers that have already been computed. We accomplish this in Java by using a static variable, also known as a class variable or global variable, that is declared outside of any method. This allows us to save information from one function call to the next.

Top-down dynamic programming is also known as memoization because it avoids duplicating work by remembering the results of function calls.
Bottom-up dynamic programming
In bottom-up dynamic programming, we compute solutions to all of the subproblems, starting with the “simplest” subproblems and gradually building up solutions to more and more complicated subproblems. To apply bottom-up dynamic programming, we must order the subproblems so that each subsequent subproblem can be solved by combining solutions to subproblems earlier in the order (which have already been solved). For our Fibonacci example, this is easy: solve the subproblems in the order 0, 1, and 2, and so forth. By the time we need to solve subproblem i, we have already solved all smaller subproblems—in particular, subproblems i–1 and i–2.
public static long fibonacci(int n)
{
long[] f = new int[n+1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];
}
When the ordering of the subproblems is clear, and space is available to store all the solutions, bottom-up dynamic programming is a very effective approach.
Next, we consider a more sophisticated application of dynamic programming, where the order of solving the subproblems is not so clear (until you see it). Unlike the problem of computing Fibonacci numbers, this problem would be much more difficult to solve without thinking recursively and also applying a bottom-up dynamic programming approach.
Longest common subsequence problem
We consider a fundamental string-processing problem that arises in computational biology and other domains. Given two strings x and y, we wish to determine how similar they are. Some examples include comparing two DNA sequences for homology, two English words for spelling, or two Java files for repeated code. One measure of similarity is the length of the longest common subsequence (LCS). If we delete some characters from x and some characters from y, and the resulting two strings are equal, we call the resulting string a common subsequence. The LCS problem is to find a common subsequence of two strings that is as long as possible. For example, the LCS of GGCACCACG and ACGGCGGATACG is GGCAACG, a string of length 7.
Algorithms to compute the LCS are used in data comparison programs like the diff command in Unix, which has been used for decades by programmers wanting to understand differences and similarities in their text files. Similar algorithms play important roles in scientific applications, such as the Smith–Waterman algorithm in computational biology and the Viterbi algorithm in digital communications theory.
Longest common subsequence recurrence
Now we describe a recursive formulation that enables us to find the LCS of two given strings s and t. Let m and n be the lengths of s and t, respectively. We use the notation s[i..m) to denote the suffix of s starting at index i, and t[j..n) to denote the suffix of t starting at index j. On the one hand, if s and t begin with the same character, then the LCS of x and y contains that first character. Thus, our problem reduces to finding the LCS of the suffixes s[1..m) and t[1..n). On the other hand, if s and t begin with different characters, both characters cannot be part of a common subsequence, so we can safely discard one or the other. In either case, the problem reduces to finding the LCS of two strings—either s[0..m) and t[1..n) or s[1..m) and t[0..n)—one of which is strictly shorter. In general, if we let opt[i][j] denote the length of the LCS of the suffixes s[i..m) and t[j..m), then the following recurrence expresses opt[i][j] in terms of the length of the LCS for shorter suffixes.
0 if i = m or j = n
opt[i][j] = opt[i+1, j+1] + 1 if s[i] = t[j]
max(opt[i, j+1], opt[i+1, j]) otherwise
Dynamic programming solution
LongestCommonSubsequence (PROGRAM 2.3.6) begins with a bottom-up dynamic programming approach to solving this recurrence. We maintain a two-dimensional array opt[i][j] that stores the length of the LCS of the suffixes s[i..m) and t[j..n). Initially, the bottom row (the values for i = m) and the right column (the values for j = n) are 0. These are the initial values. From the recurrence, the order of the rest of the computation is clear: we start with opt[m][n]. Then, as long as we decrease either i or j or both, we know that we will have computed what we need to compute opt[i][j], since the two options involve an opt[][] entry with a larger value of i or j or both. The method lcs() in PROGRAM 2.3.6 computes the elements in opt[][] by filling in values in rows from bottom to top (i = m-1 to 0) and from right to left in each row (j = n-1 to 0). The alternative choice of filling in values in columns from right to left and from bottom to top in each row would work as well. The diagram at the bottom of this page has a blue arrow pointing to each entry that indicates which value was used to compute it. (When there is a tie in computing the maximum, both options are shown.)
Program 2.3.6 Longest common subsequence
public class LongestCommonSubsequence
{
public static String lcs(String s, String t)
{ // Compute length of LCS for all subproblems.
int m = s.length(), n = t.length();
int[][] opt = new int[m+1][n+1];
for (int i = m-1; i >= 0; i--)
for (int j = n-1; j >= 0; j--)
if (s.charAt(i) == t.charAt(j))
opt[i][j] = opt[i+1][j+1] + 1;
else
opt[i][j] = Math.max(opt[i+1][j], opt[i][j+1]);
// Recover LCS itself.
String lcs = "";
int i = 0, j = 0;
while(i < m && j < n)
{
if (s.charAt(i) == t.charAt(j))
{
lcs += s.charAt(i);
i++;
j++;
}
else if (opt[i+1][j] >= opt[i][j+1]) i++;
else j++;
}
return lcs;
}
public static void main(String[] args)
{ StdOut.println(lcs(args[0], args[1])); }
}
s, t | two strings m, n | lengths of two strings opt[i][j] | length of LCS of x[i..m) and y[j..n) lcs | longest common subsequence
The function lcs() computes and returns the LCS of two strings s and t using bottom-up dynamic programming. The method call s.charAt(i) returns character i of string s.
The final challenge is to recover the longest common subsequence itself, not just its length. The key idea is to retrace the steps of the dynamic programming algorithm backward, rediscovering the path of choices (highlighted in gray in the diagram) from opt[0][0] to opt[m][n]. To determine the choice that led to opt[i][j], we consider the three possibilities:
• The character s[i] equals t[j]. In this case, we must have opt[i][j] = opt[i+1][j+1] + 1, and the next character in the LCS is s[i] (or t[j]), so we include the character s[i] (or t[j]) in the LCS and continue tracing back from opt[i+1][j+1].
• The LCS does not contain s[i]. In this case, opt[i][j] = opt[i+1][j] and we continue tracing back from opt[i+1][j].
• The LCS does not contain t[j]. In this case, opt[i][j] = opt[i][j+1] and we continue tracing back from opt[i][j+1].
We begin tracing back at opt[0][0] and continue until we reach opt[m][n]. At each step in the traceback either i increases or j increases (or both), so the process terminates after at most m + n iterations of the while loop.

Dynamic programming is a fundamental algorithm design paradigm, intimately linked to recursion. If you take later courses in algorithms or operations research, you are sure to learn more about it. The idea of recursion is fundamental in computation, and the idea of avoiding recomputation of values that have been computed before is certainly a natural one. Not all problems immediately lend themselves to a recursive formulation, and not all recursive formulations admit an order of computation that easily avoids recomputation—arranging for both can seem a bit miraculous when one first encounters it, as you have just seen for the LCS problem.
Perspective
Programmers who do not use recursion are missing two opportunities. First recursion leads to compact solutions to complex problems. Second, recursive solutions embody an argument that the program operates as anticipated. In the early days of computing, the overhead associated with recursive programs was prohibitive in some systems, and many people avoided recursion. In modern systems like Java, recursion is often the method of choice.
Recursive functions truly illustrate the power of a carefully articulated abstraction. While the concept of a function having the ability to call itself seems absurd to many people at first, the many examples that we have considered are certainly evidence that mastering recursion is essential to understanding and exploiting computation and in understanding the role of computational models in studying natural phenomena.
Recursion has reinforced for us the idea of proving that a program operates as intended. The natural connection between recursion and mathematical induction is essential. For everyday programming, our interest in correctness is to save time and energy tracking down bugs. In modern applications, security and privacy concerns make correctness an essential part of programming. If the programmer cannot be convinced that an application works as intended, how can a user who wants to keep personal data private and secure be so convinced?
Recursion is the last piece in a programming model that served to build much of the computational infrastructure that was developed as computers emerged to take a central role in daily life in the latter part of the 20th century. Programs built from libraries of functions consisting of statements that operate on primitive types of data, conditionals, loops, and function calls (including recursive ones) can solve important problems of all sorts. In the next section, we emphasize this point and review these concepts in the context of a large application. In CHAPTER 3 and in CHAPTER 4, we will examine extensions to these basic ideas that embrace the more expansive style of programming that now dominates the computing landscape.
A. No, any loop can be replaced by a recursive function, though the recursive version might require excessive memory.
Q. Are there situations when recursion is the only option available to address a problem?
A. No, any recursive function can be replaced by an iterative counterpart. In SECTION 4.3, we will see how compilers produce code for function calls by using a data structure called a stack.
Q. Which should I prefer, recursion or iteration?
A. Whichever leads to the simpler, more easily understood, or more efficient code.
Q. I get the concern about excessive space and excessive recomputation in recursive code. Anything else to be concerned about?
A. Be extremely wary of creating arrays in recursive code. The amount of space used can pile up very quickly, as can the amount of time required for memory management.
Exercises
2.3.1 What happens if you call factorial() with a negative value of n? With a large value of, say, 35?
2.3.2 Write a recursive function that takes an integer n as its argument and returns ln (n !).
2.3.3 Give the sequence of integers printed by a call to ex233(6):
public static void ex233(int n)
{
if (n <= 0) return;
StdOut.println(n);
ex233(n-2);
ex233(n-3);
StdOut.println(n);
}
2.3.4 Give the value of ex234(6):
public static String ex234(int n)
{
if (n <= 0) return "";
return ex234(n-3) + n + ex234(n-2) + n;
}
2.3.5 Criticize the following recursive function:
public static String ex235(int n)
{
String s = ex235(n-3) + n + ex235(n-2) + n;
if (n <= 0) return "";
return s;
}
Answer: The base case will never be reached because the base case appears after the reduction step. A call to ex235(3) will result in calls to ex235(0), ex235(-3), ex235(-6), and so forth until a StackOverflowError.
2.3.6 Given four positive integers a, b, c, and d, explain what value is computed by gcd(gcd(a, b), gcd(c, d)).
2.3.7 Explain in terms of integers and divisors the effect of the following Euclid-like function:
public static boolean gcdlike(int p, int q)
{
if (q == 0) return (p == 1);
return gcdlike(q, p % q);
}
2.3.8 Consider the following recursive function:
public static int mystery(int a, int b)
{
if (b == 0) return 0;
if (b % 2 == 0) return mystery(a+a, b/2);
return mystery(a+a, b/2) + a;
}
What are the values of mystery(2, 25) and mystery(3, 11)? Given positive integers a and b, describe what value mystery(a, b) computes. Then answer the same question, but replace + with * and return 0 with return 1.
2.3.9 Write a recursive program Ruler to plot the subdivisions of a ruler using StdDraw, as in PROGRAM 1.2.1.
2.3.10 Solve the following recurrence relations, all with T(1) = 1. Assume n is a power of 2.
• T(n) = T(n/2) + 1
• T(n) = 2T(n/2) + 1
• T(n) = 2T(n/2) + n
• T(n) = 4T(n/2) + 3
2.3.11 Prove by induction that the minimum possible number of moves needed to solve the towers of Hanoi satisfies the same recurrence as the number of moves used by our recursive solution.
2.3.12 Prove by induction that the recursive program given in the text makes exactly Fn recursive calls to fibonacci(1) when computing fibonacci(n).
2.3.13 Prove that the second argument to gcd() decreases by at least a factor of 2 for every second recursive call, and then prove that gcd(p, q) uses at most 2 log2 n + 1 recursive calls where n is the larger of p and q.
2.3.14 Modify Htree (PROGRAM 2.3.4) to animate the drawing of the H-tree. Next, rearrange the order of the recursive calls (and the base case), view the resulting animation, and explain each outcome.

Creative Exercises
2.3.15 Binary representation. Write a program that takes a positive integer n (in decimal) as a command-line argument and prints its binary representation. Recall, in PROGRAM 1.3.7, that we used the method of subtracting out powers of 2. Now, use the following simpler method: repeatedly divide 2 into n and read the remainders backward. First, write a while loop to carry out this computation and print the bits in the wrong order. Then, use recursion to print the bits in the correct order.
2.3.16 A4 paper. The width-to-height ratio of paper in the ISO format is the square root of 2 to 1. Format A0 has an area of 1 square meter. Format A1 is A0 cut with a vertical line into two equal halves, A2 is A1 cut with a horizontal line into two halves, and so on. Write a program that takes an integer command-line argument n and uses StdDraw to show how to cut a sheet of A0 paper into 2n pieces.
2.3.17 Permutations. Write a program Permutations that takes an integer command-line argument n and prints all n ! permutations of the n letters starting at a (assume that n is no greater than 26). A permutation of n elements is one of the n ! possible orderings of the elements. As an example, when n = 3, you should get the following output (but do not worry about the order in which you enumerate them):
bca cba cab acb bac abc
2.3.18 Permutations of size k. Modify Permutations from the previous exercise so that it takes two command-line arguments n and k, and prints all P(n, k) = n ! / (n–k)! permutations that contain exactly k of the n elements. Below is the desired output when k = 2 and n = 4 (again, do not worry about the order):
ab ac ad ba bc bd ca cb cd da db dc
2.3.19 Combinations. Write a program Combinations that takes an integer command-line argument n and prints all 2n combinations of any size. A combination is a subset of the n elements, independent of order. As an example, when n = 3, you should get the following output:
a ab abc ac b bc c
Note that your program needs to print the empty string (subset of size 0).
2.3.20 Combinations of size k. Modify Combinations from the previous exercise so that it takes two integer command-line arguments n and k, and prints all C(n, k) = n ! / (k !(n–k)!) combinations of size k. For example, when n = 5 and k = 3, you should get the following output:
abc abd abe acd ace ade bcd bce bde cde
2.3.21 Hamming distance. The Hamming distance between two bit strings of length n is equal to the number of bits in which the two strings differ. Write a program that reads in an integer k and a bit string s from the command line, and prints all bit strings that have Hamming distance at most k from s. For example, if k is 2 and s is 0000, then your program should print
0011 0101 0110 1001 1010 1100
Hint: Choose k of the bits in s to flip.
2.3.22 Recursive squares. Write a program to produce each of the following recursive patterns. The ratio of the sizes of the squares is 2.2:1. To draw a shaded square, draw a filled gray square, then an unfilled black square.

2.3.23 Pancake flipping. You have a stack of n pancakes of varying sizes on a griddle. Your goal is to rearrange the stack in order so that the largest pancake is on the bottom and the smallest one is on top. You are only permitted to flip the top k pancakes, thereby reversing their order. Devise a recursive scheme to arrange the pancakes in the proper order that uses at most 2n – 3 flips.
2.3.24 Gray code. Modify Beckett (PROGRAM 2.3.3) to print the Gray code (not just the sequence of bit positions that change).
2.3.25 Towers of Hanoi variant. Consider the following variant of the towers of Hanoi problem. There are 2n discs of increasing size stored on three poles. Initially all of the discs with odd size (1, 3, ..., 2n-1) are piled on the left pole from top to bottom in increasing order of size; all of the discs with even size (2, 4, ..., 2n) are piled on the right pole. Write a program to provide instructions for moving the odd discs to the right pole and the even discs to the left pole, obeying the same rules as for towers of Hanoi.
2.3.26 Animated towers of Hanoi. Use StdDraw to animate a solution to the towers of Hanoi problem, moving the discs at a rate of approximately 1 per second.
2.3.27 Sierpinski triangles. Write a recursive program to draw Sierpinski triangles (see PROGRAM 2.2.3). As with Htree, use a command-line argument to control the depth of the recursion.

2.3.28 Binomial distribution. Estimate the number of recursive calls that would be used by the code
public static double binomial(int n, int k)
{
if ((n == 0) && (k == 0)) return 1.0;
if ((n < 0) || (k < 0)) return 0.0;
return (binomial(n-1, k) + binomial(n-1, k-1))/2.0;
}
to compute binomial(100, 50). Develop a better implementation that is based on dynamic programming. Hint: See EXERCISE 1.4.41.
2.3.29 Collatz function. Consider the following recursive function, which is related to a famous unsolved problem in number theory, known as the Collatz problem, or the 3n+1 problem:
public static void collatz(int n)
{
StdOut.print(n + " ");
if (n == 1) return;
if (n % 2 == 0) collatz(n / 2);
else collatz(3*n + 1);
}
For example, a call to collatz(7) prints the sequence
7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
as a consequence of 17 recursive calls. Write a program that takes a command-line argument n and returns the value of i < n for which the number of recursive calls for collatz(i) is maximized. The unsolved problem is that no one knows whether the function terminates for all integers (mathematical induction is no help, because one of the recursive calls is for a larger value of the argument).
2.3.30 Brownian island. B. Mandelbrot asked the famous question How long is the coast of Britain? Modify Brownian to get a program BrownianIsland that plots Brownian islands, whose coastlines resemble that of Great Britain. The modifications are simple: first, change curve() to add a random Gaussian to the x-coordinate as well as to the y-coordinate; second, change main() to draw a curve from the point at the center of the canvas back to itself. Experiment with various values of the parameters to get your program to produce islands with a realistic look.

2.3.31 Plasma clouds. Write a recursive program to draw plasma clouds, using the method suggested in the text.
2.3.32 A strange function. Consider McCarthy’s 91 function:
public static int mcCarthy(int n)
{
if (n > 100) return n - 10;
return mcCarthy(mcCarthy(n+11));
}
Determine the value of mcCarthy(50) without using a computer. Give the number of recursive calls used by mcCarthy() to compute this result. Prove that the base case is reached for all positive integers n or find a value of n for which this function goes into an infinite recursive loop.
2.3.33 Recursive tree. Write a program Tree that takes a command-line argument n and produces the following recursive patterns for n equal to 1, 2, 3, 4, and 8.

2.3.34 Longest palindromic subsequence. Write a program LongestPalindromicSubsequence that takes a string as a command-line argument and determines the longest subsequence of the string that is a palindrome (the same when read forward or backward). Hint: Compute the longest common subsequence of the string and its reverse.
2.3.35 Longest common subsequence of three strings. Given three strings, write a program that computes the longest common subsequence of the three strings.
2.3.36 Longest strictly increasing subsequence. Given an integer array, find the longest subsequence that is strictly increasing. Hint: Compute the longest common subsequence of the original array and a sorted version of the array, where any duplicate values are removed.
2.3.37 Longest common strictly increasing subsequence. Given two integer arrays, find the longest increasing subsequence that is common to both arrays.
2.3.38 Binomial coefficients. The binomial coefficient C(n, k) is the number of ways of choosing a subset of k elements from a set of n elements. Pascal’s identity expresses the binomial coefficient C(n, k) in terms of smaller binomial coefficients: C(n, k) = C(n – 1, k – 1) + C(n – 1, k), with C(n, 0) = 1 for each integer n. Write a recursive function (do not use dynamic programming) to computer C(n, k). How long does it take to computer C(100, 15)? Repeat the question, first using top-down dynamic programming, then using bottom-up dynamic programming.
2.3.39 Painting houses. Your job is to paint a row of n houses red, green, or blue so as to minimize total cost, where cost(i, color) = cost to pain house i the specified color. You may not paint two adjacent houses the same color. Write a program to determine an optimal solution to the problem. Hint: Use bottom-up dynamic programming and solve the following subproblems for each i = 1, 2, …, n:
• red(i) = min cost to paint houses 1, 2, …, i so that the house i is red
• green(i) = min cost to paint houses 1, 2, …, i so that the house i is green
• blue(i) = min cost to paint houses 1, 2, …, i so that the house i is blue
2.4 Case Study: Percolation
The programming tools that we have considered to this point allow us to attack all manner of important problems. We conclude our study of functions and modules by considering a case study of developing a program to solve an interesting scientific problem. Our purpose in doing so is to review the basic elements that we have covered, in the context of the various challenges that you might face in solving a specific problem, and to illustrate a programming style that you can apply broadly.
2.4.2 Vertical percolation detection
2.4.4 Percolation probability estimate
Programs in this section
Our example applies a widely applicable computational technique known as Monte Carlo simulation to study a natural model known as percolation. The term “Monte Carlo simulation” is broadly used to encompass any computational technique that employs randomness to estimate an unknown quantity by performing multiple trials (known as simulations). We have used it in several other contexts already—for example, in the gambler’s ruin and coupon collector problems. Rather than develop a complete mathematical model or measure all possible outcomes of an experiment, we rely on the laws of probability.
In this case study we will learn quite a bit about percolation, a model which underlies many natural phenomena. Our focus, however, is on the process of developing modular programs to address computational tasks. We identify subtasks that can be independently addressed, striving to identify the key underlying abstractions and asking ourselves questions such as the following: Is there some specific subtask that would help solve this problem? What are the essential characteristics of this specific subtask? Might a solution that addresses these essential characteristics be useful in solving other problems? Asking such questions pays significant dividend, because they lead us to develop software that is easier to create, debug, and reuse, so that we can more quickly address the main problem of interest.
Percolation
It is not unusual for local interactions in a system to imply global properties. For example, an electrical engineer might be interested in composite systems consisting of randomly distributed insulating and metallic materials: which fraction of the materials need to be metallic so that the composite system is an electrical conductor? As another example, a geologist might be interested in a porous landscape with water on the surface (or oil below). Under which conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. It has been studied widely, and shown to be an accurate model in a dizzying variety of applications, beyond insulating materials and porous substances to the spread of forest fires and disease epidemics to evolution to the study of the Internet.
For simplicity, we begin by working in two dimensions and model the system as an n-by-n grid of sites. Each site is either blocked or open; open sites are initially empty. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. If there is a full site in the bottom row, then we say that the system percolates. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.

In a famous scientific problem that has been heavily studied for decades, scientists are interested in the following question: if sites are independently set to be open with site vacancy probability p (and therefore blocked with probability 1–p), what is the probability that the system percolates? No mathematical solution to this problem has yet been derived. Our task is to write computer programs to help study the problem.
Basic scaffolding
To address percolation with a Java program, we face numerous decisions and challenges, and we certainly will end up with much more code than in the short programs that we have considered so far in this book. Our goal is to illustrate an incremental style of programming where we independently develop modules that address parts of the problem, building confidence with a small computational infrastructure of our own design and construction as we proceed.
The first step is to pick a representation of the data. This decision can have substantial impact on the kind of code that we write later, so it is not to be taken lightly. Indeed, it is often the case that we learn something while working with a chosen representation that causes us to scrap it and start all over using a new one.
For percolation, the path to an effective representation is clear: use an n-by-n array. Which type of data should we use for each element? One possibility is to use integers, with the convention that 0 indicates an empty site, 1 indicates a blocked site, and 2 indicates a full site. Alternatively, note that we typically describe sites in terms of questions: Is the site open or blocked? Is the site full or empty? This characteristic of the elements suggests that we might use n-by-n arrays in which element is either true or false. We refer to such two-dimensional arrays as boolean matrices. Using boolean matrices leads to code that is easier to understand than the alternative.

Boolean matrices are fundamental mathematical objects with many applications. Java does not provide direct support for operations on boolean matrices, but we can use the methods in StdArrayIO (see PROGRAM 2.2.2) to read and write them. This choice illustrates a basic principle that often comes up in programming: the effort required to build a more general tool usually pays dividends.
Eventually, we will want to work with random data, but we also want to be able to read and write to files because debugging programs with random inputs can be counterproductive. With random data, you get different input each time that you run the program; after fixing a bug, what you want to see is the same input that you just used, to check that the fix was effective. Accordingly, it is best to start with some specific cases that we understand, kept in files formatted compatible with StdArrayIO (dimensions followed by 0 and 1 values in row-major order).
When you start working on a new problem that involves several files, it is usually worthwhile to create a new folder (directory) to isolate those files from others that you may be working on. For example, we might create a folder named percolation to store all of the files for this case study. To get started, we can implement and debug the basic code for reading and writing percolation systems, create test files, check that the files are compatible with the code, and so forth, before worrying about percolation at all. This type of code, sometimes called scaffolding, is straightforward to implement, but making sure that it is solid at the outset will save us from distraction when approaching the main problem.
Now we can turn to the code for testing whether a boolean matrix represents a system that percolates. Referring to the helpful interpretation in which we can think of the task as simulating what would happen if the top were flooded with water (does it flow to the bottom or not?), our first design decision is that we will want to have a flow() method that takes as an argument a boolean matrix isOpen[][] that specifies which sites are open and returns another boolean matrix isFull[][] that specifies which sites are full. For the moment, we will not worry at all about how to implement this method; we are just deciding how to organize the computation. It is also clear that we will want client code to be able to use a percolates() method that checks whether the array returned by flow() has any full sites on the bottom.
Percolation (PROGRAM 2.4.1) summarizes these decisions. It does not perform any interesting computation, but after running and debugging this code we can start thinking about actually solving the problem. A method that performs no computation, such as flow(), is sometimes called a stub. Having this stub allows us to test and debug percolates() and main() in the context in which we will need them. We refer to code like PROGRAM 2.4.1 as scaffolding. As with scaffolding that construction workers use when erecting a building, this kind of code provides the support that we need to develop a program. By fully implementing and debugging this code (much, if not all, of which we need, anyway) at the outset, we provide a sound basis for building code to solve the problem at hand. Often, we carry the analogy one step further and remove the scaffolding (or replace it with something better) after the implementation is complete.
Program 2.4.1 Percolation scaffolding
public class Percolation
{
public static boolean[][] flow(boolean[][] isOpen)
{
int n = isOpen.length;
boolean[][] isFull = new boolean[n][n];
// The isFull[][] matrix computation goes here.
return isFull;
}
public static boolean percolates(boolean[][] isOpen)
{
boolean[][] isFull = flow(isOpen);
int n = isOpen.length;
for (int j = 0; j < n; j++)
if (isFull[n-1][j]) return true;
return false;
}
public static void main(String[] args)
{
boolean[][] isOpen = StdArrayIO.readBoolean2D();
StdArrayIO.print(flow(isOpen));
StdOut.println(percolates(isOpen));
}
}
n | system size (n-by-n) isFull[][] | full sites isOpen[][] | open sites
To get started with percolation, we implement and debug this code, which handles all the straightforward tasks surrounding the computation. The primary function flow() returns a boolean matrix giving the full sites (none, in the placeholder code here). The helper function percolates() checks the bottom row of the returned matrix to decide whether the system percolates. The test client main() reads a boolean matrix from standard input and prints the result of calling flow() and percolates() for that matrix.
% more test5.txt
5 5
0 1 1 0 1
0 0 1 1 1
1 1 0 1 1
1 0 0 0 1
0 1 1 1 1
% java Percolation < test5.txt
5 5
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
false
Vertical percolation
Given a boolean matrix that represents the open sites, how do we figure out whether it represents a system that percolates? As we will see later in this section, this computation turns out to be directly related to a fundamental question in computer science. For the moment, we will consider a much simpler version of the problem that we call vertical percolation.
The simplification is to restrict attention to vertical connection paths. If such a path connects top to bottom in a system, we say that the system vertically percolates along the path (and that the system itself vertically percolates). This restriction is perhaps intuitive if we are talking about sand traveling through cement, but not if we are talking about water traveling through cement or about electrical conductivity. Simple as it is, vertical percolation is a problem that is interesting in its own right because it suggests various mathematical questions. Does the restriction make a significant difference? How many vertical percolation paths do we expect?

Determining the sites that are filled by some path that is connected vertically to the top is a simple calculation. We initialize the top row of our result array from the top row of the percolation system, with full sites corresponding to open ones. Then, moving from top to bottom, we fill in each row of the array by checking the corresponding row of the percolation system. Proceeding from top to bottom, we fill in the rows of isFull[][] to mark as true all elements that correspond to sites in isOpen[][] that are vertically connected to a full site on the previous row. PROGRAM 2.4.2 is an implementation of flow() for Percolation that returns a boolean matrix of full sites (true if connected to the top via a vertical path, false otherwise).
Testing
After we become convinced that our code is behaving as planned, we want to run it on a broader variety of test cases and address some of our scientific questions. At this point, our initial scaffolding becomes less useful, as representing large boolean matrices with 0s and 1s on standard input and standard output and maintaining large numbers of test cases quickly becomes unwieldy. Instead, we want to automatically generate test cases and observe the operation of our code on them, to be sure that it is operating as we expect. Specifically, to gain confidence in our code and to develop a better understanding of percolation, our next goals are to:
• Test our code for large random boolean matrices.
• Estimate the probability that a system percolates for a given p.

Program 2.4.2 Vertical percolation detection
public static boolean[][] flow(boolean[][] isOpen)
{ // Compute full sites for vertical percolation.
int n = isOpen.length;
boolean[][] isFull = new boolean[n][n];
for (int j = 0; j < n; j++)
isFull[0][j] = isOpen[0][j];
for (int i = 1; i < n; i++)
for (int j = 0; j < n; j++)
isFull[i][j] = isOpen[i][j] && isFull[i-1][j];
return isFull;
}
n | system size (n-by-n) isFull[][] | full sites isOpen[][] | open sites
Substituting this method for the stub in PROGRAM 2.4.1 gives a solution to the vertical-only percolation problem that solves our test case as expected (see text).
% more test5.txt
5 5
0 1 1 0 1
0 0 1 1 1
1 1 0 1 1
1 0 0 0 1
0 1 1 1 1
% java Percolation < test5.txt
5 5
0 1 1 0 1
0 0 1 0 1
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
true
To accomplish these goals, we need new clients that are slightly more sophisticated than the scaffolding we used to get the program up and running. Our modular programming style is to develop such clients in independent classes without modifying our percolation code at all.
Data visualization
We can work with much bigger problem instances if we use StdDraw for output. The following static method for Percolation allows us to visualize the contents of boolean matrices as a subdivision of the StdDraw canvas into squares, one for each site:
public static void show(boolean[][] a, boolean which)
{
int n = a.length;
StdDraw.setXscale(-1, n);
StdDraw.setYscale(-1, n);
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (a[i][j] == which)
StdDraw.filledSquare(j, n-i-1, 0.5);
}
The second argument which specifies which squares we want to fill—those corresponding to true elements or those corresponding to false elements. This method is a bit of a diversion from the calculation, but pays dividends in its ability to help us visualize large problem instances. Using show() to draw our boolean matrices representing blocked and full sites in different colors gives a compelling visual representation of percolation.
Monte Carlo simulation
We want our code to work properly for any boolean matrix. Moreover, the scientific question of interest involves random boolean matrices. To this end, we add another static method to Percolation:
public static boolean[][] random(int n, double p)
{
boolean[][] a = new boolean[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
a[i][j] = StdRandom.bernoulli(p);
return a;
}
This method generates a random n-by-n boolean matrix of any given size n, each element true with probability p.
Having debugged our code on a few specific test cases, we are ready to test it on random systems. It is possible that such cases may uncover a few more bugs, so some care is in order to check results. However, having debugged our code for a small system, we can proceed with some confidence. It is easier to focus on new bugs after eliminating the obvious bugs.
With these tools, a client for testing our percolation code on a much larger set of trials is straightforward. PercolationVisualizer (PROGRAM 2.4.3) consists of just a main() method that takes n and p from the command line and displays the result of the percolation flow calculation.
This kind of client is typical. Our eventual goal is to compute an accurate estimate of percolation probabilities, perhaps by running a large number of trials, but this simple tool gives us the opportunity to gain more familiarity with the problem by studying some large cases (while at the same time gaining confidence that our code is working properly). Before reading further, you are encouraged to download and run this code from the booksite to study the percolation process. When you run PercolationVisualizer for moderate-size n (50 to 100, say) and various p, you will immediately be drawn into using this program to try to answer some questions about percolation. Clearly, the system never percolates when p is low and always percolates when p is very high. How does it behave for intermediate values of p? How does the behavior change as n increases?
Estimating probabilities
The next step in our program development process is to write code to estimate the probability that a random system (of size n with site vacancy probability p) percolates. We refer to this quantity as the percolation probability. To estimate its value, we simply run a number of trials. The situation is no different from our study of coin flipping (see PROGRAM 2.2.6), but instead of flipping a coin, we generate a random system and check whether it percolates.
PercolationProbability (PROGRAM 2.4.4) encapsulates this computation in a method estimate(), which takes three arguments n, p, and trials and returns an estimate of the probability that an n-by-n system with site vacancy probability p percolates, obtained by generating trials random systems and calculating the fraction of them that percolate.
How many trials do we need to obtain an accurate estimate? This question is addressed by basic methods in probability and statistics, which are beyond the scope of this book, but we can get a feeling for the problem with computational experience. With just a few runs of PercolationProbability, you can learn that if the site vacancy probability is close to either 0 or 1, then we do not need many trials, but that there are values for which we need as many as 10,000 trials to be able to estimate it within two decimal places. To study the situation in more detail, we might modify PercolationProbability to produce output like Bernoulli (PROGRAM 2.2.6), plotting a histogram of the data points so that we can see the distribution of values (see EXERCISE 2.4.9).
Program 2.4.3 Visualization client
public class PercolationVisualizer
{
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
double p = Double.parseDouble(args[1]);
StdDraw.enableDoubleBuffering();
// Draw blocked sites in black.
boolean[][] isOpen = Percolation.random(n, p);
StdDraw.setPenColor(StdDraw.BLACK);
Percolation.show(isOpen, false);
// Draw full sites in blue.
StdDraw.setPenColor(StdDraw.BOOK_BLUE);
boolean[][] isFull = Percolation.flow(isOpen);
Percolation.show(isFull, true);
StdDraw.show();
}
}
n | system size (n-by-n) p | site vacancy probability isOpen[][] | open sites isFull[][] | full sites
This client takes two command-line argument n and p, generates an n-by-n random system with site vacancy probability p, determines which sites are full, and draws the result on standard drawing. The diagrams below show the results for vertical percolation.

Using PercolationProbability.estimate() represents a giant leap in the amount of computation that we are doing. All of a sudden, it makes sense to run thousands of trials. It would be unwise to try to do so without first having thoroughly debugged our percolation methods. Also, we need to begin to take the time required to complete the computation into account. The basic methodology for doing so is the topic of SECTION 4.1, but the structure of these programs is sufficiently simple that we can do a quick calculation, which we can verify by running the program. If we perform T trials, each of which involves n2 sites, then the total running time of PercolationProbability.estimate() is proportional to n2T. If we increase T by a factor of 10 (to gain more precision), the running time increases by about a factor of 10. If we increase n by a factor of 10 (to study percolation for larger systems), the running time increases by about a factor of 100.
Can we run this program to determine percolation probabilities for a system with billions of sites with several digits of precision? No computer is fast enough to use PercolationProbability.estimate() for this purpose. Moreover, in a scientific experiment on percolation, the value of n is likely to be much higher. We can hope to formulate a hypothesis from our simulation that can be tested experimentally on a much larger system, but not to precisely simulate a system that corresponds atom-for-atom with the real world. Simplification of this sort is essential in science.
You are encouraged to download PercolationProbability from the booksite to get a feel for both the percolation probabilities and the amount of time required to compute them. When you do so, you are not just learning more about percolation, but are also testing the hypothesis that the models we have just described apply to the running times of our simulations of the percolation process.
What is the probability that a system with site vacancy probability p vertically percolates? Vertical percolation is sufficiently simple that elementary probabilistic models can yield an exact formula for this quantity, which we can validate experimentally with PercolationProbability. Since our only reason for studying vertical percolation was an easy starting point around which we could develop supporting software for studying percolation methods, we leave further study of vertical percolation for an exercise (see EXERCISE 2.4.11) and turn to the main problem.
Program 2.4.4 Percolation probability estimate
public class PercolationProbability
{
public static double estimate(int n, double p, int trials)
{ // Generate trials random n-by-n systems; return empirical
// percolation probability estimate.
int count = 0;
for (int t = 0; t < trials; t++)
{ // Generate one random n-by-n boolean matrix.
boolean[][] isOpen = Percolation.random(n, p);
if (Percolation.percolates(isOpen)) count++;
}
return (double) count / trials;
}
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
double p = Double.parseDouble(args[1]);
int trials = Integer.parseInt(args[2]);
double q = estimate(n, p, trials);
StdOut.println(q);
}
}
n | system size (n-by-n) p | site vacancy probability trials | number of trials isOpen[][] | open sites q | percolation probability
The method estimate() generates trials random n-by-n systems with site vacancy probability p and computes the fraction of them that percolate. This is a Bernoulli process, like coin flipping (see PROGRAM 2.2.6). Increasing the number of trials increases the accuracy of the estimate. If p is close to 0 or to 1, not many trials are needed to achieve an accurate estimate. The results below are for vertical percolation.
% java PercolationProbability 20 0.05 10 0.0 % java PercolationProbability 20 0.95 10 1.0 % java PercolationProbability 20 0.85 10 0.7 % java PercolationProbability 20 0.85 1000 0.564 % java PercolationProbability 40 0.85 100 0.1
Recursive solution for percolation
How do we test whether a system percolates in the general case when any path starting at the top and ending at the bottom (not just a vertical one) will do the job?
Remarkably, we can solve this problem with a compact program, based on a classic recursive scheme known as depth-first search. PROGRAM 2.4.5 is an implementation of flow() that computes the matrix isFull[][], based on a recursive four-argument version of flow() that takes as arguments the site vacancy matrix isOpen[][], the current matrix isFull[][], and a site position specified by a row index i and a column index j. The base case is a recursive call that just returns (we refer to such a call as a null call), for one of the following reasons:
• Either i or j is outside the array bounds.
• The site is blocked (isOpen[i][j] is false).
• We have already marked the site as full (isFull[i][j] is true).
The reduction step is to mark the site as filled and issue recursive calls for the site’s four neighbors: isOpen[i+1][j], isOpen[i][j+1], isOpen[i][j-1], and isOpen[i-1][j]. The one-argument flow() calls the recursive method for every site on the top row. The recursion always terminates because each recursive call either is null or marks a new site as full. We can show by an induction-based argument (as usual for recursive programs) that a site is marked as full if and only if it is connected to one of the sites on the top row.

Tracing the operation of flow() on a tiny test case is an instructive exercise. You will see that it calls flow() for every site that can be reached via a path of open sites from the top row. This example illustrates that simple recursive programs can mask computations that otherwise are quite sophisticated. This method is a special case of the depth-first search algorithm, which has many important applications.
Program 2.4.5 Percolation detection
public static boolean[][] flow(boolean[][] isOpen)
{ // Fill every site reachable from the top row.
int n = isOpen.length;
boolean[][] isFull = new boolean[n][n];
for (int j = 0; j < n; j++)
flow(isOpen, isFull, 0, j);
return isFull;
}
public static void flow(boolean[][] isOpen,
boolean[][] isFull, int i, int j)
{ // Fill every site reachable from (i, j).
int n = isFull.length;
if (i < 0 || i >= n) return;
if (j < 0 || j >= n) return;
if (!isOpen[i][j]) return;
if (isFull[i][j]) return;
isFull[i][j] = true;
flow(isOpen, isFull, i+1, j); // Down.
flow(isOpen, isFull, i, j+1); // Right.
flow(isOpen, isFull, i, j-1); // Left.
flow(isOpen, isFull, i-1, j); // Up.
}
n | system size (n-by-n) isOpen[][] | open sites isFull[][] | full sites i, j | current site row, column
Substituting these methods for the stub in PROGRAM 2.4.1 gives a depth-first-search-based solution to the percolation problem. The recursive flow() sets to true the element in isFull[][] corresponding to any site that can be reached from isOpen[i][j] via a chain of neighboring open sites. The one-argument flow() calls the recursive method for every site on the top row.
% more test8.txt
8 8
0 0 1 1 1 0 0 0
1 0 0 1 1 1 1 1
1 1 1 0 0 1 1 0
0 0 1 1 0 1 1 1
0 1 1 1 0 1 1 0
0 1 0 0 0 0 1 1
1 0 1 0 1 1 1 1
1 1 1 1 0 1 0 0
% java Percolation < test8.txt
8 8
0 0 1 1 1 0 0 0
0 0 0 1 1 1 1 1
0 0 0 0 0 1 1 0
0 0 0 0 0 1 1 1
0 0 0 0 0 1 1 0
0 0 0 0 0 0 1 1
0 0 0 0 1 1 1 1
0 0 0 0 0 1 0 0
true
To avoid conflict with our solution for vertical percolation (PROGRAM 2.4.2), we might rename that class PercolationVertical, making another copy of Percolation (PROGRAM 2.4.1) and substituting the two flow() methods in PROGRAM 2.4.5 for the placeholder flow(). Then, we can visualize and perform experiments with this algorithm with the PercolationVisualizer and PercolationProbability tools that we have developed. If you do so, and try various values for n and p, you will quickly get a feeling for the situation: the systems always percolate when the site vacancy probability p is high and never percolate when p is low, and (particularly as n increases) there is a value of p above which the systems (almost) always percolate and below which they (almost) never percolate.

Having debugged PercolationVisualizer and PercolationProbability on the simple vertical percolation process, we can use them with more confidence to study percolation, and turn quickly to study the scientific problem of interest. Note that if we want to experiment with vertical percolation again, we would need to edit PercolationVisualizer and PercolationProbability to refer to PercolationVertical instead of Percolation, or write other clients of both PercolationVertical and Percolation that run methods in both classes to compare them.
Adaptive plot
To gain more insight into percolation, the next step in program development is to write a program that plots the percolation probability as a function of the site vacancy probability p for a given value of n. Perhaps the best way to produce such a plot is to first derive a mathematical equation for the function, and then use that equation to make the plot. For percolation, however, no one has been able to derive such an equation, so the next option is to use the Monte Carlo method: run simulations and plot the results.
Immediately, we are faced with numerous decisions. For how many values of p should we compute an estimate of the percolation probability? Which values of p should we choose? How much precision should we aim for in these calculations? These decisions constitute an experimental design problem. Much as we might like to instantly produce an accurate rendition of the curve for any given n, the computation cost can be prohibitive. For example, the first thing that comes to mind is to plot, say, 100 to 1,000 equally spaced points, using StdStats (PROGRAM 2.2.5). But, as you learned from using PercolationProbability, computing a sufficiently precise value of the percolation probability for each point might take several seconds or longer, so the whole plot might take minutes or hours or even longer. Moreover, it is clear that a lot of this computation time is completely wasted, because we know that values for small p are 0 and values for large p are 1. We might prefer to spend that time on more precise computations for intermediate p. How should we proceed?

PercolationPlot (PROGRAM 2.4.6) implements a recursive approach with the same structure as Brownian (PROGRAM 2.3.5) that is widely applicable to similar problems. The basic idea is simple: we choose the maximum distance that we wish to allow between values of the x-coordinate (which we refer to as the gap tolerance), the maximum known error that we wish to tolerate in the y-coordinate (which we refer to as the error tolerance), and the number of trials T per point that we wish to perform. The recursive method draws the plot within a given interval [x0, x1], from (x0, y0) to (x1, y1). For our problem, the plot is from (0, 0) to (1, 1). The base case (if the distance between x0 and x1 is less than the gap tolerance, or the distance between the line connecting the two endpoints and the value of the function at the midpoint is less than the error tolerance) is to simply draw a line from (x0, y0) to (x1, y1). The reduction step is to (recursively) plot the two halves of the curve, from (x0, y0) to (xm, f (xm)) and from (xm, f (xm)) to (x1, y1).
The code in PercolationPlot is relatively simple and produces a good-looking curve at relatively low cost. We can use it to study the shape of the curve for various values of n or choose smaller tolerances to be more confident that the curve is close to the actual values. Precise mathematical statements about quality of approximation can, in principle, be derived, but it is perhaps not appropriate to go into too much detail while exploring and experimenting, since our goal is simply to develop a hypothesis about percolation that can be tested by scientific experimentation.
Program 2.4.6 Adaptive plot client
public class PercolationPlot
{
public static void curve(int n,
double x0, double y0,
double x1, double y1)
{ // Perform experiments and plot results.
double gap = 0.01;
double err = 0.0025;
int trials = 10000;
double xm = (x0 + x1)/2;
double ym = (y0 + y1)/2;
double fxm = PercolationProbability.estimate(n, xm, trials);
if (x1 - x0 < gap || Math.abs(ym - fxm) < err)
{
StdDraw.line(x0, y0, x1, y1);
return;
}
curve(n, x0, y0, xm, fxm);
StdDraw.filledCircle(xm, fxm, 0.005);
curve(n, xm, fxm, x1, y1);
}
public static void main(String[] args)
{ // Plot experimental curve for n-by-n percolation system.
int n = Integer.parseInt(args[0]);
curve(n, 0.0, 0.0, 1.0, 1.0);
}
}
n | system size x0, y0 | left endpoint x1, y1 | right endpoint
xm, ym | midpoint fxm | value at midpoint gap | gap tolerance err | error tolerance trials | number of trials
This recursive program draws a plot of the percolation probability (experimental observations) against the site vacancy probability p (control variable) for random n-by-n systems.


Indeed, the curves produced by PercolationPlot immediately confirm the hypothesis that there is a threshold value (about 0.593): if p is greater than the threshold, then the system almost certainly percolates; if p is less than the threshold, then the system almost certainly does not percolate. As n increases, the curve approaches a step function that changes value from 0 to 1 at the threshold. This phenomenon, known as a phase transition, is found in many physical systems.
The simple form of the output of PROGRAM 2.4.6 masks the huge amount of computation behind it. For example, the curve drawn for n = 100 has 18 points, each the result of 10,000 trials, with each trial involving n2 sites. Generating and testing each site involves a few lines of code, so this plot comes at the cost of executing billions of statements. There are two lessons to be learned from this observation. First, we need to have confidence in any line of code that might be executed billions of times, so our care in developing and debugging code incrementally is justified. Second, although we might be interested in systems that are much larger, we need further study in computer science to be able to handle larger cases—that is, to develop faster algorithms and a framework for knowing their performance characteristics.
PercolationPlot.curve()
PercolationProbability.estimate()
Percolation.random()
StdRandom.bernoulli()
.
. n2 times
.
StdRandom.bernoulli()
return
Percolation.percolates()
flow()
return
return
.
. T times
.
Percolation.random()
StdRandom.bernoulli()
.
. n2 times
.
StdRandom.bernoulli()
return
Percolation.percolates()
flow()
return
return
return
.
. once for each point
.
PercolationProbability.estimate()
Percolation.random()
StdRandom.bernoulli()
.
. n2 times
.
StdRandom.bernoulli()
return
Percolation.percolates()
flow()
return
return
.
.
. T times
Percolation.random()
StdRandom.bernoulli()
.
. n2 times
.
StdRandom.bernoulli()
return
Percolation.percolates()
flow()
return
return
return
return
Function-call trace for PercolationPlot
With this reuse of all of our software, we can study all sorts of variants on the percolation problem, just by implementing different flow() methods. For example, if you leave out the last recursive call in the recursive flow() method in PROGRAM 2.4.5, it tests for a type of percolation known as directed percolation, where paths that go up are not considered. This model might be important for a situation like a liquid percolating through porous rock, where gravity might play a role, but not for a situation like electrical connectivity. If you run PercolationPlot for both methods, will you be able to discern the difference (see EXERCISE 2.4.10)?
To model physical situations such as water flowing through porous substances, we need to use three-dimensional arrays. Is there a similar threshold in the three-dimensional problem? If so, what is its value? Depth-first search is effective for studying this question, though the addition of another dimension requires that we pay even more attention to the computational cost of determining whether a system percolates (see EXERCISE 2.4.18). Scientists also study more complex lattice structures that are not well modeled by multidimensional arrays—we will see how to model such structures in SECTION 4.5.
Percolation is interesting to study via in silico experimentation because no one has been able to derive the threshold value mathematically for several natural models. The only way that scientists know the value is by using simulations like Percolation. A scientist needs to do experiments to see whether the percolation model reflects what is observed in nature, perhaps through refining the model (for example, using a different lattice structure). Percolation is an example of an increasing number of problems where computer science of the kind described here is an essential part of the scientific process.
Lessons
We might have approached the problem of studying percolation by sitting down to design and implement a single program, which probably would run to hundreds of lines, to produce the kind of plots that are drawn by PROGRAM 2.4.6. In the early days of computing, programmers had little choice but to work with such programs, and would spend enormous amounts of time isolating bugs and correcting design decisions. With modern programming tools like Java, we can do better, using the incremental modular style of programming presented in this chapter and keeping in mind some of the lessons that we have learned.
Expect bugs
Every interesting piece of code that you write is going to have at least one or two bugs, if not many more. By running small pieces of code on small test cases that you understand, you can more easily isolate any bugs and then more easily fix them when you find them. Once debugged, you can depend on using a library as a building block for any client.
Keep modules small
You can focus attention on at most a few dozen lines of code at a time, so you may as well break your code into small modules as you write it. Some classes that contain libraries of related methods may eventually grow to contain hundreds of lines of code; otherwise, we work with small files.

Limit interactions
In a well-designed modular program, most modules should depend on just a few others. In particular, a module that calls a large number of other modules needs to be divided into smaller pieces. Modules that are called by a large number of other modules (you should have only a few) need special attention, because if you do need to make changes in a module’s API, you have to reflect those changes in all its clients.
Develop code incrementally
You should run and debug each small module as you implement it. That way, you are never working with more than a few dozen lines of unreliable code at any given time. If you put all your code in one big module, it is difficult to be confident that any of it is free from bugs. Running code early also forces you to think sooner rather than later about I/O formats, the nature of problem instances, and other issues. Experience gained when thinking about such issues and debugging related code makes the code that you develop later in the process more effective.
Solve an easier problem
Some working solution is better than no solution, so it is typical to begin by putting together the simplest code that you can craft that solves a given problem, as we did with vertical percolation. This implementation is the first step in a process of continual refinements and improvements as we develop a more complete understanding of the problem by examining a broader variety of test cases and developing support software such as our PercolationVisualizer and PercolationProbability classes.
Consider a recursive solution
Recursion is an indispensable tool in modern programming that you should learn to trust. If you are not already convinced of this fact by the simplicity and elegance of Percolation and PercolationPlot, you might wish to try to develop a nonrecursive program for testing whether a system percolates and then reconsider the issue.
Build tools when appropriate
Our visualization method show() and random boolean matrix generation method random() are certainly useful for many other applications, as is the adaptive plotting method of PercolationPlot. Incorporating these methods into appropriate libraries would be simple. It is no more difficult (indeed, perhaps easier) to implement general-purpose methods like these than it would be to implement special-purpose methods for percolation.
Reuse software when possible
Our StdIn, StdRandom, and StdDraw libraries all simplified the process of developing the code in this section, and we were also immediately able to reuse programs such as PercolationVisualizer, PercolationProbability, and PercolationPlot for percolation after developing them for vertical percolation. After you have written a few programs of this kind, you might find yourself developing versions of these programs that you can reuse for other Monte Carlo simulations or other experimental data analysis problems.
The primary purpose of this case study is to convince you that modular programming will take you much further than you could get without it. Although no approach to programming is a panacea, the tools and approach that we have discussed in this section will allow you to attack complex programming tasks that might otherwise be far beyond your reach.
The success of modular programming is only a start. Modern programming systems have a vastly more flexible programming model than the class-as-a-library-of-static-methods model that we have been considering. In the next two chapters, we develop this model, along with many examples that illustrate its utility.
Q&A
Q. Editing PercolationVisualizer and PercolationProbability to rename Percolation to PercolationVertical or whatever method we want to study seems to be a bother. Is there a way to avoid doing so?
A. Yes, this is a key issue to be revisited in CHAPTER 3. In the meantime, you can keep the implementations in separate subdirectories, but that can get confusing. Advanced Java mechanisms (such as the classpath) are also helpful, but they also have their own problems.
Q. That recursive flow() method makes me nervous. How can I better understand what it’s doing?
A. Run it for small examples of your own making, instrumented with instructions to print a function-call trace. After a few runs, you will gain confidence that it always marks as full the sites connected to the start site via a chain of neighboring open sites.
Q. Is there a simple nonrecursive approach to identifying the full sites?
A. There are several methods that perform the same basic computation. We will revisit the problem in SECTION 4.5, where we consider breadth-first search. In the meantime, working on developing a nonrecursive implementation of flow() is certain to be an instructive exercise, if you are interested.
Q. PercolationPlot (PROGRAM 2.4.6) seems to involve a huge amount of computation to produce a simple function graph. Is there some better way?
A. Well, the best would be a simple mathematical formula describing the function, but that has eluded scientists for decades. Until scientists discover such a formula, they must resort to computational experiments like the ones in this section.
Exercises
2.4.1 Write a program that takes a command-line argument n and creates an n-by-n boolean matrix with the element in row i and column j set to true if i and j are relatively prime, then shows the matrix on the standard drawing (see EXERCISE 1.4.16). Then, write a similar program to draw the Hadamard matrix of order n (see EXERCISE 1.4.29). Finally, write a program to draw the boolean matrix such that the element in row n and column j is set to true if the coefficient of xj in (1 + x)i (binomial coefficient) is odd (see EXERCISE 1.4.41). You may be surprised at the pattern formed by the third example.
2.4.2 Implement a print() method for Percolation that prints 1 for blocked sites, 0 for open sites, and * for full sites.
2.4.3 Give the recursive calls for flow() in PROGRAM 2.4.5 given the following input:
3 3 1 0 1 0 0 0 1 1 0
2.4.4 Write a client of Percolation like PercolationVisualizer that does a series of experiments for a value of n taken from the command line where the site vacancy probability p increases from 0 to 1 by a given increment (also taken from the command line).
2.4.5 Describe the order in which the sites are marked when Percolation is used on a system with no blocked sites. Which is the last site marked? What is the depth of the recursion?
2.4.6 Experiment with using PercolationPlot to plot various mathematical functions (by replacing the call PercolationProbability.estimate() with a different expression that evaluates a mathematical function). Try the function f(x) = sin x + cos 10x to see how the plot adapts to an oscillating curve, and come up with interesting plots for three or four functions of your own choosing.
2.4.7 Modify Percolation to animate the flow computation, showing the sites filling one by one. Check your answer to the previous exercise.
2.4.8 Modify Percolation to compute that maximum depth of the recursion used in the flow calculation. Plot the expected value of that quantity as a function of the site vacancy probability p. How does your answer change if the order of the recursive calls is reversed?
2.4.9 Modify PercolationProbability to produce output like that produced by Bernoulli (PROGRAM 2.2.6). Extra credit: Use your program to validate the hypothesis that the data obeys a Gaussian distribution.
2.4.10 Create a program PercolationDirected that tests for directed percolation (by leaving off the last recursive call in the recursive flow() method in PROGRAM 2.4.5, as described in the text), then use PercolationPlot to draw a plot of the directed percolation probability as a function of the site vacancy probability p.
2.4.11 Write a client of Percolation and PercolationDirected that takes a site vacancy probability p from the command line and prints an estimate of the probability that a system percolates but does not percolate down. Use enough experiments to get an estimate that is accurate to three decimal places.

Creative Exercises
2.4.12 Vertical percolation. Show that a system with site vacancy probability p vertically percolates with probability 1 – (1 – pn)n, and use PercolationProbability to validate your analysis for various values of n.
2.4.13 Rectangular percolation systems. Modify the code in this section to allow you to study percolation in rectangular systems. Compare the percolation probability plots of systems whose ratio of width to height is 2 to 1 with those whose ratio is 1 to 2.
2.4.14 Adaptive plotting. Modify PercolationPlot to take its control parameters (gap tolerance, error tolerance, and number of trials) as command-line arguments. Experiment with various values of the parameters to learn their effect on the quality of the curve and the cost of computing it. Briefly describe your findings.
2.4.15 Nonrecursive directed percolation. Write a nonrecursive program that tests for directed percolation by moving from top to bottom as in our vertical percolation code. Base your solution on the following computation: if any site in a contiguous subrow of open sites in the current row is connected to some full site on the previous row, then all of the sites in the subrow become full.

2.4.16 Fast percolation test. Modify the recursive flow() method in PROGRAM 2.4.5 so that it returns as soon as it finds a site on the bottom row (and fills no more sites). Hint: Use an argument done that is true if the bottom has been hit, false otherwise. Give a rough estimate of the performance improvement factor for this change when running PercolationPlot. Use values of n for which the programs run at least a few seconds but not more than a few minutes. Note that the improvement is ineffective unless the first recursive call in flow() is for the site below the current site.
2.4.17 Bond percolation. Write a modular program for studying percolation under the assumption that the edges of the grid provide connectivity. That is, an edge can be either empty or full, and a system percolates if there is a path consisting of full edges that goes from top to bottom. Note: This problem has been solved analytically, so your simulations should validate the hypothesis that the bond percolation threshold approaches 1/2 as n gets large.

2.4.18 Percolation in three dimensions. Implement a class Percolation3D and a class BooleanMatrix3D (for I/O and random generation) to study percolation in three-dimensional cubes, generalizing the two-dimensional case studied in this section. A percolation system is an n-by-n-by-n cube of sites that are unit cubes, each open with probability p and blocked with probability 1–p. Paths can connect an open cube with any open cube that shares a common face (one of six neighbors, except on the boundary). The system percolates if there exists a path connecting any open site on the bottom plane to any open site on the top plane. Use a recursive version of flow() like PROGRAM 2.4.5, but with six recursive calls instead of four. Plot the percolation probability versus site vacancy probability p for as large a value of n as you can. Be sure to develop your solution incrementally, as emphasized throughout this section.
2.4.19 Bond percolation on a triangular grid. Write a modular program for studying bond percolation on a triangular grid, where the system is composed of 2n2 equilateral triangles packed together in an n-by-n grid of rhombus shapes. Each interior point has six bonds; each point on the edge has four; and each corner point has two.

2.4.20 Game of Life. Implement a class GameOfLife that simulates Conway’s Game of Life. Consider a boolean matrix corresponding to a system of cells that we refer to as being either live or dead. The game consists of checking and perhaps updating the value of each cell, depending on the values of its neighbors (the adjacent cells in every direction, including diagonals). Live cells remain live and dead cells remain dead, with the following exceptions:
• A dead cell with exactly three live neighbors becomes live.
• A live cell with exactly one live neighbor becomes dead.
• A live cell with more than three live neighbors becomes dead.
Initialize with a random boolean matrix, or use one of the starting patterns on the booksite. This game has been heavily studied, and relates to foundations of computer science (see the booksite for more information).

