Chapter 7 Collection and Analysis of Rate Data

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

7. Collection and Analysis of Rate Data

You can observe a lot just by watching.

—Yogi Berra, New York Yankees

Overview. In Chapters 5 and 6 we have shown that once the rate law is known, it can be substituted into the appropriate mole balance, and then through the use of the appropriate stoichiometric relationships, we can apply the CRE algorithm to analyze any isothermal reaction system. In this chapter we focus on ways of obtaining and analyzing reaction-rate data to obtain the rate law for a specific reaction.

We discuss two common types of reactors used for obtaining rate data: the batch reactor, which is used primarily for homogeneous reactions, and the differential reactor, which is used for solid-fluid heterogeneous reactions. In batch-reactor experiments, concentration, pressure, and/or volume are usually measured and recorded at different times during the course of the reaction. Data are collected from the batch reactor during transient operation, whereas measurements on the differential reactor are made during steady-state operation. In experiments with a differential reactor, the product concentration is usually monitored for different sets of feed conditions.

Three different methods of analyzing the data collected are used:

• The integral method

• The differential method

• Nonlinear regression

The integral and differential methods are used primarily in analyzing batch-reactor data. Because a number of software packages (e.g., Polymath, MATLAB) are now available to analyze data, a rather extensive discussion of nonlinear regression is included.

7.1 The Algorithm for Data Analysis

For batch systems, the usual procedure is to collect concentration-time data, which we then use to determine the rate law. Table 7-1 gives a seven-step procedure we will emphasize in analyzing reaction engineering data.

Data for homogeneous reactions is most often obtained in a batch reactor. After postulating a rate law in Step 1 and combining it with a mole balance in Step 2, we next use any or all of the methods in Step 5 to process the data and arrive at the reaction orders and specific reaction-rate constants.

Analysis of heterogeneous reactions is shown in Step 6. For gas-solid heterogeneous reactions, we need to have an understanding of the reaction and possible mechanisms in order to postulate the rate law in Step 6B. After studying Chapter 10 on heterogeneous reactions, one will be able to postulate different rate laws and then use Polymath nonlinear regression to choose the “best” rate-law and reaction-rate-law parameters (see Example 10-3 on pages 472-475).

The procedure we will use to delineate the rate law and rate-law parameters is given in Table 7-1.

TABLE 7-1 STEPS IN ANALYZING RATE DATA

1. Postulate a rate law.

A. Power-law models for homogeneous reactions

$- r_{A} = k C_{A}^{α}, - r_{A} = k C_{A}^{α} C_{B}^{β}$ $- r_{A} = k C_{A}^{α}, - r_{A} = k C_{A}^{α} C_{B}^{β}$

B. Langmuir-Hinshelwood models for heterogeneous reactions

$- r_{A}^{'} = \frac{k P_{A}}{1 + K_{A} P_{A}}, - r_{A}^{'} = \frac{k P_{A} P_{B}}{(1 + K_{A} P_{A} + P_{B})^{2}}$ $- r_{A}^{'} = \frac{k P_{A}}{1 + K_{A} P_{A}}, - r_{A}^{'} = \frac{k P_{A} P_{B}}{(1 + K_{A} P_{A} + P_{B})^{2}}$

2. Select reactor type and corresponding mole balance.

A. If batch reactor (Section 7.2), use mole balance on Reactant A

$\begin{matrix} - r_{A} = - \frac{d C_{A}}{d t} & (TE7-1.1) \end{matrix}$ $\begin{matrix} - r_{A} = - \frac{d C_{A}}{d t} & (TE7-1.1) \end{matrix}$

B. If differential PBR (Section 7.6), use mole balance on Product P (A → P)

$\begin{matrix} - r_{A}^{'} = \frac{F_{P}}{Δ W} = C_{P} v_{0} / Δ W & (TE7-1.2) \end{matrix}$ $\begin{matrix} - r_{A}^{'} = \frac{F_{P}}{Δ W} = C_{P} v_{0} / Δ W & (TE7-1.2) \end{matrix}$

3. Process your data in terms of the measured variable (e.g., N_A, C_A, or P_A). If necessary, rewrite your mole balance in terms of the measured variable (e.g., P_A).

4. Look for simplifications. For example, if one of the reactants is in excess, assume its concentration is constant. If the gas-phase mole fraction of reactant A is small, set ε≈0.

5. For a batch reactor, calculate -r_A as a function of concentration C_A to determine the reaction order.

A. Differential analysis (Section 7.4)

Combine the mole balance (TE7-1.1) and power law model (TE7-1.3)

$\begin{matrix} - r_{A} = k C_{A}^{α} & (TE7-1.3) \end{matrix}$ $\begin{matrix} - r_{A} = k C_{A}^{α} & (TE7-1.3) \end{matrix}$

$\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (TE7-1.4) \end{matrix}$ $\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (TE7-1.4) \end{matrix}$

and then take the natural log dC

$\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln (- r_{A}) = \ln k + α \ln C_{A} & (TE7-1.5) \end{matrix}$ $\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln (- r_{A}) = \ln k + α \ln C_{A} & (TE7-1.5) \end{matrix}$

(1) Find $- \frac{d C_{A}}{d t}$ $- \frac{d C_{A}}{d t}$ from C_A versus t data by either the

(a) Graphical differential

(b) Finite differential method or

(2) Either plot $[\ln (- \frac{d C_{A}}{d t})]$ $[\ln (- \frac{d C_{A}}{d t})]$ versus In C_A to find reaction order a, which is the slope of the line fit to the data

(3) Use nonlinear regression to find α and k simultaneously

B. Integral method (Section 7.3)

For $- r_{A} = k C_{A}^{α}$ $- r_{A} = k C_{A}^{α}$ , the combined mole balance and rate law is

$\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (TE7-1.4) \end{matrix}$ $\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (TE7-1.4) \end{matrix}$

Guess a and integrate Equation (TE7-1.4). Rearrange your equation to obtain the appropriate function of C_A, which when plotted as a function of time should be linear. If it is linear, then the guessed value of a is correct and the slope is the specific reaction rate, fe. If it is not linear, guess again for a. If you guess a = 0,1, and 2, and none of these orders fit the data, proceed to nonlinear regression.

C. Nonlinear regression (Polymath) (Section 7.5):

Integrate Equation (TE7-1.4) to obtain

$\begin{matrix} t = \frac{1}{k} [\frac{C_{A 0}^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)}] f o r α \neq 1 & (TE7-1.6) \end{matrix}$ $\begin{matrix} t = \frac{1}{k} [\frac{C_{A 0}^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)}] f o r α \neq 1 & (TE7-1.6) \end{matrix}$

Use Polymath regression to find a and fe. A Polymath tutorial on regression with screen shots can be found on the CRE Web site at http://umich.edu/~elements/5e/07chap/Example_7-3_Polymath_nonlinear_regression_tutorial.pdf and at http://wwv/.umich.edu/-elements/5e/software/nonlinear_regression_tutorial.pdj.

6. For differential PBR, calculate —r’_A as a function of C_A or P_A (Section 7.6)

A. Calculate $- r_{A}^{'} = \frac{v_{0} C_{P}}{Δ W}$ $- r_{A}^{'} = \frac{v_{0} C_{P}}{Δ W}$ as a function of reactant concentration, C_A or partial pressure P_A.

B. Choose a model (see Chapter 10), e.g.,

$- r_{A}^{'} = \frac{k P_{A}}{1 + K_{A} P_{A}}$ $- r_{A}^{'} = \frac{k P_{A}}{1 + K_{A} P_{A}}$

C. Use nonlinear regression to find the best model and model parameters. See example on the CRE Web site Summary Notes for Chapter 10, using data from heterogeneous catalysis.

7. Analyze your rate law model for “goodness of fit." Calculate a correlation coefficient.

7.2 Determining the Reaction Order for Each of Two Reactants Using the Method of Excess

Batch reactors are used primarily to determine rate-law parameters for homogeneous reactions. This determination is usually achieved by measuring concentration as a function of time and then using either the integral, differential, or nonlinear regression method of data analysis to determine the reaction order, a, and specific reaction-rate constant, k. If some reaction parameter other than concentration is monitored, such as pressure, the mole balance must be rewritten in terms of the measured variable (e.g., pressure, as shown in the example in Solved Problems on the CRE Web site at http://www.umich.edu/-elements/5e/07chap/pdf/excd5-l.pdf).

Process data in terms of the measured variable.

When a reaction is ineversible, it is possible in many cases to determine the reaction order a and the specific rate constant by either nonlinear regression or by numerically differentiating concentration versus time data. This latter method is most applicable when reaction conditions are such that the rate is essentially a function of the concentration of only one reactant; for example, if, for the decomposition reaction

$\begin{matrix} A \to Products \\ - r_{A} = k_{A} C_{A}^{α} & (7-1) \end{matrix}$ $\begin{matrix} A \to Products \\ - r_{A} = k_{A} C_{A}^{α} & (7-1) \end{matrix}$

Assume that the rate law is of the form $- r_{A}^{} = k_{A} C_{A}^{α} .$ $- r_{A}^{} = k_{A} C_{A}^{α} .$

then the differential method may be used.

However, by utilizing the method of excess, it is also possible to determine the relationship between — r_A and the concentration of other reactants. That is, for the irreversible reaction

A + B → Products

With the rate law

$\begin{matrix} - r_{A} = k_{A} C_{A}^{α} C_{B}^{β} & (7-2) \end{matrix}$ $\begin{matrix} - r_{A} = k_{A} C_{A}^{α} C_{B}^{β} & (7-2) \end{matrix}$

where α and β are both unknown, the reaction could first be run in an excess of B so that C_B remains essentially unchanged during the course of the reaction (i.e., C_B ≈ C_B0 ) and

$\begin{matrix} - r_{A} = k' C_{A}^{α} & (7-3) \end{matrix}$ $\begin{matrix} - r_{A} = k' C_{A}^{α} & (7-3) \end{matrix}$

where

$k' = k_{A} C_{B}^{β} \approx k_{A} C_{B 0}^{β}$ $k' = k_{A} C_{B}^{β} \approx k_{A} C_{B 0}^{β}$

Method of excess

After determining α, the reaction is carried out in an excess of A, for which the rate law is approximated as

$\begin{matrix} - r_{A} = k " C_{B}^{β} & (7-4 \end{matrix}$ $\begin{matrix} - r_{A} = k " C_{B}^{β} & (7-4 \end{matrix}$

where

$k'' = k_{A} C_{A}^{α} \approx k_{A} C_{A 0}^{α}$ $k'' = k_{A} C_{A}^{α} \approx k_{A} C_{A 0}^{α}$

Once α and β are determined, k_A can be calculated from the measurement of - r_A at known concentrations of A and B

$\begin{matrix} k_{A} = \frac{- r_{A}}{C_{A}^{α} C_{B}^{β}} = \frac{(d m^{3} / m o 1)^{α + β - 1}}{s} & (7-5) \end{matrix}$ $\begin{matrix} k_{A} = \frac{- r_{A}}{C_{A}^{α} C_{B}^{β}} = \frac{(d m^{3} / m o 1)^{α + β - 1}}{s} & (7-5) \end{matrix}$

Both a and β can be determined by using the method of excess, coupled with a differential analysis of data for batch systems.

7.3 Integral Method

The integral method is the quickest method to use to determine the rate law if the order turns out to zero, first, or second order. In the integral method, we guess the reaction order, a, in the combined batch reactor mole balance and rate law equation

$\begin{matrix} \frac{d C_{A}}{d t} = - k C_{A}^{α} & (7-6) \end{matrix}$ $\begin{matrix} \frac{d C_{A}}{d t} = - k C_{A}^{α} & (7-6) \end{matrix}$

The integral method uses a trial- and-error procedure to find the reaction order.

and integrate the differential equation to obtain the concentration as a function of time. If the order a we assumed is correct, then the appropriate plot (determined from this integration) of the concentration-time data should be linear. The integral method is used most often when the reaction order is known and it is desired to evaluate the specific reaction rate constant at different temperatures to determine the activation energy.

In the integral method of analysis of rate data, we are looking for the appropriate function of concentration corresponding to a particular rate law that is linear with time. You should be thoroughly familiar with the methods of obtaining these linear plots for reactions of zero, first, and second order.

It is important to know how to generate linear plots of functions of C_A versus t for zero-, first-, and second-order reactions.

For the reaction

A → Products

carried out in a constant-volume batch reactor, the mole balance is

$\frac{d C_{A}}{d t} = r_{A}$ $\frac{d C_{A}}{d t} = r_{A}$

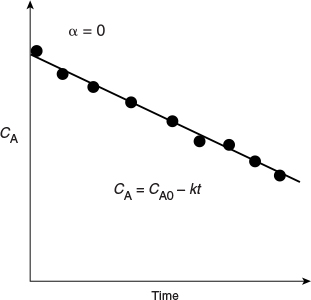
For a zero-order reaction, r_A = —k, and the combined rate law and mole balance is

$\begin{matrix} \frac{d C_{A}}{d t} = - k & (7-7) \end{matrix}$ $\begin{matrix} \frac{d C_{A}}{d t} = - k & (7-7) \end{matrix}$

Integrating with C_A = C_A0 at t = 0, we have

$\begin{matrix} C_{A} = C_{A0} - k t \end{matrix} (7 - 8)$ $\begin{matrix} C_{A} = C_{A0} - k t \end{matrix} (7 - 8)$

Zero order

A plot of the concentration of A as a function of time will be linear (Figure 7-1) with slope (—k) for a zero-order reaction carried out in a constant-volume batch reactor.

Figure 7-1 Zero-order reaction.

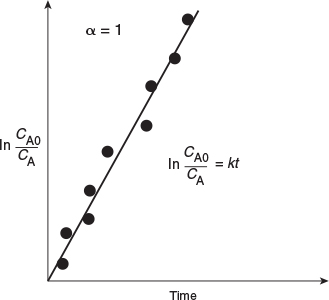
If the reaction is first order (Figure 7-2), integration of the combined mole balance and the rate law

Figure 7-2 First-order reaction.

$- \frac{d C_{A}}{d t} = k C_{A}$ $- \frac{d C_{A}}{d t} = k C_{A}$

with the limits C_A = C_A0 at t = 0 gives

In \frac{C_{A0}}{C_{A}} = K t (7 - 9)

$In \frac{C_{A0}}{C_{A}} = K t (7 - 9)$

First order

Consequently, we see that the slope of a plot of [In (C_A0/C_A)] as a function of time is indeed linear with slope k.

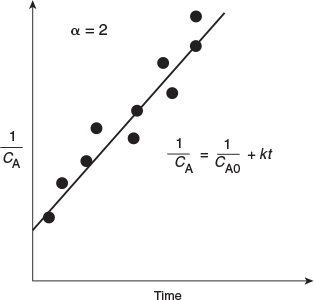
If the reaction is second order (Figure 7-3), then

Graph depicts the second-order reaction.

Figure 7-3 Second-order reaction.

$- \frac{d C_{A}}{d t} = k C_{A}^{2}$ $- \frac{d C_{A}}{d t} = k C_{A}^{2}$

Graph depicts the plot of reciprocal concentration as a function of time.

Figure 7-4 Plot of reciprocal concentration as a function of time.

Integrating, with C_A = C_A0 initially (i.e., t = 0), yields

\frac{1}{C_{A}} - \frac{1}{C_{A0}} = K t (7 - 10)

$\frac{1}{C_{A}} - \frac{1}{C_{A0}} = K t (7 - 10)$

Second order

We see that for a second-order reaction a plot of (1/C_A) as a function of time should be linear with slope k.

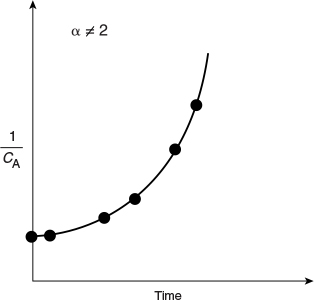
In Figures 7-1, 7-2, and 7-3, we saw that when we plotted the appropriate function of concentration (i.e., C_A, lnC_A, or 1/C_A) versus time, the plots were linear, and we concluded that the reactions were zero, first, or second order, respectively. However, if the plots of concentration data versus time had turned out not to be linear, such as shown in Figure 7-4, we would say that the proposed reaction order did not fit the data. In the case of Figure 7-4, we would conclude that the reaction is not second order. After finding that the integral method for first, second, and third orders also do not fit the data, one should use one of the other methods discussed in Table 7-1.

The idea is to arrange the data so that a linear relationship is obtained.

It is important to restate that, given a reaction-rate law, you should be able to quickly choose the appropriate function of concentration or conversion that yields a straight line when plotted against time or space time. The goodness-of-fit of such a line may be assessed statistically by calculating the linear correlation coefficient, r², which should be as close to 1 as possible. The value of r² is given in the output of Polymath’s nonlinear regression analysis.

Example 7-1 Integral Method of CRE Data Analysis

The liquid-phase reaction

Trityl (A) + Methanol (B) → Products (C)

was carried out in a batch reactor at 25°C in a solution of benzene and pyridine in an excess of methanol $(C_{B 0} = 0.5 \frac{m o 1}{d m^{3}})$ $(C_{B 0} = 0.5 \frac{m o 1}{d m^{3}})$ . (We need to point out that this batch reactor was purchased at the Sunday markets in Rica, Jofostan.) Pyridine reacts with HCl, which then precipitates as pyridine hydro-chloride thereby making the reaction irreversible. The reaction is first order in methanol. The concentration of triphenyl methyl chloride (A) was measured as a function of time and is shown below

TABLE E7-1.1 RAW DATA

t (min)	0	50	100	150	200	250	300
C_A (mol/dm³)	0.05	0.038	0.0306	0.0256	0.0222	0.0195	0.0174

(a) Use the integral method to confirm that the reaction is second order with regard to triphenyl methyl chloride.

(b) Determine the pseudo rate constant k’ = feC_B0 .

(c) Assume the reaction is first order in methanol and determine the true specific reactor rate constant, k, for this over all third-order reaction.

Solution

We use the power-law model, Equation (7-2), along with information from the problem statement that the reaction is first order in methanol, (B), i.e., ß = 1 to obtain

$\begin{matrix} - r_{A} = k C_{A}^{α} C_{B} & (E7-1.1) \end{matrix}$ $\begin{matrix} - r_{A} = k C_{A}^{α} C_{B} & (E7-1.1) \end{matrix}$

(a) Excess methanol: The initial concentration of methanol (B) is 10 times that of tri-tyl (A), so even if all A were consumed, 90% of B remains. Consequently, we will take the concentration of B as a constant and combine it with k to form

$\begin{matrix} - r_{A} = k C_{A}^{α} C_{B 0} = k' C_{A}^{α} & (E7-1.2) \end{matrix}$ $\begin{matrix} - r_{A} = k C_{A}^{α} C_{B 0} = k' C_{A}^{α} & (E7-1.2) \end{matrix}$

where k’ is the pseudo rate constant k’ = kC_B0 and k is the true rate constant. Substituting a = 2 and combining with the mole balance on a batch reactor, we obtain

$\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{2} & (E7-1.3) \end{matrix}$ $\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{2} & (E7-1.3) \end{matrix}$

Integrating with C_A = C_A0 at t = 0

$\begin{matrix} t = \frac{1}{k ’} [\frac{1}{C_{A}} - \frac{1}{C_{A 0}}] & (E7-1.4) \end{matrix}$ $\begin{matrix} t = \frac{1}{k ’} [\frac{1}{C_{A}} - \frac{1}{C_{A 0}}] & (E7-1.4) \end{matrix}$

Rearranging

$\begin{matrix} \frac{1}{C_{A}} = \frac{1}{C_{A 0}} + k' t & (E7-1.5) \end{matrix}$ $\begin{matrix} \frac{1}{C_{A}} = \frac{1}{C_{A 0}} + k' t & (E7-1.5) \end{matrix}$

from Eq. (E7-1.5), we see that if the reaction is indeed second order then a plot of (1/C_A) versus t should be linear. Using the data in Table E7-1.1, we calculate (1/C_A) to construct Table E7-1.2.

TABLE E7-1.2 PROCESSED DATA

t (min)	0	50	100	150	200	250	300
C_A (mol/dm³)	0.05	0.038	0.0306	0.0256	0.0222	0.0195	0.0174
1/C_A (dm³/mol)	20	26.3	32.7	39.1	45	51.3	57.5

(b) In a graphical solution, the data in Table E7-1.2 is used to construct a plot of (1/C_A) as a function of t, which will yield the pseudo-specific reaction rate k’. This plot is shown in Figure E7-1.1. Again, Excel or Polymath could be used to find k’ from the data in Table E7-1.2.

Graph depicts a plot of the reciprocal of C subscript A versus t for a second-order reaction.

Figure E7-1.1 Plot of the reciprocal of C_A versus t for a second-order reaction.

The slope of the line is the specific reaction rate k’. Which using the points at t = 0 and t = 200, k is calculated to be

$\begin{matrix} k' = \frac{Δ (\frac{1}{C_{A}})}{Δ t} = \frac{(44 - 20) (\frac{d m^{3}}{m o 1})}{(200 - 0) \min} = 0.12 \frac{d m^{3}}{m o 1 \cdot m} & (E7-1.6) \end{matrix}$ $\begin{matrix} k' = \frac{Δ (\frac{1}{C_{A}})}{Δ t} = \frac{(44 - 20) (\frac{d m^{3}}{m o 1})}{(200 - 0) \min} = 0.12 \frac{d m^{3}}{m o 1 \cdot m} & (E7-1.6) \end{matrix}$

We see from the Excel analysis and plot that the slope of the line is 0.12 dm³/mol · min.

(c) We now use Equation (E7-1.6), along with the initial concentration of metha-nol, to find the true rate constant, k.

$k = \frac{k'}{C_{B0}} = \frac{0.12}{0.5} \frac{{dm}^{3} / mol/min}{mol/ {dm}^{3}} = 0.24 (\frac{{dm}^{3}}{mol})^{2} / \min$ $k = \frac{k'}{C_{B0}} = \frac{0.12}{0.5} \frac{{dm}^{3} / mol/min}{mol/ {dm}^{3}} = 0.24 (\frac{{dm}^{3}}{mol})^{2} / \min$

The rate law is

- r_{A} = [0.24 {(\frac{{dm}^{3}}{mol})}^{2} / m i n] C_{A}^{2} C_{B} (E 7 - 1.7)

$- r_{A} = [0.24 {(\frac{{dm}^{3}}{mol})}^{2} / m i n] C_{A}^{2} C_{B} (E 7 - 1.7)$

We note that the integral method tends to smooth the data.

Analysis: In this example, the reaction orders are known so that the integral method can be used to (1) verify the reaction is second order in trityl and (2) to find the specific pseudo reaction rate k’ = feC_B0 for the case of excess methanol (B). Knowing k’ and C_B0, we then found the true rate constant k.

7.4 Differential Method of Analysis

To outline the procedure used in the differential method of analysis, we consider a reaction carried out isothermally in a constant-volume batch reactor and the concentration of A, recorded as a function of time. By combining the mole balance with the rate law given by Equation (7-1), we obtain

$- \frac{d C_{A}}{d t} = k_{A} C_{A}^{α}$ $- \frac{d C_{A}}{d t} = k_{A} C_{A}^{α}$

Constant-volume batch reactor

After taking the natural logarithm of both sides of Equation (5-6)

In(− \frac{d C_{A}}{d t}) = {In K}_{A} + α {In C}_{A} (7 - 11)

$In(− \frac{d C_{A}}{d t}) = {In K}_{A} + α {In C}_{A} (7 - 11)$

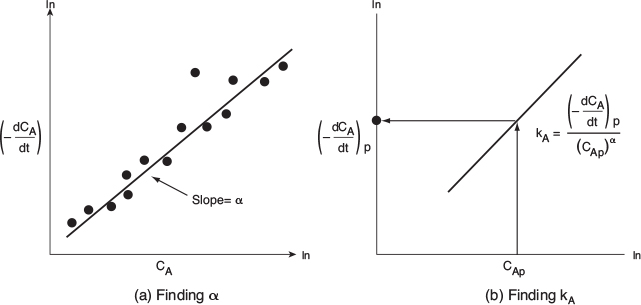
observe that the slope of a plot of [In ( — dC_A/dt)] as a function of (In C_A) is the reaction order, a (see Figure 7-5).

Graph (a) shows the differential method to determine reaction order, alpha and (b) finding k subscript A in which the horizontal and vertical axis is labeled (natural logarithm).

Figure 7-5 Differential method to determine reaction order.

Figure 7-5(a) shows a plot of [— (dC_A/dt)] versus [C_A] on log-log paper (or use Excel to make the plot) where the slope is equal to the reaction order a. The specific reaction rate, k_A, can be found by first choosing a concentration in the plot, say C_Ap, and then finding the corresponding value of [— (dC_A/dt) ] on the line, as shown in Figure 7-5(b). The concentration chosen, C_A , to find the derivative at C_Ap, need not be a data point, it just needs to be on the line. After raising C_A to the power a, we divide it into [— (dC_A/dt) ] to determine fe_A

$\begin{matrix} k_{A} = \frac{- (d C_{A} / d t)_{P}}{(C_{Ap})^{α}} & (7-12) \end{matrix}$ $\begin{matrix} k_{A} = \frac{- (d C_{A} / d t)_{P}}{(C_{Ap})^{α}} & (7-12) \end{matrix}$

To obtain the derivative (—dC_A/dt) used in this plot, we must differentiate the concentration-time data either numerically or graphically. Three methods to determine the derivative from data giving the concentration as a function of time are

Plot $\ln (- \frac{d C_{A}}{d t})$ $\ln (- \frac{d C_{A}}{d t})$ versus In C_A to find α and k_A

• Graphical differentiation

• Numerical differentiation formulas

• Differentiation of a polynomial fit to the data

Methods for finding $- \frac{d C_{A}}{d t}$ $- \frac{d C_{A}}{d t}$ from concentration-time data

We shall only discuss the graphical and numerical methods.

7.4.1 Graphical Differentiation Method

This method is very old (from slide rule days—"What’s a slide rule, Grandfather?"), when compared with the numerous software packages. So why do we use it? Because with this method, disparities in the data are easily seen. Consequently, it is advantageous to use this technique to analyze the data before planning the next set of experiments. As explained in Appendix A.2, the graphical method involves plotting (-ΔC_A/Δt) as a function of t and then using equal-area differentiation to obtain (—dC_A/dt). An illustrative example is also given in Appendix A.2.

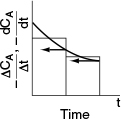
See Appendix

In addition to the graphical technique used to differentiate the data, two other methods are commonly used: differentiation formulas and polynomial fitting.

7.4.2 Numerical Method

Numerical differentiation formulas can be used when the data points in the independent variable are equally spaced, such as t_x —1₀ = t₂ - t_x = Δt. (See Table 7-2.)

TABLE 7-2 RAW DATA

Time (min)	t₀	t₁	t₂	t₃	t₄	t₅
Concentration (mol/dm³)	C_A0	C_A1	C_A2	C_A3	C_A4	C_A5

The three-point differentiation formulas¹ shown in Table 7-3 can be used to calculate dC_A/dt.

¹ B. Carnahan, H. A. Luther, and J. O. Wilkes, Applied Numerical Methods (New York: Wiley, 1969), p. 129.

TABLE 7-3 DIFFERENTIATION FORMULAS

Initial point:	${(\frac{d C_{A}}{d t})}_{t_{0}} = \frac{- 3 C_{A0} + 4 C_{A1} - C_{A2}}{2 Δ t}$ ${(\frac{d C_{A}}{d t})}_{t_{0}} = \frac{- 3 C_{A0} + 4 C_{A1} - C_{A2}}{2 Δ t}$	(7-13)
Interior points:	$(\frac{d C_{A}}{d t})_{t_{i}} = \frac{1}{2 Δ t} [(C_{A (i + 1)} - C_{A (i - 1)}] ⌊ e . g ., (\frac{d C_{A}}{d t})_{t_{3}} = \frac{1}{2 Δ t} [C_{A 4} - C_{A 2}] ⌋$ $(\frac{d C_{A}}{d t})_{t_{i}} = \frac{1}{2 Δ t} [(C_{A (i + 1)} - C_{A (i - 1)}] ⌊ e . g ., (\frac{d C_{A}}{d t})_{t_{3}} = \frac{1}{2 Δ t} [C_{A 4} - C_{A 2}] ⌋$	(7-14)
Last point:	$(\frac{d C_{A}}{d t})_{t_{5}} = \frac{1}{2 Δ t} [C_{A 3} - 4 C_{A 4} + 3 C_{A 5}]$ $(\frac{d C_{A}}{d t})_{t_{5}} = \frac{1}{2 Δ t} [C_{A 3} - 4 C_{A 4} + 3 C_{A 5}]$	(7-15)

Equations (7-13) and (7-15) are used for the first and last data points, respectively, while Equation (7-14) is used for all intermediate data points (see Step 6A.la in Example 7-2).

7.4.3 Finding the Rate-Law Parameters

Now, using either the graphical method, differentiation formulas, or the polynomial derivative, Table 7-4 can be set up.

TABLE 7-4 PROCESSED DATA

Time	t₀	t₁	t₂	t₃
Concentration	C_A0	C_A1	C_A2	C_A3
Derivative	$(- \frac{d C_{A}}{d t})_{0}$ $(- \frac{d C_{A}}{d t})_{0}$	$(- \frac{d C_{A}}{d t})_{1}$ $(- \frac{d C_{A}}{d t})_{1}$	$(- \frac{d C_{A}}{d t})_{2}$ $(- \frac{d C_{A}}{d t})_{2}$	$(- \frac{d C_{A}}{d t})_{3}$ $(- \frac{d C_{A}}{d t})_{3}$

The reaction order can now be found from a plot of ln(-dC_A/dX) as a function of lnC_A, as shown in Figure 7-5(a), since

$\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln k_{A} + α \ln C_{A} & (7-16) \end{matrix}$ $\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln k_{A} + α \ln C_{A} & (7-16) \end{matrix}$

Before solving the following example problems, review the steps to determine the reaction-rate law from a set of data points (Table 7-1).

Example 7-2 Determining the Rate Law

The reaction of triphenyl methyl chloride (trityl) (A) and methanol (B) discussed in Example 7-1 is now analyzed using the differential method.

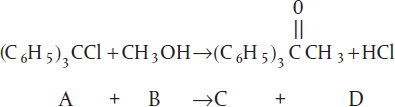
Chlorotriphenylmethane Triphenylmethyl chloride (C6H5)3 CCL represents A, Methanol (CH3OH) represents B, Triphenylmethane ((C6H5)3CH) represents C and Hydrochloric acid represents D. The reaction reads: A plus B reacts to form C plus D.

$\underset{A}{(C {}_{6}H_{5})_{3} C C 1} \underset{+}{+} \underset{B}{C H_{3} O H} \underset{\to}{\to} \underset{C}{(C {}_{6}H_{5})_{3} \overset{\overset{0}{∥}}{C C H_{3}}} \underset{+}{+} \underset{D}{\underset{}{H C 1}}$ $\underset{A}{(C {}_{6}H_{5})_{3} C C 1} \underset{+}{+} \underset{B}{C H_{3} O H} \underset{\to}{\to} \underset{C}{(C {}_{6}H_{5})_{3} \overset{\overset{0}{∥}}{C C H_{3}}} \underset{+}{+} \underset{D}{\underset{}{H C 1}}$

The concentration-time data in Table E7-2.1 was obtained in a batch reactor.

TABLE E7-2.1 RAW DATA

Time (min)	0	50	100	150	200	250	300
Concentration of A (mol/dm³) × 10³ (At t = 0, C_A = 0.05 M)	50	38	30.6	25.6	22.2	19.5	17.4

The initial concentration of methanol was 0.5 mol/dm³.

Part (1) Determine the reaction order with respect to triphenyl methyl chloride.

Part (2) In a separate set of experiments, the reaction order wrt methanol was found to be first order. Determine the specific reaction-rate constant.

Solution

Part (1) Find the reaction order with respect to trityl.

Step 1 Postulate a rate law.

$\begin{matrix} - r_{A} = k C_{A}^{α} C_{B}^{β} & (E7-2.1) \end{matrix}$ $\begin{matrix} - r_{A} = k C_{A}^{α} C_{B}^{β} & (E7-2.1) \end{matrix}$

Step 2 Process your data in terms of the measured variable, which in this case is C_A.

Step 3 Look for simplifications. Because the concentration of methanol is 10 times the initial concentration of triphenyl methyl chloride, its concentration is essentially constant

$\begin{matrix} C_{B} ≅ C_{B0} & (E7-2.2) \end{matrix}$ $\begin{matrix} C_{B} ≅ C_{B0} & (E7-2.2) \end{matrix}$

Substituting for C_B in Equation (E7-2.1)

$- r_{A} = \underset{k^{'}}{\underset{︸}{k C_{B 0}^{β}}} C_{A}^{α}$ $- r_{A} = \underset{k^{'}}{\underset{︸}{k C_{B 0}^{β}}} C_{A}^{α}$

$\begin{matrix} - r_{A} = k' C_{A}^{α} & (E7-2.3) \end{matrix}$ $\begin{matrix} - r_{A} = k' C_{A}^{α} & (E7-2.3) \end{matrix}$

Step 4 Apply the CRE algorithm.

Mole Balance

$\begin{matrix} \frac{d N_{A}}{d t} = r_{A} V & (E7-2.4) \end{matrix}$ $\begin{matrix} \frac{d N_{A}}{d t} = r_{A} V & (E7-2.4) \end{matrix}$

Rate Law:

$\begin{matrix} - r_{A} = k' C_{A}^{α} & (E7-2.3) \end{matrix}$ $\begin{matrix} - r_{A} = k' C_{A}^{α} & (E7-2.3) \end{matrix}$

Stoichiometry: Liquid V = V₀

$C_{A} = \frac{N_{A}}{V_{0}}$ $C_{A} = \frac{N_{A}}{V_{0}}$

Combine: Mole balance, rate law, and stoichiometry àC,

$\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{α} & (E7-2.5) \end{matrix}$ $\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{α} & (E7-2.5) \end{matrix}$

Evaluate: Taking the natural log of both sides of Equation (E7-2.5)

$\begin{matrix} \ln [- \frac{d C_{A}}{d t}] = \ln k' + α \ln C_{A} & (E7-2.6) \end{matrix}$ $\begin{matrix} \ln [- \frac{d C_{A}}{d t}] = \ln k' + α \ln C_{A} & (E7-2.6) \end{matrix}$

The slope of a plot of $\begin{matrix} \ln [- \frac{d C_{A}}{d t}] \end{matrix}$ $\begin{matrix} \ln [- \frac{d C_{A}}{d t}] \end{matrix}$ versus In C_A will yield the reaction order α with respect to triphenyl methyl chloride (A).

Step 5 Find $\begin{matrix} [- \frac{d C_{A}}{d t}] \end{matrix}$ $\begin{matrix} [- \frac{d C_{A}}{d t}] \end{matrix}$ as a function of C_A from concentration-time data.

Step 5A Graphical Method. We now show how to construct Table E7-2.2.

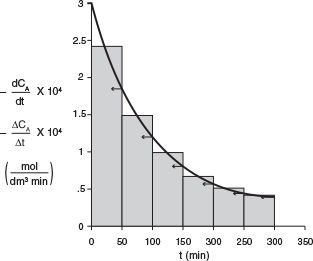
The derivative (-dC_Ajdt) is determined by calculating and plotting (—ΔCa]At) as a function of time, t, and then using the equal-area differentiation technique (Appendix A.2) to determine (-dC_Ajdt) as a function of C_A. First, we calculate the ratio (-AC_AjAt) from the first two columns of Table E7-2.2; the result is written in the third column.

TABLE E7-2.2 PROCESSED DATA

The column headers represents, t (minutes), C subscript A times (10 to the power 3) (moles per (decimeter cube)), negative (delta C subscript A over delta t) times 10 to the power 4 (moles per decimeter cube. Min), and negative (d C subscript A over dt) times 10 to the power 4 (moles per decimeter cube). t (minutes), C subscript A times (10 to the power 3) (moles per (decimeter cube)) the rows reads row 1 reads 0, 50. Row 2 reads 50, 38. Row 3 reads 100, 30.6. Row 4 reads 150, 25.6. Row 5 reads 200, 22.2. Row 6 reads 250, 19.5. Row 7 reads 300, 17.4. Row 1 and row 2 is substituted in the third column formulae and row 1 reads 2.40, row 3 reads 1.48, row 3 reads 1.00, row 4 reads 0.68, row 5 reads0.54, and row 6 reads0.42. In the fourth column, the values are substituted in the formulae and row 1 reads 3.0, row 2 reads1.86, row 3 reads 1.2, row 4 reads 0.8, row 5 reads 0.5, and row 6 reads 0.47.

We use numerical differentiation to help identify inconsistencies in the data.

Next, we use Table E 7-2.2 to plot the third column as a function of the first column in Figure E7-1.1 [i.e., (–ΔC_A/Δt) versus t]. Using equal-area differentiation, the value of (–dC_A/dt) is read off the figure (represented by the arrows); then it is used to complete the fourth column of Table E7-2.2.

Figure shows histogram bars with a curve.

Figure E7-2.1 Graphical differentiation.

The results to find (–dC_A/dt) at each time, t, and concentration, C_A, are summarized in Table E7-2.3.

Step 5B Finite Difference Method. We now show how to calculate (dC_Ajdt) using the finite difference formulas [i.e., Equations (7-13) through (7-15)].

$\begin{matrix} t = 0 & {(\frac{d C_{A}}{d t})}_{t=0} & = \frac{- 3 C_{A 0} + 4 C_{A 1} - C_{A 2}}{2 Δ t} \\ = \frac{[- 3 (50) + 4 (38 - 30.6)] \times 10^{- 3}}{100} \\ - 2.86 \times 10 {mol/dm}^{3} \cdot \min \\ - \frac{d C_{A}}{d t} \times 10^{4} = 2.86 {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 0 & {(\frac{d C_{A}}{d t})}_{t=0} & = \frac{- 3 C_{A 0} + 4 C_{A 1} - C_{A 2}}{2 Δ t} \\ = \frac{[- 3 (50) + 4 (38 - 30.6)] \times 10^{- 3}}{100} \\ - 2.86 \times 10 {mol/dm}^{3} \cdot \min \\ - \frac{d C_{A}}{d t} \times 10^{4} = 2.86 {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 50 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{1} & \frac{\begin{matrix} C_{A2} - C_{A0} \end{matrix}}{2 Δ t} = \frac{(30.6 - 50) \times 10^{- 3}}{100} \\ = - 1.94 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 50 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{1} & \frac{\begin{matrix} C_{A2} - C_{A0} \end{matrix}}{2 Δ t} = \frac{(30.6 - 50) \times 10^{- 3}}{100} \\ = - 1.94 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 100 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{2} & \frac{\begin{matrix} C_{A3} - C_{A1} \end{matrix}}{2 Δ t} = \frac{(25.6 - 38) \times 10^{- 3}}{100} \\ = - 1.24 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 100 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{2} & \frac{\begin{matrix} C_{A3} - C_{A1} \end{matrix}}{2 Δ t} = \frac{(25.6 - 38) \times 10^{- 3}}{100} \\ = - 1.24 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 150 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{3} & \frac{\begin{matrix} C_{A4} - C_{A2} \end{matrix}}{2 Δ t} = \frac{(22.2 - 30.6) \times 10^{- 3}}{100} \\ = - 0.84 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 150 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{3} & \frac{\begin{matrix} C_{A4} - C_{A2} \end{matrix}}{2 Δ t} = \frac{(22.2 - 30.6) \times 10^{- 3}}{100} \\ = - 0.84 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{4} & \frac{\begin{matrix} C_{A5} - C_{A3} \end{matrix}}{2 Δ t} = \frac{(19.5 - 25.6) \times 10^{- 3}}{100} \\ = - 0.61 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{4} & \frac{\begin{matrix} C_{A5} - C_{A3} \end{matrix}}{2 Δ t} = \frac{(19.5 - 25.6) \times 10^{- 3}}{100} \\ = - 0.61 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{5} & \frac{\begin{matrix} C_{A6} - C_{A4} \end{matrix}}{2 Δ t} = \frac{(17.4 - 22.2) \times 10^{- 3}}{100} \\ = - 0.48 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{5} & \frac{\begin{matrix} C_{A6} - C_{A4} \end{matrix}}{2 Δ t} = \frac{(17.4 - 22.2) \times 10^{- 3}}{100} \\ = - 0.48 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

$\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{5} & \frac{\begin{matrix} C_{A4} - 4 C_{A5} + 3 \end{matrix} C_{A6}}{2 Δ t} = \frac{[22.2 - 4 (19.5) + 3 (17.4)] \times 10^{- 3}}{100} \\ = - 0.36 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$ $\begin{matrix} t = 200 & (\frac{\begin{matrix} d C_{A} \end{matrix}}{d t})_{5} & \frac{\begin{matrix} C_{A4} - 4 C_{A5} + 3 \end{matrix} C_{A6}}{2 Δ t} = \frac{[22.2 - 4 (19.5) + 3 (17.4)] \times 10^{- 3}}{100} \\ = - 0.36 \times 10^{- 4} {mol/dm}^{3} \cdot \min \end{matrix}$

We now enter the above values for (−dC_A/dt) in Table E7-2.3 and use Table 7-2.2 to plot columns 2 and 3 $(- \frac{d C_{A}}{d t} \times 10, 000)$ $(- \frac{d C_{A}}{d t} \times 10, 000)$ as a function of column 4 (C_AX 1,000) on log-log paper, as shown in Figure E7-2.2. We could also substitute the parameter values in Table E7-2.3 into Excel to find α and k’. Note that most of the points for both methods fall virtually on top of one another. This table is, in a way, redundant because it is not necessary to always find (−dC_A/dt) by both techniques, graphical and finite difference.

TABLE E7-2.3 SUMMARY OF PROCESSED DATA

	Graphical	Finite Difference
	$- \frac{d C_{A}}{d t} \times 10, 000$ $- \frac{d C_{A}}{d t} \times 10, 000$	$- \frac{d C_{A}}{d t} \times 10, 000$ $- \frac{d C_{A}}{d t} \times 10, 000$
t (min)	(mol/dm³ . min)	(mol/dm³ . min)	C_A × 1,000 (mol/dm³)
0	3.0	2.86	50
50	1.86	1.94	38
100	1.20	1.24	30.6
150	0.80	0.84	25.6
200	0.68	0.61	22.2
250	0.54	0.48	19.5
300	0.42	0.36	17.4

Graph shows an excel plot to define alpha and k.

Figure E7-2.2 Excel plot to determine α and k.

From Figure E7-2.2, we found the slope to be 1.99, so that the reaction is said to be second order (α = 2.0) with respect to triphenyl methyl chloride. Recall when the cycle lengths on the x-axis and the y-axis are the same on log-log paper, then we simply measure the slope with a ruler. However, with all the software on your computer it would be more impressive to your professor or employer if you typed the data into Excel or Polymath or some other spreadsheet software and then printed the results.

To evaluate k′, we can evaluate the derivative in Figure E7-2.2 at C_AP = 20 × 10^–3 mol/dm³, which is

$\begin{matrix} (- \frac{d C_{A}}{d t})_{p} = 0 \cdot 5 \times 1 0^{- 4} mol/ {dm}^{3} · min & (E7-2.7) \end{matrix}$ $\begin{matrix} (- \frac{d C_{A}}{d t})_{p} = 0 \cdot 5 \times 1 0^{- 4} mol/ {dm}^{3} · min & (E7-2.7) \end{matrix}$

then

$\begin{matrix} k' = \frac{{(- \frac{d C_{A}}{d t})}_{p}}{C_{A p}^{2}} & (E7-2.8) \\ = \frac{0.5 \times 10^{- 4} {mol/dm}^{3} \cdot min}{(20 \times 10^{- 3} {mol/dm}^{3})^{2}} = 0.125 {dm}^{3} / mol \cdot min \end{matrix}$ $\begin{matrix} k' = \frac{{(- \frac{d C_{A}}{d t})}_{p}}{C_{A p}^{2}} & (E7-2.8) \\ = \frac{0.5 \times 10^{- 4} {mol/dm}^{3} \cdot min}{(20 \times 10^{- 3} {mol/dm}^{3})^{2}} = 0.125 {dm}^{3} / mol \cdot min \end{matrix}$

As will be shown in Section 7.5, we could also use nonlinear regression on Equation (E7-1.5) to find K′

k′ = 0.122 dm³/mol · min (E7-2.9)

The Excel graph shown in Figure E7-2.2 gives α = 1.99 and K′ = 0.13 dm³/mol · min. We now set α = 2 and regress again to find K′ = 0.122 dm³/mol · min.

ODE Regression. There are techniques and software becoming available whereby an ODE solver can be combined with a regression program to solve differential equations, such as

\begin{matrix} - \frac{d C_{A}}{d t} = k_{A}^{'} C_{A}^{α} & \begin{matrix} (E 7 - 2.5) \end{matrix} \end{matrix}

$\begin{matrix} - \frac{d C_{A}}{d t} = k_{A}^{'} C_{A}^{α} & \begin{matrix} (E 7 - 2.5) \end{matrix} \end{matrix}$

to find K_A and α from concentration-time data.

Part (2) The reaction was said to be first order with respect to methanol, ß = 1.

\begin{matrix} k' = C_{B 0}^{β} k = C_{B 0} k & \begin{matrix} (E 7 - 2.10) \end{matrix} \end{matrix}

$\begin{matrix} k' = C_{B 0}^{β} k = C_{B 0} k & \begin{matrix} (E 7 - 2.10) \end{matrix} \end{matrix}$

Assuming C_BO is constant at 0.5 mol/dm³ and solving for k yields²

$\begin{array}{l} k = \frac{k'}{C_{B 0}} = \frac{0.122 \frac{d m^{3}}{m o 1 \cdot \min}}{0.5 \frac{m o 1}{d m^{3}}} \\ k = 0.244 ({dm}^{3} / mol)^{2} / min \end{array}$ $\begin{array}{l} k = \frac{k'}{C_{B 0}} = \frac{0.122 \frac{d m^{3}}{m o 1 \cdot \min}}{0.5 \frac{m o 1}{d m^{3}}} \\ k = 0.244 ({dm}^{3} / mol)^{2} / min \end{array}$

The rate law is

\begin{matrix} - r_{A} = [0.244 (d m^{3} / mol)^{2} / \min] C_{A}^{2} C_{B} & \begin{matrix} (E 7 - 2.11) \end{matrix} \end{matrix}

$\begin{matrix} - r_{A} = [0.244 (d m^{3} / mol)^{2} / \min] C_{A}^{2} C_{B} & \begin{matrix} (E 7 - 2.11) \end{matrix} \end{matrix}$

Analysis: In this example, the differential method of data analysis was used to find the reaction order with respect to trityl (α = 1.99) and the pseudo rate constant (k′ = 0.125 (dm³/mol)/min). However, as we mentioned earlier it would probably be more impressive to your employer or professor if you typed the data into your computer and used a software package to find fe. We discuss one such software package in Section 7.5. The reaction order was rounded up to α = 2 and the data was regressed again to obtain k′ = 0.122 (dm³/mol)/min, again knowing k′ and C_B0, and the true rate constant is k = 0.244 (dm³/mol)²/min. We used two techniques to differentiate the concentration-time data to find $(\frac{d C_{A}}{d t})$ $(\frac{d C_{A}}{d t})$ : The graphical technique and the finite difference technique.

Integral method normally used to find k when order is known

By comparing the methods of analysis of the rate data presented in Examples 7-1 and 7-2, we note that the differential method tends to accentuate the uncertainties in the data, while the integral method tends to smooth the data, thereby disguising the uncertainties in it. In most analyses, it is imperative that the engineer know the limits and uncertainties in the data. This prior knowledge is necessary to provide for a safety factor when scaling up a process from laboratory experiments to design either a pilot plant or full-scale industrial plant.

² M. Hoepfner and D. K. Roper, “Describing Temperature Increases in Plasmon-Resonant Nanoparticle Systems,” journal of Thermal Analysis and Calorimetry, 98(1), (2009), pp. 197-202.

7.5 Nonlinear Regression

In nonlinear regression analysis, we search for those parameter values that minimize the sum of the squares of the differences between the measured values and the calculated values for all the data points. Not only can nonlinear regression find the best estimates of parameter values, it can also be used to discriminate between different rate-law models, such as the Langmuir-Hinshelwood models discussed in Chapter 10. Many software programs are available to find these parameter values so that all one has to do is enter the data. The Polymath software will be used to illustrate this technique. In order to carry out the search efficiently, in some cases one has to enter initial estimates of the parameter values close to the actual values. These estimates can be obtained using the linear-least-squares technique discussed on the CRE Web site Professional Reference Shelf R7.3 (http://www.umich.edu/~elements/5e/07chap/pdf/leastsquares.pdfi.

Compare the calculated parameter value with the measured value.

We will now apply nonlinear regression to reaction-rate data to determine the rate-law parameters. Here, we make initial estimates of the parameter values (e.g., reaction order, specific rate constant) in order to calculate the concentration for each data point, C_ic, obtained by solving an integrated form of the combined mole balance and rate law. We then compare the measured concentration at that point, C_im, with the calculated value, C_ic, for the parameter values chosen. We make this comparison by calculating the sum of the squares of the differences at each point ∑(C_im – C_ic)². We then continue to choose new parameter values and search for those values of the rate law that will minimize the sum of the squared differences of the measured concentrations, C_im, and the calculated concentrations values, C_ic. That is, we want to find the rate-law parameters for which the sum of all data points ∑(C_im – C_ic)² is a minimum. If we carried out N experiments, we would want to find the parameter values (e.g., E, activation energy, reaction orders) that minimize the quantity

$σ^{2} = \frac{s^{2}}{N - K} = \sum_{i = 1}^{N} \frac{(C_{i m} - C_{i c})^{2}}{N - K} (7-17)$ $σ^{2} = \frac{s^{2}}{N - K} = \sum_{i = 1}^{N} \frac{(C_{i m} - C_{i c})^{2}}{N - K} (7-17)$

where

$s^{2} = \sum_{i = 1}^{i = N} {(C}_{i m} - C_{i c})^{2}$ $s^{2} = \sum_{i = 1}^{i = N} {(C}_{i m} - C_{i c})^{2}$

N = number of runs

K = number of parameters to be determined

C_im = measured concentration rate for run i

C_ic = calculated concentration rate for run i

One notes that if we minimize s² in Equation (7-17), we minimize σ².

To illustrate this technique, let’s consider the reaction

A → Product

for which we want to learn the reaction order, a, and the specific reaction rate, k,

$- r_{A} = k C_{A}^{α}$ $- r_{A} = k C_{A}^{α}$

The reaction rate will be measured at a number of different concentrations. We now choose values of k and α, and calculate the rate of reaction (C_ic) at each concentration at which an experimental point, i, was taken. We then subtract the calculated value (C_ic) from the measured value (C_im), square the result, and sum the squares for all the runs for the values of k and α that we have chosen.

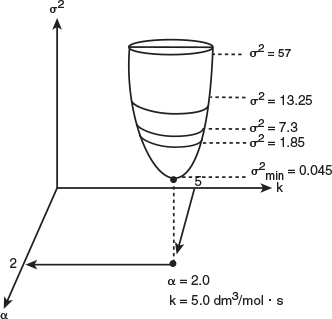
This procedure is continued by further varying α and k until we find those values of k and α that minimize the sum of the squares. Many well-known searching techniques are available to obtain the minimum value $σ_{\min}^{2} .$ $σ_{\min}^{2} .$ .³ Figure 7-6 shows a hypothetical plot of the sum of the squares as a function of the parameters α and k:

$\begin{matrix} σ^{2} = f (k, α) & (7-18) \end{matrix}$ $\begin{matrix} σ^{2} = f (k, α) & (7-18) \end{matrix}$

A three-dimensional plane shows half of a prolate spheroid in the k alpha plane.

Figure 7-6 Minimum sum of squares.

Look at the top circle. We see that there are many combinations of α and k (e.g., α = 2.2, k = 4.8 or α = 1.8, k = 5.3) that will give a value of σ² = 57. The same is true for σ² = 1.85. We need to find the combination of α and k that gives the lowest value of σ².

In searching to find the parameter values that give the minimum of the sum of squares σ², one can use a number of optimization techniques or software packages. The computerized searching procedure begins by guessing parameter values and then calculating (C_im – C_ic) and then σ² for these values. Next, a few sets of parameters are chosen around the initial guess, and σ² is calculated for these sets as well. The search technique looks for the smallest value of σ² in the vicinity of the initial guess and then proceeds along a trajectory in the direction of decreasing σ² to choose the next set of different parameter values and determine the corresponding σ² as shown as a contour plot in Figure 7-7.

³ (a) B. Carnahan and J. O. Wilkes, Digital Computing and Numerical Methods (New York: Wiley, 1973), p. 405. (b) D. J. Wilde and C. S. Beightler, Foundations of Optimization, 2nd ed. (Upper Saddle River, NJ: Prentice Hall, 1979). (c) D. Miller and M. Frenklach, Int.}. Chem. Kinet, 15 (1983), p. 677.

Starting at α = 1 and k = 1, the trajectory shown by the arrows, is continually adjusted by choosing α and k. We see in Figure 7-7 that the trajectory leads

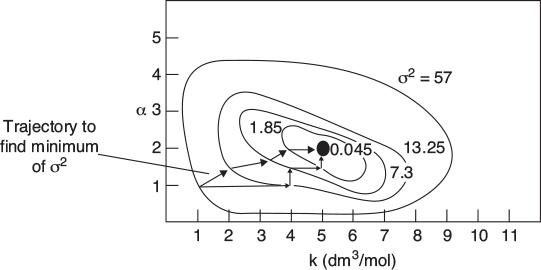
Graph shows a trajectory to find the best values of k and alpha.

Figure 7-7 Trajectory to find the best values of k and α.

us to a minimum value of σ² = 0.045 (mol/dm³)² at which point α = 2 and k = 5(dm³/mol).

If the equations are highly non linear, your initial guesses of a and k are very important. A number of software packages are available to carry out the procedure to determine the best estimates of the parameter values and the corresponding confidence limits. All we have to do is to enter the experimental values into the computer, specify the model, enter the initial guesses of the parameters, and then push the “compute” button, and the best estimates of the parameter values along with 95% confidence limits appear. If the confidence limits for a given parameter are larger than the parameter itself, the parameter is probably not significant and should be dropped from the model. After the appropriate model parameters are eliminated, the software is run again to determine the best fit with the new model equation.

7.5.1 Concentration-Time Data

We will now use nonlinear regression to determine the rate-law parameters from concentration-time data obtained in batch experiments. We recall that the combined rate-law stoichiometry mole balance for a constant-volume batch reactor is

$\begin{matrix} \frac{d C_{A}}{d t} = - k C_{A}^{α} & (7-19) \end{matrix}$ $\begin{matrix} \frac{d C_{A}}{d t} = - k C_{A}^{α} & (7-19) \end{matrix}$

We now integrate Equation (7-6) for the case α ≠ 1 to give

$C_{A 0}^{1 - α} - C_{A}^{1 - α} = (1 - α) k t$ $C_{A 0}^{1 - α} - C_{A}^{1 - α} = (1 - α) k t$

Rearranging to obtain the concentration as a function of time, we obtain

$\begin{matrix} C_{A} = [C_{A 0}^{1 - α} - (1 - α) k t]^{1 / (1 - α)} & (7-20) \end{matrix}$ $\begin{matrix} C_{A} = [C_{A 0}^{1 - α} - (1 - α) k t]^{1 / (1 - α)} & (7-20) \end{matrix}$

Now we could use either Polymath or MATLAB to find the values of α and k that would minimize the sum of squares of the differences between the measured concentrations, C_Aim, and calculated concentrations, C_Aic. That is, for N data points,

$\begin{matrix} s^{2} = Σ_{i = 1}^{N} (C_{A i m} - C_{A i c})^{2} = Σ_{i = 1}^{N} [C_{A i m} - [C_{A 0}^{1 - α} - (1 - α) k t_{i}]^{1 / (1 - α)}]^{2} & (7-21) \end{matrix}$ $\begin{matrix} s^{2} = Σ_{i = 1}^{N} (C_{A i m} - C_{A i c})^{2} = Σ_{i = 1}^{N} [C_{A i m} - [C_{A 0}^{1 - α} - (1 - α) k t_{i}]^{1 / (1 - α)}]^{2} & (7-21) \end{matrix}$

we want the values of a and k that will make s² a minimum.

If Polymath is used, one should use the absolute value, abs, for the term in brackets in Equation (7-16), that is,

$\begin{matrix} s^{2} = Σ_{i = 1}^{n} {[C_{A i m} - {a b s [C_{A 0}^{1 - α} - (1 - α) k t_{i}]}^{1 / (1 - α)}]}^{2} & (7-22) \end{matrix}$ $\begin{matrix} s^{2} = Σ_{i = 1}^{n} {[C_{A i m} - {a b s [C_{A 0}^{1 - α} - (1 - α) k t_{i}]}^{1 / (1 - α)}]}^{2} & (7-22) \end{matrix}$

Another, and perhaps easier, way to solve for the parameter values is to use time rather than concentrations, rearranging Equation (7-20) to get

t_{c} = \frac{C_{A0}^{1 - α} - C_{A}^{1 - α}}{K (1 - α)} (7 - 23)

$t_{c} = \frac{C_{A0}^{1 - α} - C_{A}^{1 - α}}{K (1 - α)} (7 - 23)$

That is, we find the values of k and a that minimize

$\begin{matrix} s^{2} = Σ_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = Σ_{i = 1}^{N} [t_{i m} - \frac{C_{A0}^{1 - α} - C_{Ai}^{1 - α}}{k (1 - α)}]^{2} & (7-24) \end{matrix}$ $\begin{matrix} s^{2} = Σ_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = Σ_{i = 1}^{N} [t_{i m} - \frac{C_{A0}^{1 - α} - C_{Ai}^{1 - α}}{k (1 - α)}]^{2} & (7-24) \end{matrix}$

Finally, a discussion oi weighted least squares as applied to a first-order reaction is provided in the Professional Reference Shelf R7.5 on the CRE Web site.

Example 7-3 Use of Regression to Find the Rate-Law Parameters^†

We shall use the reaction and data in Examples E7-1 and E7-2 to illustrate how to use regression to find α and k’.

\begin{matrix} {(C_{6} H_{5})}_{3} {CCI+CH}_{3} OH & \to & {{(C}_{6} H_{5})}_{3} {COCH}_{3} + HCI \\ A + B & \to & C + D \end{matrix}

$\begin{matrix} {(C_{6} H_{5})}_{3} {CCI+CH}_{3} OH & \to & {{(C}_{6} H_{5})}_{3} {COCH}_{3} + HCI \\ A + B & \to & C + D \end{matrix}$

The Polymath regression program is included on the CRE Web site. Recalling Equation (E5-1.5)

$\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{α} & (E7-2.5) \end{matrix}$ $\begin{matrix} - \frac{d C_{A}}{d t} = k' C_{A}^{α} & (E7-2.5) \end{matrix}$

and integrating with the initial condition when t = 0 and C_A = C_A0 for α ≠ 1.0

t = \frac{1}{k^{'}} \frac{C_{A0}^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} (E 7 - 3.1)

$t = \frac{1}{k^{'}} \frac{C_{A0}^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} (E 7 - 3.1)$

Given or assuming k’ and α, Equation (7-2.5) can be solved to calculate the time t to reach a concentration C_A or we could calculate the concentration C_A at time t. We can proceed two ways from this point, both of which will give the same result.

† See tutorial at http://www.umich.edu/~elements/5e/07chap/Example_7-3_Polymath_nonlinear_regression_tutorial.pdf.

We can search for the combination α and k that minimizes $\begin{matrix} [σ^{2} = \sum (t_{i m} - t_{i c})^{2}], \end{matrix}$ $\begin{matrix} [σ^{2} = \sum (t_{i m} - t_{i c})^{2}], \end{matrix}$ or we could solve Equation (E7-4.3) for C_A and find a and k that minimize $[σ^{2} = Σ (C_{A i m} - C_{A i c})^{2}] .$ $[σ^{2} = Σ (C_{A i m} - C_{A i c})^{2}] .$

We shall choose the former. So, substituting for the initial concentration C_A0 = 0.05 mol/dm³ into Equation (Ε7-3.1)^τ

$\begin{matrix} \begin{matrix} t = \frac{1}{k'} \frac{(0.05)^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} \end{matrix} & (E7-3.2) \end{matrix}$ $\begin{matrix} \begin{matrix} t = \frac{1}{k'} \frac{(0.05)^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} \end{matrix} & (E7-3.2) \end{matrix}$

A brief tutorial on how to input data in Polymath on the CRE Web site (http:llumich.edu/-elementsl5el07chaplExample_7-3_Polymath_nonlinear_regression_ tuto-rial.pdj) shows screen shots of how to enter the raw data in Table E7-2.1 and how to carry out a nonlinear regression on Equation (E7-3.2).

For C_A0 = 0.05 mol/dm³, that is, Equation (E7-3.1) becomes

$\begin{matrix} t_{c} = \frac{1}{k ’} \frac{(0.05)^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} & (E7-3.3) \end{matrix}$ $\begin{matrix} t_{c} = \frac{1}{k ’} \frac{(0.05)^{(1 - α)} - C_{A}^{(1 - α)}}{(1 - α)} & (E7-3.3) \end{matrix}$

We want to minimize s² to give α and k′ .

$\begin{matrix} s^{2} = \sum_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = \sum_{i = 1}^{N} [t_{i m} - \frac{0.0 5^{(1 - α)} - C_{A i c}^{(1 - α)}}{k' (1 - α)}]^{2} & (7-25) \end{matrix}$ $\begin{matrix} s^{2} = \sum_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = \sum_{i = 1}^{N} [t_{i m} - \frac{0.0 5^{(1 - α)} - C_{A i c}^{(1 - α)}}{k' (1 - α)}]^{2} & (7-25) \end{matrix}$

We shall carry out a first regression to find approximate values of a and k. Next, we use a common procedure, which is to round a off to an integer and carry out a second regression to find the best value of k after a has been set equal to an integer.

TABLE E7-3.1 RESULTS OF 1ST REGRESSION

TABLE E7-3.2 RESULTS OF 2ND REGRESSION

The results shown are

\begin{matrix} α = 2.04 \\ K^{,} = 0.147 {dm}^{3} / mol .min \end{matrix} | \begin{matrix} α = 2.0 \\ K^{,} = 0.125 {dm}^{3} / mol .min \end{matrix}

$\begin{matrix} α = 2.04 \\ K^{,} = 0.147 {dm}^{3} / mol .min \end{matrix} | \begin{matrix} α = 2.0 \\ K^{,} = 0.125 {dm}^{3} / mol .min \end{matrix}$

The first regression gives a = 2.04, as shown in Table E7-3.1. We shall round off a to make the reaction second order, (i.e., a = 2.00). Now having fixed a at 2.0, we must do another regression (cf. Table E7-3.2) on k’ because the k’ given in Table E.7-3.1 is for a = 2.04. We now regress the equation

$t = \frac{1}{k ’} [\frac{1}{C_{A}} - \frac{1}{C_{A 0}}]$ $t = \frac{1}{k ’} [\frac{1}{C_{A}} - \frac{1}{C_{A 0}}]$

The second regression gives k′ = 0.125 dm³/mol · min. We now calculate k

$k = \frac{k'}{C_{A0}} = 0.25 (\frac{d m^{3}}{m o 1})^{2} / \min$ $k = \frac{k'}{C_{A0}} = 0.25 (\frac{d m^{3}}{m o 1})^{2} / \min$

Analysis: In this example, we showed how to use nonlinear regression to find k’ and a. The first regression gave a = 2.04, which we rounded to 2.00 and then regressed again for the best value of k’ for a = 2.0, which was k′ = 0.125 (dm³/mol)/min giving a value of the true specific reaction rate of k = 0.25 (mol/dm³)²/min. We note that the reaction order is the same as that in Examples 7-1 and 7-2; however, the value of k is about 8% larger. The r² and other statistics are in Polymath’s output.

7.5.2 Model Discrimination

One can also determine which model or equation best fits the experimental data by comparing the sums of the squares for each model and then choosing the equation with a smaller sum of squares and/or carrying out an F-test. Alternatively we can compare the residual plots for each model. These plots show the error associated with each data point, and one looks to see if the error is randomly distributed or if there is a trend in the error. When the error is randomly distributed, this is an additional indication that the correct rate law has been chosen. An example of model discrimination using nonlinear regression is given in Chapter 10, Example 10-3.

7.6 Reaction-Rate Data from Differential Reactors

Data acquisition using the method of initial rates and a differential reactor is similar in that the rate of reaction is determined for a specified number of predetermined initial or entering reactant concentrations. A differential reactor (PBR) is normally used to determine the rate of reaction as a function of either concentration or partial pressure. It consists of a tube containing a very small amount of catalyst, usually arranged in the form of a thin wafer or disk. A typical arrangement is shown schematically in Figure 7-8. The criterion for a reactor being differential is that the conversion of the reactants in the bed is extremely small, as is the change in temperature and reactant concentration through the bed. As a result, the reactant concentration through the reactor is essentially constant and approximately equal to the inlet concentration. That is, the reactor is considered to be gra-dientless,⁴ and the reaction rate is considered spatially uniform within the bed.

Most commonly used catalytic reactor to obtain experimental data

⁴ B. Anderson, ed., Experimental Methods in Catalytic Research (San Diego, CA: Academic Press).

The differential reactor is relatively easy to construct at a low cost. Owing to the low conversion achieved in this reactor, the heat release per unit volume will be small (or can be made small by diluting the bed with inert solids) so that the reactor operates essentially in an isothermal manner. When operating this reactor, precautions must be taken so that the reactant gas or liquid does not bypass or channel through the packed catalyst, but instead flows uniformly across the catalyst. If the catalyst under investigation decays rapidly, the differential reactor is not a good choice because the reaction-rate parameters at the start of a run will be different from those at the end of the run. In some cases, sampling and analysis of the product stream may be difficult for small conversions in multicomponent systems.

Limitations of the differential reactor

Figure 7-8 Differential reactor.

Schematic shows a differential catalyst bed.

Figure 7-9 Differential catalyst bed.

For the reaction of species A going to product (P)

A → P

the volumetric flow rate through the catalyst bed is monitored, as are the entering and exiting concentrations (Figure 7-9). Therefore, if the weight of catalyst, AW, is known, the rate of reaction per unit mass of catalyst, —r’_A, can be calculated. Since the differential reactor is assumed to be gradientless, the design equation will be similar to the CSTR design equation. A steady-state mole balance on reactant A gives

\begin{matrix} [Flow rate in] - [Flow rate out] & + & [Rate of generation] & = & [Rate of accumulation] \\ [F_{A 0}] - [F_{Ae}] & + & [(\frac{Rate of reaction}{Mass of catalyst}) (Mass of catalyst)] & = & 0 \\ F_{A0} - F_{Ae} & + & ({r^{'}}_{A}) (Δ W) & = & 0 \end{matrix}

$\begin{matrix} [Flow rate in] - [Flow rate out] & + & [Rate of generation] & = & [Rate of accumulation] \\ [F_{A 0}] - [F_{Ae}] & + & [(\frac{Rate of reaction}{Mass of catalyst}) (Mass of catalyst)] & = & 0 \\ F_{A0} - F_{Ae} & + & ({r^{'}}_{A}) (Δ W) & = & 0 \end{matrix}$

The subscript e refers to the exit of the reactor. Solving for —r’_A,we have

$\begin{matrix} - r_{A}^{'} = \frac{F_{A 0} - F_{A e}}{Δ W} & (7-26) \end{matrix}$ $\begin{matrix} - r_{A}^{'} = \frac{F_{A 0} - F_{A e}}{Δ W} & (7-26) \end{matrix}$

The mole balance equation can also be written in terms of concentration

\begin{matrix} - r_{A}' = \frac{υ_{0} C_{A0} - υ C_{Ae}}{Δ W} & (7 - 27) \end{matrix}

$\begin{matrix} - r_{A}' = \frac{υ_{0} C_{A0} - υ C_{Ae}}{Δ W} & (7 - 27) \end{matrix}$

Differential reactor design equation

or in terms of conversion or product flow rate F_P

\begin{matrix} - r_{A}' = \frac{F_{A0} X}{Δ W} = \frac{F_{P}}{Δ W} & (7 - 28) \end{matrix}

$\begin{matrix} - r_{A}' = \frac{F_{A0} X}{Δ W} = \frac{F_{P}}{Δ W} & (7 - 28) \end{matrix}$

The term F_A0X gives the rate of formation of product, F_P, when the stoichio-metric coefficients of A and of P are identical. Adjustments to Equation (7-28) must be made when this is not the case.

For constant volumetric flow, Equation (7-28) reduces to

$\begin{matrix} - r_{A}^{'} = \frac{v_{0} (C_{A 0} - C_{A e})}{Δ W} = \frac{v_{0^{C_{P}}}}{Δ W} & (7-29) \end{matrix}$ $\begin{matrix} - r_{A}^{'} = \frac{v_{0} (C_{A 0} - C_{A e})}{Δ W} = \frac{v_{0^{C_{P}}}}{Δ W} & (7-29) \end{matrix}$

Consequently, we see that the reaction rate, $- r_{A}^{'}$ $- r_{A}^{'}$ , can be determined by measuring the product concentration, C_P.

By using very little catalyst and large volumetric flow rates, the concentration difference, (C_A0 - C_Ae), can be made quite small. The rate of reaction determined from Equation (7-29) can be obtained as a function of the reactant concentration in the catalyst bed, C_Ab

$\begin{matrix} - r_{A}^{'} = - r_{A}^{'} (C_{A b}) & (7-30) \end{matrix}$ $\begin{matrix} - r_{A}^{'} = - r_{A}^{'} (C_{A b}) & (7-30) \end{matrix}$

by varying the inlet concentration. One approximation of the concentration of A within the bed, C_Ab), would be the arithmetic mean of the inlet and outlet concentrations

$\begin{matrix} C_{A b} = \frac{C_{A 0} + C_{A e}}{2} & (7-31) \end{matrix}$ $\begin{matrix} C_{A b} = \frac{C_{A 0} + C_{A e}}{2} & (7-31) \end{matrix}$

However, since very little reaction takes place within the bed, the bed concentration is essentially equal to the inlet concentration

$C_{A b} \approx C_{A 0}$ $C_{A b} \approx C_{A 0}$

so $- r_{A}^{'}$ $- r_{A}^{'}$ is a function of C_A0

$\begin{matrix} - r_{A}^{'} = - r_{A}^{'} (C_{A 0}) & (7-32) \end{matrix}$ $\begin{matrix} - r_{A}^{'} = - r_{A}^{'} (C_{A 0}) & (7-32) \end{matrix}$

As with the method of initial rates (see the CRE Web site, http://www.umich.edu/~elements/5e/software/nonlinear_regression_tutorial.pdf), various numerical and graphical techniques can be used to determine the appropriate algebraic equation for the rate law. When collecting data for fluid-solid reacting systems, care must be taken that we use high flow rates through the differential reactor and small catalyst particle sizes in order to avoid mass transfer limitations. If data show the reaction to be first order with a low activation energy, say 8 kcal/mol, one should suspect the data are being collected in the mass transfer limited regime. We will expand on mass transfer limitations and how to avoid them in Chapter 10, and also in PDF Chapters 14 and 15 on the Web site.

Example 7-4 Using a Differential Reactor to Obtain CatalytL· Kate Data

The formation of methane from carbon monoxide and hydrogen using a nickel catalyst was studied by Pursley.⁵ The reaction

⁵J. A. Pursley, “An Investigation of the Reaction between Carbon Monoxide and Hydrogen on a Nickel Catalyst above One Atmosphere,” Ph.D. thesis, University of Michigan.

3H₂ + CO→CH₄ + H₂0

was carried out at 500°F in a differential reactor where the effluent concentration of methane was measured. The raw data is shown in Table E7-4.1.

TABLE E7-4.1 RAW DATA

Run	P_CO(atm)	$P_{H_{2}} (atm)$ $P_{H_{2}} (atm)$	$C_{C H_{4}} ({mol/dm}^{3})$ $C_{C H_{4}} ({mol/dm}^{3})$
1	1	1.0	1.73×10^-4
2	1.8	1.0	4.40×10^-4
3	4.08	1.0	10.0×10^-4
4	1.0	0.1	1.65×10^-4
5	1.0	0.5	2.47×10^-4
6	1.0	4.0	1.75×10^-4

$P_{H_{2}}$ $P_{H_{2}}$ is constant in Runs 1, 2, 3.

P_CO is constant in Runs 4, 5, 6.

The exit volumetric flow rate from a differential packed bed containing 10 g of catalyst was maintained at 300 dm³ /min for each run. The partial pressures of H₂ and CO were determined at the entrance to the reactor, and the methane concentration was measured at the reactor exit.

Determine the rate law and rate law parameters. To better understand how we will determine the rate law and its parameters, we will break the solution into three parts, (a), (b), and (c), as shown below.

(a) Relate the rate of reaction to the exit methane concentration. The reaction-rate law is assumed to be the product of a function of the partial pressure of CO, /(CO), and a function of the partial pressure of H₂, g(H₂), i-e.,

$\begin{matrix} r_{{CH}_{4}}^{'} = f (C O) \cdot g (H_{2}) & (E7-4.1) \end{matrix}$ $\begin{matrix} r_{{CH}_{4}}^{'} = f (C O) \cdot g (H_{2}) & (E7-4.1) \end{matrix}$

(b) Determine the rate-law dependence on carbon monoxide, using the data generated in part (a). Assume that the functional dependence of $r_{{CH}_{4}}^{'}$ $r_{{CH}_{4}}^{'}$ on P_CO is of the form

$\begin{matrix} r_{{CH}_{4}}^{'} \sim P_{C O}^{α} & (E7-4.2) \end{matrix}$ $\begin{matrix} r_{{CH}_{4}}^{'} \sim P_{C O}^{α} & (E7-4.2) \end{matrix}$

(c) Generate a table of the reaction rate as a function of partial pressures of carbon monoxide and hydrogen, and then determine the rate-law dependence on H₂.

Solution

(a) Calculate the Rates of Reaction. In this example the product composition, rather than the reactant concentration, is being monitored. The term $(r_{CO}^{'})$ $(r_{CO}^{'})$ can be written in terms of the flow rate of methane from the reaction

$- r_{CO}^{'} = r_{{CH}_{4}}^{'} = \frac{F_{C H_{4}}}{Δ W}$ $- r_{CO}^{'} = r_{{CH}_{4}}^{'} = \frac{F_{C H_{4}}}{Δ W}$

Substituting for $F_{C H_{4}}$ $F_{C H_{4}}$ in terms of the volumetric flow rate and the concentration of methane gives

$\begin{matrix} - r_{C H_{4}}^{'} = \frac{v_{0} C_{C H_{4}}}{Δ W} & (E7-4.3) \end{matrix}$ $\begin{matrix} - r_{C H_{4}}^{'} = \frac{v_{0} C_{C H_{4}}}{Δ W} & (E7-4.3) \end{matrix}$

Since υ₀, $F_{C H_{4}}$ $F_{C H_{4}}$ , and ΔW are known for each run, we can calculate the rate of reaction.

For run 1

$r_{C H_{4}}^{'} = (\frac{300 d m^{3}}{\min}) \frac{1.73 \times 1 0^{- 4}}{10 g - c a t} m o 1 / d m^{3} = 5.2 \times 1 0^{- 3} \frac{mol C H_{4}}{g - c a t \times \min}$ $r_{C H_{4}}^{'} = (\frac{300 d m^{3}}{\min}) \frac{1.73 \times 1 0^{- 4}}{10 g - c a t} m o 1 / d m^{3} = 5.2 \times 1 0^{- 3} \frac{mol C H_{4}}{g - c a t \times \min}$

The rate for runs 2 through 6 can be calculated in a similar manner (Table E7-4.2).

TABLE E7-4.2 RAW AND CALCULATED DATA

Run	P_CO(atm)	$P_{H_{2}} (atm)$ $P_{H_{2}} (atm)$	$C_{C H_{4}} ({mol/dm}^{3})$ $C_{C H_{4}} ({mol/dm}^{3})$	$r_{C H_{4}}^{'} (\frac{{mol CH}_{4}}{g - cat-min})$ $r_{C H_{4}}^{'} (\frac{{mol CH}_{4}}{g - cat-min})$
1	1	1.0	1.73×10⁻⁴	5.2×10⁻³
2	1.8	1.0	4.40×10⁻⁴	13.2×10⁻³
3	4.08	1.0	10.0×10⁻⁴	30.0×10⁻³
4	1.0	0.1	1.65×10⁻⁴	4.95×10⁻³
5	1.0	0.5	2.47×10⁻⁴	7.42×10⁻³
6	1.0	4.0	1.75×10⁻⁴	5.25×10⁻³

(b) Determining the Rate-Law Dependence in CO. For constant hydrogen concentration (runs 1, 2, and 3), the rate law

r_{C H_{4}}^{'} = {kP}_{C O}^{α} \cdot g (P_{H_{2}})

$r_{C H_{4}}^{'} = {kP}_{C O}^{α} \cdot g (P_{H_{2}})$

can be written as

\begin{matrix} r_{C H_{4}}^{'} = k' P_{C O}^{α} & (E7-4.4) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} = k' P_{C O}^{α} & (E7-4.4) \end{matrix}$

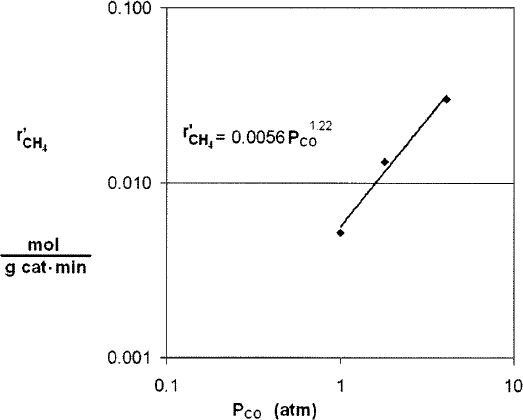
Taking the natural log of Equation (E7-5.4) gives us

\ln (r_{C H_{4}}^{'}) = \ln k^{'} + α \ln P_{CO}

$\ln (r_{C H_{4}}^{'}) = \ln k^{'} + α \ln P_{CO}$

We now plot $\ln (r_{C H_{4}}^{'})$ $\ln (r_{C H_{4}}^{'})$ versus ln P_co using runs 1, 2, and 3, for which the H₂ concentration is constant, in Figure E7-4.1. We see from the Excel plot that α = 1.22.

Graph representing reaction rate as a function of concentration shows a few points that tend to rise from left to right.

Figure E7-4.1 Reaction rate as a function of concentration.

Had we included more points, we would have found that the reaction is essentially first order with α = 1, that is

\begin{matrix} - r_{CO}^{'} = k' P_{C O} & (E7-4.5) \end{matrix}

$\begin{matrix} - r_{CO}^{'} = k' P_{C O} & (E7-4.5) \end{matrix}$

If we had used more data (not given here) we would have found α = 1.

From the first three data points in Table E7-4.2 where the partial pressure of H₂ is constant, we see the rate is linear in partial pressure of CO

r_{C H_{4}}^{'} = k' P_{C O} \cdot g (H_{2})

$r_{C H_{4}}^{'} = k' P_{C O} \cdot g (H_{2})$

Now let’s look at the hydrogen dependence.

(c) Determining the Rate-Law Dependence on H₂. From Table E7-4.2 it appears that the dependence of r’_cli on P_H cannot be represented by a power law. Comparing run 4 with run 5 and then run 5 with run 6, we see that the reaction rate first increases with increasing partial pressure of hydrogen, and subsequently decreases with increasing P_H . That is, there appears to be a concentration of hydrogen at which the rate is maximum. One set of rate laws that is consistent with these observations is:

Sketch of $r_{C H_{4}}^{'}$ $r_{C H_{4}}^{'}$ as a function of $P_{H_{2}}$ $P_{H_{2}}$

Graph shows the sketch of r prime subscript (CH subscript 4) as a function of (PH subscript 2). The horizontal axis represents "P H subscript 2" and the vertical axis represents "r prime subscript (C H subscript 4)." A concave downward curve is shown.

1. At low H₂ concentrations where $r_{C H_{4}}^{'}$ $r_{C H_{4}}^{'}$ increases as $P_{H_{2}}$ $P_{H_{2}}$ increase, the rate flow may be of the form

\begin{matrix} r_{C H_{4}}^{'} \sim P_{H_{2}}^{β_{1}} & (E7-4.6) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} \sim P_{H_{2}}^{β_{1}} & (E7-4.6) \end{matrix}$

2. At high H₂ concentrations where $r_{C H_{4}}^{'}$ $r_{C H_{4}}^{'}$ decreases as $P_{H_{2}}$ $P_{H_{2}}$ increases as P_H increases, the rate law

\begin{matrix} r_{{CH}_{4}}^{'} \sim \frac{1}{P_{H_{2}}^{β_{2}}} & (E7-4.7) \end{matrix}

$\begin{matrix} r_{{CH}_{4}}^{'} \sim \frac{1}{P_{H_{2}}^{β_{2}}} & (E7-4.7) \end{matrix}$

We would like to find one rate law that is consistent with reaction-rate data at both high and low hydrogen concentrations. After we have studied heterogeneous reactions in Chapter 10, we would recognize that Equations (E7-4.6) and (E7-4.7) can be combined into the form

\begin{matrix} r_{C H_{4}}^{'} \sim \frac{P_{H_{2}}^{β_{1}}}{1 + b P_{H_{2}}^{β_{2}}} & (E7-4.8) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} \sim \frac{P_{H_{2}}^{β_{1}}}{1 + b P_{H_{2}}^{β_{2}}} & (E7-4.8) \end{matrix}$

We will see in Chapter 10 that this combination and similar rate laws that have reac-tant concentrations (or partial pressures) in the numerator and denominator are common in heterogeneous catalysis.

Let’s see if the resulting rate law (E7-4.8) is qualitatively consistent with the rate observed.

1. For condition 1: At low $P_{H_{2}}$ $P_{H_{2}}$ , $[b (P_{H_{2}})^{β_{2}} ≪ 1]$ $[b (P_{H_{2}})^{β_{2}} ≪ 1]$ and Equation (E7-4.8) reduces to

\begin{matrix} r_{C H_{4}}^{'} \sim P_{H_{2}}^{β_{1}} & (E7-4.9) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} \sim P_{H_{2}}^{β_{1}} & (E7-4.9) \end{matrix}$

Equation (E7-4.9) is consistent with the trend in comparing runs 4 and 5.

2. For condition 2: At high $P_{H_{2}}$ $P_{H_{2}}$ , $[b (P_{H_{2}})^{β_{2}} ≫ 1]$ $[b (P_{H_{2}})^{β_{2}} ≫ 1]$ and Equation (E5-5.8) reduces to

\begin{matrix} r_{C H_{4}}^{'} \sim \frac{(P_{H_{2}})^{β_{1}}}{(P_{H_{2}})^{β_{2}}} \sim \frac{1}{(P_{H_{2}})^{β_{2} - β_{1}}} & (E7-4.10) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} \sim \frac{(P_{H_{2}})^{β_{1}}}{(P_{H_{2}})^{β_{2}}} \sim \frac{1}{(P_{H_{2}})^{β_{2} - β_{1}}} & (E7-4.10) \end{matrix}$

where β₂ > β₁. Equation (E7-4.10) is consistent with the trends in comparing runs 5 and 6.

Combining Equations (E 7-4.8) and (E7-4.5)

\begin{matrix} r_{C H_{4}}^{'} = \frac{a P_{C O} P_{H_{2}}^{β_{1}}}{1 + b P_{H_{2}}^{β_{2}}} & (E7-4.11) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} = \frac{a P_{C O} P_{H_{2}}^{β_{1}}}{1 + b P_{H_{2}}^{β_{2}}} & (E7-4.11) \end{matrix}$

Typical form of the rate law for heterogeneous catalysis

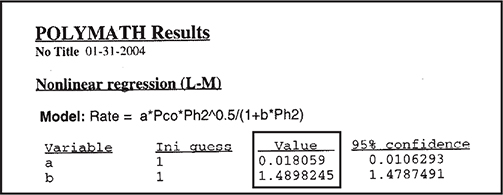
We now use the Polymath regression program to find the parameter values a, b, ß_1; and ß₂. The results are shown in Table E7-4.3.

TABLE E7-4.3 FIRST REGRESSION

Polymath and Excel regression tutorial are given in the Chapter 7 Summary Notes on the CRE Web site.

The corresponding rate law is

\begin{matrix} r_{C H_{4}}^{'} = \frac{0.025 P_{CO} P_{H_{2}}^{0.61}}{1 + 2.49 P_{H_{2}}} & (E7-4.12) \end{matrix}

$\begin{matrix} r_{C H_{4}}^{'} = \frac{0.025 P_{CO} P_{H_{2}}^{0.61}}{1 + 2.49 P_{H_{2}}} & (E7-4.12) \end{matrix}$

We could use the rate law given by Equation (E7-4.12) as is, but there are only six data points, and we should be concerned about extrapolating the rate law over a wider range of partial pressures. We could take more data, and/or we could carry out a theoretical analysis of the type discussed in Chapter 10 for heterogeneous reactions. If we assume hydrogen undergoes dissociative adsorption on the catalyst surface (cf. Figure 10-11), we would expect a dependence on the partial pressure of hydrogen to be to the 1/2 power. Because 0.61 is close to 0.5, we are going to regress the data again, setting ß₁ = 1/2 and ß₂ = 1.0. The results are shown in Table E7-4.4.

TABLE E7-4.4 SECOND REGRESSION

Note: A complete tutorial of how to enter this example into Polymath can be found on the Web site at

http://www.umich.edu/~elements/5e/software/nonlinear_regression_tutorial.pdf.

The rate law is now

r_{\overset{'}{C} H_{4}} = \frac{0.018 P_{C O} P_{H_{2}}^{1 / 2}}{1 + 1.49 P_{H_{2}}}

$r_{\overset{'}{C} H_{4}} = \frac{0.018 P_{C O} P_{H_{2}}^{1 / 2}}{1 + 1.49 P_{H_{2}}}$

where $r_{{CH}_{4}}^{'}$ $r_{{CH}_{4}}^{'}$ is in (mol/g-cat · s) and the partial pressures are in (atm).

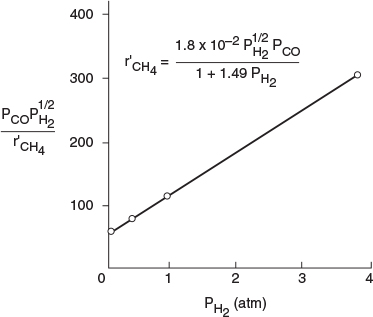
We could also have set $β_{1} = \frac{1}{2}$ $β_{1} = \frac{1}{2}$ and ß₂ = 1.0 and rearranged Equation (E7-4.il) in the form

\begin{matrix} \frac{P_{C O} P_{H_{2}}^{1 / 2}}{r_{C H_{4}}^{'}} = \frac{1}{a} + \frac{b}{a} P_{H_{2}} & (E7-4.13) \end{matrix}

$\begin{matrix} \frac{P_{C O} P_{H_{2}}^{1 / 2}}{r_{C H_{4}}^{'}} = \frac{1}{a} + \frac{b}{a} P_{H_{2}} & (E7-4.13) \end{matrix}$

Linearizing the rate law to determine the rate law parameters

A plot of $P_{C O} P_{H_{2}}^{1 / 2} / r_{C H_{4}}^{'}$ $P_{C O} P_{H_{2}}^{1 / 2} / r_{C H_{4}}^{'}$ function of $P_{H_{2}}$ $P_{H_{2}}$ should be a straight line with an intercept of 1/a and a slope of b/a. From the plot in Figure E7-4.2, we see that the rate law is indeed consistent with the rate-law data.

Figure E7-4.2 Linearized plot of data.

Analysis: The reaction-rate data in this example were obtained at steady state, and as a result, neither the integral method nor differential method of analysis can be used. One of the purposes of this example is to show how to reason out the form of the rate law and to then use regression to determine the rate-law parameters. Once the parameters were obtained, we showed how to linearize the rate-law [e.g., Equation (E7-4.13)] to generate a single plot of all the data, Figure (E7-4.2).

7.7 Experimental Planning

Four to six weeks in the lab can save you an hour in the library.

—G. C. Quarderer, Dow Chemical Co.

So far, this chapter has presented various methods of analyzing rate data. It is just as important to know in which circumstances to use each method as it is to know the mechanics of these methods. In the Expanded Material and in the Professional Reference Shelf (http://www.umich.edu/~elements/5e/07chap/prof-7-5.html) on the CRE Web site, we give a thumbnail sketch of a heuristic to plan experiments to generate the data necessary for reactor design. However, for a more thorough discussion, the reader is referred to the books and articles by Box and Hunter.⁶

⁶ G. E. P. Box, W. G. Hunter, andj. S. Hunter, Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building (New York: Wiley, 1978).

Closure. After reading this chapter, the reader should be able to analyze data to determine the rate law and rate-law parameters using the graphical and numerical techniques, as well as software packages. Nonlinear regression is the easiest method to analyze rate-concentration data to determine the parameters, but the other techniques, such as graphical differentiation, help one get a "feel" for the disparities in the data. The reader should be able to describe the care that needs to be taken in using nonlinear regression to ensure that one does not arrive at a false minimum for σ². Consequently, it is advisable to use more than one method to analyze the data.

Summary

1. Integral method:

a. Guess the reaction order and integrate the mole balance equation.

b. Calculate the resulting function of concentration for the data and plot it as a function of time. If the resulting plot is linear, you have probably guessed the correct reaction order.

c. If the plot is not linear, guess another order and repeat the procedure.

2. Differential method for constant-volume systems:

\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (S7-1) \end{matrix}

$\begin{matrix} - \frac{d C_{A}}{d t} = k C_{A}^{α} & (S7-1) \end{matrix}$

a. Plot — ΔC_A/Δt as a function of t.

b. Determine — dC_A/dt from this plot.

c. Take the In of both sides of (S7-1) to get

\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln k + α \ln C_{A} & (S7-2) \end{matrix}

$\begin{matrix} \ln (- \frac{d C_{A}}{d t}) = \ln k + α \ln C_{A} & (S7-2) \end{matrix}$

Plot ln( — dC_A/dt) versus lnC_A. The slope will be the reaction order a . We could use finite-difference formulas or software packages to evaluate ( — dC_A/ dt) as a function of time and concentration.

3. Nonlinear regression: Search for the parameters of the rate law that will minimize the sum of the squares of the difference between the measured rate of reaction and the rate of reaction calculated from the parameter values chosen. For N experimental runs and K parameters to be determined, use Polymath.

\begin{matrix} σ^{2} = \sum_{i = 1}^{N} \frac{- P_{i} (m e a s u r e d) - P_{i} (c a l c u l a t e d)]^{2}}{N - K} & (S7-3) \end{matrix}

$\begin{matrix} σ^{2} = \sum_{i = 1}^{N} \frac{- P_{i} (m e a s u r e d) - P_{i} (c a l c u l a t e d)]^{2}}{N - K} & (S7-3) \end{matrix}$

\begin{matrix} s^{2} = \sum_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = \sum_{i = 1}^{N} [t_{i m} - \frac{C_{A 0}^{1 - α} - C_{A i}^{1 - α}}{k (1 - α)}]^{2} & (S7-4) \end{matrix}

$\begin{matrix} s^{2} = \sum_{i = 1}^{N} (t_{i m} - t_{i c})^{2} = \sum_{i = 1}^{N} [t_{i m} - \frac{C_{A 0}^{1 - α} - C_{A i}^{1 - α}}{k (1 - α)}]^{2} & (S7-4) \end{matrix}$

Caution: Be sure to avoid a false minimum in σ² by varying your initial guess.

4. Modeling the differential reactor:
The rate of reaction is calculated from the equation

\begin{matrix} - r_{A}^{'} = \frac{F_{A 0} X}{Δ W} = \frac{F_{P}}{Δ W} = \frac{v_{0} (C_{A 0} - C_{A e})}{Δ W} = \frac{C_{P} v_{0}}{Δ W} & (S7-5) \end{matrix}

$\begin{matrix} - r_{A}^{'} = \frac{F_{A 0} X}{Δ W} = \frac{F_{P}}{Δ W} = \frac{v_{0} (C_{A 0} - C_{A e})}{Δ W} = \frac{C_{P} v_{0}}{Δ W} & (S7-5) \end{matrix}$

In calculating the reaction order, α

- r_{A}^{'} = k C_{A}^{α}

$- r_{A}^{'} = k C_{A}^{α}$

the concentration of A is evaluated either at the entrance conditions or at a mean value between C_A0 and C_Ae. However, power-law models such as

\begin{matrix} - r_{A}^{'} = k C_{A}^{α} C_{B}^{β} & (\begin{matrix} S7-6 \end{matrix}) \end{matrix}

$\begin{matrix} - r_{A}^{'} = k C_{A}^{α} C_{B}^{β} & (\begin{matrix} S7-6 \end{matrix}) \end{matrix}$

are not the best way to describe heterogeneous reaction-rate laws. Typically, they take the form

- r_{A}^{'} = \frac{k P_{A} P_{B}}{1 + K_{A} P_{A} + K_{B} P_{B}}

$- r_{A}^{'} = \frac{k P_{A} P_{B}}{1 + K_{A} P_{A} + K_{B} P_{B}}$

or a similar form, with the reactant partial pressures in the numerator and denominator of the rate law.

CRE Web Site Materials

• Expanded Materials (http://lumich.edu/~elements/5e/07chap/expanded.html)

1. Evaluation of Laboratory Reactors (http://umich.edu/~elements/5e/07chap/expanded_ch07_labReactor.pdf)

2. Summary of Reactor-Ratings, Gas-Liquid, Powdered Catalyst Decaying Catalyst System (http://umich.edu/~elements/5e/07chap/expanded_ch07_labReactor.pdf)

3. Experimental Planning (http://umich.edu/~elements/5e/07chap/prof-7-5.html)

4. Additional Homework Problems (on the web: http://umich.edu/~elements/5e/07chap/expanded_ch07_homeproblem.pdf (Additional Problems: http://’/umich.edu/~elements/5e/07’chap/add.html)

• Learning Resources (http://lumich.edu/~elements/’5e/07chap/learn.html)

1. Summary Notes (http://lumich.edu/~elements/5e/07chap/summary.html)

2. Self-Tests (http://umich.edu/~elements/5e/07chap/add.html)

A. Exercises (http://umich.edu/~elements/5e/07chap/add.html)

B. i>clicker Questions (http://lumich.edu/~elements/5e/07chap/iclicker_ch7_ql.html)

3. Interactive Computer Games (http://umich.edu/~elements/5e/icm/index.html)

A. Ecology (http://umich.edu/~elements/5e/icm/ecology.html)

Schematic shows a PC with arrows shooting from it toward all the four directions.

Screenshot shows a wetland analysis window.

On the left, a rectangular prism with a curved face at the top is divided into three parts. The part on the left has a sprout and a curved rightward arrow below it is labeled "F." The middle part is labeled "reaction" with height h and width w. The part on the right has a sprout with a flower and a curved rightward arrow below it labeled "F." The edges of the central part are labeled "z and z plus delta z." Beside the prism, the text reads width (w) equals 10 meters, height (h) equals 2 meters. To the right of the figure, the text reads: The wetland channel is a liquid phase system with a volumetric flow of 1 cubic meter per minute. The average width of the swamp is 10 meters and the average height is 2 meters (you won't need to remember these values). Below the figure, the text reads: We'll use the following assumptions to simplify the problem: 1. Assume the channel has a rectangular cross-section. We can now use the Cartesian coordinate system: Below the text, a three-dimensional plane is shown. Below it, the text reads, 2. Assume the cross-section of the channel has constant dimensions as we move down the z-direction; height and width are constant. At the bottom left, Previous button and the Main Menu button are shown. At the bottom right, a Continue button is shown.

B. Reactor Lab (www.reactorfab.net): See Reactor Lab Chapter 7 and P7-3_A.

4. Solved Problems

A. Example: Differential Method of Analysis of Pressure-Time Data (http://umich.edu/~elements/5e/07chap/pdf/excd5-l.pdfi

B. Example: Integral Method of Analysis of Pressure-Time Data (http://umich.edu/~elements/5e/07chap/pdj/excd5-2.pdf)

C. Example: Oxygenating Blood (http://umich.edu/~elements/5e/07chap/learn-cdp7-bb.html)

• Living Example Problem

1. Example 7-3 Data Use of Regression to Find the Rate Law Parameters (http://umich.edu/~elements/5e/07chap/live.html)

2. 7-3 Tutorial for Nonlinear Regression

3. 7-4 Tutorial for Nonlinear Regression

4. LEV Tutorial How to Load Regression Data to Polymath

5. Regression Fit of Experimental Data to Polynomial Curve

• FAQs (Frequently Asked Questions)—In Updates/FAQ icon section (http://umich.edu/~elements/5e/07chap/faq.html)

• Professional Reference Shelf (http://umich.edu/~elements/5e/07chap/prof.html)

R7.1 Method of Initial Rates (http://umich.edu/~elements/5e/07chap/prof-7-l.html)

R7.2 Method of Half Lives (http://umich.edu/~elements/5e/07chap/prof-7-2.html)

R7.3 Least-Squares Analysis of the Linearized Rate Law (http://umich.edu/~elements/5e/07chap/pdf/leastsquares.pdf)

The CRE Web site describes how the rate law

- r_{A} = k C_{A}^{α} C_{B}^{β}

$- r_{A} = k C_{A}^{α} C_{B}^{β}$

is linearized

\ln (- r_{A}) = \ln k + α \ln C_{A} + β \ln C_{B}

$\ln (- r_{A}) = \ln k + α \ln C_{A} + β \ln C_{B}$

and put in the form

Y = a_{0} + α X_{1} + β X_{2}

$Y = a_{0} + α X_{1} + β X_{2}$

and used to solve for α, ß, and fe. The etching of a semiconductor, Mn0₂, is used as an example to illustrate this technique.

R7.4 A Discussion of Weighted Least Squares (http://umich.edu/~elements/5e/07chap/prof-7-4.html) For the case when the error in measurement is not constant, we must use a weighted least-squares analysis.

R7.5 Experimental Planning (http://umich.edu/~elements/5e/07chap/prof-7-5.html)

A. Why perform the experiment?

B. Are you choosing the correct parameters?

C. What is the range of your experimental variables?

D. Can you repeat the measurement? (Precision)

E. Milk your data for all it’s worth.

F. We don’t believe an experiment until it’s proven by theory.

G. Tell someone about your result.

R7.6 Evaluation of Laboratory Reactors (http://umich.edu/~elements/5e/07chap/prof-7-6.html)

Questions and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

Questions

Q7-1_A i>clicker. Go to the Web site (http://www.umich.edu/~elements/5e/07chap/iclicker_ch7_ql.html) and view at least five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case: explaining why the question should not be on the next exam. In either case, explain your reasoning.

Q7-2a (a) Listen to the audios on the CRE Web site and pick one and say why it could be eliminated.

(b) Create an original problem based on Chapter 7 material.

(c) Design an experiment for the undergraduate laboratory that demonstrates the principles of chemical reaction engineering and will cost less than $500 in purchased parts to build. (From 1998 AIChE National Student Chapter Competition). Rules are provided on the CRE Web site.

(d) K-12 Experiment. Plant a number of seeds in different pots (corn works well). The plant and soil of each pot will be subjected to different conditions. Measure the height of the plant as a function of time and fertilizer concentration. Other variables might include lighting, pH, and room temperature. (Great grade school or high school science project.)

Q7-3_B Example 7-1. What is the error in assuming the concentration of species B is constant and what limits can you put on the calculated value of fe? (I.e., fe = 0.24 ±?)

Q7-4_A Example 7-3. Explain why the regression was carried out twice to find fe’ and fe.

Computer Simulations and Experiments

P7-1_A (a) Example 7-4: Nonlinear Regression

Regress the data to fit the rate law

r_{C H_{4}} = k P_{C O}^{α} P_{H_{2}}^{β}

$r_{C H_{4}} = k P_{C O}^{α} P_{H_{2}}^{β}$

What is the difference in the correlation and sums of squares compared with those given in Example 7-4? Why was it necessary to regress the data twice, once to obtain Table E7-4.3 and once to obtain Table E 7-4.4?

Interactive Computer Games

P7-2_A Download the Interactive Computer Game (ICG) from the CRE Web site (http://www.umich.edu/~elements/5e/icm/ecology.html). Play the game and then record your performance number for the module that indicates your mastery of the material. Your professor has the key to decode your performance number.

ICM Ecology Performance #_________________.

P7-3_A Go to Professor Herz’s Reactor Lab on the Web at www.reactoriab.net. Do (a) one quiz, or (b) two quizzes from Division 1. When you first enter a lab, you see all input values and can vary them. In a lab, click on the Quiz button in the navigation bar to enter the quiz for that lab. In a quiz, you cannot see some of the input values: you need to find those with “???” hiding the values. In the quiz, perform experiments and analyze your data in order to determine the unknown values. See the bottom of the Example Quiz page at www.reactoriab.net for equations that relate E and fe. Click on the “???” next to an input and supply your value. Your answer will be accepted if it is within ±20% of the correct value. Scoring is done with imaginary dollars to emphasize that you should design your experimental study rather than do random experiments. Each time you enter a quiz, new unknown values are assigned. To reenter an unfinished quiz at the same stage you left, click the [i] info button in the Directory for instructions. Turn in copies of your data, your analysis work, and the Budget Report.

Problems

P7-4_A When arterial blood enters a tissue capillary, it exchanges oxygen and carbon dioxide with its environment, as shown in this diagram.

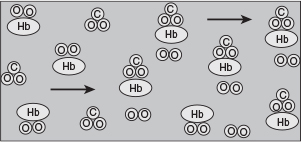
Reaction reads: The Oxoborinic acid reacts with K subscript 1 to form Boric acid and Oxygen. The Boric acid and Oxygen reacts with k subscript negative 1 to produce Oxoborinic acid.

The kinetics of this deoxygenation of hemoglobin in blood was studied with the aid of a tubular reactor by Nakamura and Staub (J. PhysioL, 173, 161).

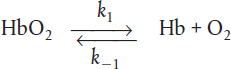
The reversible reaction reads: Metaboric acid (Hbo2) reacts with K subscript 1 and K subscript (negative 1) to form the Boric acid (Hb) and Oxygen.

{HbO}_{2} ⇄_{k_{- 1}}^{k_{1}} Hb + O_{2}

${HbO}_{2} ⇄_{k_{- 1}}^{k_{1}} Hb + O_{2}$

Although this is a reversible reaction, measurements were made in the initial phases of the decomposition so that the reverse reaction could be neglected. Consider a system similar to the one used by Nakamura and Staub: the solution enters a tubular reactor (0.158 cm in diameter) that has oxygen electrodes placed at 5-cm intervals down the tube. The solution flow rate into the reactor is 19.6 cm³/s with C_A0 = 2.33 X 10^-6 mol/cm³.

Electrode position	1	2	3	4	5	6	7
Percent decomposition of Hb0₂	0.00	1.93	3.82	5.68	7.48	9.25	11.00

(a) Using the method of differential analysis of rate data, determine the reaction order and the forward specific reaction-rate constant k_x for the deoxygenation of hemoglobin.

(b) Repeat using regression.

P7-5A The irreversible isomerization

A → B

was carried out in a batch reactor and the following concentration-time data were obtained:

t (min)	0	5	8	10	12	15	17.5	20
C_A (mol/dm³)	4.0	2.25	1.45	1.0	0.65	0.25	0.06	0.008

Determine the reaction order α and the specific reaction rate k in appropriate units.

P7-6_B The liquid-phase irreversible reaction

A → B + C

is carried out in a CSTR. To learn the rate law, the volumetric flow rate, υ₀, (hence τ = V/v₀ ) is varied and the effluent concentrations of species A are recorded as a function of the space time τ. Pure A enters the reactor at a concentration of 2 mol/dm³. Steady-state conditions exist when the measurements are recorded.

Run	1	2	3	4	5
τ (min)	15	38	100	300	1200
C_A (mol/dm³)	1.5	1.25	1.0	0.75	0.5

(a) Determine the reaction order and specific reaction-rate constant.

(b) If you were to repeat this experiment to determine the kinetics, what would you do differently? Would you run at a higher, lower, or the same temperature? If you were to take more data, where would you place the measurements (e.g., τ )?

(c) It is believed that the technician may have made a dilution factor-of-10 error in one of the concentration measurements. What do you think? How do your answers compare using regression (Polymath or other software) with those obtained by graphical methods?

Note: All measurements were taken at steady-state conditions. Be careful; this problem is sneaky.

P7-7_A The reaction

A → B + C

was carried out in a constant-volume batch reactor where the following concentration measurements were recorded as a function of time.

t (min)	0	5	9	15	22	30	40	60
C_A (mol/dm³)	2	1.6	1.35	1.1	0.87	0.70	0.53	0.35

(a) Use nonlinear least squares (i.e., regression) and one other method to determine the reaction order, α, and the specific reaction rate, k.

(b) Nicolas Bellini wants to know, if you were to take more data, where would you place the points? Why?

(c) Prof. Dr. Sven Köttlov from Jofostan University always asks his students, if you were to repeat this experiment to determine the kinetics, what would you do differently? Would you run at a higher, lower, or the same temperature? Take different data points? Explain what you think he is expecting her to say and why.

(d) It is believed that the technician made a dilution error in the concentration measured at 60 min. What do you think? How do your answers compare using regression (Polymath or other software) with those obtained by graphical methods?

P7-8_A The following data were reported [from C. N. Hinshelwood and P. J. Ackey, Proc. R. Soc. (Lond)., A115, 215] for a gas-phase constant-volume decomposition of dimethyl ether at 504°C in a batch reactor. Initially, only (CH₃)₂O was present.

Time (s)	390	777	1195	3155	∞
Total Pressure (mmHg)	408	488	562	799	931

(a) Why do you think the total pressure measurement at t = 0 is missing? Can you estimate it?

(b) Assuming that the reaction

(CH₃)₂O → CH₄ + H₂ + CO

is irreversible and goes virtually to completion, determine the reaction order and specific reaction rate k. (Ans.: k = 0.00048 min"¹)

(c) What experimental conditions would you suggest if you were to obtain more data?

(d) How would the data and your answers change if the reaction were run at a higher temperature? A lower temperature?

P7-9_A In order to study the photochemical decay of aqueous bromine in bright sunlight, a small quantity of liquid bromine was dissolved in water contained in a glass battery jar and placed in direct sunlight. The following data were obtained at 25°C:

Time (min)	10	20	30	40	50	60
ppm Br₂	2.45	1.74	1.23	0.88	0.62	0.44

(a) Determine whether the reaction rate is zero, first, or second order in bromine, and calculate the reaction-rate constant in units of your choice.

(b) Assuming identical exposure conditions, calculate the required hourly rate of injection of bromine (in pounds per hour) into a sunlit body of water, 25,000 gal in volume, in order to maintain a sterilizing level of bromine of 1.0 ppm. [Ans.: 0.43 lb/h]

Schematic shows a badge labeled "Hall of Fame" with a text, Member, at the center plus a figure with an irregular shape.

(c) Apply one or more of the six ideas in Preface Table P-4, page xxvii, to this problem. (Note: ppm = parts of bromine per million parts of brominated water by weight. In dilute aqueous solutions, 1 ppm = 1 milligram per liter.) (From California Professional Engineers’ Exam.)

P7-10_C The reactions of ozone were studied in the presence of alkenes [from R. Atkinson et al., Int.). Chem. Kinet., 15(8), 721]. The data in Table P7-9_C are for one of the alkenes studied, ris-2-butene. The reaction was carried out isothermally at 297 K. Determine the rate law and the values of the rate-law parameters.

TABLE P7-9_c RATE AS A FUNCTION OF OZONE AND BUTèNE CONCENTRATIONS

Run	Ozone Rate (mol/s·dm³×10⁷)	Ozone Concentration (mol/dm³)	Butene Concentration (mol/dm³)
1	1.5	0.01	10^-12
2	3.2	0.02	10^-11
3	3.5	0.015	10^-10
4	5.0	0.005	10^-9
5	8.8	0.001	10^-8
6	4.7*	0.018	10^-9

*Hint: Ozone also decomposes by collision with the wall.

P7-11_A Tests were run on a small experimental reactor used for decomposing nitrogen oxides in an automobile exhaust stream. In one series of tests, a nitrogen stream containing various concentrations of N0₂ was fed to a reactor, and the kinetic data obtained are shown in Figure P7-10_A. Each point represents one complete run. The reactor operates essentially as an isothermal backmix reactor (CSTR). What can you deduce about the apparent order of the reaction over the temperature range studied?

The plot gives the fractional decomposition of N0₂ fed versus the ratio of reactor volume V (in cm³) to the N0₂ feed rate, F_NO (g mol/h), at different feed concentrations of N0₂ (in parts per million by weight). Determine as many rate law parameters as you can.

The horizontal axis representing "10 to the power negative 5 times V over F subscript nitrogen dioxide, Oxygen (in cubic meter times height over g mole nitrogen dioxide). ranges from 0 to 5, in increments of 5. The vertical axis representing "Decomposition nitrogen dioxide (No subscript 2) (in percentage), ranges from 0 to 100, in increments of 50. In the graph, a circle represents 700 parts per minute of nitrogen dioxide in feed, a square represents 1896 parts per minute of nitrogen dioxide. In feed, and the inverted triangle represents 3050 parts per minute of nitrogen dioxide in the feed. Three straight lines are shown that rises up from the origin. At temperature, t equals 300 degree Celsius, from bottom to top it shows, 3050 ppm, 700 ppm, 3050 ppm, 1896 ppm, and 700 ppm. At temperature, t equals 250 degree Celsius, from bottom to top it shows, 3050 ppm, 1896 ppm, 700 ppm, and 700 ppm. At temperature, t equals 200 degree Celsius, it shows, 3050 ppm, 1896 ppm, 700 ppm, 1896 ppm, 700 ppm, 700 ppm, 3050 ppm, and 700 ppm.

Figure P7-10_A Auto exhaust data.

P7-12_A The thermal decomposition of isopropyl isocyanate was studied in a differential packed-bed reactor. From the data in Table P7-11_A, determine the reaction-rate-law parameters.

TABLE P7-11_A RAW DATA^†

Run	Rate (mol/s·dm³)	Concentration (mol/dm³)	Temperature (K)
1	4.9 × 10⁻⁴	0.2	700
2	1.1 × 10⁻⁴	0.02	750
3	2.4 × 10⁻⁴	0.05	800
4	2.2 × 10⁻⁴	0.08	850
5	1.18 × 10⁻⁴	0.1	900
6	1.82 X 10-²	0.06	950

^† Jofostan Journal of Chemiail Engineering, Vol. 15, page 743 (1995).

• Additional Homework Problems are on the CRE Web site (http://www.umich.edu/~elements/5e/07chap/add.html)

CDP7-New From time to time, new problems relating Chapter 7 material to everyday interests or emerging technologies will be placed on the Web. Also, one can go to the Web site, nebula.rowan.edu:82/home.asp, and work the home problem specific to this chapter.

Schematic shows a tree and three metal rings linked together.

Supplementary Reading

1. A wide variety of techniques for measuring the concentrations of the reacting species may or may not be found in

BURGESS, THORNTON W., Mr. Toad and Danny the Meadow Mouse Take a Walk. New York: Dover Publications, Inc., 1915.

FOGLER, H. SCOTT, AND STEVEN E. LEBLANC, with BENJAMIN RIZZO, Strategies for Creative Problem Solving, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2014.

KARRASS, CHESTER L., In Business As in Life, You Don’t Get What You Deserve, You Get What You Negotiate. Hill, CA: Stanford Street Press, 1996.

ROBINSON, J. W., Undergraduate Instrumental Analysis, 5th ed. New York: Marcel Dekker, 1995.

SKOOG, DOUGLAS A., F. JAMES HOLLER, and TIMOTHY A. NIEMAN, Principles of Instrumental Analysis, 5th ed. Philadelphia: Saunders College Publishers, Harcourt Brace College Publishers, 1998.

2. The design of laboratory catalytic reactors for obtaining rate data is presented in

RASE, H. F., Chemical Reactor Design for Process Plants, Vol. 1. New York: Wiley, 1983, Chap. 5.

3. The sequential design of experiments and parameter estimation is covered in

Box, G. E. P., J. S. HUNTER, and W. G. HUNTER, Statistics for Experimenters: Design, Innovation, and Discovery, 2nded. (Hoboken, New Jersey: Wiley, 2005).

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 7 Collection and Analysis of Rate Data

Create new playlist

Sign In

Sign Up

7. Collection and Analysis of Rate Data

7.1 The Algorithm for Data Analysis

7.2 Determining the Reaction Order for Each of Two Reactants Using the Method of Excess

7.3 Integral Method

7.4 Differential Method of Analysis

7.4.1 Graphical Differentiation Method

7.4.2 Numerical Method

7.4.3 Finding the Rate-Law Parameters

7.5 Nonlinear Regression

7.5.1 Concentration-Time Data

7.5.2 Model Discrimination

7.6 Reaction-Rate Data from Differential Reactors

7.7 Experimental Planning

Summary

CRE Web Site Materials

Questions and Problems

Questions

Computer Simulations and Experiments

Interactive Computer Games

Problems

Supplementary Reading

Table of Contents for
Chapter 7 Collection and Analysis of Rate Data