Chapter 12 Steady-State Nonisothermal Reactor Design—Flow Reactors with Heat Exchange

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

12. Steady-State Nonisothermal Reactor Design—Flow Reactors with Heat Exchange

Research is to see what everybody else sees, and to think what nobody else has thought.

—Albert Szent-Gyorgyi

Overview. This chapter focuses on chemical reactors with heat exchange. The chapter topics are arranged in the following manner:

• Section 12.1 further develops the energy balance for easy application to PFRs and PBRs.

• Section 12.2 describes PFRs and PBRs for four types of heat exchanger operations.

(1) Constant heat-transfer fluid temperature, T_a

(2) Variable fluid temperature T_a with co-current operation

(3) Variable fluid temperature T_a with countercurrent operation

(4) Adiabatic operation

• Section 12.3 describes the algorithm for PFRs and PBRs and gives examples of four types of heat exchanger operations.

• Section 12.4 applies the energy balance to a CSTR.

• Section 12.5 shows how a CSTR can operate at different steady-state temperatures and conversions, and how to decide which of these conditions are stable and which are unstable.

• Section 12.6 describes one of the most important topics of the entire text, multiple reactions with heat effects with Living Example Problems, which is a unique feature of this textbook.

• Section 12.7 discusses radial and axial temperature and concentration gradients.

• Section 12.8 Safety: The causes of batch-reactor explosions are discussed and hint of things to come when we do a CSI analysis on the Monsanto and T2 Laboratory explosions in Chapter 13.

The Chapter 12 Professional Reference Shelf (R12.4) on the CRE Web site (http://www.umich.edu/~elements/5e/12chap/pdf/sulfuricacid.pdf) describes a typical nonisothermal industrial reactor and reaction, SO₂ oxidation, and gives many practical details.

12.1 Steady-State Tubular Reactor with Heat Exchange

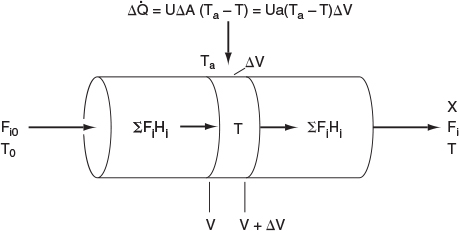
In this section, we consider a tubular reactor in which heat is either added or removed through the cylindrical walls of the reactor (Figure 12-1). In modeling plug-flow reactors, we shall assume that there are no radial gradients in the reactor and that the heat flux through the wall per unit volume of reactor is as shown in Figure 12-1.¹

Schematic shows a horizontal cylindrical tubular reactor with heat gain or loss.

Figure 12-1 Tubular reactor with heat gain or loss.

¹ Radial gradients are discussed in Section 12.7 and in PDF Chapters 17 and 18 on the Web site (http://www.umich.edu/~elements/5e/17chap/Fogler_Web_Ch17.pdf and http://www.umich.edu/~elements/5e/18chap/Fogler_Web_Ch18.pdf).

12.1.1 Deriving the Energy Balance for a PFR

We will carry out an energy balance on the volume AV. i.e., W˙s=0 ${\dot{W}}_{s} = 0$ , so Equation 11-10) becomes

Heat Added Δ Q ˙ + + Energy In Σ F i H i | V - - Energy Out Σ F i H i | V + Δ V = = 00 (12-1)

$\begin{matrix} \begin{matrix} Heat \\ Added \end{matrix} & + & \begin{matrix} Energy \\ In \end{matrix} & - & \begin{matrix} Energy \\ Out \end{matrix} & = & 0 \\ Δ \dot{Q} & + & Σ F_{i} H_{i} |_{V} & - & Σ F_{i} H_{i} |_{V + Δ V} & = & 0 & (12-1) \end{matrix}$

The heat flow to the reactor, ΔQ˙ $Δ \dot{Q}$ , is given in terms of the overall heat-transfer coefficient, U, the heat exchange area, ΔA, and the difference between the ambient temperature, T_a, and the reactor temperature T

Δ Q ˙ = U Δ A (T a - T) = U a Δ V (T a - T)

$Δ \dot{Q} = U Δ A (T_{a} - T) = U a Δ V (T_{a} - T)$

where a is the heat exchange area per unit volume of reactor. For a tubular reactor

a = A V = π D L π D 2 L 4 = 4 D

$a = \frac{A}{V} = \frac{π D L}{\frac{π D^{2} L}{4}} = \frac{4}{D}$

where D is the reactor diameter. Substituting for ΔQ˙ $Δ \dot{Q}$ in Equation 12-1), dividing by ΔV and then taking the limit as ΔV — 0, we get

U a (T a - T) - d Σ ( F i H i ) d V = 0

$U a (T_{a} - T) - \frac{d Σ (F_{i} H_{i})}{d V} = 0$

Expanding

U a (T a - T) - Σ d F i d V H i - Σ F i d H i d V = 0 (12-2)

$U a (T_{a} - T) - Σ \frac{d F_{i}}{d V} H_{i} - Σ F_{i} \frac{d H_{i}}{d V} = 0 (12-2)$

From a mole balance on species i, we have

d F i d V = r i = ν i (- r A) (12-3)

$\frac{d F_{i}}{d V} = r_{i} = ν_{i} (- r_{A}) (12-3)$

Differentiating the enthalpy Equation 11-19) with respect to V

d H i d V = C P i d T d V (12-4)

$\frac{d H_{i}}{d V} = C_{P_{i}} \frac{d T}{d V} (12-4)$

Substituting Equations (12-3) and (12-4) into Equation (12-2), we obtain

Ua(Ta−T)−ΣvHiiΔHRX(−rA)−ΣFiCPidTdV=0 $Ua (T_{a} - T) - \underset{\overset{︸}{Δ H_{RX}}}{Σ v {}_{i}H_{i}} (- r_{A}) - Σ F_{i} C_{P_{i}} \frac{d T}{d V} = 0$

Rearranging, we arrive at

This form of the energy balance will also be applied to multiple reactions.

dTdV=rAΔHRxQgHeat“Generated”−Ua(T−Ta)QrHeat“Removed”ΣFiCPi(12-5) $\begin{matrix} \frac{d T}{d V} = \frac{\overset{\begin{matrix} \begin{matrix} Q_{g} \\ Heat \end{matrix} \\ “Generated” \end{matrix}}{\overset{︷}{r_{A} Δ H_{Rx}}} - \overset{\begin{matrix} \begin{matrix} Q_{r} \\ Heat \end{matrix} \\ “Removed” \end{matrix}}{\overset{︷}{Ua (T - T_{a})}}}{Σ F_{i} C_{P_{i}}} & (12-5) \end{matrix}$

which is Equation (T11-1G) in Table 11-1 on pages 521-523.

dTdV=Qg−QrΣFiCPi(T11-1G) $\begin{matrix} \frac{d T}{d V} = \frac{Q_{g} - Q_{r}}{Σ F_{i} C_{P_{i}}} & (T11-1G) \end{matrix}$

where

Q g = r A Δ H R x \equiv (- r A) (- Δ H R x) (12-5a)

$Q_{g} = r_{A} Δ H_{R x} \equiv (- r_{A}) (- Δ H_{R x}) (12-5a)$

Q r = U a (T - T a) (12-5b)

$Q_{r} = U a (T - T_{a}) (12-5b)$

To help remember that Q_r is the "heat” removed from the reacting mixture, we note the driving force is from “T” to “T_a", i.e., Ua (T - T_a).

For exothermic reactions, Q_g will be a positive number. We note that when the heat “generated,” Q_g, is greater than the heat “removed,” Q_r (i.e., Q_g > Q_r), the temperature will increase down the reactor. When Q_r > Q_g, the temperature will decrease down the reactor.

For endothermic reactions ΔH_Rx will be a positive number and therefore the heat generated, Q_g in Equation (12-5a), will be a negative number. The heat removed, Q_r in Equation (12-5b), will also be a negative number because heat is removed rather than added, T_a > T. See Chapter 12 Expanded Material for a sample calculation (http://www.umich.edu/~elements/5e/12chap/CH12ExpandedMaterialEndothermicReactions.pdf). Example 12-2 for the case of constant ambient temperature also illustrates this point.

Equation (12-5) is coupled with the mole balances on each species, Equation 12-3). Next, we express r_A as a function of either the concentrations for liquid systems or molar flow rates for gas systems, as described in Chapter 6. We will use the molar flow rate form of the energy balance for membrane reactors and also extend this form to multiple reactions.

We could also write Equation 12-5) in terms of conversion by recalling Fi=FA0(Θi+viX) $F_{i} = F_{A 0} (Θ_{i} + v_{i} X)$ and substituting this expression into the denominator of Equation (12-5).

PFR energy balance

dTdV=rAΔHRx−Ua(T−Ta)FA0(ΣΘiCPi+ΔCPX)=Qg−QrΣFiCPi(12-6) $\begin{matrix} \frac{dT}{d V} = \frac{r_{A} Δ H_{Rx} - Ua (T - T_{a})}{F_{A 0} (Σ Θ_{i} C_{P_{i}} + Δ C_{P} X)} = \frac{Q_{g} - Q_{r}}{Σ F_{i} C_{P_{i}}} & (12-6) \end{matrix}$

For a packed-bed reactor dW = ρ_b dV where ρ_b is the bulk density

PBR energy balance

dTdW=r′AΔHRx−Ua(T−Ta)ρbΣFiCPi(12-7) $\begin{matrix} \frac{d T}{d W} = \frac{r_{A}^{'} Δ H_{Rx} - \frac{Ua (T - T_{a})}{ρ_{b}}}{Σ F_{i} C_{{P_{}}_{i}}} & (12-7) \end{matrix}$

Equations (12-6) and (12-7) are also given in Table 11-1 as Equations (T11-1D) and (T11-1F). As noted earlier, having gone through the derivation to these equations, it will be easier to apply them accurately to CRE problems with heat effects.

12.1.2 Applying the Algorithm to Flow Reactors with Heat Exchange

We continue to use the algorithm described in the previous chapters and simply add a fifth building block, the energy balance.

Gas Phase

If the reaction is in gas phase and pressure drop is included, there are four differential equations that must be solved simultaneously. The differential equation describing the change in temperature with volume (i.e., distance) as we move down the reactor

Energy balance

d T d V = g (X, T, T a) (A)

$\frac{d T}{d V} = g (X, T, T_{a}) (A)$

must be coupled with the mole balance

Mole balance

d X d V = - r A F A 0 = f (X, T, p) (B)

$\frac{d X}{d V} = \frac{- r_{A}}{F_{A 0}} = f (X, T, p) (B)$

and with the pressure drop equation

Pressure drop

d p d V = - h (p, X, T) (C)

$\frac{d p}{d V} = - h (p, X, T) (C)$

and solved simultaneously. If the temperature of the heat-exchange fluid, T_a, varies down the reactor, we must add the energy balance on the heat-exchange fluid. In the next section, we will derive the following equation for co-current heat transfer

Heat exchanger

d T a d V = U a ( T - T a ) m ˙ c o C P C 0 (D)

$\frac{d T_{a}}{d V} = \frac{U a (T - T_{a})}{{\dot{m}}_{c o} C_{P_{C 0}}} (D)$

Numerical integration of the coupled differential equations (A) to (D) is required.

along with the equation for countercurrent heat transfer. A variety of software packages (e.g., Polymath) can be used to solve these coupled differential equations: (A), (B), (C), and (D).

Liquid Phase

For liquid-phase reactions, the rate is not a function of total pressure, so our mole balance is

d X d V = - r A F A 0 = f (X, T) (E)

$\frac{d X}{d V} = \frac{- r_{A}}{F_{A 0}} = f (X, T) (E)$

Consequently, we need to only solve equations (A), (D), and (E) simultaneously.

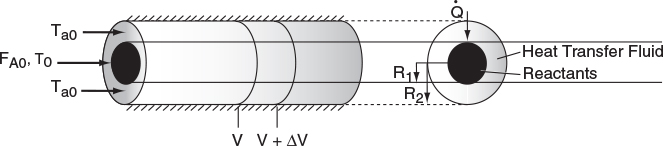
12.2 Balance on the Heat-Transfer Fluid

12.2.1 Co-current Flow

The heat-transfer fluid will be a coolant for exothermic reactions and a heating medium for endothermic reactions. If the flow rate of the heat-transfer fluid is sufficiently high with respect to the heat released (or absorbed) by the reacting mixture, then the heat-transfer fluid temperature will be virtually constant along the reactor. In the material that follows, we develop the basic equations for a coolant to remove heat from exothermic reactions; however, these same equations apply to endothermic reactions where a heating medium is used to supply heat.

We now carry out an energy balance on the coolant in the annulus between R₁ and R₂, and axially between V and V + ΔV, as shown in Figure 12-2. The mass flow rate of the heat-exchange fluid (e.g., coolant) is m˙c ${\dot{m}}_{c}$ . We will consider the case when the reactor is cooled and the outer radius of the coolant channel R₂ is insulated. Recall that by convention Q˙ $\dot{Q}$ is the heat added to the system.

Schematic shows the aerial and front view of co-current, double-pipe heat exchanger.

Figure 12-2 Co-current, double-pipe heat exchanger.

For co-current flow, the reactant and the coolant flow in the same direction.

Schematic shows a horizontal hollow cylinder.

The energy balance on the coolant in the volume between V and (V + ΔV) is

[Rate of energy in at V] m c H c | V ˙ - - [Rate of energy out at V + ΔV] m ˙ c H c | V + ΔV + + ⎡ ⎣ ⎢ Rate of heat added by condition through the inner wall ⎤ ⎦ ⎥ U a (T - T a) ΔV = = 00

$\begin{matrix} [\begin{matrix} Rate of energy \\ in at V \end{matrix}] & - & [\begin{matrix} Rate of energy \\ out at V + ΔV \end{matrix}] & + & [\begin{matrix} \begin{matrix} Rate of heat added \\ by condition through \\ the inner wall \end{matrix} \end{matrix}] & = & 0 \\ \dot{m_{c} H_{c} |_{V}} & - & {\dot{m}}_{c} H_{c} |_{V + ΔV} & + & U a (T - T_{a}) ΔV & = & 0 \end{matrix}$

where T_a is the temperature of the heat transfer fluid, i.e., coolant, and T is the temperature of the reacting mixture in the inner tube.

Dividing by ΔV and taking limit as ΔV → 0

- m ˙ c d H c d V + U a (T - T a) = 0 (12-8)

$- {\dot{m}}_{c} \frac{d H_{c}}{d V} + U a (T - T_{a}) = 0 (12-8)$

Analogous to Equation (12-4), the change in enthalpy of the coolant can be written as

d H c d V = C P c d T a d V (12-9)

$\frac{d H_{c}}{d V} = C_{P_{c}} \frac{d T_{a}}{d V} (12-9)$

The variation of coolant temperature T_a down the length of reactor is

dTadV=Ua(T−Ta)m˙cCPc(12-10) $\begin{matrix} \frac{d T_{a}}{d V} = \frac{Ua (T - T_{a})}{{\dot{m}}_{c} C_{P_{c}}} & (12-10) \end{matrix}$

The equation is valid whether the heat-transfer fluid is a coolant or a heating medium.

Typical heat-transfer fluid temperature profiles for both exothermic and endothermic reactions when the heat transfer fluid enters at T_a0 are shown in Figure 12-3, parts (a) and (b) respectively.

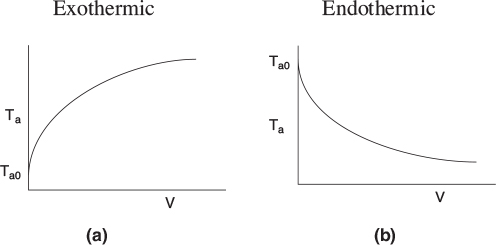
Graph (a) shows Exothermic and graph (b) shows Endothermic.

Figure 12-3 Heat-transfer fluid temperature profiles for co-current heat exchanger. (a) Coolant. (b) Heating medium.

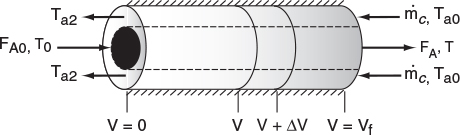
12.2.2 Countercurrent Flow

In countercurrent heat exchange, the reacting mixture and the heat-transfer fluid (e.g., coolant) flow in opposite directions. At the reactor entrance, V = 0, the reactants enter at temperature T₀, and the coolant exits at temperature T_a2. At the end of the reactor, the reactants and products exit at temperature T, while the coolant enters at T_a0.

Again, we write an energy balance on the coolant over a differential reactor volume to arrive at

dTadV=Ua(Ta−T)m˙cCPc(12-11) $\begin{matrix} \frac{d T_{a}}{d V} = \frac{Ua (T_{a} - T)}{{\dot{m}}_{c} C_{P_{c}}} & (12-11) \end{matrix}$

At the entrance, V = 0 ∴ X = 0 and T_a = T_a2.

At the exit, V = V_f ∴ T_a = T_a0.

We note that the only difference between Equations (12-10) and (12-11) is a minus sign, i.e., (T – T_a) vs. (T_a – T).

The solution to a countercurrent flow problem to find the exit conversion and temperature requires a trial-and-error procedure, as shown in Table 12-1.

Trial and error procedure required

TABLE 12-1. PROCEDURE TO SOLVE FOR THE EXIT CONDITIONS FOR PFRS WITH COUNTERCURRENT HEAT EXCHANGE

1. Consider an exothermic reaction where the coolant stream enters at the end of the reactor (V = V_f) at a temperature T_a2, say 300 K. We have to carry out a trial-and-error procedure to find the temperature of the coolant T_a2 exiting the reactor at V = 0 (cf. Figure 12-4).

Figure 12-4 Countercurrent, double-pipe heat exchanger.

2. Guess an exit coolant temperature T_a2 at the feed entrance (X = 0, V = 0) to the reactor to be T_a2 = 340 K, as shown in Figure 12-5(a).

Two graphs labeled (a) at left and (b) at right represent trial and error procedure.

Figure 12-5 Trial-and-error results for countercurrent heat exchanger.

3. Use an ODE solver to calculate X, T, and T_a as a function of V.

We see from Figure 12-5 (a) that our guess of 340 K for T_a2 at the feed entrance (V = 0 and X = 0) gives an entering temperature of the coolant of 310 K (V = V_f), which does not match the actual entering coolant temperature of 300 K.

4. Now guess another coolant temperature at V = 0 and X = 0 of, say, 330 K. After carrying out the simulation with this guess, we see from Figure 12-5(b) that a coolant temperature at V = 0 of T_a2 = 330 K will give a coolant entering temperature at V_f of 300 K, which matches the actual T_a0.

12.3 Algorithm for PFR/PBR Design with Heat Effects

We now have all the tools to solve reaction engineering problems involving heat effects in PFRs and PBRs for the cases of both constant and variable coolant temperatures.

Table 12-2 gives the algorithm for the design of PFRS and PBRS with heat exchange: In Case A Conversion is the reaction variable and in Case B Molar Flow Rates are the reaction variables. The procedure in Case Ð’ must be used to analyze multiple reactions with heat effects.

TABLE 12-2. ALGORITHM FOR PFR/PBR DESIGN FOR GAS-PHASE REACTIONS WITH HEAT EFFECTS

The elementary gas phase reaction

A + B ⇄ 2C

is to be carried out in a PBR with a co-current heat exchanger.

A. Conversion as the Reaction Variable

1. Mole Balance:

d X d W = r ' A - F A 0 (T12-1.1)

$\frac{d X}{d W} = \frac{{}^{-}{r_{A}^{'}}}{F_{A 0}} (T12-1.1)$

2. Rate Law:

- r' A = k 1 (C A C B - C 2 c K c) (T12-1.2)

$- {r'}_{A} = k_{1} (C_{A} C_{B} - \frac{C_{c}^{2}}{K_{c}}) (T12-1.2)$

k = k 1 (T 1)exp [E R (1 T 1 - 1 T 1)] (T12-1.3)

$\begin{matrix} k = k_{1} (T_{1})exp [\frac{E}{R} (\frac{1}{T_{1}} - \frac{1}{T} 1)] & (T12-1.3) \end{matrix}$

for Δ C P ≅ 0 . K C = K C 2 (T 2)exp [Δ H o R x R (1 T 2 - 1 T)] (T 12-1.4)

$\begin{matrix} for Δ C_{P} ≅ 0 . & K_{C} = K_{C 2} (T_{2})exp [\frac{Δ H_{R x}^{o}}{R} (\frac{1}{T_{2}} - \frac{1}{T})] & \begin{matrix} (T 12–1.4) \end{matrix} \end{matrix}$

Again we note that because δ ≡ 0, K_C ≡ K_e

3. Stoichiometry (gas phase):

Following the Algorithm

• Mole Balance

• Rate Law

• Stoichiometry

• Energy Balance

• Parameters

• Solution

• Analysis

C A = C A 0 ( 1 - X ) ( 1 + ε X ) T 0 T p (S 4-9)

$\begin{matrix} C_{A} = \frac{C_{A 0} (1 - X)}{(1 + ε X)} \frac{T_{0}}{T} p & \begin{matrix} (S 4-9) \end{matrix} \end{matrix}$

ϵ = y A 0 δ = 1 3 (2-1-1) = 0

$ϵ = y_{A 0} δ = \frac{1}{3} (2–1–1) = 0$

C A = C A 0 (1 - X) T 0 T p (T 12-1.5)

$\begin{matrix} C_{A} = C_{A 0} (1 - X) \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.5) \end{matrix} \end{matrix}$

C B = C A 0 (Θ B - X) T 0 T p (T 12-1.6)

$\begin{matrix} C_{B} = C_{A 0} (Θ_{B} - X) \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.6) \end{matrix} \end{matrix}$

C C = 2 C A 0 X T 0 T p (T 12-1.7)

$\begin{matrix} C_{C} = 2 C_{A 0} X \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.7) \end{matrix} \end{matrix}$

C I = C I 0 T 0 T p (T 12-1.8)

$\begin{matrix} C_{I} = C_{I 0} \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.8) \end{matrix} \end{matrix}$

d p d W = - α 2 p (1 + ε X) T T 0 (5-30)

$\begin{matrix} \frac{d p}{d W} = - \frac{α}{2 p} (1 + ε X) \frac{T}{T_{0}} & \begin{matrix} (5-30) \end{matrix} \end{matrix}$

ε = 0

$ε = 0$

d p d W = - α 2 p T T 0 (T 12-1.9)

$\begin{matrix} \frac{d p}{d W} = - \frac{α}{2 p} \frac{T}{T_{0}} & \begin{matrix} (T 12–1.9) \end{matrix} \end{matrix}$

Combine Rate Law and Stoichiometry to find X_e

- r A = k 1 C 2 A 0 [(1 - X) (Θ B - X) - 4 X 2 K C] (T 0 T p) 2 (T 12-1.10)

$\begin{matrix} - r_{A} = k_{1} C_{A 0}^{2} [(1 - X) (Θ_{B} - X) - \frac{4 X^{2}}{K_{C}}] (\frac{T_{0}}{T} p)^{2} & \begin{matrix} (T 12–1.10) \end{matrix} \end{matrix}$

at equilibrium —r_A = 0 and X = X_e

Solving for X_e

X e = ( Θ B + 1 ) K C - [ ( ( Θ B + 1 ) K c ) 2 - 4 K C Θ B ( K C - 4 ) ] 1 / 2 2 ( K C - 4 ) (T 12-1.11)

$\begin{matrix} X_{e} = \frac{(Θ_{B} + 1) K_{C} - [((Θ_{B} + 1) K_{c})^{2} - 4 K_{C} Θ_{B} (K_{C} - 4)]^{1 / 2}}{2 (K_{C} - 4)} & \begin{matrix} (T 12–1.11) \end{matrix} \end{matrix}$

4. Energy Balances:

Reactor: d T d W = ( U a ρ b ) ( T a - T ) + ( - r A ) ( - Δ H R x ) F A 0 [ C P A + Θ B C P B + X Δ C P ] (T 12-1.12)

$\begin{matrix} Reactor: \frac{d T}{d W} = \frac{(\frac{U a}{ρ_{b}}) (T_{a} - T) + (- r_{A}) (- Δ H_{R x})}{F_{A 0} [C_{P_{A}} + Θ_{B} C_{P_{B}} + X Δ C_{P}]} & \begin{matrix} (T 12–1.12) \end{matrix} \end{matrix}$

Co-current coolant: d T a d W = ( U a ρ b ) ( T - T a ) m ˙ c C P C o o 1 (T 12-1.13)

$\begin{matrix} Co-current coolant: \frac{d T_{a}}{d W} = \frac{(\frac{U a}{ρ_{b}}) (T - T_{a})}{{\dot{m}}_{c} C_{P_{C o o 1}}} & \begin{matrix} (T 12–1.13) \end{matrix} \end{matrix}$

B. Molar Flow Rates as the Reaction Variable

1. Mole Balance:

d F A d W = r' A (T 12-1.14)

$\begin{matrix} \frac{d F_{A}}{d W} = r_{A}^{'} & \begin{matrix} (T 12–1.14) \end{matrix} \end{matrix}$

d F B d W = r' B (T 12-1.15)

$\begin{matrix} \frac{d F_{B}}{d W} = r_{B}^{'} & \begin{matrix} (T 12–1.15) \end{matrix} \end{matrix}$

d F C d W = r' C (T 12-1.16)

$\begin{matrix} \frac{d F_{C}}{d W} = r_{C}^{'} & \begin{matrix} (T 12–1.16) \end{matrix} \end{matrix}$

F I = F I 0 (T 12-1.17)

$\begin{matrix} F_{I} = F_{I 0} & \begin{matrix} (T 12–1.17) \end{matrix} \end{matrix}$

Following the Algorithm

2. Rate Law (elementary reaction):

- r' A = k 1 (C A C B - C 2 C K C) (T 12-1.2)

$\begin{matrix} - r_{A}^{'} = k_{1} (C_{A} C_{B} - \frac{C_{C}^{2}}{K_{C}}) & \begin{matrix} (T 12–1.2) \end{matrix} \end{matrix}$

k = k 1 (T 1) exp [E R (1 T 1 - 1 T)] (T 12-1.3)

$\begin{matrix} k = k_{1} (T_{1}) \exp [\frac{E}{R} (\frac{1}{T_{1}} - \frac{1}{T})] & \begin{matrix} (T 12–1.3) \end{matrix} \end{matrix}$

K c = K C 2 (T 2) exp [Δ H o R x R (1 T 2 - 1 T)] (T 12-1.4)

$\begin{matrix} K_{c} = K_{C 2} (T_{2}) \exp [\frac{Δ H_{R x}^{o}}{R} (\frac{1}{T_{2}} - \frac{1}{T})] & \begin{matrix} (T 12–1.4) \end{matrix} \end{matrix}$

3. Stoichiometry (gas phase):

r' B = r' A (T 12-1.18)

$\begin{matrix} r_{B}^{'} = r_{A}^{'} & \begin{matrix} (T 12–1.18) \end{matrix} \end{matrix}$

r' C = - 2 r' A (T 12-1.19)

$\begin{matrix} r_{C}^{'} = - 2 r_{A}^{'} & \begin{matrix} (T 12–1.19) \end{matrix} \end{matrix}$

C A = C T 0 F A F T T 0 T p (T 12-1.20)

$\begin{matrix} C_{A} = C_{T 0} \frac{F_{A}}{F_{T}} \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.20) \end{matrix} \end{matrix}$

C B = C T 0 F B F T T 0 T p (T 12-1.21)

$\begin{matrix} C_{B} = C_{T 0} \frac{F_{B}}{F_{T}} \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.21) \end{matrix} \end{matrix}$

C C = C T 0 F C F T T 0 T p (T 12-1.22)

$\begin{matrix} C_{C} = C_{T 0} \frac{F_{C}}{F_{T}} \frac{T_{0}}{T} p & \begin{matrix} (T 12–1.22) \end{matrix} \end{matrix}$

F T = F A + F B + F C + F I (T 12-1.23)

$\begin{matrix} F_{T} = F_{A} + F_{B} + F_{C} + F_{I} & \begin{matrix} (T 12–1.23) \end{matrix} \end{matrix}$

d p d W = - α p F T F T 0 T T 0 (T 12-1.24)

$\begin{matrix} \frac{d p}{d W} = - \frac{α}{p} \frac{F_{T}}{F_{T 0}} \frac{T}{T_{0}} & \begin{matrix} (T 12–1.24) \end{matrix} \end{matrix}$

4. Energy Balances:

R e a c t o r : d T d W = ( U a ρ b ) ( T a - T ) + ( - r A ) ( - Δ H R x ) F A C P A + F B C P B + F C C P C + F I C P I (T 12-1.25)

$\begin{matrix} Reactor: & \frac{d T}{d W} = \frac{(\frac{U a}{ρ b}) (T_{a} - T) + (- r_{A}) (- Δ H_{R x})}{F_{A} C_{P_{A}} + F_{B} C_{P_{B}} + F_{C} C_{P_{C}} + F_{I} C_{P_{I}}} & \begin{matrix} (T 12–1.25) \end{matrix} \end{matrix}$

Heat Exchangers: Same as for A. Conversion as the Reaction Variable

Case A: Conversion as the Independent Variable Example Calculation

5. Parameter Evaluation:

Now we enter all the explicit equations with the appropriate parameter values.

k 1, E, R, C T 0, T a, T 0, T 1, T 2, K A 2, Θ B, Θ I, Δ H o R x, C P A, C P B, C P C, U a, ρ b

$k_{1}, E, R, C_{T 0}, T_{a}, T_{0}, T_{1}, T_{2}, K_{A 2}, Θ_{B}, Θ_{I}, Δ H_{R x}^{o}, C_{P_{A}}, C_{P_{B}}, C_{P_{C}}, U a, ρ_{b}$

Base Case for Parameter Values

E = 25 kcal/mol

ΔH_Rx = −20 kcal/mol

k = 0.004 d m 6 m o 1 \cdot k g \cdot s @ 310 K

$k = 0.004 \frac{d m^{6}}{m o 1 \cdot k g \cdot s} @ 310 K$

K_C = 1000 ⋅303 K

α = 0.0002/kg

F_A0 = 5 mol/s

C_T0 = 0.3 mol/dm³

C P A = C P B = C P C = 20 cal/mol/K

$C_{P_{A}} = C_{P_{B}} = C_{P_{C}} = 20 cal/mol/K$

C P I = 40 cal/mol K

$C_{P_{I}} = 40 cal/mol K$

(U a ρ b) = Uarho = 0.5 cal kg \cdot s \cdot K

$(\frac{U a}{ρ b}) = Uarho = 0.5 \frac{cal}{kg ⋅ s ⋅ K}$

m ˙ c = 1000 g / s

${\dot{m}}_{c} = 1000 g/s$

C P Cool = 18 cal/g/K

$C_{P_{Cool}} = 18 cal/g/K$

Θ_B = 1

Θ_I = 1

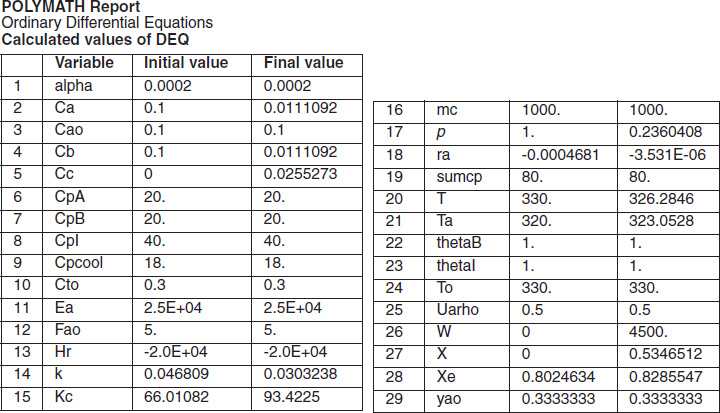
with initial values T₀ = 330 K, T_ao = 320 K, and X = 0 at W = 0 and final values: W_f = 5000 kg.

6. Solution:

Equations (T12-1.1) through (T12-1) are entered into the Polymath program along with the corresponding parameter values.

Living Example Problem

Differential equations

1 d(Ta)/d(W) = Uarho*(T-Ta)/(mc*Cpmc)

2 d(p)/d(W) = -alpha/2*(T/To)/p

3 d(T)/d(W) = (Uarho*(Ta-T)+(-ra)*(-Hr))/(Fao*sumcp)

4 d(X)/d(W) = -ra/Fao

Explicit equations

1 Hr = -20000

2 alpha = .0002

3 To = 330

4 Uarho = 0.5

5 mc = 1000

6 Cpcool = 18

7 Kc = 1000*(exp(Hr/1.987*(1/303-1/T)))

8 Fao = 5

9 thetaI = 1

10 CpI = 40

11 CpA = 20

12 thetaB = 1.0

13 CpB = 20

14 Cto = 0.3

15 Ea = 25000

16 Xe = ((thetaB+1)*Kc- (((thetaB+1)*Kc)^2-4*(Kc-4)*(Kc*thetaB))^0.5)/(2*(Kc-4))

17 k = .004*exp(Ea/1.987*(1/310-1/T)

18 yao = 1/(1+thetaB+thetaI)

19 Cao = yao*Cto

20 sumcp = (thetaI*CpI+CpA+thetaB*CpB)

21 Ca = Cao*(1-X)*p*To/T

22 Cb = Cao*(thetaB-X)*p*To/T

23 Cc = Cao*2*X*p*To/T

24 ra = -k*(Ca*Cb-Cc^2/Kc)

http://www.umich.edu/~elements/5e/live/chapterl2fT12-3/LEP-T12-2.pol

7. Analysis:

The temperature profiles are shown in Figure TE12-1.1. One notes that due to the exothermic heat of reaction, the temperature of the gas in the reactor increases sharply near the entrance then decreases as the reactants are consumed and the fluid is cooled as it moves down the reactor. Figure TE12-1.2 shows the conversion X increases and approaches its equilibrium value X_e at approximately W = 1125 kg of catalyst where the rate approaches zero. At this point the conversion cannot increase further unless X_e increases. The increase in X_e occurs because of the cooling of the reactor’s contents by the heat exchanger thus shifting the equilibrium to the right. By the end of the reactor the equilibrium conversion has been increased to 82.9% and the conversion in the reactor to 53.4%. One notes from Figure TE12.2-3, that owing to the cooling and consumption of reac-tants the conversion does not increase significantly above a catalyst weight of 2000 kg, even though X is much below X_e (see Problem P12-1_A).
The following figures in Table 12-2 show representative profiles that would result from solving the above equations for different parameter values. The reader is encouraged to download the Living Example Problem for Table 12-2 and vary a number of parameters, as discussed in P12-1_A. Be sure you can explain why these curves look the way they do.

Graph is titled A plus B <-.> 2C exothermic gas phase reaction.

Figure TE12-1.1

Figure TE12-1.2

Figure TE12-1.3

Be sure you can explain why these curves look the way they do.

A set of four graphs, (a), (b), (c), and (d) are shown.

In set (a), the first graph shows a horizontal V-axis, points T subscript a and T subscript 0 along the vertical T-axis, a curve that is almost bell shaped, and a horizontal dashed line from T subscript a on the T-axis intersecting the right edge of the curve. The second graph shows a horizontal V-axis, a vertical X-axis, a curve labeled X subscript e that slides from a point on the X-axis, rises, and extends, and a curve that starts from the origin, rises, and extends to the right. Text above the graphs read: Constant T subscript a reversible exothermic reaction in a PFR with heat exchange. In set (b), the first graph shows a horizontal V-axis, points T subscript 0 and T subscript a on the vertical axis, a curve that is almost inverted bell shaped, and a horizontal dashed line at T subscript a on the vertical axis intersecting the curve. The second graph shows a horizontal V-axis, a vertical X-axis, a curve labeled X subscript e that slides from a point on the X-axis and rises, and a wavy curve that starts from the origin, rises, and extends to the right. Text above the graphs read: Constant T subscript a endothermic reaction in a PFR with heat exchange. In set (c), the first graph shows a horizontal V-axis, a vertical T-axis, and two curves that are almost bell shaped, labeled T and T subscript a. The second graph shows a horizontal V-axis, a vertical T-axis, a curve labeled X subscript e that slides from a point on the T-axis, rises, and extends, and a wavy curve that starts from the origin, rises, and extends to the right. Text above the graphs read: Variable T subscript a exothermic counter-current exchange. In set (d), the first graph shows a horizontal V-axis, a vertical T-axis, and two curves labeled T and T subscript a that rise from two points on the T-axis. The second graph shows a horizontal V-axis, a vertical T-axis, an inverted S-curve labeled X subscript e that slides from a point on the T-axis, and a curve that starts from the origin, rises, and extends to the right, and intersects the previous curve. Text above the graphs read: Variable T subscript a exothermic co-current exchange.

12.3.1 Applying the Algorithm to an Exothermic Reaction

Example 12-1 Butane Isomerization Continued—OOPS!

when plant engineer Maxwell Anthony looked up the vapor pressure at the exit to the adiabatic reactor in Example 11-3, where the temperature is 360 K, he learned the vapor pressure for isobutene was about 1.5 MPa, which is greater than the rupture pressure of the glass vessel the company had hoped to use. Fortunately, when Max looked in the storage shed, he found there was a bank of 10 tubular reactors, each of which was 5 m³. The bank reactors were double-pipe heat exchangers with the reactants flowing in the inner pipe and with Ua = 5,000 kJ/m³-h-K. Max also bought some thermodynamic data from one of the companies he found on the Internet that used Colorimeter experiments to find ΔH_Rx for various reactions. One of the companies had the value of ΔH_Rx for his reaction on sale this week for the low, low price of $25,000.00. For this value of AH_fe the company said it is best to use an initial concentration of A of 1.86 mol/dm³. The entering temperature of the reactants is 305 K and the entering coolant temperature is 315 K. The mass flow rate of the coolant, m˙C ${\dot{m}}_{C}$ , is 500 kg/h and the heat capacity of the coolant, CPC $C_{P_{C}}$ , is 28 kJ/kg·K. The temperature in any one of the reactors cannot rise above 325 K. Carry out the following analyses with the newly purchased values from the Internet:

(a) Co-current heat exchange: Plot X, X_e, T, T_a, and −r_A, down the length of the reactor.

(b) Countercurrent heat exchange: Plot X, X_e, T, T_a, and −r_A down the length of the reactor.

(c) Constant ambient temperature, T_a: Plot X, X_e, T, and −r_A down the length of the reactor.

(d) Adiabatic operation: Plot X, X_e, T, T_a, and −r_A, down the length of the reactor.

(e) Compare parts (a) through (d) above and write a paragraph describing what you find.

Additional information

Recall from Example 11-3 that CPA $C_{P_{A}}$ = 141 kJ/kmol·K, CP0=ΣΘiCPi=159 kJ/kmol⋅K $C_{P 0} = Σ Θ_{i} C_{P i} = 159 kJ/kmol \cdot K$ , and data from the company Maxwell got off the Internet are ΔH_Rx = –34,500 kJ/kmol with ΔCPA=0 $Δ C_{P_{A}} = 0$ and C_A0 = 1.86 kmol/m³.

Solution

We shall first solve part (a), the co-current heat exchange case and then make small changes in the Polymath program for parts (b) through (d).

The molar flow rate of A to each of the ten reactors in parallel

F A0 = (0.9) (163 kmol/h) \times 1 10 = 14.7 kmol A h

$F_{A0} = (0.9) (163 kmol/h) \times \frac{1}{10} = 14.7 \frac{kmol A}{h}$

The mole balance, rate law, and stoichiometry are the same as in the adiabatic case previously discussed in Example 11-3; that is,

Same as Example 11-3

The Algorithm

Mole Balance:

dXdV=−rAFA0(E11−3.1) $\begin{matrix} \frac{d X}{d V} = \frac{- r_{A}}{F_{A 0}} & (E11-3.1) \end{matrix}$

Rate Law and Stoichiometry:

rA=−kCA0[1−(1+1KC)X](E11−3.7) $\begin{matrix} r_{A} = - k C_{A0} [1 - (1 + \frac{1}{K_{C}}) X] & (E11-3.7) \end{matrix}$

With

k=31.1 exp[7906(T−360360T)] h−1(E11−3.10) $\begin{matrix} k = 31.1 exp [7906 (\frac{T - 360}{360 T})] h^{- 1} & (E11-3.10) \end{matrix}$

KC=3.03 exp[−4150(T−333)333T](E11−3.11) $\begin{matrix} K_{C} = 3.03 exp [\frac{- 4150 (T - 333)}{333 T}] & (E11-3.11) \end{matrix}$

Q g Q r d T d V = = = r A Δ H Rx U a (T - T a) Q g - Q r F A 0 C P 0

$\begin{matrix} Q_{g} & = & r_{A} Δ H_{Rx} \\ Q_{r} & = & U a (T - T_{a}) \\ \frac{d T}{d V} & = & \frac{Q_{g} - Q_{r}}{F_{A 0} C_{P 0}} \end{matrix}$

The equilibrium conversion is

Xe=KC1+KC(E11−3.12) $\begin{matrix} X_{e} = \frac{K_{C}}{1 + K_{C}} & (E11-3.12) \end{matrix}$

Energy Balance

The energy balance on the reactor is

dTdV=rA ΔHRx−Ua(T−Ta)FA0∑ΘiCPiCP0=rAΔHRx−Ua(T−Ta)FA0CP0(E12−1.1) $\begin{matrix} \frac{d T}{d V} = \frac{r_{A} Δ H_{Rx} - Ua (T - T_{a})}{F_{A0} \underset{C_{P_{0}}}{\underset{︸}{\sum Θ_{i} C_{P_{i}}}}} = \frac{r_{A} Δ H_{Rx} - Ua (T - T_{a})}{F_{A0} C_{P_{0}}} & (E12-1.1) \end{matrix}$

Part (a) Co-current Heat Exchange

We are now going to solve the coupled, ordinary differential and explicit equations (E11-3.1), (E11-3.7), (E11-3.10), (E11-3.11), (E11-3.12), and (E12-1.1), and the appropriate heat-exchange balance using Polymath. After entering these equations we will enter the parameter values. By using co-current heat exchange as our Polymath base case, we only need to change one line in the program for each of the other three cases and solve for the profiles of X, X_e, T, T_a, and -r_A, and not have to re-enter the program.

For co-current flow, the balance on the heat transfer fluid is

dTadV=Ua(T-Ta)m˙CCPC(E12−1.2) $\begin{matrix} \frac{d T_{a}}{d V} = \frac{U a ({T-T}_{a})}{{\dot{m}}_{C} C_{P_{C}}} & (E12-1.2) \end{matrix}$

with T₀ = 305 K and T_a = 315 K at V = 0. The Polymath program and solution are shown in Table E12-1.1.

Living Example Problem

TABLE E12-1.1. PART (a) CO-CURRENT HEAT EXCHANGE

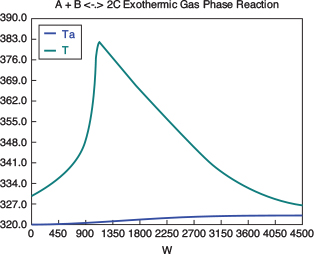
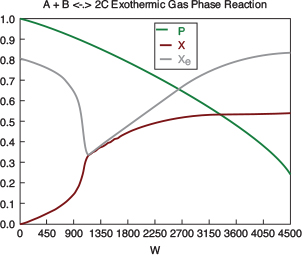
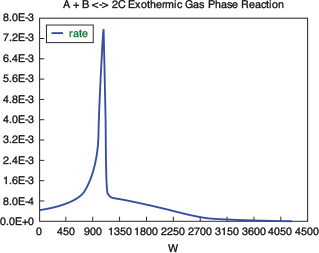
Figure E12-1.1 shows the profiles for the reactor temperature, T, the coolant temperature, T_a, the conversion, X, the equilibrium conversion, X_e, and the reaction rate, -r_A. Note that at the entrance to the reactor the reactor temperature T is below the coolant temperature, but as reacting mixture moves into and through the reactor the mixture heats up and T becomes great than T_a. When you load the Polymath Living Example Problem (LEP) code on your computer, one of the things you will want to explore is the value of the ambient temperature, T_a, or the entering temperature, T₀, below which the reaction might never take off or “ignite."

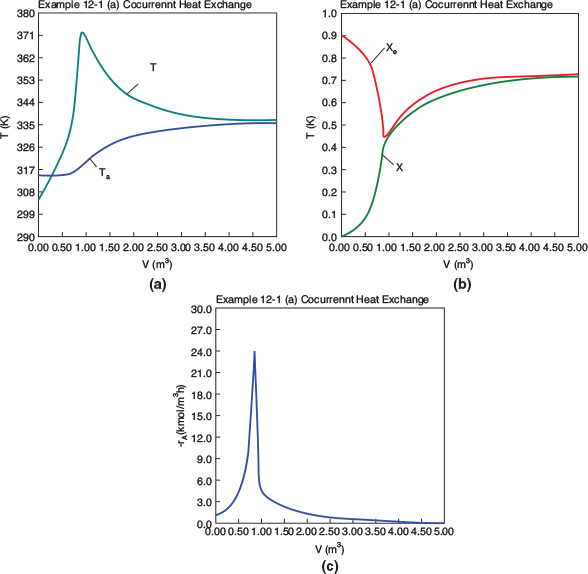
Graph (a) titled Example 12-1 (a) Co-current Heat Exchange, graph (b) titled Example 12-1 (a) Co-current Heat Exchange show two curves each and graph (c) titled Example 12-1 (a) Co-current Heat Exchange shows a curve.

Graph (a) shows the horizontal axis representing V cubic meters that ranges from 0.00 to 5.00, in increments of 0.50 and the vertical axis T (K) that ranges from 290 to 380, in increments of 9. Graph (b) shows the horizontal axis representing V cubic meters marked from 0.00 to 5.00, in increments of 0.50 and the vertical axis T (K) marked from 0.0 to 1.0, in increments of 0.1. A curve representing X subscript e starts from a point near 0.9 on the vertical axis, slides steeply, and rises. Another curve representing X starts from the origin, increases gradually and extends to the right. Graph (c) shows the horizontal axis representing V cubic meters marked from 0.00 to 5.00, in increments of 0.50 and the vertical axis negative r subscript A of (kmol per m cubed h) marked from 0.0 to 30.0, in increments of 0.3. A curve from a point near 0.1 on the vertical axis, rises and slides steeply, and extends horizontally.

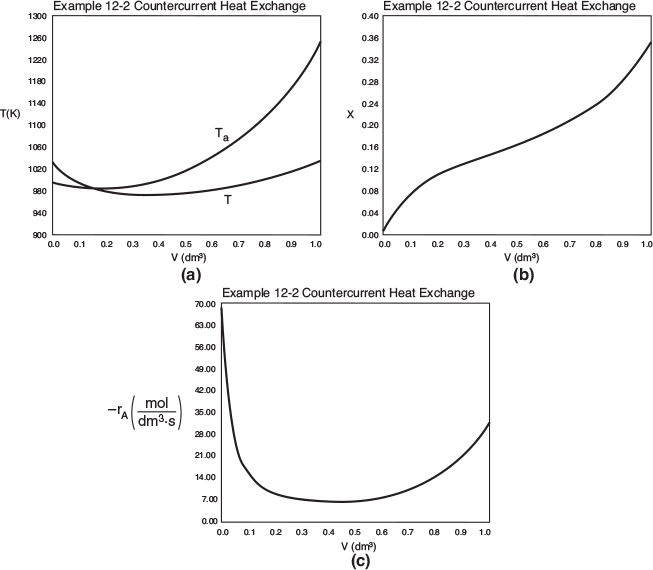
Figure E12-1.1 Profiles down the reactor for co-current heat exchange (a) temperature, (b) conversion, (c) reaction rate.

Analysis: Part (a) Co-current Exchange: We note that reactor temperature goes through a maximum. Near the reactor entrance, the reactant concentrations are high and therefore the reaction rate is high [c.f. Figure E12-1.1(a)] and Q_g > Q_r. Consequently, the temperature and conversion increase with increasing reactor volume while X_e decreases because of the increasing temperature. Eventually, X and X_e come close together (V = 0.95 m³) and the rate becomes very small as the reaction approaches equilibrium. At this point, the reactant conversion X cannot increase unless X_e increases. We also note that when the ambient heat-exchanger temperature, T_a, and the reactor temperature, T, are essentially equal, there is no longer a temperature driving force to cool the reactor. Consequently, the temperature does not change farther down the reactor, nor does the equilibrium conversion, which is only a function of temperature.

Part (b) Countercurrent Heat Exchange:

For countercurrent flow, we only need to make two changes in the program. First, multiply the right-hand side of Equation (E12-1.2) by minus one to obtain

d T a d V = - U a ( T - T a ) m ˙ C C P c (E 12-1.12)

$\begin{matrix} \frac{d T_{a}}{d V} = - \frac{U a (T - T_{a})}{{\dot{m}}_{C} C_{P_{c}}} & \begin{matrix} (E 12-1.12) \end{matrix} \end{matrix}$

Next, we guess T_a at V = 0 and see if it matches T_a0 at V = 5 m³. If it doesn’t, we guess again. In this example, we will guess T_a (V = 0) = 340.3 K and see if T_a = T_a0 = 315 K at V = 5 m³.

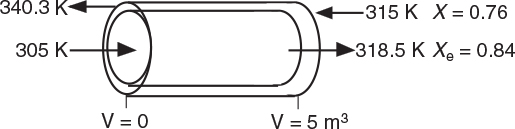
Illustration shows Countercurrent heat exchange through a horizontal cylinder.

TABLE E12-1.2. PART (b) COUNTERCURRENT HEAT EXCHANGE

Good guess!

Living Example Problem

At V = 0, we guessed an entering coolant temperature of 340.3 K and found that at V = V_f, the calculation showed that it matched the emerging coolant temperature T_a0 = 315 K!! (Was that a lucky guess or what?!) The variable profiles are shown in Figure E12-1.2.

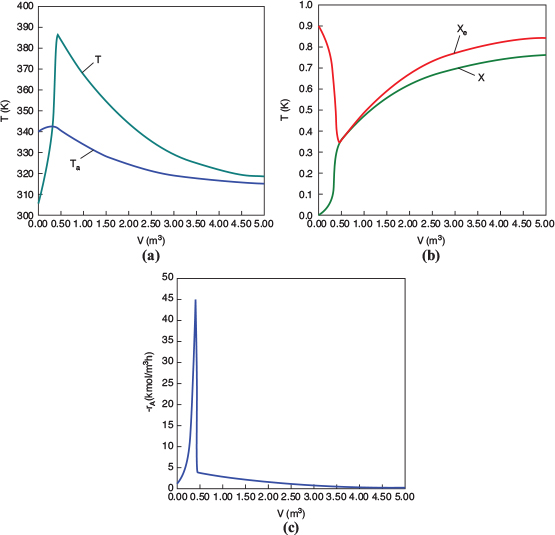
Graph shows three graphs labeled (a), (b), and (c).

Graph (a) shows the horizontal axis representing V cubic meters marked from 0.00 to 5.00, in increments of 0.50 and the vertical axis T (K) marked from 300 to 400, in increments of 10. A curve representing T starts from a point near 305 on the vertical axis, increases and slides steeply, and extends horizontally. A curve representing T subscript a starts from 340 on the vertical axis, increases gradually, slides, and extends horizontally. Graph (b) shows the horizontal axis representing V cubic meters marked from 0.00 to 5.00, in increments of 0.50 and the vertical axis T (K) marked from 0.0 to 1.0, in increments of 0.1. A curve representing X subscript e starts from a point near 0.9 on the vertical axis, slides steeply, and rises. A curve representing X starts from the origin, increases gradually and extends to the right. Graph (c) shows the horizontal axis representing V cubic meters marked from 0.00 to 5.00, in increments of 0.50 and the vertical axis negative r subscript A of (kmol per m cubed h) marked from 0 to 50, in increments of 5. A curve from a point near 0.2 on the vertical axis, rises and slides steeply and extends horizontally.

Figure E12-1.2 Profiles down the reactor for countercurrent heat exchange (a) temperature, (b) conversion, (c) reaction rate.

We observe that at V = 0.5 m³, X = 0.36 and the rate, −r_A, drop to a low value as X approaches X_e. Because X can never be greater than X_e the reaction will not proceed further unless X_e is increased. In this case the reactor is cooled, causing the temperature to decrease and resulting in an increase in the equilibrium conversion beyond a reactor volume of V = 0.5 m³.

Analysis: Part (b) Countercurrent Exchange: We note that near the entrance to the reactor, the coolant temperature is above the reactant entrance temperature. However, as we move down the reactor, the reaction generates “heat” and the reactor temperature rises above the coolant temperature. We note that X_e reaches a minimum (corresponding to the reactor temperature maximum) near the entrance to the reactor. At this point (V = 0.5 m³), X cannot increase above X_e. As we move down the reactor, the reactants are cooled and the reactor temperature decreases allowing X and X_e to increase. A higher exit conversion, X, and equilibrium conversion, X_e, are achieved in the countercurrent heat-exchange system than for the co-current system.

Part (c) Constant T_a

For constant Ta, use the Polymath program in part (a), but multiply the right side of Equation (E12-1.2) by zero in the program, i.e.,

d T a d V = U a ( T - T a ) m ˙ C C P C * 0 (E 12-1.13)

$\begin{matrix} \frac{d T_{a}}{d V} = \frac{U a (T - T_{a})}{{\dot{m}}_{C} C_{P_{C}}} * 0 & \begin{matrix} (E 12–1.13) \end{matrix} \end{matrix}$

TABLE E12-1.3. PART (c) CONSTANT T_a

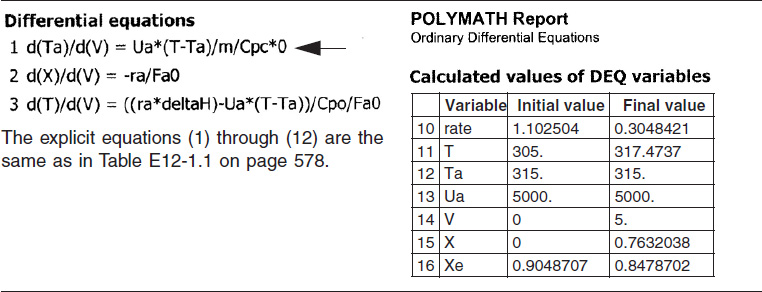
The initial and final values are shown in the Polymath report and the variable profiles are shown in Figure E12-1.3.

Three graphs representing Example 12-1 (c) Constant T subscript a are labeled (a), (b), and (c).

Graph (a) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis T marked from 300 to 390, in increments of 9. A curve representing T starts from a point between 300 and 309 on the vertical axis, increases steeply, slides, and extends horizontally. A horizontal line T subscript a starts from a point between 309 and 318 on the vertical axis. Graph (b) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis X marked from 0.0 to 1.0, in increments of 0.1. A curve representing X subscript e starts from a point 0.9 on the vertical axis, slides steeply, rises, and extends horizontally. Another curve representing X starts from the origin, increases gradually and extends to the right. Graph (c) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis negative r subscript A of (kmol per m cubed h) marked from 0.0 to 30.0, in increments of 3.0. A curve from a point between 0.0 and 3.0 on the vertical axis, rises and slides steeply, and extends horizontally.

Figure E12-1.3 Profiles down the reactor for constant heat-exchange fluid temperature T_a; (a) temperature, (b) conversion, (c) reaction rate.

We note that for the parameter values chosen, the profiles for T, X, X_e and −r_A are similar to those for countercurrent flow. For example, as X and X become close to each other at V = 1.0 m³, but beyond that point X_e increases because the reactor temperature decreases.

Analysis: Part (c) Constant T_a: When the coolant flow rate is sufficiently large, the coolant temperature, T_a, will be essentially constant. If the reactor volume is sufficiently large, the reactor temperature will eventually reach the coolant temperature, as is the case here. At this exit temperature, which is the lowest achieved in this example, the equilibrium conversion, X_e, is the largest of the four cases studied in this example.

Part (d) Adiabatic Operation

In Example 11-3, we solved for the temperature as a function of conversion and then used that relationship to calculate k and K_C. An easier way is to solve the general or base case of a heat exchanger for co-current flow and write the corresponding Polymath program. Next, use Polymath [part (a)], but multiply the parameter Ua by zero, i.e.,

Ua=5,000*0

and run the simulation again.

TABLE E12-1.4. PART (d) ADIABATIC OPERATION

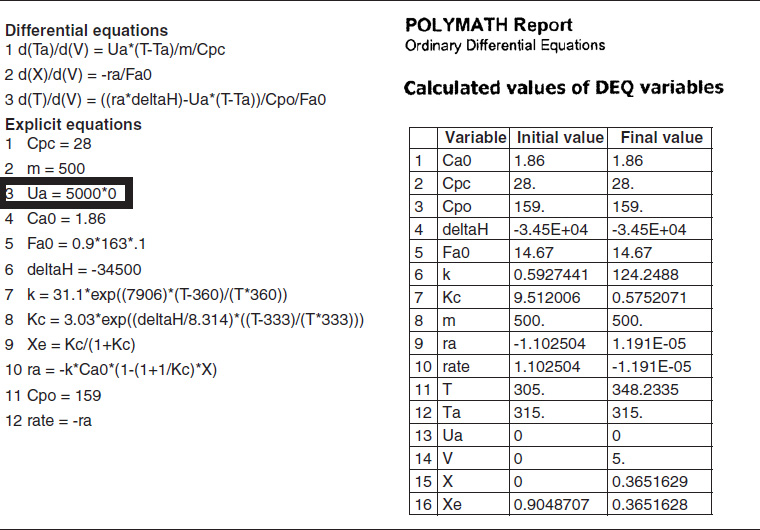
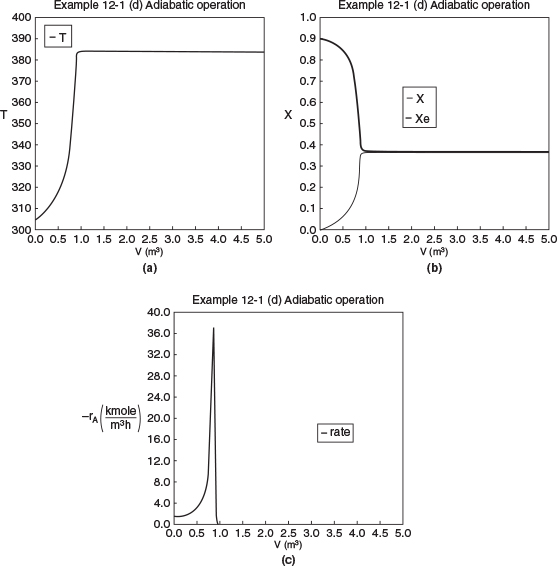
The initial and exit conditions are shown in the Polymath report, while the profiles of T, X, X_e, and −r_A are shown in Figure E12-1.4.

Three graphs representing Example 12-1 (d) Adiabatic operation are labeled (a), (b), and (c).

Graph (a) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis T marked from 300 to 400, in increments of 10. A curve representing T starts from a point near 305 on the T-axis, increases steeply and extends horizontally. Graph (b) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis X marked from 0.0 to 1.0, in increments of 0.1. A curve representing X subscript e starts from a point near 0.9 on the vertical axis, slides steeply and a curve representing X starts from the origin, increases gradually and extends to the right. Graph (c) shows the horizontal axis representing V cubic meters marked from 0.0 to 5.0, in increments of 0.5 and the vertical axis negative r subscript A of (kmol per m cubed h) marked from 0.0 to 40.0, in increments of 4.0. A curve from a point near 0.2 on the vertical axis, rises steeply and slides steeply to intersect the horizontal axis at 1.0.

Figure E12-1.4 Profiles down the reactor for adiabatic reactor; (a) temperature, (b) conversion, (c) reaction rate.

Analysis: Part (d) Adiabatic Operation. Because there is no cooling, the temperature of this exothermic reaction will continue to increase down the reactor until equilibrium is reached, X = X_e = 0.365 at T = 384 K, which is the adiabatic equilibrium temperature. The profiles for X and X_e are shown in Figure E12-1.4(b) where one observes that X_e decreases down the reactor because of the increasing temperature until it becomes equal to the reactor conversion (i.e., X ≡ X_e), which occurs circa 0.9 m³. There is no change in temperature, X or X_e, after this point because the reaction rate is virtually zero and thus the remaining reactor volume serves no purpose.

Finally, Figure E12-1.4(c) shows −r_A increases as we move down the reactor as the temperature increases, reaching a maximum and then decreasing until X and X_e approach each other and the rate becomes virtually zero.

Overall Analysis: This is an extremely important example, as we applied our CRE PFR algorithm with heat exchange to a reversible exothermic reaction. We analyzed four types of heat-exchanger operations. We see that the countercurrent exchanger and the constant T_a cases give the highest conversion and adiabatic operation gives the lowest conversion.

12.3.2 Applying the Algorithm to an Endothermic Reaction

In Example 12-1 we studied the four different types of heat exchanger on an exothermic reaction. In this section we carry out the same study on an endothermic reaction.

Example 12-2 Production of Acetic Anhydride

Jeffreys, in a treatment of the design of an acetic anhydride manufacturing facility, states that one of the key steps is the endothermic vapor-phase cracking of acetone to ketene and methane is²

² G. V. Jeffreys, A Problem in Chemical Engineering Design: The Manufacture of Acetic Anhydride, 2nd ed. (London: Institution of Chemical Engineers).

CH₃COCH₃ → CH₂CO + CH₄

He states further that this reaction is first-order with respect to acetone and that the specific reaction rate is given by

ln k = 34.34 - 3 4 , 2 2 2 T (E 12-2.1)

$\begin{matrix} \ln k = 34.34 - \frac{34, 222}{T} & \begin{matrix} (E 12–2.1) \end{matrix} \end{matrix}$

where k is in reciprocal seconds and T is in Kelvin. It is desired to feed 7850 kg of acetone per hour to a tubular reactor. The reactor consists of a bank of 1000 one-inch, schedule-40 tubes. We shall consider four cases of heat exchanger operation. The inlet temperature and pressure are the same for all cases at 1035 K and 162 kPa (1.6 atm) and the entering heating-fluid temperature available is 1250 K. The heat-exchange fluid has a flow rate, m˙C ${\dot{m}}_{C}$ , of 0.111 mol/s, with a heat capacity of 34.5 J/mol·K.

Gas-phase endothermic reaction examples:

1. Adiabatic

2. Heat exchange T_a is constant

3. Co-current heat exchange with variable T_a

4. Countercurrent exchange with variable T_a

A bank of 1000 one-inch, schedule-40 tubes, 1.79 m in length corresponds to 1.0 m³ (0.001 m³/tube = 1.0 dm³/tube) and gives 20% conversion. Ketene is unstable and tends to explode, which is a good reason to keep the conversion low. However, the pipe material and schedule size should be checked to learn if they are suitable for these temperatures and pressures. In addition, the final design and operating conditions need to be cleared by the safety committee before operation can begin.

Case 1 The reactor is operated adiabatically.

Case 2 Constant heat-exchange fluid temperature T_a = 1250 K

Case 3 Co-current heat exchange with T_a0 = 1250 K

Case 4 Countercurrent heat exchange with T_a0 = 1250 K

Additional information

C H 3 C O C H 3 (A) : H A (T R) = - 216.67 k J / m o l, C P A = 163 J / m o l \cdot K

$C H_{3} C O C H_{3} (A) : H_{A} (T_{R}) = - 216.67 k J / m o l, C_{P_{A}} = 163 J / m o l \cdot K$

C H 2 C O (B) : H B (T R) = - 61.09 k J / m o l, C P B = 83 J / m o l \cdot K

$C H_{2} C O (B) : H_{B} (T_{R}) = - 61.09 k J / m o l, C_{P_{B}} = 83 J / m o l \cdot K$

CH4(C):HC(TR)=−74.81kJ/mol,CPC=71J/mol⋅KU=110J/s⋅m2⋅K $\begin{array}{l} C H_{4} (C) : H_{C} (T_{R}) = - 74.81 k J / m o l, C_{P_{C}} = 71 J / m o l \cdot K \\ U = 110 J/s \cdot m^{2} \cdot K \end{array}$

Solution

Let A = CH₃COCH₃, B = CH₂CO, and C = CH₄. Rewriting the reaction symbolically gives us

A → B + C

Algorithm for a PFR with Heat Effects

1. Mole Balance:

d X d V = - r A F A 0 (E 12-2.2)

$\begin{matrix} \frac{d X}{d V} = - \frac{r_{A}}{F_{A 0}} & \begin{matrix} (E 12–2.2) \end{matrix} \end{matrix}$

2. Rate Law:

- r A = k C A (E 12-2.3)

$\begin{matrix} - r_{A} = k C_{A} & \begin{matrix} (E 12–2.3) \end{matrix} \end{matrix}$

Rearranging (E12-2.1)

k = 8.2 \times 1014 exp [- 3 4 , 2 2 2 T] = 3.58 exp [34, 222 (1 1 0 3 5 - 1 T)] (E 12-2.4)

$\begin{matrix} k = 8.2 \times 1 0^{14} \exp [- \frac{34, 222}{T}] = 3.58 \exp [34, 222 (\frac{1}{1035} - \frac{1}{T})] & \begin{matrix} (E 12–2.4) \end{matrix} \end{matrix}$

3. Stoichiometry (gas-phase reaction with no pressure drop):

C A ϵ = = C A 0 ( 1 - X ) T 0 ( 1 + ϵ X ) T y A 0 δ = 1 (1 + 1-1) = 1 (E 12.2.5)

$\begin{matrix} C_{A} & = & \frac{C_{A 0} (1 - X) T_{0}}{(1 + ϵ X) T} & \begin{matrix} (E 12.2.5) \end{matrix} \\ ϵ & = & y_{A 0} δ = 1 (1 + 1-1) = 1 \end{matrix}$

4. Combining yields

- r A = k C A 0 ( 1 - X ) 1 + X T 0 T (E 12-2.6)

$\begin{matrix} - r_{A} = \frac{k C_{A 0} (1 - X)}{1 + X} \frac{T_{0}}{T} & \begin{matrix} (E 12–2.6) \end{matrix} \end{matrix}$

Before combining Equations (E12-2.2) and (E12-2.6), it is first necessary to use the energy balance to determine T as a function of X.

5. Energy Balance:

a. Reactor balance

d T d V = U a ( T a - T ) + ( r A ) [ Δ H \circ R x + Δ C P ( T - T R ) ] F A 0 ( Σ Θ i C P i + X Δ C P ) (E 12-2.7)

$\begin{matrix} \frac{d T}{d V} = \frac{U a (T_{a} - T) + (r_{A}) [Δ H_{R x}^{\circ} + Δ C_{P} (T - T_{R})]}{F_{A 0} (Σ Θ_{i} C_{P_{i}} + X Δ C_{P})} & \begin{matrix} (E 12–2.7) \end{matrix} \end{matrix}$

b. Heat Exchanger. We will use the heat-exchange fluid balance for co-current flow as our base case. We will then show how we can very easily modify our ODE solver program (e.g., Polymath) to solve for the other cases by simply multiplying the appropriate line in the code by either zero or minus one.

For co-current flow:

d T a d V = U a ( T - T a ) m ˙ C P c (E 12-2.8)

$\begin{matrix} \frac{d T_{a}}{d V} = \frac{U a (T - T_{a})}{\dot{m} C_{P_{c}}} & \begin{matrix} (E 12–2.8) \end{matrix} \end{matrix}$

6. Calculation of Mole Balance Parameters on a Per Tube Basis:

FA0=7,850 kg/h58 kg/kmol×11,000 Tubes=0.135 kmol/h=0.0376 mol/sCA0=PA0RT=162 kPa8.31kpa⋅m3kmol⋅K(1035 K)=0.0188kmolm3=18.8 mol/m3v0=FA0CA0=2.0 dm3/s, V=1 m31000 tubes=0.001 m3tube=1.0 dm3tube $\begin{array}{l} F_{A0} = \frac{7, 850 kg/h}{58 kg/ kmol} \times \frac{1}{1, 000 Tubes} = 0.135 kmol/h = 0.0376 mol/s \\ C_{A 0} = \frac{P_{A0}}{R T} = \frac{162 k P a}{8.31 \frac{kpa \cdot m^{3}}{kmol \cdot K} (1035 K)} = 0.0188 \frac{kmol}{m^{3}} = 18.8 {mol/m}^{3} \\ v_{0} = \frac{F_{A0}}{C_{A0}} = 2.0 {dm}^{3} / s, V= \frac{1 m^{3}}{1000 tubes} = \frac{0.001 m^{3}}{tube} = \frac{1.0 {dm}^{3}}{tube} \end{array}$

7. Calculation of Energy Balance Parameters:

Thermodynamics:

a. ΔH∘Rx(TR) $Δ H_{R x}^{\circ} (T_{R})$ : At 298 K, using the standard heats of formation

Δ H \circ R x (T R) = = = H \circ B (T R) + H \circ C (T R) - H \circ A (T R) (- 61.09) + (- 74.81) - (- 216.67) kJ/mol 80.77 kJ/mol

$\begin{matrix} Δ H_{R x}^{\circ} (T_{R}) & = & H_{B}^{\circ} (T_{R}) + H_{C}^{\circ} (T_{R}) - H_{A}^{\circ} (T_{R}) \\ = & (- 61.09) + (- 74.81) - (- 216.67) kJ/mol \\ = & 80.77 kJ/mol \end{matrix}$

b. ΔC_P: Using the mean heat capacities

Δ C P = C P B + C P C - C P A = (83 + 71 - 163) J / m o 1 \cdot K

$Δ C_{P} = C_{P_{B}} + C_{P_{C}} - C_{P_{A}} = (83 + 71 - 163) J / m o 1 \cdot K$

Δ C P = - 9 J / m o 1 \cdot K

$Δ C_{P} = - 9 J / m o 1 \cdot K$

Heat Exchange:

Energy balance. The heat-transfer area per unit volume of pipe is

a = π D L ( π D 2 / 4 ) L = 4 D = 4 0 . 0 2 6 6 m = 150 m - 1

$a = \frac{π D L}{(π D^{2} / 4) L} = \frac{4}{D} = \frac{4}{0.0266 m} = 150 m^{- 1}$

U = 110 J / m 2 \cdot s \cdot K

$U = 110 J / m^{2} \cdot s \cdot K$

Combining the overall heat-transfer coefficient with the area yields

Ua = 16,500 J/m³ · s · K

TABLE E12-2.1. SUMMARY OF PARAMETER VALUES

ΔHoRx(TR)=80.77 kJ/molFA0=0.0376 mol/sCPA=163 J/mol A/KCPCool≡CPc=34.5 J/mol/KParameter ValuesΔCP=−9 J/mol⋅KCA0=18.8 mol/m3Ua=16,500 J/mol3s⋅KT0=1035KTR=298 Km˙C=0.111 mol/SVf=0.001m3 $\begin{matrix} Parameter Values \\ Δ H_{Rx}^{o} (T_{R}) = 80.77 kJ / mol & Δ C_{P} = - 9 J / mol \cdot K & T_{0} = 1035 K \\ F_{A 0} = 0.0376 mol /s & C_{A 0} = 18.8 mol / m^{3} & T_{R} = 298 K \\ C_{PA} = 163 J / mol A/K & U_{a} = 16, 500 J / {mol}^{3} s \cdot K & {\dot{m}}_{C} = 0.111 mol / S \\ C_{P_{Cool}} \equiv C_{Pc} = 34.5 J /mol/K & V_{f} = 0.001 m^{3} \end{matrix}$

We will solve for all four cases of heat exchanger operation for this endother-mic reaction example in the same way we did for the exothermic reaction in Example 12-1. That is, we will write the Polymath equations for the case of co-current heat exchange and use that as the base case. We will then manipulate the different terms in the heat-transfer fluid balance (Equations 12-10 and 12-11) to solve for the other cases. We will start with the adiabatic case where we multiply the heat-transfer coefficient in the base case by zero.

Adiabatic endothermic reaction in a PFR

Case 1 Adiabatic

We are going to start with the adiabatic case first to show the dramatic effects of how the reaction dies out as the temperature drops. In fact, we are now going to extend the length of each tube to make the total reactor volume 5 dm³ in order to observe this effect of a reaction dying out as well as showing necessity of adding a heat exchanger. For the adiabatic case, we simply multiply the value of Ua in our Polymath program by zero. No other changes are necessary. For the adiabatic case, the answer will be the same whether we use a bank of 1000 reactors, each a 1-dm³ reactor, or one of 1 m³. To illustrate how an endothermic reaction can virtually die out completely, let’s extend the single-pipe volume from 1 dm³ to 5 dm³.

Ua = 16,500 * 0

The Polymath program is shown in Table E12-2.2. Figure E12-2.1 shows the graphical output.

Adiabatic conversion and temperature, and reaction rate profiles.

In graph (a) at left, the horizontal axis representing volume V (cubic decimeter) ranges from 0.5 to 4 in increments of 0.5. The vertical axis at left represents temperature T in Kelvin ranging from 900 to 1150 in increments of 50. The vertical axis at right represents conversion X ranging from 0.1 to 0.5 in increments of 0.1. A curve starts from 1035 Kelvin, decreases swiftly initially and then it bends and decreases gradually, ending at 905 Kelvin. Another curve starts from conversion 0, increases swiftly initially and then it bends and increases gradually, ending at conversion 0.28. Small perpendicular lines are drawn from a point on the curves where they bend. In graph (b) at right, the horizontal axis representing volume V (cubic decimeter) ranges from 0.00 to 5.00 in increments of 1.00. The vertical axis represents negative r subscript A (mole per cubic decimeter second) ranging from 0.0 to 68.0 in increments of 6.8. A curve representing rate starts from 67 of the vertical axis, decreases swiftly up to the bottom of the vertical axis, and then it decreases gradually up to 0.37 of the vertical axis. The end of the curve is indicated as Reaction died.

Figure E12-2.1 Adiabatic conversion and temperature (a), and reaction rate (b) profiles.

A box labeled Reaction Rate with a cross at the top of the box labeled RIP.

Death of a reaction

Living Example Problem

TABLE E12-2.2. POLYMATH PROGRAM AND OUTPUT FOR ADIABATIC OPERATION

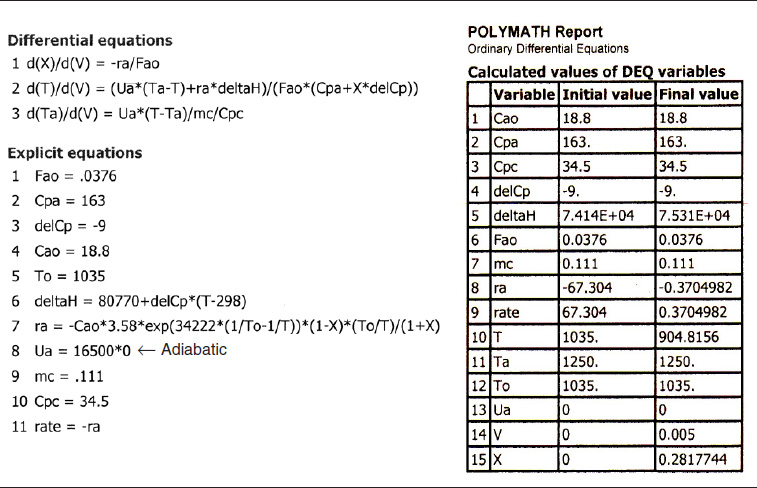
Analysis: Case 1 Adiabatic Operation: As temperature drops, so does k and hence the rate, −r_A, drops to an insignificant value. Note that for this adiabatic endothermic reaction, the reaction virtually dies out after 3.5 dm³, owing to the large drop in temperature, and we observe very little conversion is achieved beyond this point. one way to increase the conversion would be to add a diluent such as nitrogen, which could supply the sensible heat for this endothermic reaction. However, if too much diluent is added, the concentration, and hence the rate, will be quite low. On the other hand, if too little diluent is added, the temperature will drop and virtually extinguish the reaction. How much diluent to add is left as an exercise. Figures E12-2.1 (a) and (b) give the reactor volume as 5 dm³ in order to show the reaction “dying out.” However, because the reaction is nearly complete near the entrance to the reactor, i.e., −r_A ≅ 0, we are going to study and compare the heat-exchange systems in a 1-dm³ reactor (0.001 m³) in the next three cases.

Case 2 Constant heat-exchange fluid temperature, T_a

We make the following changes in our program on line 3 of the base case (a)

d T a d V = U a ( T - . T a ) m ˙ C P * 0

$\frac{d T_{a}}{d V} = \frac{U a (T - . T_{a})}{\dot{m} C_{P}} * 0$

Ua = 16,500 J/m³/s/K

and V_f = 0.001 m³

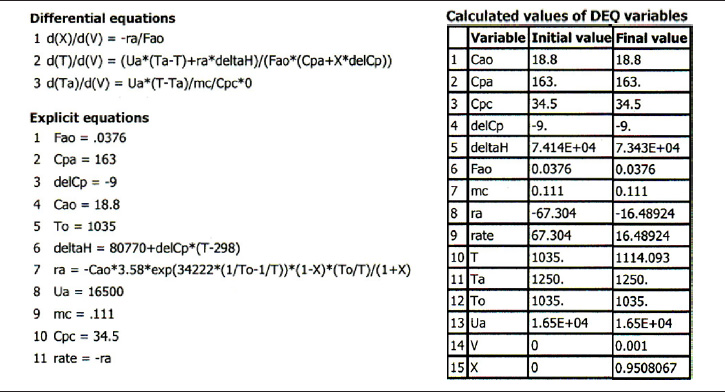
TABLE E12-2.3. POLYMATH PROGRAM AND OUTPUT FOR CONSTANT T_s

Living Example Problem

The profiles for T, X, and −r_A are shown in Figure E12-2.2, parts (a), (b), and (c) respectively.

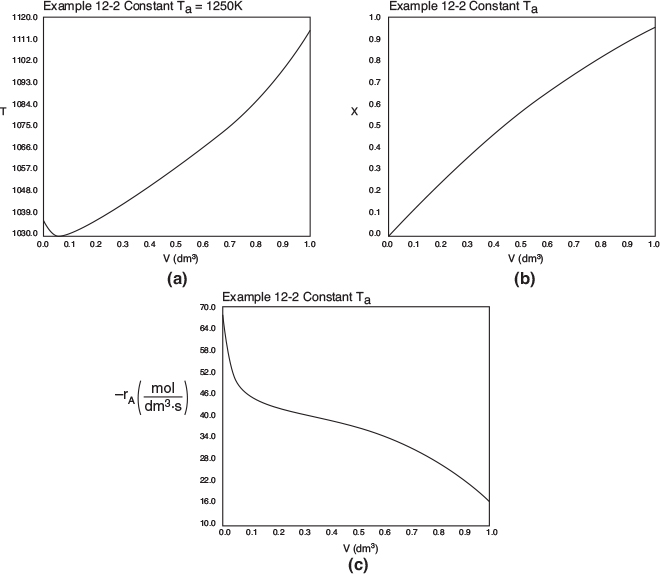
Three graphs representing Example 12-2 Constant T subscript a equals 1250K are labeled (a), (b), and (c).

In graph (a), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled T ranges from 1030.0 to 1120.0, in increments of 9.0. A curve from a point between 1030.0 and 1039.0 slides, intersects the horizontal axis at a point between 0.0 and 0.1, rises, and extends. In graph (b), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled X ranges from 0.0 to 1.0, in increments of 0.1. A curve from the origin rises and extends. In graph (c), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled negative r subscript A times (mol over cubic decimeters dot s) ranges from 10.0 to 70.0, in increments of 10.0. A curve from a point between 64.0 and 70.0 slides, extends horizontally, and slides.

Figure E12-2.2 Profiles for constant heat exchanger fluid temperature, T_a; (a) temperature, (b) conversion, (c) reaction rate.

Analysis: Case 2 Constant T_a: Just after the reactor entrance, the reaction temperature drops as the sensible heat from the reacting fluid supplies the energy for the endothermic reaction. This temperature drop in the reactor also causes the rate of reaction to drop. As we move farther down the reactor, the reaction rate drops further as the reactants are consumed. Beyond V = 0.08 dm³, the heat supplied by the constant T_a heat exchanger becomes greater than that “consumed” by the endothermic reaction and the reactor temperature rises. In the range between V = 0.2 dm³ and V = 0.6 dm³, the rate decreases slowly owing to the depletion of reactants, which is counteracted, to some extent, by the increase in temperature and hence the rate constant k. Consequently, we are eventually able to achieve an exit conversion of 95%.

Case 3 Co-current Heat Exchange

The energy balance on a co-current exchanger is

d T a d V = U a ( T - T a ) m ˙ C C P C

$\frac{d T_{a}}{d V} = \frac{U a (T - T_{a})}{{\dot{m}}_{C} C_{P_{C}}}$

with T_a0 = 1250 K at V = 0

TABLE E12-2.4. POLYMATH PROGRAM AND OUTPUT FOR CO-CURRENT EXCHANGE

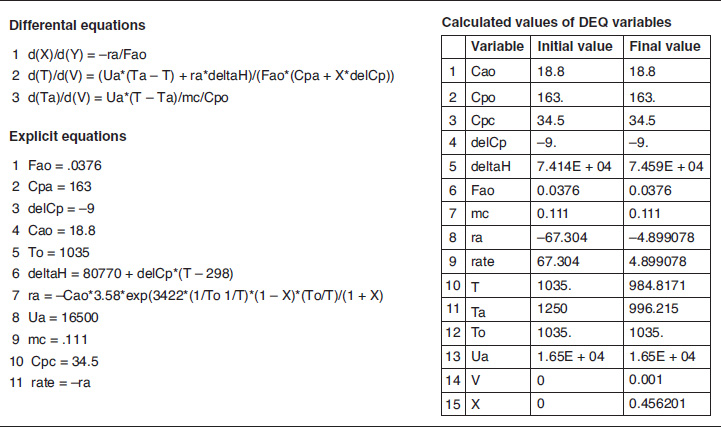
The variable profiles for T, T_a, X, and −r_A are shown in Figure E12-2.3, parts (a), (b), and (c) respectively. Because the reaction is endothermic, T_a needs to start off at a high temperature at V = 0.

Three graphs representing Example 12-2 Co-current Heat Exchange are labeled (a), (b), and (c).

In graph (a), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled T(K) ranges from 980 to 1250, in increments of 27. A curve labeled T subscript a from a point between 1223 and 1250 slides and extends horizontally and a curve labeled T from a point at 1034 slides and extends horizontally. In graph (b), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled X ranges from 0.00 to 0.46, in increments of 0.05. A curve from the origin rises and extends. In graph (c), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled negative r subscript A times (mol over cubic decimeters dot s) ranges from 0.00 to 70.0, in increments of 7.0. A curve from a point between 63.00 and 70.00 slides and extends horizontally.

Figure E12-2.3 Profiles down the reactor for an endothermic reaction with co-current heat exchange; (a) temperature, (b) conversion, and (c) reaction rate.

Analysis: Case 3 Co-Current Exchange: In co-current heat exchange, we see that the heat-exchanger fluid temperature, T_a, drops rapidly initially and then continues to drop along the length of the reactor as it supplies the energy to the heat drawn by the endothermic reaction. Eventually T_a decreases to the point where it approaches T and the rate of heat exchange is small; as a result, the temperature of the reactor, T, continues to decrease, as does the rate, resulting in a small conversion. Because the reactor temperature for co-current exchange is lower than that for Case 2 constant T_a, the reaction rate will be lower. As a result, significantly less conversion will be achieved than in the case of constant heat-exchange temperature T_a.

Case 4 Countercurrent Heat Exchange

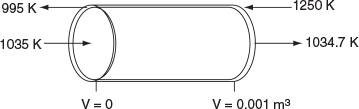
Countercurrent heat exchange shows a horizontal cylinder.

For countercurrent exchange, we first multiply the rhs of the co-current heat-exchanger energy balance by -1, leaving the rest of the Polymath program in Table 12-2.5 the same.

d T a d V = - U a ( T - T a ) m ˙ C p C

$\frac{d T_{a}}{d V} = - \frac{U a (T - T_{a})}{\dot{m} C_{p_{C}}}$

Next, guess T_a (V = 0) = 995.15 K to obtain T_a0 = 1250 K at V = 0.001m³. (Don’t you believe for a moment 995.15 K was my first guess.) Once this match is obtained as shown in Table E12-2.5, we can report the profiles shown in Figure E12-2.4.

Three graphs representing Example 12-2 Countercurrent Heat Exchange are labeled (a), (b), and (c).

In graph (a), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled T (K) ranges from 900 to 1300, in increments of 40. A curve labeled T from a point between 1020 and 1060 slides and rises. A curve labeled T subscript a from a point between 980 and 1020 slides and rises. In graph (b), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled X ranges from 0.00 to 0.40, in increments of 0.04. A curve that starts near the origin rises, slides, rises, and extends. In graph (c), the horizontal axis labeled V cubic decimeters ranges from 0.0 to 1.0, in increments of 0.1 and the vertical axis labeled negative r subscript A times (mol over (cubic decimeters dot s)) ranges from 0.00 to 70.0, in increments of 7.0. A curve from a point near 70.00 slides, extends horizontally, and rises.

Figure E12-2.4 Profiles down the reactor for countercurrent heat exchange; (a) temperature, (b) conversion, (c) reaction rate.

Good guess!

TABLE E12-2.5. POLYMATH PROGRAM AND OUTPUT FOR COUNTERCURRENT EXCHANGE

Polymath Report for ordinary differential equations shows a table labeled Calculated values of DEQ variables with column headers: Variable, Initial value, and Final value.

Analysis: Case 4 Countercurrent Exchange: At the front of the reactor, V = 0, the reaction takes place very rapidly, drawing energy from the sensible heat of the gas and causing the gas temperature to drop because the heat exchanger cannot supply energy at an equal or greater rate to that being drawn by the endothermic reaction. Additional “heat” is lost at the entrance in the case of countercurrent exchange because the temperature of the exchange fluid, T_a , is below the entering reactor temperature, T. One notes there is a minimum in the reaction rate, -r_A, profile that is rather flat. In this flat region, the rate is “virtually” constant between V = 0.2 dm³ and V = 0.8 dm³, because the increase in k caused by the increase in T is balanced by the decrease in rate brought about by the consumption of reactants. Just past the middle of the reactor, the rate begins to increase slowly as the reactants become depleted and the heat exchanger now supplies energy at a rate greater than the reaction draws energy and, as a result, the temperature eventually increases. This lower temperature coupled with the consumption of reactants causes the rate of reaction to be low in the plateau, resulting in a lower conversion than either the co-current or constant T_a heat exchange cases.

Summary of 4 Cases. The exit temperatures and conversion are shown in the Summary Table E12-2.6.

TABLE E12-2.6. SUMMARY TABLE

Heat Exclusion	X	T(K)	T(K)
Adiabatic	0.28	905	---
Constant T_a	0.95	1114	1250
Co-current	0.456	985	996
Countercurrent	0.35	1034	995

AspenTech: Example 12-2 has also been formulated in AspenTech and can be downloaded on your computer directly from the CRE Web site.

Screenshot shows buttons for Mixers/Splitters, Separators, Heat Exchangers, Columns, Reactors (selected), Pressure Changers, Manipulators, Solids, User Models, and Retired. Reactors button displays RPlug.

12.4 CSTR with Heat Effects

In this section we apply the general energy balance [Equation (11-22)] to a CSTR at steady state. We then present example problems showing how the mole and energy balances are combined to design reactors operating adiabatically and non-adiabatically.

In Chapter 11 the steady-state energy balance was derived as

Q˙−W˙s−FA0ΣΘiCPi(T−Ti0)−[ΔH∘Rx(TR)+ΔCP(T−TR)]FA0X = 0(11−28) $\begin{matrix} \dot{Q} - {\dot{W}}_{s} - F_{A0} Σ Θ_{i} C_{P_{i}} ({T - T}_{i 0}) - [Δ H_{R x}^{\circ} (T_{R}) + Δ C_{P} ({T - T}_{R})] F_{A0} X = 0 & (11-28) \end{matrix}$

Recall that W˙s ${\dot{W}}_{s}$ is the shaft work, i.e., the work done by the stirrer or mixer in the CSTR on the reacting fluid inside the CSTR. Consequently, because the convention that W˙s ${\dot{W}}_{s}$ done by the system on the surroundings is positive, the CSTR stirrer work will be a negative number, e.g., W˙s ${\dot{W}}_{s}$ =-1,000J/s. (See problem P12-6_B, a California Professional Engineers’ Exam Problem.)

Note: In many calculations the CSTR mole balance derived in Chapter 2

(F_A0X = −r_AV

These are the forms of the steady-state balance we will use.

will be used to replace the term following the brackets in Equation (11-28), that is, (F_A0X) will be replaced by (−r_AV) to arrive at Equation (12-12).

Rearranging yields the steady-state energy balance

Q˙−W˙s−FA0ΣΘiCPi(T-Ti0)+(rAV)(ΔHRx)=0(12−12) $\begin{matrix} \dot{Q} - {\dot{W}}_{s} - F_{A0} Σ Θ_{i} C_{P_{i}} ({T-T}_{i 0}) + (r_{A} V) (Δ H_{R x}) = 0 & (12-12) \end{matrix}$

Although the CSTR is well mixed and the temperature is uniform throughout the reaction vessel, these conditions do not mean that the reaction is carried out isothermally. Isothermal operation occurs when the feed temperature is identical to the temperature of the fluid inside the CSTR.

The Q˙ $\dot{Q}$ Term in the CSTR

For endothermic reactions (T>T_a2>T_a1)

For endothermic reactions (T_1a>T_2a>T)

12.4.1 Heat Added to the Reactor, Q˙ $\dot{Q}$

Figure 12-6 shows the schematics of a CSTR with a heat exchanger. The heat-transfer fluid enters the exchanger at a mass flow rate m_c (e.g., kg/s) at a temperature T_a1 and leaves at a temperature T_a2. The rate of heat transfer from the exchanger to the reactor fluid at temperature T is³

Schematic shows a CSTR at the left and a heat exchanger at the right.

Figure 12-6 CSTR tank reactor with heat exchanger. (Diagram on right courtesy of Pfaudler, Inc.)

Q ˙ = U A ( T a 1 - T a 2 ) l n [ ( T - T a 1 ) / ( T - T a 2 ) ] (12-13)

$\begin{matrix} \dot{Q} = \frac{U A (T_{a 1} - T_{a 2})}{l n [(T - T_{a 1}) / (T - T_{a 2})]} & \begin{matrix} (12-13) \end{matrix} \end{matrix}$

³ Information on the overall heat-transfer coefficient may be found in J. R. Welty, G. L. Rorrer, and D. G. Foster, Fundamentals of Momentum Heat and Mass Transfer, 6th ed. (New Jersey: Wiley, 2015), p. 370.

The following derivations, based on a coolant (exothermic reaction), apply also to heating mediums (endothermic reaction). As a first approximation, we assume a quasi-steady state operation for the coolant flow and neglect the accumulation term (i.e., dT_a/dt = 0). An energy balance on the heat-exchanger fluid entering and leaving the exchanger is

Energy balance on heat-exchanger fluid

⎡ ⎣ ⎢ ⎢ ⎢ ⎢ Rate of energy i n by flow ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ - ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ Rate of energy o u t by flow ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ - ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ Rate of heat transfer f r o m exchanger to reactor ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = 0 (12-14)

$\begin{matrix} \begin{matrix} [\begin{matrix} Rate of \\ energy \\ in \\ by flow \end{matrix}] & - & [\begin{matrix} Rate of \\ energy \\ out \\ by flow \end{matrix}] & - & [\begin{matrix} Rate of \\ heat transfer \\ from exchanger \\ to reactor \end{matrix}] & = 0 \end{matrix} & \begin{matrix} (12-14) \end{matrix} \end{matrix}$

m ˙ c C P c (T a 1 - T R) - m ˙ c C P c (T a 2 - T R) - U A ( T a 1 - T a 2 ) ln [ ( T - T a 1 ) / ( T - T a 2 ) ] = 0 (12-15)

$\begin{matrix} {\dot{m}}_{c} C_{P_{c}} (T_{a 1} - T_{R}) - {\dot{m}}_{c} C_{P_{c}} (T_{a 2} - T_{R}) - \frac{U A (T_{a 1} - T_{a 2})}{\ln [(T - T_{a 1}) / (T - T_{a 2})]} = 0 & \begin{matrix} (12-15) \end{matrix} \end{matrix}$

where CPc $C_{P_{c}}$ is the heat capacity of the heat exchanger fluid and T_R is the reference temperature. Simplifying gives us

Q ˙ = m ˙ c C P c (T a 1 - T a 2) = U A ( T a 1 - T a 2 ) ln [ ( T - T a 1 ) / ( T - T a 2 ) ] (12-16)

$\begin{matrix} \dot{Q} = {\dot{m}}_{c} C_{P_{c}} (T_{a 1} - T_{a 2}) = \frac{U A (T_{a 1} - T_{a 2})}{\ln [(T - T_{a 1}) / (T - T_{a 2})]} & \begin{matrix} (12-16) \end{matrix} \end{matrix}$

Solving Equation (12-16) for the exit temperature of the heat-exchanger fluid yields

T a 2 = T - (T - T a 1) exp (- U A m ˙ c C P c) (12-17)

$\begin{matrix} T_{a 2} = T - (T - T_{a 1}) \exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{c}}}) & \begin{matrix} (12-17) \end{matrix} \end{matrix}$

From Equation (12-16)

Q ˙ = m ˙ c C P c (T a 1 - T a 2) (12-18)

$\begin{matrix} \dot{Q} = {\dot{m}}_{c} C_{P_{c}} (T_{a 1} - T_{a 2}) & \begin{matrix} (12-18) \end{matrix} \end{matrix}$

Substituting for T_a2 in Equation (12-18), we obtain

Heat transfer to a CSTR

Q˙=mc˙CPc{(Ta1−T)[1−exp(−UAmc˙CPc)]}(12−19) $\begin{matrix} \dot{Q} = \dot{m_{c}} C_{P_{c}} {(T_{a 1} - T) [1 - \exp (\frac{- U A}{\dot{m_{c}} C_{P_{c}}})]} & (12-19) \end{matrix}$

For large values of the heat-exchanger fluid flow rate, mc˙ $\dot{m_{c}}$ , the exponent will be small and can be expanded in a Taylor series (e^−x = 1 − x + · · ·) where second-order terms are neglected in order to give

Q ˙ = m ˙ c C P c (T a 1 - T) [1 - (1 - U A m ˙ c C P c)]

$\dot{Q} = {\dot{m}}_{c} C_{P_{c}} (T_{a 1} - T) [1 - (1 - \frac{U A}{{\dot{m}}_{c} C_{P_{c}}})]$

Then

Valid only for large heat-transfer fluid flow rates!!

Q˙=UA(Ta−T)(12−20) $\begin{matrix} \dot{Q} = U A (T_{a} - T) & \begin{matrix} (12 - 20) \end{matrix} \end{matrix}$

where T_a1 ≅ T_a2 = T_a.

With the exception of processes involving highly viscous materials such as in Problem P12-6_B, a Caltfornta Professtonal Engineers’ Exam Problem, the work done by the stirrer can usually be neglected. Setting Ws˙ $\dot{W_{s}}$ equal to zero in Equation (11-27), neglecting ΔC_P, substituting for Q˙ $\dot{Q}$ , and rearranging, we have the following relationship between conversion and temperature in a CSTR

U A F A 0 (T a - T) - Σ Θ i C P i (T - T 0) - Δ H o R x X = 0 (12-21)

$\begin{matrix} \frac{U A}{F_{A 0}} (T_{a} - T) - Σ Θ_{i} C_{P_{i}} (T - T_{0}) - Δ H_{R x}^{o} X = 0 & \begin{matrix} (12-21) \end{matrix} \end{matrix}$

Solving for X

X=UAFA0(T−Ta)+ΣΘiCPi(T−T0)[−ΔH0Rx(TR)](12−22) $\begin{matrix} X = \frac{\frac{U A}{F_{A0}} (T - T_{a}) + Σ Θ_{i} C_{P_{i}} (T - T_{0})}{[- Δ H_{Rx}^{0} (T_{R})]} & \begin{matrix} (12 - 22) \end{matrix} \end{matrix}$

Equation (12-22) is coupled with the mole balance equation

V=FA0X−rA(X,T)(12−23) $\begin{matrix} V = \frac{F_{A0} X}{- r_{A} (X, T)} & \begin{matrix} (12 - 23) \end{matrix} \end{matrix}$

to design CSTRs.

To help us more easily see the effect of the operating parameters of T, T₀, and T_a, we collect terms and define CP0 $C_{P_{0}}$ , along with κ and T_c.

We now will further rearrange Equation (12-21) after letting

CP0=ΣΘiCPi $C_{P_{0}} = Σ Θ_{i} C_{P_{i}}$

then

C P 0 (U A F A 0 C P 0) T a + C P 0 T 0 - C P 0 (U A F A 0 C P 0 + 1) T - Δ H \circ Rx X = 0

$C_{P_{0}} (\frac{U A}{F_{A 0} C_{P_{0}}}) T_{a} + C_{P_{0}} T_{0} - C_{P_{0}} (\frac{U A}{F_{A 0} C_{P_{0}}} + 1) T - Δ H_{Rx}^{\circ} X = 0$

Let κ and T_C be non-adiabatic parameters defined by

Non-adiabatic CSTR heat exchange parameters: κ and T_c

κ=UAFA0CP0andTc=κTa+T01+κ $κ = \frac{U A}{F_{A0} C_{P_{0}}} and T_{c} = \frac{κ T_{a} + T_{0}}{1 + κ}$

Then

- X Δ H o R x = C P 0 (1 + κ) (T - T c) (12-24)

$\begin{matrix} - X Δ H_{R x}^{o} = C_{P_{0}} (1 + κ) (T - T_{c}) & \begin{matrix} (12-24) \end{matrix} \end{matrix}$

The parameters κ and T_c are used to simplify the equations for non-adiabatic operation. Solving Equation (12-24) for conversion

X=CP0(1+κ)(T−Tc)−ΔH∘Rx(12−25) $\begin{matrix} X = \frac{C_{P_{0}} (1 + κ) (T - T_{c})}{- Δ H_{Rx}^{\circ}} & \begin{matrix} (12 - 25) \end{matrix} \end{matrix}$

Solving Equation (12-24) for the reactor temperature

T=Tc+(−ΔH∘Rx)(X)CP0(1+κ)(12−26) $\begin{matrix} T = T_{c} + \frac{(- Δ H_{Rx}^{\circ}) (X)}{C_{P_{0}} (1 + κ)} & \begin{matrix} (12 - 26) \end{matrix} \end{matrix}$

Table 12-3 shows three ways to specify the design of a CSTR. This procedure for nonisothermal CSTR design can be illustrated by considering a first-order irreversible liquid-phase reaction. To solve CSTR problems of this type we have three variables X, T, and V and we can only specify two and then solve for the third. The algorithm for working through either cases A (X specified), B (T specified), or C (V specified) is shown in Table 12-3. Its application is illustrated in Example 12-3.

Forms of the energy balance for a CSTR with heat exchange

TABLE 12-3 WAYS TO SPECIFY THE SIZING OF A CSTR

Illustration shows ways to specify the sizing of a CSTR.

A: Specify X: Find V and T, B: Specify T: Find X and V, and C: Specify V: Find X and T are shown from left to right. A leads to Calculate T from equation (12-26). Below it, an equation reads: T equals T subscript c plus ((negative delta H subscript (RX) degrees) of (X)) over (C subscript (P subscript 0) (1 plus K)). It further leads to Calculate k: k equals (A e to the power (negative E over (RT))), Calculate negative r subscript A (X, T) (example, negative r subscript A equals k C subscript (A0) (1 minus X), Calculate V: V equals ((F subscript (A0) X) over (negative r subscript A)). B leads to Calculate X subscript (EB) from equation (12-25). Below it, an equation reads: X subscript (EB) equals ((C subscript (P subscript 0) (1 plus K)) (T minus T subscript c) over (negative delta H subscript (RX)). It further leads to Calculate k: k equals (Ae to the power (negative E over (RT))), Calculate negative r subscript A (X, T) (example, negative r subscript A equals k C subscript (A0) (1 minus X), Calculate V: V equals ((F subscript (A0)X) over (negative r subscript A)). Below A and B, text reads: X subscript (MB) conversion calculated from the mole balance: X subscript (EB) equals conversion calculated from the energy balance. The intersection of the energy balance curve X subscript EB of (T) and the mole balance curve X subscript MB of (T) in the figure gives the steady-state CSTR exit conversion and temperature. C leads to Use equation (12-25) to plot X subscript (EB) versus T. Below it, a graph shows point T subscript 0 marked on the horizontal T-axis and the vertical X subscript (EB) axis. It leads to Solve Equation (12-23) for X subscript MB equals f of (T) to find X subscript MB versus T (example, for a first-order reaction). Below it, an equation reads: X subscript (MB) equals (tau A exp (negative E over (RT)) over (1 plus tau A exp (negative E over (RT))). It further leads to Plot X subscript (EB) and X subscript (MB) as a function of T on the same figure. Below it, a graph shows a S curve intersecting a line labeled X subscript (EB) and X subscript (MB). The point of intersection is connected to the horizontal axis labeled T and the vertical axis labeled X. Below it, text reads: CSTR steady state when X subscript (EB) equals X subscript (MB).

Example 12-3 Production of Propylene Glycol in an Adiabatic CSTR

Propylene glycol is produced by the hydrolysis of propylene oxide:

Production, uses, and economics

Over 900 million pounds of propylene glycol were produced in 2010 and the selling price was approximately $0.80 per pound. Propylene glycol makes up about 25% of the major derivatives of propylene oxide. The reaction takes place readily at room temperature when catalyzed by sulfuric acid.

You are the engineer in charge of an adiabatic CSTR producing propylene gly-col by this method. Unfortunately, the reactor is beginning to leak, and you must replace it. (You told your boss several times that sulfuric acid was corrosive and that mild steel was a poor material for construction. He wouldn’t listen.) There is a nice-looking, bright, shiny overflow CSTR of 300-gal capacity standing idle; it is glass-lined, and you would like to use it.

We are going to work this problem in lb_m, s, ft³, and lb-moles rather than g, mol, and m³ in order to give the reader more practice in working in both the English and metric systems. Why?? Many plants still use the English system of units.

You are feeding 2500 lb_m/h (43.04 lb-mol/h) of propylene oxide (P.O.) to the reactor. The feed stream consists of (1) an equivolumetric mixture of propylene oxide (46.62 ft³/h) and methanol (46.62 ft³/h), and (2) water containing 0.1 wt % H₂SO₄. The volumetric flow rate of water is 233.1 ft³/h, which is 2.5 times the methanol-P.O. volumetric flow rate. The corresponding molar feed rates of methanol and water are 71.87 lb-mol/h and 802.8 lb-mol/h, respectively. The water-propylene oxide-methanol mixture undergoes a slight decrease in volume upon mixing (approximately 3%), but you neglect this decrease in your calculations. The temperature of both feed streams is 58°F prior to mixing, but there is an immediate 17°F temperature rise upon mixing of the two feed streams caused by the heat of mixing. The entering temperature of all feed streams is thus taken to be 75°F (Figure E12-3.1).

Schematic shows a CSTR with a mixture in it labeled V equals 300 gallon.

Figure E12-3.1 Propylene glycol manufacture in a CSTR.

Furusawa et al. state that under conditions similar to those at which you are operating, the reaction is first-order in propylene oxide concentration and apparent zero-order in excess of water with the specific reaction rate⁴

k = A e - E / R T = 16.96 \times 1012 (e - 32, 400 / R T) h - 1

$k = A e^{- E / R T} = 16.96 \times 1 0^{12} (e^{- 32, 400 / R T}) h^{- 1}$

⁴ T. Furusawa, H. Nishimura, and T. Miyauchi, J. Chem. Eng. Jpn, 2, 95.

The units of E are Btu/lb-mol and Τ is in °R.

There is an important constraint on your operation. Propylene oxide is a rather low-boiling-point substance. With the mixture you are using, you feel that you cannot exceed an operating temperature of 125 °F, or you will lose too much propylene oxide by vaporization through the vent system.

(a) Can you use the idle CSTR as a replacement for the leaking one if it will be operated adiabatically?

(b) If so, what will be the conversion of propylene oxide to glycol?

Solution

(All data used in this problem were obtained from the CRC Handbook of Chemistry and Physics unless otherwise noted.) Let the reaction be represented by

A + B → C

where

A is p0ropylene oxide (CPA=35Btu/1b-mol⋅°F) $(C_{P_{A}} = 35 Btu/1b-mol \cdot ° F)$ ⁵

⁵ CPA $C_{P_{A}}$ and CPC $C_{P_{C}}$ are estimated from the observation that the great majority of low-molecular-weight oxygen-containing organic liquids have a mass heat capacity of 0.6 cal/g ·°C ±15%.

B is water (CPB=18Btu/1b-mol⋅°F) $(C_{P_{B}} = 18 Btu/1b-mol \cdot ° F)$

C is propylene glycol (CPC=46Btu/1b-mol⋅°F) $(C_{P_{C}} = 46 Btu/1b-mol \cdot ° F)$

M is methanol (CPM=19.5Btu/1b-mol⋅°F) $(C_{P_{M}} = 19.5 Btu/1b-mol \cdot ° F)$

In this problem, neither the exit conversion nor the temperature of the adia-batic reactor is given. By application of the mole and energy balances, we can solve two equations with two unknowns (X and Τ ), as shown on the right-hand pathway in Table 12-3. Solving these coupled equations, we determine the exit conversion and temperature for the glass-lined reactor to see if it can be used to replace the present reactor.

Following the Algorithm

1. Mole Balance and Design Equation:

F A 0 - F A + r A V = 0

$F_{A 0} - F_{A} + r_{A} V = 0$

The design equation in terms of X is

V = F A 0 X - r A (E 12-3.1)

$\begin{matrix} V = \frac{F_{A 0} X}{- r_{A}} & \begin{matrix} (E 12–3.1) \end{matrix} \end{matrix}$

2. Rate Law:

- r A = k C A (E 12-3.2)

$\begin{matrix} - r_{A} = k C_{A} & \begin{matrix} (E 12–3.2) \end{matrix} \end{matrix}$

k = 16.961012 exp [- 32, 400 / R / T] h - 1

$k = 16.961 0^{12} \exp [- 32, 400 / R / T] h^{- 1}$

3. Stoichiometry (liquid phase, υ = υ₀):

C A = C A 0 (1 - X) (E 12-3.3)

$\begin{matrix} C_{A} = C_{A 0} (1 - X) & \begin{matrix} (E 12–3.3) \end{matrix} \end{matrix}$

4. Combining yields

V = F A 0 X k C A 0 ( 1 - X ) = v 0 X k ( 1 - X ) (E 12-3.4)

$\begin{matrix} V = \frac{F_{A 0} X}{k C_{A 0} (1 - X)} = \frac{v_{0^{X}}}{k (1 - X)} & \begin{matrix} (E 12–3.4) \end{matrix} \end{matrix}$

Solving for X as a function of T and recalling that τ = V/υ₀ gives

X M B = τ k 1 + τ k = τ A e - E / R T 1 + τ A e - E / R T (E 12-3.5)

$\begin{matrix} X_{M B} = \frac{τ k}{1 + τ k} = \frac{τ A e^{- E / R T}}{1 + τ A e^{- E / R T}} & \begin{matrix} (E 12–3.5) \end{matrix} \end{matrix}$

This equation relates temperature and conversion through the mole balance.

5. The energy balance for this adiabatic reaction in which there is negligible energy input provided by the stirrer is

X E B = \sum Θ i C P i ( T - T i 0 ) - [ Δ H o R x ( T R ) + Δ C P ( T - T R ) ] (E 12-3.6)

$\begin{matrix} X_{E B} = \frac{\sum Θ_{i} C_{P_{i}} (T - T_{i 0})}{- [Δ H_{R x}^{o} (T_{R}) + Δ C_{P} (T - T_{R})]} & \begin{matrix} (E 12–3.6) \end{matrix} \end{matrix}$

This equation relates X and T through the energy balance. We see that two equations, Equations (E12-3.5) and (E12-3.6), and two unknowns, X and T, must be solved (with X_EB = X_MB = X).

6. Calculations:

Rather than putting all those numbers in the mole and heat balance equations yourself, you can outsource this task, for a small fee, to Sven Köttlov Consulting Company, located on the third floor of the downtown Market Center Building (called the “MCB") in Riça, Jofostan.

(a) Evaluate the mole balance terms (C_A0, Θ_i, τ): The total liquid volumetric flow rate entering the reactor is

I know these are tedious calculations, but someone’s gotta know how to do it.

v0==V=vA0+vM0+vB046.62+46.62+233.1=326.3ft3/h300gal=40.1ft3(E12-3.7) $\begin{matrix} v_{0} = & v_{A0} + v_{M0} + v_{B0} \\ = & 46.62 + 46.62 + 233.1 = 326.3 {ft}^{3} / h & (E12-3.7) \\ V = & 300 gal = 40.1 {ft}^{3} \end{matrix}$

τ=Vv0=40.1ft3326.3ft3/h=0.123h(E12-3.8) $\begin{matrix} τ = \frac{V}{v_{0}} = \frac{40.1 {ft}^{3}}{326.3 {ft}^{3} /h} = 0.123 h & \begin{matrix} (E12-3.8) \end{matrix} \end{matrix}$

CA0==FA0v0=43.0lb-mol/h326.3ft3/h0.132lb-mol/ft3(E12-3.9) $\begin{matrix} \begin{matrix} C_{A0} = & \frac{F_{A0}}{v_{0}} = \frac{43.0 lb-mol/h}{326.3 {ft}^{3} / h} \\ = & 0.132 {lb-mol/ft}^{3} \end{matrix} & \begin{matrix} (E12-3.9) \end{matrix} \end{matrix}$

For methanol:For water:ΘM=FM0FA0=71.87lb-mol/h43.0lb-mol/h=1.67ΘB=FB0FA0=802.8 lb-mol/h43.0lb-mol/h=18.65 $\begin{matrix} For methanol: & Θ_{M} = \frac{F_{M0}}{F_{A0}} = \frac{71.87 lb-mol/h}{43.0 lb-mol/h} = 1.67 \\ For water: & Θ_{B} = \frac{F_{B 0}}{F_{A0}} = \frac{802.8 lb-mol/h}{43.0 lb-mol/h} = 18.65 \end{matrix}$

The conversion calculated from the mole balance, X_MB , is found from Equation (E12-3.5)

XMB=(16.93×1012h−1)(0.1229h)exp(−32,400/1.987T)1+(16.96×1012h−1)(0.1229h)exp(−32,400/1.987T) $\begin{matrix} X_{MB} & = \frac{(16.93 \times 10^{12} h^{- 1}) (0.1229 h) exp (- 32, 400 / 1.987 T)}{1 + (16.96 \times 10^{12} h^{- 1}) (0.1229 h) exp (- 32, 400 / 1.987 T)} \end{matrix}$

Plot X_MB as a function of temperature.

XMB=(2.084×1012)exp (−16,306/T)1+(2.084×1012)exp(−16,306/T),Tis inR∘(E12-3.10) $\begin{matrix} \begin{matrix} X_{MB} & = \frac{(2.084 \times 10^{12}) exp (- 16, 306 / T)}{1 + (2.084 \times 10^{12}) exp (- 16, 306 / T)}, T is in {}^{\circ}R \end{matrix} & \begin{matrix} (E12-3.10) \end{matrix} \end{matrix}$

(b) Evaluating the energy balance terms

(1) Heat of reaction at temperature T

Δ H R x (T) = Δ H o R x (T R) + Δ C P (T - T R) (11-26)

$\begin{matrix} Δ H_{R x} (T) = Δ H_{R x}^{o} (T_{R}) + Δ C_{P} (T - T_{R}) & \begin{matrix} (11-26) \end{matrix} \end{matrix}$

Δ C P = C P C - C P B - C P A = 46 - 18 - 35 = - 7 B t u / 1 b - m o 1 / \circ F

$Δ C_{P} = C_{P_{C}} - C_{P_{B}} - C_{P_{A}} = 46 - 18 - 35 = - 7 B t u / 1 b - m o 1 /^{\circ} F$

Δ H Rx = - 36, 000 - 7 (T - T R) (E 12-3.11)

$\begin{matrix} Δ H_{Rx} = - 36, 000 - 7 (T - T_{R}) & \begin{matrix} (E 12–3.11) \end{matrix} \end{matrix}$

(2) Heat capacity term

ΣΘiCPi===CPA+ΘB+CPB+ΘMCPM35+(18.65)(18)+(1.67)(19.5)403.3Btu/lb-mol.F∘(E12-3.12) $\begin{matrix} \begin{matrix} Σ Θ_{i} C_{P_{i}} = & C_{P_{A}} + Θ_{B} + C_{P_{B}} + Θ_{M} C_{P_{M}} \\ = & 35 + (18.65) (18) + (1.67) (19.5) \\ = & 403.3 Btu/lb-mol. {}^{\circ}F \end{matrix} & \begin{matrix} (E12-3.12) \end{matrix} \end{matrix}$

T0==TR=T00+ΔTmix=58∘F+17∘F=75∘F535∘R68∘F=528∘R(E12-3.13) $\begin{matrix} \begin{matrix} T_{0} = & T_{00} + Δ T_{mix} = 58^{\circ} F + 17^{\circ} F = 75^{\circ} F \\ = & 535^{\circ} R \\ T_{R} = & 68^{\circ} F = 528^{\circ} R \end{matrix} & \begin{matrix} (E12-3.13) \end{matrix} \end{matrix}$

The conversion calculated from the energy balance, X_EB, for an adiabatic reaction is given by Equation (11-29)

X E B = - Σ Θ i C P i ( T - T i 0 ) Δ H o R x ( T R ) + Δ C P ( T - T R ) (11-29)

$\begin{matrix} X_{E B} = - \frac{Σ Θ_{i} C_{P_{i}} (T - T_{i 0})}{Δ H_{R x}^{o} (T_{R}) + Δ C_{P} (T - T_{R})} & \begin{matrix} (11-29) \end{matrix} \end{matrix}$

Substituting all the known quantities into the energy balance gives us

XEB=(403.3Btu/lb-mol⋅F∘)(T−535)∘F−[−36,400−7(T−528)]Btu/lb-mol $X_{EB} = \frac{(403.3 Btu/lb-mol \cdot {}^{\circ}F) (T - 535)^{\circ} F}{- [- 36, 400 - 7 (T - 528)] Btu/lb-mol}$

XEB=403.3(T−535)36,400+7(T−528)(E12-3.14) $\begin{matrix} X_{EB} = \frac{403.3 (T - 535)}{36, 400 + 7 (T - 528)} & \begin{matrix} (E12-3.14) \end{matrix} \end{matrix}$

Adiabatic CSTR

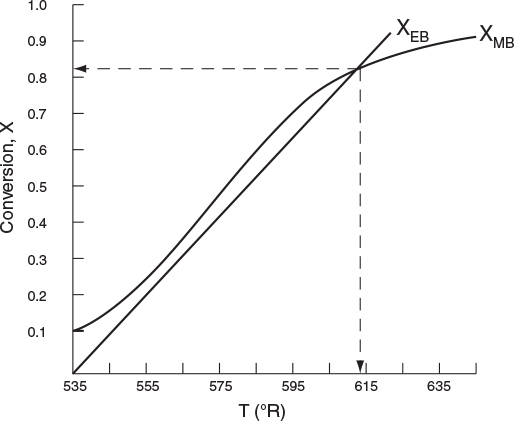
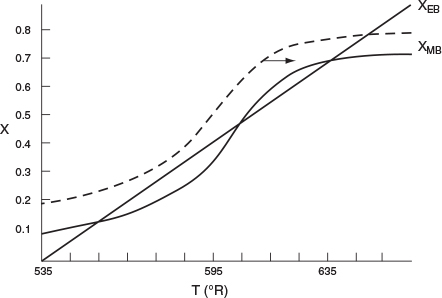
7. Solving. There are a number of different ways to solve these two simultaneous algebraic equations (E12-3.10) and (E12-3.14). The easiest way is to use the Polymath nonlinear equation solver. However, to give insight into the functional relationship between X and T for the mole and energy balances, we shall obtain a graphical solution. Here, X is plotted as a function of T for both the mole and energy balances, and the intersection of the two curves gives the solution where both the mole and energy balance solutions are satisfied, i.e., X_EB = X_MB. In addition, by plotting these two curves we can learn if there is more than one intersection (i.e., multiple steady states) for which both the energy balance and mole balance are satisfied. If numerical root-finding techniques were used to solve for X and T, it would be quite possible that you would find only one root when there is actually more than one. If Polymath were used, you could learn if multiple roots exist by changing your initial guesses in the nonlinear equation solver. We shall discuss multiple steady states further in Section 12-5. We choose Τ and then calculate X (Table E12-3.1). The calculations for X_MB and X_EB are plotted in Figure E12-3.2. The virtually straight line corresponds to the energy balance, Equation (E12-3.14), and the curved line corresponds to the mole balance, Equation (E12-3.10). We observe from this plot that the only intersection point is at 83% conversion and 613°R. At this point, both the energy balance and mole balance are satisfied. Because the temperature must remain below 125°F (585°R), we cannot use the 300-gal reactor as it is now.

A graph depicts the conversions X subscript EB and X subscript MB as a function of temperature.

Figure E12-3.2 The conversion X_EB and X_MB as a function of temperature.

TABLE E12-3.1 CALCULATIONS OF X_EB AND X_MB AS A FUNCTION OF T

T (°R)	X_MB [Eq. (E12-3.10)]	X_EB [Eq. (E12-3.14)]
535	0.108	0.000
550	0.217	0.166
565	0.379	0.330
575	0.500	0.440
585	0.620	0.550
595	0.723	0.656
605	0.800	0.764
615	0.860	0.872
625	0.900	0.980

The reactor cannot be used because it will exceed the specified maximum temperature of 585°R.

Analysis: After using Equations (E12-3.10) and (E12-3.14) to make a plot of conversion as a function of temperature, we see that there is only one intersection of X_EB(T) and X_MB(T), and consequently only one steady state. The exit conversion is 83% and the exit temperature (i.e., the reactor temperature) is 613°R (153°F), which is above the acceptable limit of 585°R (125°F) and we thus cannot use the CSTR operating at these conditions.

Ouch! Looks like our plant will not be able to be completed and our multimillion-dollar profit has flown the coop. But wait, don’t give up, let’s ask reaction engineer Maxwell Anthony to fly to our company’s plant in the country of Jofostan to look for a cooling coil heat exchanger that we could place in the reactor. See what Max found in Example 12-4.

Example 12-4 CSTR with a Cooling Coil

Fantastic! Max has located a cooling coil in an equipment storage shed in the small, mountainous village of Ölofasis, Jofostan, for use in the hydrolsis of propylene oxide discussed in Example 12-3. The cooling coil has 40 ft² of cooling surface and the cooling-water flow rate inside the coil is sufficiently large that a constant coolant temperature of 85°F can be maintained. A typical overall heat-transfer coefficient for such a coil is 100 Btu/h · ft² -°F. Will the reactor satisfy the previous constraint of 125°F maximum temperature if the cooling coil is used?

Solution

If we assume that the cooling coil takes up negligible reactor volume, the conversion calculated as a function of temperature from the mole balance is the same as that in Example 12-3, Equation (E12-3.10).

1. Combining the mole balance, stoichiometry, and rate law, we have, from Example 12-3

XMB=τk1+τk=(2.084×1012)exp(−16,306/T)1+(2.084×1012)exp(−16,306/T)(E12-3.10) $\begin{matrix} X_{MB} = \frac{τ k}{1 + τ k} = \frac{(2.084 \times 10^{12}) exp (- 16, 306 / T)}{1 + (2.084 \times 10^{12}) exp (- 16, 306 / T)} & \begin{matrix} (E12-3.10) \end{matrix} \end{matrix}$

T is in °R.

2. Energy balance. Neglecting the work by the stirrer, we combine Equations (11-27) and (12-20) to write

U A ( T a - T ) F A 0 - X [Δ H \circ R X (T R) + Δ C P (T - T R)] = Σ Θ i C P i (T - T 0) (E 12-4.1)

$\begin{matrix} \frac{U A (T_{a} - T)}{F_{A 0}} - X [Δ H_{R X}^{\circ} (T_{R}) + Δ C_{P} (T - T_{R})] = Σ Θ_{i} C_{P_{i}} (T - T_{0}) & \begin{matrix} (E 12–4.1) \end{matrix} \end{matrix}$

Solving the energy balance for X_EB yields

XEB=ΣΘiCPi(T−T0)+[UA(T−Ta)/FA0]−[ΔH∘Rx(TR)+ΔCP(T−TR)](E12-4.2) $\begin{matrix} X_{EB} = \frac{Σ Θ_{i} C_{P_{i}} (T - T_{0}) + [U A (T - T_{a}) / F_{A0}]}{- [Δ H_{Rx}^{\circ} (T_{R}) + Δ C_{P} (T - T_{R})]} & \begin{matrix} (E12-4.2) \end{matrix} \end{matrix}$

The cooling-coil term in Equation (E12-4.2) is

U A F A 0 - (100 Btu h \cdot ft 2 \cdot F \circ) ( 40 ft 2 ) ( 43.04 lb-mol/h ) = 92.9 B t u lb-mol \cdot F \circ (E 12-4.3)

$\begin{matrix} \frac{U A}{F_{A 0}} - (100 \frac{Btu}{h \cdot ft^{2} \cdot {}^{\circ}F}) \frac{(40 ft^{2})}{(43.04 lb−mol/h)} = \frac{92.9 B t u}{lb−mol \cdot {}^{\circ}F} & \begin{matrix} (E 12–4.3) \end{matrix} \end{matrix}$

Recall that the cooling temperature is

T_a = 85°F = 545°R

The numerical values of all other terms of Equation (E12-4.2) are identical to those given in Equation (E12-3.13), but with the addition of the heat exchange term, X_EB becomes

XEB=403.3(T−535)+92.9(T−545)36,400+7(T−528)(E12-4.4) $\begin{matrix} X_{EB} = \frac{403.3 (T - 535) + 92.9 (T - 545)}{36, 400 + 7 (T - 528)} & \begin{matrix} (E12-4.4) \end{matrix} \end{matrix}$

We now have two equations, Equations (E12-3.10) and (E12-4.4), and two unknowns, X and T, which we can solve with Polymath. Recall Examples E4-5 and E8-6 to review how to solve nonlinear, simultaneous equations of this type with Polymath. (See Problem P12-1(f) on page 642 to plot X versus T on Figure E12-3.2.) We could generate Figure E12-3.2 by “fooling” Polymath to plot X and T, as explained in the tutorial on the Web site (http://www.umich.edu/~elements/5e/software/Polymath_fooling_tutorial.pdf).

Living Example Problem

The Polymath program and solution to these two Equations (E12-3.10) for X_MB, and (E12-4.4) for X_EB, are given in Table E12-4.1. The exiting temperature and conversion are 103.7°F (563.7°R) and 36.4%, respectively, i.e.,

TABLE E12-4.1 POLYMATH: CSTR WITH HEAT EXCHANGE

T=564∘R andX=0.36 $T = 564^{\circ} R and X = 0.36$

Analysis: We are grateful to the people of the village of Ölofasis in Jofostan for their help in finding this shiny new heat exchanger. By adding heat exchange to the CSTR, the X_MB(T) curve is unchanged but the slope of the X_EB(T) line in Figure E12-3.2 increases and intersects the X_MB curve at X = 0.36 and T = 564°R. This conversion is low! We could try to reduce to cooling by increasing T_a or T₀ to raise the reactor temperature closer to 585°R, but not above this temperature. The higher the temperature in this irreversible reaction, the greater the conversion.

We will see in the next section that there may be multiple exit values of conversion and temperature (Multiple Steady States, MSS) that satisfy the parameter values and entrance conditions.

12.5 Multiple Steady States (MSS)

In this section, we consider the steady-state operation of a CSTR in which a first-order reaction is taking place. An excellent experimental investigation that demonstrates the multiplicity of steady states was carried out by Vejtasa and Schmitz.⁶ They studied the reaction between sodium thiosulfate and hydrogen peroxide

⁶ S. A. Vejtasa and R. A. Schmitz, AIChE J., 16 (3), 415 (1970).

2Na₂S₂O₃ + 4H₂O₂ Na₂S₃O₆ + Na₂SO₄ + 4H₂O

in a CSTR operated adiabatically. The multiple steady-state temperatures were examined by varying the flow rate over a range of space times, τ.

Reconsider the X_MB(T) curve, Equation (E12-3.10), shown in Figure E12-3.2, which has been redrawn and shown as dashed lines in Figure E12-3.2A. Now consider what would happen if the volumetric flow rate υ₀ is increased (τ decreased) just a little. The energy balance line, X_EB(T), remains unchanged, but the mole balance line, X_MB, moves to the right, as shown by the curved, solid line in Figure E12-3.2A. This shift of X_MB(T) to the right results in the X_EB(T) and X_MB(T) intersecting three times, indicating three possible steady-state conditions at which the reactor could operate.

Figure E12-3.2A Plots of X_EB(T) and X_MB(T) for different spaces times τ.

When more than one intersection occurs, there is more than one set of conditions that satisfy both the energy balance and mole balance (i.e., X_EB = X_MB); consequently, there will be multiple steady states at which the reactor may operate. These three steady states are easily determined from a graphical solution, but only one could show up in the Polymath equation solver solution. Thus, when using the Polymath nonlinear equation solver, we need to either choose different initial guesses to find if there are other solutions. We could also fool Polymath to obtain the plot in Figure E12-3.2A by using the ODE solver and setting dTdt=0.1 $\frac{d T}{d t} = 0.1$ and then plot X_MB and X_EB versus T, as in Example 12-3. Tutorials on “How to Fool Polymath” and generate G(T) and R(T) plots can be found at http://www.umich.edu/~elements/5e/software/Polymath_fooling_tutorial.pdf

“Fooling” Polymath

We begin by recalling Equation (12-24), which applies when one neglects shaft work and ΔC_P (i.e., ΔC_P = 0 and therefore ΔHRx=ΔHoRx $Δ H_{R x} = Δ H_{R x}^{o}$ )

- X Δ H o R x = C P 0 (1 + κ) (T - T c) (12-24)

$\begin{matrix} - X Δ H_{R x}^{o} = C_{P 0} (1 + κ) (T - T_{c}) & \begin{matrix} (12-24) \end{matrix} \end{matrix}$

where

CP0=ΣΘiCPi(12−26a) $\begin{matrix} C_{P0} = Σ Θ_{i} C_{P_{i}} & (12 - 26 a) \end{matrix}$

κ=UACP0FA0(12−26b) $\begin{matrix} κ = \frac{U A}{C_{P0} F_{A0}} & \begin{matrix} (12 - 26 b) \end{matrix} \end{matrix}$

and

Tc=T0FA0CP0+UATaUA+CP0FA0=κTa+T01+κ(12−27) $\begin{matrix} T_{c} = \frac{T_{0} F_{A0} C_{P 0} + {U A T}_{a}}{U A + C_{P0} F_{A0}} = \frac{κ T_{a} + T_{0}}{1 + κ} & \begin{matrix} (12 - 27) \end{matrix} \end{matrix}$

Using the CSTR mole balance X=−rAVFA0 $X = \frac{- r_{A} V}{F_{A 0}}$ , Equation (12-24) may be rewritten as

(- r A V / F A 0) (- Δ H o R x) = C P 0 (1 + κ) (T - T c) (12-28)

$\begin{matrix} (- r_{A} V / F_{A 0}) (- Δ H_{R x}^{o}) = C_{P 0} (1 + κ) (T - T_{c}) & \begin{matrix} (12-28) \end{matrix} \end{matrix}$

The left-hand side is referred to as the heat-generated term

G(T) = Heat-generated term

G(T)=(−ΔH∘Rx)(−rAV/FA0)(12−29) $\begin{matrix} G (T) = (- Δ H_{Rx}^{\circ}) (- r_{A} V / F_{A0}) & \begin{matrix} (12 - 29) \end{matrix} \end{matrix}$

The right-hand side of Equation (12-28) is referred to as the heat-removed term (by flow and heat exchange) R(T)

R(T) = Heat-removed term

R(T)=CP0(1+κ)(T−Tc)(12−30) $\begin{matrix} R (T) = C_{P0} (1 + κ) (T - T_{c}) & (12 - 30) \end{matrix}$

To study the multiplicity of steady states, we shall plot both R(T) and G(T) as a function of temperature on the same graph and analyze the circumstances under which we will obtain multiple intersections of R(T) and G(T).

12.5.1 Heat-Removed Term, R (T)

Vary Entering Temperature. From Equation (12-30) we see that R(T) increases linearly with temperature, with slope C_P0 (1 + κ) and intercept T_c. As the entering temperature T₀ is increased, the line retains the same slope but shifts to the right as the intercept T_c increases, as shown in Figure 12-7.

Graph depicts variation of heat-removed line with inlet temperature.

Figure 12-7 Variation of heat-removed line with inlet temperature.

Heat-removed curve R(T)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 12 Steady-State Nonisothermal Reactor Design—Flow Reactors with Heat Exchange

Create new playlist

Sign In

Sign Up

12. Steady-State Nonisothermal Reactor Design—Flow Reactors with Heat Exchange

12.1 Steady-State Tubular Reactor with Heat Exchange

12.1.1 Deriving the Energy Balance for a PFR

12.1.2 Applying the Algorithm to Flow Reactors with Heat Exchange

12.2 Balance on the Heat-Transfer Fluid

12.2.1 Co-current Flow

12.2.2 Countercurrent Flow

12.3 Algorithm for PFR/PBR Design with Heat Effects

12.3.1 Applying the Algorithm to an Exothermic Reaction

12.3.2 Applying the Algorithm to an Endothermic Reaction

12.4 CSTR with Heat Effects

12.4.1 Heat Added to the Reactor, ˙QQ˙<math alttext="" xmlns:m="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><mover><mrow><mi>Q</mi></mrow><mrow><mo>˙</mo></mrow></mover></mrow></math>

12.5 Multiple Steady States (MSS)

12.5.1 Heat-Removed Term, R (T)

Table of Contents for
Chapter 12 Steady-State Nonisothermal Reactor Design—Flow Reactors with Heat Exchange

12.4.1 Heat Added to the Reactor, Q˙ $\dot{Q}$