2. Conversion and Reactor Sizing

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

2. Conversion and Reactor Sizing

Be more concerned with your character than with your reputation, because character is what you really are while reputation is merely what others think you are.

—John Wooden, former head coach, UCLA Bruins

Overview. In the first chapter, the general mole balance equation was derived and then applied to the four most common types of industrial reactors. A balance equation was developed for each reactor type and these equations are summarized in Table S1-1 in Chapter 1. In Chapter 2, we will show how to size and arrange these reactors conceptually, so that the reader may see the structure of chemical reaction engineering (CRE) design and will not get lost in the mathematical details.

In this chapter, we

Define conversion
Rewrite all balance equations for the four types of industrial reactors in Chapter 1 in terms of the conversion, X
Show how to size (i.e., determine the reactor volume) these reactors once the relationship between the reaction rate and conversion is known that is given, i.e., –r_A = f(X)
Show how to compare CSTR and PFR sizes
Show how to decide the best arrangements for reactors in series, a most important principle

In addition to being able to determine CSTR and PFR sizes given the rate of reaction as a function of conversion, you will be able to calculate the overall conversion and reactor volumes for reactors arranged in series.

2.1 Definition of Conversion

Conversion helps us measure how far a reaction has progressed. In defining conversion, we choose one of the reactants as the basis of calculation and then relate the other species involved in the reaction to this basis. In virtually all instances, we must choose the limiting reactant as the basis of calculation. For single reactions, we can use conversion to develop the stoichiometric relationships and design equations by considering the general reaction

\begin{matrix} a A + b B \to c C + d D & (2 - 1) \end{matrix}

The uppercase letters represent chemical species, and the lowercase letters represent stoichiometric coefficients. We shall choose species A as our limiting reactant and, thus, our basis of calculation. The limiting reactant is the reactant that will be completely consumed first after the reactants have been mixed. We next divide the reaction expression through by the stoichiometric coefficient of the limiting reactant, that is, of species A, in order to arrange the reaction stoichiometry in the form

\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2 - 2) \end{matrix}

“A” is our basis of calculation

to put every quantity on a “per mole of A” basis, our limiting reactant.

Now we ask such questions as “How can we quantify how far a reaction (e.g., Equation (2-2)) proceeds to the right?” or “How many moles of C are formed for every mole of A consumed?” A convenient way to answer these questions is to define a parameter called conversion. The conversion X_A is the number of moles of A that have reacted per mole of A fed to the system:

$X_{A} = \frac{Moles o f A r e a c t e d}{M o 1 e s o f A f e d}$

Definition of X

Because we are defining conversion with respect to our basis of calculation (A in Equation (2-2)), we eliminate the subscript A for the sake of brevity and let X ≡ X_A. For irreversible reactions, the maximum conversion is 1.0, that is, complete conversion. For reversible reactions, the maximum conversion is the equilibrium conversion X_e (i.e., X_max = X_e). We will take a closer look at equilibrium conversion in Section 4.3.

2.2 Batch Reactor Design Equations

In most batch reactors (BRs), the longer a reactant stays in the reactor, the more the reactant is converted to product until either equilibrium is reached or the reactant is exhausted. Consequently, in batch systems, the conversion X is a function of the time the reactants spend in the reactor. If N_A0 is the number of moles of A initially present in the reactor (i.e., t = 0), then the total number of moles of A that have reacted (i.e., have been consumed) after a time t is [N_A0X].

[Moles of A reacted (consumed)] [Moles of A fed] · $[\frac{M o l e s o f A r e a c t e d}{M o l e s o f A f e d}]$

\begin{matrix} \begin{matrix} [\begin{matrix} Moles of A \\ reacted \\ (\begin{matrix} consumed \end{matrix}) \end{matrix}] & = & [N_{A0}] & \cdot & [X] \end{matrix} & (2 - 3) \end{matrix}

Now, the number of moles of A that remain in the reactor after a time t, N_A, can be expressed in terms of N_A0 and X:

$\begin{matrix} [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} Moles of A \\ in reactor \end{matrix} \end{matrix} \\ at time t \end{matrix} \end{matrix}] & = & [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} Moles of A \\ initially fed \end{matrix} \end{matrix} \\ to reactor at \end{matrix} \end{matrix} \\ t = 0 \end{matrix} \end{matrix}] & - & [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} Moles of A that \\ have been \end{matrix} \end{matrix} \\ consumed by \end{matrix} \end{matrix} \\ chemical reaction \end{matrix} \end{matrix}] \\ [\begin{matrix} N_{A} \end{matrix}] & = & [\begin{matrix} N_{A0} \end{matrix}] & - & [\begin{matrix} N_{A0} X \end{matrix}] \end{matrix}$

The number of moles of A in the reactor after a conversion X has been achieved is

\begin{matrix} N_{A} = N_{A0} - N_{A0} X = N_{A0} (1 - X) & (2 - 4) \end{matrix}

Moles of A in the reactor at a time t

When no spatial variations in reaction rate exist, the mole balance on species A for a batch system is given by the following equation (cf. Equation (1-5)):

\begin{matrix} \frac{d N_{A}}{d t} = r_{A} V & (2 - 5) \end{matrix}

This equation is valid whether or not the reactor volume is constant. In the general reaction, Equation (2-2), reactant A is disappearing; therefore, we multiply both sides of Equation (2-5) by –1 to obtain the mole balance for the batch reactor in the form

$- \frac{d N_{A}}{d t} = (- r_{A}) V$

The rate of disappearance of A, –r_A, in this reaction might be given by a rate law similar to Equation (1-2), such as –r_A = kC_AC_B.

For batch reactors, we are interested in determining how long to leave the reactants in the reactor to achieve a certain conversion X. To determine this length of time, we write the mole balance, Equation (2-5), in terms of conversion by differentiating Equation (2-4) with respect to time, remembering that N_A0 is the number of moles of A initially present in the reactor and is therefore a constant with respect to time.

$\frac{d N_{A}}{d t} = 0 - N_{A 0} \frac{d X}{d t}$

Combining the above with Equation (2-5) yields

$- N_{A 0} \frac{d X}{d t} = r_{A} V$

For a batch reactor, the design equation in differential form is

\begin{matrix} N_{A 0} \frac{d X}{d t} = {- r}_{A} V & (\begin{matrix} 2 - 6 \end{matrix}) \end{matrix}

Batch reactor (BR) design equation

We call Equation (2-6) the differential form of the BR mole balance and it is often referred to as the design equation for a batch reactor because we have written the mole balance in terms of conversion. The differential forms of the batch reactor mole balances, Equations (2-5) and (2-6), are often used in the interpretation of reaction rate data (Chapter 7) and for reactors with heat effects (Chapters 11–13), respectively. Batch reactors are frequently used in industry for both gas-phase and liquid-phase reactions. The laboratory bomb calorimeter reactor is widely used for obtaining reaction rate data. Liquid-phase reactions are frequently carried out in batch reactors when small-scale production is desired or operating difficulties rule out the use of continuous-flow systems.

Uses of a BR

To determine the time to achieve a specified conversion X, we first separate the variables in Equation (2-6) as follows:

$d t = N_{A 0} \frac{d X}{- {r_{A}}_{} V}$

Batch time t to achieve a conversion X

Next, this equation is integrated with the limits that the reaction begins at time equals zero where there is no conversion initially (i.e., when t = 0, X = 0) and ends at time t when a conversion X is achieved (i.e., when t = t, then X = X). Carrying out the integration, we obtain the time t necessary to achieve a conversion X in a batch reactor

\begin{matrix} t = N_{A 0} \int_{0}^{X} \frac{d X}{- r_{A} V} & (2 - 7) \end{matrix}

An illustration depicting batch reactor with impeller, which is connected to the shaft is displayed. A liquid is present within the batch reactor.

The longer the reactants are left in the reactor, the greater the conversion will be. Equation (2-6) is the differential form of the design equation, and Equation (2-7) is the integral form of the design equation for a batch reactor.

2.3 Design Equations for Flow Reactors

For a batch reactor, we saw that conversion increases with time spent in the reactor. For continuous-flow systems, this time usually increases with increasing reactor volume; for example, the bigger/longer the reactor, the more time it will take the reactants to flow completely through the reactor and thus, the more time to react. Consequently, the conversion X is a function of reactor volume V. If F_A0 is the molar flow rate of species A fed to a system operated at steady state, the molar rate at which species A is reacting within the entire system will be F_A0X.

$[F_{A 0}] \cdot [X] = \frac{M o l e s o f A f e d}{t i m e} \cdot \frac{M o l e s o f A r e a c t e d}{M o l e s o f A f e d}$

$[F_{A 0}] \cdot [X] = \frac{M o l e s o f A f e d}{t i m e}$

The molar flow rate of A leaving the system F_A equals the molar feed rate of A into the system F_A0 minus the rate of reaction of A within the system (F_A0X). The preceding sentence can be expressed mathematically as

$\begin{matrix} [\begin{matrix} \begin{matrix} Molar flow rate \\ at which A leaves \\ the system \end{matrix} \end{matrix}] & = & [\begin{matrix} \begin{matrix} Molar flow rate \\ at which A is \\ fed to the system \end{matrix} \end{matrix}] & - & [\begin{matrix} \begin{matrix} \begin{matrix} Molar rate at \\ which A is \\ consum ed within \end{matrix} \end{matrix} \\ the system \end{matrix}] \\ [F_{A}] & = & [F_{A0}] & - & [F_{A0} X] \end{matrix}$

Rearranging gives

\begin{matrix} F_{A} = F_{A0} (1 - X) & (2 - 8) \end{matrix}

The entering molar flow rate of species A, F_A0 (mol/s), is just the product of the entering concentration, C_A0 (mol/dm³), and the entering volumetric flow rate, υ₀(dm³/s).

\begin{matrix} \begin{matrix} F_{A0} = C_{A0} υ_{0} & (2-9) \end{matrix} \end{matrix}

For liquid systems, the volumetric flow rate, υ, is constant and equal to υ₀, and C_A0 is commonly given in terms of molarity, for example, C_A0 = 2 mol/dm³.

Liquid phase

For gas systems, C_A0 can be calculated from the entering mole fraction, y_A0, the temperature, T₀, and pressure, P₀, using the ideal gas law or some other gas law. For an ideal gas (see Appendix B):

\begin{matrix} C_{A 0} = \frac{P_{A 0}}{R T_{0}} = \frac{y_{A 0} p_{0}}{R T_{0}} & (2 - 10) \end{matrix}

Gas phase

Now that we have a relationship [Equation (2-8)] between the molar flow rate and conversion, it is possible to express the design equations (i.e., mole balances) in terms of conversion for the flow reactors examined in Chapter 1.

2.3.1 CSTR (Also Known as a Backmix Reactor or a Vat)

Recall that the CSTR is modeled as being well mixed such that there are no spatial variations in the reactor. For the general reaction

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2 - 2) \end{matrix}$

the CSTR mole balance Equation (1-7) can be arranged to

\begin{matrix} V = \frac{F_{A 0} - F_{A}}{- r_{A}} & (2 - 11) \end{matrix}

We now substitute for F_A in terms of F_A0 and X

F_{A} = F_{A 0} - F_{A 0} X (2 - 12)

and then substitute Equation (2-12) into (2-11)

$V = \frac{F_{A 0} - (F_{A 0} - F_{A 0} X)}{- r_{A}}$

Simplifying, we see that the CSTR volume necessary to achieve a specified conversion X is

\begin{matrix} V = \frac{F_{A 0} X}{(- r_{A})_{e x i t}} & (2 - 13) \end{matrix}

An illustration depicts the CSTR reactor. — The input and output rates of CSTR reactor are depicted when perfect mixing takes place. The molar flow rates coming into the system (F subscript A0) and leaving it (F subscript A) are marked in the illustration. The conversion X is marked near the output.

Because the reactor is perfectly mixed, the exit composition from the reactor is identical to the composition inside the reactor, and, therefore, the rate of reaction, –r_A, is evaluated at the exit conditions.

Evaluate –r_A at the CSTR exit conditions!!

2.3.2 Tubular Flow Reactor (PFR)

We model the tubular reactor as having the fluid flowing in plug flow—that is, no radial gradients in concentration, temperature, or reaction rate.¹ As the reactants enter and flow axially down the reactor, they are consumed and the conversion increases along the length of the reactor. To develop the PFR design equation, we first multiply both sides of the tubular reactor design equation given in Chapter 1, Equation (1-12), by –1. We then express the mole balance equation for species A in the reaction as

¹ This constraint will be removed when we extend our analysis to nonideal (industrial) reactors in Chapters 16–18.

\frac{- d F_{A}}{d V} = - r_{A} (2 - 14)

For a flow system, F_A has previously been given in terms of the entering molar flow rate F_A0 and the conversion X

F_{A} = F_{A 0} - F_{A 0} X (2 - 12)

Differentiating

dF_A = –F_A0 dX

and substituting into Equation (2-14) gives the differential form of the design equation for a plug-flow reactor (PFR)

\begin{matrix} F_{A 0} \frac{d X}{d V} = - r_{A} & (\begin{matrix} 2 - 15 \end{matrix}) \end{matrix}

We now separate the variables and integrate with the limits V = 0 when X = 0 to obtain the plug-flow reactor volume necessary to achieve a specified conversion X

\begin{matrix} V = F_{A0} \int_{0}^{X} \frac{d X}{- r_{A}} & (2 - 16) \end{matrix}

A diagram representing a plug flow reactor which resembles a tube through which the fluid flows is shown.

To carry out the integrations in the batch and plug-flow reactor design equations (2-7) and (2-16), as well as to evaluate the CSTR design equation (2-13), we need to know how the reaction rate –r_A varies with the concentration (hence conversion) of the reacting species. This relationship between reaction rate and concentration is developed in Chapter 3.

2.3.3 Packed-Bed Reactor (PBR)

Packed-bed reactors are tubular reactors filled with catalyst particles. In PBRs, it is the weight of catalyst W that is important, rather than the reactor volume. The derivation of the differential and integral forms of the design equations for packed-bed reactors are analogous to those for a PFR (cf. Equations (2-15) and (2-16)). That is, substituting Equation (2-12) for F_A in Equation (1-15) gives

\begin{matrix} F_{A 0} \frac{d X}{d W} = - r_{A}^{'} & (2 - 17) \end{matrix}

PBR design equation

The differential form of the design equation (i.e., Equation (2-17)) must be used when analyzing reactors that have a pressure drop along the length of the reactor. We discuss pressure drop in packed-bed reactors in Chapter 5.^†

In the absence of pressure drop, that is, ΔP = 0, we can integrate Equation (2-17) with limits X = 0 at W = 0, and when W = W then X = X to obtain

\begin{matrix} W = F_{A0} \int_{0}^{X} \frac{d X}{- r_{A}^{'}} & (2 - 18) \end{matrix}

A diagram of a packed bed reactor is shown and it resembles a tube filled with particles (catalyst particles) through which the fluid flows. The input molar flow rate is F subscript A0 and the output is F subscript A.

Equation (2-18) can be used to determine the catalyst weight W (i.e., mass) necessary to achieve a conversion X when the total pressure remains constant.

2.4 Sizing Continuous-Flow Reactors

In this section, we are going to show how we can size CSTRs and PFRs (i.e., determine their reactor volumes) using the appropriate mole balance in terms of conversion and knowledge of the rate of reaction, –r_A, as a function of conversion, X (i.e., –r_A = f(X)). The rate of disappearance of A, –r_A, is almost always a function of the concentrations of the various species present (see Chapter 3). When only one reaction is occurring, each of the concentrations can be expressed as a function of the conversion X (see Chapter 4); consequently, –r_A can be expressed as a function of X.

As an example, we shall choose a particularly simple functional dependence on concentration, that is, first-order.

–r_A = kC_A = kC_A0 (1 – X)

Here, k is the specific reaction rate and is a function of temperature only, and C_A0 is the entering concentration of A. We note in Equations (2-13) and (2-16) that the reactor volume is a function of the reciprocal of –r_A. For this first-order dependence, a plot of the reciprocal rate of reaction (1/–r_A) as a function of conversion yields a curve similar to the one shown in Figure 2-1, where

$\frac{1}{- r_{A}} = \frac{1}{k C_{A 0}} (\frac{1}{1 - X})$

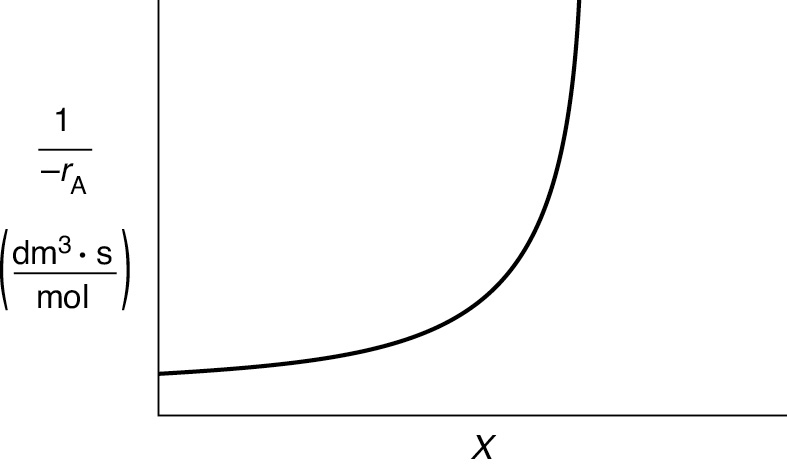
A graph plotting the inverse of reaction rate, 1 over negative r subscript A (decimeter cubed times second over moles) versus x is shown. The curve is concaved upwards and exponentially increasing. — **Figure 2-1** Typical curve of the reciprocal rate as a function of conversion.

^† Be sure to watch the YouTube video (https://www.youtube.com/watch?v=S9mUAXmNqxs).

We can use Figure 2-1 to size CSTRs and PFRs for different entering flow rates. By sizing we mean either determine the reactor volume for a specified conversion or determine the conversion for a specified reactor volume. Before sizing flow reactors, let’s consider some insights. If a reaction is carried out isothermally, the rate is usually greatest at the start of the reaction when the concentration of reactant is greatest (i.e., when there is negligible conversion [X ≡ 0]). Hence, the reciprocal rate (1/–r_A) will be small. Near the end of the reaction, when the reactant has been mostly used up and thus the concentration of A is small (i.e., the conversion is large), the reaction rate will be small. Consequently, the reciprocal rate (1/–r_A) is large.

For all irreversible reactions of greater than zero order (see Chapter 3 for zero-order reactions), as we approach complete conversion where all the limiting reactant is used up, that is, X = 1, the reciprocal rate approaches infinity as does the reactor volume, that is,

$As X \to 1, {- r}_{A} \to 0, thus, \frac{1}{{- r}_{A}} \to \infty and therefore V \to \infty$

A → B + C

Consequently, we see that an infinite reactor volume is necessary to reach complete conversion, X = 1.0.

“To infinity and beyond”—Buzz Lightyear

For reversible reactions (e.g., A ⇄ B), the maximum conversion is the equilibrium conversion X_e. At equilibrium, the reaction rate is zero (r_A ≡ 0). Therefore,

$\begin{matrix} as & X \to X_{e,} - r_{A} \to 0, thus, \frac{1}{{- r}_{A}} \to \infty and therefore V \to \infty \end{matrix}$

A ⇄ B + C

and we see that an infinite reactor volume would also be necessary to obtain the exact equilibrium conversion, X = X_e. We will discuss X_e further in Chapter 4.

Examples of Reactor Design and Staging Given –r_A = f(X)

To illustrate the design of continuous-flow reactors (i.e., CSTRs and PFRs), we consider the irreversible isothermal gas-phase isomerization

A → B

Researchers at the Central Lab performed experiments to determine the rate of chemical reaction as a function of the conversion of reactant A and the results are shown in Table 2-1. The temperature was constant at 500 K (440°F), the total pressure was constant at 830 kPa (8.2 atm), and the initial charge to the reactor was pure A. The entering molar flow of reactant A is F_A0 = 0.4 mol/s.

^†Proprietary coded data courtesy of Jofostan Central Research Laboratory, Çölow, Jofostan, and published in Jofostan Journal of Chemical Engineering Research, Volume 21, page 73 (2023).

If we know –r_A as a function of X, we can size any isothermal reaction system.

Recalling the CSTR and PFR design equations, (2-13) and (2-16), we see that the reactor volume varies directly with the molar flow rate F_A0 and with the reciprocal of –r_A, $(\frac{1}{- r_{A}})$ , for example, $V = (\frac{F_{A0}}{- r_{A}}) X$ . Consequently, to size reactors, we first convert the raw data in Table 2-1, which gives –r_A as a function of X first to $(\frac{1}{- r_{A}})$ as a function of X. Next, we multiply by the entering molar flow rate, F_A0, to obtain $(\frac{F_{A0}}{- r_{A}})$ as a function of X as shown in Table 2-2 of the processed data for F_A0 = 0.4 mol/s.

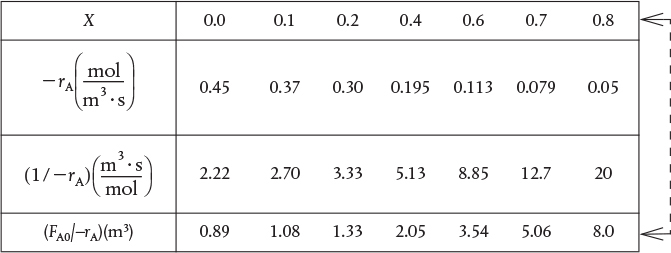
We shall use the data in this table for the next five Example Problems.

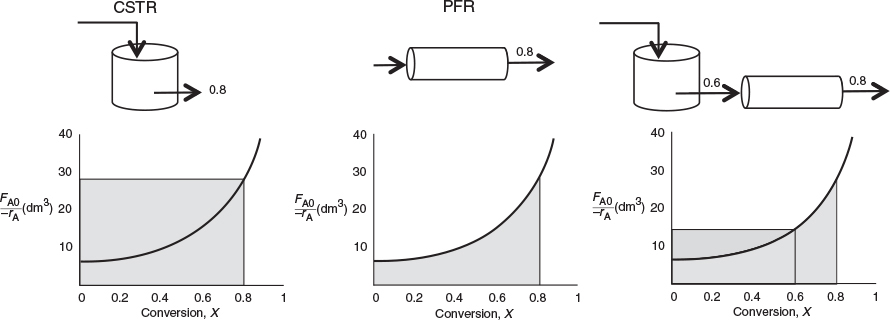
To size reactors for different entering molar flow rates, F_A0, we would use rows 1 and 4, as shown by the arrows in Table 2-2 to construct the following figure:

A graph plots the inverse of reaction rate against conversion, X. — **Figure 2-2(a)** Levenspiel plot of processed data 1 in Table 2-2.

A levenspiel plot of the inverse of reaction rate - 1 over negative r subscript A with unit, meter cubed times seconds over moles, is plotted. The horizontal axis represents X in the range 0.0 to 1.0 in increments of 0.2. The vertical axis represents reciprocal rate. The curve is concaved upwards and increasing. The curve passes through coordinates such as (0.38,5) and (0.8,20).

However, for a given F_A0, rather than using Figure 2-2(a) to size reactors, it is often more advantageous to plot $(\frac{F_{A 0}}{{- r}_{A}})$ as a function of X, which is called a Levenspiel plot.^† We are now going to carry out a number of examples where we have specified the flow rate F_A0 to be 0.4 mol A/s.

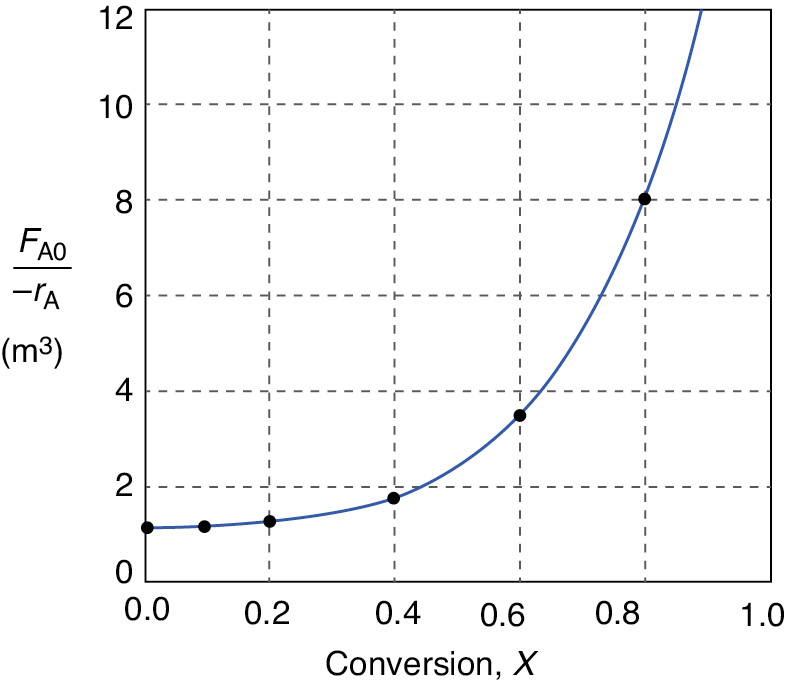
Plotting $(\frac{F_{A 0}}{{- r}_{A}})$ as a function of X using the data in Table 2-2 we obtain the plot shown in Figure 2-2(b).

Levenspiel plot

We are now going to use the Levenspiel plot of the processed data (Figure 2-2(b)) to size a CSTR and a PFR.

^†After Professor Octave Levenspiel (1/1/1926–3/5/2017), Oregon State University, Corvallis, OR.

Example 2–1 Sizing a CSTR

The reaction described by the data in Table 2-2

A → B

is to be carried out in a CSTR. Species A enters the reactor at a molar flow rate of $F_{A 0} = 0.4 \frac{m o 1}{s}$ , which is the flow rate used to construct the Levenspiel plot in Figure 2-2(b).

Using the data in either Table 2-2 or Figure 2-2(b), calculate the volume necessary to achieve 80% conversion in a CSTR.
Shade the area in Figure 2-2(b) that would give the CSTR volume necessary to achieve 80% conversion.

Solutions

Equation (2-13) gives the volume of a CSTR as a function of F_A0, X, and –r_A

$V = \frac{F_{A 0} X}{{(- r_{A})}_{e x i t}} (2 - 13)$

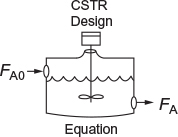
In a CSTR, the composition, temperature, and conversion of the effluent stream are identical to that of the fluid within the reactor, because perfect mixing is assumed. Therefore, we need to find the value of –r_A (or reciprocal thereof) at X = 0.8. From either Table 2-2 or Figure 2-2(a), we see that when X = 0.8, then

${(\frac{1}{- r_{A}})}_{X = 0.8} = 20 \frac{m^{3} \cdot s}{mol}$

Substitution into Equation (2-13) for an entering molar flow rate, F_A0, of 0.4 mol A/s and X = 0.8 gives

$V = 0.4 \frac{mol}{s} (\frac{20 m^{3} \cdot s}{mol}) (0.8) = 6.4 m^{3} (E 2 - 1.1)$

V = 6.4 m³ = 6400 = dm³ = 6400 liters Answer
Shade the area in Figure 2-2(b) that yields the CSTR volume to achieve 80% conversion. Rearranging Equation (2-13) gives

$V = [\frac{F_{A 0}}{{- r}_{A}}] X (2 - 13)$

In Figure E2-1.1, the volume is equal to the area of a rectangle with a height (F_A0/–r_A = 8 m³) and a base (X = 0.8). This rectangle is shaded in the figure.

$V = {[\frac{F_{A 0}}{{- r}_{A}}]}_{X = 0.8} (0.8) (E 2 - 1.2)$

V = Levenspiel rectangle area = height × width

V = [8 m³][0.8] = 6.4 m³ = 6400 dm³ = 6400 L Answer

Representative Industrial CSTR Dimensions

The CSTR volume necessary to achieve 80% conversion is 6.4 m³ when operated at 500 K, 830 kPa (8.2 atm), and with an entering molar flow rate of A of 0.4 mol/s. This volume corresponds to a reactor about 1.5 m in diameter and 3.6 m high. It’s a large CSTR, but this is a gas-phase reaction, and CSTRs are normally not used for gas-phase reactions. CSTRs are used primarily for liquid-phase reactions. Oops!

A Levenspiel plot for CSTR is shown. — **Figure E2-1.1** Levenspiel CSTR plot.

A graph plots rate of reaction as a function of conversion with the molar flow of the species A and conversion, X. The horizontal axis represents the conversion, X in the range 0.0 to 1.0 in increments of 0.2. The vertical axis represents input molar flow rate over negative r subscript A and is in the range of 0 to 12 in increments of 2. The curve increases slightly in the beginning and after a point increases steeply. The curve passes through (0.4,1.9) and (0.8,8). The volume of CSTR is mentioned as 6.4 cubed meters. A rectangular region is shaded and with borders as the axes, a dashed line intersecting at 8 in the vertical axis and a line intersecting 0.8 at horizontal axis. Note: All values taken are approximate.

Plots of (F_A0/=r_A) versus X are often referred to as Levenspiel plots (after Prof. Octave Levenspiel).

Analysis: Given the conversion, the rate of reaction as a function of conversion along with the molar flow of the species A, we saw how to calculate the volume of a CSTR. From the data and information given, we calculated the volume to be 6.4 m³ for 80% conversion. We showed how to carry out this calculation using the design equation (2-13) and also using a Levenspiel plot.

Example 2–2 Sizing a PFR

The reaction described by the data in Tables 2-1 and 2-2 is to be carried out in a PFR. The entering molar flow rate of A is again, F_A0 = 0.4 mol/s.

First, use one of the integration formulas given in Appendix A.4 to determine the PFR reactor volume necessary to achieve 80% conversion.
Next, shade the area in Figure 2-2(b) that would give the PFR volume necessary to achieve 80% conversion.
Finally, make a qualitative sketch of the conversion, X, and the rate of reaction, –r_A, down the length (volume) of the reactor.

Solution

We start by repeating rows 1 and 4 of Table 2-2 to produce the results shown in Table 2-3

(a) Numerically evaluate PFR volume. For the PFR, the differential form of the mole balance is

$F_{A 0} \frac{d X}{d V} = {- r}_{A} (2 - 15)$

Rearranging and integrating gives

$V = F_{A 0} \int_{0}^{0.8} \frac{d X}{{- r}_{A}} = \int_{0}^{0.8} \frac{F_{A 0}}{{- r}_{A}} d X (2 - 16)$

We shall use the five-point quadrature formula (Equation (A-23)) given in Appendix A.4 to numerically evaluate Equation (2-16). The five-point formula with a final conversion of 0.8 gives four equal segments between X = 0 and X = 0.8, with a segment length of $Δ X = \frac{0.8}{4} = 0.2$ . The function inside the integral is evaluated at X = 0, X = 0.2, X = 0.4, X = 0.6, and X = 0.8.

$V = \frac{Δ X}{3} [\frac{F_{A 0}}{{- r}_{A} (X = 0)} + \frac{{4 F}_{A 0}}{{- r}_{A} (X = 0.2)} + \frac{{2 F}_{A 0}}{{- r}_{A} (X = 0.4)} + \frac{{4 F}_{A 0}}{{- r}_{A} (X = 0.6)} + \frac{F_{A 0}}{{- r}_{A} (X = 0.8)}]$ (E2-2.1)

Using values of [F_A0/(–r_A)] corresponding to the different conversions in Table 2-3 yields

$V = (\frac{0.2}{3}) [0.89 + 4 (1.33) + 2 (2.05) + 4 (3.54 + 8.0] m^{3} = (\frac{0.2}{3}) (32.47 m^{3})$

$\begin{matrix} V = 2.165 m^{3} = 2615 {dm}^{3} \end{matrix}$

An image shows PFRs connected in parallel. The diameter and the length of the reactors are marked as 0.1 meters and 2.8 meters. The number of reactors connected is mentioned as 100. The fluid enters at 0.4 moles per second and the conversion X is 0.8.

The PFR reactor volume necessary to achieve 80% conversion is 2165 dm³. This volume could be achieved by using a bank of 100 PFRs that are each 0.1 m in diameter with a length of 2.8 m (e.g., see margin figure or Figures 1-8(a) and (b)).

Note: As we proceed through later chapters and have analytical formulas for –r_A, we will use integration tables or software packages (e.g., Polymath, rather than quadrate formulas, such as Equation (E2-2.1)).
The PFR volume, that is, the integral in Equation (2-16), can also be evaluated from the area under the curve of a plot of (F_A0 /–r_A) versus X.

$V = \int_{0}^{0.8} \frac{F_{A 0}}{- r_{A}} d X$ = Area under the curve between X = 0 and X = 0.8
(see shaded area in Figure E2-2.1)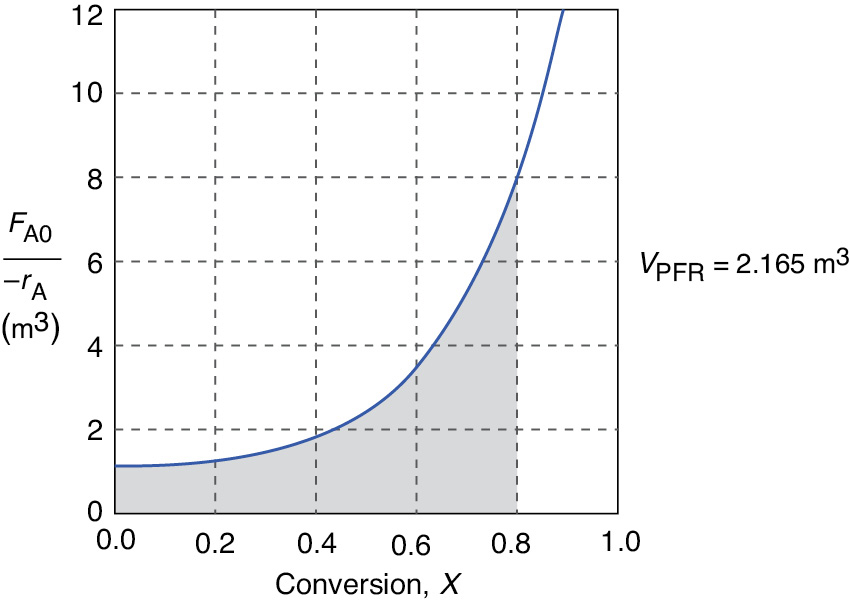

Figure E2-2.1 Levenspiel PFR plot.

A graph plots the values of Molar flow rate inward over negative r subscript A against values of conversion. The horizontal axis represents the conversion, X and ranges from 0.0 to 1.0 in increments of 0.2. The vertical axis ranges from 0 to 12 in increments of 2. The curve is a concave upward and increasing curve which increases slightly in the beginning and after a point increases steeply. The volume of PFR is mentioned as 2.165 cubed meters. The region from 0.0 to 0.8 below the curve is shaded. The curve passes through (0.8, 8). Note: All values taken are approximate.

PFR

The area under the curve will give the tubular reactor volume necessary to achieve the specified conversion of A. For 80% conversion, the shaded area is roughly equal to 2165 dm³ (2.165 m³).
Sketch the profiles of =r_A and X down the length of the reactor.

We know that as we proceed down the reactor, the conversion increases as more and more reactant is converted to product. Consequently, as the reactant is consumed, the concentration of reactant decreases, as does the rate of disappearance of A for isothermal reactions.
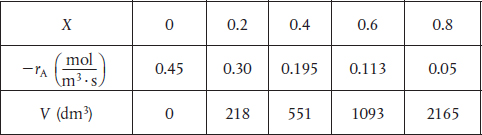
1. For X = 0.2, we calculate the corresponding reactor volume using Simpson’s rule (given in Appendix A.4 as Equation (A-21)) with increment =X = 0.1 and the data in rows 1 and 4 in Table 2-2.
  
  $\begin{matrix} V & = F_{A 0} \int_{0}^{0.2} \frac{d X}{- r_{A}} = \frac{Δ X}{3} [\frac{F_{A 0}}{- r_{A} (X = 0)} + \frac{4 F_{A 0}}{- r_{A} (X = 0.1)} + \frac{F_{A 0}}{- r_{A} (X = 0.2)}] & (E 2 - 2.2) \\ = (\frac{0.1}{3} [0.89 + 4 (1.08) + 1.33]) m^{3} = \frac{0.1}{3} (6.54 m^{3}) = 0.218 m^{3} = 218 m^{3} \\ = 218 m^{3} \end{matrix}$
  
  This volume (218 m³) is the volume at which X = 0.2. From Table 2-2, we see the corresponding rate of reaction at X = 0.2 is ${- r}_{A} = 0.3 \frac{m o l}{{d m}^{3} \cdot s} \cdot$ .
  
  Therefore at X = 0.2, then – r_A = 0.3 mol/m³ · s and V = 218 dm³.
2. For X = 0.4, we can again use Table 2-3 and Simpson’s rule with ΔX = 0.2 to find the reactor volume necessary for a conversion of 40%.
  
  $\begin{matrix} V & = \frac{Δ X}{3} [\frac{F_{A 0}}{- r_{A} (X = 0)} + \frac{4 F_{A 0}}{- r_{A} (X = 0.2)} + \frac{F_{A 0}}{- r_{A} (X = 0.4)}] \\ = (\frac{0.2}{3} [0.89 + 4 (1.33)] + 2.05) m^{3} = 0.551 m^{3} \\ = 551 d m^{3} \end{matrix}$
  
  From Table 2-2 we see that at X = 0.4, –r_A = 0.195 mol m³ · s and V = 551 dm³.
  
  We can continue in this manner to arrive at Table E2-2.1.
  
  TABLE E2-2.1 CONVERSION AND REACTION RATE PROFILES
  
  The data in Table E2-2.1 are plotted in Figures E2-2.2(a) and (b).
  
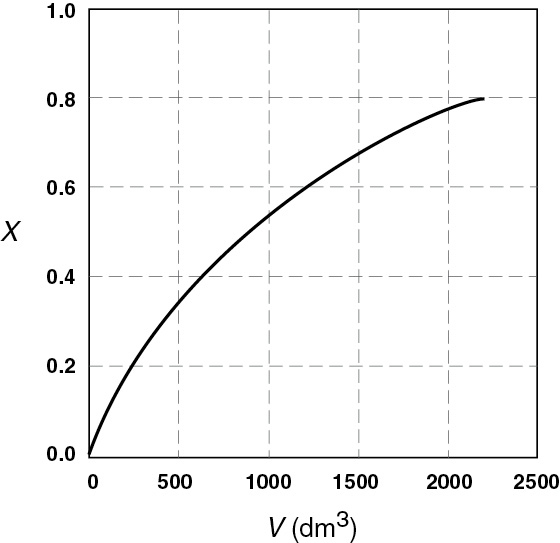
  Figure E2-2.2(a) Conversion profile.
  
  A graph plots conversion against the volume. The horizontal axis represents the volume, ranging from 0 to 2500 in increments of 2500. The vertical axis represents conversion X, ranging from 0.0 to 1.0 in increments of 0.2. The curve is concave downward and increasing. The curve starts at the origin and passes through (250,0.2) and (2000,0.76). Note: All values taken are approximate.
  
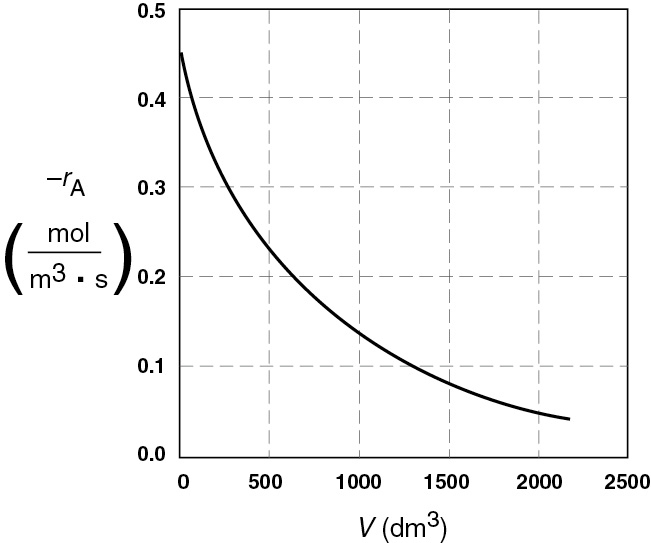
  Figure E2-2.2(b) Reaction rate profile.
  
  A graph plots the values of rate of reaction against the volume. The horizontal axis represents the volume in the range 0 to 2500 in increments of 500. The vertical axis represents rate of reaction in the range 0.0 to 1.0 in increments of 0.2. The curve is concave upward and decreasing. The curve passes through coordinates such as (250,0.3) and (1300,0.1). Note: All values taken are approximate.
  
  For isothermal reactions, the conversion increases and the rate decreases as we move down the PFR.

Analysis: One observes that for most all isothermal reactions the reaction rate, –r_A, decreases as we move down the reactor while the conversion increases. These plots are typical for reactors operated isothermally.

Example 2–3 Comparing CSTR and PFR Sizes

Compare the volumes of a CSTR and a PFR required for the same conversion using the data in Figure 2-2(b). Which reactor would require the smaller volume to achieve a conversion of 80%: a CSTR or a PFR? The entering molar flow rate and the feed conditions are the same in both cases.

Solution

We will again use the data in Table 2-3.

TABLE 2-3 PROCESSED DATA 2

X	0.0	0.1	0.2	0.4	0.6	0.7	0.8
(F_A0/–r_A)(m³)	0.89	1.08	1.33	2.05	3.54	5.06	8.0

The CSTR volume was 6.4 m³ and the PFR volume was 2.165 m³. When we combine Figures E2-1.1 and E2-2.1 on the same graph, Figure 2-3.1(a), we see that the crosshatched area above the curve is the difference in the CSTR and PFR reactor volumes. Figure E2-3.1(b) shows the rate of reaction, –r_A, as a function of conversion. We note that at 80% conversion the rate is approximately one-tenth the initial rate.

For isothermal reactions greater than zero order (see Chapter 3), the CSTR volume will always be greater than the PFR volume for the same conversion and reaction conditions (temperature, flow rate, etc.).

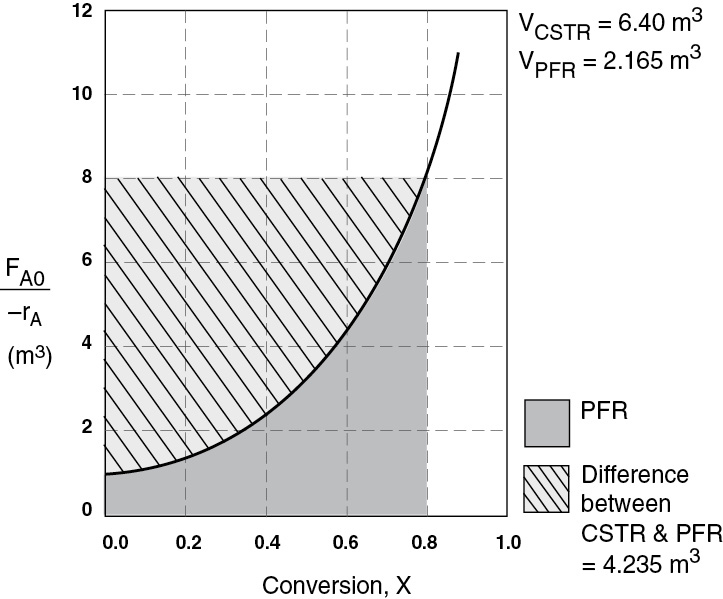
A graph compares the reactor sizes for PFR and CSTR. — **Figure E2-3.1(a)** Comparison of CSTR and PFR reactor sizes for X = 0.8.

A graph plots the values of volume for both CSTR and PFR. The horizontal axis represents the conversion (X), ranging from 0.0 to 1.0 in increments of 500. The vertical axis represents volume (F subscript A0 over negative r subscript A), ranging from 0 to 12 in increments of 2. The curve is concave upwards and increasing. The region within 0.8 and 8 below and above the curve is shaded differently. The volume of CSTR and PFR are mentioned as 6.40 and 2.166 cubic meters.

A graph compares the reaction rate and conversion X. — **Figure E2-3.1(b)** –r_A as a function of X obtained from Table 2-2.1.

A graph plots rate of reaction against the conversion X. The horizontal axis represents the conversion X, ranging from 0.0 to 1.0 in increments of 0.2. The vertical axis represents rate of reaction ranging from 0.0 to 0.5 in increments of 0.1. The curve is concave upward and decreasing. The lowest point is marked as (0.8, 0.05).

Analysis: We see that the reason the isothermal CSTR volume is usually greater than the PFR volume is that the CSTR is always operating at the lowest reaction rate (e.g., –r_A = 0.05 mol m³ · s in Figure E2-3.1(b)). The PFR, on the other hand, starts at a high rate at the entrance and gradually decreases to the exit rate, thereby requiring less volume because the volume is inversely proportional to the rate. However, there are exceptions such as autocatalytic reactions, product-inhibited reactions, and nonisothermal exothermic reactions; these trends will not always be the case, as we will see in Chapters 9 and 11.

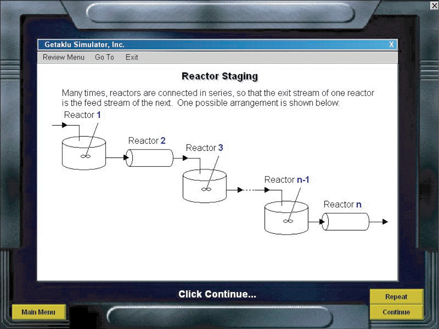
2.5 Reactors in Series

Many times, reactors are connected in series so that the exit stream of one reactor is the feed stream for another reactor. When this arrangement is used, it is often possible to speed calculations by defining conversion in terms of location at a point downstream rather than with respect to any single reactor. That is, the conversion X is the total number of moles of A that have reacted up to that point per mole of A fed to the first reactor.

For reactors in series

$\begin{matrix} X_{i} = \frac{T o t a 1 m o 1 e s o f A r e a c t e d u p t o p o i n t i}{M o 1 e s o f A f e d t o t h e f i r s t r e a c t o r} \end{matrix}$

Only valid for NO side streams!!

However, this definition can only be used when the feed stream only enters the first reactor in the series and there are no side streams either fed or withdrawn. The molar flow rate of A at point i is equal to the moles of A fed to the first reactor, minus all the moles of A reacted up to point i.

Caution.

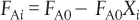
F_A_i = F_A0 – F_A0X_i

For the reactors shown in Figure 2-3, X₁ at point i = 1 is the conversion achieved in the PFR, X₂ at point i = 2 is the total conversion achieved at this point in the PFR and the CSTR, and X₃ is the total conversion achieved by all three reactors.

A figure depicts series connection of PFRs and CSTR. — **Figure 2-3** Reactors in series.

An image of 3 reactors PFR and CSTR in the order PFR-CSTR-PFR is shown. The species A enters the PFR of volume upper V subscript 1 with flow rate F subscript A0 and output flow rate of F subscript A1. This enters CSTR of volume upper V subscript 2 and comes out with flow rate upper F subscript upper A2 and enters PFR of volume upper V subscript 3 and comes out with flow rate upper F subscript upper A3. The output of each reactors are shown as i equals 1, i equals 2, and i equals 3. The conversion of the reactors are mentioned as upper X subscript 1, X subscript 2, and upper X subscript 3.

To demonstrate these ideas, let us consider three different schemes of reactors in series: two CSTRs, two PFRs, and then a combination of PFRs and CSTRs in series. To size these reactors, we shall use the impeccable data in Table 2-1 from Jofostan Central Research laboratories that gives the reaction rate at different conversions.

2.5.1 CSTRs in Series

The first scheme to be considered is the two CSTRs in series shown in Figure 2-4.

A figure depicts the series connection of 2 CSTRs. — **Figure 2-4** Two CSTRs in series.

2 CSTRs connected to each other are shown. The species A enters the CSTR with flow rate F subscript A0. The conversion in between is X1 equals 0.4 and the output flow rate of the first 1 is the input flow rate of the second. The second CSTR has the output flow rate as F subscript A2 and the conversion is X2 equals 0.8. The reaction rate of the first CSTR is negative r subscript A1 and the reaction rate of the second CSTR is negative r subscript A2.

For the first reactor, the rate of disappearance of A is –r_A1 at conversion X₁.

A mole balance on reactor 1 gives

In – Out + Generation = 0

\begin{matrix} Reactor 1: & F_{A 0} - F_{A 1} + r_{A 1} V_{1} = 0 (2 - 19) \end{matrix}

The molar flow rate of A at point 1 is

F_{A 1} = F_{A 0} - F_{A 0} X_{1} (2 - 20)

Combining Equations (2-19) and (2-20), and rearranging

\begin{matrix} V_{1} = \frac{F_{A0} X_{1}}{- r_{A}} & (2 - 21) \end{matrix}

Reactor 1

In the second reactor, the rate of disappearance of A, –r_A2, is evaluated at the conversion of the exit stream of reactor 2, X₂. A steady-state mole balance on the second reactor is

In – Out + Generation = 0

\begin{matrix} Reactor 2: & F_{A1} - F_{A2} + r_{A2} V_{2} = 0 (2 - 22) \end{matrix}

The molar flow rate of A at point 2 is

F_{A 2} = F_{A 0} - F_{A 0} X_{2} (2 - 23)

combining Equations (2-22) and (2-23) and rearranging

$V_{2} = \frac{F_{A 1} - F_{A 2}}{- r_{A 2}} = \frac{(F_{A 0} - F_{A 0} X_{1}) - (F_{A 0} - F_{A 0} X_{2})}{- r_{A 2}}$

\begin{matrix} V_{2} = \frac{F_{A 0}}{- r_{A 2}} (X_{2} - X_{1}) & (2 - 24) \end{matrix}

Reactor 2

For the second CSTR, recall that –r_A2 is evaluated at X₂ and then use (X₂–X₁) to calculate V₂.

In the examples that follow, we shall again use the molar flow rate of A used in Example 2-1 (i.e., F_A0 = 0.4 mol A/s) and the reaction conditions given in Table 2-3 in Example 2-3 processed data 2.

Example 2–4 Comparing Volumes for CSTRs in Series

For the two CSTRs in series, 40% conversion is achieved in the first reactor. What is the volume of each of the two reactors necessary to achieve 80% overall conversion of the entering species A? (See Table 2-3.)

Solution

For Reactor 1, we observe from either Table 2-3 or Figure 2-2(b) that when X = 0.4, then

$(\frac{F_{A 0}}{- r_{A 1}})_{X = 0.4} = 2.05 m^{3}$

Then, using Equation (2-13)

$V_{1} = (\frac{A_{A 0}}{- r_{A 1}})_{4_{1}} X_{1} = (\frac{F_{A 0}}{- r_{A 1}})_{0.4} X_{1} = (2.05) (0.4) = 0.82 m^{3} = 820 d m^{3}$

V₁ = 820 dm³ (liters) Answer

For Reactor 2, when X₂ = 0.8, then $(\frac{F_{A 0}}{- r_{A}})_{X = 0.8} = 8.0 m^{3}$

Using Equation (2-24)

$V_{2} = (\frac{F_{A 0}}{- r_{A 2}}) (X_{2} - X_{1})$ (2-24)

V₂ = (8.0 m³)(0.8 – 0.4) = 3.2 m³ = 3200 dm³

V₂ = 3200 dm³ (liters) Answer

To achieve the same overall conversion, the total volume for two CSTRs in series is less than that required for one CSTR.

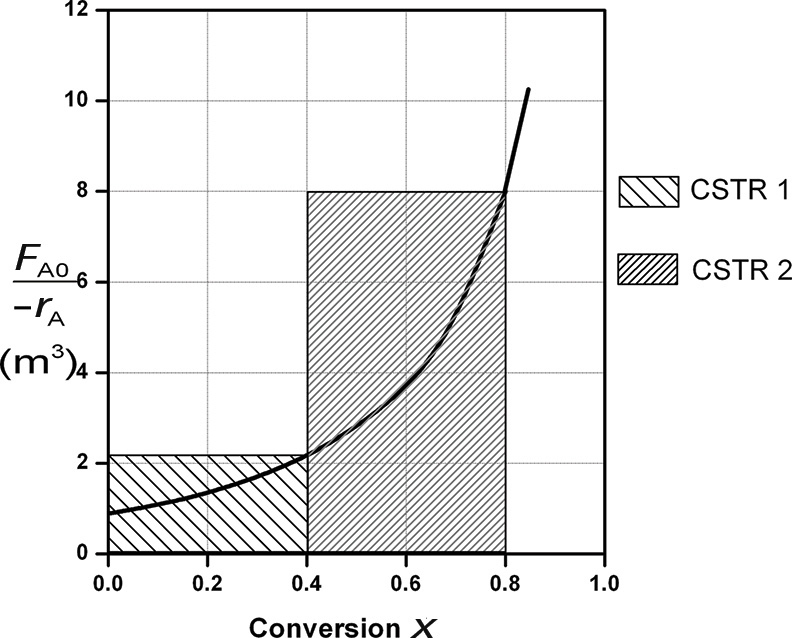
A graph plots volume against conversion X for two CSTRs in series. — **Figure E2-4.1** Two CSTRs in series.

A graph plots volume (F subscript A0 over negative r subscript A) in cubic meters for different values of conversion. The horizontal axis represents the conversion in the range 0.0 to 1.0 in increments of 0.2. The vertical axis represents rate of reaction in the range 0 to 12 in increments of 2. The curve is concave upward and increasing. The curve passes through (0.4,2) and (0.8,8). Rectangular areas representing CSTR 1 and 2, enclosed by lines representing X equals 0.4, 0.8 and volume 2, 8 is shown. Note: All values taken are approximate.

The shaded areas in Figure E2-4.1 could also have been used to determine volumes of CSTR 1 and CSTR 2.

Note again that for CSTRs in series, the rate –r_A1 is evaluated at a conversion of 0.4 and rate –r_A2 is evaluated at a conversion of 0.8. The total volume for these two reactors in series is

V = V₁ + V₂ = 0.82 m³ + 3.2 m³ = 4.02 m³ = 4020 dm³ Answer

By comparison, the volume necessary to achieve 80% conversion in one CSTR is

$y = (\frac{F_{A 0}}{- r_{A 1}}) X = (8.0) (0.8) = 6.4 m^{3} = 6400 d m^{3}$ Answer

We need only –r_A = f(X) and F_A0 to size reactors.

Notice in Example 2-4 that the sum of the two CSTR reactor volumes (4.02 m³) in series is less than the volume of one CSTR (6.4 m³) to achieve the same overall conversion.

Analysis: When we have reactors in series, we can speed our analysis and calculations by defining an overall conversion at a point in the series, rather than the conversion of each individual reactor. In this example, we saw that 40% was achieved at point 1, the exit to the first reactor, and that a total of 80% conversion was achieved by the time we exit the second reactor. Using two CSTRs in series will give a smaller total volume than one CSTR to achieve the same conversion.

Approximating a PFR by a Large Number of CSTRs in Series

Consider approximating a PFR with a number of small, equal-volume CSTRs of V_i in series (Figure 2-5). We want to compare the total volume of all these CSTRs in series with the volume of one plug-flow reactor for the same conversion, say 80%.

A figure depicts series connection of PFRs and CSTRs. — **Figure 2-5** Modeling a PFR with CSTRs in series.

PFR and CSTRs in series is shown. The PFR is represented by stacked horizontal cylinders numbered from 1 to 5. The CSTRs are represented as vertical cylinders placed next to each other. The output of each CSTR is fed into the next.

Useful Concept!

The fact that we can model a PFR with a large number of CSTRs is an important result.

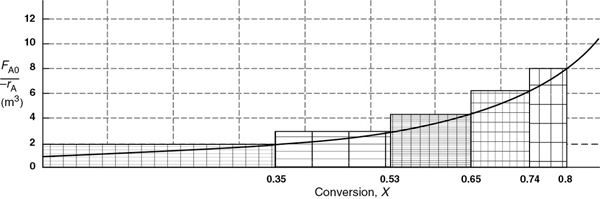
A graph plots the volume against conversion for CSTRs in series with one PFR. — **Figure 2-6** Levenspiel plot showing comparison of CSTRs in series with one PFR.

A Levenspiel plot shows the values of volume (F subscript A0 over negative r subscript A) for different conversion values. The horizontal axis represents the conversion ranging from 0.0 to 0.8 in increments of 0.1. The vertical axis represents rate of reaction ranging from 0 to 12 in increments of 2. The curve is concave upward and increasing. The conversion 0.0 to 0.35 corresponds to volume of 2, 0.35 to 0.53 corresponds to 2.5, 0.53 to 0.65 corresponds to 4.2, 0.65 to 0.74 corresponds to 6.2, and 0.74 to 0.8 corresponds to a volume of 8 cubic meters.

From Figure 2-6, we note a very important observation! The total volume to achieve 80% conversion for five CSTRs of equal volume in series is “roughly” the same as the volume of a PFR. As we make the volume of each CSTR smaller and increase the number of CSTRs, the total volume of the CSTRs in series and the volume of the PFR will become identical. That is, we can model a PFR with a large number of CSTRs in series. This concept of using many CSTRs in series to model a PFR will be used later in a number of situations, such as modeling catalyst decay in packed-bed reactors or transient heat effects in PFRs.

2.5.2 PFRs in Series

We saw that two CSTRs in series gave a smaller total volume than a single CSTR to achieve the same conversion. This case does not hold true for the two plug-flow reactors connected in series shown in Figure 2-7.

A figure shows 2 PFRs in series connection. — **Figure 2-7** Two PFRs in series.

A figure shows 2 PFRs connected in series. The species A with molar flow rate F subscript A0 enter the second PFR with flow rate, F subscript A1 and conversion, X1 equals 0.4. The output molar flow rate of second PFR is FA subscript 2 and the conversion is X2 (0.8).

We can see from Figure 2-8 and from the following equation

$\int_{0}^{X_{2}} F_{A 0} \frac{d X}{- r_{A}} \equiv \int_{0}^{X_{1}} F_{A 0} \frac{d X}{- r_{A}} + \int_{X_{1}}^{X_{2}} F_{A 0} \frac{d X}{- r_{A}}$

PFRs in series

that it is immaterial whether you place two plug-flow reactors in series or have one continuous plug-flow reactor; the total reactor volume required to achieve the same conversion is identical!

The overall conversion of two PFRs in series is the same as one PFR with the same total volume.

2.5.3 Combinations of CSTRs and PFRs in Series

The final sequences we shall consider in this chapter are combinations of CSTRs and PFRs in series. An industrial example of reactors in series is shown in the photo in Figure 2-9 where two CSTRs in series are followed by a PFR. This sequence is used to dimerize propylene (A) into isohexanes (B), for example,

$\begin{matrix} 2 {CH}_{3} - CH = {CH}_{2} \to {CH}_{3} \overset{{CH}_{3}}{\overset{|}{C}} = CH - {CH}_{2} - {CH}_{3} \\ 2 A \to B \end{matrix}$

A photograph of Dimensol G unit is shown. — **Figure 2-9** Dimersol G (an organometallic catalyst) unit (two CSTRs and one tubular reactor in series) to dimerize propylene into isohexanes. Institut Français du Pétrole process. Photo courtesy of Editions Technip (Institut Français du Pétrole).

Not sure whether the size of these CSTRs is in the Guiness Book of World Records.

A schematic of the industrial reactor system in Figure 2-9 is shown in Figure 2-10.

A figure depicts series connection of 2 CSTR and 1 PFR. — **Figure 2-10** Schematic of a real system.

An illustration of 2 CSTR and an PFR connected in series is shown. The species A with flow rate F subscript A0 and with conversion X equals 0 enters into first CSTR. The outward molar flow rate is F subscript A1 and conversion is X subscript 1, which is fed into the second CSTR. The outward flow rate from the second one is F subscript A2 and the conversion is X subscript 2. This is fed into PFR and the outward flow rate is F subscript A3 and conversion is X subscript 3.

For the sake of illustration, let’s assume that the reaction carried out in the reactors in Figure 2-10 follows the same $(\frac{F_{A 0}}{- r_{A}})$ versus X curve given by Table 2-3.

The volumes of the first two CSTRs in series (see Example 2-4) are:

Reactor 1: $V_{1} = \frac{F_{A 0} X_{1}}{- r_{A 1}}$ (2-13)

Reactor 2: $V_{2} = \frac{F_{A 0} (X_{2} - X_{1})}{- r_{A 2}}$ (2-14)

In this series arrangement, –r_A2 is evaluated at X₂ for the second CSTR.

Starting with the differential form of the PFR design equation

$F_{A 0} \frac{d X}{d V} = - r_{A}$ (2-15)

rearranging and integrating between limits, when V = 0, then X = X₂, and when V = V₃, then X = X₃ we obtain

Reactor 3: $V_{3} = \int_{X_{2}}^{X_{3}} \frac{F_{A 0}}{- r_{A}} d X$ (2-25)

The corresponding reactor volumes for each of the three reactors can be found from the shaded areas in Figure 2-11.

A graph comparing the volume and conversion X for reactors with volumes V1, V2 and V3 is shown. — **Figure 2-11** Levenspiel plot to determine the reactor volumes V₁, V₂, and V₃.

A Levenspiel plot for finding the reactor volumes V1, V2 and V3 is shown. The horizontal axis represents the conversion. The vertical axis represents rate of reaction in the range 0 to 120 in increments of 20. The curve is concave upward and increasing. Rectangular regions for conversions X1, X2, X3 are shaded differently and the corresponding volumes are V1, V2, and V3 for the CSTR 1, CSTR 2, and CSTR respectively. While V1, V2 are taken as rectangular regions, V3 is calculated as the region under the curve.

The (F_A0/–r_A) versus X curves we have been using in the previous examples are typical of those found in isothermal reaction systems. We will now consider a real reaction system that is carried out adiabatically. Isothermal reaction systems are discussed in Chapter 5 and adiabatic systems in Chapter 11, where we will see that for adiabatic exothermic reactions the temperature increases with increasing conversion.

Example 2–5 An Adiabatic Liquid-Phase Isomerization

The isomerization of butane

n-C₄H₁₀ ⇄ i - C₄H₁₀

A label representing the Butane NFPA Diamond is shown. It is a tilted square, with the diagonals dividing into 4 parts. 3 of them are numbered as 1,4,0 and are colored as red, blue, and yellow.

Butane NFPA Diamond

was carried out adiabatically in the liquid phase. The data for this reversible reaction are given in Table E2-5.1. (Example 11.3 shows how the data in Table E2-5.1 were generated.)

TABLE E2-5.1 RAW DATA

X	0.0	0.2	0.4	0.6	0.65
–r_A(kmol/m³ · h)	39	53	59	38	25

Don’t worry how we got this data or why the (1/–r_A) looks the way it does; we will see how to construct this table in Chapter 11, Example 11-3. It is real data for a real reaction carried out adiabatically, and the reactor scheme shown below in Figure E2-5.1 is used.

A figure depicts the series connection of 2 CSTR and 1 PFR. — **Figure E2-5.1** Reactors in series.

An illustration depicting 2 CSTR and a PFR connected in series in the order CSTR-PFR-CSTR is shown. A species or liquid enters into first CSTR with volume V1 has a reaction rate r A1 and conversion X1 is 0.2. This is fed into the PFR with volume V2 and the conversion X2 is 0.6. It is fed into the second CSTR with volume V3 and the conversion X3 is 0.65.

Real Data for a Real Reaction

Calculate the volume of each of the reactors for an entering molar flow rate of n-butane of 50 kmol/hr, that is, F_A0 = 50 kmol/h.

Solution

Taking the reciprocal of –r_A and multiplying by F_A0, we obtain Table E2-5.2.

For example, at $X = 0 : \frac{F_{A0}}{- r_{A}} = \frac{50 kmol/h}{39 kmol/h \cdot m^{3}} = 1.28 m^{3}$

†Data from Table E11-3.1.

For the first CSTR,

when X = 0.2, then $\frac{F_{A 0}}{- r_{A}} = 0.94 m^{3}$

$\begin{matrix} V_{1} = \frac{F_{A 0}}{- r_{A}} X_{1} = (0.94 m^{3}) (0.2) = 0.1 88 m^{3} & (E2-5.1) \end{matrix}$

$\begin{matrix} V_{1} = 0.188 m^{3} = 188 {dm}^{3} & (E2-5.2) \end{matrix}$
For the PFR,

$V_{2} = \int_{0.2}^{0.6} (\frac{F_{A 0}}{- r_{A}}) d X$

Using Simpson’s three-point formula with ΔX = (0.6 – 0.2)/2 = 0.2, and X₁ = 0.2, X₂ = 0.4, and X₃ = 0.6

$y_{2} = \int_{0.2}^{0.6} \frac{F_{A 0}}{- r_{A}} d X = \frac{Δ X}{3} [\frac{F_{A 0}}{- r_{A}})_{X = 0.2} + 4 \frac{F_{A 0}}{- r_{A}})_{X = 0.4} + \frac{F_{A 0}}{- r_{A}})_{X = 0.6}]$

$\begin{matrix} = \frac{0.2}{3} [0.94 + 4 (0.85) + 1.32] m^{3} & (E2-5.3) \end{matrix}$

$\begin{matrix} V_{2} = 0.38 m^{3} = 380 d m^{3} & (E2-5.4) \end{matrix}$
For the last reactor and the second CSTR, mole balance on A for the CSTR:

In – Out + Generation = 0

$\begin{matrix} F_{A2} - F_{A3} + r_{A3} V_{3} = 0 & (E2-5.5) \end{matrix}$

Rearranging

F_A2 = F_A0 – F_A0X₂

F_A3 = F_A0 – F_A0X₃

$V_{3} = \frac{(F_{A 0} - F_{A 0} X_{2}) - (F_{A 0} - F_{A 0} X_{3})}{- r_{A 3}}$

Simplifying

$\begin{matrix} V_{3} = (\frac{F_{A 0}}{- r_{A 3}}) (X_{3} - X_{2}) & (E2-5.7) \end{matrix}$

We find from Table E2-5.2 that at X₃ = 0.65, then $\frac{F_{A 0}}{- r_{A 3}} = 2.0 m^{3}$

V₃ = 2 m³ (0.65 – 0.6) = 0.1 m³

$\begin{matrix} V_{3} = 0.1 m^{3} = 100 d m^{3} & (E2-5.8) \end{matrix}$

A Levenspiel plot of (F_A0/–r_A) versus X is shown in Figure E2-5.2.

Figure E2-5.2 Levenspiel plot for adiabatic reactors in series.

A Levenspiel plot compares the volume for different conversion values for two CSTRs and PFR. The horizontal axis represents the conversion ranging from 0 to 0.7 in increments of 0.1. The vertical axis represents reciprocal rate with molar flow, F subscript A0, ranging from 0 to 2.5 in increments of 0.5. The curve is concave upward and increasing. The volumes are V1, V2, and V3 for the CSTR 1, PFR , and CSTR 2 respectively and are shaded differently. The conversion of the reactors and the corresponding values in vertical axis are: V 1- 0 to 0.2 corresponds to volumes of 0 to 1 cubic meters, V 1- 0 to 0.2 corresponds to 0 to 1, V 2- 0.2 to 0.6 below the curve, V 3- 0.6 to 0.65 corresponds to 0 to 2.

For this adiabatic reaction, the three reactors in series resulted in an overall conversion of 65%. The maximum conversion we can achieve is the equilibrium conversion, which is 68%, and is shown by the dashed line in Figure E2-5.2. Recall that at equilibrium, the rate of reaction is zero and an infinite reactor volume is required to reach equilibrium $(V - \frac{1}{- r_{A}} \sim \frac{1}{0} = \infty)$ .

Analysis: For exothermic reactions that are not carried out isothermally, the rate usually increases at the start of the reaction because reaction temperature increases. However, as the reaction proceeds the rate eventually decreases as the conversion increases because the reactants are consumed. These two competing effects give the bowed shape of the curve in Figure E2-5.2, which will be discussed in detail in Chapters 11 and 12. Under these circumstances, we saw that a CSTR will require a smaller volume than a PFR at low conversions.

2.5.4 Comparing the CSTR and PFR Volumes and Reactor Sequencing

If we look at Figure E2-5.2, the area under the curve (PFR volume) between X = 0 and X = 0.2, we see that the PFR area is greater than the rectangular area corresponding to the CSTR volume, that is, V_PFR > V_CSTR. However, if we compare the areas under the curve between X = 0.6 and X = 0.65, we see that the area under the curve (PFR volume) is smaller than the rectangular area corresponding to the CSTR volume, that is, V_CSTR > V_PFR. This result often occurs when the reaction is carried out adiabatically, which is discussed when we look at heat effects in Chapter 11.

Which arrangement is best?

A figure depicts the PFR and CSTR series arrangement in which the output of PFR is given as input to CSTR. Another arrangement is also depicted where the output of CSTR is given as input to PFR.

In the sequencing of reactors, one is often asked, “Which reactor should go first to give the highest overall conversion? Should it be a PFR followed by a CSTR, or two CSTRs, then a PFR, or …?” The answer is “It depends.” It depends not only on the shape of the Levenspiel plot (F_A0/–r_A) versus X, but also on the relative reactor sizes. As an exercise, examine Figure E2-5.2 to learn if there is a better way to arrange the two CSTRs and one PFR. Suppose you were given a Levenspiel plot of (F_A0/–r_A) versus X for three reactors in series, along with their reactor volumes V_CSTR1 = 3 m³, V_CSTR2 = 2 m³, and V_PFR = 1.2 m³, and were asked to find the highest possible conversion X. What would you do? The methods we used to calculate reactor volumes all apply, except the procedure is reversed and a trial-and-error solution is needed to find the exit overall conversion from each reactor (see Problem P2-5_B).

Given upper V and left bracket upper F subscript upper A 0 over negative r subscript upper A versus upper X right bracket find upper X (encircled)

The previous examples show that if we know the molar flow rate to the reactor and the reaction rate as a function of conversion, then we can calculate the reactor volume necessary to achieve a specified conversion. The reaction rate does not depend on conversion alone, however. It is also affected by the initial concentrations of the reactants, the temperature, and the pressure. Consequently, the experimental data obtained in the laboratory and presented in Table 2-1 as –r_A as a function of X are useful only in the design of full-scale reactors that are to be operated at the identical conditions as the laboratory experiments (temperature, pressure, and initial reactant concentrations). However, such circumstances are seldom encountered and we must revert to the methods we describe in Chapters 3 and 4 to obtain –r_A as a function of X.

It is important to remember that if the rate of reaction is available or can be obtained solely as a function of conversion, –r_A = f(X), or if it can be generated by some intermediate calculations, one can design a variety of reactors and combinations of reactors.

Only need –r_A = f(X) to size flow reactors

Ordinarily, laboratory data are used to formulate a rate law, and then the reaction rate–conversion functional dependence is determined using the rate law. The preceding sections show that with the reaction rate–conversion relationship, that is, –r_A = f(X), different reactor schemes can readily be sized. In Chapters 3 and 4, we show how we obtain this relationship between reaction rate and conversion from rate law and reaction stoichiometry.

A figure depicts the equations derived in Chapter 3 and 4 and the combined result. — The text shown reads: "Chapter 3 shows how to find negative r subscript upper A equals function of left parenthesis upper C subscript upper A plus Chapter 4 shows how to find upper C subscript upper A equals g of x implies Chapters 3 and 4 are combined to get negative r subscript upper A equals f of x."

2.6 Some Further Definitions

Before proceeding to Chapter 3, some terms and equations commonly used in reaction engineering need to be defined. We also consider the special case of the plug-flow design equation when the volumetric flow rate is constant.

2.6.1 Space Time

The space time tau, τ, is obtained by dividing the reactor volume by the volu-metric flow rate entering the reactor

\begin{matrix} τ \equiv \frac{V}{υ_{0}} & (2 - 26) \end{matrix}

τ is an important quantity!

The space time is the time necessary to process one reactor volume of fluid based on entrance conditions. For example, consider the tubular reactor shown in Figure 2-12, which is 20 m long and 0.2 m³ in volume. The dashed line in Figure 2-12 represents 0.2 m³ of fluid directly upstream of the reactor. The time it takes for this upstream fluid volume to enter the reactor completely is called the space time tau. It is also called the holding time or mean residence time.

A figure depicts upstream volume in a tubular reactor. — **Figure 2-12** Tubular reactor showing identical volume upstream.

An illustration depicts a tubular reactor with fluid flowing through it. 3 points a, b, and c are marked. The distance between the points a to b and b to c is mentioned as 20 meters. The volume of reactor between points a and b is 0.2 cubed meters and points b and c is also 0.2 cubed meters.

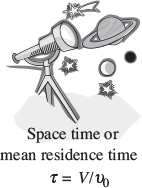
Space time or mean residence time tau equals upper V over nu subscript 0.

For example, if the reactor volume is 0.2 m³ and the inlet volumetric flow rate is 0.01 m³/s, it would take the upstream equivalent reactor volume (V = 0.2 m³), shown by the dashed lines, a time τ equal to

$τ = \frac{0.2 m^{3}}{0.01 m^{3} / s} = 20 s$

to enter the reactor (V = 0.2 m³). In other words, it would take 20 s for the fluid molecules at point a to move to point b, which corresponds to a space time of 20 s. We can substitute for F_A0 = υ₀C_A0 in Equations (2-13) and (2-16) and then divide both sides by to write our mole balance in the following forms:

$\begin{matrix} For a PFR & τ_{p} = (\frac{V_{p}}{υ_{0}}) = C_{A 0} \int_{0}^{X} \frac{d X}{- r_{A}} \end{matrix}$

and

$\begin{matrix} For a CSTR & τ_{CSTR} = (\frac{V_{CSTR}}{υ_{0}}) = \frac{C_{A 0}}{- r_{A}} X \end{matrix}$

For plug flow, the space time is equal to the mean residence time in the reactor, t_m (see Chapter 16). This time is the average time that the molecules spend in the reactor. A range of typical processing times in terms of the space time (residence time) for industrial reactors is shown in Table 2-4.

² P. Trambouze, H. Landeghem, and J. P. Wauquier, Chemical Reactors, Paris: Editions Technip, 1988; Houston: Gulf Publishing Company, 1988, p. 154.

Practical guidelines

Table 2-5 shows an order of magnitude of the space times for six industrial reactions and associated reactors.

Typical industrial reaction space times

Table 2-6 gives typical sizes for batch and CSTR reactors (along with the comparable size of a familiar object) and the costs associated with those sizes. All reactors are glass lined and the prices include heating/cooling jacket, motor, mixer, and baffles. The reactors can be operated at temperatures between 20°F and 450°F, and at pressures up to 100 psi.

An icon of the reference shelf with books.

†Doesn’t include instrumentation costs.

Cliparts of water basket, garbage can, and a Jacuzzi is shown.

2.6.2 Space Velocity

The space velocity (SV) is another term used by reaction engineers and is defined as

$\begin{matrix} \begin{matrix} S V \equiv \frac{v_{0}}{V} & S V = \frac{1}{τ} \end{matrix} & (2 - 27) \end{matrix}$

³ Walas, S. M. Chemical Reactor Data, Chemical Engineering, 79 (October 14, 1985).

The space velocity might be regarded at first sight as the reciprocal of the space time. However, there can be a difference in the two quantities’ definitions. For the space time, the entering volumetric flow rate is measured at the entrance conditions, but for the space velocity, other conditions are often used. The two space velocities commonly used in industry are the liquid-hourly and gas-hourly space velocities, LHSV and GHSV, respectively. The entering volumetric flow rate, υ₀, in the LHSV is frequently measured as that of a liquid feed rate at 60°F or 75°F, even though the feed to the reactor may be a vapor at some higher temperature. Strange but true.

$L H S V = \frac{υ_{0} | l i q u i d}{V}$ (2-28)

Slight differences in space velocities

The gas volumetric flow rate, υ₀, in the GHSV is normally reported at standard temperature and pressure (STP).

$G H S V = \frac{υ_{0} | S T P}{V}$ (2-29)

Example 2–6 Reactor Space Times and Space Velocities

Calculate the space time, τ, and space velocities for the reactor in Examples 2-1 and 2-3 for an entering volumetric flow rate of 2 dm³/s.

Solution

The entering volumetric flow rate is 2 dm³/s (0.002 m³/s).

From Example 2-1, the CSTR volume was 6.4 m³ and the corresponding space time, τ, and space velocity, SV are

$τ = \frac{V}{v_{0}} = \frac{6.4 m^{3}}{0.002 m^{3} / s} = 3200 s = 0.89 h$

It takes 0.89 h to put 6.4 m³ into the reactor and the corresponding space velocity, SV, is

$S V = \frac{1}{τ} = \frac{1}{0.89 h} = 1.125 h^{- 1}$

From Example 2-3, the PFR volume was 2.165 m³, and the corresponding space time and space velocity are

$τ = \frac{V}{v_{0}} = \frac{2.165 m^{3}}{0.002 m^{3} / s} = 1083 s = 0.30 h$

$S V = \frac{1}{τ} = \frac{1}{0.30 h} = 3.3 h^{- 1}$

Analysis: This example gives an important industrial concept. These space times are the times for each of the reactors to take the volume of fluid equivalent to one reactor volume and put it into the reactor.

Summary

In these last examples we have seen that in the design of reactors that are to be operated at conditions (e.g., temperature and initial concentration) identical to those at which the reaction rate–conversion data –r_A = f(X) were obtained, we can size (determine the reactor volume) both CSTRs and PFRs alone or in various combinations. In principle, it may be possible to scale up a laboratory-bench or pilot-plant reaction system solely from knowledge of –r_A as a function of X or C_A. However, for most reactor systems in industry, a scale-up process cannot be achieved in this manner because knowledge of –r_A solely as a function of X is seldom, if ever, available under identical conditions. By combining the information in Chapters 3 and 4, we shall see how we can obtain –r_A = f(X) from information obtained either in the laboratory or from the literature. This relationship will be developed in a two-step process. In Step 1, we will find the rate law that gives the rate as a function of concentration (Table 3-1) and in Step 2, we will find the concentrations as a function of conversion (Figure 4-3). Combining Steps 1 and 2 in Chapters 3 and 4, we obtain –r_A = f(X). We can then use the methods developed in this chapter, along with integral and numerical methods, to size reactors.

Coming attractions in Chapters 3 and 4

2.7 And Now… A Word from Our Sponsor–Safety 2 (AWFOS–S2 The NFPA Diamond)

In this AWFOS–S, we describe the National Fire Protection Agency (NFPA) Diamond which quickly identifies risks of hazardous materials. This identification is extremely important to first responders in an emergency. Each color in the diamond represents a different type of hazard, while the numbers in the hazard refer to a degree of concern one should have about the material. The different types of hazards and levels of concern of the NFPA diamond are shown in Figure 2-13.

A figure illustrates NFPA diamond and its components. — **Figure 2-13** Components of each color of the NFPA Diamond. (Image: Dmitry Kovalchuk/Shutterstock)

An image of a rhombus with 4 colors which represents 4 different hazards with degree of concern. Hazards and degree of concern mentioned are Fire hazard: 4- below 73 degrees, 3- below 100 degrees, 2- below 200 degrees, 1- above 200 degrees, 0- will not burn; Instability hazard: 4- may detonate, 3- shock and heat may detonate, 2- violent Chemical change, 1- unstable if heated, 0- stable; Specific hazard: ACID- Acidic material, ALK- alkali, COR- corrosive, OX- oxidizer, trefoil symbol- radiation hazard, upper W struck through- use no water; Health hazard: 4- deadly, 3- extreme danger, 2- hazardous, Slightly danger, 0- normal material.

A tutorial on how to fill in the numbers in the diamond for the insecticide dichlorodiphenyltrichloroethane (DDT) using the CAMEO Chemicals Website (https://cameochemicals.noaa.gov) is given in the NFPA Diamond tutorial on the safety Website (http://umich.edu/~safeche/nfpa.html, http://umich.edu/~safeche/assets/pdf/CAMEO.pdf). The NFPA Diamond for the chemical DDT discussed in Example 1-1, DDT, is shown in Figure 2-14.

A label representing NFPA diamond is shown. — **Figure 2-14** NFPA Diamond Levels of Concern for DDT. (Image: Idea.s/Shutterstock)

A label representing NFPA diamond levels for concern. It is a rhombus formed by 4 rhombi. The top-most diamond is red in color and has the number 2 in it. The far-right diamond is yellow in color and has the number 0 in it. The bottom-most diamond is white in color. The far-left diamond is blue in color and has the number 2 in it.

We see that the number two in the red (top-most) diamond indicates DDT has a flash point below 200°F, the zero in the yellow (far-right) diamond indicates it is stable, the blank in the white (bottom-most) diamond indicates no specific hazard, and the two in the blue (far-left) diamond indicates DDT is hazardous to one’s health.

The following photographs show two examples of how the NFPA Diamond is used in industry.

Two photographs of NFPA Diamond labels pasted on a tank and chemical storage unit are shown. An NFPA diamond label with numbers 2-4-0 is pasted on a tank indicated that it contains highly flammable propane gas. The colors blue, red, yellow and white are present in the label and they indicate health, fire, instability and specific hazards. The numbers 2 (health), 4 (fire), and 0 (instability) for propane indicate that it is highly flammable. Similarly, a NFPA Diamond label is pasted on a chemical storage unit and it has the numbers 4-4-2. — **Figure 2-15** NFPA Diamond in Action. (Photos: left, Gado Images/Getty; right, TFoxFoto/Shutterstock)

The NFPA Diamond along with its companion GHS Diamond (see AWFOS-S3) is shown on the Process Safety Across the Chemical Engineering Curriculum Web site. For tutorials and NFPA data sheets see

NFPA Diamond Tutorial: https://cse.wwu.edu/files/safety-tutorials/Gen_Chem_Tutorial/HTML/GCST_10.htm

CAMEO Chemicals Tutorial: http://umich.edu/~safeche/assets/pdf/CAMEO.pdf

Quick Card: https://www.nfpa.org/Assets/files/AboutTheCodes/704/NFPA704_HC2012_QCard.pdf

Data Sheets: https://cameochemicals.noaa.gov/chemical/694https://cameochemicals.noaa.gov/chemical/4145

FAQs: https://www.nfpa.org/Assets/files/AboutTheCodes/704/704_FAQs.pdf

The CRE Algorithm

Mole Balance, Ch 1
Rate Law, Ch 3
Stoichiometry, Ch 4
Combine, Ch 5
Evaluate, Ch 5
Energy Balance, Ch 11

Closure

In this chapter, we have shown that if you are given the rate of reaction as a function of conversion, that is, –r_A = f(X), you will be able to size CSTRs and PFRs, and arrange the order of a given set of reactors to determine the maximum overall conversion. After completing this chapter, the reader should be able to:

Define the parameter conversion and rewrite the mole balances in terms of conversion
Show that by expressing –r_A as a function of conversion X, a number of reactors and reaction systems can be sized or a conversion calculated from a given reactor size
Arrange reactors in series to achieve the maximum conversion for a given Levenspiel plot

Summary

The conversion X is the moles of A reacted per mole of A fed.

For batch systems:

$X = \frac{N_{A 0} - N_{A}}{N_{A 0}}$ (S2-1)

For flow sytems:

$X = \frac{F_{A 0} - F_{A}}{F_{A 0}}$ (S2-2)

For reactors in series with no side streams, the conversion at point i is

$X_{i} = \frac{Total moles of A reacted up to Point i}{Moles A fed to the first reactor}$ (S2-3)
The differential and integral forms of the reactor design equations (i.e., GMBEs) are shown in Table S2-1.

TABLE S2-1 MOLE BALANCE FOR BR, CSTR, PFR, AND PBR TERMS OF CONVERSION
If the rate of disappearance of A is given as a function of conversion, the following graphical techniques can be used to size a CSTR and a plug-flow reactor.
1. Graphical Integration Using Levenspiel Plots
  
  First image and graph shows, CSTR and a graph of the volume as a function of conversion with the molar flow of the species A and conversion, X. The horizontal axis represents the conversion, X in the range 0 to 1 in increments of 0.2. The vertical axis is the range of 0 to 40 in increments of 10. The curve is concave upward and increasing. The region of the graph bounded by the lines drawn at 0.8 at horizontal axis and 30 at vertical axis. Second image shows, PFR and a graph of the volume as a function of conversion with the molar flow of the species A and conversion, X. The horizontal axis represents the conversion, X in the range 0 to 1 in increments of 0.2. The vertical axis is the range of 0 to 40 in increments of 10. The curve is concave upward and increasing. The region of the graph bounded by the lines drawn at 0.8 below the curve is shaded. Third image and graph shows, CSTR and PFR series connection and a graph of the volume as a function of conversion with the molar flow of the species A and conversion, X. The horizontal axis represents the conversion, X in the range 0 to 1 in increments of 0.2. The vertical axis is the range of 0 to 40 in increments of 10. The curve is concave upward and increasing. The region of the graph bounded by the lines drawn at 0.6 at horizontal axis and 15 at vertical axis and the region below the curve till X=0.8 is shaded separately.
  
  The PFR integral could also be evaluated by
2. Numerical Integration
  
  See Appendix A.4 for quadrature formulas such as the five-point quadrature formula with ΔX = 0.8/4 of five equally spaced points, X₁ = 0, X₂ = 0.2, X₃ = 0.4, X₄ = 0.6, and X₅ = 0.8.
Space time, τ, and space velocity, SV, are given by

$τ = \frac{V}{v_{0}}$ (S2-4)

$\begin{matrix} S V = \frac{υ_{0}}{V} (at STP for gas-phase reaction) & (S2-5) \end{matrix}$

CRE Web Site Materials

(http://www.umich.edu/~elements/6e/02chap/obj.html)

A figure represents the materials that can be accessed from CRE website. — An image shows useful links and evaluation. Useful links are: Living example problems- Polymath, Python, Matlab and Wolfram; Extra Help- Multiple resources extra problems, screencasts and lecture notes; Additional Materials- New technical material, detailed derivations and web modules; Professional reference shelf- Material important to the practicing engineer that is not necessarily covered in all CRE courses; YouTube Videos- Humorous videos covering topics varying from example problems to light hearted breaks from studying. Evaluation: Self tests- Interactive problems with solutions to provide extra practice of concepts; i>Clicker Questions- Interactive multiple choice questions to help access your understanding of the material.

Web Module Hippopotamus Digestive System

A figure depicts the Hippopotamus digestive system modeled as a CSTR and PFR in series. — An CSTR of volume V subscript 1 and a PFR of volume V subscript 2 are connected in series. The species A with flow rate F subscript A0 times X subscript 0 enters into CSTR and the output of CSTR has flow rate, F subscript A1 and conversion, X subscript 1. This enters the PFR. The output of PFR has molar flow rate and conversion of F subscript A2 and X subscript 2 respectively.

(http://umich.edu/~elements/6e/web_mod/hippo/index.htm)

An image of CSTR and a graph of the inverse of reaction rate and conversion X representing autocatalytic reaction is shown. — An image of CSTR and a graph of the of rate of reaction and conversion, X is shown. The horizontal axis represents the conversion, X in the range 0 to X. The vertical axis represents 1 over negative r subscript AM. The curve is a parabola concave upward. The region of the graph bounded by the lines drawn at X subscript 1 at horizontal axis and vertex of parabola at vertical axis. The vertex is marked as V subscript 1.

Interactive Computer Games

Reactor Staging (http://umich.edu/~elements/6e/icm/staging.html)

A snapshot shows a simulator displaying information on reactor staging. — A simulator showing information of reactor staging shows CSTRs and PFRs connected in series alternatively. The reactors are numbered from 1 to n. There are buttons like main menu, repeat and continue.

Questions and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

A = • B = ▪ C = ♦ D = ♦♦

Questions

Q2-1_A QBR (Questions Before Reading). Will or could there ever be a case where the CSTR volume is represented by something other than a square or rectangle on a Levenspiel plot?

Q2-2_A i>clicker. Go to the Web site http://www.umich.edu/~elements/6e/02chap/iclicker_ch2_q1.html and view at least five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case: explaining why the question should not be on the next exam. In either case, explain your reasoning.

Q2-3 (a) Without referring back, make a list of the most important items you learned in this chapter.

(b) Overall, what do you believe were the three major purposes of the chapter?

Q2-4 Go to the Web site www.engr.ncsu.edu/learningstyles/ilsweb.html. Take the Inventory of Learning Style test, and record your learning style according to the Soloman/Felder inventory, and then use Appendix I.2 to suggest two ways to facilitate your learning style in each of the four categories.

Global/Sequential_____

Active/Reflective_____

Visual/Verbal_____

Sensing/Intuitive_____

Q2-5_A Go to the Chapter 2 Video Screencasts Web page (http://www.umich.edu/~elements/6e/02chap/learn-cheme-videos.html).

View one or more of the screencast 5- to 6-minute videos and write a two-sentence evaluation.
What did the speaker do well and what could be improved?

Q2-6_A AWFOS-S2

What is the NFPA diamond and why is it important?
Go to Wikipedia and search ethylene oxide to find the NFPA diamond numbers.
Draw the NFPA diamond for the chemicals propylene, isohexane, and isobutane that we discussed in Figure 2-6, and Example 2-5.

Interactive Computer Games

P2-1_A ICG Staging. Download the Interactive Computer Game (ICG) from the CRE Web site, http://www.umich.edu/~elements/6e/icm/staging.html. Play this game and then record your performance number, which indicates your mastery of the material. Your professor has the key to decode your performance number. Note: To play this game you must have Windows 2000 or a later version.

Write the ICG Reactor Staging Performance here # ______________________.

A snapshot of computer game screen which shows staging screen with main menu button. The game asks the user to click on the correct door representing the correct answer for question related to CSTR.

Problems

Before solving the problems, state or sketch qualitatively the expected results or trends.

P2-2_A

Revisit the data in Table 2-1 Raw Data and calculate the batch reactor (BR) times to achieve 10%, 50%, and 80% conversion when 100 moles of A are charged to a 400 dm³ reactor.
Revisit Examples 2-1 through 2-3. How would your answers change if the flow rate, F_A0, were cut in half? If it were doubled? What conversion can be achieved in a 4.5 m³ PFR and in a 4.5 m³ CSTR?
Revisit Example 2-2. Being a company about to go bankrupt, you can only afford a 2.5 m³ CSTR. What conversion can you achieve?
Revisit Example 2-3. What conversion could you achieve if you could convince your boss, Dr. Pennypincher, to spend more money to buy a 1.0 m³ PFR to attach to a 2.40 CSTR?
Revisit Example 2-4. How would your answers change if the two CSTRs (one 0.82 m³ and the other 3.2 m³) were placed in parallel with the flow, F_A0, divided equally between the reactors?
Revisit Example 2-5. (1) What is the worst possible way to arrange the two CSTRs and one PFR? (2) What would be the reactor volumes if the two intermediate conversions were changed to 20% and 50%, respectively? (3) What would be the conversions, X₁, X₂, and X₃, if all the reactors had the same volume of 100 dm³ and were placed in the same order?
Revisit Example 2-6. If the term $C_{A 0} \int_{0}^{X} \frac{d X}{- r_{A}}$ is 2 seconds for 80% conversion, how much fluid (m³/min) can you process in a 3 m³ reactor?

P2-3_B You have two CSTRs and two PFRs, each with a volume of 1.6 m³. Use Figure 2-2(b) on page 45 to calculate the conversion for each of the reactors in the following arrangements.

Two CSTRs in series. (Ans: X₁ = 0.435, X₂ = 0.66)
Two PFRs in series.
Two CSTRs in parallel with the feed, F_A0, divided equally between the two reactors.
Two PFRs in parallel with the feed divided equally between the two reactors.
A PFR followed by a CSTR.
(f) A CSTR followed by a PFR. (Ans: X_CSTR = 0.435, X_PFR = 0.71)
A PFR followed by two CSTRs. Is this a good arrangement or is there a better one?
Caution: Part (h) is a C level problem. A CSTR and a PFR in parallel with the flow equally divided. Calculate the overall conversion, X_ov

$X_{o v} = \frac{F_{A 0} - F_{A C S T R} - F_{A P F R}}{F_{A 0}}, with F_{A C S T R} = \frac{F_{A 0}}{2} - \frac{F_{A 0}}{2} X_{C S T R}, and F_{A P F R} = \frac{F_{A 0}}{2} (1 - X_{P F R})$

P2-4_B The exothermic reaction of stillbene (A) to form the economically important trospophene (B) and methane (C), that is,

A → B+ C

was carried out adiabatically and the following data recorded:

The entering molar flow rate of A was 300 mol/min.

Calculate the batch reactor (BR) times to achieve 40% and 80% conversion when 400 moles of A are charged to a 400 dm³ reactor.
What are the PFR and CSTR volumes necessary to achieve 40% conversion? (V_PFR = 72 dm³, V_CSTR = 24 dm³)
Over what range of conversions would the CSTR and PFR reactor volumes be identical?
What is the maximum conversion that can be achieved in a 105-dm³ CSTR?
What conversion can be achieved if a 72-dm³ PFR is followed in series by a 24-dm³ CSTR?
What conversion can be achieved if a 24-dm³ CSTR is followed in a series by a 72-dm³ PFR?
Plot the conversion and rate of reaction as a function of PFR reactor volume up to a volume of 100 dm³.

P2-5_B The financially important reaction to produce the valuable product B (not the real name) was carried out in Jesse Pinkman’s garage (see Breaking Bad Season 3, Episode 7). This Breaking Bad, fly-by-night company, is on a shoestring budget and has very little money to purchase equipment. Fortunately, cousin Bernie has a reactor surplus company and you can get reactors from Bernie. The reaction

A → B + C

takes place in the liquid phase. Below is the Levenspiel plot for this reaction. You have up to $10,000 to use to purchase reactors from those given below.

A Levenspiel plot graphs the values of volume for different conversion (X) values. — A graph plots values of volume against conversion X. The horizontal axis represents the conversion ranging from 0 to 0.9 in increments of 0.1. The vertical axis represents volume with molar flow rate, F subscript A0, ranging from 0 to 80 in increments of 10. The rate decreases steadily from a volume of 50 in the beginning and from 0.2 of X it is stable till 0.6 of X, after which it increases.

What reactors do you choose, how do you arrange them, and what is the highest conversion you can get for $10,000? Approximately what is the corresponding highest conversion with your arrangement of reactors?

Scheme and sketch your reactor volumes.

A figure shows rectangular blocks representing reactors connected in series. In the end, it is mentioned as et cetera, implying more reactors could be connected.

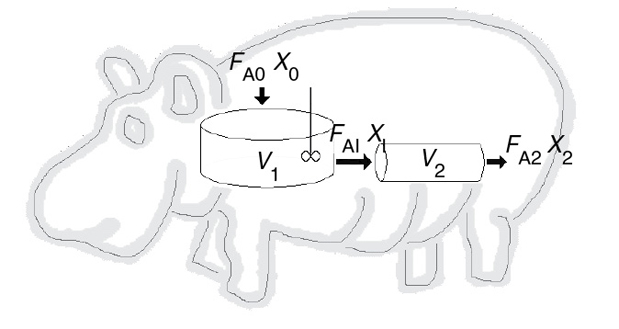
P2-6_B Read the Web Module “Chemical Reaction Engineering of Hippopotamus Stomach” on the CRE Web site (http://www.umich.edu/~elements/6e/web_mod/hippo/index.htm).

Two similar images of hippopotamus swimming.

Write five sentences summarizing what you learned from the Web Module.
Work problems (1) and (2) in the Hippo Web Module.
The hippo has picked up a river fungus, and now the effective volume of the CSTR stomach compartment is only 0.2 m³. The hippo needs 30% conversion to survive. Will the hippo survive?
The hippo had to have surgery to remove a blockage. Unfortunately, the surgeon, Dr. No, accidentally reversed the CSTR and the PFR during the operation. Oops!! What will be the conversion with the new digestive arrangement? Can the hippo survive?

P2-7_B OEQ (Old Exam Question). The adiabatic exothermic irreversible gas-phase reaction

2A + B → 2C

is to be carried out in a flow reactor for an equimolar feed of A and B. A Levenspiel plot for this reaction is shown in Figure P2-7_B.

A graph plots the values of volume against conversion. — **Figure P2-7_B** Levenspiel plot.

A graph plots the values of volume for different conversion values. The horizontal axis represents the conversion in the range 0 to 0.9 in increments of 0.1. The vertical axis represents the volume with molar flow rate as F subscript A0, ranging from 0 to 500,000 in increments of 10. The rate decreases steadily in the beginning and from 0.5 of X it increases. The maximum volume observed is 500,000 cubic meters and minimum is 100,000 cubic meters.

What PFR volume is necessary to achieve 50% conversion?
What CSTR volume is necessary to achieve 50% conversion?
What is the volume of a second CSTR added in series to the first CSTR (Part b) necessary to achieve an overall conversion of 80%? (Ans: V_CSTR = 1.5 × 10⁵ m³)
What PFR volume must be added to the first CSTR (Part b) to raise the conversion to 80%?
What conversion can be achieved in a 6 × 10⁴ m³ CSTR? In a 6 × 10⁴ m³ PFR?
Think critically (cf. Introduction, Section H, page xxix) to critique the answers (numbers) to this problem.

P2-8_A Estimate the reactor volumes of the two CSTRs and the PFR shown in the photo in Figure 2-9. Hint: Use the dimensions of the door as a scale.

P2-9_D Don’t calculate anything. Just go home and relax.

P2-10_C OEQ (Old Exam Question). The curve shown in Figure 2-1 is typical of a reaction carried out isothermally, and the curve shown in Figure P2-10_C (see Example 11-3) is typical of a gas–solid catalytic exothermic reaction carried out adiabatically.

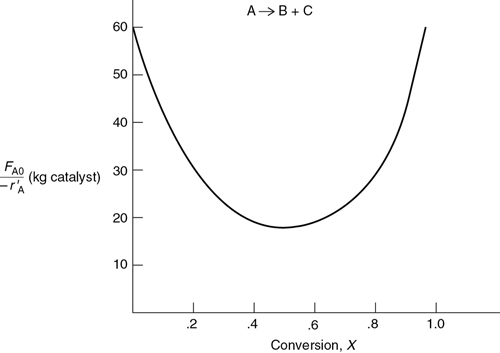
A graph plots the weights of catalyst against conversion values. — **Figure P2-10_C** Levenspiel plot for an adiabatic exothermic heterogeneous reaction.

A Levenspiel plot compares the weight of catalyst with conversion values. The horizontal axis represents the conversion ranging from 0 to 1.0 in increments of 0.2. The vertical axis represents catalyst weight with molar flow rate as F subscript A0, ranging from 10 to 60 in increments of 10. The curve is a parabola open upwards. The vertex of the parabola is at (0.5,18) and the parabola passes through (0,60). Note: All values taken are approximate.

Assuming that you have a fluidized CSTR and a PBR containing equal weights of catalyst, how should they be arranged for this adiabatic reaction? Use the smallest amount of catalyst weight to achieve 80% conversion of A.
What is the catalyst weight necessary to achieve 80% conversion in a fluidized CSTR? (Ans: W = 23.2 kg of catalyst)
What fluidized CSTR weight is necessary to achieve 40% conversion?
What PBR weight is necessary to achieve 80% conversion?
What PBR weight is necessary to achieve 40% conversion?
Plot the rate of reaction and conversion as a function of PBR catalyst weight, W.

Additional information: F_A0 = 2 mol/s.

An image of a reactor with fluidized catalyst pellets. The direction inside the reactor is represented by 2 arrows in clockwise and counter-clockwise directions and the flow direction is upwards.

P2-11 The experiments on reaction A → B were carried out and the conversion-rate data is given in Table P2-11.

What are the batch reactor times to achieve 10%, 50%, and 80% for the reactor A → B when the initial concentration is 2 molar?
Plot the reaction rate, –r_A, as a function of time up to a time necessary to achieve 80% conversion.

Additional Homework Problems can be found on the CRE Web site under Chapter 2 $\begin{matrix} A. EXERCISES \end{matrix}$ hot button.

Supplementary Reading

Further discussion of the proper staging of reactors in series for various rate laws, in which a plot of (=1/r_A) versus X is given, may or may not be presented in

THORNTON W. BURGESS, The Adventures of Poor Mrs. Quack, New York: Dover Publications, Inc., 1917.

CHESTER L. KARRASS, Effective Negotiating: Workbook and Discussion Guide, Beverly Hills, CA: Karrass Ltd., 2004.

OCTAVE LEVENSPIEL, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999, Chapter 6, pp. 139–156.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2. Conversion and Reactor Sizing

Create new playlist

Sign In

Sign Up

2. Conversion and Reactor Sizing

2.1 Definition of Conversion

2.2 Batch Reactor Design Equations

2.3 Design Equations for Flow Reactors

2.3.1 CSTR (Also Known as a Backmix Reactor or a Vat)

2.3.2 Tubular Flow Reactor (PFR)

2.3.3 Packed-Bed Reactor (PBR)

2.4 Sizing Continuous-Flow Reactors

2.5 Reactors in Series

2.5.1 CSTRs in Series

2.5.2 PFRs in Series

2.5.3 Combinations of CSTRs and PFRs in Series

2.5.4 Comparing the CSTR and PFR Volumes and Reactor Sequencing

2.6 Some Further Definitions

2.6.1 Space Time

2.6.2 Space Velocity

2.7 And Now… A Word from Our Sponsor–Safety 2 (AWFOS–S2 The NFPA Diamond)

Summary

CRE Web Site Materials

Questions and Problems

Questions

Interactive Computer Games

Problems

Supplementary Reading

Table of Contents for
2. Conversion and Reactor Sizing