4. Stoichiometry

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

4. Stoichiometry

If you are thinking about someone while reading this book, you are most definitely in love.

—Tim Newberger Undergraduate ChE Student W2013

Overview. In Chapter 2, we carried out the sizing and sequencing of flow reactors given the reaction rate, –r_A, as a function of conversion X. To find –r_A = f(X) is a two-step process. In Chapter 3, we described (Step 1) how the rate of reaction, –r_A, is related to concentration and temperature, that is, –r_A = [k_A(T)fn(C_A, C_B ...)]. In this chapter, we show how concentration can be related to conversion (Step 2), C_i = g(X), and once we do that, we will have –r_A = f(X) and can design a multitude of reaction systems. We will use stoichiometric tables, along with the definitions of concentration, to find the concentration as a function of conversion.

For batch systems the reactor is most always rigid, so V = V₀, and one then uses the stoichiometric table to express concentration as a function of conversion: C_A = N_A/V₀ = C_A0(1 – X).
For liquid-phase flow systems, the volumetric flow rate is considered to be constant, υ = υ₀, and C_A = (F_A0/υ₀)(1 – X) = C_A0(1 – X).
For gas-phase flow systems, the process becomes more complicated, as the volumetric flow rate for gases can vary with conversion, temperature, and pressure, and we need to develop the relationship relating υ and X, that is, υ = υ₀(1+ɛX)(P₀/P)(T/T₀) and thus

$C_{A} = \frac{C_{A 0} (1 - X)}{(1 + ε X)} \frac{P}{P_{0}} \frac{T_{0}}{T} = C_{A 0} \frac{(1 - X)}{(1 + ε X)} p \frac{T_{0}}{T}$
For most gas–solid catalyst reactions, the rate laws are typically written in terms of partial pressures, which can also be written in terms of conversion.

$P_{A} = C_{A} R T = P_{A 0} \frac{(1 - X)}{(1 + ε X)} \frac{P}{P_{0}} = P_{A 0} \frac{(1 - X)}{(1 + ε X)} p$

After completing this chapter, you will be able to write the rate of reaction as a function of conversion and calculate the equilibrium conversion for both batch and flow reactors.

Now that we have shown how the rate law can be expressed as a function of concentrations, we need only express concentration as a function of conversion and sequence in order to carry out calculations similar to those presented in Chapter 2 to size reactors. If the rate law depends on more than one species, we must relate the concentrations of the different species to each other. This relationship is most easily established with the aid of a stoichiometric table. This table presents the stoichiometric relationships between reacting molecules for single reactions. That is, it tells us how many molecules of one species will be formed during a chemical reaction when a given number of molecules of another species disappears. These relationships will be developed for the general reaction

$\begin{matrix} a A + b B ⇆ c C + d D & (2-1) \end{matrix}$

Recall that we have already used stoichiometry to relate the relative rates of reaction for Equation (2-1):

\begin{matrix} \frac{r_{A}}{- a} = \frac{r_{B}}{- b} = \frac{r_{C}}{c} = \frac{r_{D}}{d} & (3 - 1) \end{matrix}

This stoichiometric relationship relating reaction rates will be used in Chapters 6 and 8.

In formulating our stoichiometric table, we shall take species A as our basis of calculation (i.e., the limiting reactant) and then divide through by the stoichiometric coefficient of A

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2-2) \end{matrix}$

in order to put everything on a basis of “per mole of A.”

Next, we develop the stoichiometric relationships for reacting species that give the change in the number of moles of each species (i.e., A, B, C, and D).

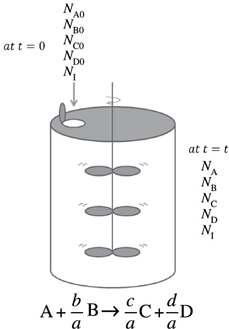
A figure shows a starving artist's rendition of a batch system. — **Figure 4-1** Batch reactor. (Schematic with special permission by Renwahr.) (*http://encyclopedia.che.engin.umich.edu/Pages/Reactors/Batch/Batch.html*)

A schematic representation by Renwahr shows the batch reactor carrying out the reaction given by the equation (2-2). The batch reactor is shown in the form of a sphere. At time t equals 0, number of moles of species A, B, C and D, and inerts I (N subscript AO, N subscript BO, N subscript CO, and N subscript IO, respectively) are placed into the reactor and the port hole is closed. At time t, the number of moles of species A, B, C and D, and inerts I remaining, are denoted as N subscript A, N subscript B, N subscript C, and N subscript I, respectively.

4.1 Batch Reactors (BRs)

Batch reactors (BRs) are primarily used for the production of specialty chemicals and to obtain reaction rate data in order to determine reaction-rate laws and rate-law parameters such as k, the specific reaction rate.

Figure 4-1 shows a starving artist’s rendition of a batch system in which we will carry out the reaction given by Equation (2-2). At time t = 0, we will open the reactor and place a number of moles of species A, B, C, and D, and inerts I (N_A0, N_B0, N_C0, N_D0, and N_I0, respectively) into the reactor and then of course close the port hole.

Species A is our basis of calculation, and N_A0 is the number of moles of A initially present in the reactor. After a time t, N_A0X moles of A are consumed in the system as a result of the chemical reaction, leaving (N_A0 – N_A0X) moles of A in the system. That is, the number of moles of A remaining in the reactor after a conversion X has been achieved is

N_A = N_A0 – N_A0X = N_A0(1 – X)

We now will use conversion in a similar fashion to express the number of moles of B, C, and D in terms of conversion.

To determine the number of moles of each species remaining after N_A0X moles of A have reacted, we form the stoichiometric table (Table 4-1). This stoichiometric table presents the following information:

TABLE 4-1 STOICHIOMETRIC TABLE FOR A BATCH SYSTEM

Species	Initially (mol)	Change (mol)	Remaining (mol)
A	N_A0	−(N_A0X)	N_A = N_A N_A0 – N_A0X
B	N_B0	$- \frac{b}{a} (N_{A0} X)$	$N_{B} = N_{B 0} - \frac{b}{a} N_{A0} X$
C	N_C0	$\frac{c}{a} (N_{A0} X)$	$N_{C} = N_{C 0} + \frac{c}{a} N_{A0} X$
D	N_D0	$\frac{d}{a} (N_{A0} X)$	$N_{D} = N_{D 0} + \frac{d}{a} N_{A0} X$
I (inerts)	N_I0	–	N_I = N_I0
Totals	N_T0		$N_{T} = N_{T0} + \underset{δ}{\underset{︸}{(\frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1)}} N_{A0} X$

Batch Reactor

Column 1: the species in the reaction

Column 2: the number of moles of each species initially present

Column 3: the change in the number of moles brought about by reaction

Column 4: the number of moles remaining in the system at time t

Components of the stoichiometric table

To calculate the number of moles of species B remaining at time t, we recall that at time t the number of moles of A that have reacted is N_A0X. For every mole of A that reacts, b/a moles of B must react; therefore, the total number of moles of B that have reacted is

$\begin{matrix} Moles B reacted = \frac{Moles B reacted}{Moles A reacted} \cdot Moles A reacted \\ = \frac{b}{a} (N_{A0} X) \end{matrix}$

Because B is disappearing from the system, the sign of the “change” is negative. N_B0 is the number of moles of B initially in the system. Therefore, the number of moles of B remaining in the system, N_B, at a time t, is the number of moles of B initially minus the moles of B that have reacted and is given in the last column of Table 4-1 as

$N_{B} = N_{B0} - \frac{b}{a} N_{A0} X$

The complete stoichiometric table delineated in Table 4-1 is for all species in the general reaction

\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2 - 2) \end{matrix}

Let’s take a look at the totals in the last column of Table 4-1. The stoichiometric coefficients in parentheses $\begin{matrix} (d / a + c / a - b / a - 1) \end{matrix}$ represent the change in the total number of moles per mole of A reacted. Because this term occurs so often in our calculations, it is given the symbol δ:

\begin{matrix} δ = \frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1 & (4 - 1) \end{matrix}

The parameter δ

Definition of δ

$δ = \frac{Change in the total number of moles}{Moles of A reacted}$

The total number of moles can now be calculated from the equation

N_T = N_T0 + δ(N_A0X)

We recall from Chapters 1 and 3 that the kinetic rate law (e.g., $- r_{A} = k C_{A}^{2}$ ) is a function solely of the intensive properties of the reacting system (e.g., temperature, pressure, concentration, and catalysts, if any). The reaction rate, –r_A, usually depends on the concentration of the reacting species raised to some power. Consequently, to determine the reaction rate as a function of conversion, X, we need to know the concentrations of the reacting species as a function of conversion, X. Let’s do it!

We want C_j = h_j (X)

4.1.1 Batch Concentrations for the Generic Reaction, Equation (2-2)

The concentration of A is the number of moles of A per unit volume

$C_{A} = \frac{N_{A}}{V}$

Batch concentration

After writing similar equations for B, C, and D, we use the stoichiometric table to express the concentration of each component in terms of the conversion X:

$\begin{matrix} C_{A} = \frac{N_{A}}{V} = \frac{N_{A0} (1 - X)}{V} & (4-2) \end{matrix}$

$\begin{matrix} C_{B} = \frac{N_{B}}{V} = \frac{N_{B 0} - (b / a) N_{A0} X}{V} & (4-3) \end{matrix}$

$\begin{matrix} C_{C} = \frac{N_{C}}{V} = \frac{N_{C 0} + (c / a) N_{A0} X}{V} & (4-4) \end{matrix}$

$\begin{matrix} C_{D} = \frac{N_{D}}{V} = \frac{N_{D 0} + (d / a) N_{A0} X}{V} & (4-5) \end{matrix}$

Because almost all batch reactors are solid vessels, the reactor volume is constant, so we can take V =V₀, then

$\begin{matrix} C_{A} = \frac{N_{A}}{V_{0}} = \frac{N_{A0} (1 - X)}{V_{0}} \end{matrix}$

\begin{matrix} C_{A} = C_{A0} (1 - X) & (4 - 6) \end{matrix}

Constant Volume, V = V₀

We will soon see that Equation (4-6) for constant-volume batch reactors also applies to continuous-flow liquid-phase systems.

We further simplify these equations by defining the parameter Θ_i, which allows us to factor out N_A0 in each of the expressions for concentration

$\begin{matrix} Θ_{i} = \frac{N_{i 0}}{N_{A0}} = \frac{C_{i 0}}{C_{A0}} = \frac{y_{i 0}}{y_{A0}}, \\ Θ_{i} = \frac{Moles of species “ i ” initially}{Moles of species A initially} \end{matrix}$

$C_{B} = \frac{N_{A0} [N_{B 0} / N_{A0} - (b / a) X]}{V_{0}} = \frac{N_{A0} [Θ_{B} - (b / a) X]}{V_{0}}$

\begin{matrix} C_{B} = C_{A0} (Θ_{B} - \frac{b}{a} X) & (4 - 7) \end{matrix}

with $Θ_{B} = \frac{N_{B0}}{N_{A 0}}$

Feed

Equalmolar:

Θ_B = 1

Stoichiometric:

$Θ_{B} = \frac{b}{a}$

for an equalmolar feed Θ_B = 1 and for a stoichiometric feed Θ_B = b/a.

Continuing for species C and D

$\begin{matrix} C_{C} = \frac{N_{A0} [Θ_{C} + (c / a) X]}{V_{0}} \\ C_{C} = C_{A0} (Θ_{C} + \frac{c}{a} X) & (4-8) \end{matrix}$

$with Θ_{C} = \frac{N_{C0}}{N_{A0}}$

Concentration for constant-volume batch reactors and for liquid-phase continuous-flow reactors

$\begin{matrix} C_{D} = \frac{N_{A0} [Θ_{D} + (d / a) X]}{V_{0}} \\ C_{D} = C_{A0} (Θ_{D} + \frac{d}{a} X) & (4-9) \end{matrix}$

$with Θ_{D} = \frac{N_{D 0}}{N_{A0}}$

For constant-volume batch reactors, for example, steel containers V = V₀, we now have concentration as a function of conversion. If we know the rate law, we can now obtain –r_A = f(X) to couple with the differential mole balance in terms of conversion in order to solve for the reaction time, t, to achieve a spec-ified conversion, X.

For liquid-phase reactions taking place in solution, the solvent usually dominates the situation. For example, most liquid-phase organic reactions do not change density during the course of the reaction and represent still another case for which the constant-volume simplifications apply. As a result, changes in the density of the solute do not affect the overall density of the solution significantly and therefore it is essentially a constant-volume reaction process, V = V₀ and υ = υ₀. Consequently, Equations (4-6)–(4-9) can be used for liquid-phase reactions as well as constant-volume (V = V₀) gas-phase reactions. An important exception to this general rule exists for some polymerization processes.

For liquids V = V₀ and υ = υ₀

To summarize for constant-volume batch systems and for liquid-phase reactions, we can use a rate law for Reaction (2-2) such as –r_A = k_AC_AC_B to obtain = f(X); that is,

$- r_{A} = k C_{A} C_{B} = k C_{A0}^{2} (1 - X) (Θ_{B} - \frac{b}{a} X) = f (X)$

A graph depicting V subscript PFR. — The plot of F subscript A0 over negative r subscript A versus X is depicted. The graph is a curve which is concave up and increasing. The region below the curve is represented as V subscript PFR.

Substituting for the given parameters k, C_A0, and Θ_B, we can now use the techniques in Chapter 2 to size the CSTRs and PFRs for liquid-phase reactions.

Example 4–1 Expressing C_j = h_j (X) for a Liquid-Phase Batch Reaction

Soap is necessary to clean such things as dirty softball and soccer players’ uniforms, dirty hands, and foul mouths. Soap consists of the sodium and potassium salts of various fatty acids, such as oleic, stearic, palmitic, lauric, and myristic acids. The saponification reaction for the formation of soap from aqueous caustic soda and glyceryl stearate is

3NaOH(aq) (C₁₇ H₃₅COO)₃C₃ H₅ → 3C₁₇ H₃₅COONa + C₃ H₅(OH)₃

Letting X represent the conversion of sodium hydroxide (the moles of sodium hydroxide reacted per mole of sodium hydroxide initially present), set up a stoichiometric table expressing the concentration of each species in terms of its initial concentration and the conversion, X.

Solution

Because we have taken sodium hydroxide as our basis of calculation, we divide through by the stoichiometric coefficient of sodium hydroxide to put the reaction expression in the form

$\begin{matrix} NaOH + \frac{1}{3} (C_{17} H_{35} {COO)}_{3} C_{3} H_{5} \to C_{17} H_{35} COONa + \frac{1}{3} C_{3} H_{5} (OH)_{3} \end{matrix}$

$\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} A & + \end{matrix} & \frac{1}{3} \end{matrix} B & \to \end{matrix} & C \end{matrix} & + \end{matrix} & \frac{1}{3} D \end{matrix}$

Choosing a basis of calculation

We may next perform the calculations shown in Table E4-1.1. Because this reaction is a liquid-phase reaction, the density ρ is considered to be constant; therefore, V = V₀

$\begin{matrix} C_{A} = \frac{N_{A}}{V} = \frac{N_{A}}{V_{0}} = \frac{N_{A0} (1 - X)}{V_{0}} = C_{A0} (1 - X) \\ Θ_{B} = \frac{C_{B0}}{C_{A0}} Θ_{C} = \frac{C_{C 0}}{C_{A0}} Θ_{D} = \frac{C_{D0}}{C_{A0}} \end{matrix}$

TABLE E4-1.1 STOICHIOMETRIC TABLE FOR LIQUID-PHASE SOAP REACTION

Species	Symbol	Initially	Change	Remaining	Concentration
NaOH	A	N_A0	–N_A0 X	N_A0 (1 – X)	C_A0 (1 – X)
(C₁₇ H₃₅COO)₃C₃ H₅	B	N_B0	$- \frac{1}{3} N_{A0} X$	$N_{A0} (Θ_{B} - \frac{X}{3})$	$C_{A0} (Θ_{B} - \frac{X}{3})$
C₁₇ H₃₅COONa	C	N_C0	N_A0 X	N_A0(Θ_C + X)	C_A0(Θ_C + X
C₃ H₅(OH)₃	D	N_D0	$- \frac{1}{3} N_{A0} X$	$N_{A0} (Θ_{D} + \frac{X}{3})$	$C_{A0} (Θ_{D} + \frac{X}{3})$
Water (inert)	I	N₁₀	–	N₁₀	C_I0
Totals		N_T0	0	N_T = N_T0

Stoichiometric table (batch)

Analysis: The purpose of this example was to show how the generic reaction in Table 4-1 is applied to a real reaction and how to develop the corresponding stoichiometric table.

Example 4–2 What Is the Limiting Reactant?

Having set up the stoichiometric table in Example 4-1, one can now readily use it to calculate the concentrations at a given conversion. If the initial mixture consists of sodium hydroxide at a concentration of 10 mol/dm³ (i.e., 10 mol/L or 10 kmol/m³) and glyceryl stearate at a concentration of 2 mol/dm³, what are the concentrations of glycerol stearate, B, and of glycerine, D, when the conversion of sodium hydroxide is (a) 20% and (b) 90%?

NFPA Diamond of Nitrogen Tetroxide. — A 2-dimensional rhombus shown with four divisions and different shades represents the diamond levels of Nitrogen Tetroxide. The level of health hazard is 3, fire and instability hazards are 0, and OX is a specific hazard.

Glyceryl Stearate (Chapter 2 AWFOS–S2)

Solution

Only the reactants NaOH and (C₁₇ H₃₅COO)₃C₃ H₅ are initially present; therefore, Θ_C = Θ_D = 0.

For 20% conversion of NaOH

$\begin{matrix} C_{D} = C_{A0} (\frac{X}{3}) = (10) (\frac{0.2}{3}) = 0.67 mol/L = 0.67 mol/d m^{3} \\ C_{B} = C_{A0} (Θ_{B} - \frac{X}{3}) = 10 (\frac{2}{10} - \frac{0.2}{3}) = 10 (0.133) = 1.33 mol/d m^{3} \end{matrix}$
For 90% conversion of NaOH

$C_{D} = C_{A0} (\frac{X}{3}) = 10 (\frac{0.9}{3}) = 3 mol/d m^{3}$

Let us find C_B

$C_{B} = 10 (\frac{2}{10} - \frac{0.9}{3}) = 10 (0.2 - 0.3) = - 1 mol/d m^{3}$

Oops!! Negative concentration—impossible! What went wrong?

Analysis: We purposely chose the wrong basis of calculation to make the point that we must choose the limiting reactant as our basis of calculation!! Ninety-percent conversion of NaOH is not possible because glyceryl stearate is the limiting reactant and is used up before 90% of the NaOH can be reacted. Glyceryl stearate should have been our basis of calculation and therefore we should not have divided the reaction as written by the stoichiometric coefficient of 3. It’s always important to make sure you learn something from a mistake, such as choosing the wrong basis of calculation. There is no such thing as failure, unless one fails to learn from it.

The basis of calculation must be the limiting reactant.

#LifeLesson!

4.2 Flow Systems

The form of the stoichiometric table for a continuous-flow system (see Figure 4-2) is virtually identical to that for a batch system (Table 4-1), except that we replace N_j₀ by F_j₀ and N_j by F_j (Table 4-2). Again taking A as the basis, we divide Equation (2-1) through by the stoichiometric coefficient of A to obtain

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2-2) \end{matrix}$

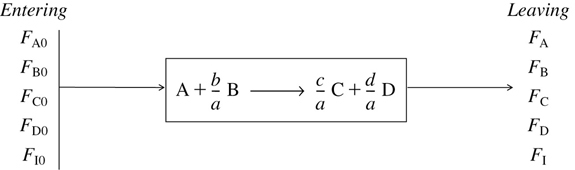
The figure illustrates the flow reactor. — **Figure 4-2** Flow reactor.

The flow reaction takes place as follows. The entering and the leaving group are at the sides. The reaction is as follows. Upper A plus b over a, times upper B gives c over a, times upper C plus d over a, times upper D. The entering group includes F subscript A0, F subscript B0, F subscript C0, F subscript D0, and F subscript I0. The leaving group includes F subscript A, F subscript B, F subscript C, F subscript D, and F subscript I.

TABLE 4-2 STOICHIOMETRIC TABLE FOR A FLOW SYSTEM

Species	Feed Rate to Reactor (mol/time)	Change within Reactor (mol/time)	Effluent Rate from Reactor (mol/time)
A	F_A0	–F_A0X	F_A = F_A0 (1 – X)
B	F_B0 = Θ_BF_A0	$- \frac{b}{a} F_{A0} X$	$F_{B} = F_{A0} (Θ_{B} - \frac{b}{a} X)$
C	F_C0 = Θ_CF_A0	$\frac{c}{a} F_{A0} X$	$F_{C} = F_{A0} (Θ_{C} + \frac{c}{a} X)$
D	F_D0 = Θ_DF_A0	$\frac{d}{a} F_{A0} X$	$F_{D} = F_{A0} (Θ_{D} + \frac{d}{a} X)$
I	F_I0= Θ_IF_A0	–	F_I = F_A0θ_I
Totals	F_T0		$F_{T} = F_{T0} + (\frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1) F_{A0} X$
			F_T = F_T0 + δF_A0 X

Stoichiometric table for a flow system

where

$Θ_{B} = \frac{F_{B0}}{F_{A0}} = \frac{C_{B0} υ_{0}}{C_{A0} υ_{0}} = \frac{C_{B0}}{C_{A0}} = \frac{y_{B0}}{y_{A0}}$

and Θ_C, Θ_D, and Θ_I are defined similarly

and, as before,

\begin{matrix} δ = \frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1 & (4 - 1) \end{matrix}

4.2.1 Equations for Concentrations in Flow Systems

For a flow system, the concentration C_A at a given point can be determined from the molar flow rate F_A and the volumetric flow rate υ at that point:

\begin{matrix} C_{A} = \frac{F_{A}}{υ} = \frac{moles/time}{liters/time} = \frac{moles}{liter} & (4 - 10) \end{matrix}

Definition of concentration for a flow system

Units of υ are typically given in terms of liters per second, cubic decimeters per second, or cubic feet per minute. We now can write the concentrations of A, B, C, and D for the general reaction given by Equation (2-2) in terms of their respective entering molar flow rates (F_A0, F_B0, F_C0, F_D0), the conversion, X, and the volumetric flow rate, υ.

$\begin{matrix} C_{A} = \frac{F_{A}}{υ} = \frac{F_{A0}}{υ} (1 - X) & C_{B} = \frac{F_{B}}{υ} = \frac{F_{B0} - (b / a) F_{A0} X}{υ} \\ C_{C} = \frac{F_{C}}{υ} = \frac{F_{C 0} + (c / a) F_{A0} X}{υ} & C_{D} = \frac{F_{D}}{υ} = \frac{F_{D 0} - (d / a) F_{A0} X}{υ} & (4-11) \end{matrix}$

We now focus on determining the volumetric flow rate, υ.

4.2.2 Liquid-Phase Concentrations

For liquids, the fluid volume change with reaction is negligible when no phase changes are taking place. Consequently, we can take

υ = υ₀

Then

Tap water flows to a container placed below the tap.

\begin{matrix} C_{A} = \frac{F_{A0}}{υ_{0}} (1 - X) = C_{A0} (1 - X) & (4-12) \end{matrix}

\begin{matrix} C_{B} = C_{A0} (Θ_{B} - \frac{b}{a} X), & (4-13) \end{matrix}

For liquids

C_A = C_A0(1 – X)

$C_{B} = C_{A0} (Θ_{B} - \frac{b}{a} X)$

Therefore, for a given rate law we have –r_A = g(X)

and so forth, for C_C and C_D.

Consequently, using any one of the rate laws in Chapter 3, we can now find –r_A = f(X) for liquid-phase reactions. However, for gas-phase reactions the volumetric flow rate most often changes during the course of the reaction because of a change in the total number of moles or a change in temperature or pressure. Hence, one cannot always use Equation (4-13) to express concentration as a function of conversion for gas-phase reactions. No worries. In the next section we will sort this out.

4.2.3 Gas-Phase Concentrations

In our previous discussions, we considered primarily systems in which the reaction volume or volumetric flow rate did not vary as the reaction progressed. Most batch and liquid-phase and some gas-phase systems fall into this category. There are other systems, though, in which either V or υ does vary, and these will now be considered.

A situation where one encounters a varying flow rate occurs quite frequently in gas-phase reactions that do not have an equal number of product and reactant moles. For example, in the synthesis of ammonia

N₂ + 3H₂ ⇄ 2NH₃

4 mol of reactants gives 2 mol of product. In flow systems where this type of reaction occurs, the molar flow rate will be changing as the reaction progresses. Because equal numbers of moles occupy equal volumes in the gas phase at the same temperature and pressure, the volumetric flow rate will also change.

#We’reGood The same stoichiometric table holds for both liquid-phase and gas-phase reactions.

In the stoichiometric tables presented on the preceding pages, it was not necessary to make assumptions concerning a volume change in the first four columns of the table (i.e., the species, initial number of moles or molar feed rate, change within the reactor, and the remaining number of moles or the molar effluent rate). All of these columns of the stoichiometric table are independent of the volume or density, and they are identical for constant-volume (constant-density) and varying-volume (varying-density) situations. Only when concentration is expressed as a function of conversion does variable density enter the picture.

Flow Reactors with Variable Volumetric Flow Rate. To derive the concentrations of each species in terms of conversion for a gas-phase flow system, we shall start by using the relationships for the total concentration. The total concentration, C_T, at any point in the reactor is the total molar flow rate, F_T, divided by the volumetric flow rate, υ (cf. Equation (4-10)). In the gas phase, the total concentration is also found from the gas law, C_T = P/ZRT. Equating these two relationships gives

$\begin{matrix} C_{T} = \frac{F_{T}}{υ} = \frac{P}{Z R T} & (4-14) \end{matrix}$

At the entrance to the reactor

$\begin{matrix} C_{T0} = \frac{F_{T0}}{υ_{0}} = \frac{P_{0}}{Z_{0} R T_{0}} & (4-15) \end{matrix}$

Taking the ratio of Equation (4-14) to Equation (4-15) and assuming negligible changes in the compressibility factor occur, that is, Z ≅ Z₀, during the course of the reaction, we have upon rearrangement

\begin{matrix} υ = υ_{0} (\frac{F_{T}}{F_{T0}}) \frac{P_{0}}{P} (\frac{T}{T_{0}}) & (4 - 16) \end{matrix}

Gas-phase reactions

We can now express the concentration of species j for a flow system in terms of its flow rate, F_j, the temperature, T, and total pressure, P.

$C_{j} = \frac{F_{j}}{υ} = \frac{F_{j}}{υ_{0} (\frac{F_{T}}{F_{T} 0} \frac{P_{0}}{P} \frac{T}{T_{0}})} = (\frac{F_{T0}}{υ_{0}}) (\frac{F_{j}}{F_{T}}) (\frac{P}{P_{0}}) (\frac{T_{0}}{T})$

\begin{matrix} C_{j} = C_{T0} = (\frac{F_{j}}{F_{T}}) (\frac{P}{P_{0}}) (\frac{T_{0}}{T}) & (4 - 17) \end{matrix}

Use this gas-phase concentration equation for membrane reactors (Chapter 6) and for multiple reactions (Chapter 8).

The total molar flow rate is just the sum of the molar flow rates of each of the species in the system and is

$\begin{matrix} \begin{matrix} F_{T} = F_{A} + F_{B} + F_{C} + F_{D} + F_{I} + ... = Σ_{j = 1}^{n} & F_{j} \end{matrix} & (4-18) \end{matrix}$

We can also write Equation (4-17) in terms of the mole fraction of species j, y_j, and the pressure ratio, p, with respect to the initial or entering conditions, that is, sub “0”

$\begin{matrix} y_{i} = \frac{F_{j}}{F_{T}} \\ p = \frac{P}{P_{0}} \end{matrix}$

\begin{matrix} C_{j} = C_{T0} y_{j} p \frac{T_{0}}{T} & (\begin{matrix} 4 - 19 \end{matrix}) \end{matrix}

A figure shows a balloon. — The blown balloon is taken as an example of the gas phase.

The molar flow rates, F_j, are found by solving the mole balance equations. The concentration given by Equation (4-17) will be used for measures other than conversion when we discuss membrane reactors (Chapter 6) and multiple gas-phase reactions (Chapter 8).

Now, let’s express the concentration in terms of conversion for gas flow systems. From Table 4-2, the total molar flow rate can be written in terms of conversion and is

F_T = F_T0 + F_A0 δX

We divide this equation through by F_T0

$\frac{F_{T}}{F_{T0}} = 1 + \frac{F_{A0}}{F_{T0}} δ X = 1 + \overset{ε}{\overset{︷}{y_{A0} δ}} X$

Then

$\begin{matrix} \frac{F_{T}}{F_{T0}} = 1 + ε X & (4-20) \end{matrix}$

where y_A0 is the mole fraction of A at the inlet (i.e., (F_A0/F_T0)), and where δ is given by Equation (4-1) and ɛ is given by

$ε = (\frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1) \frac{F_{A0}}{F_{T0}} = y_{A0} δ$

\begin{matrix} ε = y_{A0} δ & (4 - 21) \end{matrix}

Relationship between δ and ɛ

Equation (4-21) holds for both batch and flow systems. To interpret ɛ, let’s rearrange Equation (4-20) at complete conversion (i.e., X = 1 and F_T = F_T_f)

$ε = \frac{F_{T f} - F_{T0}}{F_{T0}}$

\begin{matrix} ε = \frac{Chane in total number of moles for complete conversion}{Total moles fed} & (4 - 22) \end{matrix}

Interpretation of ɛ

Substituting for (F_T/F_T0) in Equation (4-16) for the volumetric flow rate, υ, we have

\begin{matrix} υ = υ_{0} (1 + ε X) \frac{P_{0}}{P} (\frac{T}{T_{0}}) & (4 - 23) \end{matrix}

Gas-phase volumetric flow rate

The concentration of species j in a flow system is

$\begin{matrix} C_{j} = \frac{F_{j}}{v} & (4-24) \end{matrix}$

The molar flow rate of species j is

F_j = F_j₀ + v_j (F_A0X) = F_A0= (Θ_j + v_jX)

where v_j is the stoichiometric coefficient for species j, which is negative for reactants and positive for products. For example, for the reaction

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (2-2) \end{matrix}$

ν_A = –1, ν_B = –b/a, ν_C = c/a, ν_D = d/a, and Θ_j = F_j₀/F_A0.

Substituting for the gas volumetric flow rate, υ, using Equation (4-23) and for F_j, we have

$C_{j} = \frac{F_{A0} (Θ_{j} + ν_{j} X)}{υ_{0} ((1 + ε X) \frac{P_{0}}{P} \frac{T}{T_{0}})}$

Rearranging

\begin{matrix} C_{j} = \frac{C_{A0} (Θ_{j} + v_{j} X)}{1 + ε X} (\frac{P}{P_{0}}) \frac{T_{0}}{T} & (4 - 25) \end{matrix}

Gas-phase concentration as a function of conversion

Recall that y_A0 = F_A0/F_T0, C_A0 = y_A0C_T0, and ɛ is given by Equation (4-21) (i.e., ɛ = y_A0δ).

The stoichiometric table for the gas-phase reaction (2-2) is given in Table 4-3.

TABLE 4-3 CONCENTRATIONS IN A VARIABLE-VOLUME GAS FLOW SYSTEM

$C_{A} = \frac{F_{A}}{υ} = \frac{F_{A0} (1 - X)}{υ}$	$= \frac{F_{A0} (1 - X)}{υ_{0} (1 - ε X)} (\frac{T_{0}}{T}) \frac{P}{P_{0}}$	$= C_{A0} (\frac{1 - X}{1 + ε X}) \frac{T_{0}}{T} (\frac{P}{P_{0}})$
$C_{B} = \frac{F_{B}}{υ} = \frac{F_{A0} [Θ_{B} - (b / a) X]}{υ}$	$= \frac{F_{A0} [Θ_{B} - (b / a) X]}{υ_{0} (1 + ε X)} (\frac{T_{0}}{T}) \frac{P}{P_{0}}$	$= C_{A0} (\frac{Θ_{B} - (b / a) X}{1 + ε X}) \frac{T_{0}}{T} (\frac{P}{P_{0}})$
$C_{C} = \frac{F_{C}}{υ} = \frac{F_{A0} [Θ_{C} + (c / a) X]}{υ}$	$= \frac{F_{A0} [Θ_{C} + (c / a) X]}{υ_{0} (1 + ε X)} (\frac{T_{0}}{T}) \frac{P}{P_{0}}$	$= C_{A0} (\frac{Θ_{C} + (c / a) X}{1 + ε X}) \frac{T_{0}}{T} (\frac{P}{P_{0}})$
$C_{D} = \frac{F_{D}}{υ} = \frac{F_{A0} [Θ_{D} + (d / a) X]}{υ}$	$= \frac{F_{A0} [Θ_{D} + (d / a) X]}{υ_{0} (1 + ε X)} (\frac{T_{0}}{T}) \frac{P}{P_{0}}$	$= C_{A0} (\frac{Θ_{D} + (d / a) X}{1 + ε X}) \frac{T_{0}}{T} (\frac{P}{P_{0}})$
$C_{I} = \frac{F_{I}}{υ} = \frac{F_{A0} Θ_{I}}{υ}$	$= \frac{F_{A0} Θ_{I}}{υ_{0} (1 + ε X)} (\frac{T_{0}}{T}) \frac{P}{P_{0}}$	$= \frac{C_{A0} Θ_{I}}{1 + ε X} \frac{T_{0}}{T} (\frac{P}{P_{0}})$

At last!

We now have

C_j = h_j (X)

and

–r_A = g(X)

for variable-volume gas-phase reactions.

One of the major objectives of this chapter is to learn how to express any given rate law –r_A as a function of conversion. The schematic diagram in Figure 4-3 helps to summarize our discussion on this point. The concentration of the reactant species B in the generic reaction is expressed as a function of conversion in both flow and batch systems for various conditions of temperature, pressure, and volume.

At last, by coupling Table 4-3 with the rate law for single gas-phase reactions, we obtain what we needed and used in Chapter 2 to size and sequence flow reactors, that is,

–r_A = f(X)

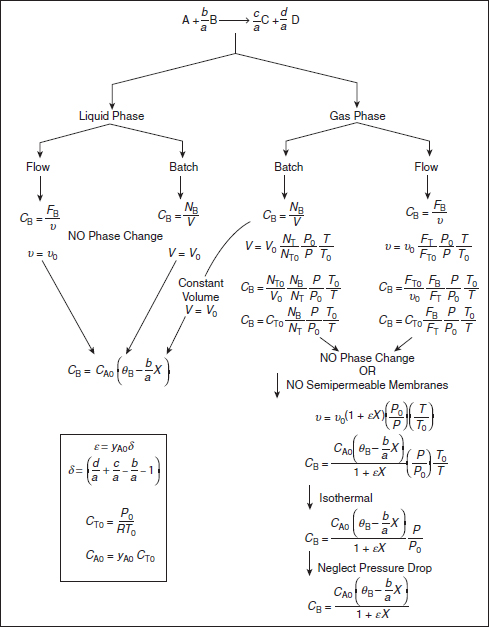
Steps to express as a function of conversion. — **Figure 4-3** Expressing concentration as a function of conversion.

The flow chart is as follows: upper A plus b over a, times upper B gives c over a, times upper C plus d over a, times upper D. This reaction is divided into liquid phase and gas phase. Liquid phase is divided as flow and batch. Flow is represented with Upper C subscript upper B equals upper F subscript upper B over v and batch is represented with Upper C subscript upper B equals upper N subscript upper B over V. No phase change occurs in the liquid phase. Here, v equals v subscript 0 and upper V equals upper V subscript 0 combines with the constant volume upper V equals upper V subscript 0 to give Upper C subscript upper B equals upper C subscript upper A0 times (theta subscript upper B minus b over a, times X). Gas phase comprises of batch and flow types. The batch type is as follows: Upper C subscript upper B equals upper N subscript upper B over v; upper V equals upper V subscript 0, times upper N subscript upper T over upper N subscript upper T0, times upper P subscript 0 over upper P, times upper T over upper T subscript 0; Upper C subscript upper B equals upper N subscript upper T0 over upper V subscript 0, times upper N subscript upper B over upper N subscript upper T, times upper P over upper P subscript 0, times upper T subscript 0 over upper T; Upper C subscript upper B equals upper C subscript upper T0, times upper N subscript upper B over upper N subscript upper T, times upper P over upper P subscript 0, times upper T subscript 0 over upper T; The flow system is as follows: Upper C subscript upper B equals upper F subscript upper B over nu; v equals v subscript 0, times upper F subscript upper T over upper F subscript upper T0, times upper P subscript 0 over upper P, times upper T over upper T subscript 0; Upper C subscript upper B equals upper F subscript upper T0 over v subscript 0, times upper F subscript upper B over upper F subscript upper T, times upper P over upper P subscript 0, times upper T subscript 0 over upper T; Upper C subscript upper B equals upper C subscript upper T0, times upper F subscript upper B over upper F subscript upper T, times upper P over upper P subscript 0, times upper T subscript 0 over upper T. No phase change or no semi permeable membranes are observed in the gas phase. v equals v subscript 0 ( 1 plus epsilon X) times (upper P subscript 0 over upper P) times (upper T over upper T subscript 0); upper C subscript upper B equals upper C subscript upper A0 times (theta subscript upper B minus b over a, times X) over 1 plus epsilon X, times (upper P over upper P subscript 0) times upper T subscript 0 over upper T; under isothermal conditions, upper C subscript upper B equals upper C subscript upper A0, times (theta subscript upper B minus, b over a, times X) over 1 plus epsilon X, times upper P over upper P subscript 0; Under neglect pressure drop, upper C subscript upper B equals upper C subscript upper A0, times (theta subscript upper B minus b over a, times X) over 1 plus epsilon X. Also the following equations are provided: Epsilon equals y subscript upper A0 times delta; delta equals (d over a, plus c over a, minus b over a, minus 1); upper C subscript upper T0 baseline equals upper P subscript 0 over upper R upper T subscript 0; upper C subscript upper A0 baseline equals y subscript upper A0 times upper C subscript upper T0.

Example 4–3 Determining C_j = h_j (X) for a Gas-Phase Reaction

A mixture of 28% SO₂ and 72% air is charged to a flow reactor in which is oxidized.

2SO₂ + O₂ → 2SO₃

First, set up a stoichiometric table using only the symbols (i.e., Θ_i, F_i ).
Next, prepare a second table evaluating the species concentrations as a function of conversion for the case when the total pressure is 1485 kPa (14.7 atm) and the temperature is constant at 227°C.
Evaluate the parameters and make a plot of each of the concentrations SO₂, SO₃, N₂ as a function of conversion.

Solution

Stoichiometric table. Taking SO₂ as the basis of calculation, we divide the reaction through by the stoichiometric coefficient of our chosen basis of calculation

$SO_{2} + \frac{1}{2} O_{2} \to {SO}_{3}$

The stoichiometric table is given in Table E4-3.1.

TABLE E4-3.1 STOICHIOMETRIC TABLE FOR $SO_{2} + \frac{1}{2} O_{2} \to {SO}_{3}$

Species	Symbol	Initially	Change	Remaining
SO₂	A	F_A0	–F_A0X	F_A F_A0 (1 – X)
O₂	B	F_B0 = Θ_BF_A0	$- \frac{F_{A0} X}{2}$	$F_{B} = F_{A0} (Θ_{B} - \frac{1}{2} X)$
SO₃	C	0	+F_A0X	F_C = F_A0X
N₂	I	F_I0 = Θ_IF_A0	–	F_I = F_I0 = Θ_IF_A0
Totals		F_T0		$F_{T} = F_{T0} - \frac{F_{A0} X}{2}$

Expressing the concentration as a function of conversion. From the definition of conversion, we substitute not only for the molar flow rate of SO₂ (A) in terms of conversion but also for the volumetric flow rate as a function of conversion

$C_{A} = \frac{F_{A}}{υ} = \frac{F_{A0} (1 - X)}{υ}$

Recalling Equation (4-23), we have

$\begin{matrix} υ = υ_{0} (1 + ε X) \frac{P_{0}}{P} (\frac{T}{T_{0}}) & (4 - 23) \end{matrix}$

Neglecting pressure drop in the reaction, P = P₀, yields

$υ = υ_{0} (1 + ε X) \frac{T}{T_{0}}$

Neglecting pressure drop, P = P₀, that is, $p = \frac{p}{p_{0}} \approx 1$

If the reaction is also carried out isothermally, T = T₀, we obtain

υ = υ₀(1 + ɛX)

$\begin{matrix} C_{A} = \frac{F_{A0} (1 - X)}{υ_{0} (1 + ε X)} = C_{A0} (\frac{1 - X}{1 + ε X}) & (E4-3 .1) \end{matrix}$

Isothermal operation, T = T₀

Similarly for B also with T = T₀ and P = P₀ (i.e., p = 1)

$\begin{matrix} C_{B} = C_{A0} \frac{(Θ_{B} - \frac{b}{a} X)}{1 + ε X} p \frac{T_{0}}{T} = \frac{C_{A0} (Θ_{B} - \frac{1}{2} X)}{1 + ε X} & (E4-3 .2) \end{matrix}$
Parameter evaluation and plots of concentrations as a function of conversion. The inlet concentration of A is equal to the inlet mole fraction of A multiplied by the total inlet molar concentration. The total concentration can be calculated from an equation of state such as the ideal gas law. Recall that y_A0 = 0.28, T₀ = 500 K, and P₀ = 1485 kPa.

$C_{A0} = y_{A0} C_{T0} = y_{A0} (\frac{P_{0}}{R T_{0}})$

$\begin{matrix} = 0.28 [\frac{1485 kPa}{8.314 kPa \cdot {dm}^{3} / (mol \cdot K) \times 500 K}] \\ = \begin{matrix} 0.1 {mol/dm}^{3} & \underline{\begin{matrix} Answer \end{matrix}} \end{matrix} \end{matrix}$

The total concentration at constant temperature and pressure is

Images

$C_{T0} = \frac{P_{o}}{R T_{o}} = \frac{1485 kpa}{[8.314 kPa \cdot {dm}^{3} / (mol \cdot K)] (500 K)} = 0.357 \frac{mol}{{dm}^{3}} (E4-3.4)$

We now evaluate ɛ.

$ɛ = y_{A 0} δ = (0.28) (1 - 1 - \frac{1}{2}) = - 0.14 (E4-3.5)$

Initially, 72% of the total number of moles is air containing 21% O₂ and 79% N₂, along with 28% SO₂.

$\begin{matrix} \begin{array}{l} F_{A0} = (0.28) (F_{T0}) \\ F_{B0} = (0.72) (0.21) (F_{T0}) \\ Θ_{B} = \frac{F_{B 0}}{F_{A0}} = \frac{(0.72) (0.21)}{0.28} = 0.54 \\ Θ_{I} = \frac{F_{I 0}}{F_{A0}} = \frac{(0.72) (0.79)}{0.28} \end{array} & \underline{Answer} \end{matrix}$

Substituting for C_A0 and ɛ in the species concentrations:

${SO}_{2 :} C_{A} = C_{A0} (\frac{1 - X}{1 + ϵ X}) = 0.1 (\frac{1 - X}{1–0.14 X}) {mol/dm}^{3} (E4-3.6)$

O_{2 :} C_{B} = C_{A0} (\frac{Θ_{B} - \frac{1}{2} X}{1 + ϵ X}) = \frac{0.1 (0.54–0.5 X)}{1–0.14 X} {mol/dm}^{3} (E4-3.7)

{S O}_{3 :} C_{c} = (\frac{C_{A0} X}{1 + ϵ X}) = \frac{0.1 X}{1–0.14 X} {mol/dm}^{3} (E4-3.8)

\begin{matrix} \begin{matrix} N_{2} : & C_{1} = \frac{C_{A0} Θ_{1}}{1 + ε X} \end{matrix} = \frac{(0.1) (2.03)}{1 - 0.14 X} {mol/dm}^{3} & (E4-3.9) \end{matrix}

The concentrations of different species at various conversions are calculated in Table E4-3.2 and plotted in Figure E4-3.1. Note that the concentration of is changing even though it is an inert species in this reaction!! #Seriously?

TABLE E4-3.2 CONCENTRATION AS A FUNCTION OF CONVERSION

		C_i (mol/dm³)
Species		X = 0.0	X = 0.25	X = 0.5	X = 0.75	X = 1.0
SO₂	C_A =	0.100	0.078	0.054	0.028	0.000
O₂	C_B =	0.054	0.043	0.031	0.018	0.005
SO₃	C_C =	0.000	0.026	0.054	0.084	0.116
N₂	C_I =	0.203	0.210	0.218	0.227	0.236
Total	C_T =	0.357	0.357	0.357	0.357	0.357

The plot of concentration versus conversion. — **Figure E4-3.1** Concentration as a function of conversion.

A graph with the vertical axis representing concentration (moles per cubic decimeter) and the horizontal axis representing conversion, X is shown. Concentration on the vertical axis ranges from 0.00 to 0.25 in increments of 0.05. Conversion on the horizontal axis ranges from 0.1 to 1.0 in increments of 0.1. Four lines are plotted which represent four compounds. The line representing dinitrogen, starts at 0.21 when X is 0 and linearly increases to 0.24, at X equals 1. The line representing sulfur dioxide, starts at 0.10 when X is 0 and linearly decreases to 0, at X equals 1. The line representing sulfur trioxide, starts at 0 when X is 0 and linearly increases to 0.12, at X equals 1. The line representing oxygen, starts at 0.05 when X is 0 and linearly decreases to 0.01, at X equals 1. The mentioned values are approximate.

Note: Because the volumetic flow rate varies with conversion, υ = υ₀(1 – 0.14X), the concentration of inerts (N₂) is not constant.

Now we could use techniques presented in Chapter 2 to size reactors.

We are now in a position to express –r_A as a function of X and use the techniques in Chapter 2 to size and sequence reactors. However, we will use a better method to solve CRE problems, namely a Table of Integrals (Appendix A) or the Polymath, MATLAB, Wolfram, or Python software, discussed in the next chapter.

Analysis: In this example, we first formed a stoichiometric table in terms of molar flow rates. We then showed how to express the concentrations of each species in a gas-phase reaction in which there is a change in the total number of moles. Next, we plotted each species concentration as a function of conversion and noted that the concentration of the inert, N₂, was not constant but increased with increasing conversion because of the decrease in the total molar flow rate, F_T, with conversion.

As previously mentioned many, if not most, rate laws for catalyst reactions are given in terms of partial pressures. Luckily, partial pressures are easily related to conversion with the aid of the ideal gas law and Equation (4-17).

$P_{i} = C_{i} R T = C_{T0} \frac{F_{i}}{F_{T}} \overset{p}{\overset{︷}{(\frac{P}{P_{0}})}} \frac{T_{0}}{T} R T = \overset{P_{T 0}}{\overset{︷}{C_{T0} R T_{0}}} \overset{y_{i}}{\overset{︷}{\frac{F_{i}}{F_{T}}}} p$

The following equation is used when the mole balance is written in terms of molar flow rates:

\begin{matrix} P_{i} = P_{T0} (\frac{F_{i}}{F_{T}}) p \end{matrix} (4 - 26)

However, when the mole balance is written in terms of conversion, we use Equation (4-25):

$\begin{matrix} P_{i} = C_{i} R T = C_{A0} \frac{(Θ_{i} + v_{i} X)}{(1 + ε X)} \frac{P}{P_{0}} \frac{T_{0}}{T} R T \\ = \overset{P_{A 0}}{\overset{︷}{C_{A0} {R T}_{0}}} \frac{(Θ_{i} + v_{i} X)}{(1 + ε X)} p \end{matrix}$

\begin{matrix} P_{i} = P_{A0} \frac{(Θ_{i} + v_{i} X)}{1 + ε X} p \end{matrix} (4 - 27)

For example, the rate law for the hydrodemethylation of toluene (T) to form methane (M) and benzene (B) given by Equation (10-80) on page 483 can now be written in terms of conversion.

$- {r'}_{T} = \frac{k P_{A 0}^{2} (1 - X) (Θ_{H_{2}} - X)}{1 + K_{B} P_{A 0} X + K_{B} P_{A 0} (1 - X)} (p)^{2}$

T + H₂ → M + B

If you haven’t decided which computer to buy or borrow, or don’t have your integral tables, I suppose you could resort to the graphical techniques in Chapter 2 and use a Levenspiel plot, $F_{A0} / - r_{A}^{'}$ versus X, to achieve a specified conversion of toluene. However, that may put you at a severe disadvantage as other chemical reaction engineers will be using software packages (e.g., Poly-math) to solve chemical reaction engineering problems.

Example 4–4 Expressing the Rate Law for SO₂ Oxidation in Terms of Partial Pressures and Conversions

The SO₂ oxidation discussed in Example 4-3 is to be carried out over a solid platinum catalyst. As with almost all gas–solid catalytic reactions, the catalytic rate law is expressed in terms of partial pressures instead of concentrations. The rate law for this SO₂ oxidation was found experimentally to be¹

$- r_{S 0_{2}}^{'} = \frac{k [P_{{SO}_{2}} \sqrt{P_{O_{2}}} - \frac{P_{{SO}_{3}}}{K_{P}}]}{{(1 + \sqrt{P_{O_{2}} K_{O_{2}}} + P_{{SO}_{3}} K_{{SO}_{3}})}^{2}}, {mol SO}_{2} oxidized/ (h) / (g-cat) (E4-4 .1)$

¹ O. A. Uychara and K. M. Watson, Ind. Engrg. Chem, 35, 541.

where P_i (kPa, bar, or atm) is the partial pressure of species i.

The reaction is to be carried out isothermally at 400°C. At this temperature, the rate constant k per gram of catalyst (g-cat), the adsorption constants for O₂ ( $K_{O_{2}}$ ) and SO₂ ( $K_{{SO}_{2}}$ ), and the pressure equilibrium constant, K_P, were experimentally found to be

k = 9.7 mol SO₂/atm^3/2/h/g-cat

$K_{O_{2}} = 38.5 {atm}^{- 1}, K_{{SO}_{3}} = 42.5 {atm}^{- 1}, and K_{P} = 930 {atm}^{- 1 / 2}$

The total pressure and the feed composition (e.g., 28% SO₂) are the same as in Example 4-3. Consequently, the entering partial pressure of SO₂ is 4.1 atm. There is virtually no pressure drop in this reactor.

Write the rate law as a function of conversion evaluating all other parameters.
Prepare a Levenspiel plot by sketching the reciprocal rate [1/(−r_A)] as a function of X up to the equilibrium conversion X_e, and note where the rate goes to zero and [1/(–r_A)] goes to infinity.

Solution

Part (a)

No Pressure Drop and Isothermal Operation

For SO₂

First we need to recall the relationship between partial pressure and concentration, followed by the relationship between concentration and conversion. Because we know how to express concentration as a function of conversion, we therefore know how to express partial pressure as a function of conversion.

$P_{{SO}_{2}} = C_{{SO}_{2}} R T = \frac{F_{{SO}_{2}}}{υ} R T = \frac{F_{{SO}_{2,} 0} (1 - X) R T}{υ_{0} (1 + ɛ X) \frac{T}{T_{0}} \frac{P_{0}}{P}} = \frac{F_{{SO}_{2}, 0}}{υ_{0}} \frac{R T_{0} (1 - X) \frac{P}{P_{0}}}{1 + ɛ X}$

$P_{{SO}_{2}} = \frac{P_{{SO}_{2,} 0} (1 - X) \frac{P}{P_{0}}}{(1 + ɛ X)} = \frac{P_{{SO}_{2,} 0} (1 - X) P}{(1 + ɛ X)} (E4-4 .2)$

$P_{i} = P_{A0} \frac{(Θ_{i} + v_{i} X)}{(1 + ε X)} \frac{P}{P_{0}} = P_{A0} \frac{(Θ_{i} + v_{i} X)}{(1 + ε X)} p$

For no pressure drop P = P₀, that is, p = 1

$P_{{SO}_{2}} = \frac{P_{{SO}_{2}, 0} (1 - X)}{(1 + ε X)}$

\begin{matrix} P_{{SO}_{2}, 0} = y_{{SO}_{2}, 0}) P_{0} = 4.1)atm & (E4-4.3) \end{matrix}

For SO₃

\begin{matrix} P_{{SO}_{3}} = C_{{SO}_{3}} R T = \frac{C_{{SO}_{2}, 0} {R T}_{0} X}{(1 + ε X)} = \frac{P_{{SO}_{2}, 0} X}{1 + ε X} & (E4-4.4) \end{matrix}

For O₂

P_{O_{2}} = C_{O_{2}} R T = C_{{SO}_{2,} 0} \frac{(Θ_{B} - \frac{1}{2} X) R T_{0}}{1 + ε X} = P_{{SO}_{2,} 0} \frac{(Θ_{B} - \frac{1}{2} X)}{1 + ε X} (E4-4 .5)

From Example 4-3

Θ_B = 0.54

Factoring out $\frac{1}{2}$ in Equation (E4-4.5) gives

\begin{matrix} P_{O_{2}} = P_{{SO}_{2}, 0} = \frac{(Θ_{B} - \frac{1}{2} X)}{(1 + ε X)} = \frac{P_{{SO}_{2}, 0} (1.08 - X)}{2 (1 + ε X)} & (E4-4.6) \end{matrix}

From Equation (E4-3.5)

\begin{matrix} ε = - 0.14 & (E4-3.5) \end{matrix}

Substitute for the partial pressure in the rate-law equation (E4-4.1)

$- {r^{'}}_{{SO}_{2}}^{} = k [\frac{P_{{SO}_{2, 0}}^{3 / 2} (\frac{1 - x}{1–0.14 X}) \sqrt{\frac{(1.08 - X)}{2 (1–0.14 X)}} - \frac{P_{{SO}_{2, 0}} X}{(1–0.14 X)} (\frac{1}{930 {atm}^{- 1 / 2}})}{(1 + \sqrt{\frac{38.5 P_{{SO}_{2, 0}} (1.08 - X)}{2 (1 - 0.14 X)}} + \frac{42.5 P_{{SO}_{2, 0}} X}{(1 - 0.14 X)})^{2}}] (E4-4.7)$

with k = 9.7 mol SO₂/atm^3/2/h/g-cat P_SO₂,₀ = 4.1 atm, $P_{{SO}_{2, 0}}^{3 / 2}$ = 8.3 atm ^3/2

\begin{matrix} - r_{{SO}_{2}}^{'} = 9.7 \frac{mol}{hg-cat {atm}^{3 / 2}} [\frac{\frac{8.3 {atm}^{3 / 2} (1 - X)}{(1 - 0.14 X)} \sqrt{\frac{1.08 - X}{2 (1 - 0.14 X)}} - \frac{0.0044 {atm}^{3 / 2} X}{(1 - 0.14 X)}}{(1 + \sqrt{\frac{79 (1.08 - X)}{(1 - 0.14 X)}} + \frac{174 X}{1 - 0.14 X})^{2}}] & (E4-4.8) \end{matrix}

$- r_{A}^{'} = f (x)$

Part (b)

We can now use Equation (E4-4.8) to plot the reciprocal rate as a function of X as shown in Figure E4-4.1 to design a packed-bed catalytic reactor. We note at the equilibrium conversion, X_e, the reciprocal rate goes to infinity. We could now use a Levenspiel plot to find the catalyst weight W in a packed-bed reactor (PBR) to achieve a specified conversion.

F_{A0} \frac{d X}{d W} = - r_{A}' (2-17)

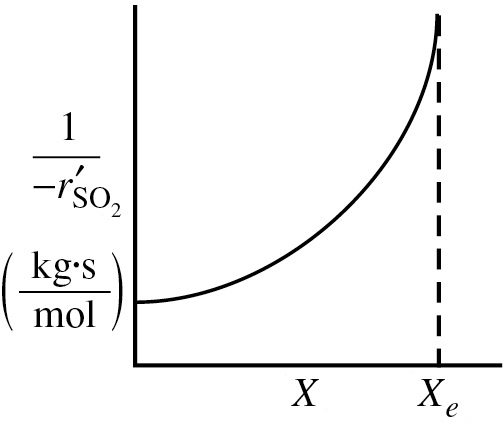
Plot of oxidation of sulfur dioxide's reciprocal rate versus conversion. — **Figure E4-4.1** Reciprocal rate of SO₂ oxidation as a function of conversion.

A graph with the vertical axis representing the reciprocal rate of sodium dioxide oxidation (1 over negative r dash of SO2) in Kilogram seconds per mole and the horizontal axis representing X is shown. The graph is a concave upward and increasing curve drawn from the vertical axis. The maximum value is obtained at the end, corresponding to X equals X subscript e.

Levenspiel plots are useful for conceptually visualizing the differences in reactor sizes and the sequencing of reactors. However, we will see in Chapter 5 that using numerical software packages are so much better ways to solve for the catalysis weight, W, than using Levenspiel plots. For example, we would couple Equation (E4-4.8) with Equation (2-17) and use an ordinary differential equation (ODE) solver, such as Polymath or MATLAB, to find the conversion X as a function of catalyst weight W. So, be sure to buy, rent, or borrow a laptop computer before attempting to solve the problems in Chapter 5 and beyond.

Analysis: In most heterogeneous catalytic reactions, rate laws are expressed in terms of partial pressures instead of concentration. However, we see that through the use of the ideal gas law we could easily express the partial pressure as a function of concentration then use the stoichiometric table and conversion in order to express the rate law as a function of conversion. In addition, for most all heterogeneous reactions you will usually find a term like (1 + K_AP_A + K_BP_B + . . .) in the denominator of the rate law, as will be explained in Chapter 10.

4.3 Reversible Reactions and Equilibrium Conversion

Thus far in this chapter, we have focused mostly on irreversible reactions. The procedure one uses for the isothermal reactor design of reversible reactions is virtually the same as that for irreversible reactions, with one notable exception: the maximum conversion that can be achieved at the reaction temperature is the equilibrium conversion, X_e. In the following example, it will be shown how our algorithm for reactor design is easily extended to reversible reactions.

Need to first calculate X_e

Example 4–5 Calculating the Equilibrium Conversion

The reversible gas-phase decomposition of nitrogen tetroxide, N₂O₄, to nitrogen dioxide, NO₂,

N₂O₄ ⇄ 2NO₂

Nitrogen Tetroxide

is to be carried out at constant temperature. The feed consists of pure N₂O₄ at 340 K and 202.6 kPa (2 atm). The concentration equilibrium constant, K_C, at 340 K is 0.1 mol / dm³ and the rate constant $k_{N_{2} O_{4}}$ and the rate constant is 0.5 min^–1.

Set up a stoichiometric table and then calculate the equilibrium conversion of N₂O₄ in a constant-volume batch reactor.
Set up a stoichiometric table and then calculate the equilibrium conversion of N₂O₄ in a flow reactor.
Assuming the reaction is elementary, express the rate of reaction solely as a function of conversion for a flow system and for a batch system.
Determine the CSTR volume necessary to achieve 80% of the equilibrium conversion.

Solution

N₂O₄ ⇄ 2NO₂

A ⇄ 2B

At equilibrium, the concentrations of the reacting species are related by the relationship dictated by thermodynamics (cf. see Equation (3-10) and Appendix C).

$K_{C} = \frac{C_{Be}^{2}}{C_{Ae}} (E4-5.1)$

Batch system—constant volume, V = V₀.

TABLE E4-5.1 STOICHIOMETRIC TABLE FOR BATCH REACTOR

Species

Symbol

Initially

Change

Remaining

N₂O₄

A

N_A0

–N_A0X

N_A = N_A0(1 – X)

NO₂

B

0

+2N_A0X

N_B = 2N_A0X

N_T0 = N_A0

N_T = N_T0 + N_A0X

Living Example Problem

For batch systems C_i = N_i/V

$C_{A} = \frac{N_{A}}{V} = \frac{N_{A}}{V_{0}} = \frac{N_{A0} (1 - X)}{V_{0}} = C_{A0} (1 - X) (E4-5.2)$

$C_{B} = \frac{N_{B}}{V} = \frac{N_{B}}{V_{0}} = \frac{2 N_{A0} X}{V_{0}} = 2 C_{A0} X (E4-5.3)$

$\begin{matrix} C_{A 0} & = \frac{y_{A 0} P_{0}}{R T_{0}} = \frac{(1) (2 atm)}{(0.082 atm \cdot {dm}^{3} / mol \cdot K) (340 K)} \\ \begin{matrix} \begin{matrix} = 0.07174 mol / {dm}^{3} \end{matrix} & Answer \end{matrix} \end{matrix}$

At equilibrium in a batch reactor, X = X_eb, we substitute Equations (E4-5.2) and (E4-5.3) into Equation (E4-5.1)

$K_{c} = \frac{C_{Be}^{2}}{C_{Ae}} = \frac{4 C_{A0}^{2} X_{e b}^{2}}{C_{A0} (1 - X_{e b})} = \frac{4 C_{A0} X_{e b}^{2}}{1 - X_{e b}}$

(math-math-math-math) to get

$X_{e b} = \sqrt{\frac{K_{c} (1 - X)}{4 C_{A0}}} (E4-5.4)$

We will use the software package Polymath to solve for the equilibrium conversion and let Xeb represent the equilibrium conversion in a constant-volume batch reactor. Equation (E4-5.4) written in Polymath format becomes

f(Xeb) = Xeb – [Kc* (1 – Xeb)/(4*Cao)] ^0.5

The Polymath program and solution are given in Table E4-5.2.

When looking at Equation (E4-5.4), you probably asked yourself, “Why not use the quadratic formula to solve for the equilibrium conversion in both batch and flow systems?” That is from Equation (E4-5.4) we would have

$\begin{matrix} B a t c h : & X_{e b} = \frac{1}{8} [(- 1 + \sqrt{1 + 16 C_{A0} / K_{C}}) / (C_{A0} / K_{C})] \end{matrix}$

and from Equation (E4-5.8) we would have

$\begin{matrix} F l o w : & X_{e f} = [\frac{(ε - 1) + \sqrt{{(ε + 1)}^{2} + 4 (ε + {4 C}_{A0} / K_{C})}}{2 (ε + 4 C_{A0} / K_{C})}] \end{matrix}$

There is a Polymath tutorial in the Summary Notes for Chapter 1 on the CRE Web site.

The answer is that future problems will be nonlinear and require Polymath solutions; therefore, this simple exercise increases the reader’s ease in using Polymath.

TABLE E4-5.2 POLYMATH PROGRAM AND SOLUTION FOR BOTH BATCH AND FLOW SYSTEMS

Polymath Tutorial Chapter 1

As seen in Table E4-5.2, the equilibrium conversion in a constant-volume batch reactor (X_eb) is

$X_{e b} = 0.44$

Note: A tutorial on Polymath can be found in the summary notes for Chapter 1 and on the CRE Web site (www.umich.edu/~elements/6e/tutorials/Polymath_LEP_tutorial.pdf).
Flow system. The stoichiometric table is the same as that for a batch system except that the number of moles of each species, N_i, is replaced by the molar flow rate of that species, F_i.

For constant temperature and pressure, the volumetric flow rate υ = υ₀(1 + ɛX), is and the resulting concentrations of species A and B are

TABLE E4-5.3 STOICHIOMETRIC TABLE FOR CONTINUOUS-FLOW REACTOR

Species

Symbol

Entering

Change

Leaving

N₂O₂

A

F_A0

–F_A0X

F_A = F_A0(1–X)

NO₂

B

0

+2F_A0X

F_B = 2F_A0X

F_T = F_A0

F_T = F_T0 + F_A0 X

$C_{A} = \frac{F A}{υ} = \frac{F_{A0} (1 - X)}{υ} = \frac{F_{A0} (1 - X)}{υ_{0} (1 + ɛ X)} = \frac{C_{A0} (1 - X)}{1 + ɛ X} (E4-5.5)$

$C_{B} = \frac{F_{B}}{υ} = \frac{2 F_{A0} X}{υ_{0} (1 + ɛ X)} = \frac{2 C_{A0} X}{(1 + ɛ X)} (E4-5.6)$

At equilibrium, X = X_ef, we can substitute Equations (E4-5.5) and (E4-5.6) into Equation (E4-5.1) to obtain the expression

$K_{C} = \frac{{C_{B e}}^{2}}{C_{A e}} = \frac{[2 C_{A0} X_{e f} / (1 + ɛ X_{e f})]^{2}}{C_{A0} (1 - X_{e f}) / (1 + ɛ X_{e f})}$

Simplifying gives

$K_{C} = \frac{4 C_{A0} {X_{e f}}^{2}}{(1 - X_{e f}) (1 + ɛ X_{e f})} (E4-5.7)$

Rearranging to use Polymath yields

$X_{e f} = \sqrt{\frac{K_{C} (1 - X_{e f}) (1 + ɛ X_{e f})}{4 C_{A0}}} (E4-5.8)$

For a flow system with pure N₂O₄ feed, ɛ = y_A0 δ = 1(2–1)=1.

We shall let Xef represent the equilibrium conversion in a flow system. Equation (E4-5.8) written in the Polymath format becomes

$f (Xef) = Xef - {[kc * (1 - Xef) * (1 + eps * Xef) / 4 / cao]}^{^} 0.5$

This solution is also shown in Table E4-5.3 $\begin{matrix} X_{e f} = 0.51 \end{matrix}$ .

Note that the equilibrium conversion in a flow reactor (i.e., X_ef = 0.51), with no pressure drop, is greater than the equilibrium conversion in a constant-volume batch reactor (X_eb = 0.44). Recalling Le Châtelier's principle, can you suggest an explanation for this difference in X_e? This example is continued in Problem P4-1_A (a). Be sure to use Wolfram and/or Python in the Living Example Problems (LEPs) to see how the ratio (X_eb/X_ef ) varies with ɛ and C_T0.

LEP Sliders
Rate laws. Assuming that the reaction follows an elementary rate law, then

$\begin{matrix} - r_{A} = k_{A} [C_{A} - \frac{C_{B}^{2}}{K_{C}}] & (E4-5.9) \end{matrix}$
1. For a constant volume (V = V₀) batch system
  
  Here, C_A = N_A/V₀ and C_B = N_B/V₀. Substituting Equations (E4-5.2) and (E4-5.3) into the rate law, we obtain the rate of disappearance of A as a function of conversion
  
  $\begin{matrix} - r_{A} = k_{A} [C_{A} - \frac{C_{B}^{2}}{K_{C}}] = k_{A} [C_{A0} (1 - X) - \frac{4 C_{A0}^{2} X^{2}}{K_{C}}] & (E4-5.10) \end{matrix}$
  
  –r_A =f(X) for a batch reactor with V = V₀
2. For a flow system
  
  Here, C_A = F_A/υ and C_B = F_B/υ with υ = υ₀ (1 + ɛX). Consequently, we can substitute Equations (E4-5.5) and (E4-5.6) into Equation (E4-5.9) to obtain
  
  $\begin{matrix} - r_{A} = k_{A} [\frac{C_{A0} (1 - X)}{1 + ε X} - \frac{4 C_{A0}^{2} X^{2}}{K_{C} (1 + ε X)^{2}}] & (E4-5.11) \end{matrix}$
  
  –r_A = f (X) for a flow reactor
  
  As expected, the dependence of reaction rate on conversion, that is, –r_A = f(X), for a constant-volume batch system (i.e., Equation (E4-5.10)) is different than that for a flow system (Equation (E4-5.11)) for gas-phase reactions.
  
  If we substitute the values for C_A0, K_C, ɛ, and k_A = 0.5 min^–1 in Equation (E4-5.11), we obtain –r_A solely as a function of X for the flow system.
  
  $- r_{A} = \frac{0.5}{min} [0.072 \frac{mol (1 - X)}{{dm}^{3} (1 + X)} \frac{4 (0.075 {mol/dm}^{3})^{2} X^{2}}{0.01 {mol/dm}^{3} (1 + X)^{2}}]$
  
  $- r_{A} = 0.036 [\frac{(1 - X)}{(1 + X)} - \frac{2.88 X^{2}}{(1 + X)^{2}}] (\frac{mol}{{dm}^{3} \cdot min}) (E4-5.12)$
  
  We can now use Equation (E4-5.12) to prepare our Levenspiel plot to find either the CSTR or PFR volume.
  
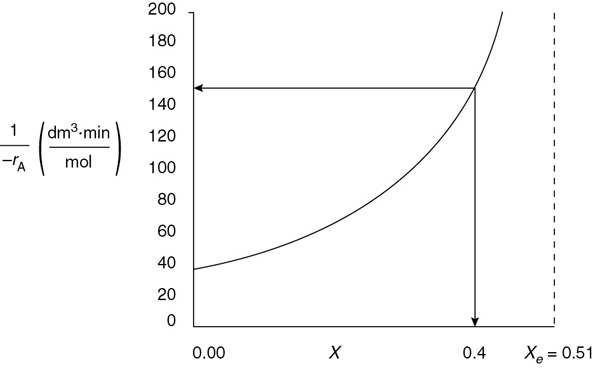
  Figure E4-5.1 Levenspiel plot for a flow system.
  
  A graph represents the Levenspiel plot. The vertical axis represents 1 over negative r subscript A (in decimeter cube minute per mole) and ranges from 0 to 200 in increments of 20. The horizontal axis represents X. The graph is concave upward and increasing, extending from point 38 on the vertical axis, corresponding to X equals 0. It increases to 150, when X equals 0.4. A dashed vertical line is drawn from the horizontal axis at X subscript e equals 0.51 (at the end).
  
  X_e = 0.51
  
  We see as we approach equilibrium, X_e = 0.51, –r_A goes to zero and (1/–r_A) goes to infinity.
CSTR volume. Just for fun (and this really is fun), let’s fast forward and calculate the CSTR reactor volume necessary to achieve 80% of the equilibrium conversion of 51% (i.e., X = 0.8X_e = (0.8)(0.51) = 0.4) for a molar feed rate of A of 3 mol/min.

Plotting the reciprocal of Equation (E4-5.12) to obtain Levenspiel plot as we did in Chapter 2, it can be seen in Figure E4-5.1 when X = 0.4 then as

$(\frac{1}{- r_{A}})_{x = 0.4} = 143 \frac{{dm}^{3} \min}{mol}$

then for F_A0 = 3 mol/min

Keeping an eye on things to come

$\begin{matrix} V & = F_{A0} X (\frac{1}{- r_{A}})_{X = 0.4} \\ = (\frac{3 mol}{\min}) (0.4) (143) \frac{{dm}^{3} \min}{mol} \\ V & {= 171 dm}^{3} \end{matrix}$

A quicker way to find the CSTR volume, rather than drawing a Levenspiel plot, is to simply evaluate Equation (E4-5.12) at X = 0.4

$- r_{A} = 0.036 [\frac{(1–0.4)}{(1 + 0.4)} - \frac{2.88 (0.4)^{2}}{(1 + (0.4))^{2}}] = 0.0070 {mol/dm}^{3} / \min$

Using Equation (2-13), we can now find the reactor volume

$\begin{matrix} V = & \frac{F_{A 0} X}{- r_{A} |_{X}} = \frac{F_{A0} (0.4)}{- r_{A} |_{0.4}} = \frac{(3)mol/min)(0.4)}{0.0070) \frac{mol}{{dm}^{3} \cdot min}} \\ V= & {\begin{matrix} 171 dm \end{matrix}}^{3} = 0.171 m^{3} \end{matrix}$

The CSTR volume required to achieve 40% conversion is 0.171 m³. See Problem P4-1A (b) to calculate the PFR volume.

Species	Symbol	Initially	Change	Remaining
N₂O₄	A	N_A0	–N_A0X	N_A = N_A0(1 – X)
NO₂	B	0	+2N_A0X	N_B = 2N_A0X
		N_T0 = N_A0		N_T = N_T0 + N_A0X

Species	Symbol	Entering	Change	Leaving
N₂O₂	A	F_A0	–F_A0X	F_A = F_A0(1–X)
NO₂	B	0	+2F_A0X	F_B = 2F_A0X
		F_T = F_A0		F_T = F_T0 + F_A0 X

Analysis: The purpose of this example was to calculate the equilibrium conversion first for a constant-volume batch reactor in part (a), and then for a constant pressure flow reactor in part (b). One notes that there is a change in the total number of moles in this reaction and, as a result, these two equilibrium conversions (batch and flow) are not the same!! We next showed in part (c) how to express –r_A = f(X) for a reversible gas-phase reaction. Here we noted that the equations for the reaction-rate laws as a function of conversion, that is, –r_A = f(X), are different for batch and flow reactors. Finally, in Part (d) having –r_A = f(X), we specified a molar flow rate of A (i.e., 3.0 mol A/min) and calculated the CSTR volume necessary to achieve 40% conversion. We did this calculation to give insight to the types of analyses we, as chemical reaction engineers, will carry out as we move into similar but more complex calculations in Chapters 5 and 6.

4.4 And Now... A Word from Our Sponsor–Safety 4 (AWFOS–S4 The Swiss Cheese Model)

The Swiss Cheese Model shown in Figure 4-4 is another risk assessment tool, one that offers a deeper understanding into the layers of protection for chemical processes. This section (i.e., 4.4) is presented to give an overview of the model while the Process Safety Across the Chemical Engineering Curriculum Web site (http://umich.edu/~safeche/swiss_cheese.html) gives more in-depth explanation. A layer of protection is either a preventative action put in place to reduce the chance that an incident will occur, or a mitigating action put in place to lessen the severity of an accident. These layers of protection can include using inherently safer designs, following proper lab procedures, wearing adequate personal protective equipment (PPE), and having an emergency response plan.

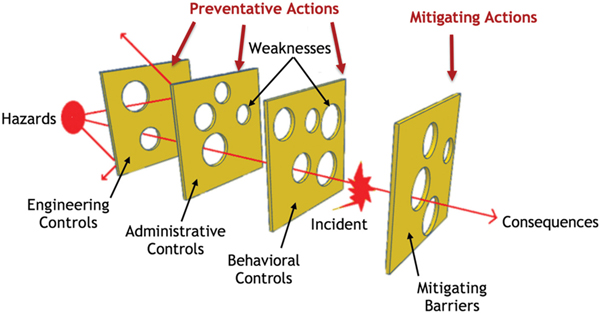
The figure depicts the Swiss cheese model. — **Figure 4-4** Swiss Cheese Model.

A pictorial representation of the Swiss cheese model is shown. Four cheese like structures are placed vertically in an order. The cheese models are labeled as Engineering controls, administrative controls, behavioral controls, and mitigating barriers, from left to right. First three-cheeses include preventative actions. The last cheese includes mitigating actions. Holes are present on the cheese which represent the weaknesses. The hazard rays pass through the weaknesses (holes) and after passing through the third cheese model, it becomes an incident. It comes out of the fourth model (mitigating barriers) as a consequence.

Even with the different levels or layers of protection, represented in Figure 4-4 as Swiss cheese slices, there is a possibility that a hazard will result in an incident. For an incident to occur, there must be vulnerability in each layer of protection, represented by holes in the slices of cheese. A hole is a weakness in that layer of protection (e.g., a backup cooling system, a faulty pressure relief valve). The size and number of holes in the cheese represent the relative lack of reliability of that layer. This model illustrates the importance of having redundant and strong protective layers so that hazards do not pass through multiple protective actions undetected and unresolved.

Understanding and implementing each protective level is important when running a chemical process. Table 4-4 shows and discusses each of the three control “cheese” slices (i.e., Engineering, Administrative, and Behavioral) while Table 4-5 shows and discusses the mitigating barriers.

TABLE 4-4 PREVENTATIVE ACTIONS

Engineering Controls	Administrative Controls	Behavioral Controls
Engineering controls involve preventative actions that are designed into the system, for example, pressure relief valves on heat exchangers.	Administrative controls involve managerial actions taken to ensure everyone involved in the process possesses the same knowledge of the established safety procedures, for example, Management of Change (MoC) procedures: Before making a change to a process, employees are required to identify, review, and approve modifications to ensure changes are implemented safely.	Behavioral controls focus on actions that individuals can take to prevent an accident from occurring by using proper tools, and following lab procedures, MoC and safety checklists as instructed.

TABLE 4-5 MITIGATING ACTIONS

Mitigating Barriers
These barriers focus on actions that lessen the severity or impact of an accident, for example, having an emergency response plan, wearing personal protective equipment (PPE), or the installation of a fire suppression system.

Engineering Controls, Administrative Controls, and Behavioral Controls represent Preventative Actions designed to reduce the likelihood of an incident occurring, while Mitigating Barriers represent Mitigating Actions designed to lessen the impact or severity of an incident. It’s important to recognize that all of these layers of protection will have some weaknesses.

The main purpose of the Swiss Cheese Model is to visualize the vulnerability and how a hazard may be able to pass through the many different preventative actions in place.

Further Reading on the Swiss Cheese Model:

Board, U.S. Chemical Safety and Hazard Investigation. Fire at Praxair St. Louis: Dangers of Propylene Cylinders. Washington DC, 2006.

D. Hatch, P. McCulloch, and I. Travers. “Visual HAZOP,” Chem. Eng., (917), 27–32 (2017, November).

USCSB. “CSB Safety Video: Dangers of Propylene Cylinders.” Online video clip. YouTube, 10 October 2007. Web. 8 May 2018.

Closure. Having completed this chapter, you should be able to write the rate law solely in terms of conversion and the reaction-rate parameters, (e.g., k, K_C) for both liquid-phase and gas-phase reactions. Once expressing –r_A = f(X) is accomplished, you can proceed to use the techniques in Chapter 2 to calculate reactor sizes and conversion for single CSTRs, PFRs, and PBRs, as well as those connected in series. However, in Chapter 5 we will show you how to carry out these calculations much more easily by instead using a Table of Integrals or software such as Polymath, MATLAB, Python, or Wolfram without having to resort to Levenspiel plots. After studying this chapter, you should also be able to calculate the equilibrium conversion for both constant-volume batch reactors and for constant-pressure flow reactors. We have now completed the following building blocks of our CRE tower.

Building blocks of CRE tower is shown. — The building blocks of CRE tower consists of mole balance, rate law, and stoichiometry from bottom to top.

In Chapter 5, we will focus on the fourth and fifth blocks: Combine and Evaluate. In Chapter 5, we will focus on the combine and evaluation building blocks, which will then complete our algorithm for isothermal chemical reactor design.

The CRE Algorithm

Mole Balance, Chapter 1
Rate Law, Chapter 3
Stoichiometry, Chapter 4
Combine, Chapter 5
Evaluate, Chapter 5
Energy Balance, Chapter 11

Summary

The stoichiometric table for the reaction given by Equation (S4-1) being carried out in a flow system is

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (S4-1) \end{matrix}$

In the case of ideal gases, Equation (S4-3) relates volumetric flow rate to conversion.

Batch reactor constant volume: V = V₀

$\begin{matrix} V = V_{0} & \begin{matrix} (S4-2) \end{matrix} \end{matrix}$

Flow systems: Gas:

$\begin{matrix} v = v_{0} (\frac{P_{0}}{P}) (1 + ε X) \frac{T}{T_{0}} & (S4-3) \end{matrix}$

Liquid: ()

$\begin{matrix} v = v_{0} & (S4- \end{matrix} 4)$

Species	Entering	Change	Leaving
A	F_A0	–F_A0X	F_A0(1 = X)
B	F_B0	$- (\frac{b}{a}) F_{A0} X$	$F_{A0} (Θ_{B} - \frac{b}{a} X)$
C	F_C0	$(\frac{c}{a}) F_{A0} X$	$F_{A0} (Θ_{C} + \frac{c}{a} X)$
D	F_D0	$(\frac{d}{a}) F_{A0} X$	$F_{A0} (Θ_{D} + \frac{d}{a} X)$
I	F_I0	- - -	F_I0
Totals	F_T0	δF_A0X	F_T = F_T0 +δF_A0X

Definitions of δ and ɛ: For the general reaction given by Equation (S4-1), we have

\begin{matrix} δ = \frac{d}{a} + \frac{c}{a} - \frac{b}{a} - 1 & (S4-5) \end{matrix}

$δ = \frac{Change in total number of moles}{mole of A reacted}$

and

$\begin{matrix} ε = y_{A0} δ & (S4-6) \end{matrix}$

$ε = \frac{Change in total number of moles for complete conversion}{Total number of moles fed to the reactor}$

For incompressible liquids or for batch gas-phase reactions taking place in a constant volume, V = V₀, the concentrations of species A and C in the reaction given by Equation (S4-1) can be written as

$\begin{matrix} C_{A} = \frac{F_{A}}{v} = \frac{F_{A0}}{v_{0}} (1 - X) = C_{A0} (1 - X) & (S4-7) \end{matrix}$

$\begin{matrix} C_{c} = C_{A0} (Θ_{C} + \frac{c}{a} X) & (S4-8 \end{matrix})$

Equations (S4-7) and (S4-8) also hold for gas-phase reactions carried out in constant-volume batch reactors.
For gas-phase reactions in continuous-flow reactors, we use the definition of concentration (C_A = F_A/υ) along with the stoichiometric table and Equation (S4-3) to write the concentration of A and C in terms of conversion.

$\begin{matrix} C_{A} = \frac{F_{A}}{v} = \frac{F_{A0} (1 - X)}{v} = C_{A0} [\frac{1 - X}{1 + ɛ X}] P (\frac{T_{0}}{T}) & (S4-9 \end{matrix})$

$\begin{matrix} C_{c} = \frac{F_{c}}{v} = C_{A0} [\frac{Θ_{c} + (c / a) X}{1 + ε X}] P (\frac{T_{0}}{T}) & (S4-10) \end{matrix}$

$with Θ_{c} = \frac{F_{c0}}{F_{A0}} = \frac{C_{c0}}{C_{A0}} = \frac{y_{c 0}}{y_{A 0}} and p = \frac{p}{p_{0}}$
In terms of gas-phase molar flow rates, the concentration of species i is

$\begin{matrix} C_{i} = C_{T 0} \frac{F_{i}}{F_{T}} \frac{P}{P_{0}} \frac{T_{0}}{T} & (S4-11) \end{matrix}$

Equation (S4-11) must be used for membrane reactors (Chapter 6) and for multiple reactions (Chapter 8).
Many catalytic rate laws are given in terms of partial pressure, for example,

$\begin{matrix} - r_{A}^{'} = \frac{K_{A} P_{A}}{1 + K_{A} P_{A}} & (S4-12) \end{matrix}$

The partial pressure is related to conversion through the stoichiometric table. For any species “i” in the reaction

$\begin{matrix} P_{i} = P_{A 0} \frac{(Θ_{i} + v_{i} X)}{(1 + ɛ X)} & (S4-13) \end{matrix}$

For species A

$P_{A} = P_{A 0} \frac{(1 - X)}{(1 + ɛ X)} p$

Substituting in the rate law

$\begin{matrix} - r_{A}^{'} = \frac{K_{A} P_{A 0} \frac{(1 - X)}{(1 + ɛ X)} P}{1 + K_{A} P_{A 0 \frac{(1 - X)}{(1 + ɛ X)} P}} = \frac{{k P}_{A 0} (1 - X) p}{(1 + ɛ X) + K_{A} p_{A 0} (1 - X) P} & (S4-14) \end{matrix}$

CRE Web Site Materials (http://www.umich.edu/~elements/6e/04chap/obj.html#/)

Useful links and evaluation from CRE Web site. — The useful links of CRE Web site materials include the following: living example problems, extra help, additional materials, professional reference shelf, computer simulation problem statements, and YouTube videos. The evaluation includes self tests and i>clicker questions.

Interactive Computer Games (http://umich.edu/~elements/6e/icm/index.html) Quiz Show II Jeopardy (http://umich.edu/~elements/6e/icm/kinchal2.html). A Jeopardy Game competition between AIChE student chapters is held at the annual AIChE meeting.

Screenshot of a question from a Jeopardy competition. — The screenshot of the game titled kinetics challenge 2 is shown. The conditions of the reaction are provided. A question is displayed with four options. The fourth option is selected. Send checked answer option is available on the left side, below the four choices of answers. It is displayed as correct. The main menu and continue options are available on the left and the right side at the bottom.

Questions and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

A = • B = ▪ C = ♦ D = ♦♦

Questions

Q4-1_A QBR (Question Before Reading). What are the differences in writing the concentrations as a function of conversion for gas-phase and liquid-phase reactions?

Q4-2_A i>clicker. Go to the Web site (http://www.umich.edu/~elements/6e/04chap/iclicker_ch4_q1.html) and view at leave five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case, explaining why the question should not be on the next exam. In either case, explain your reasoning.

Q4-3_A Example 4-1. Would the example be correct if water were considered an inert? Explain.

Q4-4_A Example 4-2. How would the answer change if the initial concentration of glyceryl stearate were 3 mol/dm³? Rework Example 4-2 correctly using the information given in the problem statement.

Q4-5_A Example 4-3. Under what conditions will the concentration of the inert nitrogen be constant? Plot Equation (E4-5.2) in terms of (1/–r_A) as a function of X up to value of X = 0.99. What did you find?

Q4-6_A Can you name the English rock group that was famous worldwide in the 1970s and 1980s and whose lead singer was Freddie Mercury? The group had a resurgence in 2019 when Adam Lambert took over for Freddie, who had died in 1991. Hint: See Problem P5-22_A.

Q4-7_A What did you learn from the Swiss Cheese Model (e.g., make a list)?

Q4-8_A Go to the LearnChemE screencast link for Chapter 4 (http://www.umich.edu/~elements/6e/04chap/learn-cheme-videos.html).

View one or more of the screencast 5- to 6-minute videos and write a two-sentence evaluation.
What did the screencast do well and what could be improved?

Q4-9_A AWFOS–S4 Swiss Cheese Model.

What is the main purpose of implementing the Swiss Cheese Model in a workplace?
Categorize engineering controls, administrative controls, behavioral controls, and mitigating barriers as preventative actions or mitigating actions. List an example of each.
What happens when all of the weaknesses/vulnerabilities in the controls/barriers line up?
What was the takeaway lesson from this safety section?

Computer Simulations and Experiments

P4-1_A (a) Example 4-4: SO₂ Oxidation

Wolfram and Python

Vary Θ_B and observe the change in reaction rate. Go to the extremes and explain what is causing the curve to change the way it does.
Vary the parameters and list the parameters that have the greatest and the least effect on the reaction rate.
Write a set of conclusions about the experiments you carried out by varying the sliders in parts (i) through (iii).

Polymath
Using the molar flow rate of SO₂ (A) of 3 mol/h and Figure E4-4.1, calculate the fluidized bed (i.e., CSTR catalyst weight) necessary for 40% conversion.
Next, consider the entering flow rate of SO₂ is 1000 mol/h. Plot (F_A0/–r_A) as a function of X to determine the fluidized bed catalyst weight necessary to achieve 30% conversion, and 99% of the equilibrium conversion, that is, X = 0.99 X_e.

(b) Example 4-5: Equilibrium Conversion

Using Figure E4-5.1 and the methods in Chapter 2, estimate the PFR volume for 40% conversion for a molar flow rate of A of 5 dm³/min.
Using Figure E4-5.1 and the methods in Chapter 2, estimate the time to achieve 40% conversion in a batch reactor when the initial concentration is 0.05 mol/dm³.

Wolfram and Python
What values of K_C and C_A0 cause X_ef to be the farthest away from X_eb?
What values of K_C and C_A0 will cause X_eb and X_ef to be the closest together?
Observe the plot of the ratio of $(\frac{X_{e b}}{X_{e r}})$ as a function of y_A₀. Vary the values of K_C and C_T0. What conclusions can you draw?
Write a set of conclusions from your experiment (i) through (vi).

Interactive Computer Games

P4-2_A Load the Interactive Computer Games (ICG) Kinetic Challenge from the CRE Web site. Play the game and then record your performance number for the module that indicates your mastering of the material. Your professor has the key to decode your performance number. ICG Kinetics Challenge Performance # ______________.

A Jeopardy Game competition between AIChE student chapters is held at the annual AIChE meeting. You might find one of these questions asked.

Kinetics Challenge II

Rate	Law	Stoich
100	100	100
200	200	200
300	300	300

Problems

P4-3_A The elementary reversible reaction

2A ⇄ B

is carried out in a flow reactor where pure A is fed at a concentration of 4.0 mol/dm³. If the equilibrium conversion is found to be 60%,

What is the equilibrium constant, K_C if the reaction is a gas-phase reaction? (Ans: Gas: K_C = 0.328 dm³/mol)
What is the K_C if the reaction is a liquid-phase reaction? (Ans: Liquid: K_C = 0.469 dm³/mol)
Write =r_A solely as a function of conversion (i.e., evaluating all symbols) when the reaction is an elementary, reversible, gas-phase, isothermal reaction with no pressure drop with k_A = 2 dm⁶/mol•s and K_C = 0.5 all in proper units.
Repeat (c) for a constant-volume batch reactor.

P4-4_B Stoichiometry. The elementary gas reaction

2A + B → C

is carried out isothermally in a PFR with no pressure drop. The feed is equal molar in A and B, and the entering concentration of A is 0.1 mol/dm³. Set up a stoichiometric table and then determine the following.

What is the entering concentration (mol/dm³) of B?
What are the concentrations of A and C (mol/dm³) at 25% conversion of A?
What is the concentration of B (mol/dm³) at 25% conversion of A? (Ans: C_B = 0.1 mol/dm³)
What is the concentration of B (mol/dm³) at 100% conversion of A?
If at a particular conversion the rate of formation of C is 2 mol/min/dm³, what is the rate of formation of A at the same conversion?
Write =r_A solely as a function of conversion (i.e., evaluating all symbols) when the reaction is an elementary, irreversible, gas-phase, isothermal reaction with no pressure drop with an equal molar feed and with C_A0 = 2.0 mol/dm³ at, k_A = 2 dm⁶/mol•s.
What is the rate of reaction at X = 0.5?

P4-5_A Set up a stoichiometric table for each of the following reactions and express the concentration of each species in the reaction as a function of conversion, evaluating all constants (e.g., =, =). Next, assume the reaction follows an elementary rate law, and write the reaction rate solely as a function of conversion, that is, –r_A = f(X).

For the liquid-phase reaction

Ethylene oxide (C2H4O) reacts with water (H2O) in the presence of sulfuric acid (H2SO4) as a catalyst to form ethylene glycol (C2H6O2).

the entering concentrations of ethylene oxide and water, after mixing the inlet streams, are 16.13 and 55.5 mol/dm³, respectively. The specific reaction rate is k = 0.1 dm³/mol · s at 300 K with E = 12500 cal/mol.
1. After finding –r_A = f(X), calculate the CSTR space-time, τ, for 90% conversion at 300 K and also at 350 K.
2. If the volumetric flow rate is 200 liters per second, what are the corresponding reactor volumes? (Ans: At 300 K: V = 439 dm³ and at 350 K: V = 22 dm³)
For the isothermal gas-phase pyrolysis

C₂H₆ → C₂H₄ = H₂

pure ethane enters a flow reactor at 6 atm and 1100 K, with ΔP = 0. Set up a stoichiometric table and then write –r_A = f(X). How would your equation for the concentration and reaction rate, that is, –r_A = f(X), change if the reaction were to be carried out in a constant-volume batch reactor?
For the isothermal, isobaric, catalytic gas-phase oxidation

Ethylene (C2H4) reacts with half a molecule of oxygen (Half of O2) to form ethylene oxide (C2H4O).

the feed enters a PBR at 6 atm and 260°C, and is a stoichiometric mixture of only oxygen and ethylene. Set up a stoichiometric table and then write $- r_{A}^{'}$ as a function of partial pressures. Express the partial pressures and $- r_{A}^{'}$ as a function of conversion for (1) a fluidized batch reactor and (2) a PBR. Finally, write $- r_{A}^{'}$ solely as a function of the rate constant and conversion.
Set up a stoichiometric table for the isothermal, catalytic gas-phase reaction carried out in a fluidized CSTR.

Benzene reacts with two molecules of hydrogen (2H2) to form cyclohexene.

A fluidized CSTR contains the fluidized catalyst pellets in it. It is cylindrical in the middle and funnel like at the top and the bottom ends.

The feed is stoichiometric and enters at 6 atm and 170°C. What catalyst weight is required to reach 80% conversion in a fluidized CSTR at 170°C and at 270°C? The rate constant is defined with respect to benzene and υ₀ = 50 dm³/min.

$K_{B} = \frac{53 mol}{Kgcat \cdot \min \cdot {atm}^{3}} at 300 k with E = 80 kJ/mol$

First write the rate law in terms of partial pressures and then express the rate law as a function of conversion. Assume ΔP ≡ 0.

P4-6_A Orthonitroanaline (an important intermediate in dyes—called fast orange) is formed from the reaction of orthonitrochlorobenzene (ONCB) and aqueous ammonia (see explosion in Figure E13-2.1 in Example 13-2).

Orthonitrochlorobenzene and two molecules of ammonia (2NH3) react to form orthonitroaniline and ammonium chloride (NH4Cl).

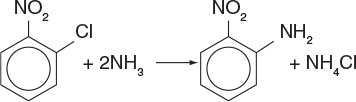
The liquid-phase reaction is first order in both ONCB and ammonia with k = 0.0017 m³/kmol · min at 188°C with E = 11273 cal/mol. The initial entering concentrations of ONCB and ammonia are 1.8 and 6.6 kmol/m³, respectively (more on this reaction in Chapter 13).
1. Set up a stoichiometric table for this reaction for a flow system.
2. Write the rate law for the rate of disappearance of ONCB in terms of concentration.
3. Explain how parts (a) and (b) would be different for a batch system.
(d) Write –r_A solely as a function of conversion.

–r_A = ______
What is the initial rate of reaction (X = 0)

at 188°C? –r_A = ______

at 25°C? –r_A = ______

at 288°C? –r_A = ______
What is the rate of reaction when X = 0.90

at 188°C? –r_A = ______

at 25°C? –r_A = ______

at 288°C? –r_A = ______
What would be the corresponding CSTR reactor volume at 25°C to achieve 90% conversion and at 288°C for a feed rate of 2 dm³/min

at 25°C? V = ______

at 288°C? V = ______

P4-7_B OEQ (Old Exam Question). Consider the following elementary gas-phase reversible reaction to be carried out isothermally with no pressure drop and for an equal molar feed of A and B with C_A0 = 2.0 mol/dm³.

2A + B ⇄ C

What is the concentration of B initially? C_B0 = ____ (mol/dm³)
What is the limiting reactant? ______
What is the exit concentration of B when the conversion of A is 25%? C_B = _____ (mol/dm³)
Write –r_A solely as a function of conversion (i.e., evaluating all symbols) when the reaction is an elementary, reversible, gas-phase, isothermal reaction with no pressure drop with an equal molar feed and with C_A0 = 2.0 mol/dm³, k_A = 2 dm⁶/mol²•s, and K_C = 0.5 all in proper units –r_A = ____.
What is the equilibrium conversion?
What is the rate when the conversion is
1. 0%?
2. 50%?
3. 0.99 X_e?

P4-8_B OEQ (Old Exam Question). The gas-phase reaction

$\frac{1}{2} N_{2} + \frac{3}{2} H_{2} \to {NH}_{3}$

is to be carried out isothermally first in a flow reactor. The molar feed is 50% H₂ and 50% N₂, at a pressure of 16.4 atm and at a temperature of 227°C.

Construct a complete stoichiometric table.
Express the concentrations in mol/dm³ of each for the reacting species as a function of conversion. Evaluate C_A0,δ, and ɛ, and then calculate the concentrations of ammonia and hydrogen when the conversion of H₂ is 60%. (Ans: $C_{H_{2}} = 0.1 {mol/dm}^{3}$ )
Suppose by chance the reaction is elementary with $k_{N_{2}} = 40 {dm}^{3} / mol/s$ . Write the rate of reaction solely as a function of conversion for (1) a flow reactor and for (2) a constant-volume batch reactor.

P4-9_B OEQ (Old Exam Question). There were 820 million pounds of phthalic anhydride produced in the United States in 1995. One of the end uses of phthalic anhydride is in the fiberglass of sailboat hulls. Phthalic anhydride can be produced by the partial oxidation of naphthalene in either a fixed or a fluidized catalytic bed. A flow sheet for the commercial process is shown below. Here, the reaction is carried out in fixed bed reactor with a vanadium pentoxide catalyst packed in 25 mm diameter tubes. A production rate of 31,000 tons per year would require 15,000 tubes.

The synthesis of phthalic anhydride. — Two molecules of Naphthalene reacts with 9 molecules of oxygen (9O2) to give 2 molecules of phthalic anhydride (C6H4(CO)2O) plus 4 molecules of carbon-di-oxide (4CO2) plus four molecules of water (4 H2O).

Assume the reaction is first order in oxygen and second order in naphthalene with k_N = 0.01 dm⁶/mol²/s.

The manufacturing process of Phthalic anhydride. — Naphthalene along with steam and air, is passed to the evaporator. Steam is passed to the evaporator and the naphthalene gets evaporated. Then it is moved to the reactor. The reactor is attached to a salt bath cooler. Water is fed to the salt bath and gas cooler. The reactor is attached with the gas cooler. Steam gets evaporated from the salt bath cooler and the gas cooler. From the gas cooler, the compound is passed to the switch condensers (separators), Oil is passed into the separators. Waste is released to the scrubber. From the separators, the mixture is sent to the crude PA storage tank, followed by vacuum distillation, and finally pure phthalic anhydride is obtained.

Adapted from Process Technology and Flowsheet Volume II. Reprints from Chemical Engineering, McGraw Hill Pub. Co., p. 111.

Set up a stoichiometric table for this reaction for an initial mixture of 3.5% naphthalene and 96.5% air (mol %), and use this table to develop the relations listed in parts (b) and (c). The initial/entering pressure and temperature are P₀ = 10 atm and T₀ = 500 K.
Express the following solely as a function of the conversion of naphthalene, X for a constant-volume isothermal batch reactor V = V₀. (1) The concentration of O₂, C_O₂. (2) The total pressure P. (3) The rate of reaction, –r_N. (4) Then calculate the time to achieve 90% conversion.
Repeat (b) for an isothermal flow reactor to find C_O₂, volumetric flow rate and the reaction rate –r_N as a function of conversion.
What CSTR and PFR volumes are necessary to achieve 98% conversion of naphthalene for an entering volumetric flow rate of 10 dm³/s.
Write a few sentences about the above flow sheet to manufacture phthalic anhydride.

P4-10_B OEQ (Old Exam Question). The elementary reversible reaction

2A ⇄ B

is carried out isothermally in a flow reactor with no pressure drop and where pure A is fed at a concentration of 4.0 mol/dm³. If the equilibrium conversion is found to be 60%

What is the equilibrium constant, K_C, if the reaction occurs in the gas phase?
What is the K_C if the reaction is a liquid-phase reaction?

P4-11_B Consider the elementary gas-phase reversible reaction is carried out isothermically

A ⇄ 3C

Pure A enters at a temperature of 400 K and a pressure of 10 atm. At this temperature, K_C = 0.25(mol/dm³)². Write the rate law and then calculate the equilibrium conversion for each of the following situations:

The gas-phase reaction is carried out in a constant-volume batch reactor.
The gas-phase reaction is carried out in a constant-pressure batch reactor.
Can you explain the reason why there would be a difference in the two values of the equilibrium conversion?

P4-12_B Repeat parts (a)–(c) of Problem P4-11_B for the reaction

3A ⇄ C

Pure A enters at 400 K, 10 atm and the equilibrium constant is K_C = 2.5 (dm³/mol)².

Compare the equilibrium conversions in Problems P4-11_B and P4-12_B. Explain the trends, for example, is X_e for constant pressure always greater than X_e for constant volume? Explain the reasons for the similarities and differences in the equilibrium conversions in the two reactions.

P4-13_C OEQ (Old Exam Question). Consider a cylindrical batch reactor that has one end fitted with a frictionless piston attached to a spring (Figure P4-13_C). The reaction

A + B → 8C

with the rate law

$- r_{A} = k_{1} C_{A}^{2} C_{B}$

The badge of the member of the hall of fame.

Reaction in a Cylindrical Batch reactor. — **Figure P4-13_C**

A cylindrical batch reactor is placed. A frictionless piston on the cylinder is attached to a spring, which is, in turn fixed to a vertical fixed support. The reaction occurs at the space in the cylinder, enclosed by the piston.

is taking place in this type of reactor.

Write the rate law solely as a function of conversion, numerically evaluating all possible symbols. (Ans: –r_A = 5.03 × 10^–9 [(1 − X)³/(1 + 3X)^3/2] lb mol/ft³·s.)
What is the conversion and rate of reaction when V = 0.2 ft³? (Ans: X = 0.259, –r_A = 8.63 × 10^–10 lb mol/ft³·s.)

Additional information:

Equal moles of A and B are present at t = 0

Initial volume: 0.15 ft³

Value of k₁: 1.0 (ft³/lb mol)²=s·^–1

The spring constant is such that the relationship between the volume of the reactor and pressure within the reactor is

V = (0.1)(P) (V in ft³, P in atm)

Temperature of system (considered constant): 140°F

Gas constant: 0.73 ft³·atm/lb mol·°R

Supplementary Reading

Further elaboration of the development of the general balance equation may be found on the CRE Web site www.umich.edu/~elements/6e/index.html and also may or may not be found in

G. KEILLOR AND T. RUSSELL, Dusty and Lefty: The Lives of the Cowboys (Audio CD), St. Paul, MN: Highbridge Audio, 2006.

R. M. FELDER, R. W. ROUSSEAU, and L. G. Bullard, Elementary Principles of Chemical Processes, 4th ed. Global Edition, Singapore: John Wiley & Sons Singapore PTE Ltd., 2017, Chap. 4.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

at 188°C?	–r_A = ______
at 25°C?	–r_A = ______
at 288°C?	–r_A = ______

at 188°C?	–r_A = ______
at 25°C?	–r_A = ______
at 288°C?	–r_A = ______

at 25°C?	V = ______
at 288°C?	V = ______

Table of Contents for 4. Stoichiometry

Create new playlist

Sign In

Sign Up

4. Stoichiometry

4.1 Batch Reactors (BRs)

4.1.1 Batch Concentrations for the Generic Reaction, Equation (2-2)

4.2 Flow Systems

4.2.1 Equations for Concentrations in Flow Systems

4.2.2 Liquid-Phase Concentrations

4.2.3 Gas-Phase Concentrations

4.3 Reversible Reactions and Equilibrium Conversion

4.4 And Now... A Word from Our Sponsor–Safety 4 (AWFOS–S4 The Swiss Cheese Model)

Summary

CRE Web Site Materials (http://www.umich.edu/~elements/6e/04chap/obj.html#/)

Questions and Problems

Questions

Computer Simulations and Experiments

Interactive Computer Games

Problems

Supplementary Reading

Table of Contents for
4. Stoichiometry