10. Catalysis and Catalytic Reactors
It isn’t that they can’t see the solution. It is that they can’t see the problem.
—G. K. Chesterton
10.1 Catalysts
Catalysts have been used by humankind for over 2000 years.1 The first observed uses of catalysts were in the making of wine, cheese, and bread. For example, it was found that it was always necessary to add small amounts of bread from the previous batch to make the current batch. However, it wasn’t until 1835 that Berzelius began to tie together observations of earlier chemists by suggesting that small amounts of a foreign substance could greatly affect the course of chemical reactions. This mysterious force attributed to the substance was called catalytic (from the ancient Greek katálusis, “to dissolve away the inertness”). In 1894, Ostwald expanded Berzelius’s explanation by stating that catalysts were substances that accelerate the rate of chemical reactions without being consumed during the reaction. During the 180 years since Berzelius’s work, catalysts have come to play a major economic role in the world market. In the United States alone, sales of process catalysts will reach over $20 billion by 2020, the major uses being in petroleum refining and in chemical production.
1 S. T. Oyama and G. A. Somorjai, J. Chem. Educ., 65, 765.
10.1.1 Definitions
What is catalysis?
A catalyst is a substance that affects the rate of a reaction but emerges from the process unchanged. A catalyst usually changes a reaction rate by promoting a different molecular path (“mechanism”) for the reaction. For example, gaseous hydrogen and oxygen are virtually inert at room temperature, but react rapidly when exposed to platinum. The reaction coordinate (cf. Figure 3-2) shown in Figure 10-1 is a measure of the progress along the reaction path as H2 and O2 approach each other and pass over the energy barrier to form H2O. Catalysis is the occurrence, study, and use of catalysts and catalytic processes. Commercial chemical catalysts are immensely important. Approximately one-third of the material gross national product of the United States involves a catalytic process somewhere between raw material and finished product.2 The development and use of catalysts is a major part of the constant search for new ways of increasing product yield and selectivity in chemical reactions. Because a catalyst makes it possible to obtain an end product by a different pathway with a lower energy barrier, it can affect both the yield and the selectivity.
2 V. Haensel and R. L. Burwell, Jr., Sci. Am., 225(10), 46.
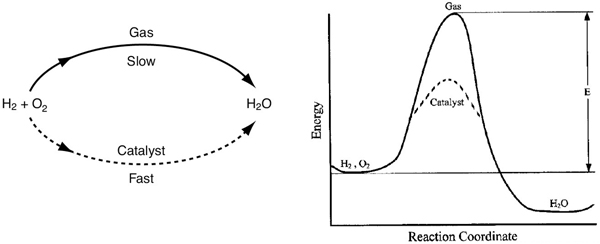
Figure 10-1 Different reaction paths.
Catalysts can accelerate the reaction rate but cannot change the equilibrium.
Normally when we talk about a catalyst, we mean one that speeds up a reaction, although strictly speaking, a catalyst can either accelerate or slow the formation of a particular product species. A catalyst changes only the rate of a reaction; it does not affect the equilibrium.
The 2007 Nobel Prize for Chemistry was awarded to Gerhard Ertl for his pioneering work on heterogeneous catalytic reactions. A heterogeneous catalytic reaction involves more than one phase; usually the catalyst is a solid and the reactants and products are in liquid or gaseous form. One example is the production of benzene, which is mostly manufactured today from the dehydrogenation of cyclohexane (obtained from the distillation of petroleum crude oil) using platinum-on-alumina as the catalyst:
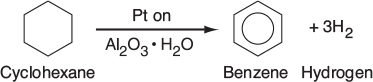
The simple and complete separation of the fluid product mixture from the solid catalyst makes heterogeneous catalysis economically attractive, especially because many catalysts are quite valuable and their reuse is demanded.
A heterogeneous catalytic reaction occurs at or very near the fluid–solid interface. The principles that govern heterogeneous catalytic reactions can be applied to both catalytic and noncatalytic fluid–solid reactions. The two other types of heterogeneous reactions involve gas–liquid and gas–liquid–solid systems. Reactions between a gas and a liquid are usually mass transfer–limited as will be discussed in Chapter 14.
10.1.2 Catalyst Properties
Ten grams of this catalyst possess more surface area than a U.S. football field.
Because a catalytic reaction occurs at the fluid–solid interface, a large interfacial area is almost always essential in attaining a significant reaction rate. In many catalysts, this area is provided by an inner porous structure (i.e., the solid contains many fine pores, and the surface of these pores supplies the area needed for the high rate of reaction), see Figures 10-4(b) and 10-9. The area possessed by some porous catalysis materials is surprisingly large. A typical silica-alumina cracking catalyst has a pore volume of 0.6 cm3/g and an average pore radius of 4 nm. The corresponding surface area can be the order of 300 m2/g of these porous catalysts. Examples include the Raney nickel used in the hydrogenation of vegetable and animal oils, platinum-on-alumina used in the reforming of petroleum naphthas to obtain higher octane ratings, and promoted iron used in ammonia synthesis. Sometimes pores are so small that they will admit only small molecules and prevent large ones from entering and being catalyzed. Materials with this type of pore are called molecular sieves, and they may be derived from natural substances such as certain clays and zeolites, or they may be totally synthetic, such as some crystalline aluminosilicates (see Figure 10-2). These sieves can form the basis for quite selective catalysts; the pores can control the residence time of various molecules near the catalytically active surface to a degree that essentially allows only the desired molecules to react. One example of the high selectivity of zeolite catalysts is the formation of para-xylene from toluene and methane shown in Figure 10-2(b).3 Here, methane and toluene enter through the zeolite pore and react on the interior surface to form a mixture of ortho-, meta-, and para-xylenes. However, the size of the pore mouth is such that only para-xylene can exit through the pore mouth, as meta- and ortho-xylene with their methyl group on the side cannot fit through the pore mouth. There are interior sites that can isomerize ortho-xylene and meta-xylene to para-xylene. Hence, we have a very high selectivity to form para-xylene.
3 R. I. Masel, Chemical Kinetics and Catalysis, New York: Wiley Interscience, 2001, p. 741.
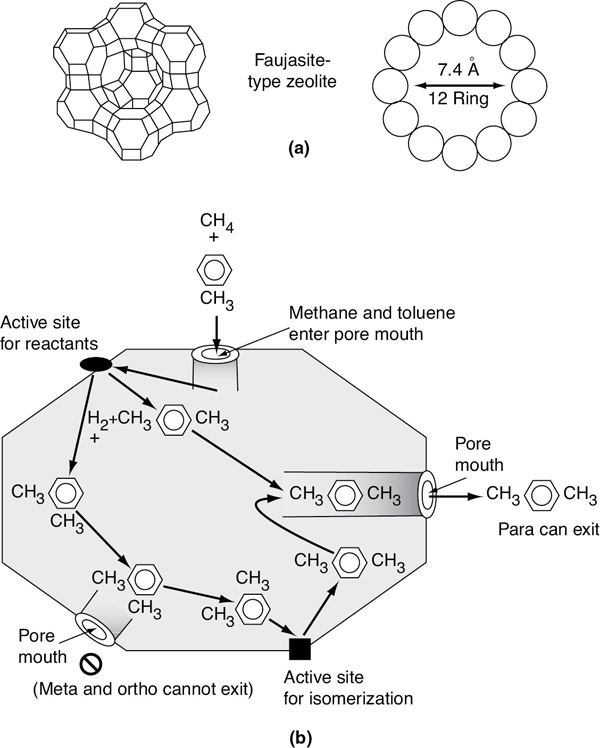
Figure 10-2 (a) Framework structures and (b) pore cross sections of two types of zeolites. (a) Faujasite-type zeolite has a three-dimensional channel system with pores at least 7.4 Å in diameter. A pore is formed by 12 oxygen atoms in a ring. (b) Schematic of reaction CH4 and C6H5CH3. (Note that the size of the pore mouth and the interior of the zeolite are not to scale.) ((a) From N. Y. Chen and T. F. Degnan, Chem. Eng. Prog., 84(2), 33 (1988). Reproduced by permission of the American Institute of Chemical Engineers. Copyright © 1988 AIChE. All rights reserved.)
Catalyst types:
Porous
Molecular sieves
Monolithic
Supported
Unsupported
Typical zeolite catalyst
High selectivity to para-xylene
A very thorough and well-written book.
In some cases, a catalyst consists of minute particles of an active material dispersed over a less-active substance called a support. The active material is frequently a pure metal or metal alloy. Such catalysts are called supported catalysts, as distinguished from unsupported catalysts. Catalysts can also have small amounts of active ingredients added called promoters, which increase their activity. Examples of supported catalysts are the packed-bed catalytic converter in an automobile, the platinum-on-alumina catalyst used in petroleum reforming, and the vanadium pentoxide on silica used to oxidize sulfur dioxide in manufacturing sulfuric acid. Typical unsupported catalysts include platinum gauze for ammonia oxidation, promoted iron for ammonia synthesis, and the silica-alumina dehydrogenation catalyst used in butadiene manufacture.
10.1.3 Catalytic Gas–Solid Interactions
In this section, we focus our attention on gas-phase reactions catalyzed by solid surfaces. For a catalytic reaction to occur, at least one and frequently all of the reactants must become attached to the surface. This attachment is known as adsorption and takes place by two different processes: physical adsorption and chemisorption. Physical adsorption is similar to condensation. The process is exothermic, and the heat of adsorption is relatively small, being on the order of 1–15 kcal/mol. Here, the forces of attraction between the gas molecules and the solid surface are weak. These van der Waals forces consist of interaction between permanent dipoles, between a permanent dipole and an induced dipole, and/or between neutral atoms and molecules. The amount of gas physically adsorbed decreases rapidly with increasing temperature, and above its critical temperature only very small amounts of a substance are physically adsorbed.
The type of adsorption that affects the rate of a chemical reaction is chemisorption. Here, the adsorbed atoms or molecules are held to the surface by valence forces of the same type as those that occur between bonded atoms in molecules. As a result, the electronic structure of the chemisorbed molecule is perturbed significantly, causing it to be extremely reactive. Interaction with the catalyst causes bonds of the adsorbed reactant to be stretched, making them easier to break.
Figure 10-3 shows the bonding from the adsorption of ethylene on a platinum surface to form chemisorbed ethylidyne. Like physical adsorption, chemisorption is an exothermic process, but the heats of adsorption are generally of the same magnitude as the heat of a chemical reaction (i.e., 40–400 kJ/mol). If a catalytic reaction involves chemisorption, it must be carried out within the temperature range where chemisorption of the reactants is appreciable.
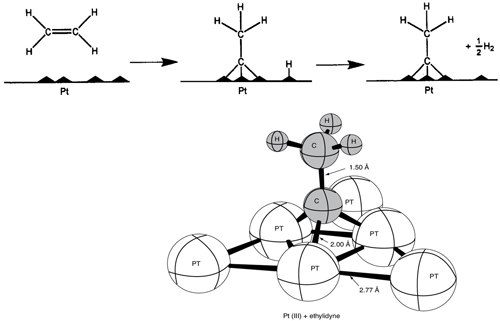
Figure 10-3 Ethylidyne chemisorbed on platinum. (Adapted from G. A. Somorjai, Introduction to Surface Chemistry and Catalysis. © 1994 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.)
Chemisorption on active sites is what catalyzes the reaction.
In a landmark contribution to catalytic theory, H. S. Taylor suggested that a reaction is not catalyzed over the entire solid surface but only at certain active sites or centers.4 He visualized these sites as unsaturated atoms in the solids that resulted from surface irregularities, dislocations, edges of crystals, and cracks along grain boundaries. Other investigators have taken exception to this definition, pointing out that other properties of the solid surface are also important. The active sites can also be thought of as places where highly reactive intermediates (i.e., chemisorbed species) are stabilized long enough to react. This stabilization of a reactive intermediate is key in the design of any catalyst. Consequently, for our purposes we will define an active site as a point on the catalyst surface that can form strong chemical bonds with an adsorbed atom or molecule.
4 H. S. Taylor, Proc. R. Soc. London, A108, 105 (1928).
TOF
One parameter used to quantify the activity of a catalyst is the turnover frequency (TOF), f. It is the number of molecules reacting per active site per second at the conditions of the experiment. When a metal catalyst such as platinum is deposited on a support, the metal atoms are considered active sites. The dispersion, D, of the catalyst is the fraction of the metal atoms deposited on a catalyst that are on the surface. The TOFs for a number of reactions are shown in the Additional Material for Chapter 10 on the Web site (http://www.umich.edu/~elements/6e/10chap/expanded_ch10_TOF.pdf).
10.1.4 Classification of Catalysts
One common way to classify catalysts is in terms of the type of reaction they catalyze.
Table 10-1 gives a list of representative reactions and their corresponding catalysts. Further discussion of each of these reaction classes and the materials that catalyze them can be found on the CRE Web site’s Professional Reference Shelf R10.1 (http://www.umich.edu/~elements/6e/10chap/prof.html).

TABLE 10-1 TYPES OF REACTIONS AND REPRESENTATIVE CATALYSTS
Reaction |
Catalysts |
1. Halogenation–dehalogenation |
CuCl2, AgCl, Pd |
2. Hydration–dehydration |
Al2O3, MgO |
3. Alkylation–dealkylation |
AlCl3, Pd, Zeolites |
4. Hydrogenation–dehydrogenation |
Co, Pt, Cr2O3, Ni |
5. Oxidation |
Cu, Ag, Ni, V2O5 |
6. Isomerization |
AlCl3, Pt/Al2O3, Zeolites |
If, for example, we were to form styrene from an equimolar mixture of ethylene and benzene, we could first carry out an alkylation reaction to form ethyl benzene, which is then dehydrogenated to form styrene. We need both an alkylation catalyst and a dehydrogenation catalyst:
10.2 Steps in a Catalytic Reaction
A photograph of different types and sizes of catalysts is shown in Figure 10-4(a). A schematic diagram of a tubular reactor packed with catalytic pellets is shown in Figure 10-4(b). The overall process by which heterogeneous catalytic reactions proceed can be broken down into the sequence of individual steps shown in Table 10-2 and pictured in Figure 10-5 for an isomerization reaction.

Figure 10-4(a) Catalyst particles of different shapes (spheres, cylinders) and sizes (0.1–1 cm). (Photo courtesy of BASF Corporation.)

Figure 10-4(b) Catalytic packed-bed reactor—schematic.
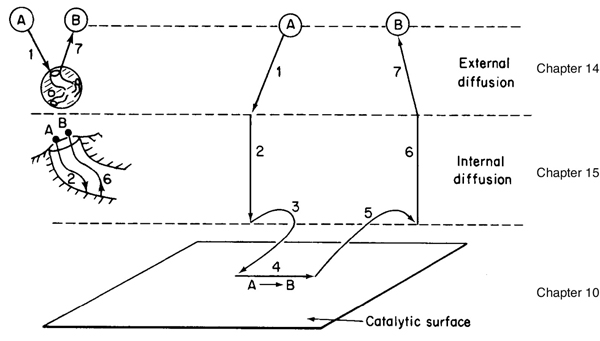
Figure 10-5 Steps in a heterogeneous catalytic reaction.
Each step in Table 10-2 is shown schematically in Figure 10-5.
A reaction takes place on the surface, but the species involved in the reaction must get to and from the surface.
The overall rate of reaction is limited by the rate of the slowest step in the sequence. When the diffusion steps (1, 2, 6, and 7 in Table 10-2) are very fast compared with the surface reaction-rate steps (3, 4, and 5), the concentrations in the immediate vicinity of the active sites are indistinguishable from those in the bulk fluid. In this situation, the transport or diffusion steps do not affect the overall rate of the reaction. In other situations, if the reaction steps are very fast compared with the diffusion steps, mass transport does affect the reaction rate. In systems where diffusion from the bulk gas or liquid to the external catalyst surface or to the mouths of catalyst pores affects the rate, that is, Steps 1 and 7, changing the flow conditions past the catalyst should change the overall reaction rate (see Chapter 14). Once inside the porous catalysts, on the other hand, diffusion within the catalyst pores, that is, Steps 2 and 6, may limit the rate of reaction and, as a result, the overall rate will be unaffected by external flow conditions even though diffusion affects the overall reaction rate (see Chapter 15).
TABLE 10-2 STEPS IN A CATALYTIC REACTION
|
There are many variations of the situation described in Table 10-2. Sometimes, of course, two reactants are necessary for a reaction to occur, and both of these may undergo the steps listed above. Other reactions between two substances may have only one of them adsorbed.
In this chapter we focus on:
3. Adsorption
4. Surface reaction
5. Desorption
With this introduction, we are ready to treat individually the steps involved in catalytic reactions. In this chapter, only Steps 3, 4, and 5—that is, adsorption, surface reaction, and desorption—are considered as we assume that the diffusion steps (1, 2, 6, and 7) are very fast so that the overall reaction rate is not affected by mass transfer in any fashion. Further treatment of the effects involving diffusion limitations is provided in Figure 14-5 in Chapter 14 and Figure 15-5 in Chapter 15.
Where Are We Heading?† As we saw in Chapter 7, one of the tasks of a chemical reaction engineer is to analyze rate data and to develop a rate law that can be used in reactor design. Rate laws in heterogeneous catalysis seldom follow power-law models (Eq. 3-3) and hence are inherently more difficult to formulate from the data. To develop an in-depth understanding and insight as to how the rate laws are formed from heterogeneous catalytic data, we are going to proceed in somewhat of a reverse manner than what is normally done in industry when one is asked to develop a rate law. That is, we will first postulate catalytic mechanisms and then derive rate laws for the various mechanisms. The mechanism will typically have an adsorption step, a surface reaction step, and a desorption step, one of which is usually rate-limiting. Suggesting mechanisms and rate-limiting steps is not the first thing we normally do when presented with data. However, by deriving equations for different mechanisms, we will observe the various forms of the rate law one can have in heterogeneous catalysis. Knowing the different forms that catalytic rate equations can take, it will be easier to view the trends in the data and deduce the appropriate rate law. This deduction is usually what is done first in industry before a mechanism is proposed. Knowing the form of the rate law, one can then numerically evaluate the rate-law parameters and postulate a reaction mechanism and rate-limiting step that are consistent with the experimental data. Finally, we use the rate law to design catalytic reactors. This procedure is shown in Figure 10-6. The dashed lines represent feedback to obtain new data in specific regions (e.g., concentrations, temperature) to evaluate the rate-law parameters more precisely or to differentiate between reaction mechanisms.
† “If you don’t know where you are going, you’ll probably wind up someplace else.” Yogi Berra, New York Yankees.
An algorithm
Knowing the various forms a catalytic rate law can take will help us interpret the data.
An overview
#ChanceCard: Do not pass go. Proceed directly to Section 10.2.3.
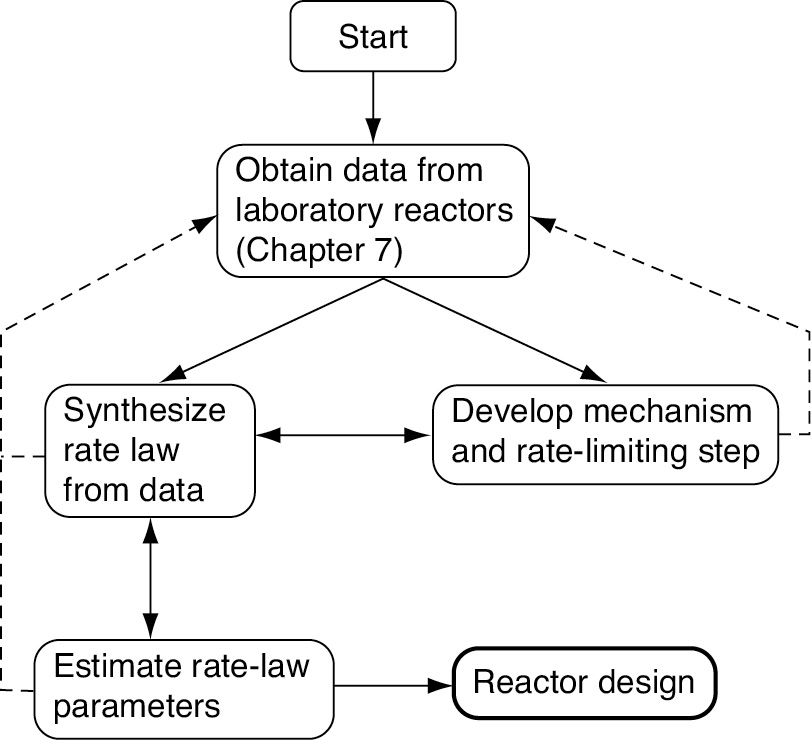
Figure 10-6 Collecting information for catalytic reactor design.
We will now discuss each of the steps shown in Figure 10-5 and Table 10-2. As mentioned earlier, this chapter focuses on Steps 3, 4, and 5 (the adsorption, surface reaction, and desorption steps) by assuming that Steps 1, 2, 6, and 7 are very rapid. Consequently, to understand when this assumption is valid, we shall give a quick overview of Steps 1, 2, 6, and 7. These steps involve diffusion of the reactants to and within the catalyst pellet. While these diffusion steps are covered in detail in Figure 14-5 in Chapter 14 and Figure 15-5 in Chapter 15, it’s worthwhile to give a brief description of these two mass-transfer steps to better understand the entire sequence of steps. If you have had the core course in Mass Transfer or Transport Phenomena you can skip Sections 10.2.1 and 10.2.2, and go directly to Section 10.2.3.
10.2.1 Mass Transfer Step 1: Diffusion from the Bulk to the External Surface of the Catalyst—An Overview
For the moment, let’s assume that the transport of A from the bulk fluid to the external surface of the catalyst is the slowest step in the sequence shown in Figure 10-5. We lump all the resistance to transfer of reactant species A from the bulk fluid to the surface, in the mass transfer boundary layer surrounding the pellet. In this step the reactant A, which is at a bulk concentration CAb must travel (diffuse) through the boundary layer of thickness δ to the external surface of the pellet where the concentration is CAs, as shown in Figure 10-7. The rate of transfer (and hence rate of reaction, ) for this slowest step is

Figure 10-7 Diffusion through the external boundary layer (also see Figures 14-2 and 14-3).
Rate = kC (CAb – CAs)
where the mass transfer coefficient, kC, is a function of the hydrodynamic conditions, namely the fluid velocity, U, and the particle diameter, Dp.
External and internal mass transfer in catalysis are covered in detail in Chapters 14 and 15.
As we will see (Chapter 14), the mass transfer coefficient is inversely proportional to the boundary layer thickness, δ, and directly proportional to the diffusion coefficient (i.e., the diffusivity DAB).
At low velocities of fluid flow over the pellet, the boundary layer across which A and B must diffuse is thick, and it takes a long time for A to travel to the surface, resulting in a small mass transfer coefficient kC. As a result, mass transfer across the boundary layer is slow and limits the rate of the overall reaction. As the velocity over the pellet is increased, the boundary layer becomes thinner and the mass transfer rate is increased. At very high velocities, the boundary layer thickness, δ, is so small that it no longer offers any significant resistance to the diffusion across the boundary layer. As a result, external mass transfer no longer limits the rate of reaction. This external resistance also decreases as the particle size is decreased. As the fluid velocity increases and/or the particle diameter decreases, the mass transfer coefficient increases until a plateau is reached, as shown in Figure 10-8. On this plateau, CAb ≈ CAs, and one of the other steps in the sequence, that is, Steps 2–6, is the slowest step and limits the overall reaction rate. Further details on external mass transfer are discussed in Chapter 14.

Figure 10-8 Effect of particle size and fluid velocity on the overall reaction rate.
High external fluid velocities decrease the resistance to external mass transfer.
10.2.2 Mass Transfer Step 2: Internal Diffusion—An Overview
Now consider that we are operating at a fluid velocity where external diffusion is no longer the rate-limiting step and that internal diffusion is the slowest step. In Step 2 of Figure 10-5, the reactant A diffuses from the external pellet surface at a concentration is CA. As A diffuses into the interior of the pellet, it reacts with catalyst deposited on the sides of the catalyst pellet’s inner pore walls.
The smaller the size of the catalyst pellet, the smaller the resistance to internal mass transfer (i.e., diffusion).
For large pellets, it takes a long time for the reactant A to diffuse into the interior, compared to the time that it takes for the reaction to occur on the interior pore surface. Under these circumstances, the reactant is only consumed near the exterior surface of the pellet and the catalyst near the center of the pellet is wasted catalyst. On the other hand, for very small pellets it takes very little time to diffuse into and out of the pellet interior and, as a result, internal diffusion no longer limits the rate of reaction. When internal mass transfer does not limit the rate of reaction, the concentration inside the pores of the catalyst pellet is equal to the concentration at the external pellet surface, CAs. As a result the corresponding rate law is
Rate = kr CAs
where CAs is the concentration at the external pellet surface and kr is an overall rate constant, which is a function of particle size. The overall rate constant, kr, increases as the pellet diameter decreases. In Chapter 15, we show that Figure 15-5 can be combined with Equation (15-34) to arrive at the plot of kr as a function of DP, shown in Figure 10-9(b).

Figure 10-9 Effect of particle size on the overall reaction-rate constant. (a) Branching of a single pore with deposited metal; (b) decrease in rate constant with increasing particle diameter (see Chapter 15).
We see in Figure 10-9 that for small particle sizes, internal diffusion is no longer the slow step and that the surface reaction sequence of adsorption, surface reaction, and desorption (Steps 3, 4, and 5 in Figure 10-5) limit the overall rate of reaction. Consider now one more important point about internal diffusion and surface reaction. Steps (2–6) are not at all affected by flow conditions external to the pellet.
In the material that follows, we are going to choose our pellet size and external fluid velocity such that neither external diffusion (Chapter 14), nor internal diffusion (Chapter 15), limits the reaction. Instead, we assume that either Step 3 (adsorption), Step 4 (surface reaction), or Step 5 (desorption), or a combination of these steps, limits the overall rate of reaction.
10.2.3 Adsorption Isotherms
Because chemisorption is a necessary part of a catalytic process, we shall discuss it before treating catalytic reaction rates. The letter S will represent an active site; alone, it will denote a vacant site, with no atom, molecule, or complex adsorbed on it. The combination of S with another letter (e.g., A⋅S) will mean that one unit of species A has been chemically adsorbed on the site S. Species A can be an atom, molecule, or some other atomic combination, depending on the circumstances. Consequently, the adsorption of A on a site S is represented by
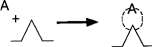
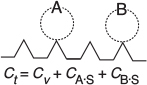
The total molar concentration of active sites per unit mass of catalyst is equal to the number of active sites per unit mass divided by Avogadro’s number and will be labeled Ct (mol/g-cat). The molar concentration of vacant sites, Cυ(mol/g-cat), is the number of vacant sites per unit mass of catalyst divided by Avogadro’s number. In the absence of catalyst deactivation, we assume that the total concentration of active sites, Ct, remains constant. Some further definitions include
Pi = partial pressure of species i in the gas phase (atm, bar, or kPa)
Ci·S = surface concentration of sites occupied by species i (mol/g-cat)
A conceptual model depicting species A and B adsorbed on two different sites is shown in Figure 10-10.

Figure 10-10 Vacant and occupied sites.
For the system shown in Figure 10-10, the total concentration of sites is
Site balance
This equation is referred to as a site balance. A typical value for the total concentration of sites could be the order of 1022 sites/g-cat. To express the site concentration in terms of (moles/g-cat) we divide by Avogadro’s number to get “moles of sites/g-cat.”
Now consider the adsorption of a nonreacting gas onto the surface of a catalyst. Adsorption data are frequently reported in the form of adsorption isotherms. Isotherms portray the amount of a gas adsorbed on a solid at different pressures at a given temperature.
Postulate models; then see which one(s) fit(s) the data.
First, an adsorption mechanism is proposed, and then the isotherm (see Figure 10-11, page 455) obtained from the mechanism is compared with the experimental data. If the isotherm predicted by the model agrees with the experimental data, the model may reasonably describe what is occurring physically in the real system. If the predicted curve does not agree with the experimental data, the model fails to match the physical situation in at least one important characteristic and perhaps more.
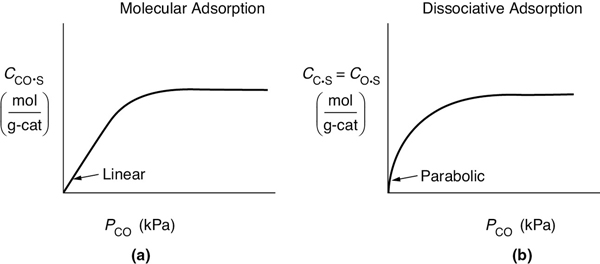
Figure 10-11 Langmuir isotherms for (a) molecular adsorption (b) dissociative adsorption of CO.
We will consider two types of adsorption: molecular adsorption and dissociative adsorption. To illustrate the difference between molecular adsorption and dissociative adsorption, we will postulate two models for the adsorption of carbon monoxide on a metal surface active site. In the molecular adsorption model, carbon monoxide is adsorbed as molecules, CO,
as is the case on nickel

In the dissociative adsorption model, carbon monoxide is adsorbed as oxygen and carbon atoms instead of molecular CO
as is the case on iron5
5 R. I. Masel, Principles of Adsorption and Reaction on Solid Surfaces, New York: Wiley, 1996.
Two models:
1. Adsorption as CO
2. Adsorption as C and O
The former is called molecular or nondissociated adsorption (e.g., CO) and the latter is called dissociative adsorption (e.g., C and O). Whether a molecule adsorbs nondissociatively or dissociatively depends on the surface.
Molecular Adsorption: The adsorption of carbon monoxide molecules will be considered first. Because the carbon monoxide does not react further after being adsorbed, we need only to consider the molecular adsorption process:
Molecular adsorption
In obtaining a rate law for the rate of adsorption, the reaction in Equation (10-2) can be treated as an elementary reaction. The rate of attachment of the carbon monoxide molecules to the active site on the surface is proportional to the number of collisions that CO molecules make with a surface active site per second. In other words, a specific fraction of the molecules that strike the surface become adsorbed. The collision rate is, in turn, directly proportional to the carbon monoxide partial pressure, PCO. Because carbon monoxide molecules adsorb only on vacant sites and not on sites already occupied by other carbon monoxide molecules, the rate of attachment is also directly proportional to the concentration of vacant sites, Cν. Combining these two facts along with the law of mass action means that the rate of attachment of carbon monoxide molecules to the surface is directly proportional to the product of the partial pressure of CO (PCO) and the concentration of vacant sites (Cν); that is,
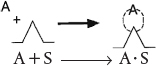
PCO = CCORT
The rate of detachment of molecules from the surface can be a first-order process; that is, the detachment of carbon monoxide molecules from the surface is usually directly proportional to the concentration of sites occupied by the adsorbed molecules (e.g., CCO·S):

The net rate of adsorption is equal to the rate of molecular attachment to the surface minus the rate of detachment from the surface. If kA and k-A are the constants of proportionality for the attachment and detachment processes, then
The ratio KA = kA/k-A is the adsorption equilibrium constant. Using KA to rearrange Equation (10-3) gives
The adsorption rate constant, kA, for molecular adsorption is virtually independent of temperature, while the desorption constant, k·A, increases exponentially with increasing temperature. Consequently, the equilibrium adsorption constant KA decreases exponentially with increasing temperature.
Site balance
Because carbon monoxide is the only material adsorbed on the catalyst, the site balance gives
At equilibrium, the net rate of adsorption equals zero, that is, rAD ≡ 0. Setting the left-hand side of Equation (10-4) equal to zero and solving for the concentration of CO adsorbed on the surface, we get
Using Equation (10-5) to give in terms of CCO·S and the total number of sites Ct, we can solve for the equilibrium value of CCO·S in terms of constants and the pressure of carbon monoxide
Rearranging gives us a Langmuir isotherm6
6 Named after Irving Langmuir (1881–1957), who first proposed it. He received the Nobel Prize in 1932 for his discoveries in surface chemistry (https://www.nobelprize.org/nobel_prizes/chemistry/laureates/1932/langmuir-bio.html).
Langmuir adsorption isotherm
This equation thus gives the equilibrium concentration of carbon monoxide adsorbed on the surface, CCO·S, as a function of the partial pressure of carbon monoxide, and is an equation for the adsorption isotherm. This particular type of isotherm equation is called a Langmuir isotherm.7 Figure 10-11(a) shows a single-site Langmuir isotherm for molecular adsorption in terms of the adsorbed concentration (mass of CO adsorbed per unit mass of catalyst) as a function of the partial pressure of CO, that is, Equation (10-7).
7 Ibid.
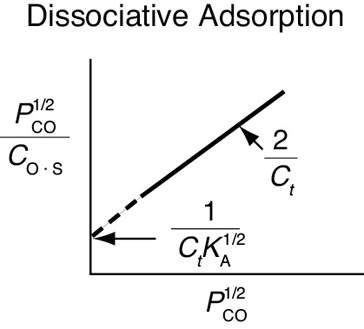
Now, for the case of dissociative adsorption, Equation (10-11), Figure 10-11(b) shows the concentration of the dissociated atoms of C and O adsorbed per unit mass of catalyst of a function of partial pressure of CO, that is, Equation (10-11).
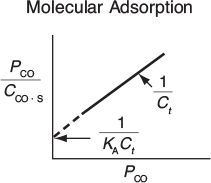
One method of checking whether or not a model (e.g., molecular adsorption vs. dissociative adsorption) predicts the behavior of the experimental data is to linearize the model’s equation and then plot the indicated variables against one another. For example, the molecular adsorption isotherm, Equation (10-7), may be arranged in the form
Molecular adsorption
and the linearity of a plot of PCO/CCO·S as a function of PCO will determine whether the data conform to molecular adsorption, that is, a Langmuir single-site isotherm.
Dissociative Adsorption: We next derive the isotherm for carbon monoxide disassociating into separate atoms as it adsorbs on the surface, that is,
Dissociative adsorption
When the carbon monoxide molecule dissociates upon adsorption, it is referred to as the dissociative adsorption of carbon monoxide. As in the case of molecular adsorption, the rate of adsorption is proportional to the partial pressure of carbon monoxide in the system because this rate is governed by the number of gaseous CO collisions with the surface. For a molecule to dissociate as it adsorbs, however, two adjacent vacant active sites are required, rather than the single site needed when a substance adsorbs in its molecular form. The probability of two vacant sites occurring adjacent to one another is proportional to the square of the concentration of vacant sites, cf. the law of mass action. These two observations mean that the rate of adsorption is proportional to the product of the carbon monoxide partial pressure and the square of the vacant-site concentration, .
For desorption to occur, two occupied sites must be adjacent, meaning that the rate of desorption is proportional to the product of the occupied-site concentration, (C·S) × (O·S). The net rate of adsorption can then be expressed as
Factoring out kA, the equation for dissociative adsorption is
where

Rate of dissociative adsorption
For dissociative adsorption, both kA and k·A increase exponentially with increasing temperature, while the adsorption equilibrium constant KA decreases with increasing temperature because adsorption is an exothermic reaction step.
At equilibrium, rAD ≡ 0, and
For CC·S = CO·S
Substituting for CC·S and CO·S in a site balance equation (10-1),
Site balance:
Solving for Cυ
This value may be substituted into Equation (10-10) to give an expression that can be solved for the equilibrium value of CO·S as a function of the partial pressure of CO. The resulting equation for the isotherm shown in Figure 10-11(b) is
Langmuir isotherm for carbon monoxide dissociative adsorption as atomic carbon and oxygen
Taking the inverse of both sides of the equation, then multiplying through by (PCO)1/2, yields
If dissociative adsorption is the correct model, a plot of versus should be linear with slope (2/Ct).
When more than one substance is present, the adsorption isotherm equations are somewhat more complex. The principles are the same, though, and the isotherm equations are easily derived. It is left as an exercise to show that the adsorption isotherm of A in the presence of another adsorbate B is given by the relationship
When the adsorption of both A and B are first-order processes, the desorptions are also first order, and both A and B are adsorbed as molecules. The derivations of other Langmuir isotherms are relatively easy.
In obtaining the Langmuir isotherm equations, several aspects of the adsorption system were presupposed in the derivations. The most important of these, and the one that has been subject to the greatest doubt, is that a uniform surface is assumed. In other words, any active site has the same attraction for an impinging molecule as does any other active site. Isotherms different from the Langmuir isotherm, such as the Freundlich isotherm, may be derived based on various assumptions concerning the adsorption system, including different types of nonuniform surfaces.
Note assumptions in the model and check their validity.
10.2.4 Surface Reaction
The rate of adsorption of species A onto a solid surface site
is given by
After a reactant has been adsorbed onto the surface, that is, A · S, it is capable of reacting in a number of ways to form the reaction product. Three of these ways are:
Single site. The surface reaction may be a single-site mechanism in which only the site on which the reactant is adsorbed is involved in the reaction. For example, an adsorbed molecule of A may isomerize (or perhaps decompose) directly on the site to which it is attached, such as pentene isomerization

The pentane isomerization can be written in generic form as

Each step in the reaction mechanism is elementary, so the surface reaction rate law is
Single Site
where KS is the surface-reaction equilibrium constant KS = kS/k–S
Ks = (dimensionless)
Dual site. The surface reaction may be a dual-site mechanism in which the adsorbed reactant interacts with another site (either unoccupied or occupied) to form the product.
First type of dual-site mechanism

For example, adsorbed A may need to react with an adjacent vacant site to further become destabilized to yield a vacant site and a site on which the product is adsorbed. In case of the dehydration of butanol, the reaction products adsorb on two adjacent sites.
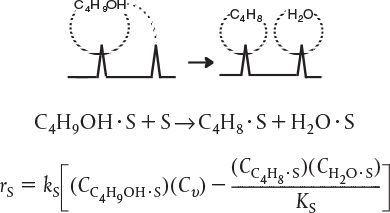
For the generic reaction
the corresponding surface-reaction rate law is
Dual Site
A second dual-site mechanism is the reaction between two adsorbed species, such as the reaction of CO with O.
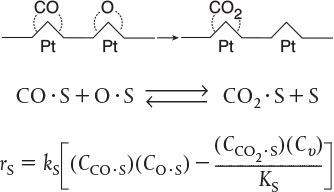
For the generic reaction

the corresponding surface-reaction rate law is
A third dual-site mechanism is the reaction of two species adsorbed on different types of sites S and S′, such as the reaction of CO with O.
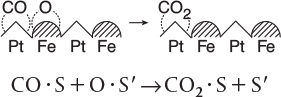
For the generic reaction
the corresponding surface-reaction rate law is

Langmuir-Hinshelwood kinetics
Reactions involving either single- or dual-site mechanisms, which were described earlier, are sometimes referred to as following Langmuir-Hinshelwood kinetics.
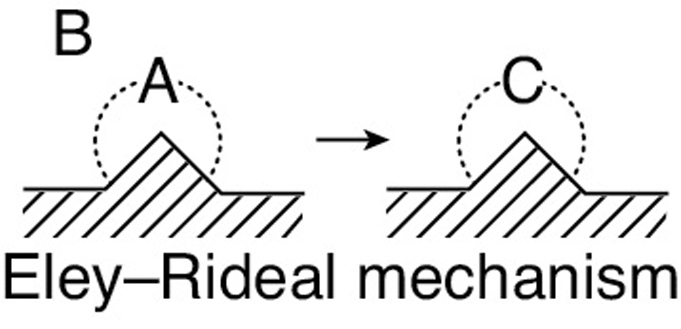
Eley–Rideal. A third mechanism is the reaction between an adsorbed molecule and a molecule in the gas phase, such as the reaction of propylene and benzene (cf. the reverse reaction in Figure 10-13 on page 463.)
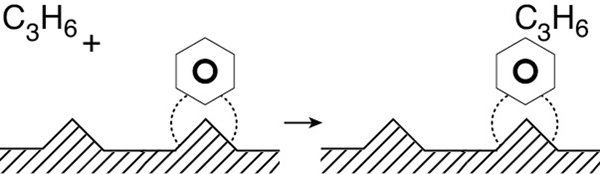
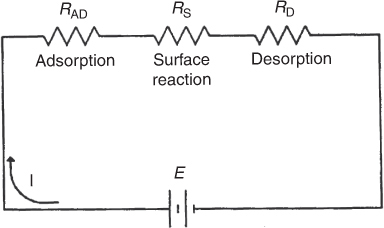
Figure 10-12 Electrical analog to heterogeneous reactions.

Figure 10-13 Sequence of steps in a reaction-limited catalytic reaction.
For the generic reaction
the corresponding surface-reaction rate law is
Surface reaction models
This type of mechanism is referred to as an Eley–Rideal mechanism.
KDC = (atm)
10.2.5 Desorption
In each of the preceding cases, the products of the surface reaction adsorbed on the surface are subsequently desorbed into the gas phase. For the desorption of a species (e.g., C)
the rate of desorption of C is
where KDC is the desorption equilibrium constant with units of atm. Now let’s look at the above desorption step of C•S from right to left. We note that the desorption step for C•S is just the reverse of the adsorption step. Consequently, the rate of desorption of C, rDC, is just opposite in sign to the rate of adsorption of C, rADC
rDC = –rADC
In addition, we see that the desorption equilibrium constant KDC is just the reciprocal of the adsorption equilibrium constant for C, KC
in which case the rate of desorption of C can be written
In the material that follows, the form of the equation for the desorption step that we will use to develop our rate laws will be similar to Equation (10-21).
10.2.6 The Rate-Limiting Step
When heterogeneous reactions are carried out at steady state, the rates of each of the three reaction steps in series (adsorption, surface reaction, and desorption) are equal to one another
However, one particular step in the series is usually found to be rate-limiting or rate-controlling. That is, if we could make that particular step go faster, the entire reaction would proceed at an accelerated rate. Consider the analogy to the electrical circuit shown in Figure 10-12. A given concentration of reactants is analogous to a given driving force or electromotive force (EMF). The current I (with units of coulombs/s) is analogous to the rate of reaction, (mol/s·g-cat), and a resistance Ri (with units of Ohms, Ω) is associated with each step in the series. Because the resistances are in series, the total resistance Rtot is just the sum of the individual resistances, for adsorption (RAD), surface reaction (RS), and desorption (RD). The current, I, for a given voltage, E, is
The concept of a rate-limiting step
Who is slowing us down?
Because we observe only the total resistance, Rtot, it is our task to find which resistance is much larger (say, 100 Ω) than the other two resistances (say, 0.1 Ω). Thus, if we could lower the largest resistance, the current I (i.e., ), would be larger for a given voltage, E. Analogously, we want to know which step in the adsorption–reaction–desorption series is limiting the overall rate of reaction.
An algorithm to determine the rate-limiting step

The approach in determining catalytic and heterogeneous mechanisms is usually termed the Langmuir-Hinshelwood approach, since it is derived from ideas proposed by Hinshelwood based on Langmuir’s principles for adsorption.8 The Langmuir-Hinshelwood approach was popularized by Hougen and Watson and occasionally includes their names.9 It consists of first assuming a sequence of steps in the reaction. In writing this sequence, one must choose among such mechanisms as molecular or atomic adsorption, and single- or dual-site reaction. Next, rate laws are written for the individual steps as shown in the preceding section, assuming that all steps are reversible. Finally, a rate-limiting step is postulated, and steps that are not rate-limiting are used to eliminate all coverage-dependent terms. The most questionable assumption in using this technique to obtain a rate law is the hypothesis that the activity of the surface is essentially uniform as far as the various steps in the reaction are concerned.
8 C. N. Hinshelwood, The Kinetics of Chemical Change, Oxford: Clarendon Press, 1940.
9 O. A. Hougen and K. M. Watson, Ind. Eng. Chem., 35, 529 (1943).
Industrial Example of Adsorption-Limited Reaction
An example of an adsorption-limited reaction is the synthesis of ammonia from hydrogen and nitrogen
over an iron catalyst that proceeds by the following mechanism:10
10 From the literature cited in G. A. Somorjai, Introduction to Surface Chemistry and Catalysis, New York: Wiley, 1994, p. 482.
Dissociative adsorption of N2 is rate-limiting.
The rate-limiting step is believed to be the adsorption of the N2 molecule as an N atom on an iron active site.
Industrial Example of Surface-Limited Reaction
An example of a surface-limited reaction is the reaction of two noxious automobile exhaust products, CO and NO
carried out over a copper catalyst to form more environmentally acceptable products, N2 and CO2
Surface reaction is rate-limiting.
Analysis of the rate law suggests that CO2 and N2 are weakly adsorbed, that is, have infinitesimally small adsorption constants (see Problem P10-9B).
What If Two Steps Are Equally Rate Limiting?
If two steps, say surface reaction and desorption, are equally slow then one must resort to applying the Pseudo-Steady-State Hypothesis (PSSH) to the adsorbed species as shown in the Chapter 10 expanded material (http://www.umich.edu/~elements/6e/10chap/expanded_ch10_PSSH.pdf).
10.3 Synthesizing a Rate Law, Mechanism, and Rate-Limiting Step
We now wish to develop rate laws for catalytic reactions that are not diffusion-limited. In developing the procedure of how to obtain a rate law, a mechanism and a rate-limiting step, consistent with experimental observation, we shall discuss the catalytic decomposition of cumene to form benzene and propylene. The overall reaction is
Adsorption
Surface reaction
Desorption
A conceptual model depicting the sequence of steps in this platinum-catalyzed reaction is shown in Figure 10-13. Figure 10-13 is only a schematic representation of the adsorption of cumene; a more realistic model is the formation of a complex of the π orbitals of benzene with the catalytic surface, as shown in Figure 10-14.

Figure 10-14π-orbital complex on surface.
The nomenclature in Table 10-3 will be used to denote the various species in this reaction: C = cumene, B = benzene, and P = propylene. The reaction sequence for this decomposition is shown in Table 10-3.
TABLE 10-3 STEPS IN A LANGMUIR-HINSHELWOOD KINETIC MECHANISM
These three steps represent the mechanism for cumene decomposition.
Equations (10-22)–(10-24) represent the mechanism proposed for this reaction.
Ideal gas law PC = CCRT
When writing rate laws for these steps, we treat each step as an elementary reaction; the only difference is that the species concentrations in the gas phase are replaced by their respective partial pressures
CC → PC
There is no theoretical reason for this replacement of the concentration, CC, with the partial pressure, PC; it is just the convention initiated in the 1930s and used ever since. Fortunately, PC can be calculated easily and directly from CC using the ideal gas law (i.e., PC = CCRT ).
The rate expression for the adsorption of cumene as given in Equation (10-22) is
If rAD has units of (mol/g-cat·s) and CC·S has units of (mol cumene adsorbed/g-cat) and PC has units of kPa, bar or atm, then typical units of kA, k·A, and KC would be
The rate law for the surface-reaction step producing adsorbed benzene and propylene in the gas phase
is
with the surface reaction equilibrium constant being
Typical units for kS and KS are s–1 and kPa (or atm or bar) respectively.
Propylene is not adsorbed on the surface. Consequently, its concentration on the surface is zero, that is,
CP·S = 0
The rate of benzene desorption (see Equation (10-24)) is
Typical units of kD and KDB are s–1 and kPa or bar, respectively. By viewing the desorption of benzene
from right to left, we see that desorption is just the reverse of the adsorption of benzene. Consequently, as mentioned earlier, it is easily shown that the benzene adsorption equilibrium constant KB is just the reciprocal of the benzene desorption constant KDB
and Equation (10-28) can be written as
Because there is no accumulation of reacting species on the surface, the rates of each step in the sequence are all equal as discussed in Figure 10-12:
For the mechanism postulated in the sequence given by Equations (10-22)–(10-24), we wish to determine which step is rate-limiting. We first assume one of the steps to be rate-limiting (rate-controlling) and then formulate the reaction-rate law in terms of the partial pressures of the species present. From this expression, we can determine the variation of the initial reaction rate with the initial partial pressures and the initial total pressure. If the predicted rate varies with pressure in the same manner as the rate observed experimentally, the implication is that the assumed mechanism and rate-limiting step are correct.
We will first start our development of the rate laws with the assumption that the adsorption step is rate-limiting and derive the rate law, and then proceed in the following reactions to assume that each of the other two steps’ surface reaction and desorption limit the overall rate and then derive the rate law for each of these other two limiting cases.
10.3.1 Is the Adsorption of Cumene Rate-Limiting?
To answer this question, we shall first assume that the adsorption of cumene is indeed the rate-limiting step (RLS)
derive the corresponding rate law, and then check to see whether it is consistent with experimental observation. By postulating that this (or any other) step is rate-limiting, we are assuming that the adsorption rate constant of this step (in this case kA) is small with respect to the specific rates of the other steps (in this case kS and kD).11 The rate of adsorption is
11 Strictly speaking, one should compare the product kAPC with kS and kD.
Need to express Cυ and CC·S in terms of PC, PB, and PP.
Dividing rAD by kAPC, we note . The reason we do this is that in order to compare terms, the ratios , and must all have the same units . Luckily for us, the end result is the same, however.
Because we cannot measure either Cυ or CC · S , we must replace these variables in the rate law with measurable quantities in order for the equation to be meaningful.
For steady-state operation we have
For adsorption-limited reactions, kA is very small and kS and kD are very, very large by comparison. Consequently, the ratios rS / kS and rD / kD are very small (approximately zero), whereas the ratio rAD / kA is relatively large.
The surface reaction-rate law is
Again, for adsorption-limited reactions, the surface-specific reaction rate kS is large by comparison, and we can set
and solve Equation (10-31) for CC · S
From Equation (10-33) we see that in order to be able to express CC · S solely in terms of the partial pressures of the species present, we must evaluate CB · S . The rate of desorption of benzene is
Using find CB · S and CC · S in terms of partial pressures.
However, for adsorption-limited reactions, kD is large by comparison, and we can set
and then solve Equation (10-29) for CB · S
After combining Equations (10-33) and (10-35), we have
Replacing CC·S in the rate equation by Equation (10-36) and then factoring Cυ, we obtain
Thermodynamics: Let’s look at how the thermodynamic constant-pressure equilibrium constant, KP, found its way into Equation (10-37) and how we can find its value for any reaction. First we observe that at equilibrium rAD = 0, Equation (10-37) rearranges to
We also know from thermodynamics (Appendix C) that for the reaction
also at equilibrium , we have the following relationship for partial pressure equilibrium constant KP
Consequently, the following relationship must hold
The thermodynamic equilibrium constant, Kp
The equilibrium constant can be determined from thermodynamic data and is related to the change in the Gibbs free energy, ΔG∘, by the equation (see Equation (C-2) in Appendix C)
where R is the ideal gas constant and T is the absolute temperature.
Back to the rate law task at hand. The concentration of vacant sites, Cυ, can now be eliminated from Equation (10-37) by utilizing the site balance to give the total concentration of sites, Ct, which is assumed constant12
Total sites = Vacant sites + Occupied sites
12 #SurfaceReactionRate, Some (I won’t mention any names, but they know who they are) prefer to write the surface reaction rate in terms of the fraction of the surface of sites covered (i.e., fA rather than the number of sites CA·S covered, the difference being the multiplication factor of the total site concentration, Ct. In any event, the final form of the rate law is the same because Ct, KA, kS, and so on, are all lumped into the reaction-rate constant, k.
Because cumene and benzene are adsorbed on the surface, the concentration of occupied sites is (CC·S + CB·S), and the total concentration of sites is
Site balance
Substituting Equations (10-35) and (10-36) into Equation (10-40), we have
Solving for Cυ, we have
Combining Equations (10-41) and (10-37), we find that the rate law for the catalytic decomposition of cumene, assuming that the adsorption of cumene is the rate-limiting step, is
Cumene reaction rate law iff adsorption were the limiting step
We now, as we usually do, sketch a plot of the initial rate of reaction as a function of the initial partial pressure, in this case cumene, PC0. Initially, no products are present; consequently, PP = PB = 0. The initial rate is given by
If the cumene decomposition is adsorption rate limited, then from Equation (10-43) we see that the initial rate will be linear with the initial partial pressure of cumene, as shown in Figure 10-15.

Figure 10-15 Adsorption-limited reaction.
Iff adsorption were rate-limiting, the data should show increasing linearly with PCO.
Before checking to see whether Figure 10-15 is consistent with experimental observation, we shall derive the corresponding rate laws for the other possible rate-limiting steps and then develop corresponding initial rate plots for the case when the surface reaction is rate-limiting and then for the case when the desorption of benzene is rate-limiting.
10.3.2 Is the Surface Reaction Rate-Limiting?
We next assume the surface reaction step
is the rate-limiting step (RLS) and derive a rate law in terms of the partial pressures of C and B. The rate law for the surface reaction is
Single-site mechanism
Since we cannot readily measure the concentrations of the adsorbed species, we must utilize the adsorption and desorption steps to eliminate CC·S and CB·S from this equation.
From the adsorption rate expression in Equation (10-25) and the condition that kA and kD are very large by comparison with kS when the surface reaction is limiting (i.e., rAD/kA⋍ 0),13 we obtain a relationship for the surface concentration for adsorbed cumene
13 See footnote 11 on page 466.
CC·S = KCPCCυ
In a similar manner, the surface concentration of adsorbed benzene can be evaluated from the desorption rate expression, Equation (10-29), together with the approximation
Using find CB · S and CC · S in terms of partial pressures.
then we get the same result for CB•S as before when we had adsorption limitation, that is,
CB·S = KBPBCυ
Substituting for CB·S and CC·S in Equation (10-26) gives us
where the thermodynamic equilibrium constant was used to replace the ratio of surface reaction and adsorption constants, that is,
The only variable left to eliminate is and we use a site balance to accomplish this, that is,
Site balance
Substituting for concentrations of the adsorbed species, CB·S, and CC·S, factoring out Cυ, and rearranging yields
Substituting for Cυ in Equation (10-26a)
Cumene rate law iff surface-reaction-limiting
The initial rate of reaction is
Using Equation (10-45), we make the sketch of the initial rate of reaction, , as a function of the initial partial pressure of cumene, PC0, as shown in Figure 10-16 for the case when surface-reaction limit is the limiting step.
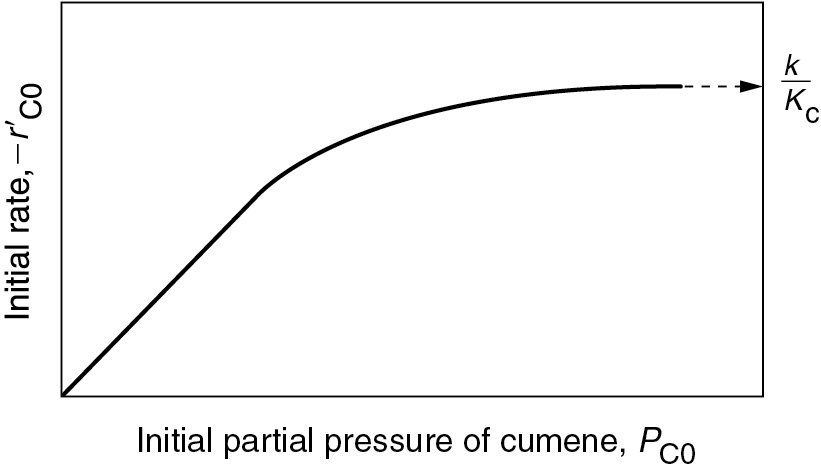
Figure 10-16 Surface-reaction-limited.
At low partial pressures of cumene
and we observe that the initial rate will increase linearly with the initial partial pressure of cumene:
Iff surface reaction were rate-limiting, the data would show this behavior.
At high partial pressures
and Equation (10-45) becomes
and the initial rate is independent of the initial partial pressure of cumene.
10.3.3 Is the Desorption of Benzene the Rate-Limiting Step (RLS)?
To answer this question, we now want to determine the initial rate, , and a function of partial pressure of cumene, PC, for the desorption step
The rate expression for the desorption of benzene is
From the rate expression for surface reaction, Equation (10-26), we set
For desorption-limited reactions, both kA and kS are very large compared with kD, which is small.
to obtain
Similarly, for the adsorption step, Equation (10-25), we set
then substitute for CC·S in Equation (10-46) to obtain
Combining Equations (10-26b), (10-29), and (10-47) gives us
where KC is the cumene adsorption constant, KS is the surface reaction equilibrium constant, and KP is the thermodynamic gas-phase equilibrium constant, Equation (10-38), for the reaction. The expression for Cυ is obtained from a site balance:
After substituting for the respective surface concentrations, we solve the site balance for Cυ
Replacing Cυ in Equation (10-48) by Equation (10-49) and multiplying the numerator and denominator by PP, we obtain the rate expression for desorption control
Cumene decomposition rate law iff desorption were limiting
To determine the dependence of the initial rate of reaction on the initial partial pressure of cumene, we again set PP = PB = 0, and the rate law reduces to
If desorption limits, the initial rate is independent of the initial partial pressure of cumene.
with the corresponding plot of shown in Figure 10-17. If desorption were rate limiting, we would see that the initial rate of reaction would be independent of the initial partial pressure of cumene.
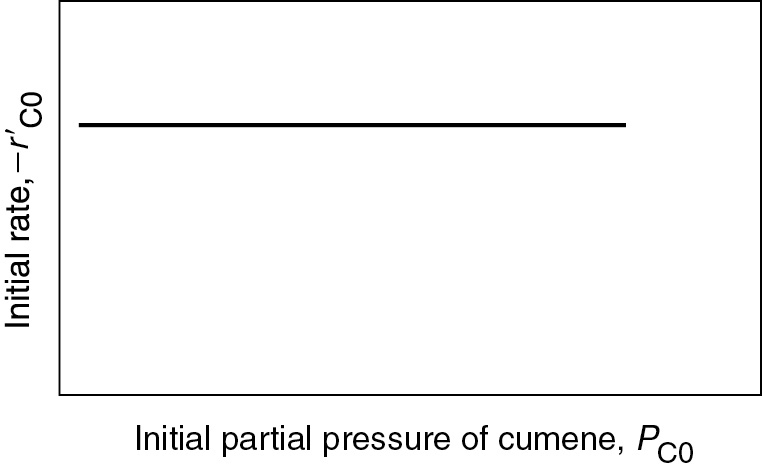
Figure 10-17 Desorption-limited reaction.
10.3.4 Summary of the Cumene Decomposition

Now that we know what the functionality of initial rate versus partial pressure looks like when we assume each of the step is the RLS, it gives us a foot up in interpreting reaction rate data. The experimental observations of as a function of PC0 are shown in Figure 10-18. From the plot in Figure 10-18, we can clearly see that neither adsorption nor desorption is rate-limiting. For the reaction and mechanism given by
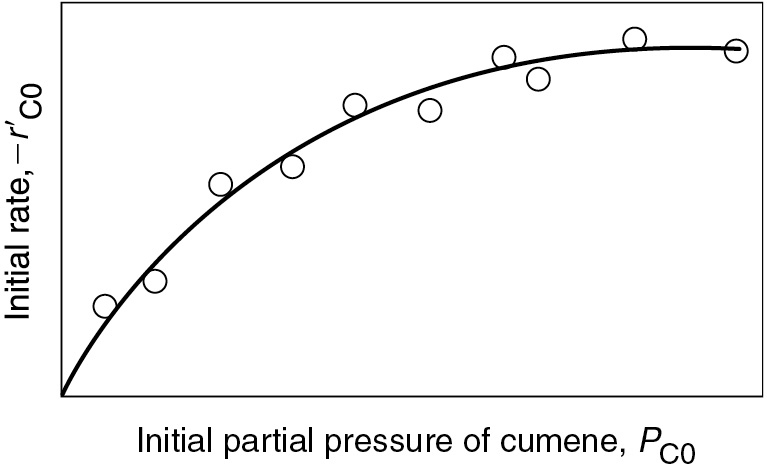
Figure 10-18 Actual initial rate as a function of partial pressure of cumene.
the rate law derived by assuming that the surface reaction is the rate-limiting step (RLS) agrees with the data.
Cumene decomposition is surface-reaction-limited.
Surface-reaction-limited mechanism is consistent with experimental data.
The rate law for the case of no inerts adsorbing on the surface is
The forward cumene decomposition reaction is a single-site mechanism involving only adsorbed cumene, while the reverse reaction of propylene in the gas phase reacting with adsorbed benzene is an Eley–Rideal mechanism.
If we were to have an adsorbing inert in the feed, the inert would not participate in the reaction but would occupy active sites on the catalyst surface:
Our site balance is now
Because the adsorption of the inert is at equilibrium, the concentration of sites occupied by the inert is
Substituting for the inert sites in the site balance, the rate law for surface reaction control when an adsorbing inert is present is
Adsorbing inerts
One observes that the rate decreases as the partial pressure of adsorbing inerts, PI, increases.
10.3.5 Reforming Catalysts
We now consider a dual-site mechanism, which is a reforming reaction found in petroleum refining to upgrade the octane number of gasoline.
The more compact the molecule, the greater the octane number.
Catalyst manufacture
One common reforming catalyst is platinum on alumina. Platinum on alumina (Al2O3) (see SEM photo in Figure 10-19) is a bifunctional catalyst that can be prepared by exposing alumina pellets to a chloroplatinic acid solution, drying, and then heating in air at 775–875 K for several hours. Next, the material is exposed to hydrogen at temperatures around 725–775 K to produce very small clusters of Pt on alumina. These clusters have sizes on the order of 10 Å, while the alumina pore sizes on which the Pt is deposited are on the order of 100–10,000 Å (i.e., 10–1000 nm).

Figure 10-19 Platinum on alumina. (Masel, Richard. Chemical Kinetics and Catalysis, p. 700. © John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.)
Gasoline |
|
C5 |
10% |
C6 |
10% |
C7 |
20% |
C8 |
25% |
C9 |
20% |
C10 |
10% |
C11-12 |
5% |
As an example of catalytic reforming, we shall consider the isomerization of n-pentane to i-pentane
Normal pentane has an octane number of 62, while iso-pentane, which is more compact, has an octane number of 90! The n-pentane adsorbs onto the platinum, where it is dehydrogenated to form n-pentene. The n-pentene desorbs from the platinum and adsorbs onto the alumina, where it is isomerized to i-pentene, which then desorbs and subsequently adsorbs onto platinum, where it is hydrogenated to form i-pentane. That is,
We shall focus on the isomerization step to develop the mechanism and the rate law
The procedure for formulating a mechanism, rate-limiting step, and corresponding rate law is given in Table 10-4.
TABLE 10-4 ALGORITHM FOR DETERMINING THE REACTION MECHANISM AND RATE-LIMITING STEP
Isomerization of n-pentene (N) to i-pentene (I) over alumina Reformingreaction to increaseoctane number of gasoline Step 1. Select a mechanism. (Let’s choose a Dual-Site Mechanism) Treat each reaction step as an elementary reaction when writing rate laws. Step 2. Assume a rate-limiting step. We choose the surface reaction first, because more than 75% of all heterogeneous reactions that are not diffusion-limited are surface-reaction-limited. We note that the PSSH must be used when more than one step is rate limiting (see Section 10.3.6). The rate law for the surface reaction step is
Step 3. Find the expression for concentration of the adsorbed species Ci·S. Use the other steps that are not limiting to solve for Ci·S (e.g., CN·S and CI·S). For this reaction Step 4. Write a site balance. Step 5. Derive the rate law. Combine Steps 2, 3, and 4 to arrive at the rate law |
Step 6. Compare with data. Compare the rate law derived in Step 5 with experimental data. If they agree, there is a good chance that you have found the correct mechanism and rate-limiting step. If your derived rate law (i.e., model) does not agree with the data
|
An observation: We note that in Table 10-4 for the dual-site mechanism, the denominator of the rate law for is squared (i.e., in Step 5 [1/( )2)]), while for a single-site mechanism, it is not squared (i.e., Step 6 [1/( )]). This fact is useful when analyzing catalytic reactor data.
TABLE 10-5 IRREVERSIBLE SURFACE-REACTION-LIMITED RATE LAWS
Single site Dual site Eley–Rideal |

We need a word of caution at this point. Just because the mechanism and rate-limiting step may fit the rate data does not imply that the mechanism is correct.14 Usually, spectroscopic measurements are needed to confirm a mechanism absolutely. However, the development of various mechanisms and rate-limiting steps can provide insight into the best way to correlate the data and develop a rate law.
14 R. I. Masel, Principles of Adsorption and Reaction on Solid Surfaces, New York: Wiley, 1996, p. 506, www.masel.com. This is a terrific book.
10.3.6 Rate Laws Derived from the Pseudo-Steady-State Hypothesis (PSSH)
In Section 9.1 we discussed the PSSH, where the net rate of formation of reactive intermediates was assumed to be zero. An alternative way to derive a catalytic rate law rather than setting
is to assume that each species adsorbed on the surface is a reactive intermediate. Consequently, the net rate of formation of species i adsorbed on the surface will be zero
The PSSH is primarily used when more than one step is rate-limiting. The isomerization example shown in Table 10-4 is reworked using the PSSH in the Chapter 10 Expanded Material on the CRE Web site (http://www.umich.edu/~elements/6e/10chap/expanded_ch10_PSSH.pdf).
10.3.7 Temperature Dependence of the Rate Law
Consider a surface-reaction-limited irreversible isomerization
A → B
in which both A and B are adsorbed on the surface, and the rate law is
The specific reaction rate, k, will usually follow an Arrhenius temperature dependence and increase exponentially with temperature. However, the adsorption of all species on the surface is exothermic. Consequently, the higher the temperature, the smaller the adsorption equilibrium constant. That is, as the temperature increases, KA and KB decrease resulting in less coverage of the surface by A and B. Therefore, at high temperatures, the denominator of catalytic rate laws approaches 1. That is, at high temperatures (low coverage)
The rate law could then be approximated as
Neglecting the adsorbed species at high temperatures
or for a reversible isomerization we would have
Algorithm
Deduce
Rate law
Find
Mechanism
Evaluate
Rate-law parameters
Design
PBR
CSTR
The algorithm we can use as a start in postulating a reaction mechanism and rate-limiting step is shown in Table 10-4. Again, we can never really prove a mechanism to be correct by comparing the derived rate law with experimental data. Independent spectroscopic experiments are usually needed to confirm the mechanism. We can, however, prove that a proposed mechanism is inconsistent with the experimental data by following the algorithm in Table 10-4. Rather than taking all the experimental data and then trying to build a model from the data, Box et al. describe techniques of sequential data collection and model building.15
15 G. E. P. Box, J. S. Hunter, and W. G. Hunter, Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed., Hoboken, New Jersey: Wiley, 2005.
10.4 Heterogeneous Data Analysis for Reactor Design

In this section, we focus on four operations that chemical reaction engineers need to be able to accomplish:
Developing an algebraic rate law consistent with experimental observations,
Analyzing the rate law in such a manner that the rate-law parameters (e.g., k, KA) can readily be determined from the experimental data,
Finding a mechanism and rate-limiting step consistent with the experimental data, and
Designing a catalytic reactor to achieve a specified conversion
We shall use the hydrodemethylation of toluene to illustrate these four operations.
Hydrogen and toluene are reacted over a solid mineral catalyst containing clinoptilolite (a crystalline silica-alumina) to form methane and benzene16
16 J. Papp, D. Kallo, and G. Schay, J. Catal., 23, 168.
We wish to design a packed-bed reactor and a “fluidized bed” CSTR to process a feed consisting of 30% toluene, 45% hydrogen, and 25% inerts. Toluene is fed at a rate of 50 mol/min at a temperature of 640=C and a pressure of 40 atm (4052 kPa). To design the PBR, we must first determine the rate law from the differential reactor data presented in Table 10-6. In this table, we are given the rate of reaction of toluene as a function of the partial pressures of hydrogen (H2), toluene (T), benzene (B), and methane (M). In the first two runs, methane was introduced into the feed together with hydrogen and toluene, while the other product, benzene, was fed to the reactor together with the reactants only in runs 3, 4, and 6. In runs 5 and 16, both methane and benzene were introduced in the feed. Because the conversion was less than 1% in the differential reactor, the partial pressures of the products, methane and benzene, formed in these runs were essentially zero, and the reaction rates were equivalent to initial rates of reaction.
TABLE 10-6 DATA FROM A DIFFERENTIAL REACTOR
Partial Pressure (atm) |
|||||
Run |
Toluene (T), PT |
Hydrogen (H2), PH2 |
Methane (M), PM |
Benzene (B), PB |
|
Set A |
|
|
|
|
|
1 |
71.0 |
1 |
1 |
1 |
0 |
2 |
71.3 |
1 |
1 |
4 |
0 |
Set B |
|
|
|
|
|
3 |
41.6 |
1 |
1 |
0 |
1 |
4 |
19.7 |
1 |
1 |
0 |
4 |
5 |
42.0 |
1 |
1 |
1 |
1 |
6 |
17.1 |
1 |
1 |
0 |
5 |
Set C |
|
|
|
|
|
7 |
71.8 |
1 |
1 |
0 |
0 |
8 |
142.0 |
1 |
2 |
0 |
0 |
9 |
284.0 |
1 |
4 |
0 |
0 |
Set D |
|
|
|
|
|
10 |
47.0 |
0.5 |
1 |
0 |
0 |
11 |
71.3 |
1 |
1 |
0 |
0 |
12 |
117.0 |
5 |
1 |
0 |
0 |
13 |
127.0 |
10 |
1 |
0 |
0 |
14 |
131.0 |
15 |
1 |
0 |
0 |
15 |
133.0 |
20 |
1 |
0 |
0 |
16 |
41.8 |
1 |
1 |
1 |
1 |
Unscramble the data to find the rate law.
10.4.1 Deducing a Rate Law from the Experimental Data
To unscramble the data, let’s first look at run 3. In run 3, there is no possibility of the reverse reaction taking place because the concentration of methane is zero, that is, PM = 0, whereas in run 5 the reverse reaction could take place because all products are present. Comparing runs 3 and 5, we see that the initial rate is essentially the same for both runs, and we can assume that the reaction is virtually irreversible.

We now ask what qualitative conclusions can be drawn from the data about the dependence of the rate of disappearance of toluene, , on the partial pressures of toluene, hydrogen, methane, and benzene.
Dependence on the product methane. If methane were adsorbed on the surface, the partial pressure of methane would appear in the denominator of the rate expression and the rate would vary inversely with methane concentration
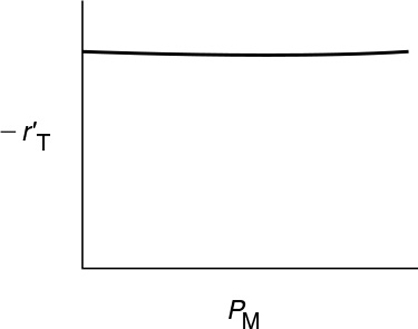
However, comparing runs 1 and 2 we observe that a fourfold increase in the pressure of methane has little effect on . Consequently, we assume that methane is either very weakly adsorbed (i.e., KMPM ≪ 1) or goes directly into the gas phase in a manner similar to propylene in the cumene decomposition previously discussed.
Dependence on the product benzene. In runs 3 and 4, we observe that, for fixed concentrations (partial pressures) of hydrogen and toluene, the rate decreases with increasing concentration of benzene. A rate expression in which the benzene partial pressure appears in the denominator could explain this dependency
The type of dependence of on PB given by Equation (10-68) suggests that benzene is adsorbed on the clinoptilolite surface.
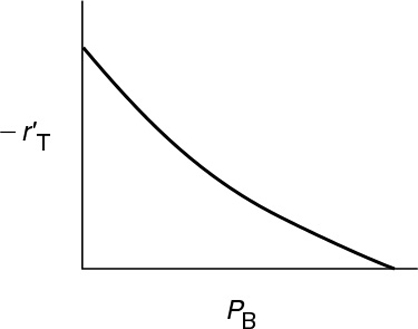
If it is in the denominator, it is probably on the surface.
Dependence on toluene. At low concentrations of toluene (runs 10 and 11), the rate increases with increasing partial pressure of toluene, while at high toluene concentrations (runs 14 and 15), the rate is virtually independent of the toluene partial pressure. A form of the rate expression that would describe this behavior is
A combination of Equations (10-68) and (10-69) suggests that the rate law may be of the form

Dependence on hydrogen. When we compare runs 7, 8, and 9 in Table 10-6, we see that the rate increases linearly with increasing hydrogen concentration, and we conclude that the reaction is first order in H2. In light of this fact, hydrogen is either not adsorbed on the surface or its coverage of the surface is extremely low for the pressures used. If H2 were adsorbed, would have a dependence on PH2 analogous to the dependence of on the partial pressure of toluene, PT (see Equation (10-69)). For first-order dependence on H2,

Deduced the rate law from data using our knowledge of catalysis
Combining Equations (10-67)–(10-71), we find that the rate law
is in qualitative agreement with the data shown in Table 10-6.
10.4.2 Finding a Mechanism Consistent with Experimental Observations
We now propose a mechanism for the hydrodemethylation of toluene. Because the partial pressure of H2 only appears in the numerator, we assume that the reaction follows an Eley–Rideal mechanism. Applying the Eley–Rideal mechanism, toluene is adsorbed on the surface and then reacts with hydrogen in the gas phase to produce benzene adsorbed on the surface and methane in the gas phase. Benzene is then desorbed from the surface. Because approximately 75%–80% of all heterogeneous reaction mechanisms are surface-reaction-limited rather than adsorption- or desorption-limited, we begin by assuming the reaction between adsorbed toluene and gaseous hydrogen to be reaction-rate-limited. Symbolically, this mechanism and associated rate laws for each elementary step are
Approximately 75% of all heterogeneous reaction mechanisms are surface-reaction-limited.
Proposed Mechanism
Eley–Rideal mechanism
The rate law for the surface reaction step is
For surface-reaction-limited mechanisms we see that we need to replace CT·S and CB·S in Equation (10-73) by quantities that we can measure, for example, concentration or partial pressure.
For surface-reaction-limited mechanisms, we use the adsorption rate Equation (10-72) for toluene to obtain CT·S17, that is,
17 See footnote 11 on page 466.
Then
and we use the desorption rate Equation (10-74) for benzene to obtain CB·S:
Then
The total concentration of sites is
Substituting Equations (10-75) and (10-76) into Equation (10-77) and rearranging, we obtain
Perform a site balance to obtain Cυ.
Next, substitute for CT·S and CB·S, in terms of partial pressures and then substitute for in Equation (10-73) to obtain the rate law for the case when the reaction is surface-reaction-rate-limited
We have shown by comparing runs 3 and 5 that we can neglect the reverse reaction, that is, the thermodynamic equilibrium constant KP is very, very large. Consequently, we obtain
Rate law for Eley–Rideal surface-reaction-limited mechanism
Again we note that the adsorption equilibrium constant of a given species is exactly the reciprocal of the desorption equilibrium constant of that species.
10.4.3 Evaluation of the Rate-Law Parameters
In the original work on this reaction by Papp et al.,18 over 25 models were tested against experimental data, and it was concluded that the preceding mechanism and rate-limiting step (i.e., the surface reaction between adsorbed toluene and H2 gas) is the correct one. Assuming that the reaction is essentially irreversible, the rate law for the reaction on clinoptilolite is
18 Ibid.
We now wish to determine how best to analyze the data to evaluate the rate-law parameters, k, KT, and KB. This analysis is referred to as parameter estimation.19 We will use nonlinear least squares which require initial estimates of the parameters. These estimates can be obtained from a linear least-squares analysis. To use linear least square, we now rearrange our rate law to obtain a linear relationship between our measured variables. For the rate law given by Equation (10-80), we see that if both sides of Equation (10-80) are divided by PH2PT and the equation is then inverted
19 See the Supplementary Reading for Chapter 10 on the CRE Web site (page 539) for a variety of techniques for estimating the rate-law parameters.
Linearize the rate equation to extract the rate-law parameters.
The regression techniques described in Chapter 7 could be used to determine the rate-law parameters by using the equation
A linear least-squares analysis of the data shown in Table 10-6 is presented on the CRE Web site.
One can use the linearized least-squares analysis (PRS 7.3) to obtain initial estimates of the parameters k, KT, KB, in order to obtain convergence in nonlinear regression. However, in many cases it is possible to use a nonlinear regression analysis directly, as described in Sections 7.5 and 7.6, and in Example 10-1.
Example 10–1 Nonlinear Regression Analysis to Determine the Model Parameters k, KB, and KT and Site Concentration Ratio CT•S/CB•S
Use nonlinear regression, as discussed in Section 7.5, along with the data in Table 10-6, to find the best estimates of the rate-law parameters k, KB, and KT in Equation (10-80).
Write the rate law solely as a function of the partial pressures.
Find the ratio of the sites occupied by toluene, CT•S, to those occupied by benzene, CB•S, at 40% conversion of toluene.
Solution
The data from Table 10-6 were entered into the Polymath nonlinear least-squares program with the following modification. The rates of reaction in column 1 were multiplied by 1010, so that each of the numbers in column 1 was entered directly (i.e., 71.0, 71.3, …). The model equation was
![]()
Following the step-by-step regression procedure in Chapter 7 and on the CRE Web site Summary Notes, we arrive at the following parameter values shown in Table E10-1.1 for this Living Example Problem (LEP). A tutorial is also given for LEP 10-1.
TABLE E10-1.1 PARAMETER VALUES

The best estimates are shown in the upper-right-hand box of Table E10-1.1.
Converting the rate law to kilograms of catalyst and minutes,
we have
Ratio of sites occupied by toluene to those occupied by benzene

After we have the adsorption constants, KT and KB, we can calculate the ratio of sites occupied by the various adsorbed species. For example, taking the ratio of Equation (10-75) to Equation (10-76), the ratio of toluene-occupied sites to benzene-occupied sites at 40% conversion is
We see that at 40% conversion there are approximately 12% more sites occupied by toluene than by benzene. This fact is common knowledge to every chemical engineering student at Jofostan University, Riça, Jofostan.
Analysis: This example shows once again how to determine the values of rate-law parameters from experimental data using Polymath nonlinear regression. It also shows how to calculate the different fraction of sites, both vacant and occupied, as a function of conversion.
10.4.4 Reactor Design
Our next step is to express the partial pressures PT, PB, and PH2 as a function of X, combine the partial pressures with the rate law, , as a function of conversion, and carry out the integration of the packed-bed design equation
Example 10–2 Catalytic Reactor Design
The hydrodemethylation of toluene is to be carried out in a PBR catalytic reactor.
The molar feed rate of toluene to the reactor is 50 mol/min, and the reactor inlet is at 40 atm and 640°C. The feed consists of 30% toluene, 45% hydrogen, and 25% inerts. Hydrogen is used in excess to help prevent coking. The pressure-drop parameter, α, is 9.8 × 10–5 kg–1.
Plot and analyze the conversion, the pressure ratio, p, and the partial pressures of toluene, hydrogen, and benzene as a function of PBR catalyst weight.
Determine the catalyst weight in a fluidized CSTR with a bulk density of 400 kg/m3 (0.4 g/cm3) to achieve 65% conversion.
Solution
PBR with pressure drop
Mole Balance:
Balance on toluene (T), the limiting reactant
Rate Law: From Equation (E10-1.1) we have
with k = 0.00087 mol/atm2/kg-cat/min, KB = 1.39 atm–1, and KT = 1.038 atm–1.
Stoichiometry:
Relating Toluene (T) Benzene (B) Hydrogen (H2)
Because ε = 0, we can use the integrated form of the pressure-drop term.
P0 = total pressure at the entrance
α = 9.8 = 10–5 kg–1
Note that PT0 designates the inlet partial pressure of toluene. In this example, the inlet total pressure is designated P0 to avoid any confusion. The inlet mole fraction of toluene is 0.3 (i.e., yT0 = 0.3), so that the inlet partial pressure of toluene is
PT0 = (0.3)(40) = 12 atm
Pressure drop in PBRs is discussed in Section 5.5.
We now calculate the maximum catalyst weight we can have, such that the exiting pressure will not fall below atmospheric pressure (i.e., 1.0 atm) for the specified feed rate. This weight is calculated by substituting the entering pressure of 40 atm and the exiting pressure of 1 atm into Equation (5-33), that is,
Maximum catalyst weight for conditions given.
TABLE E10-2.1 POLYMATH PROGRAM AND OUTPUT


Conversion profile down the packed bed
Evaluate: Consequently, we will set our final weight at 10000 kg and determine the conversion profile as a function of catalyst weight up to this value. Equations (E10-2.1)–(E10-2.5) are shown in the Polymath program in Table E10-2.1. The conversion is shown as a function of catalyst weight in Figure E10-2.1, and profiles of the partial pressures of toluene, hydrogen, and benzene are shown in Figure E10-2.2. We note that the pressure drop causes (cf. Equation E10-2.5) the partial pressure of benzene to go through a maximum as one traverses the reactor.

Figure E10-2.1 Conversion and pressure ratio profiles.

Note the partial pressure of benzene goes through a maximum. Why?
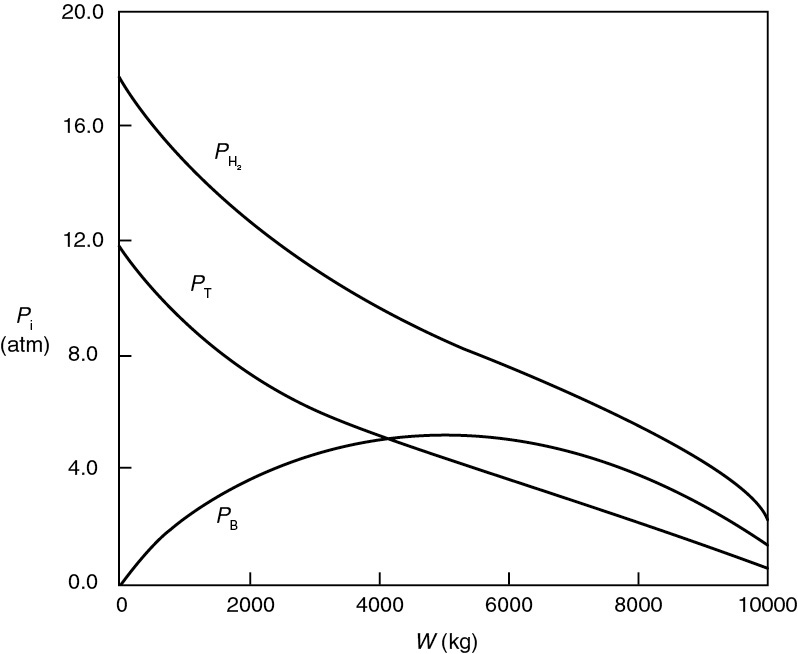
Figure E10-2.2 Partial pressure profiles.
If one had neglected ΔP it could have been very embarrassing.
See YouTube video, “Reaction Engineering Gone Wrong,” accessible from the CRE Web site home page.
PBR Analysis: For the case of no pressure drop, the conversion that would have been achieved with 10000 kg of catalyst would have been 79%, compared with 68.2% when there is pressure drop in the reactor. To carry out this calculation, for the case of no pressure drop, we use the Polymath Living Example Program (LEP) on the CRE Web site and simply multiply the pressure-drop parameter by zero, that is, line (5) would read α = 0.000098*0. For the feed rate given, eliminating or minimizing pressure drop would increase the production of benzene by up to 61 million pounds per year! Finally, we note in Figure E10-2.2 that the partial pressure of benzene (PB) goes through a maximum. This maximum can be explained by recalling that PB is just the product of the benzene mole fraction (yB) times the total pressure (P) (i.e., PB = yBPT). Near the middle to end of the bed, benzene is no longer being formed so that yB stops increasing. However, because of the pressure drop, the total pressure decreases and, as a result, so does PB.
“Fluidized” CSTR
We will now calculate the fluidized CSTR catalyst weight necessary to achieve the same (ca.) conversion as in the packed-bed reactor at the same operating conditions. The bulk density in the fluidized reactor is 0.4 g/cm3 with p = 1. The design equation is
Mole Balance:
In
–
Out
+
Gen
=
Accum
FT0
–
FT
+
=
0
Rearranging
Rate Law and
Stoichiometry same as in part (a) PBR calculation.
Combine and Evaluate: Writing Equation (E10-2.2) in terms of conversion (E10-2.3) and then substituting X = 0.65 and PT0 = 12 atm, we have
The corresponding reactor volume is
This volume would correspond to a cylindrical reactor 2 m in diameter and 10 m high.

Analysis: This example used real data and the CRE algorithm to design a PBR and CSTR. An important point is that it showed how one could be embarrassed by not including pressure drop in the design of a packed-bed reactor. We also note that for both the PBR and fluidized CSTR, the values of the catalyst weight and reactor volume are quite high, especially for the low feed rates given. Consequently, the temperature of the reacting mixture should be increased to reduce the catalyst weight, provided that side reactions and catalyst decay do not become a problem at higher temperatures.
How can the weight of catalyst be reduced?
Raise the temperature?
Example 10-2 illustrated the major activities pertinent to catalytic reactor design described earlier in Figure 10-6. In this example, the rate law was extracted directly from the data and then a mechanism was found that was consistent with experimental observation. Conversely, developing a feasible mechanism may guide one in the synthesis of the rate law.
10.5 Reaction Engineering in Microelectronic Fabrication
10.5.1 Overview
We now extend the principles of the preceding sections to one of the newer technologies in chemical engineering. Chemical engineers are now playing an important role in the electronics industry. Specifically, they are becoming more involved in the manufacture of electronic and photonic devices, recording materials, and especially microfluidics and medical lab-on-a-chip devices.

Surface reactions play an important role in the manufacture of microelectronic devices. One of the single most important developments of the twentieth century was the invention of the integrated circuit. Advances in the development of integrated circuitry have led to the production of circuits that can be placed on a single semiconductor chip the size of a pinhead and perform a wide variety of tasks by controlling the electron flow through a vast network of channels. These channels, which are made from semiconductors such as silicon, gallium arsenide, indium phosphide, and germanium, have led to the development of a multitude of novel microelectronic devices. Examples of microelectronic sensing devices manufactured using chemical reaction engineering principles are shown in the left-hand margin.

The manufacture of an integrated circuit requires the fabrication of a network of pathways for electrons. The principal reaction engineering steps of the fabrication process include depositing material on the surface of a material called a substrate (e.g., by chemical vapor deposition, abbreviated as CVD), changing the conductivity of regions of the surface (e.g., by boron doping or ion inplantation), and removing unwanted material (e.g., by etching). By applying these steps systematically, miniature electronic circuits can be fabricated on very small semiconductor chips. The fabrication of microelectronic devices may include as few as 30 or as many as 200 individual steps to produce chips with up to 109 elements per chip. An abbreviated discussion of the steps involved to produce a typical metal-oxide semiconductor field-effect transition (MOSFET) is given in the Additional Material for this chapter on the Web site (http://umich.edu/~elements/6e/10chap/pdf/Steps_in_Microchip_Fabrication.pdf).
10.5.2 Chemical Vapor Deposition (CVD)
The mechanisms by which CVD occurs are very similar to those of heterogeneous catalysis discussed earlier in this chapter. The reactant(s) adsorbs on the surface and then reacts on the surface to form a new surface. This process may be followed by a desorption step, depending on the particular reaction.
Ge used in solar cells
The growth of a germanium epitaxial film as an interlayer between a gallium arsenide layer and a silicon layer has received attention in the microelectronics industry.20 Epitaxial germanium is also an important material in the fabrication of tandem solar cells. The growth of germanium films can be accomplished by CVD. A proposed mechanism is
20 H. Ishii and Y. Takahashi, J. Electrochem. Soc., 135, p. 1539.
Mechanism
At first it may appear that a site has been lost when comparing the right- and left-hand sides of the surface reaction step. However, the newly formed germanium atom on the right-hand side is a site for the future adsorption of H2(g) or GeCl2(g), and there are three sites on both the right- and left-hand sides of the surface reaction step. These sites are shown schematically in Figure 10-20.

Figure 10-20 Manufacture of phthalic anhydride.
The surface reaction between adsorbed molecular hydrogen and germanium dichloride is believed to be rate-limiting. The reaction follows an elementary rate law with the rate being proportional to the fraction of the surface covered by GeCl2 times the square of the fraction of the surface covered by molecular hydrogen.
Rate law for rate-limiting step
where
The deposition rate (film growth rate) is usually expressed in nanometers per second and is easily converted to a molar rate (mol/m2 · s) by multiplying by the molar density of solid germanium (mol/m3).
The difference between developing CVD rate laws and rate laws for catalysis is that the site concentration (e.g., Cυ) is replaced by the fractional surface area coverage (e.g., the fraction of the surface that is vacant, fv). The total fraction of surface available for adsorption should, of course, add up to 1.0.
Area balance
We will first focus our attention on the adsorption of GeCl2. The rate of jumping on to the surface is proportional to the partial pressure of GeCl2, PGeCl2, and the fraction of the surface that is vacant, fv and the rate of jumping off is proportional to fraction area covered with GeCl2. The net rate of GeCl2 adsorption is
Since the surface reaction is rate-limiting, in a manner analogous to catalysis reactions, we have for the adsorption of GeCl2
Adsorption of GeCl2 not rate-limiting
Solving Equation (10-84) for the fractional surface coverage of GeCl2 gives
For the dissociative adsorption of hydrogen on the Ge surface, the equation analogous to Equation (10-84) is
Since the surface reaction is rate-limiting
Adsorption of H2 is not rate-limiting.
Then
Recalling the rate of deposition of germanium, we substitute for fGeCl2 and fH in Equation (10-82) to obtain
We solve for fv in an identical manner to that for Cv in heterogeneous catalysis. Substituting Equations (10-85) and (10-87) into Equation (10-83) gives
Rearranging yields
Finally, substituting for in Equation (10-88), we find that
and lumping KA, KH, and kS into a specific reaction rate k′ yields
Rate of deposition of Ge
We now need to relate the partial pressure of GeCl2 to the partial pressure of GeCl4 in order to calculate the conversion of GeCl4. If we assume that the gas-phase reaction
Equilibrium in gas phase
is in equilibrium, we have
and if hydrogen is weakly adsorbed , and letting k = k′ KP, we obtain the rate of deposition as
Rate of deposition of Ge when H2 is weakly adsorbed
We now can use stoichiometry to express each of the species’ partial pressures in terms of conversion and the entering partial pressure of GeCl4, PGeCl4,0, and then proceed to calculate the conversion.
It should be noted that it is possible that GeCl2 may also be formed by the reaction of GeCl4 and a Ge atom on the surface, in which case a different rate law would result.
10.6 Model Discrimination
We have seen that for each mechanism and each rate-limiting step we can derive a rate law. Consequently, if we had three possible mechanisms and three rate-limiting steps for each mechanism, we would have nine possible rate laws to compare with the experimental data. We will use the regression techniques discussed in Chapter 7 to identify which model equation best fits the data by choosing the one with the smaller sums of squares and/or carrying out an F-test. We could also compare the nonlinear regression residual plots for each model, which not only show the error associated with each data point but also show if the error is randomly distributed or if there is a trend in the error. If the error is randomly distributed, this result is an additional indication that the correct rate law has been chosen.

Regression
We need to raise a caution here about choosing the model with the smallest sums of squares. The caution is that the model parameter values that give the smallest sum must be realistic. In the case of heterogeneous catalysis, all values of the adsorption equilibrium constants must be positive. In addition, if the temperature dependence is given, because adsorption is exothermic, the adsorption equilibrium constant must decrease with increasing temperature. To illustrate these principles, let’s look at the following example.

Example 10–3 Hydrogenation of Ethylene to Ethane
The hydrogenation (H) of ethylene (E) to form ethane (EA),
H2 + C2H4 → C2H6
is carried out over a cobalt molybdenum catalyst (Collect. Czech. Chem. Commun., 51, 2760). Carry out a nonlinear regression analysis to determine which of the following rate laws best describes the data in Table E10-3.1.
Procedure
Enter data
Enter model
Make initial estimates of parameters
Run regression
Examine parameters and variance
Observe error distribution
Choose model
TABLE E10-3.1 DIFFERENTIAL REACTOR DATA
Run Number |
Reaction Rate (mol/kg-cat. · s) |
PE (atm) |
PEA (atm) |
PH (atm) |
1 |
1.04 |
1 |
1 |
1 |
2 |
3.13 |
1 |
1 |
3 |
3 |
5.21 |
1 |
1 |
5 |
4 |
3.82 |
3 |
1 |
3 |
5 |
4.19 |
5 |
1 |
3 |
6 |
2.391 |
0.5 |
1 |
3 |
7 |
3.867 |
0.5 |
0.5 |
5 |
8 |
2.199 |
0.5 |
3 |
3 |
9 |
0.75 |
0.5 |
5 |
1 |

Solution
Polymath was chosen as the software package to solve this problem. The data in Table E10-3.1 were entered into the program. A screen-shot-by-screen-shot tutorial and set of instructions on how to carry out the regression is given on the CRE Web site, at the end of the Summary Notes for Chapter 7 (http://www.umich.edu/~elements/6e/07chap/summary.html). After entering the data and following the step-by-step procedures, the results shown in Table E10-3.2 were obtained.
TABLE E10-3.2 RESULTS OF THE POLYMATH NONLINEAR REGRESSION
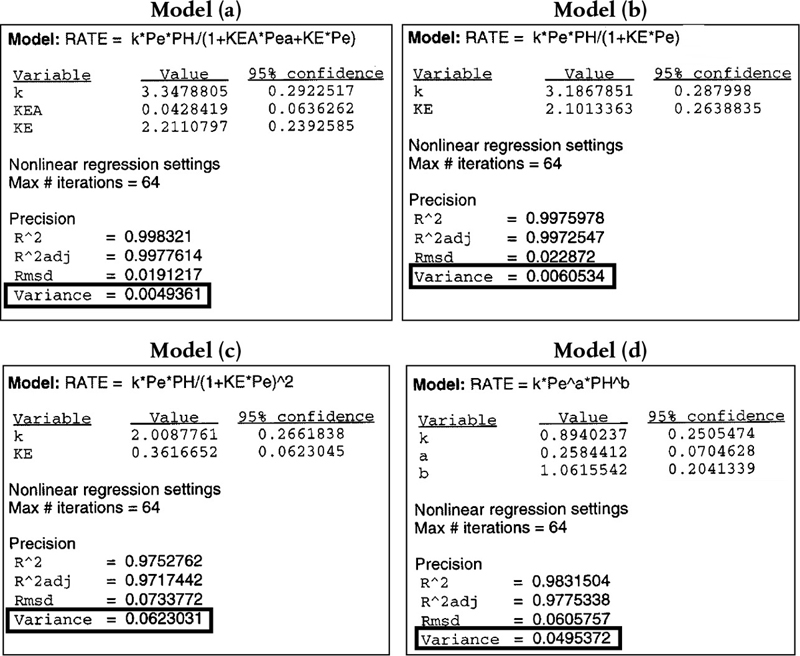
Model (a) Single site, surface-reaction, rate-limited with hydrogen weakly adsorbed

From Table E10-3.2 data, we can obtain
We now examine the sums of squares (variance) and range of variables themselves. The sums of squares is reasonable and, in fact, the smallest of all the models at 0.0049. However, let’s look at KEA. We note that the value for the 95% confidence limit of ±0.0636 is greater than the nominal value of KEA = 0.043 atm–1 itself (i.e., KEA = 0.043 ± 0.0636). The 95% confidence limit means that if the experiment were run 100 times and then 95 times it would fall within the range (–0.021) < KEA < (0.1066). Because KEA can never be negative, we are going to reject this model. Consequently, we set KEA = 0 and proceed to model (b).
Model (b) Single site, surface-reaction, rate-limited with ethane and hydrogen weakly adsorbed
From Table E10-3.2 we can obtain
The value of the adsorption constant KE = 2.1 atm–1 is reasonable and is not negative within the 95% confidence limit. Also, the variance is small at .
Model (c) Dual site, surface-reaction, rate-limited with hydrogen and ethane weakly adsorbed From Table E10-3.2 we can obtain
While KE is small, it never goes negative within the 95% confidence interval. The variance of this model at is much larger than the other models. Comparing the variance of model (c) with model (b)
We see that the is an order of magnitude greater than , and therefore we eliminate model (c).21
21 See G. F. Froment and K. B. Bishoff, Chemical Reaction Analysis and Design, 2nd ed. New York: Wiley, 1990, p. 96.
Model (d) Empirical
Similarly for the power-law model, we obtain from Table E10-3.2
As with model (c), the variance is quite large compared to model (b)
So we also eliminate model (d). For heterogeneous reactions, Langmuir-Hinshelwood rate laws are preferred over power-law models.

Analysis: Choose the Best Model. In this example, we were presented with four rate laws and were asked which law best fits the data. Because all the parameter values are realistic for model (b) and the sums of squares are significantly smaller for model (b) than for the other models, we choose model (b). We note again that there is a caution we need to point out regarding the use of regression! One cannot simply carry out a regression and then choose the model with the lowest value of the sums of squares. If this were the case, we would have chosen model (a), which had the smallest sums of squares of all the models with σ2 = 0.0049. However, one must consider the physical realism of the parameters in the model. In model (a), the 95% confidence interval was greater than the parameter itself, thereby yielding negative values of the parameter, KAE, which is physically impossible.
10.7 Catalyst Deactivation
In designing fixed and ideal fluidized bed catalytic reactors, we have assumed up to now that the activity of the catalyst remains constant throughout the catalyst’s life. That is, the total concentration of active sites, Ct, accessible to the reaction does not change with time. Unfortunately, Mother Nature is not so kind as to allow this behavior to be the case in most industrially significant catalytic reactions. One of the most insidious problems in catalysis is the loss of catalytic activity that occurs as the reaction takes place on the catalyst. A wide variety of mechanisms have been proposed by Butt and Petersen, to explain and model catalyst deactivation.22,23,24
22 J. B. Butt and E. E. Petersen, Activation, Deactivation and Poisoning of Catalysts, New York: Academic Press, 1988.
23 D. T. Lynch and G. Emig, Chem. Eng. Sci., 44(6), 1275–1280 (1989).
24 R. Hughes, Deactivation of Catalysts, San Diego: Academic Press, 1984.
Catalytic deactivation adds another level of complexity to sorting out the reaction-rate law parameters and pathways. In addition, we need to make adjustments for the decay of the catalysts in the design of catalytic reactors. However, please don’t worry, this adjustment is usually made by a quantitative specification of the catalyst’s activity, a(t). In analyzing reactions over decaying catalysts, we divide the reactions into two categories: separable kinetics and non-separable kinetics. In separable kinetics, we separate the rate law and activity
When the kinetics and activity are separable, it is possible to study catalyst decay and reaction kinetics independently. However, nonseparability
must be accounted for by assuming the existence of a nonideal surface or by describing deactivation by a mechanism composed of several elementary steps.23,24
We shall consider only separable kinetics and define the activity of the catalyst at time t, a(t), as the ratio of the rate of reaction on a catalyst that has been used for a time t to the rate of reaction on a fresh catalyst (t = 0):
a(t): catalyst activity
Because of the catalyst decay, the activity decreases with time and a typical curve of the activity as a function of time is shown in Figure 10-21.
Figure 10-21 Activity as a function of time.
Combining Equations (10-92) and (3-2), the rate of disappearance of reactant A on a catalyst that has been utilized for a time t is
Reaction-rate law accounting for catalyst activity
The rate of catalyst decay, rd, can be expressed in a rate law analogous to Equation (10-93)
Catalyst decay rate law
For example, p[a(t)] = [a(t)]2
where p[a(t)] is some function of the catalyst activity, kd is the specific decay constant, and h(Ci) is the functionality of rate of decay, rd, on the species concentrations in the reacting mixture. For the cases presented in this chapter, this functionality either will be independent of concentration (i.e., h = 1) or as in the case of catalytic poisoning it could be a linear function of species concentration (i.e., h = Ci).
The functionality of the activity term, p[a(t)], in the decay law can take a variety of forms. For example, for a first-order decay
and for a second-order decay
The particular function, p(a), will vary with the gas catalytic system being used and the reason or mechanism for catalytic decay.
10.7.1 Types of Catalyst Deactivation
There are three categories into which the loss of catalytic activity can traditionally be divided: sintering or aging, fouling or coking, and poisoning.
Sintering
Fouling
Poisoning
10.7.1A Deactivation by Sintering (Aging)25
25 See G. C. Kuczynski, ed., Sintering and Catalysis, vol. 10 of Materials Science Research, New York: Plenum Press, 1975.
Sintering, also referred to as aging, is the loss of catalytic activity due to a loss of active surface area resulting from the prolonged exposure to high gas-phase temperatures. The active surface area may be lost either by growth of the metals deposited on the support or by narrowing or closing of the pores inside the catalyst pellet. A change in the surface structure may also result from either surface recrystallization or the formation or elimination of surface defects (active sites). The reforming of heptane over platinum on alumina is an example of catalyst deactivation as a result of sintering.
Figure 10-22 shows the loss of surface area resulting from the flow of the solid porous catalyst support at high temperatures to cause pore closure. Figure 10-23 shows growth of small metal crystallites into larger particles where the interior atoms are not accessible to reactions thereby leading to a loss of metal surface area of the catalyst. Professor Abhaya Datye has recently identified that the dominant mechanism for this sintering of industrial catalysts involves the transport of mobile species, a process called Ostwald ripening.26
26 T. W. Hansen, A. T. Delariva, S. R. Challa, and A. K. Datye, “Sintering of Catalytic Nanoparticles: Particle Migration or Ostwald Ripening?” Acc. Chem. Res., 46(8), 17-20–17-30 (2013).
Sintering is usually negligible at temperatures below 40% of the melting temperature of the solid.27 However, sintering can occur at lower temperatures when mobile species are generated through a reaction of the solid with the gas phase, for example the formation of volatile PtO2 due to reaction of Pt and O2.
27 R. Hughes, Deactivation of Catalysts, San Diego: Academic Press, 1984.
The catalyst support becomes soft and flows, resulting in pore closure.

Figure 10-22 Decay by sintering: pore closure; loss of reactive surface area.
The catalyst support becomes soft and flows, resulting in pore closure.
Figure 10-23 Decay by sintering: agglomeration of deposited metal sites; loss of reactive surface area.
The atoms move along the surface and agglomerate.
Deactivation by sintering may in some cases be a function of the mainstream gas concentration. Although other forms of the sintering decay rate laws exist, one of the most commonly used sintering decay laws is second order with respect to the present activity
Integrating, with a = 1 at time t = 0, for constant kd during the time t yields
Sintering: second-order decay
The amount of sintering is usually measured in terms of the active surface area of the catalyst Sa
The sintering decay constant, kd, follows the Arrhenius equation
Minimizing sintering
The decay activation energy, Ed, for the reforming of heptane on Pt/Al2O3 is on the order of 70 kcal/mol, which is rather high. As mentioned earlier, sintering can be reduced by keeping the temperature below 0.3–0.4 times the metal’s melting point temperature, that is, (T < 0.3 Tmelting).
For the case where the temperature varies during the reaction time t, Equations (10-93), (10-94), along with the energy balance must be solved simultaneously.
We will now stop and consider reactor design for a fluid–solid system with decaying catalyst. To analyze these reactors, we only add one step to our algorithm; that is, determine the catalyst decay law. The sequence is shown here.
The algorithm
Example 10–4 Calculating Conversion with Catalyst Decay in Batch Reactors
The first-order isomerization
A → B
is being carried out isothermally in a batch reactor on a catalyst that is decaying as a result of aging. Derive an equation for conversion as a function of time.
Solution
Mol Balance:
where Xd is the conversion of A when the catalyst is decaying.
Reaction-Rate Law:
Decay Law: For second-order decay by sintering:
One extra step (number 3) is added to the algorithm.

Stoichiometry:
Combining gives us
Let k = k′W/V. Substituting for catalyst activity a, we have
where Xd is the conversion when there is decay. We want to compare the conversion with and without catalyst decay.
For no decay kd = 0
The Polymath program and a comparison of the conversion with decay Xd and without decay X are shown below.


Analytical Solution
One can also obtain an analytical solution for this reaction order with catalyst decay. Separating variables and integrating yields
Solving for the conversion Xd at any time, t, in a decaying catalyst we find that
the analytical solution without decay
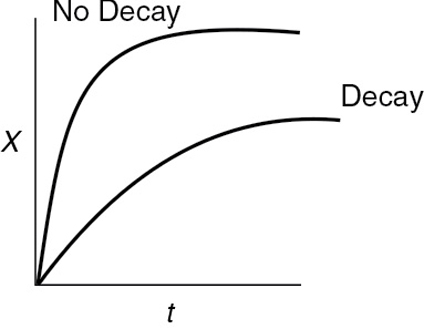
Parameters
Analysis: One observes that for long times the conversion in reactors with catalyst decay approaches a rather flat plateau and reaches conversion of about 30%. This is the conversion that will be achieved in a batch reactor for a first-order reaction when the catalyst decay law is second order. By comparison, we obtain virtually complete conversion in 500 seconds when there is no decay. The purpose of this example was to demonstrate the algorithm for isothermal catalytic reactor design for a decaying catalyst. In problem P10-1B(d), you are asked to sketch the temperature–time trajectories for various values of k and kd.
10.7.1B Deactivation by Coking or Fouling
This mechanism of decay (see Figures 10-24, 10-25, and 10-26) is common to reactions involving hydrocarbons. It results from a carbonaceous (coke) material being deposited on the surface of a catalyst. The amount of coke on the surface after a time t has been found to obey the following empirical relationship
where CC is the concentration of carbon on the surface (g/m2) and n and A are empirical fouling parameters, which can be functions of the feed rate. This expression was originally developed by Voorhies and has been found to hold for a wide variety of catalysts and feed streams. Representative values for Equation (10-101) for the cracking of a crude oil in fixed-bed of catalyst given
CC = 0.52 t0.38

Figure 10-24 Schematic of decay by coking; loss of reactive surface area.

Figure 10-25 Catalyst decay fresh catalyst.

Figure 10-26 Catalyst decay spent catalyst.
Another relationship for the weight percent coke for the cracking of East Texas light gas oil is28,29
28 A. Voorhies, Ind. Eng. Chem., 37, 318.
29 C. O. Prater and R. M. Lago, Adv. Catal., 8, 293.
Different functionalities between the activity and amount of coke on the surface have been observed. One commonly used form is
or, in terms of time, we combine Equations (10-101) and (10-102)
For light Texas gas oil being cracked at 750=F over a synthetic catalyst for short times, the decay law is
where t is in seconds.
Activity for deactivation by coking
Other commonly used forms are
and
A dimensionless fouling correlation has been developed by Pacheco and Petersen.30
30 M. A. Pacheco and E. E. Petersen, J. Catal., 86, 75.
Minimizing coking
When possible, coking can be reduced by running at elevated pressures (2000–3000 kPa) and hydrogen-rich streams. A number of other techniques for minimizing fouling are discussed by Bartholomew.31 Catalysts deactivated by coking can usually be regenerated by burning off the carbon.
31 R. J. Farrauto and C. H. Bartholomew, Fundamentals of Industrial Catalytic Processes, 2nd ed. New York: Blackie Academic and Professional, 2006. This book is one of the most definitive resources on catalyst decay.
10.7.1C Deactivation by Poisoning
Deactivation by this mechanism occurs when the poisoning molecules become irreversibly chemisorbed to active sites, thereby reducing the number of sites available for the main reaction. The poisoning molecule, P, may be a reactant and/or a product in the main reaction, or it may be an impurity in the feed stream.
It’s going to cost you. #Really?
10.7.1D Poison in the Feed
Many petroleum feed stocks contain trace impurities such as sulfur, lead, and other components that are too costly to remove, yet poison the catalyst slowly over time. For the case of an impurity, P, in the feed stream, such as sulfur, for example, in the reaction sequence
the surface sites would change with time as shown in Figure 10-27.
Progression of sites being poisoned

Figure 10-27 Decay by poisoning.
If we assume the rate of depletion of the poison from the reactant gas stream onto the catalyst sites, rP, is proportional to the number of sites that are unpoisoned (Ct0 – CP·S) and the concentration of poison in the gas phase is CP then
Total site balance at time t Ct = Ct0 – CP·S
rP·S = kd(Ct0 – CP·S)CP
where CP·S is the concentration of poisoned sites and Ct0 is the total number of sites initially available. Because every molecule that is adsorbed from the gas phase onto a site is assumed to poison the site, this rate is also equal to the rate of removal of total active sites (Ct) from the surface
Dividing through by Ct0 and letting f be the fraction of the total number of sites that have been poisoned yields
The fraction of sites available for adsorption (1 = f ) is essentially the activity a(t). Consequently, Equation (10-108) becomes
A number of examples of catalysts with their corresponding catalyst poisons are given by Farrauto and Bartholomew.32
32 Ibid.
10.7.2 Decay in Packed-Bed Reactors
In packed-bed reactors where the poison is removed from the gas phase by being adsorbed on the specific catalytic sites, the deactivation process can move through the packed bed as a wave front. Here, at the start of the operation, only those sites near the entrance to the reactor will be deactivated because the poison (which is usually present in trace amounts) is removed from the gas phase by the adsorption; consequently, the catalyst sites farther down the reactor will not be affected. However, as time continues, the sites near the entrance of the reactor become saturated, and the poison must travel farther downstream before being adsorbed (removed) from the gas phase and attaching to a site to deactivate it. Figure 10-28 shows the corresponding activity profile for this type of poisoning process. We see in Figure 10-28 that by time t4 the entire bed has become deactivated. The corresponding overall conversion at the exit of the reactor might vary with time as shown in Figure 10-29. The partial differential equations that describe the movement of the reaction front shown in Figure 10-28 are derived and solved in an example on the CRE Web site, at the very end of the Summary Notes for Chapter 10 (http://www.umich.edu/~elements/6e/10chap/summary-example3.html).

Figure 10-28 Movement of activity front in a packed bed.

Figure 10-29 Exit conversion as a function of time.
10.7.2A Poisoning by Either Reactants or Products
For the case where the main reactant also acts as a poison, the rate laws are
An example where one of the reactants acts as a poison is in the reaction of CO and H2 over ruthenium to form methane, with
Similar rate laws can be written for the case when the product B acts as a poison.
For separable deactivation kinetics resulting from contacting a poison at a constant concentration and no spatial variation
Separable deactivation kinetics
where . The solution to this equation for the case of first-order decay, n = 1
is
10.7.2B Empirical Decay Laws
Table 10-7 gives a number of empirical decay laws along with the reaction systems to which they apply.
Key resource for catalyst deactivation
One should also see Fundamentals of Industrial Catalytic Processes, by Farrauto and Bartholomew, which contains rate laws similar to those in Table 10-7, and also gives a comprehensive treatment of catalyst deactivation.33
33 Ibid.
Examples of reactions with decaying catalysts and their decay laws
TABLE 10-7 DECAY RATE LAWS
Functional Form of Activity |
Decay Reaction Order |
Differential Form |
Integral |
Form Examples |
Linear |
0 |
a = 1 – β0t |
Conversion of para-hydrogen on tungsten when poisoned with oxygena |
|
Exponential |
1 |
a = e–β1t |
||
Paraffin dehydrogenation on Cr? Al2O3c Cracking of gas oild Vinyl chloride monomer formatione |
||||
Hyperbolic |
2 |
Vinyl chloride monomer formationf, g Cyclohexane dehydrogenation on Pt/Al2O3g Isobutylene hydrogenation on Nih |
||
Reciprocal power |
a = A0t–β3 |
Cracking of gas oil and gasoline on clayi |
||
a = A0t–β4 |
Cyclohexane aromatization on NiAlj |
aD. D. Eley and E. J. Rideal, Proc. R. Soc. London, A178, 429 (1941).
bR. N. Pease and L. Y. Steward, J. Am. Chem. Soc., 47, 1235 (1925).
cE. F. K. Herington and E. J. Rideal, Proc. R. Soc. London, A184, 434 (1945).
dV. W. Weekman, Ind. Eng. Chem. Process Des. Dev., 7, 90 (1968).
eA. F. Ogunye and W. H. Ray, Ind. Eng. Chem. Process Des. Dev., 9, 619 (1970).
fA. F. Ogunye and W. H. Ray, Ind. Eng. Chem. Process Des. Dev., 10, 410 (1971).
gH. V. Maat and L. Moscou, Proc. 3rd lnt. Congr. Catal. Amsterdam: North-Holland, 1965, p. 1277.
hA. L. Pozzi and H. F. Rase, Ind. Eng. Chem., 50, 1075 (1958).
iA. Voorhies, Jr., Ind. Eng. Chem., 37, 318 (1945); E. B. Maxted, Adv. Catal., 3, 129 (1951).
jC. G. Ruderhausen and C. C. Watson, Chem. Eng. Sci., 3, 110 (1954).
Source: J. B. Butt, Chemical Reactor Engineering–Washington, Advances in Chemistry Series 109, Washington, D.C.: American Chemical Society, 1972, p. 259. Also see CES 23, 881(1968).
10.8 Reactors That Can Be Used to Help Offset Catalyst Decay
We will now consider three reaction systems that can be used to help offset systems with decaying catalyst. We will classify these systems as those having slow, moderate, and rapid losses of catalytic activity. To offset the decline in chemical reactivity of decaying catalysts in continuous-flow reactors, the following three methods are commonly used:
Matching the reactor type with speed of catalyst decay
Slow decay – Temperature–Time Trajectories (10.8.1)
Moderate decay – Moving-Bed Reactors (10.8.2)
Rapid decay – Straight-Through Transport Reactors (10.8.3)
10.8.1 Temperature–Time Trajectories
In many large-scale reactors, such as those used for hydrotreating, and reaction systems where deactivation by poisoning occurs, the catalyst decay is relatively slow. In these continuous-flow systems, constant conversion is usually necessary in order that subsequent processing steps (e.g., separation) are not upset. One way to maintain a constant conversion with a decaying catalyst in a packed or fluidized bed is to increase the reaction rate by steadily increasing the feed temperature to the reactor. Operation of a “fluidized” bed in this manner is shown in Figure 10-30.

Figure 10-30 Reactor with preheater to continually increase feed temperature.
We are going to increase the feed temperature, T, in such a manner that the reaction rate remains constant with time:
We will use a first-order reaction to illustrate the salient points. For a first-order reaction with decay we have
k(T0)CA = a(t, T)k(T)CA
Slow rate of catalyst decay
We will neglect any variations in concentration so that the product of the activity (a) and specific reaction rate (k) is constant and equal to the specific reaction rate, k0 at time t = 0 and temperature T0; that is
Note that for any power-law model, the reactant concentration dependence cancels out.
The goal is to find how the temperature should be increased with time (i.e., the temperature–time trajectory) to maintain constant conversion by keeping the rate , constant. Using the Arrhenius equation to substitute for k in terms of the activation energy, EA, gives
Solving for 1/T yields
Gradually raising the temperature can help offset effects of catalyst decay.
The decay law also follows an Arrhenius-type temperature dependence
Substituting Equation (10-115) into (10-116) and rearranging yields
Integrating with a = 1 at t = 0 for the case n = (1 = Ed/EA), we obtain
Solving Equation (10-114) for a and substituting in (10-118) gives

Equation (10-119) tells us how the temperature of the catalytic reactor should be increased with time in order for the reaction rate and conversion to remain constant. However one would first want to solve this equation for temperature, T, as a function of time, t, in order to correctly operate the preheater shown in Figure 10-30.
In many industrial reactions, the decay rate law changes as temperature increases. In hydrocracking, the temperature–time trajectories are divided into three regimes. Initially, there is fouling of the acidic sites of the catalyst followed by a linear regime due to slow coking and, finally, accelerated coking characterized by an exponential increase in temperature. The temperature–time trajectory for a deactivating hydrocracking catalyst is shown in Figure 10-31.
Figure 10-31 Temperature–time trajectories for deactivating hydrocracking catalyst, runs 3 and 4. (Krishnaswamy, S., and J. R. Kittrell. Analysis of Temperature–Time Data for Deactivating Catalysts. Industry and Engineering Chemistry Process Design and Development, 1979, 18(3), 399–403. Copyright © 1979, American Chemical Society. Reprinted by permission.)
Comparison of Model with Industrial Data
For a first-order decay, Krishnaswamy and Kittrell’s expression, Equation (10-119), for the temperature–time trajectory reduces to
Comparing theory and experiment
One observes the model compares favorably with the experimental data.
10.8.2 Moving-Bed Reactors
Reaction systems with relatively rapid catalyst decay require the continual regeneration and/or replacement of the catalyst. Two types of reactors currently in commercial use that accommodate production with decaying catalysts are the moving-bed for moderate decay and straight-through transport reactor for rapid decay. A schematic diagram of a moving-bed reactor (used for catalytic cracking) is shown in Figure 10-32.
The freshly regenerated catalyst enters the top of the reactor and then moves through the reactor as a compact packed bed. The catalyst is coked continually as it moves through the reactor until it exits the reactor into the kiln, where air is used to burn off the carbon. The regenerated catalyst is lifted from the kiln by an airstream and then fed into a separator before it is returned to the reactor. The catalyst pellets are typically between one-quarter and one-eighth inch in diameter.
The Chemical Safety Board video on the Process Safety Across the Chemical Engineering Curriculum Web site (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344ReactionEngrModule(3)PS-Exxon.pdf) shows an animation of the moving-bed reactor at the ExxonMobil Torrance, California refinery.
The reactant feed stream enters at the top of the reactor and flows rapidly through the reactor relative to the flow of the catalyst through the reactor (Figure 10-33). If the feed rates of the catalyst and the reactants do not vary with
Moving-bed reactor, used for reactions with moderate rate of catalyst decay
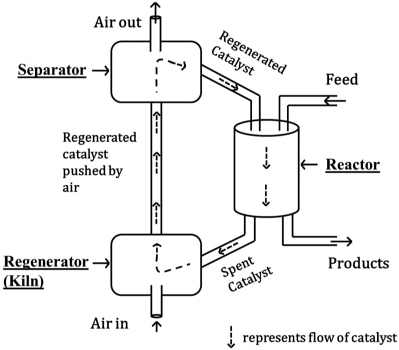
Figure 10-32 Catalytic cracking unit with catalytic regeneration.
Figure 10-33 Moving-bed reactor schematic. The value of the catalyst contained in a reactor of this type is approximately $1 million.
time, the reactor operates at steady state; that is, conditions at any point in the reactor do not change with time. The mole balance on reactant A over ΔW is
Dividing by ΔW, letting ΔW approach zero, and expressing the flow rate in terms of conversion gives
Mole Balance
The rate of reaction at any time t is
The activity, as before, is a function of the time the catalyst has been in contact with the reacting gas stream. The decay rate law is
Decay Law
We now need to relate the contact time to the weight of the catalyst. Consider a point z in the reactor, where the reactant gas has passed cocurrently through a catalyst weight W. Because the solid catalyst is moving through the bed at a rate Us (mass per unit time), the time t that the catalyst has been in contact with the gas when the catalyst reaches a point z is
If we now differentiate Equation (10-122)
and combine it with the decay rate law, we obtain
The activity equation is combined with the mole balance
The design equation for moving-bed reactors
these two coupled differential equations (i.e., Equations (10-124) and (10-125)) are numerically solved simultaneously with an ODE solver, for example, Polymath.
Example 10–5 Catalytic Cracking in a Moving-Bed Reactor
The catalytic cracking of a gas-oil charge, A, to form C5= (B) and to form coke and dry gas (C) is to be carried out in a screw-type conveyor, moving-bed reactor at 900°F:
This cracking of gas oil can also be written as
While pure hydrocarbons are known to crack according to a first-order rate law, the fact that the gas-oil exhibits a wide spectrum of cracking rates gives rise to the fact that the lumped cracking rate is well represented by a second-order rate law with the following specific reaction rate:34
34 Estimated from V. W. Weekman and D. M. Nace, AIChE J., 16, 397 (1970).
The catalytic deactivation is independent of gas-phase concentration and follows a first-order decay rate law, with a decay constant, kd of 0.72 reciprocal minutes. The feed stream is diluted with nitrogen so that as a first approximation, volume changes can be neglected with reaction. The reactor contains 22 kg of catalyst that moves through the reactor at a rate of 10 kg/min. The gas-oil is fed at a rate of 30 mol/min at a concentration of 0.075 mol/dm3.
Determine the conversion that can be achieved in this reactor.†
† AWFOS–S. Be sure to see the animation of a moving-bed reactor and description of the ExxonMobil Torrance, California accident (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344ReactionEngrModule(3)PS-Exxon.pdf).
Solution
Mole Balance:
Rate Law:
Decay Law. First-order decay:
Moving beds: moderate rate of catalyst decay
Using Equation (10-124), we obtain
Integrating
Stoichiometry. If υ ≈ υ0, then

Combining we have
The polymath program is shown below along with a conversion profile.


Explore this problem using Wolfram or Python and then use Polymath to change the decay law and make two observations.
For the simple rate law and activity law given here, we also could have solved this problem analytically as shown below.
Separating and integrating yields (E10-5.7)
Numerical evaluation:
If there were no catalyst decay, the conversion would be
Analysis: The purpose of this example was to show step-by-step how to apply the algorithm to a moving-bed reactor that has been used to reduce the effects of catalyst decay that would occur in a PBR. #Splaining. You would have some explaining to do if your company was expecting 71% conversion and you only observed 55%.
We will now rearrange Equation (E10-5.8) to a form more commonly found in the literature. Let λ be a dimensionless decay time
and Da2 be the Damköhler number for a second-order reaction (a reaction rate divided by a transport rate) for a packed-bed reactor
Through a series of manipulations we arrive at the equation for the conversion in a moving bed where a second-order reaction is taking place35
35 Ibid.
Second-order reaction in a moving-bed reactor
Similar equations are given or can easily be obtained for other reaction orders or decay laws.
10.8.3 Straight-Through Transport Reactors (STTR)
This reactor is used for reaction systems in which the catalyst deactivates very rapidly. Commercially, the STTR is used in the production of gasoline from the cracking of heavier petroleum fractions where coking of the catalyst pellets occurs very rapidly. In the STTR, the catalyst pellets and the reactant feed enter together and are transported very rapidly through the reactor. The bulk density of the catalyst particle in the STTR is significantly smaller than in moving-bed reactors, and the particles are carried through at the same velocity as the gas velocity. In some places the STTR is also referred to as a circulating fluidized bed (CFB). A schematic diagram is shown in Figure 10-34.
A mole balance on the reactant A over the differential reactor volume
ΔV = AC Δz
is
STTR: Used when catalyst decay (usually coking) is very rapid
Figure 10-34 Straight-through transport reactor.
Dividing by Δz and taking the limit as Δz → 0, letting ρb be the bulk density of the suspended catalyst and recalling that , we obtain
In terms of conversion [FA = FA0 (– X)] and catalyst activity , the reactor mole balance is written as
For a catalyst particle traveling through the reactor with a particle velocity UP, the time the catalyst pellet has been in the reactor when it reaches a height z is just
Substituting for time t in terms of distance z (i.e., a(t) = a(z/UP)), the mole balance now becomes
The entering molar flow rate, FA0, can be expressed in terms of the gas velocity U0, CA0, and AC
FA0 = U0ACCA0
Substituting for FA0, we have
Equation (10-132) describes how the conversion varies as we move up the reactor.
Example 10–6 Decay in a Straight-Through Transport Reactor
The vapor-phase cracking of a gas-oil is to be carried out in a straight-through transport reactor (STTR) that is 10-m high and 1.5 m in diameter. Gas-oil is a mixture of normal and branched paraffins (C12–C40), naphthenes, and aromatics, all of which will be lumped as a single species, A. We shall lump the primary hydrocarbon products according to distillate temperature into two respective groups, dry gas (C1–C4) species B and gasoline (C5–C14) species C. The reaction
A typical cost of the catalyst in the reactor system is $1 million.
can be written symbolically as
Both B and C are adsorbed on the surface. The rate law for a gas-oil cracking reaction on fresh catalyst can be approximated by
with k′ = 0.0014 kmol/kg-cat·s·atm, KA = 0.05 atm–1, KB = 0.15 atm–1, and KC = 0.1 atm–1. The catalyst decays by the deposition of coke, which is produced in most cracking reactions along with the reaction products. The decay law is
Pure gas-oil enters at a pressure of 12 atm and a temperature of 400=C. The bulk density of catalyst in the STTR is 80 kg-cat/m3.
Plot the activity, a(z), and conversion, X(z), of gas-oil up the 10-m reactor for entering gas velocity U0 = 2.5 m/s.
Solution
Mole Balance:
The height of the catalyst particle at time “t” after entering the STTR is

Differentiating, we can find a relation between the time the catalyst particle has been in the STTR and reached a height z, which we can use to find the activity a.
Rate Law:
On fresh catalyst
We assume the solid particles travel up the reactor at the same velocity as the gas, that is, UP = Ug = =/Ac
Combining Equations (E10-6.2)–(E10-6.4) gives
Decay Law. Assuming that the catalyst particle and gas travel up the reactor at the velocity UP = Ug, we obtain the contact time with the catalyst at a height z to be
where
Stoichiometry (gas-phase isothermal and no pressure drop):
Parameter Evaluation:
Equations (E10-6.1), (E10-6.5), (E10-6.7), and (E10-6.8)–(E10-6.10) are now combined and solved using an ODE solver. The Polymath program is shown in Table E10-6.1, and the computer output is shown in Figure E10-6.1.
TABLE E10-6.1 EQUATIONS FOR THE STTR: LANGMUIR-HINSHELWOOD KINETICS
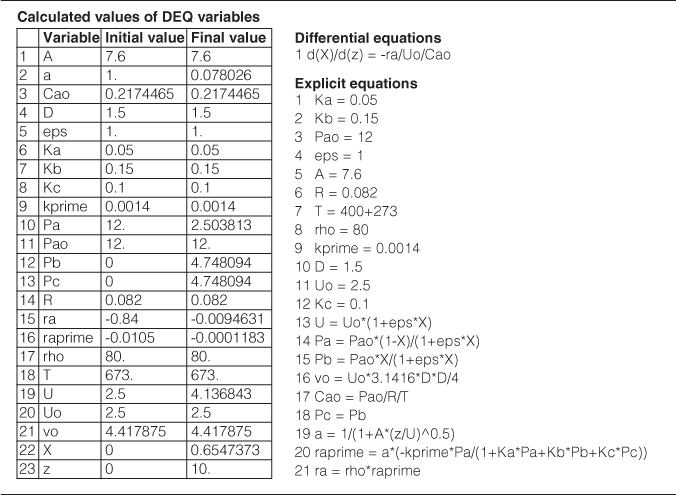


Figure E10-6.1 Activity and conversion profiles.
Use Wolfram to learn how the conversion and activity profiles shown above in Figure E10-6.1 change as you vary the parameters.
Analysis: In this example we applied the algorithm to a STTR in which the gas velocity and, hence, particle velocity increases as we move through the reactor. The decay is quite rapid and the activity is only 15% of its initial value at z = 3 m into the reactor and the conversion begins to plateau at z = 6 m at 60% conversion. If there were no catalyst decay (a = 1), the conversion would have been 97% at z = 6 m.
10.9 And Now… A Word from Our Sponsor–Safety 10 (AWFOS–S10 Exxon Mobil Torrance Refinery Explosion Involving a Straight–Through Transport Reactor [STTR])
This incident and video can be found on the Process Safety Across the Chemical Engineering Curriculum Web site and it is highly recommended to view the video first. On Monday February 18, 2015 an explosion occurred at ExxonMobil’s Torrance California refinery’s electrostatic precipitator unit, a pollution control device associated with the fluid catalytic cracking (FCC) unit. While the explosion occurred in the precipitator, the pre-initiating events took place in the catalyst regeneration unit attached to a STTR, as shown in Figure 10-35. In this incident, the spent catalyst from the STTR is covered with carbon compounds that are burned off in a regenerator. On a routine maintenance shut down, catalyst particles got lodged in the regenerator door allowing flammable vapor to flow out of the regeneration unit and proceed downstream to an electrostatic precipitator (ESP) where it found a spark and exploded.
Watch the Video: (https://www.csb.gov/exxonmobil-refinery-explosion-/)
Incident Report Available At:: (https://www.csb.gov/assets/1/20/exxonmobil_report_for_public_release.pdf?15813)
CSB Incident Report No. 2015-02-I CA ExxonMobil Torrance Refinery, February 18, 2015. If you need more detailed information that can be found in the video, review pages 1–22 of this report.

Figure 10-35 A STTR and regeneration unit.
Figure 14-8 in Chapter 14 shows a schematic for the removal of coke from a catalyst pellet. The time necessary to completely burn the coke off the pellet is
as described by the shrinking core model in Section 14.6, read to learn about Coke Regeneration.
It is important that chemical engineers have an understanding of what the accident was, why it happened, and how it could have been prevented in order ensure similar accidents may be prevented. Applying a safety algorithm to the incident will help achieve this goal. In order to become familiar with a strategy for accident awareness and prevention, view the Chemical Safety Board video on the explosion and fill out the incident report as shown below.
Safety Analysis of the Incident
Activity: The activity in this incident is the maintenance operation of a fluid catalytic cracking (FCC) unit at a refinery.
Hazard: The hazard in this incident is the flammability of light hydrocarbons.
Incident: The incident here is leakage of light hydrocarbons through the reactor into air-side of the unit and finally into the electrostatic precipitator where they found a source of ignition and exploded.
Initiating Event: The initiating event was the lowering of pressure of steam in the reactor which allowed light hydrocarbons to flow back into the reactor and move toward the air-side through the regenerator, as well as the failure of the Spent Catalyst Slide Valve to completely seal the regenerator from the reactor.
Preventative Actions and Safeguards: Some preventive actions or safeguards include strict inspection to control use of old equipment that may have undergone erosion due to use beyond their life, revaluation of operating procedure, and safe operating limits during Safe Park, extensive consideration of all possible failure scenarios. Other considerations include use of an alternative technology that avoids a possible ignition source (use of scrubber instead of ESP) when flammable substances are involved, regular inspection of plant equipment to determine their fitness, installation of gas detectors in the regenerator to detect presence of flammable gases that may flow to the ESP.
Contingency Plan/Mitigating Actions: Immediate shutdown of electrostatic precipitator or the FCC unit when a part of the plant is being opened, replaced, and so on, or when a safety critical safeguard, such as the barrier of catalyst, could not be established.
Lessons Learned: The lessons learned from this incident are that safe operating limits must be defined for all operations and process conditions must be verified to ensure that the process is safe. The equipment critical for safety must be maintained regularly to ensure that it performs its function and an assessment of various possible hazards must be made while changing practices, and they must be done only in consultation with experts from different fields.
A BowTie diagram for this incident is shown in Figure 10-36.
Figure 10-36 BowTie Diagram.
Review the ExxonMobil Safety Module (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344ReactionEngrModule(3)PS20419-Exxon.pdf) and the Catalyst Regeneration Web site.
In order to get the above BowTie diagram on one page, we had to divide it at the initiating event.
Summary
Types of adsorption:
Chemisorption
Physical adsorption
The Langmuir isotherm relating the concentration of species A on the surface to the partial pressure of A in the gas phase is
The sequence of steps for the solid-catalyzed isomerization
is:
Mass transfer of A from the bulk fluid to the external surface of the pellet
Diffusion of A into the interior of the pellet
Adsorption of A onto the catalytic surface
Surface reaction of A to form B
Desorption of B from the surface
Diffusion of B from the pellet interior to the external surface
Mass transfer of B away from the solid surface to the bulk fluid
Assuming that mass transfer is not rate-limiting, the rate of adsorption is
The rate of surface reaction is
The rate of desorption is
At steady state
If there are no inhibitors present, the total concentration of sites is (S10-7)
If we assume that the surface reaction is rate-limiting, we set
and solve for CA·S and CB·S in terms of PA and PB. After substitution of these quantities in Equation (S10-4), the concentration of vacant sites is eliminated with the aid of Equation (S10-7)
Recall that the equilibrium constant for desorption of species B is the reciprocal of the equilibrium constant for the adsorption of species B
and the thermodynamic equilibrium constant, KP, is
Chemical vapor deposition (CVD)
Catalyst deactivation. The catalyst activity is defined as
The rate of reaction at any time t is
The rate of catalyst decay is
For first-order decay
For second-order decay
For slow catalyst decay, the idea of a temperature–time trajectory is to increase the temperature in such a way that the rate of reaction remains constant.
The coupled differential equations to be solved for a moving-bed reactor are
For nth-order activity decay and m order in a gas-phase concentration of species i in a moving bed where the solids move up with the velocity US
The coupled equations to be solved in a straight-through transport reactor are
where Up is the particle velocity up the STTR. For coking
For the case when there is no slip between the catalyst particles and the gas velocity (S10-27)
ODE Solver Algorithm
The isomerization A → B is carried out over a decaying catalyst in a moving-bed reactor with pressure drop. Pure A enters the reactor and the catalyst flows through the reactor at a rate of 2.0 kg/s.
LEP Explore this problem using Python and/or Wolfram on the CRE Web site.
CRE Web Site Materials
(http://www.umich.edu/~elements/6e/10chap/obj.html#/)
Interactive Computer Games

Heterogeneous Catalysis (http://umich.edu/%7Eelements/6e/icm/hetcat.html)
After Reading Each Page in This Book, Ask Yourself a Question About What You Read
Questions, Simulations, and Problems
The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.
A = • B = ▪ C = ♦ D = ♦♦

Questions
Q10-1A QBR (Question Before Reading). The rate laws for heterogeneous reactions usually have concentration terms in both the numerator and denominator. How can this function come about?
Q10-2A i>clicker. Go to the Web site (http://www.umich.edu/~elements/6e/10chap/iclicker_ch10_q1.html) and view at least five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case: explaining why the question should not be on the next exam. In either case, explain your reasoning.
Q10-3A Read over the problems at the end of this chapter. Make up an original problem that uses the concepts presented in this chapter. See Problem P5-1A for guidelines. To obtain a solution:
Create your data and reaction.
Use a real reaction and real data.
The journals listed at the end of Chapter 1 may be useful for part (b).
Choose an FAQ from Chapter 10 and explain why it was most helpful.
Listen to the audios
 on the Summary Notes, pick one, and explain why it was most helpful.
on the Summary Notes, pick one, and explain why it was most helpful.
Q10-4B For the decomposition of cumene discussed in this chapter, if an adsorbing inert is present, how would you compare the initial rate as a function of total pressure when desorption is the RLS, as shown in Figure 10-18?
Q10-5A Choose five Chapter 10 i>clicker questions, pick the one that was the most challenging, and explain why.
Q10-6A Revisit Example 10-4. What if you were asked to sketch or explain the difference in the temperature–time trajectories and to find the catalyst lifetimes (say a = 0.1) for first- and for second-order decay when EA = 35 kcal/mol, Ed = 10 kcal/mol, kd0 = 0.01 day–1, and T0 = 400 K? What would you say? Describe how the trajectory of the catalyst lifetime would change if EA = 10 kcal/mol and Ed = 35 kcal/mol? At what values of kd0 and ratios of Ed to EA would temperature–time trajectories not be effective? Describe what your temperature–time trajectory would look like if n = 1 + Ed/EA?
Q10-7A Write a question for this problem that involves critical thinking and explain why it involves critical thinking.
Q10-8A Go to the LearnChemE screencast link for Chapter 10 (http://www.umich.edu/~elements/6e/10chap/learn-cheme-videos.html). View one or more of the screencast 5- to 6-minute videos.
List two items you learned from Professor Dave’s Lecture.
List four similarities between the Ely–Rideal mechanisms and the Langmuir-Hinshelwood screen-cast.
Write a two-sentence evaluation of the videos you viewed.
Q10-9A AWFOS–S10 View the CSB video (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344Reaction-EngrModule(3)PS-Exxon.pdf). After watching the Chemical Safety Board video, what points do you feel should have been emphasized more in the Safety Analysis of the Incident algorithm and the BowTie Diagram? Write three or so sentences describing your takeaway lesson from this incident.
Computer Simulations and Experiments
P10-1B
Example 10-1: Nonlinear Regression to Determine Model Parameters and Site Concentration Ratio = CT·S/CB·S
Wolfram and Python
Find the critical value of KB at which fraction of vacant sites starts to increase with conversion for the initial settings. Repeat for KT.Vary only one parameter at a time.
Find the value KB where the curve for versus conversion X changes from convex to concave and explain why this shape change occurs.
Write a set of conclusions for your experiments (i) and (ii).
Example 10-2: Catalytic Reactor Design
Wolfram and Python
Describe how the partial pressure profiles change as you vary the sliders for α, KT, and k.
What if the molar flow rate were reduced by 50%; how would X and p change?
After reviewing Generating Ideas and Solutions on the Web site (http://www.umich.edu/~elements/6e/toc/SCPS,3rdEdBook(Ch07).pdf), choose one of the brainstorming techniques (e.g., lateral thinking) to suggest two questions that should be included in this problem.
Write two conclusions from your experiments with the sliders in this example.
Polymath
What catalyst weight would be required for 60% conversion?
Which parameter will you vary so that PB = PH2 at the middle of the reactor (i.e., W = 5000 kg).
Example 10-3: Hydrogenation Ethylene to Ethane
Use Polymath to learn how your answers would change if the following data for run 10 were incorporated in your regression table.
How do the rate laws (e) and (f)
compare with the nonlinear analysis with the other rate laws used to model the data?
Example 10-4: Calculating Conversion with Catalyst Decay in Batch Reactors
Wolfram and Python
What is the maximum conversion that can be achieved if there is no catalyst decay?
Vary k and kd and describe what you find. Can you explain why there is no effect of catalyst decay on conversion at a high value of k?
Vary E and kd and then write a few sentences and three conclusions describing the results of your experiments.
Explain why conversion with catalyst decay increases with increasing Ed and decreases with increasing E.
Polymath
Vary the ratio of (k/kd) and describe what you find.
Repeat this example (i.e., the plotting of X vs. t) for a second-order reaction with (CA0 = 1 mol/dm3) and first-order decay, and describe the differences from the base case.
Repeat this example for a first-order reaction and first-order decay and describe the differences from the base case.
Repeat this example for a second-order reaction (CA0 = 1 mol/dm3) and a second-order decay and describe the differences from the base case.
Example 10-5: Catalytic Cracking in a Moving-Bed Reactor
Wolfram and Python
Suppose kd and US are at their maximum values. What could you do to increase conversion?
Vary the parameters and write a set of conclusions.
Polymath
Use Polymath to learn what the conversion would be if there is no catalyst decay.
What if the solids and reactants entered from opposite ends of the reactor? How would your answers change?
What if the decay in the moving bed were second order? By how much must the catalyst charge, US, be increased to obtain the same conversion?
What if ε = 2 (e.g., A → 3B) instead of zero. How would the results be affected?
Example 10-6: Decay in a Straight-Through Transport Reactor
Wolfram and Python
What happens to a and X when T is varied?
What happens to a and X when U0 is varied?
Vary the parameters and write a set of conclusions.
Polymath
What if you varied the parameters PA0, Ug, A, and k′ in the STTR? What parameter has the greatest effect on either increasing or decreasing the conversion?
Ask questions such as: What is the effect of varying the ratio of k to Ug or of k to A on the conversion? Make a plot of conversion versus distance as Ug is varied between 0.5 and 50 m/s.
Sketch the activity and conversion profiles for Ug = 0.025, 0.25, 2.5, and 25 m/s.
What gas velocity do you suggest operating at?
What is the corresponding entering volumetric flow rate?
What concerns do you have operating at the velocity you selected? Would you like to choose another velocity? If so, what is it? Which parameter will you vary so that conversion increases but activity decreases? Explain, if you can, this unusual behavior.
Interactive Computer Game
P10-2A Download the Interactive Computer Games (ICG) from the CRE Web site (http://www.umich.edu/~elements/6e/icm/install.html). Play the game and then record your performance number for the game, which indicates your mastery of the material. Your professor has the key to decode your performance number. (This ICG is a little longer than the other ICGs.)
ICG Heterogeneous Catalysis Performance # _____________
Problems
P10-3A t-Butyl alcohol (TBA) is an important octane enhancer that is used to replace lead additives in gasoline (Ind. Eng. Chem. Res., 27, 2224 (1988)). TBA was produced by the liquid-phase hydration (W) of isobutene (I) over an Amberlyst-15 catalyst. The system is normally a multiphase mixture of hydrocarbon, water, and solid catalysts. However, the use of cosolvents or excess TBA can achieve reasonable miscibility.
The reaction mechanism is believed to be
Derive a rate law assuming:
The surface reaction is rate-limiting.
The adsorption of isobutene is limiting.
The reaction follows Eley–Rideal kinetics
and the surface reaction is limiting.
Isobutene (I) and water (W) are adsorbed on different sites.
TBA is not on the surface, and the surface reaction is rate-limiting.
What generalization can you make by comparing the rate laws derived in parts (a) through (d)?
P10-4B OEQ (Old Exam Question). Consider the catalytic reaction as a function of the initial partial pressures
The rate of disappearance of species A was obtained in a differential reactor and is shown below.
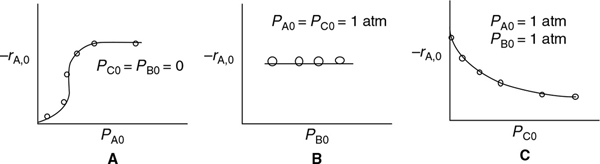
What species are on the surface?
What does Figure B tell you about the reversibility and what’s adsorbed on the surface?
Derive the rate law and suggest a rate-liming step consistent with the above figures.
How would you plot your data to linearize the initial rate data in Figure A?
Assuming pure A is fed, and the adsorption constants for A and C are KA = 0.5 atm–1 and KC = 0.25 atm–1 respectively, at what conversion are the number of sites with A adsorbed on the surface and C adsorbed on the surface equal? (Ans: X = 0.66)
P10-5A The rate law for the hydrogenation (H) of ethylene (E) to form ethane (A) over a cobalt-molybdenum catalyst (Collection Czech. Chem. Commun., 51, 2760 (1988)) is
Suggest a mechanism and rate-limiting step consistent with the above rate law.
What was the most difficult part in finding the mechanism?
P10-6B The formation of propenol on a catalytic surface is believed to proceed by the following mechanism
Suggest a rate-limiting step and derive a rate law.
P10-7B OEQ (Old Exam Question). The dehydration of n-butyl alcohol (butanol) over an alumina-silica catalyst was investigated by J. F. Maurer (Ph.D. thesis, University of Michigan). The data in Figure P10-7B were obtained at 750°F in a modified differential reactor. The feed consisted of pure butanol.
Suggest a mechanism and rate-limiting step that are consistent with the experimental data.
Evaluate the rate-law parameters.
At the point where the initial rate is a maximum, what is the fraction of vacant sites? What is the fraction of occupied sites by both A and B? % vacant = 0.41
What generalizations can you make from studying this problem?
Write a question that requires critical thinking and then explain why your question requires critical thinking. Hint: See Preface Section G.
Apply to this problem one or more of the six ideas discussed in Table P-4 in the Complete Preface-Introduction on the Web site (http://www.umich.edu/~elements/6e/toc/Preface-Complete.pdf).
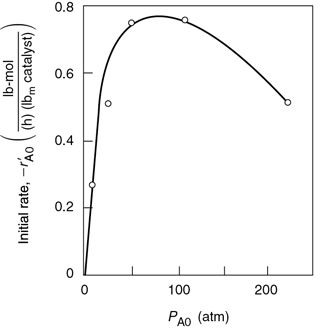
Figure P10-7B Initial reaction rate as function of initial partial pressure of butanol.
P10-8B OEQ (Old Exam Question). The catalytic dehydration of methanol (ME) to form dimethyl ether (DME) and water was carried out over an ion exchange catalyst (K. Klusacek, Collection Czech. Chem. Commun., 49, 170 (1984)). The packed bed was initially filled with nitrogen, and at t = 0. The N2 feed is switched to pure methanol vapor entering the reactor at 413 K, 100 kPa, and 0.2 cm3/s. The following partial pressures were recorded at the exit to the differential reactor containing 1.0 g of catalyst in 4.5 cm3 of reactor volume.

TABLE P10-8B PARTIAL PRESSURE OF H2, ME, AND DME EXITING THE REACTOR AFTER TIME
t(s) |
|||||||
0 |
10 |
50 |
100 |
150 |
200 |
300 |
|
PN2 (kPa) |
100 |
50 |
10 |
2 |
0 |
0 |
0 |
PME (kPa) |
0 |
2 |
15 |
23 |
25 |
26 |
26 |
PH2O (kPa) |
0 |
10 |
15 |
30 |
35 |
37 |
37 |
PDME (kPa) |
0 |
38 |
60 |
45 |
40 |
37 |
37 |
Use parts (a) through (f) to lead you to suggest a mechanism, rate-limiting step, and rate law consistent with this data.
Using the data above, sketch the exit concentrations as a function of time.
Which species took longer than others to exit the reactor in the gas phase? What could have caused this difference in exit times?
What species are adsorbed on the surface?
Are any species not adsorbed on the surface? If so, which ones?
Which set of figures in Figure P10-8B correctly describes the functionality of the chemical reaction rate with the partial pressure PW, PDME, and PME?
Derive a rate law for the catalytic dehydration of methanol. Dimethyl Ether 2ME → DME + W.
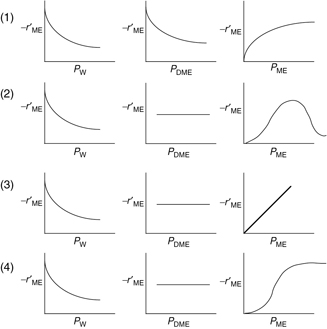
Figure P10-8B Rate data.
P10-9B In 1981, the U.S. government put forth the following plan for automobile manufacturers to reduce emissions from automobiles over the next few years.
Year |
|||
1981 |
1993 |
2010 |
|
Hydrocarbons |
0.41 |
0.25 |
0.125 |
CO |
3.4 |
3.4 |
1.7 |
NO |
1.0 |
0.4 |
0.2 |
All values are in grams per mile. An automobile emitting 3.74 lbm of CO and 0.37 lb m of NO on a journey of 1000 miles would meet the current government requirements.

To remove oxides of nitrogen (assumed to be NO) from automobile exhaust, a scheme has been proposed that uses unburned carbon monoxide (CO) in the exhaust to reduce the NO over a solid catalyst, according to the reaction
Experimental data for a particular solid catalyst indicate that the reaction rate can be well represented over a large range of temperatures by
Propose an adsorption–surface reaction–desorption mechanism and rate-limiting step that are consistent with the experimentally observed rate law. Do you need to assume any species are weakly adsorbed to get agreement with Equation (P10-9.1)?
A certain engineer thinks that it would be desirable to operate with a very large stoichiometric excess of CO to minimize catalytic reactor volume. Do you agree or disagree? Explain.
What would be the relevance of the problem if everyone were driving a hybrid by 2018? A driverless car by 2020?
P10-10B OEQ (Old Exam Question). Methyl ethyl ketone (MEK) is an important industrial solvent that can be produced from the dehydrogenation of butan-2-ol (Bu) over a zinc oxide catalyst (Ind. Eng. Chem. Res., 27, 2050 (1988)):
The following data giving the reaction rate for MEK were obtained in a differential reactor at 490°C.
PBu (atm) |
2 |
0.1 |
0.5 |
1 |
2 |
1 |
PMEK (atm) |
5 |
0 |
2 |
1 |
0 |
0 |
PH2 (atm) |
0 |
0 |
1 |
1 |
0 |
10 |
0.044 |
0.040 |
0.069 |
0.060 |
0.043 |
0.059 |
Suggest a rate law consistent with the experimental data.
Suggest a reaction mechanism and rate-limiting step consistent with the rate law. Hint: Some species might be weakly adsorbed.
Apply to this problem one or more of the six ideas discussed in Table P-4 in the Complete preface-introduction on the Web site (http://www.umich.edu/~elements/6e/toc/Preface-Complete.pdf).
Plot conversion (up to 90%) and reaction rate as a function of catalyst weight for an entering molar flow rate of pure butan-2-ol of 10 mol/min at an entering pressure P0 = 10 atm up to a catalyst weight Wmax = 23 kg.
Write a question that requires critical thinking and then explain why your question requires critical thinking. Hint: See Preface Section G.
Repeat part (d), accounting for pressure drop and α = 0.03 kg–1. Plot p and X as a function of catalyst weight down the reactor.
P10-11B Cyclohexanol was passed over a catalyst to form water and cyclohexene:
It is suspected that the reaction may involve a dual-site mechanism, but it is not known for certain. It is believed that the adsorption equilibrium constant for cyclohexanol is around 1.0 and is roughly one or two orders of magnitude greater than the adsorption equilibrium constants for the other compounds. Using the data in Table P10-11B
TABLE P10-11B DATA FOR CATALYTIC FORMATION OF CYCLOHEXENE
Run |
Reaction Rate (mol/dm3 · s) × 105 |
Partial Pressure of Cyclohexanol (atm) |
Partial Pressure of Cyclohexene (atm) |
Partial Pressure of Steam (H2O) (atm) |
1 |
3.3 |
1 |
1 |
1 |
2 |
1.05 |
5 |
1 |
1 |
3 |
0.565 |
10 |
1 |
1 |
4 |
1.826 |
2 |
5 |
1 |
5 |
1.49 |
2 |
10 |
1 |
6 |
1.36 |
3 |
0 |
5 |
7 |
1.08 |
3 |
0 |
10 |
8 |
0.862 |
1 |
10 |
10 |
9 |
0 |
0 |
5 |
8 |
10 |
1.37 |
3 |
3 |
3 |
Suggest a rate law and mechanism consistent with the data given here.
Determine the values of the rate-law parameters. (Ind. Eng. Chem. Res., 32, 2626–2632.)
Why do you think estimates of the rate-law parameters were given?
For an entering molar flow rate of cychlohexanol of 10 mol/s at a partial pressure of 15 atm, what catalyst weight is necessary to achieve 85% conversion when the bulk density is 1500 gm/dm3?
P10-12B OEQ (Old Exam Question). Experimental data for the gas-phase catalytic reaction
A + B → C
is shown below. The limiting step in the reaction is known to be irreversible, so that the overall reaction is irreversible. The reaction was carried out in a differential reactor to which A, B, and C were all fed.
Run Number |
PA (atm) |
PB (atm) |
PC (atm) |
Reaction rate (mol)/(g-cat · s) |
1 |
1 |
1 |
2 |
0.114 |
2 |
1 |
10 |
2 |
1.140 |
3 |
10 |
1 |
2 |
0.180 |
4 |
1 |
20 |
2 |
2.273 |
5 |
1 |
20 |
10 |
0.926 |
6 |
20 |
1 |
2 |
0.186 |
7 |
0.1 |
1 |
2 |
0.0243 |
Suggest a rate law consistent with the experimental data. Hint: Sketch as a function of PA, as a function of PB, and as a function of PC.
From your rate expression, which species can you conclude are adsorbed on the surface?
Suggest a rate law and then show that your mechanism is constant with the rate law in part (a).
For an entering partial pressure of A of 2 atm in a PBR, what is the ratio of A to C sites at 80% conversion of A?
At what conversion are the number of A and C sites equal? (Ans: X = 0.235)
What reactor volume is necessary to achieve 90% conversion of A for a stoichiometric feed and flow of A 2 mol/s? (Ans: W = 8.9 g-cat)
If necessary, feel free to use none, any, or all of the following parameter values:
P10-13B Solar Energy Capture: Water Splitting. Hydrogen and O2 can be combined in fuel cells to generate electricity. Solar energy can be used to split water to generate the raw reactants H2 and O2 for fuel cells. One method of solar thermal reduction is with NiFe2O4 in the sequence

We note NiFe2O4 is regenerated in this process.36
36 J. R. Scheffe, J. Li, and A. W. Weimer, “A spinel ferrite/hercynite water-splitting redox cycle,” Int. J. Hydrogen Energy, 35, 3333–3340 (2010).
Derive a rate law for Step (2), assuming that water adsorbs on the solid solution as a single-site mechanism and that the reaction is irreversible.
Repeat (a) when the reaction is reversible and the solid solution adsorption site for water (S′) is different than the NiFe2O4 site for the adsorption of H2, (S).
How would your rate law change if we included the effect of hυ in Step 1?
P10-14A Vanadium oxides are of interest for various sensor applications, owing to the sharp metal–insulator transitions they undergo as a function of temperature, pressure, or stress. Vanadium triisopropoxide (VTIPO) was used to grow vanadium oxide films by chemical vapor deposition (J. Electrochem. Soc., 136, 897 (1989)). The deposition rate as a function of VTIPO pressure for two different temperatures follows.
T = 120°C:
Growth Rate (μm/h) |
0.004 |
0.015 |
0.025 |
0.04 |
0.068 |
0.08 |
0.095 |
0.1 |
VTIPO Pressure (torr) |
0.1 |
0.2 |
0.3 |
0.5 |
0.8 |
1.0 |
1.5 |
2.0 |
T = 200°C:
Growth Rate (μm/h) |
0.028 |
0.45 |
1.8 |
2.8 |
7.2 |
VTIPO Pressure (torr) |
0.05 |
0.2 |
0.4 |
0.5 |
0.8 |
In light of the material presented in this chapter, analyze the data and describe your results. Specify where additional data should be taken.
P10-15A OEQ (Old Exam Question). Titanium dioxide is a wide-bandgap semiconductor that is showing promise as an insulating dielectric in VLSI capacitors and for use in solar cells. Thin films of TiO2 are to be prepared by chemical vapor deposition from gaseous titanium tetraisopropoxide (TTIP). The overall reaction is
The reaction mechanism in a CVD reactor is believed to be (K. L. Siefering and G. L. Griffin, J. Electro-chem. Soc., 137, 814 (1990))
where I is an active intermediate and P1 is one set of reaction products (e.g., H2O, C3H6), and P2 is another set. Assuming the homogeneous gas-phase reaction for TTIP is in equilibrium, derive a rate law for the deposition of TiO2. The experimental results show that at 200=C the reaction is second order at low partial pressures of TTIP and zero order at high partial pressures, while at 300=C the reaction is second order in TTIP over the entire pressure range. Discuss these results in light of the rate law you derived.
P10-16B The dehydrogenation of methylcyclohexane (M) to produce toluene (T) was carried out over a 0.3% Pt/ catalyst in a differential catalytic reactor. The reaction is carried out in the presence of hydrogen (H2) to avoid coking (J. Phys. Chem., 64, 1559 (1960)).
Describe how you would determine the model parameters for each of the following rate laws.
Use the data in Table P10-16B below.
Which rate law best describes the data? Hint: Neither or KM can take on negative values.
Where would you place additional data points?
Suggest a mechanism and rate-limiting step consistent with the rate law you have chosen.
TABLE P10-16B DEHYDROGENATION OF METHYLCYCLOHEXANE
PH2 (atm) |
PM (atm) |
|
1 |
1 |
1.2 |
1.5 |
1 |
1.25 |
0.5 |
1 |
1.30 |
0.5 |
0.5 |
1.1 |
1 |
0.25 |
0.92 |
0.5 |
0.1 |
0.64 |
3 |
3 |
1.27 |
1 |
4 |
1.28 |
3 |
2 |
1.25 |
4 |
1 |
1.30 |
0.5 |
0.25 |
0.94 |
2 |
0.05 |
0.41 |
P10-17A OEQ (Old Exam Question). Sketch qualitatively the reactant, product, and activity profiles as a function of length at various times for a packed-bed reactor for each of the following cases. In addition, sketch the effluent concentration of A as a function of time. The reaction is a simple isomerization:
A → B
Rate law:
Decay law:
Case I:
Sketch similar profiles for the rate laws in parts (a) and (c) in a moving-bed reactor with the solids entering at the same end of the reactor as the reactant.
Repeat part (d) for the case where the solids and the reactant enter at opposite ends.
P10-18B The elementary irreversible gas-phase catalytic reaction
is to be carried out in a moving-bed reactor at constant temperature. The reactor contains 5 kg of catalyst. The feed is stoichiometric in A and B. The entering concentration of A is 0.2 mol/dm3. The catalyst decay law is zero order with kD = 0.2 s–1 and k = 1.0 dm6/(mol · kg-cat ·s) and the volumetric flow rate is ν0 = 1 dm3/s.
What conversion will be achieved for a catalyst feed rate of 0.5 kg/s? (Ans: X = 0.2)
Sketch the catalyst activity as a function of catalyst weight (i.e., distance) down the reactor length for a catalyst feed rate of 0.5 kg/s.
What is the maximum conversion that could be achieved (i.e., at an infinite catalyst loading rate)?
What catalyst loading rate is necessary to achieve 40% conversion? (Ans: US = 1.5 kg/s)
At what catalyst loading rate (kg/s) will the catalyst activity be exactly zero at the exit of the reactor?
What does an activity of zero mean? Can catalyst activity be less than zero?
How would your answer in part (a) change if the catalyst and reactant were fed at opposite ends? Compare with part (a).
Now consider the reaction to be zero order with
k = 0.2 mol/kg-cat · min.
The economics:
The product sells for $160 per gram mole.
The cost of operating the bed is $10 per kilogram of catalyst exiting the bed.
What is the feed rate of solids (kg/min) that will give the maximum profit? (Ans: Us = 4 kg/min.) Note: For the purpose of this calculation, ignore all other costs, such as the cost of the reactant, the cost to the company of providing free lunches to workers, and so on.
P10-19B OEQ (Old Exam Question). With the increasing demand for xylene in the petrochemical industry, the production of xylene from toluene disproportionation has gained attention in recent years (Ind. Eng. Chem. Res., 26, 1854 (1987)). This reaction,
was studied over a hydrogen mordenite catalyst that decays with time. As a first approximation, assume that the catalyst follows second-order decay
and the rate law for low conversions is
with kT = 20 g mol/h·kg-cat·atm and kd = 1.6 h–1 at 735 K.
Compare the conversion–time curves in a batch reactor containing 5 kg-cat at different initial partial pressures (1 atm, 10 atm, etc.). The reaction volume containing pure toluene initially is 1 dm3 and the temperature is 735 K.
What conversion can be achieved in a moving-bed reactor containing 50 kg of catalyst with a catalyst feed rate of 2 kg/h? Toluene is fed at a pressure of 2 atm and a rate of 10 mol/min.
Explore the effect of catalyst feed rate on conversion.
Suppose that ET = 25 kcal/mol and Ed = 10 kcal/mol. What would the temperature–time trajectory look like for a CSTR? What if ET = 10 kcal/mol and Ed = 25 kcal/mol?
The decay law more closely follows the equation
with kd = 0.2 atm–1. Redo parts (b) and (c) for these conditions.
P10-20A The vapor-phase cracking of gas-oil in Example 10-6 is carried out over a different catalyst, for which the rate law is
Assuming that you can vary the entering pressure and gas velocity, what operating conditions would you recommend?
What could go wrong with the conditions you chose?
Now assume the decay law is
where the concentration, Ccoke, in mol/dm3, can be determined from a stoichiometric table.
For a temperature of 400=C and a reactor height of 15 m, what gas velocity do you recommend? Explain. What is the corresponding conversion?
The reaction is now to be carried in an STTR 15 m high and 1.5 m in diameter. The gas velocity is 2.5 m/s. You can operate in the temperature range between 100°C and 500°C. What temperature do you choose, and what is the corresponding conversion?
What would the temperature–time trajectory look like for a CSTR?
Additional information:
ER = 3000 cal/mol
ED = 15000 cal/mol
P10-21C When the impurity cumene hydroperoxide is present in trace amounts in a cumene feed stream, it can deactivate the silica-alumina catalyst over which cumene is being cracked to form benzene and propylene. The following data were taken at 1 atm and 420°C in a differential reactor. The feed consists of cumene and a trace (0.08 mol %) of cumene hydroperoxide (CHP).
Benzene in Exit Stream (mol %) |
2 |
1.62 |
1.32 |
1.06 |
0.85 |
0.56 |
0.37 |
0.24 |
t (s) |
0 |
50 |
100 |
150 |
200 |
300 |
400 |
500 |
Determine the order of decay and the decay constant. (Ans: kd = 4.27 × 10–3 s–1)
As a first approximation (actually a rather good one), we shall neglect the denominator of the catalytic rate law and consider the reaction to be first order in cumene. Given that the specific reaction rate with respect to cumene is k = 3.8 = 103 mol/kg fresh cat ·s·atm, the molar flow rate of cumene (99.92% cumene, 0.08% CHP) is 200 mol/min, the entering concentration is 0.06 kmol/m3, the catalyst weight is 100 kg, and the velocity of solids is 1.0 kg/min, what conversion of cumene will be achieved in a moving-bed reactor?
P10-22C The decomposition of spartanol to wulfrene and CO2 is often carried out at high temperatures (J. Theor. Exp., 15, 15 (2014)). Consequently, the denominator of the catalytic rate law is easily approximated as unity, and the reaction is first order with an activation energy of 150 kJ/mol. Fortunately, the reaction is irreversible. Unfortunately, the catalyst over which the reaction occurs decays with time on stream. The following conversion–time data were obtained in a differential reactor:
For T = 500 K:
t (days) |
0 |
20 |
40 |
60 |
80 |
120 |
X % |
1 |
0.7 |
0.56 |
0.45 |
0.38 |
0.29 |
For T = 550 K:
t (days) |
0 |
5 |
10 |
15 |
20 |
30 |
40 |
X % |
2 |
1.2 |
0.89 |
0.69 |
0.57 |
0.42 |
0.33 |
If the initial temperature of the catalyst is 480 K, determine the temperature–time trajectory to maintain a constant conversion.
What is the catalyst lifetime?
P10-23B The hydrogenation of ethylbenzene to ethylcyclohexane over a nickel–mordenite catalyst is zero order in both reactants up to an ethylbenzene conversion of 75% (Ind. Eng. Chem. Res., 28 (3), 260 (1989)). At 553 K, k = 5.8 mol ethylbenzene/(dm3 of catalyst · h). When a 100-ppm thiophene concentration entered the system, the ethylbenzene conversion began to drop.
Time (h) |
0 |
1 |
2 |
4 |
6 |
8 |
12 |
Conversion |
0.92 |
0.82 |
0.75 |
0.50 |
0.30 |
0.21 |
0.10 |
The reaction was carried out at 3 MPa and a molar ratio of H2/ETB = 10. Discuss the catalyst decay. Be quantitative where possible.
Supplementary Reading
1. A terrific discussion of heterogeneous catalytic mechanisms and rate-controlling steps may or may not be found in
THORNTON W. BURGESS, The Adventures of Grandfather Frog. New York: Dover Publications, Inc., 1915.
R. I. MASEL, Principles of Adsorption and Reaction on Solid Surfaces. New York: Wiley, 1996. A great reference.
G. A. SOMORJAI, Introduction to Surface Chemistry and Catalysis. New York: Wiley, 1994.
2. A truly excellent discussion of the types and rates of adsorption together with techniques used in measuring catalytic surface areas is presented in
R. I. MASEL, Principles of Adsorption and Reaction on Solid Surfaces. New York: Wiley, 1996.
3. Techniques for discriminating between mechanisms and models can be found in
G. E. P. BOX, J. S. HUNTER, and W. G. HUNTER, Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed. Hoboken, NJ: Wiley, 2005.
4. Examples of applications of catalytic principles to microelectronic manufacturing can be found in
JOHN B. BUTT, Reaction Kinetics and Reactor Design. Second Edition, Revised and Expanded. New York: Marcel Dekker, Inc., 1999.
D. M. DOBKIN AND M. K. ZURAW, Principles of Chemical Vapor Deposition. The Netherlands: Kluwer Academic Publishers, 2003.

