13. Unsteady-State Nonisothermal Reactor Design

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

13. Unsteady-State Nonisothermal Reactor Design

Chemical engineers are not gentle people, they like high temperatures and high pressures.

—Prof. Steven LeBlanc

Overview. Up to now we have focused on the steady-state operation of nonisothermal reactors. In this chapter, the unsteady-state energy balance will be developed and then applied to CSTRs, as well as well-mixed batch and semibatch reactors. We will use the difference between the rate of “heat generated,” $\overset{\cdot}{Q_{g}}$ , and the rate of “heat removed,” $\overset{\cdot}{Q_{r}}$ , to arrive at the user-friendly form of the energy balance

$\frac{d T}{d t} = \frac{\dot{Q_{g}} - \dot{Q_{r}}}{Σ N_{i} C_{P i}}$

Section 13.1 shows how to arrange the general energy balance (Equation (11-9)) in a more simplified form for unsteady-state operation.
Section 13.2 discusses the application of the energy balance to the operation of batch reactors and discusses reactor safety and the reasons for the explosion of an industrial batch reactor.
Section 13.3 discusses the startup of a CSTR and how to avoid exceeding the practical stability limit.
Section 13.4 shows how to apply the energy balance to semi-batch reactor in which the ambient temperature varies.
Section 13.5 discusses a case study of the T2 Laboratory explosion involving multiple reactions in a batch reactor.
Section 13.6 closes the chapter with a continuing discussion of Safety, which is another focus of this chapter. The example problems and homework problems were chosen to emphasize the hazards of runaway reactions.

13.1 The Unsteady-State Energy Balance

We start by deriving the user-friendly form of the energy balance that can be easily used in making reactor calculations. As I have stated before, the reason I derive the equations rather than just giving the final result is (1) the reader can see what assumptions are used at what points along the way in the derivation to the user-friendly energy balance, and (2) it is my experience that if the reader goes line-by-line through the derivation, they will be less likely to insert the incorrect numbers into symbols in the equation when making a calculation.

We begin by recalling the unsteady-state form of the energy balance developed in Chapter 11.

$\dot{Q} - {\dot{W}}_{s} + Σ_{i = 1}^{m} F_{i} H_{i} |_{i n} - Σ_{i = 1}^{m} F_{i} H_{i} |_{o u t} = (\frac{d Ê_{s y s}}{d t}) (11-9)$

We shall first concentrate on evaluating the change in the total energy of the system wrt time, $({d \hat{E}}_{sys} / d t)$ . The total energy of the system is the sum of the products of specific energies, E_i (e.g., J/mol i), of the various species in the system volume and the number of moles, N_i (mol i), of that species

${\hat{E}}_{s y s} = \underset{i = 1}{\overset{m}{Σ}} N_{i} E_{i} = N_{A} E_{A} + N_{B} E_{B} + N_{C} E_{C} + N_{D} E_{D} + N_{I} E_{I} (13-1)$

In evaluating ${\hat{E}}_{sys}$ , as before we neglect changes in the potential and kinetic energies and substitute for the internal energy U_i in terms of the enthalpy H_i

Equation to evaluate E caret subscript sys is given. — Equation 13-2, E caret subscript sys equals summation with the limit i equals 1 to m, upper N subscript i upper E subscript i equals summation with the limit i equals 1 to m, upper N subscript i upper U subscript i equals [summation with the limit i equals 1 to m, upper N subscript i (upper H subscript i minus P V subscript i)] subscript sys equals summation with the limit i equals 1 to m, N subscript i H subscript i minus P. The term, summation with the limit i equals 1 to m, upper N subscript i upper V subscript i is negligible.

We note the last term on the right-hand side of Equation (13-2) is just the total pressure times the total volume, that is, PV, and this term is virtually always smaller than the other terms in Equation (13-2), and thus will be neglected.^† For brevity, we shall write all summations as

^† Marat Orazov while a student at University of California, Berkeley, pointed out that the last term in Equation (13-2) need not be neglected for the special case of an ideal gas with a constant total number of moles. The denominator on the r.h.s. of Equation (13-9) in this case is just ΣN_i (C_P_i – R).

$Σ = \underset{i = 1}{\overset{m}{Σ}}$

unless otherwise stated.

When no spatial variations are present in the system volume, and time variations in the product of the total pressure and volume (PV) are neglected, the energy balance, after substitution of Equation (13-2) into (11-9), gives

$\dot{Q} - {\dot{W}}_{S} + Σ F_{i 0} H_{i 0} |_{i n} - Σ F_{i} H_{i} |_{o u t} = [Σ N_{i} \frac{d H_{i}}{d t} + Σ H_{i} \frac{d N_{i}}{d t}]_{s y s} (13-3)$

Recalling Equation (11-19)

$H_{i} = H_{i}^{o} (T_{R}) + \int_{T_{R}}^{T} C_{P_{i}} d T (11-19)$

and differentiating with respect to time, we obtain

$\frac{d H_{i}}{d t} = C_{P_{i}} \frac{d T}{d t} (13-4)$

Then, substituting Equation (13-4) into (13-3) gives

$\begin{matrix} \dot{Q} - {\dot{W}}_{S} + Σ F_{i 0} H_{i 0} - Σ F_{i} H_{i} = Σ N_{i} C_{P_{i}} \frac{d T}{d t} + Σ H_{i} \frac{d N_{i}}{d t} & (13-5) \end{matrix}$

The mole balance on species i is

$\begin{matrix} \begin{matrix} \begin{matrix} \frac{d N_{i}}{d t} = - v_{i} r_{A} V + F_{i 0} - F_{i} \end{matrix} \end{matrix} & (13 - 6) \end{matrix}$

Using Equation (13-6) to substitute for dN_i/dt, Equation (13-5) becomes

$\dot{Q} - {\dot{W}}_{s} + Σ F_{i 0} H_{i 0} - Σ F_{i} H_{i}$

$\begin{matrix} = Σ N_{i} C_{P_{i}} \frac{d T}{d t} + Σ ν_{i} H_{i} (- r_{A} V) + Σ F_{i 0} H_{i} - Σ F_{i} H_{i} & (13-7) \end{matrix}$

Rearranging, and recalling Σv_iH_i, = ΔH_Rx, we have

This form of the energy balance should be used when there is a phase change.

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} - Σ F_{i 0} (H_{i} - H_{i 0}) + (- Δ H_{Rx}) (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (13 -8) \end{matrix}$

Substituting for H_i and H_i₀ for the case of no phase change gives us

Energy balance on a transient CSTR or semibatch reactor

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} - Σ F_{i 0} C_{P_{i}} (T_{i} - T_{i 0}) + [- Δ H_{Rx} (T)] (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (13 - 9) \end{matrix}$

Equation (13-9) applies to a semibatch reactor, as well as to the unsteady-state operation of a CSTR, and is also shown in Table 11-1 as Equation (T11-1.I).

For liquid-phase reactions where ΔC_P is usually small and can be neglected and thus the following approximation is often made

C_P_s : Heat capacity of solution

$Σ N_{i} C_{i} ≅ Σ N_{i 0} C_{P_{i}} = N_{A 0} \overset{C_{P_{s}}}{\overset{⏞}{Σ Θ_{i} C p_{i}}} = N_{A 0} C_{P_{s}}$

where C_P_s is the heat capacity of the solution. The units of the batch term (N_A0C_{P_s}) are (cal/K) or (J/K) or (Btu/°R), and analogously for the flow term

Σ F_i0C_{P_i} = F_A0C_{P_s}

the units are (J/s · K) or (cal/s · K) or (Btu/h · °R).¹ With this approximation and assuming that every species enters the reactor at the same temperature T₀, we have

¹ If the heat capacities were given in terms of mass (i.e., C_{P_sm} = J/g · K), then both F_A0 and N_A0 would have to be converted to mass

for batch

$\begin{matrix} m_{A 0} C_{p_{s m}} = N_{A 0} C_{P_{S}} \\ (g) (J/ g \cdot K) = (m o l) \frac{J}{(m o l \cdot K)} = \frac{J}{K} \end{matrix}$

and for flow

$\begin{matrix} \dot{m}_{A 0} C_{P_{s m}} = F_{A 0} C_{P_{S}} \\ (g / s) (J / g \cdot K) = (\frac{m o l}{s}) (J/ m o 1 \cdot K) = \frac{J}{K \cdot s} \end{matrix}$

However, we note that the units of the product of mass flow rate and mass heat capacities would still be the same as the product of molar flow and molar heat capacities (e.g., cal/s · K), respectively.

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} - F_{A 0} C_{P_{s}} (T - T_{0}) + [- Δ H_{Rx} (T)] (- r_{A} V)}{N_{A0} C_{P_{s}}} & (13 -10) \end{matrix}$

C_{P_s} = ΣΘ_i C_{P_i}

13.2 Energy Balance on Batch Reactors (BRs)

A batch reactor is usually well mixed, so that we may neglect spatial variations in the temperature and species concentrations.

An illustration depicts the energy balance on Batch Reactors. — Two diagrams of the batch reactor is shown. The first diagram shows a cylindrical vessel. It has a stirrer to mix the reactants X any Y. The inlet temperature T subscript a 1 with the concentration m subscript c is passed into the reactor to get the outlet temperature T subscript a 2. A diagram labels the components of the batch reactors. The second diagram shows a cylindrical vessel. An array of half pipes is wrapped around the vessel, the conventional jacket is fitted below, the panels that are placed inside the vessel is called a fine-type baffle. A stirrer touches the bottom of the vessel.

The energy balance on batch reactors (BR) is found by setting the inlet and outlet flows to zero, that is, F_i₀ = F_i = 0, in Equation (13-9)

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} + (- Δ H_{Rx}) (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (13 -11) \end{matrix}$

Next we use the energy balance on the heat exchanger to obtain, $\dot{Q}$ , Equation (12-19), and realize that the heat “added” to the batch reactor, $\dot{Q}$ , is just the negative of the heat “removed” from the batch reactor, ${\dot{Q}}_{r b}$ , that is, $\dot{Q} = - {\dot{Q}}_{r b}$ . Neglecting shaft work (recall we could not do this in Problem P12-6_B) we get

Equation reads, d T over d t equals upper Q subscript g b minus upper Q subscript r b minus upper upper W subscript s over summation upper N subscript i upper C upper P i.

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{Σ N_{i} C_{T_{i}}} & (13 - 12) \end{matrix}$

where the terms for heat generated, $\dot{Q_{g b}}$ , and heat removed, $\dot{Q_{r b}}$ , for a batch system are

$\begin{matrix} {\dot{Q}}_{g b} = (- Δ H_{Rx}) (- r_{A} V) & (13 - 13) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{r b} = \dot{m C_{P_{C}}} (T - T_{a 1}) [1 - exp (- \frac{U A}{\dot{m C_{P_{C}}}})] & (13 -14) \end{matrix}$

with an added bonus we obtained in Equation (12-17)

$\begin{matrix} T_{a 2} = T - (T - T_{a 1}) [exp (- \frac{U A}{\dot{m} C_{P_{C}}})] & (13 - 15) \end{matrix}$

Equations (13-12) and (13-13) are the preferred form of the energy balance when the number of moles, N_i, is used in the mole balance, rather than the conversion, X.

To write the energy balance in terms of conversion, recall that the number of moles of species i at any X is

N_i = N_A0 (Θ_i + v_iX)

Consequently, in terms of conversion, the user-friendly form of the energy balance becomes

Reminder: The sign convention

Heat Added

$\dot{Q} = + 10 j/s$

Heat Removed

$\dot{Q} = - 10 j/s$

Work Done by System

${\dot{W}}_{s} = + 10 J/s$

Work Done on System

${\dot{W}}_{s} = - 10 J/s$

Batch reactor energy balance

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{rb}}{N_{A0} (Σ Θ_{i} C_{P_{i}} + Δ C_{P} X)} & (13 -16) \end{matrix}$

Equation (13-12) must be coupled with the mole balance

Batch reactor mole balance

$\begin{matrix} N_{A 0} \frac{d X}{d t} = - r_{A} V & (2 -6) \end{matrix}$

13.2.1 Adiabatic Operation of a Batch Reactor

Batch reactors operated adiabatically are often used to determine the reaction orders, activation energies, and specific reaction rates of exothermic reactions by monitoring the temperature–time trajectories for different initial conditions. In the steps that follow, we will derive the temperature–conversion relationship for adiabatic operation.

For adiabatic operation $(\dot{Q} = 0)$ of a batch reactor F_i0 = 0) and when the work done by the stirrer can be neglected $({\dot{W}}_{S} ≅ 0)$ , Equation (13-10) can be written as

$\begin{matrix} \frac{d T}{d t} = \frac{(- Δ H_{R x}) (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (13-17) \end{matrix}$

It is shown in the Summary Notes of Chapter 13 on the CRE Web site (http://www.umich.edu/~elements/6e/13chap/RelationshipBetweenXandT.pdf ) that if we combine Equation (13-17) with Equation (2-6), we can do a lot of rearranging and integrating to arrive at the following user-friendly equation for an adiabatic batch reactor.

$\begin{matrix} X = \frac{Σ Θ_{i} C_{P_{i} (T - T_{0})}}{- Δ H_{R x} (T)} & (13 - 18) \end{matrix}$

$\begin{matrix} T = T_{0} + \frac{[- Δ H_{Rx} (T_{0})] X}{Σ Θ_{i} C_{P_{i}} + X Δ C_{P}} & (13 -19) \end{matrix}$

We note that for adiabatic conditions, the relationship between temperature and conversion is the same for BRs, CSTRs, PBRs, and PFRs. Once we have T as a function of X for a batch reactor, we can construct a table similar to Table E11-3.1 and use techniques analogous to those discussed in Section 11.3.2 to evaluate the following design equation that determines the time necessary to achieve a specified conversion.

$\begin{matrix} t = N_{A 0} \int_{0}^{X} \frac{d X}{- r_{A} V} & (2-9) \end{matrix}$

However, if you do not have that much time on your hands to form a table and use Chapter 2 integration techniques, then use a software package such as Poly-math, Wolfram, Python, or MATLAB to solve the coupled differential forms of mole balance equation (2-6) and the energy balance equation (13-19) simultaneously.

A graph of X versus T shows an inclined line sloping upward that indicates that the increase in conversion increases the temperature.

Temperature–conversion relationship for any reactor operated adiabatically

#TimeOnYourHands

$\begin{matrix} N_{A0} \frac{d X}{d t} = - r_{A} V & (2 - 6) \end{matrix}$

Example 13–1 Batch Reactor with an Exothermic Reaction

It is still winter, and although you were hoping for a transfer to the plant in the tropical southern coast of Florida, you unfortunately are still the engineer of the CSTR from Example 12-3, in charge of the production of propylene glycol.

The formation of propylene glycol is represented. Ethylene oxide, a 3-carbon compound with an Oxygen group connecting the first 2 carbon undergoes hydrolysis in the presence of sulphuric acid (H2SO4). The H plus and OH minus ions combine with the first and the second carbons of the oxide and form propylene glycol.

You are considering the installation of a new, attractive-looking, glass-lined 1000-dm³ CSTR, and you decide to make a quick check of the reaction kinetics and maximum adiabatic temperature. You have a stylish, nicely decorated and instrumented 40-dm³ (~10 gal) stirred batch reactor you ordered from a company. You charge (i.e., fill) this reactor with 4 dm³ (~1 gal) of ethylene oxide, 4 dm³ (~1 gal) of methanol, and 10 dm³ (~2.5 gal) of water containing 0.1 wt % H₂SO₄. For safety reasons, the reactor is located on a boating pier on the banks of Lake Walloon (you don’t want the entire plant to be destroyed if the reactor explodes). At this time of year in northern Michigan, the initial temperature of all materials is 276 K (3°C). We have to be careful here! If the reactor temperature increases above 350 K (77°C), a secondary, more exothermic reaction will take over, causing runaway and subsequent explosion, similar to what happened in the T2 Laboratory plant explosion in Florida (see page 717).

Although you requested obtaining the data for this reaction from the Jofostan national research laboratory, the purchasing department decided to save money and buy it off the Internet. The values it purchased are

$\begin{matrix} E = 1800 cal/mol, Δ H_{Rx}^{0} = 20202 cal/mol, C_{P_{A}} = 35 cal/mol/K, \\ C_{P_{B}} = 18 cal/mol/K, C_{P_{C}} = 46 cal/mol/K, and C_{P_{M}} = 19.5 cal/mol/K \end{matrix}$

Prof. Dr. Sven Köttlov objected to this Internet purchase and said that it should be recorded that he is skeptical of these parameter values. The initial concentrations of pure ethylene oxide and methanol are 13.7 and 24.7 mol/dm³, respectively. Consequently, the initial number of moles added to the reactor are

$\begin{matrix} A: Ethylene oxide: & N_{A0} = (13.7 {mol/dm}^{3}) (4 {dm}^{3}) = 54.8 mol \\ B: Water: & N_{B0} = (55.5 {mol/dm}^{3}) (10 {dm}^{3}) = 555 mol \\ M: Methanol: & N_{M} = (24.7 {mol/dm}^{3}) (4 {dm}^{3}) = 98.8 mol \end{matrix}$

The sulfuric acid catalyst takes up negligible space, so the total volume is 18 dm³, while the data and the reaction-rate law are given in Example 12-3. We are going to carry out two scenarios: (1) to learn how fast the temperature rises and how long it takes to reach 350 K for adiabatic operation, and (2) how long would it take to reach 345 K if we added a heat exchanger.

Adiabatic Operation: Plot conversion and temperature X and T as a function of time for adiabatic operation. How many minutes should it take the mixture inside the reactor to reach a conversion of 51.5%? What is the corresponding adiabatic temperature?
Heat Exchange: Plot the temperature and conversion as a function of time when a heat exchanger is added. The product of the overall heat transfer coefficient and exchange surface area is UA = 10 cal/s/K with T_a₁ = 290 K and the coolant rate is 10 g/s, and it has a heat capacity of 4.16 cal/g/K.

Solution

The initial temperature is 3°C, and if the reactor temperature increases to above 77°C, a dangerous exothermic side reaction can occur, as was reported in Jofostan Journal of Chemical Safety, Vol. 19, p. 201 (2009).

As before, there is approximately a 10°C (18°F) rise in temperature immediately after mixing.

Illustration of footsteps represents the phrase "Following the algorithm."

1. Mole Balance, Chapter 2, rearranging Equation (2-6) we have

$\begin{matrix} \frac{d X}{d t} = \frac{- r_{A} V}{N_{A 0}} & (E13-1.1) \end{matrix}$

2. Rate Law: Apparent first order

$\begin{matrix} - r_{A} = k C_{A} & (E13-1.2) \end{matrix}$

3. Stoichiometry:

$\begin{matrix} N_{A} = N_{A 0} (1 - X) & (2-4) \end{matrix}$

Recall that for a liquid-phase batch reaction V = V₀

$\begin{matrix} C_{A} = \frac{N_{A}}{V} = \frac{N_{A}}{V_{0}} = \frac{N_{A 0} (1 - X)}{V_{0}} = C_{A 0} (1 - X) & (E13.1.3) \end{matrix}$

4. Combining Equations (E13-1.1), (E13-1.2), and (2-4) above, we have

$\begin{matrix} \frac{d X}{d t} = k (1 - X) & (E13-1.4) \end{matrix}$

Changing the data in Example 12-3 from English units to mks units, we have

$\begin{matrix} k = (4.71 \times 1 0^{9}) \exp [(\frac{E}{R}) \frac{1}{T}] s^{- 1} & (E13-1.5) \end{matrix}$

With $\frac{E}{R} = 9059 K$

Choosing 297 K as a reference temperature for k, and putting Equation (E13-1.5) in the form of Equation (3-21), we get

$\begin{matrix} k = (2.73 \times 10^{- 4}) exp [9059 K (\frac{1}{297} - \frac{1}{T}) s^{- 1}] & (E13-1.6) \end{matrix}$

5. Energy Balance:

Part (a) Adiabatic Operation.

Recalling Equation (13-12)

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{Σ N_{i} C_{p_{i}}} = \frac{{\dot{Q}}_{g b}}{Σ N_{i} C_{p_{i}}} = \frac{(- Δ H_{Rx}) (- r_{A} V)}{Σ N_{i} C_{p_{i}}} & (13 - 17) \end{matrix}$

with

${\dot{Q}}_{g b} = (- Δ H_{Rx}) (- r_{A} V)$

we could couple this ODE, Equation (13-17), with the mole balance ODE, Equation (E13-1.1), and solve these two equations simultaneously to obtain X and T as a function of t. However, for adiabatic operation we can use the explicit relationship, Equation (13-19), directly to couple with the mole balance that is

$\begin{matrix} T = T_{0} + \frac{[- Δ H_{Rx} (T_{0})] X}{Σ Θ_{i} C_{P_{i}} + Δ C_{P} X} & (E13-1.7) \end{matrix}$

6. Parameters:

$\begin{array}{l} C_{P_{S}} & = \sum Θ_{i} C_{P_{i}} = C_{P_{A}} + C_{P_{B}} Θ_{B} + C_{P_{M}} Θ_{M} (E13-1.8) \\ C_{P_{S}} & = 35 + 18 (\frac{555}{54.8}) + 19.5 (\frac{98.8}{54.8}) \\ = 35 + 182.3 + 35.2 = 252.5 \frac{c a l}{m o l \cdot K} \end{array}$

The lumped heat capacity of the solution, C_{P_S} is

$\begin{matrix} C_{P_{s}} = 252.2 \frac{cal}{mol \cdot K} \end{matrix}$

In the equation for the heat of reaction (i.e., Eq. (E13-1.9) below), we are going to neglect the second term on the right-hand side, that is,

We can do this because ΔC_P is –7 cal/mol/K and for a 50-K temperature difference, ΔC_P (T–T_R) = 350 cal/mol, which is negligible with respect to the heat of reaction of –20202 cal/mol

$\begin{matrix} Δ H_{Rx} (T) = {Δ H}_{Rx}^{\circ} = - 20202 cal/mol & (E13-1.10) \end{matrix}$

In calculating the inlet temperature after mixing, T₀, we must include the temperature rise 10°C (18°F) resulting from the heat of mixing the two solutions that are initially at 3°C

$T_{0} = 276 + 10 = 286 K$

$T = T_{0} + \frac{X (- Δ H_{Rx})}{C_{P_{S}}} = 286 K + \frac{X (- 1 (- 20, 202)) \frac{cal}{mol}}{252.5 cal/mol \cdot K}$

$\begin{matrix} T=286+80X & (E13-1.11) \end{matrix}$

Adiabatic energy balance

A summary of the heat and mole balance equations is given in Table E13-1.1.

TABLE E13-1.1 SUMMARY FOR FIRST-ORDER ADIABATIC BATCH REACTION

$\begin{array}{l} \frac{d X}{d t} = k (1 - X) & (E13-1.4) \\ k = (2.73 \times 1 0^{- 4}) \exp [9059 K (\frac{1}{297} - \frac{1}{T})] s^{- 1} & (E13-1.6) \\ T = 286 + 80 X & (E13-1.11) \end{array}$

where T is in K and t is in seconds.

A table similar to that used in Example 11-3 can now be constructed or one can make better use of his or her time using Polymath.

The software package Polymath will be used to combine Equations (E13-1.4), (E13-1.6), and (E13-1.11) to determine conversion and temperature as a function of time. Table E13-1.2 shows the program, and Figures E13-1.1 and E13-1.2 show the solution results.

TABLE E13-1.2 POLYMATH PROGRAM

Differential equations

1 d(X)/d(t) = k*(1-X)

Explicit equations

1 T = 286+80*X

2 k = .000273*exp(9059*(1/297-1/T))

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	k	8.446E-05	0.0858013
2	T	286.	366.
3	t	0	2500.
4	X	0	1.

The Polymath equations do not include the runaway reaction that “ignites” at 350 K. A switching technique, SW, can be used to prevent the temperature from numerically going to infinity and could be used here as described in detail in Example 13-6.

We note for the initial temperature of 286 K that the reaction starts off relatively slowly then at approximately 1200 sec (20 minutes) “ignites” and the temperature rises rapidly to 370 K, at which point we reach complete conversion.

Image of Living Example Problems (LEPs) sliders.

LEP Sliders

A graph of temperature versus time is depicted to represent the runaway reaction. — **Figure E13-1.1** Temperature–time trajectory.

A graph for temperature- time trajectory is shown. The horizontal axis representing t (seconds) is marked from 0 to 4000, in increments of 400. The vertical axis representing T (Kelvin) is marked from 280 to 380, in increments of 10. From the graph, the inferred data is as follows: The temperature increases from 285.0 to 360 Kelvin from 0 to 1600 seconds, where the runaway temperature is 300 Kelvin at 1200 seconds. Note: the mentioned values are approximate.

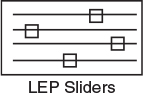
A graph of conversion versus time is depicted. — **Figure E13-1.2** Conversion–time trajectory.

A graph for conversion- time trajectory is shown. The horizontal axis representing t (seconds) is marked from 400 to 4000, in increments of 400. The vertical axis representing inverse conversion (negative X) is marked from 0.0 to 1.0, in increments of 0.1. From the graph, the inferred data is as follows: The concentration increases from 0.0 at the initial stage, increases steadily and reaches 1.0 at 1620 seconds. The mentioned values are approximate.

Part (b) Heat Exchanger in a Batch Reactor.

We now consider the case where a heat exchanger is added to the batch reactor. The coolant enters at 290 K and the flow rate, ${\dot{m}}_{c}$ , through the exchanger is 10 g/s. The mole balance, Equation (E13-1.1), and the physical properties, Equations (E13-1.2)–(E13-1.6) and (E13-1.8), remain the same.

$\begin{matrix} \frac{d X}{d t} = \frac{- r_{A} V}{N_{A0}} & (E13-1.1) \end{matrix}$

Neglecting ΔC_P the energy balance is

$\begin{matrix} \frac{d X}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{N_{A0} C_{P_{s}}} & (E13-1.12) \end{matrix}$

with

$\begin{matrix} {\dot{Q}}_{r b} = {\dot{m}}_{c} C_{P_{C}} {(T - T_{a 1}) [1 - exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{C}}})]} & (E13-1.13) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{r b} = (- r_{A} V) (- Δ H_{Rx}^{\circ}) & (E13-1.14) \end{matrix}$

$\begin{matrix} - r_{A} V = N_{A0} k (1 - X) & (E13-1.15) \end{matrix}$

The Polymath Program is shown in Table E13-1.3 with parameters

$\begin{matrix} \begin{matrix} C_{P_{S}} = Σ Θ_{i} C_{P_{i}} = 252.5 c a l / m o l / K C_{P_{C}} = 4.16 c a l / g / K \overset{}{\overset{\cdot}{m} c = 10 g / s} \\ N_{A0} = 54.8 mol, UA=10 cal/K/S \end{matrix} \\ T_{a l} = 290 K, T_{0} = 286 K \end{matrix}$

Mole balance

Energy balance

and the other terms remain the same as in Part (a).

Parameters

Polymath solution

TABLE E13-1.3 POLYMATH PROGRAM

Differential equations

1 d(T)/d(t) = (Qg-Qr)/Cps/Nao

2 d(X)/d(t) = k*(1-X)

Explicit equations

1 UA = 10

2 DeltaH = -20202

3 Ta1 = 290

4 Cpc = 4.18

5 Cps = 252.5

6 mc = 10

7 R = 1.987

8 E = 18000

9 k = .000273*exp((E/R)*(1/297-1/T))

10 Ta2 = T-(T-Ta1)*exp(-UA/mc/Cpc)

11 Qr = mc*Cpc*(T-Ta1)*(1-exp(-UA/mc/Cpc))

12 Nao = 54.8

13 Qg = Nao* k*(1-X)*(-DeltaH)

14 DeltaQ = Qr-Qg

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	Cpc	4.18	4.18
2	Cps	252.5	252.5
3	DeltaH	-2.02E+04	-2.02E+04
4	DeltaQ	-129.0845	155.5059
5	E	1.8E+04	1.8E+04
6	k	8.447E-05	0.0007724
7	mc	10.	10.
8	Nao	54.8	54.8
9	Qg	93.50939	0.0004296
10	Qr	-35.57509	155.5063
11	R	1.987	1.987
12	T	286.	307.4849
13	t	0	4000.
14	Ta1	290.	290.
15	Ta2	289.1489	293.7202
16	UA	10.	10.
17	X	0	0.9999995

One notes after comparing Figures E13-1.1 and E13-1.3 that the temperature profiles are not as steep as the adiabatic case. As expected the temperature of this exothermic reaction first increases as $({\dot{Q}}_{g b} > {\dot{Q}}_{r b})$ , goes through a maximum and then as the reactants have been consumed the temperature decreases because the heat “removed” is greater that the heat “generated,” that is, $({\dot{Q}}_{r b} > {\dot{Q}}_{g b})$ . As a result the specific reaction-rate constant goes through a maximum as the fluid becomes heated at first and then later cooled. Figure E13-1.4 shows the LEP slider variable while Figure E13-1.5 shows the trajectories of the “heat generated,” Q_gb, and “heat removed,” Q_rb. A plot of Q_gb and Q_rb as a function of time can often be useful in understanding the reaction dynamics. Whenever $({\dot{Q}}_{g b} > {\dot{Q}}_{r b})$ the reacting mixture temperature will increase and whenever $({\dot{Q}}_{r b} > {\dot{Q}}_{g b})$ the temperature will decrease.

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{N_{A0} Σ Θ_{i} C_{P_{i}}} & (E13-1.16) \end{matrix}$

A graph of temperature versus time is depicted. — **Figure E13-1.3** Polymath temperature–time trajectory.

A graph for polymath temperature- time trajectory is shown. The horizontal axis representing t (seconds) is marked from 0 to 4000, in increments of 400. The vertical axis representing temperature is marked from 280 to 360, in increments of 8. From the graph, the inferred data is as follows: The curve representing negative T (Kelvin) starts from 286 at the initial time, rises steadily and reaches a peak value of 344 at 239 seconds, and then ends with 312 at 4000 seconds. The curve representing negative T subscript a 2 (Kelvin) starts from 289 at the initial time, rises steadily and reaches a peak value of 298 at 239 seconds, and then ends with 297 at 4000 seconds. Note: the mentioned values are approximate.

An illustration of LEP sliders is shown. — **Figure E13-1.4** LEP sliders.

A screenshot of LEP sliders for various parameters is shown. The screenshot displays four profiles such as temperature, conversion, specific reaction rate, and heat, in which heat is selected. The sliders are adjusted for parameters such as UA, delta H, Ta1, Cpc, Cps, mc, and Nao.

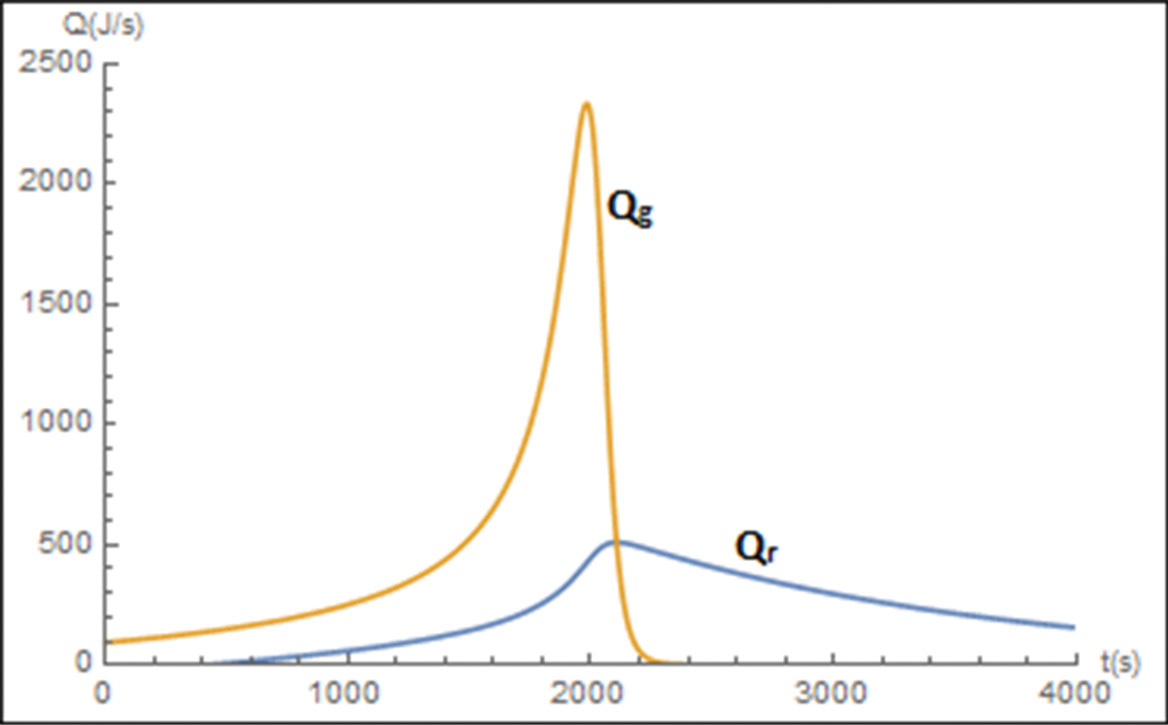
A graph of Q (in joule per second) versus t (in seconds) is shown. — **Figure E13-1.5** Wolfram heat-generated as heat-removed trajectories.

A graph compares the wolfram heat generated and heat removed trajectories. The horizontal axis represents time, ranging from 0 to 4000 in increments of 1000 seconds. The vertical axis represents the heat energy, ranging from 0 to 2500, in increments of 500 joules per second. The curve representing Q subscript g starts from (0, 100), increases rapidly to the peak value at (2000, 2400), and decreases to the lowest value at (2200, 0). The curve representing Q subscript r, starts at (200, 0), increases to the peak value at (2050, 480) and falls to the lowest value on the horizontal axis at (4000, 100). Note: all values are approximate.

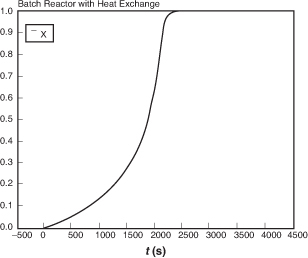
A graph of conversion versus time denotes an example of the batch reactor with heat exchange. — **Figure E13-1.6** Polymath conversion–time trajectory.

The graph for the Polymath Conversion-time trajectory is shown. The horizontal axis representing time (seconds) ranges from negative 500 to 4500 in increments of 500. The vertical axis representing the conversion (x) ranges from 0.0 to 1.0 in increments of 0.1. The graph is an increasing curve, where the conversion at time zero seconds is 0.0, which then increases steeply over time that is the conversion reaches the conversion of 0.3 at 1500 seconds and ends at 1.0 at 2490 seconds. Overall, the graph indicates that the conversion increases as time increases. Note: the mentioned values are approximate.

Analysis:

(a) Adiabatic. The initial temperature is rather low, so the reaction is slow at first. However, as the exothermic reaction proceeds, it heats up and becomes virtually autocatalytic as it goes from a small conversion at 1600 seconds to complete conversion just a few seconds later. As seen in Figure E13-1.6, the conversion reaches X = 1.0 and the temperature reaches its maximum value, where it remains.

(b) Heat Exchange. Because the temperature is maintained at a lower value in the heat exchange case than in the adiabatic case, there will be less conversion for the parameter values UA, T_ai, T₀, ${\dot{m}}_{c}$ , and so on, given in the problem statement. However, if you change these values as suggested in LEP Problem P13-1_B (a), you will find situations where the conversion remains very low and other cases where the temperature curve is extremely steep.

13.2.2 Case History of a Batch Reactor with Interrupted Isothermal Operation Causing a Runaway Reaction

In Chapters 5 and 6 we discussed the design of reactors operating isothermally. This operation may be achieved by efficient control of a heat exchanger. The following example shows what can happen when the heat exchanger suddenly fails.

Example 13–2 Safety in Chemical Plants with Exothermic Runaway Reactions²

² Adapted from the problem by Ronald Willey, Seminar on a Nitroaniline Reactor Rupture. Prepared for SAChE, Center for Chemical Process Safety, American Institute of Chemical Engineers, New York (1994). Also see Process Safety Progress, vol. 20, no. 2 (2001), pp. 123–129. The values of ΔH_Rx and UA were estimated from the plant data of the temperature–time trajectory in the article by G. C. Vincent, Loss Prevention, 5, 46–52.

A serious accident occurred at the Monsanto plant in Sauget, Illinois, on August 8, 1969, at 12:18 A.M. (see Figure E13-2.1). (Sauget (pop. 200) is the home of the 1988 Mon-Clar League Softball Champions.) The blast was heard as far as 10 mi away in Belleville, Illinois, where people were awakened from a deep sleep. The explosion occurred in a batch reactor that was used to produce nitroaniline from ammonia and o-nitrochlorobenzene (ONCB):

A 6-membered aromatic compound has groups NO2, and Cl (ortho to each other). On the addition of 2 molecules of ammonia. The chlorine is replaced with the NH2 group in the second position. NH4Cl is liberated.

This reaction is normally carried out isothermally at 175°C and about 500 psi over a 24-hour period. The ambient temperature of the cooling water in the heat exchanger is 25°C. By adjusting the coolant flow rate, the reactor temperature could be maintained at 175°C. At the maximum coolant rate, the ambient temperature is 25°C throughout the heat exchanger. Also review the T2 Laboratories Safety Modules (http://umich.edu/~safeche/assets/pdf/courses/Problems/344ReactionEngrModule(1)PS-T2.pdf).

Let me tell you something about the operation of this reactor. Over the years, the heat exchanger would fail from time to time, but the technicians would be “Johnny on the Spot” and run out and get it up and running within 10 minutes or so, and there was never any problem. It is believed that one day someone in management looked at the reactor and said, “It looks as if your reactor is only a third full and you still have room to add more reactants and to make more product and more money. How about filling it up to the top so we could triple production?” They did, and started the reactor up at 9:45 P.M. Around midnight the reactor exploded and the aftermath is shown in Figure E13-2.1.

On the day of the accident, two changes in normal operation occurred.

The reactor was charged with 9.044 kmol of ONCB, 33.0 kmol of NH₃, and 103.7 kmol of H₂O. Normally, the reactor is charged with 3.17 kmol of ONCB, 103.6 kmol of H₂O, and 43 kmol of NH₃.

A decision was made to triple production.

Figure E13-2.1 Aftermath of the explosion. (St. Louis Globe/Democrat photo by Roy Cook. Courtesy of St. Louis Mercantile Library.)
The reaction is normally carried out isothermally at 175°C over a 24-hour period. However, approximately 45 minutes after the reaction was started, cooling to the reactor failed, but only for 10 minutes, after which cooling was again up and running at the 55-minute mark. Cooling may have been halted for 10 minutes or so on previous occasions when the normal charge of 3.17 kmol of ONCB was used and no ill effects occurred.

The reactor had a rupture disk designed to burst when the pressure exceeded approximately 700 psi. If the disk would have ruptured, the pressure in the reactor would have dropped, causing the water to vaporize, and the reaction would have been cooled (quenched) by the latent heat of vaporization.

Plot and analyze the temperature–time trajectory up to a period of 120 minutes after the reactants were mixed and brought up to 175°C (448K).
Show that all of the following three conditions had to have been present for the explosion to occur: (1) increased ONCB charge, (2) cooling stopped for 10 minutes at a time early in the reaction, and (3) relief-system failure.

Additional information:

Rate law: -r_ONCB = kC_ONCBC_NH3

with $k = 0.00017 \frac{m^{3}}{k m o 1 \cdot \min}$ at 188°C (461 K) and E = 11273 cal/mol

The reaction volume for the new charge of 9.0448 kmol of ONCB

V = V_aqNH3 = V_ONCB

Because ammonia is soluble in water, the aqueous ammonia volume will not change much as ammonia is added, and thus we will assume the volume is constant at 3.9 m³ (i.e., VaqNH₃ ≡ Vaqam = 3.9 m³) for both cases. The volume of ONCB is

$V_{ONCB} = \frac{N_{ONCB} \cdot {M W}_{ONCB}}{ρ_{ONCB}} = \frac{(0.94 kmol) (157.5 \frac{kg}{kmol})}{1199 \frac{kg}{m^{3}}} = 1.19 m^{3}$

The total volume for the increased charge to the reactor is

LEP Sliders

The total volume for the increased charge to the reactor is

V = 3.9 m³ + 1.19 m³ = 5.1 m³

Case history

The reaction volume for the previous 3.17 kmol ONCB charge was Assume that

V = 3.9 m³ + 0.42 m³ = 4.32 m³

$Δ H_{R x} = - 5.9 \times 1 0^{5} k c a l / kmol$

$C_{P_{O N C B}} = C_{P_{A}} = 40 c a l / m o l \cdot K$

$C_{P_{H_{2^{O}}}} = c_{P_{W}} = 18 cal / m o 1 \cdot K C_{P_{N H_{3}}} = C_{P_{B}} = 8.38 c a l / m o l \cdot K$

Assume that ΔC_p ≈ 0

$U A = \frac{35.85 k c a 1}{\min^{\circ} C} {with T}_{a} = 298 K$

Solution

$A + 2 B \to C + D$

Mole Balance:

$\begin{matrix} \frac{d X}{d t} = - r_{A} \frac{V}{N_{A0}} = \frac{- r_{A}}{C_{A0}} & (E13-2.1) \end{matrix}$

Rate Law:

$\begin{matrix} - r_{A} = k C_{A} C_{B} & (E13-2.2) \end{matrix}$

Stoichiometry (liquid phase):

$\begin{matrix} C_{A} = C_{A0} (1 - X) & (E13-2.3) \end{matrix}$

with

$\begin{matrix} C_{B} = C_{A0} (Θ_{B} - 2 X) & (E13-2.4) \end{matrix}$

$Θ_{B} = \frac{N_{B 0}}{N_{A 0}}$

Combine:

$\begin{matrix} - r_{A} = k C_{A0}^{2} (1 - X) (Θ_{B} - 2 X) & (E13-2.5) \end{matrix}$

An illustration depicts footsteps, and represents the phrase "following the algorithm".

Substituting our parameter values into Equation (3-21)

$\begin{matrix} k = k (T_{0}) \exp [\frac{E}{R} (\frac{1}{T_{0}} - \frac{1}{T_{1}})] & (3-21) \end{matrix}$

We obtain

$\begin{matrix} k = 0.00017 exp [\frac{11273}{1.987} (\frac{1}{461} - \frac{1}{T})] \frac{m^{3}}{kmol \cdot min} \end{matrix}$

Energy Balance:

$\begin{matrix} \frac{d T}{d t} = \frac{Q_{g} - Q_{r}}{Σ N_{i} C_{P_{i}}} & (\begin{matrix} E13-2.6 \end{matrix}) \end{matrix}$

For ΔC_P = 0,

$\begin{matrix} Σ N_{i} C_{P_{i}} = N C_{P} = N_{A0} C_{P_{A}} + N_{B0} C_{P_{B}} + N_{w} C_{P_{w}} & (\begin{matrix} E13-2.7 \end{matrix}) \end{matrix}$

Parameter evaluation for day of explosion:

NC_P = (9.04)(40) + (103.7)(18) + (33)(8.38)

NC_P = 2505 kcal/K

Substituting for $Σ N_{i} C_{P_{i}}, {\dot{Q}}_{g}, and {\dot{Q}}_{r}$ in Equation (E13-2.6) one obtains

$\begin{matrix} \frac{d T}{d t} = \frac{\overset{Q_{g}}{\overset{⏞}{(r_{A} V) (Δ H_{Rx})}} - \overset{Q_{r}}{\overset{⏞}{U A (T - T_{a})}}}{N_{A0} C_{P_{A}} + N_{B 0} C_{P_{B}} + N_{W} C_{P_{W}}} & (E13-2.8) \end{matrix}$

Q_g = (r_AV) (ΔH_Rx)

Q_r = UA T – T_a)

A. Isothermal Operation up to 45 Minutes

The reaction takes place isothermally at 175°C (448 K) up to the time the heat exchanger fails and cooling stops at 45 minutes. We will calculate the conversion, X, the temperature, T, as well as Q_r and Q_g at the point that the heat exchanger fails. Next we calculate T, X, Q_r, and Q_g again 10 minutes later at the point when cooling is restored, and then again compare Q_g and Q_r.

Combining Equations (E13-2.1) with (E13-2.5) and canceling yields

$\begin{matrix} \frac{d X}{d t} = k C_{A 0} (1 - X) (Θ_{B} - 2 X) & (E13-2.9) \end{matrix}$

$Θ_{B} = \frac{33}{9.04} = 3.64$

Integrating Equation (E13-2.9) gives us

$\begin{matrix} t = [\frac{V}{k N_{A 0}}] (\frac{1}{Θ_{B} - 2}) 1 n [\frac{Θ_{B} - 2 X}{Θ_{B} (1 - X)}] & (E13-2.10) \end{matrix}$

At 175°C = 448 K, k = 0.000119m³/kmol · min.

Substituting for k and the other parameter values

$45 \min = [\frac{5.119 . m^{3}}{0.0001167 m^{3} / k m o l. \min (9.044 k m o l)}] \times (\frac{1}{1.64}) \ln [\frac{3.64 - 2 X}{3.64 (1 - X)}]$

The calculation and results can also be obtained from the Polymath output.

Solving for X, we find that at t = 45 min, then X = 0.034.

We can now calculate the rate of generation, Q_g, at this temperature and conversion and compare it with the maximum rate of heat removal, Q_r, that is available for a constant coolant temperature of T_a = 298 K. The rate of generation, Q_g, is

$\begin{matrix} Q_{g} = r_{A} V Δ H_{Rx} = k \frac{N_{A0} (1 - X) N_{A0} [(N_{B0} / N_{A0}) - 2 X] V (- Δ H_{Rx})}{V^{2}} & (\begin{matrix} E13-2.11 \end{matrix}) \end{matrix}$

Comparing Q_r and Q_g at the Time Cooling Stops

At this time (i.e., t = 45 min, X = 0.034, T = 175°C), we calculate k, then Q_r and Q_g. At 175°C, k = 0.000119 m³/min · kmol.

$Q_{g} = (0.000119) \frac{{(9.044)}^{2} (1 - 0.034)}{5.1} [\frac{33}{9.044} - 2 (0.034)] 5.9 \times 10^{5}$

$Q_{g} = 3904 kcal/min$

The corresponding maximum cooling rate is

$\begin{matrix} \begin{matrix} Q_{r} & = & U A (T - 298) \\ = & 35.85 (448 - 298) \end{matrix} & (E13-2.12) \end{matrix}$

$Q_{r} = 5378 kcal/min$

Therefore

$\begin{matrix} Q_{r} > Q_{g} & (E13-2.13) \end{matrix}$

The reaction can be controlled. There would have been no explosion had the cooling not failed.

B. Adiabatic Operation for 10 Minutes

Unexpectedly, the cooling failed from 45 to 55 minutes after the reaction was started. We will now use the conditions at the end of the period of isothermal operation as our initial conditions for the adiabatic operation period between 45 and 55 minutes

t = 45 min X = 0.034 T = 448 K

Between t = 45 and t = 55 minutes, Q_r = 0. The Polymath program was modified to account for the time of adiabatic operation by using an “if statement” for Q_r in the program, that is,

Q_r = if (t > 45 and t < 55) then (0) else (UA(T - 298))

A similar “if statement” is used for isothermal operation between t = 0 and t = 45 minutes, that is, (dT/dt) = 0 and as shown in the Polymath and Wolfram Program.

Comparing Q_r and Q_g after 10 minutes of Adiabatic Operation

For the 45- to 55-minute period without cooling, the temperature rose from 448 K to 468 K, and the conversion increased from 0.034 to 0.0432. Using this temperature and conversion in Equation (E13-2.11), we calculate the rate of generation Q_g at 55 minutes and see that it has increased to

Q_g = 6638 kcal / min

The maximum rate of cooling at this reactor temperature is found from Equation (E13-2.12) to be

Q_r = 6101 kcal/min

Everything is OK.

Interruptions in the cooling system have happened before with no ill effects.

${\dot{Q}}_{g} > {\dot{Q}}_{r}$ Oh no, looks like we may be in trouble.

We can also use the LEP Polymath Program to find these values for X, T, Q_r, and Q_g. In addition we note that by changing the run time from t = 45 to t = 55 minutes and by including an “if statement,” we can include the complete calculation of trajectory temperature and conversion versus time. The “if” statement will include the time of isothermal operation up to 45 minutes,

$\frac{d T}{d t} = {if (t<45) than (0)rlse((Q}_{g} - Q_{r})/ {NC}_{p}$

and adiabatic operation between 45 and 55 and heat exchange thereafter.

Q_r = if (45 < t < 55) then (0) else (UA (T – 298))

Here, we see that at the end of the 10-minute down time, the heat exchange system is now operating again, but now

$\begin{matrix} Q_{g} > Q_{r} & (E13-2.14) \end{matrix}$

and the temperature will continue to increase. We have a Runaway Reaction!! The point of no return has been passed and the temperature will continue to increase, as will the rate of reaction until the explosion occurs.

C. Batch Operation with Heat Exchange

Return of the cooling occurs at 55 minutes after startup. The values at the end of the period of adiabatic operation (T = 468 K, X = 0.0433) become the initial conditions for the period of restored operation with the heat exchange. The cooling is turned on at its maximum capacity, Q_r = UA(T – 298), at 55 minutes. Table E13-2.1 gives the Poly-math program to determine the temperature–time trajectory. (Note that one can change N_A0 and N_B0 to 3.17 and 43 kmol in the program and show that, if the cooling is shut off for 10 minutes, at the end of that 10 minutes, Q_r will still be greater than Q_g and no explosion will occur and one should really do that calculation.)

The point of no return

TABLE E13-2.1 POLYMATH PROGRAM

Differential equations

1 d(T)/d(t) = if (t<t1) then (0) else ((Qg-Qr)/NCp)

2 d(X)/d(t) = (-ra)*V/Nao

Explicit equations

1 Nao = 9.044 #kmol

2 Nbo = 33 #kmol

3 Nw = 103.7 #kmol

4 mao = Nao*157.55 #kg

5 mbo = Nbo*17.03 #kg

6 mw = Nw*18.03 #kg

7 NCp = Nao*40+Nw*18+Nbo*8.38 #kcal/K

8 Va = mao/1199 #m3

9 Vaqam = (mbo+mw)/rhoaqam #m3

10 V = Va+Vaqam #m3

11 DeltaHrx = -590000 #kcal/kmol

12 k = .00017*exp(11273/(1.987)*(1/461-1/T)) # m3/(kmol.min)

13 t2 = 55 #min

14 UA = 35.85 #kcal/(min C)

15 t1 = 45 #min

16 Qr = if(t>t1 and t<t2) then (0) else (UA*(T-298)) # kcal/min

17 Theata = Nbo/Nao

18 ra = -k*nao^2*(1-X)*(Theata-2*X)/V^2 # kmol/(m3.min)

19 Qg = ra*V*DeltaHrx # kcal/min

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	DeltaHrx	-5.9E+05	-5.9E+05
2	k	0.0001189	2.900631
3	mao	1424.882	1424.882
4	mbo	561.99	561.99
5	mw	1869.711	1869.711
6	Nao	9.044	9.044
7	Nbo	33.	33.
8	NCp	2504.9	2504.9
9	Nw	103.7	103.7
10	Qg	4116.257	1.356334
11	Qr	5377.5	6.87E+04
12	ra	-0.0013711	-4.518E-07
13	t	0	122.
14	T	448.	2214.403
15	t1	45.	45.
16	t2	55.	55.
17	Theata	3.648828	3.648828
18	UA	35.85	35.85
19	V	5.088392	5.088392
20	Va	1.188392	1.188392
21	Vaqam	3.9	3.9
22	X	0	1.

The complete temperature–time trajectory is shown in Figure E13-2.2. One notes the long plateau after the cooling is turned back on. Using the values of Q_g and Q_r at 55 minutes and substituting into Equation (E13-2.8), we find that

$\frac{d T}{d t} = \frac{(6638 k c a l / \min - (6101 k c a l / \min)}{2505 k c a l /^{\circ} C} = 0 . 2^{o} C / \min$

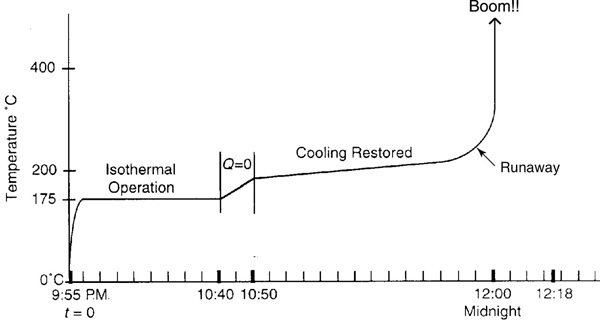
Temperature versus time trajectory is shown graphically. — **Figure E13-2.2** Temperature–time trajectory.

A graph shows the time versus temperature. The horizontal axis represents the time. The vertical axis represents the temperature in degrees Celsius. The isothermal reactions occur at 9:55 P.M to 10:40 P.M at 175 degrees Celsius. The temperature increases from 175 to 180 degrees Celsius between 10:40 to 10:50 P.M where the Q value is zero. At between 10:50 to 12:00 midnight, the cooling restores, as the temperature increases to 200 degrees Celsius (runaway temperature), in seconds the explosion hits at 400 degrees Celsius.

Consequently, even though (dT/dt) is positive, the temperature increases very slowly at first, 0.2°C/min. By 11:45, the temperature has reached 240°C and both the “heat generated” and the temperature begin to increase more rapidly. This rapid increase is a result of the Arrhenius temperature dependence, which causes the temperature to increase exponentially. The reaction is running away! One observes in Figure E13-2.2 that 119 minutes after the batch reaction was started, the temperature increases sharply and the reactor explodes at approximately midnight. If the mass and heat capacity of the stirrer and reaction vessel had been included, the NC_p term would have increased by about 5% and extended the time until the explosion occurred by 15 or so minutes, which would predict the actual time the explosion occurred, at 12:18 A.M.

When the temperature reached 300°C, a secondary reaction, the decomposition of nitroaniline to noncondensable gases such as CO, N₂, and NO₂, occurred, releasing even more energy. The total energy released was estimated to be 6.8 × 10⁹ J, which is enough energy to lift the entire 2500-ton building 300 m (the length of three football fields) straight up. In Problem P13-1_B (b) you are asked to use the Wolfram sliders to explore this example, that is, E13-2, and find such things as the value of amount of reactant fed below which no explosion would have occurred.

D. Safety Disk Rupture Failure

We note that the pressure-safety-relief disk should have ruptured when the temperature reached 265°C (ca. 700 psi) but did not and the temperature continued to rise. If it had ruptured and all the water had vaporized, then 10⁶ kcal would have been drawn from the reacting solution, thereby lowering its temperature and quenching the runaway reaction.

If the disk had ruptured at 265°C (700 psi), we know from fluid mechanics that the maximum mass flow rate, ${\dot{m}}_{vap}$ , out of the 2-in. orifice to the atmosphere (1 atm) would have been 830 kg/min at the time of rupture. The corresponding heat removed would have been

The explosion occurred shortly after midnight.

Illustration of a person running out of control from a place where the chemical reactions are taking place.

Runaway Reaction

A diagram of a safety disk is shown. A spring is attached to the valve on the top. The relief valve is on the top of the pressure gauge and the rupture disk is set at the bottom.

$\begin{array}{l} Q_{r} & = {\dot{m}}_{v a p} Δ H_{v a p} + U A (T - T_{a}) \\ = 830 \frac{k g}{\min} \times 540 \frac{k c a l}{k g} + 35.83 \frac{k c a l}{\min \cdot K} (538 - 298) K \\ = 4.48 \times 1 0^{5} \frac{k c a l}{\min} + 8604 \frac{k c a l}{\min} \\ = 456604 \frac{k c a l}{\min} \end{array}$

This value of Q_r is much greater than the “heat generated” Q_g

(Q_g = 26990 kcal/min), so that the reaction could have been easily quenched.

Analysis: Runaway reactions are the most deadly in the chemical industry. Elaborate safety measures are usually installed to prevent them from occurring. However, as we show in this example, the backup plan failed. If any one of the following three things had not occurred, the explosion would not have happened.

Tripled production
Heat-exchanger failure for 10 minutes early in the operation
Failure of the relieving device (rupture disk)

In other words, all the above had to happen to cause the explosion. If the relief valve had operated properly, it would not have prevented reaction runaway but it could have prevented the explosion. In addition to using rupture disks as relieving devices, one can also use pressure relief valves. In many cases, sufficient care is not taken to obtain data for the reaction at hand and to use it to properly size the relief device. This data can be obtained using a specially designed batch reactor called the Advanced Reactor Safety Screening Tool (ARSST) described in the Professional Reference Shelf (http://www.umich.edu/~elements/6e/13chap/pdf/CD_ARSST_ProfRef.pdf ). You can now see this example on the Web site Process Safety Across the Chemical Engineering Curriculum (http://umich.edu/~safeche) and click on Chemical Reaction Engineering Course. Another example of runaway reactions in CRE is Module 2, on the safety Web site, the Synthron explosion. This semibatch reactor shows a similar situation where reactants were added at a rate such that the heat generated ${\dot{Q}}_{g}$ was greater than the heat removed ${\dot{Q}}_{r}$ .

An icon of the reference shelf with books.

13.3 Batch and Semibatch Reactors with a Heat Exchanger

In our past discussions of reactors with heat exchangers, we assumed that the ambient temperature T_a was spatially uniform throughout the exchangers. This assumption is a good one if the system is a tubular reactor with the external pipe surface exposed to the atmosphere, or if the system is a CSTR or BR where the coolant flow rate through the exchanger is so rapid that the coolant temperatures entering and leaving the exchanger are virtually the same.

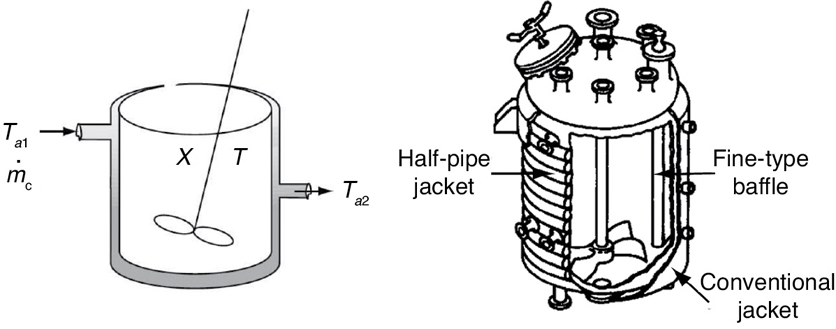
We now consider the case where the coolant temperature varies along the length of the exchanger while the temperature in the reactor is spatially uniform. The coolant enters the exchanger at a mass flow rate, ${\dot{m}}_{c}$ , at a temperature, T_a₁, and leaves at a temperature, T_a₂ (see Figure 13-1). Figure 13-1 could represent a CSTR as shown, or for a batch reactor (BR) if the inlet and outlet flow rate were set to zero, that is, F_A = F_A0 = 0, or for a semibatch reactor (SBR) if the outlet streams are set equal to zero, that is, F_A = F_B = 0.

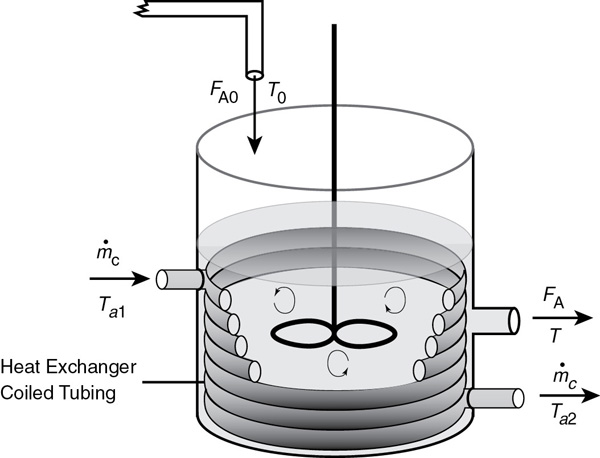
An illustration of the heat exchanger in a tank reactor. — **Figure 13-1** Tank reactor with heat exchanger.

A diagram of the tank reactor is shown. A cylindrical vessel is wrapped with coiling tubes for heat exchange with a stirrer in the center. A heat exchange happens within the vessel when coolant enters the vessel at a mass flow rate (m over dot subscript c) at T subscript a1 (temperature) and leaves at the other end of the coil at T subscript a2 with the same mass flow rate after the heat exchange. The inlet and the outlet flow rate are F subscript A0 and F subscript A, with temperatures T subscript 0 and T, respectively.

As a first approximation, we assume a quasi-steady state for the coolant flow and neglect the accumulation term (i.e., dT_a/dt = 0). As a result, Equation (12-19) will give the rate of heat transfer from the exchanger to the reactor

$\begin{matrix} \dot{Q} = {\dot{m}}_{C} C_{p_{c}} (T_{a 1} - T) [1 - \exp (- U A / {\dot{m}}_{C} C_{p_{c}})] & (12-19) \end{matrix}$

The energy balance on a semibatch reactor is

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} = Σ F_{i 0} C_{P_{i}} (T - T_{i 0}) - [Δ H_{Rx} (T)] (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (13 - 9) \end{matrix}$

Using a slight rearrangement of the heat exchanger energy balance equation, that is, Equation (12-9) and neglecting shaft work, ${\dot{W}}_{s}$

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g s} - {\dot{Q}}_{r s}}{Σ N_{i} C_{P_{i}}} & (13 -20) \end{matrix}$

where the “heat generated,” ${\dot{Q}}_{g s}$ , for a the semibatch reactor is the same as that for a BR,

$\begin{matrix} {\dot{Q}}_{g s} = (r_{A} V) (Δ H_{Rx}) & (13 -21) \end{matrix}$

however, the “heat removed” for a semibatch reactor, ${\dot{Q}}_{r s}$ , is

$\begin{matrix} {\dot{Q}}_{r s} = Σ F_{i 0} C_{P_{i}} (T - T_{i 0}) + \dot{m} C_{P_{C}} [T - T_{a 1}] [1 - exp (\frac{- U A}{\dot{m} C_{P_{C}}})] & (13 -22) \end{matrix}$

Note: The subscript “s” in ${\dot{Q}}_{r s} and {\dot{Q}}_{g s}$ means these equations only apply to a semibatch reactor.

For large coolant flow rates, we showed in Section 12.4.1 that the exponent in Equation (13-22) could be expanded and therefore Equation (13-22) can be written as

$\begin{matrix} \frac{d T}{d t} = \frac{\overset{{\dot{Q}}_{g s}}{\overset{⏞}{(r_{A} V) (Δ H_{Rx})}} - \overset{{\dot{Q}}_{r s}}{\overset{⏞}{[Σ F_{i 0} (T - T_{10}) + U A (T - T_{a})]}}}{Σ N_{i} C_{P_{i}}} & (13-23) \end{matrix}$

One added complexity for the semibatch reactor is that the heat-transfer area, A, could vary with time. For example, as the tank in Figure 13-1 fills up, more of the reacting fluid comes in contact with the heat-exchanger area, consequently this area changes significantly as the fluid level rises. This change in area will depend on the reactor geometry, how the exchanger is placed in the reactor, and the initial and final fluid volumes in the reactor. In the semibatch reactor examples that follow, we will assume the surface area, A, remains virtually constant, although this assumption will be analyzed in Problem P13-1_B (d) (vii).

13.3.1 Startup of a CSTR

In reactor startup, it is often very important how temperature and concentrations approach their steady-state values. For example, a significant overshoot in temperature may cause a reactant or product to degrade, or the overshoot may be unacceptable for safe operation, such as initiating a secondary reaction that causes runaway. If either case were to occur, we would say that the system exceeded its practical stability limit. The practical limit is specific to the specific reaction and conditions under which the reaction is carried out, and is usually determined by the reaction safety engineer. Although we can solve the unsteady temperature–time and concentration–time equations numerically to see whether such a limit is exceeded, it is often more insightful to study the approach to steady state by using the temperature–concentration phase plane. To illustrate these concepts, we shall confine our analysis to a liquid-phase reaction carried out in a CSTR.

A qualitative discussion of how a CSTR approaches steady state is given in PRS R13.5 on the CRE Web site (http://www.umich.edu/~elements/6e/13chap/prof-steadystate.html). This analysis, summarized in Figure PRS13.5 in the Summary is developed to show the four different regions into which the phase plane is divided and how they allow one to sketch the approach to the steady state.

Startup of a CSTR

An icon of the reference shelf with books.

Example 13–3 Startup of a CSTR

Again, we consider the production of propylene glycol (C) in a CSTR with a heat exchanger in Example 12-3. Initially there is only water, C_wi = 55.3 kmol/m³, at T_i = 297 K and 0.1 wt % H₂SO₄ in the 1.89 m³ reactor. The feed stream consists of 36.3 kmol/h of propylene oxide (A), 453.6 kmol/h of water (B) containing 0.1 wt % H₂SO₄, and 45.4 kmol/h of methanol A + B → C (M).

The water coolant flows through the heat exchanger at a rate of 2.27 kg/s (453.6 kmol/h). The molar densities of pure propylene oxide (A), water (B), and methanol (M) are ρ_A0 = 14.8 kmol/m³, ρ_B0 = 55.3 kmol/ m³, and ρ_M0 = 24.7 kmol/ m³, respectively.

Plot the temperature and concentration of propylene oxide as a function of time, and also the concentration of A as a function of temperature for different entering temperatures and initial concentrations of A in the reactor to learn whether the practical stability limit of 355 K is exceeded.

Additional information:

$\begin{array}{l} U A = 7262 & \frac{k c a l}{h \cdot K} with T_{a 1} = 288.7 K, with C_{P_{W}} = 18 k c a l / kmo l \cdot k \\ C_{P_{A}} = 35 k c a l / {kmo l \cdot k, C}_{P_{B}} = 18 kca l /kmo l \cdot k \\ C_{P_{C}} = 46 k c a l / {kmo l \cdot k, C}_{P_{M}} = 19.5 kca l /kmo l \cdot k \end{array}$

Is the practical stability limit exceeded?

Again, the temperature of the mixed reactant streams entering the CSTR is T₀ = 297 K.

An illustration of the heat exchanger in CSTR. — A diagram of the CSTR is shown. A cylindrical vessel is wrapped with coiling tubes for heat exchange with a stirrer in the center. A heat exchange happens within the vessel when coolant enters the vessel at a mass flow rate (m over dot c) at T subscript a1 (temperature) and leaves at the other end of the coil at T subscript a 2 with the same mass flow rate after the heat exchange. The inlet flow rate is given by F subscript A0, F subscript B0, and F subscript M0 at T subscript 0 and v subscript 0. The outlet flow rate is F subscript A, with temperature T.

Solution

A + B → C

Mole Balances:

Initial Conditions

$\begin{matrix} A: & \frac{d C_{A}}{d t} = r_{A} + \frac{(C_{A 0} - C_{A}) v_{0}}{V} & C_{A i} = 0 & (E13-3.1) \end{matrix}$

$\begin{matrix} B: & \frac{d C_{B}}{d t} = r_{B} + \frac{(C_{B 0} - C_{B}) v_{0}}{V} & C_{B i} = 55.3 \frac{k m o 1}{m^{3}} & (E13-3.2) \end{matrix}$

$\begin{matrix} C: & \frac{d C_{C}}{d t} = r_{C} + \frac{- C_{C} v_{0}}{V} & C_{C i} = 0 & (E13-3.3) \end{matrix}$

$\begin{matrix} M : & \frac{d C_{M}}{d t} = \frac{v_{0} (C_{M 0} - C_{M})}{V} & C_{M i} = 0 & (E13-3.4) \end{matrix}$

Rate Law:

$\begin{matrix} - r_{A} = k C_{A} & (E13-3.5) \end{matrix}$

Stoichiometry:

$\begin{matrix} - r_{A} = - r_{B} = r_{C} & (E13.3.6) \end{matrix}$

Energy Balance:

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g s} - {\dot{Q}}_{r s}}{N C_{P}} & (E13-3.7) \end{matrix}$

where

$\begin{matrix} {\dot{Q}}_{g s} = (r_{A} V) (Δ H_{R x}) & (E13.3.8) \end{matrix}$

An illustration depicts footsteps, and represents the phrase "following the algorithm".

using

$\begin{matrix} \sum F_{i 0} C_{P_{i}} = F_{A 0} \sum Θ_{i} C_{P_{i}} & (E13-3.9) \end{matrix}$

the “heat removed” term from the unsteady startup of a CSTR is similar to that for the “heat removed” term from a semi batch reactor. Recalling Equations (12-12) and (12-19)

$\begin{matrix} {\dot{Q}}_{r s} = \overset{{\dot{Q}}_{r s 1}}{\overset{⏞}{F_{A 0} Σ Θ_{i} C_{P_{i}} (T - T_{0})} +} \overset{{\dot{Q}}_{r s 2}}{\overset{⏞}{{\dot{m}}_{c} C_{P_{C}} (T - T_{a 1}) [1 - exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{c}}})]}} & (E13-3.10) \end{matrix}$

${\dot{Q}}_{r s} = {\dot{Q}}_{r s 1} + {\dot{Q}}_{r s 2}$

${\dot{Q}}_{r s 1}$ is the sensible heat removed by flow of material into the reactor and being heated while ${\dot{Q}}_{r s 2}$ is the heat removed by the heat exchanger.

$\begin{matrix} T_{a 2} = T - (T - T_{a 1}) exp (- \frac{U A}{{\dot{m}}_{c} C_{P_{C}}}) & (12 -17) \end{matrix}$

Evaluation of Parameters:

$\begin{array}{l} N C_{P} = \sum N_{i} C_{P_{i}} & \begin{matrix} = C_{P_{A}} N_{A} + C_{P_{B}} N_{B} + C_{P_{C}} N_{C} + C_{P_{M}} N_{M} & (E13-3.11) \end{matrix} \\ = 35 (C_{A} V) + 18 (C_{B} V) + 46 (C_{C} V) + 19.5 (C_{M} V) \end{array}$

$\begin{array}{l} \begin{matrix} \sum Θ_{i} C_{P_{i}} & = C_{P_{A}} + \frac{F_{B 0}}{F_{A 0}} C_{P_{B}} + \frac{F_{M 0}}{F_{A 0}} C_{P_{M}} \\ = 35 + 18 \frac{F_{B 0}}{F_{A 0}} + 19.5 \frac{F_{M 0}}{F_{A 0}} \end{matrix} & (E13-3.12) \end{array}$

$\begin{matrix} υ_{0} = \frac{F_{A 0}}{ρ_{A 0}} + \frac{F_{B 0}}{ρ_{B 0}} + \frac{F_{M 0}}{ρ_{M 0}} = (\frac{F_{A 0}}{1 4. 8} + \frac{F_{B 0}}{55.3} + \frac{F_{M 0}}{2 4. 7}) \frac{m^{3}}{h} & (E13-3.13) \end{matrix}$

Neglecting because ΔC_p it changes the heat of reaction insignificantly over the temperature range of the reaction, the heat of reaction is assumed constant at its reference temperature

$Δ H_{R x} = - 20013 \frac{k c a l}{k m o l A}$

The Polymath program is shown in Table E13-3.1.

Figures E13-3.1 and E13-3.2 show the concentration of propylene oxide and reactor temperature as a function of time, respectively, for an initial temperature of T_i = 297 K and only water in the tank (i.e., C_A_i = 0). One observes that both the temperature and concentration oscillate around their steady-state values (T = 331 K, C_A = 0.658 kmol/m³) as steady state is approached.

Figure E13-3.3 combines Figures E13-3.1 and E13-3.2 into a phase plot of C_A versus T. The final steady-state operating concentration of A is 0.658 kmol/m³ at a temperature of 331.5 K. The arrows on the phase-plane plots show the trajectories with increasing time. The maximum temperature reached during startup is 337.5 K, which is below the practical stability limit of 355 K.

Unacceptable startup

The concentration versus time graph for Propylene oxide is shown. — **Figure E13-3.1** Propylene oxide concentration as a function of time for C_A_i = 0 and *T_i* = 297 K.

A graph shows the concentration of propylene oxide as a function of time. The horizontal axis represents time in hours, ranging from 0.0 to 4.0 in increments of 0.8. The vertical axis represents the concentration in kilomole per meter cubed, from 0.0 to 2.5 in increments of 0.5. The concentration is 0 in the initial hour. It rapidly increases, reaches 2.25 at 0.7 hours, decreases to 0.5 in 1.7 hours, increases to 0.7, and remains constant till 4 hours. The mentioned values are approximate.

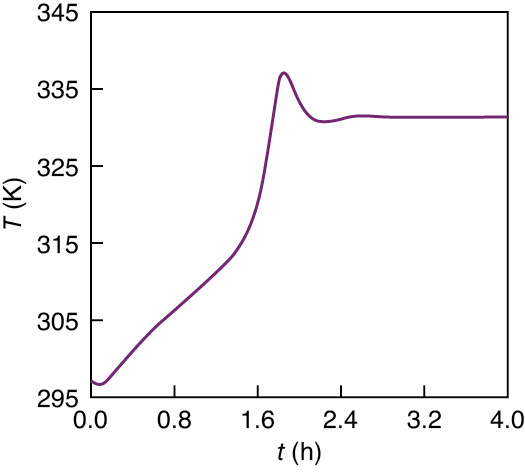
The temperature versus time graph for CSTR startup. — **Figure E13-3.2** Temperature–time trajectory for CSTR startup for C_A_i = 0 and *T_i* = 297 K.

A graph shows the temperature versus time plot. The horizontal axis represents time in hours, ranging from 0.0 to 4.0 in increments of 0.8. The vertical axis represents the temperature in kelvin, ranging from 295 to 345 in increments of 10. The temperature is initially 298 Kelvin, gradually increases, and reaches 335 kelvin at 1.7 hours. Then, it decreases to 329 Kelvin in 2.3 hours, and remains constant till 4 hours. The mentioned values are approximate.

The concentration versus temperature graph is shown. — **Figure E13-3.3** Concentration–temperature phase-plane trajectory using Figures E13-3.1 and E13-3.2.

A graph shows the Temperature versus concentration. The horizontal axis represents the temperature T in Kelvin, ranging from 290 to 340 in increments of 10. The vertical axis represents the concentration C subscript A in kilo mole per meter cubed, ranging from 0.0 to 2.5 in increments of 0.5. The concentration increases from 0 to 2.3 at 297 Kelvin, after which it gradually decreases with increase in temperature. The concentration is at 0.5 when the temperature is 338 Kelvin. Then, the trajectory exhibits that the temperature decreases with increase in concentration. At 330 kelvin, the concentration is 0.75-kilo mole per meter cubed. The mentioned values are approximate.

Next, consider Figure E13-3.4, which shows three different phase-plane trajectories for three different sets of initial conditions:

(1) T_i = 297 K C_A_i = 0 (same as Figure E13-3.3)

(2) T_i = 339 K C_A_i = 0

(3) T_i = 344 K C_A_i = 2.26 kmol/m³

After 3 hours, the reaction is operating at steady state and all three trajectories converge on the final steady-state temperature of 331 K and the corresponding steady-state concentrations

$\begin{matrix} \begin{matrix} C_{A} = 0.658 kmol/ m^{3} C_{C} = 2.25 {kmol/m}^{3} \\ C_{B} = 34 kmol/ m^{3} C_{M} = 3.63 {kmol/m}^{3} \end{matrix} \\ T = 331.5 K \end{matrix}$

One can use the Wolfram sliders in the LEP for Example 13-3 to observe how the parameters change the trajectories as the temperature and concentration approach steady state.

For this reaction system, the plant safety office believes that an upper temperature limit of 355 K should not be exceeded in the tank. This temperature is the practical stability limit. The practical stability limit represents a temperature above which it is undesirable to operate because of unwanted side reactions, safety considerations, damage to equipment, or secondary runaway reactions, such as in the T2 Explosion. Consequently, we see that if we started at an initial temperature of

An illustration of the LEP slider is shown.

Oops! The practical stability limit was exceeded.

TABLE E13-3.1 POLYMATH PROGRAM FOR CSTR STARTUP

Differential equations

1 d(Ca)/d(t) = 1/tau*(Ca0-Ca)+ra

2 d(Cb)/d(t) = 1/tau*(Cb0-Cb)+rb

3 d(Cc)/d(t) = 1/tau*(0-Cc)+rc

4 d(Cm)/d(t) = 1/tau*(Cm0-Cm)

5 d(T)/d(t) = (Qg-Qr)/NCp

Explicit equations

1 Fa0 = 36.3

2 T0 = 297

3 V = 1.89

4 UA = 7262

5 dh = -20013

6 Ta1 = 288.7

7 k = 16.96e12*exp(-18012/1.987/(T))

8 Fb0 = 453.6

9 Fm0 = 45.4

10 mc = 453.6

11 ra = -k*Ca

12 rb = -k*Ca

13 rc = k*Ca

14 Nm = Cm*V

15 Na = Ca*V

16 Nb = Cb*V

17 Nc = Cc*V

18 ThetaCp = 35+Fb0/Fa0*18+Fm0/Fa0*19.5

19 v0 = Fa0/14.8+Fb0/55.3+Fm0/24.7

20 Ta2 = T-(T-Ta1)*exp(-UA/(18*mc))

21 Ca0 = Fa0/v0

22 Cb0 = Fb0/v0

23 Cm0 = Fm0/v0

24 Qr2 = mc*18*(Ta2-Ta1)

25 tau = V/v0

26 NCp = Na*35+Nb*18+Nc*46+Nm*19.5

27 Qr1 = Fa0*ThetaCp*(T-T0)

28 Qr = Qr1+Qr2

29 Qg = ra*V*dh

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	Ca	0	0.658258
2	Ca0	2.905559	2.905559
3	Cb	55.3	34.06019
4	Cb0	36.30749	36.30749
5	Cc	0	2.247301
6	Cm	0	3.63395
7	Cm0	3.63395	3.63395
8	dh	-2.001E+04	-2.001E+04
9	Fa0	36.3	36.3
10	Fb0	453.6	453.6
11	Fm0	45.4	45.4
12	k	0.9420055	22.56758
13	mc	453.6	453.6
14	Na	0	1.244108
15	Nb	104.517	64.37375
16	Nc	0	4.2474
17	NCp	1881.306	1531.581
18	Nm	0	6.868166
19	Qg	0	5.619E+05
20	Qr	3.992E+04	5.619E+05
21	Qr1	0	3.56E+05
22	Qr2	3.992E+04	2.059E+05
23	ra	0	-14.85529
24	rb	0	-14.85529
25	rc	0	14.85529
26	T	297.	331.4976
27	t	0	4.
28	T0	297.	297.
29	Ta1	288.7	288.7
30	Ta2	293.5896	313.9124
31	tau	0.1512812	0.1512812
32	ThetaCp	284.314	284.314
33	UA	7262.	7262.
34	V	1.89	1.89
35	v0	12.49329	12.49329

T_i = 344 K and an initial concentration of 2.26 kmol/m³, the practical stability limit of 355 K would be exceeded as the reactor approached its steady-state temperature of 331 K. See the concentration–temperature trajectory in Figure E13-3.4.

Figures E13-3.1 through E13-3.4 show the concentration and temperature–time trajectories for the start up of a CSTR for different initial conditions.

The reader is encouraged to use Wolfram to explore this problem to learn the answers to questions such as: (1) what parameter values lead to the greatest and smallest number of oscillations before steady state is reached (see Problem P13-1_B (c)).

Analysis: One of the purposes of this example was to demonstrate the use of phase plots, for example, T versus C_A, in analyzing CSTR startup. Phase plots allow us to see how the steady state is approached for different sets of initial conditions and if the practical stability limit is exceeded causing a secondary, more exothermic reaction to set in.

13.3.2 Semibatch Operation

Example 13–4 Heat Effects in a Semibatch Reactor

The second-order saponification of ethyl acetate is to be carried out in a semibatch reactor shown schematically in Figure E13-4.1.

$\begin{matrix} C_{2} H_{5} (C H_{3} C O O) (a q) + N a O H (a q) ⇆ N a (C H_{3} C O O) (a q) + C_{2} H_{5} OH(a q) \\ \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} A \end{matrix} & + \end{matrix} \end{matrix} & B \end{matrix} \end{matrix} & ⇆ \end{matrix} \end{matrix} & C \end{matrix} \end{matrix} & + \end{matrix} \end{matrix} & D \end{matrix} \end{matrix}$

Aqueous sodium hydroxide is to be fed at a concentration of 1 kmol/m³, a temperature of 300 K, and a volumetric rate of 0.004 m³/s to an initial volume of 0.2 m³ of water and ethyl acetate. The concentration of water in the feed, C_W0, is 55 kmol/m³. The initial concentrations of ethyl acetate and water in the reactor are 5 and 30.7 kmol/m³, respectively. The reaction is exothermic and it is necessary to add a heat exchanger to keep its temperature below 315 K. A super-shiny heat exchanger with UA = 3000 J/s · K obtained from the downtown Sunday markets in Riça, Jofostan, is available and ready for use. The coolant enters at a mass flow rate of 100 kg/s and a temperature of 285 K.

Are the heat exchanger and coolant flow rate adequate to keep the reactor temperature below 315 K?
Plot the reactor temperature, T, and the concentrations, C_A, C_B, and C_C as a function of time.

Additional information:³

³ Value for k from J. M. Smith, Chemical Engineering Kinetics, 3rd ed. New York: McGraw-Hill, 1981, p. 205. Note that ΔH_Rx and K_C were calculated from values given in Perry’s Chemical Engineers’ Handbook, 6th ed. New York: McGraw-Hill, 1984, pp. 3–147.

$k = 0.39175 \exp [5472.7 (\frac{1}{273} - \frac{1}{T} 1] m^{3} / kmol.s$

$K_{C} = 1 0^{3885.44 / T}$

$Δ H_{R x}^{o} = - 79, 076 k j / kmol/ k$

$C_{P_{A}} = 170.7 k j / k m o l / K = 170700 J / k m o 1 / K$

$C_{P_{B}} = C_{P_{C}} = C_{P_{D}} ≅ C_{P_{W}} = C_{P} = 75.24 k J / kmol \cdot k = 75246 J / k mol/K$

Feed: $C_{W 0} = 55 {kmol/m}^{3} C_{Bo} = 1.0 {kmol/m}^{3}$

Initially: $C_{W i} = 30.7 k m o l / m^{3} C_{A i} = 5 k m o l / m^{3} C_{Bi} = 0$

An illustration of the semibatch reactor. — **Figure E13-4.1** Semibatch reactor with heat exchange.

A diagram shows a square-shaped vessel with a stirrer. It is closed except for two circular openings at the top. The water and sodium hydroxide is fed from the top. The concentration of the mixtures fed through the inlet are C subscript W0 and C subscript B0. The initial concentrations of ethyl acetate, water, and sodium hydroxide inside the vessel are marked as C subscript W i, C subscript A i, and C subscript B i. The vessel is connected to an inductor. The mass flow m dot subscript c is constant, while the temperature T subscript a 1 become T subscript a 2 after the reaction.

Solution

1. Mole Balances: (See Chapter 6.)

$\begin{matrix} \frac{d C_{A}}{d t} = r_{A} - \frac{v_{0} C_{A}}{V} & (E13-4.1) \end{matrix}$

$\frac{d C_{B}}{d t} = r_{B} + \frac{v_{0} (C_{B 0} - C_{B})}{V} (E13-4.2)$

$\begin{matrix} \frac{d C_{C}}{d t} = r_{C} - \frac{C_{C} v_{0}}{V} & (E13-4.3) \end{matrix}$

C_D = >C_C

$\begin{matrix} \frac{d N_{W}}{d t} = C_{w_{0}} υ_{0} & (E13-4.4) \end{matrix}$

Initially, the number of moles of water in the reactor is, N_W_i,

N_Wi = V_iC_W0 = (0.2 m³)(30.7 kmol/m³) = 6.14 kmol

2. Rate Law:

$\begin{matrix} - r_{A} = k (C_{A} C_{B} - \frac{C_{C} C_{D}}{K_{C}}) & (E13.4.5) \end{matrix}$

3. Stoichiometry:

$\begin{matrix} - r_{A} = - r_{B} = r_{C} = r_{D} & (E13-4.6) \end{matrix}$

$\begin{matrix} N_{A} = C_{A} V & (E13-4.7) \end{matrix}$

$\begin{matrix} V = V_{0} + v_{0} t & (E13-4.8) \end{matrix}$

4. Energy Balance:

The user-friendly energy balance is

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g s} - {\dot{Q}}_{r s}}{Σ N_{i} C_{P_{i}}} & (13 - 20) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{g s} = (r_{A} V) (Δ H_{Rx}) & (13 - 21) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{r s} = \sum F_{i 0} C_{P_{i}} (T - T_{i 0}) + {\dot{m}}_{c} C_{P_{W}} [T - T_{a 1}] [1 - \exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{W}}})] & (13-22) \end{matrix}$

Only species B (NaOH) and water flow into the reactor, so Equation (13-22) becomes

$\begin{matrix} {\dot{Q}}_{r s} = \overset{{\dot{Q}}_{r s 1}}{\overset{⏞}{(F_{B 0} C_{P_{B}} + F_{w} C_{Pw}) (T - T_{0})} +} \overset{{\dot{Q}}_{r s 2}}{\overset{⏞}{{\dot{m}}_{c} C_{P_{w}} [T - T_{a 1}] [1 - exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{w}}})]}} & (E13-4.9) \end{matrix}$

${\dot{Q}}_{r s 1}$ is the heat removed by mass flow, and ${\dot{Q}}_{r s 2}$ is the heat removed through heat exchange.

An illustration depicts footsteps, and represents the phrase "following the algorithm".

TABLE E13-4.1 POLYMATH PROGRAM AND OUTPUT FOR SEMIBATCH REACTOR

Differential equations

1 d(Ca)/d(t) = ra-(v0*Ca)/V

2 d(Cb)/d(t) = rb+(v0*(Cb0-Cb)/V)

3 d(Cc)/d(t) = rc-(Cc*v0)/V

4 d(T)/d(t) = (Qg-Qr)/NCp

5 d(Nw)/d(t) = v0*Cw0

Explicit equations

1 v0 = 0.004

2 Cb0 = 1

3 UA = 3000

4 cp = 75240

5 T0 = 300

6 dh = -7.9076e7

7 Cw0 = 55

8 k = 0.39175*exp(5472.7*((1/273)-(1/T)))

9 Cd = Cc

10 Vi = 0.2

11 Kc = 10^(3885.44/T)

12 cpa = 170700

13 V = Vi+v0*t

14 Fb0 = Cb0*v0

15 ra = -k*((Ca*Cb)-((Cc*Cd)/Kc))

16 Na = V*Ca

17 Nb = V*Cb

18 Fw = Cw0*v0

19 Nc = V*Cc

20 rb = ra

21 rc = -ra

22 Qr1 = ((Fb0*cp) + (Fw*cp))*(T - T0)

23 Nd = V*Cd

24 rate = -ra

25 NCp = cp*(Nb+Nc+Nd+Nw)+cpa*Na

26 Cpc = 18

27 Ta1 = 285

28 mc = 100

29 Qr2 = mc*Cpw*(T-Ta1)*(1-exp(-UA/mc/Cpw))

30 Ta2 = T-(T-Ta1)*exp(-UA/mc/Cpw)

31 Qr = Qr1 + Qr2

32 Qg = ra*V*dh

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	Ca	5.	3.981E-13
2	Cb	0	0.2682927
3	Cb0	1.	1.
4	Cc	0	0.6097561
5	Cd	0	0.6097561
6	Cp	7.524E+04	7.524E+04
7	cpa	1.707E+05	1.707E+05
8	Cpc	18.	18.
9	Cw0	55.	55.
10	dh	-7.908E+07	-7.908E+07
11	Fb0	0.004	0.004
12	Fw	0.22	0.22
13	k	2.379893	4.211077
14	Kc	8.943E+12	3.518E+12
15	mc	100.	100.
16	Na	1.	6.529E-13
17	Nb	0	0.44
18	Nc	0	1.
19	NCp	6.327E+05	6.605E+06
20	Nd	0	1.
21	Nw	6.14	85.34
22	Qg	0	6.19E-07
23	Qr	2.19E+04	1.993E+05
24	Qr1	0	1.633E+05
25	Qr2	2.19E+04	3.604E+04
26	ra	0	-4.773E-15
27	rate	0	4.773E-15
28	rb	0	-4.773E-15
29	rc	0	4.773E-15
30	t	0	360.
31	T	300.	309.6878
32	T0	300.	300.
33	Ta1	285.	285.
34	Ta2	297.1669	305.0248
35	UA	3000.	3000.
36	V	0.2	1.64
37	v0	0.004	0.004
38	Vi	0.2	0.2

In Jofostan we have the added bonus that we can ask Prof. Dr. Sven Köttlov to calculate the temperature of the heat-exchange fluid at its exit using Equation (12-17)

$\begin{matrix} T_{a 2} = T - (T - T_{a 1}) exp [\frac{- U A}{{\dot{m}}_{c} C_{P_{w}}}] & (12 - 17) \end{matrix}$

#AddedBonus

5. Evaluation of Parameters:

$F_{B 0} = ν_{0} C_{B 0} = (0.004 \frac{m^{3}}{s}) (1 \frac{k m o l}{m^{3}}) = 0.004 \frac{k m o l}{s},$

$F_{w} = ν_{0} C_{w} = (0.004 \frac{m^{3}}{s}) (55 \frac{k m o l}{m^{3}}) = 0.220 \frac{k m o l}{s}$

$C_{P_{A}} = 170700 J / k m o l / K, C_{P} = 75246 J / k m o l / K$

We note the heat capacities for B, C, and water are essentially the same at C_P

NC_P = C_{P_A}N_A + C_P (N_B + N_C + N_D + N_W)

The Polymath program is given in Table E13-4.1, and the graphical output of the Polymath program—given in terms of temperatures T and T_a and concentrations (C_A, C_B, and C_C)—are shown in Figures E13-4.2 and E13-4.3.

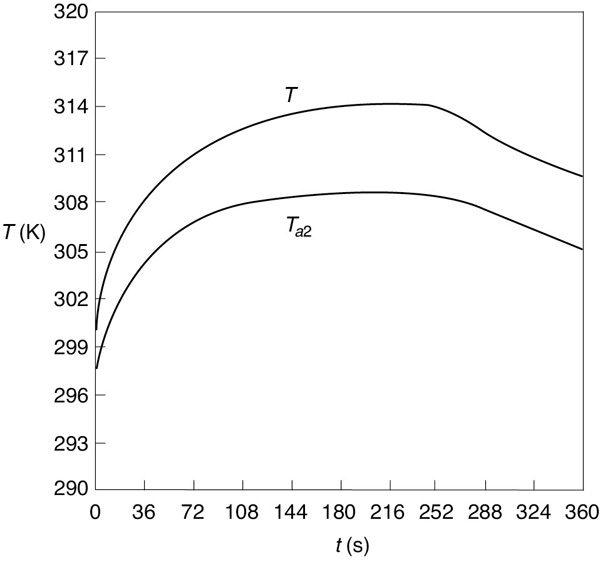
A temperature versus time graph for a semibatch reactor. — **Figure E13-4.2** Temperature–time trajectories in a semibatch reactor.

A graph plots temperature in a semibatch reactor as a function of time. The horizontal axis represents time (in seconds), ranging from 0 to 360 in increments of 36. The vertical axis represents temperature, ranging from 290 to 320, in increments of 3. The T curve increases from 300 to 314 Kelvin in 252 seconds, and decreases to 311 Kelvin in 360 seconds. The T subscript a2 curve increases from 295 Kelvin to 307 Kelvin in 288 seconds, and decreases to 305 Kelvin in 360 seconds. The mentioned values are approximate.

A graph plots the concentration for a time duration in a semi-batch reactor. — **Figure E13-4.3** Concentration–time trajectories in a semibatch reactor.

In the graph, the horizontal axis represents time, and is marked from 0 to 360 in increments of 36. The vertical axis represents concentration, and is marked from 0 to 5, in increments of 0.5. The Cc curve increases from 0 to 0.75 (Kmol/m3) at 260 seconds, and decreases to 0.5 (Kmol/m3) at 360 seconds. The Ca curve decreases from 5.0 (Kmol/m3) to 0 (Kmol/m3) at 252 seconds. The Cb curve increases to 0.25 (Kmol/m3) at 360 seconds.

Wrong Reactor Choice!

Analysis: From Figure E13-4.3 we see that the concentration of species B is essentially zero, owing to the fact that it is consumed virtually as fast as it enters the reactor up to a time of 252 seconds. By the time we reach 252 seconds, all species A has been consumed, and the reaction rate is virtually zero and no more of species C or D is produced and no more B is consumed. Because species B continues to enter the reactor at a volumetric flow rate ν₀, after 252 seconds, the fluid volume continues to increase and the concentrations of C and D are diluted. The figure shows that before 252 seconds, $({\dot{Q}}_{g s} > {\dot{Q}}_{r s})$ , both the reactor temperature and the coolant temperature increase. However, after 252 seconds, the reaction rate, and hence ${\dot{Q}}_{r s}$ , are virtually zero so that $({\dot{Q}}_{g s} > {\dot{Q}}_{r s})$ and the temperature decreases. Because of the impractical short reaction time (252 seconds), a semibatch reactor would never be used for this reaction at this temperature; instead, we would most likely use a CSTR or PFR. See Problem P13-1_B (d) to reflect on this example.

A figure representing LEP sliders is shown. Sliders are represented as squares on horizontal lines.

A real-life LEP example of the Synthron Runaway Reaction in a semibatch reactor is given in the Additional Material on the CRE Web site (http://www.umich.edu/~elements/6e/13chap/obj.html#/additional-materials/) and also on the Safety Web site (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344ReactionEngrModule(2)PS-Monsanto.pdf ).

13.4 Nonisothermal Multiple Reactions

For q multiple reactions with m species occurring in either a semibatch or batch reactor, Equation (13-9) can be generalized in the same manner as the steady-state energy balance to give

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{m}}_{c} C_{P_{c}} (T_{a 1} - T) [1 - exp (- U A / {\dot{m}}_{c} C_{P_{c}})] + Σ_{i = 1}^{q} r_{i j} V Δ H_{Rx i j (T)} - Σ_{j = 1}^{m} F_{j 0} C_{P_{j}} (T - T_{0})}{Σ_{j = 1}^{m} N_{j 0} C_{P_{j}}} & (13 -24) \end{matrix}$

For large coolant flow rates (i.e., ṁ_c), Equation (13-24) becomes

$\begin{matrix} \frac{d T}{d t} = \frac{V Σ_{i = 1}^{q} r_{i j} Δ H_{Rx i j} - U A (T - T_{a}) Σ_{j = 1}^{m} F_{j 0} C_{P_{j}} (T - T_{0})}{Σ_{j = 1}^{m} N_{j} C_{P_{j}}} & (13 -25) \end{matrix}$

Rearranging Equation (13-25) and letting

$\begin{matrix} {\dot{Q}}_{g} = V Σ_{i = 1}^{q} r_{i j} Δ H_{Rx i j} & (13 -26) \end{matrix}$

and

$\begin{matrix} {\dot{Q}}_{r} = U A (T - T_{a}) + Σ F_{j 0} C_{P_{j}} (T - T_{0}) & (13 -27) \end{matrix}$

we can write Equation (13-25) in a more compact form

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g} - {\dot{Q}}_{r}}{Σ_{j = 1}^{m} N_{j} C_{P_{j}}} & (13 -28) \end{matrix}$

One exothermic reaction and one endothermic reaction! Will the temperature increase or decrease?

Example 13–5 Multiple Reactions in a Semibatch Reactor

The series reactions

$2 A \underset{(1)}{\overset{k_{1 A}}{\to}} B \underset{(2)}{\overset{k_{2 B}}{\to}} 3 C$

are catalyzed by H₂SO₄. All reactions are first order in the reactant concentration. However, Reaction (1) is exothermic and Reaction (2) is endothermic. The reaction is to be carried out in a semibatch reactor that has a heat exchanger inside with UA = 35000 cal/h · K and a constant exchanger temperature, T_a, of 298 K. Pure A enters at a concentration of 4 mol/dm³, a volumetric flow rate of 240 dm³/h, and a temperature of 305 K. Initially, there is a total of 100 dm³ of liquid in the reactor, which contains 1.0 mol/dm³ of A and 1.0 mol/dm³ of the catalyst H₂SO₄. The reaction rate is independent of the catalyst concentration. The initial temperature inside the reactor is 290 K.

Plot and analyze the species concentrations and reactor temperature as a function of time.
Analyze the results in (a) and comment on any maximums or minimums in the trajectories.

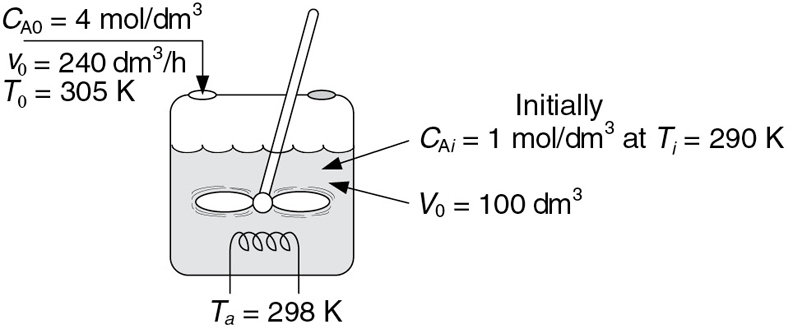
An illustration of semi-batch reactor is shown. — An image shows a semi-batch reactor with heater that maintains constant temperature T a at 298 K. The fluid or species A enters the reactor at a concentration of 4 mol per decimeter cubed, with a volumetric flow rate of 240 decimeter cubed per hour, and a temperature of 305 Kelvin. Initially, there is a total of 100 decimeter cubed of liquid in the reactor, which contains 1.0 mol per decimeter cubed of A at a temperature of 290 K and 1.0 mol per decimeter cubed.

Additional information:

$\begin{matrix} \begin{matrix} k_{1 A} = 1.25 h^{- 1} at 320 K with E_{1 A} = 9500 cal/mol & {\begin{matrix} C_{P} \end{matrix}}_{A} = 30 cal/mol \cdot K \end{matrix} \\ \begin{matrix} k_{2 B} = 0.08 h^{- 1} at 300 K with E_{2 B} = 7000 cal/mol & {\begin{matrix} C_{P} \end{matrix}}_{B} = 60 cal/mol \cdot K \end{matrix} \end{matrix}$

$\begin{matrix} Δ H_{Rx1A} = - 6500 cal/mol A & C_{P_{C}} = 20 cal/mol \cdot K \\ Δ H_{Rx2B} = + 8000 cal/mol B & C_{P_{H_{2} {SO}_{4}}} = 35 cal/mol \cdot K \end{matrix}$

Solution

Reaction (1) $2 A \to B$

Reaction (2) $B \to 3 C$

1. Mole Balances:

$\begin{matrix} \frac{d C_{A}}{d t} = r_{A} + \frac{(C_{A 0} - C_{A})}{V} v_{0} & (E13-5-1) \end{matrix}$

$\begin{matrix} \frac{d C_{B}}{d t} = r_{B} - \frac{C_{B}}{V} v_{0} & (E13-5.2) \end{matrix}$

$\begin{matrix} \frac{d C_{c}}{d t} = r_{c} - \frac{C_{c}}{V} v_{0} & (E13-5.3) \end{matrix}$

2. Rates:

(a) Rate Laws:

$\begin{matrix} - r_{1 A} = k_{1 A} C_{A} & (E13-5.4) \end{matrix}$

$\begin{matrix} - r_{2 B} = k_{2 B} C_{B} & (E13-5.5) \end{matrix}$

(b) Relative Rates:

$\begin{matrix} r_{1 B} = - \frac{1}{2} r_{1 A} & (E13-5.6) \end{matrix}$

$\begin{matrix} r_{2 C} = - 3 r_{2 B} & (E13-5.7) \end{matrix}$

(c) Net Rates:

$\begin{matrix} r_{A} = r_{1 A} = - k_{1 A} C_{A} & (E13-5.8) \end{matrix}$

$\begin{matrix} r_{B} = r_{1 B} + r_{2 B} = \frac{- r_{1 A}}{2} + r_{2 B} = \frac{k_{1 A} C_{A}}{2} - k_{2 B} C_{B} & (E13-5.9) \end{matrix}$

$\begin{matrix} r_{C} = 3 k_{2 B} C_{B} & (E13-5.10) \end{matrix}$

3. Stoichiometry (liquid phase): Use C_A, C_B, C_C

$\begin{matrix} N_{i} = C_{i} V & E13-5.11) \end{matrix}$

$\begin{matrix} V = V_{0} + v_{0} t & (E13-5.12) \end{matrix}$

H₂SO₄ already in the tank

$N_{H_{2} S O_{4}} = (C_{H_{2} S O_{4, 0}}) V_{0} = \frac{1 m o 1}{d m^{3}} \times 100 d m^{3} = 100 mol$

Only A enters the tank

$F_{A 0} = C_{A 0} v_{0} = \frac{4 m o 1}{d m^{3}} \times 240 \frac{d m^{3}}{h} = 960 \frac{m o 1}{h}$

An illustration depicts footsteps, and represents the phrase "following the algorithm".

4. Energy Balance:

A slight rearrangement of (13-25) for this semibatch reactor gives

$\begin{matrix} \frac{d T}{d t} = \frac{UA (T_{a} - T) - Σ F_{j 0} C_{P_{j}} (T - T_{0}) + V \underset{i = 1}{\overset{q}{Σ}} Δ H_{Rxij} r_{i j}}{\underset{j = 1}{\overset{m}{Σ}} N_{j} C_{P_{j}}} & (E13-5.13) \end{matrix}$

Expanding

$\begin{matrix} \frac{d T}{d t} = \frac{UA (T_{a} - T) - F_{A 0} C_{P_{A}} (T - T_{0}) + [(Δ H_{Rx1A}) (r_{1 A}) + (Δ H_{Rx2B}) (r_{2 B})] V}{[C_{A} C_{P_{A}} + C_{B} C_{P_{B}} + C_{C} C_{P_{C}}] V + N_{H_{2^{{so}_{4}}}} C_{P_{H_{2^{{so}_{4}}}}}} & (13-5.14) \end{matrix}$

Substituting the parameter values into Equation (E13-5.14)

$\begin{matrix} \frac{d T}{d t} = \frac{35000 (298 - T) - (4) (240) (30) (T - 305) + [(- 6500) + (- k_{1 A} C_{A}) + (+ 8000) (- k_{2 B} C_{B})] V}{(30 C_{A} + 60 C_{B} + 20 C_{C}) (100 + 240 t) + (100) (35)} & (E13-5.15) \end{matrix}$

Equations (E13-5.1)–(E13-5.3) and (E13-5.8)–(E13-5.12) can be solved simultaneously with Equation (E13-5.14) using an ODE solver. The Polymath program is shown in Table E13-5.1. The concentration–time and temperature–time trajectories are shown in Figures E13-5.1 and E13-5.2.

TABLE E13-5.1 POLYMATH PROGRAM FOR STARTUP OF A CSTR

Differential equations

1 d(Ca)/d(t) = ra+(Ca0-Ca)*vo/V

2 d(Cb)/d(t) = rb-Cb*vo/V

3 d(Cc)/d(t) = rc-Cc*vo/V

4 d(T)/d(t) = (Qg-Qr)/((Ca*30+Cb*60+Cc*20)*V+100*35

Explicit equations

1 UA = 35000

2 dHrx1 = -6500

3 dHrx2 = 8000

4 vo = 240

5 V = 100+vo*t

6 Cao = 4

7 Qr = UA*(T-298) + Cao*vo*30*(T-305)

8 k1a = 1.25*exp((9500/1.987)*(1/320-1/T))

9 k2b = 0.08*exp((7000/1.987)*(1/300-1/T))

10 ra = -k1a*Ca

11 Qg = (dHrx1*(-k1a*Ca)+dHrx2*(-k2b*Cb))*V

12 rc = 3*k2b*Cb

13 rb = k1a*Cb/2-k2b*Cb

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	Ca	1.	0.2165095
2	Cao	4.	4.
3	Cb	0	0.8114253
4	Cc	0	2.262699
5	dHrx1	-6500.	-6500.
6	dHrx2	8000.	8000.
7	k1a	0.2664781	9.133834
8	k2b	0.0533618	0.7215678
9	Qg	1.732E+05	3.758E+06
10	Qr	-7.12E+05	4.337E+06
11	ra	-0.2664781	-1.977562
12	rb	0.133239	0.4032827
13	rc	0	1.756495
14	t	0	1.5
15	T	290.	369.1375
16	UA	3.5E+04	3.5E+04
17	V	100.	460.
18	vo	240.	240.

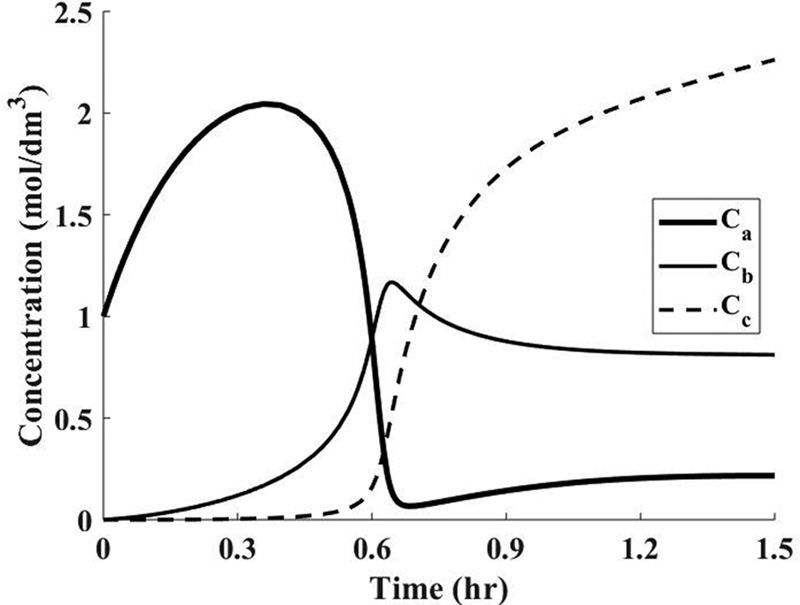
A graph plots concentration against time. — **Figure E13-5.1** Concentration–time.

In the graph, the horizontal axis represents time, and is marked from 0 to 1.5 hours in increments of 0.3. The vertical axis represents concentration, and is marked from 0 to 2.5, in increments of 3. The C a curve increases from 1 to 2 (mol per decimeter cubed) at 0.4 hours, and decreases to 0.1 (mol per decimeter cubed) at 0.65 hours, and steadily raises to 0.25(mol per decimeter cubed) at 1.5 hours. The C b curve exponentially increases from 0 to 1.10 at 0.65 hours and then settles on 0.9 at 1.5 hours. The C c curve is at 0 till 0.56 hours and increases exponentially to 1.75 at 0.8 hours and then slowly increases to 2.25 at 1.5 hours.

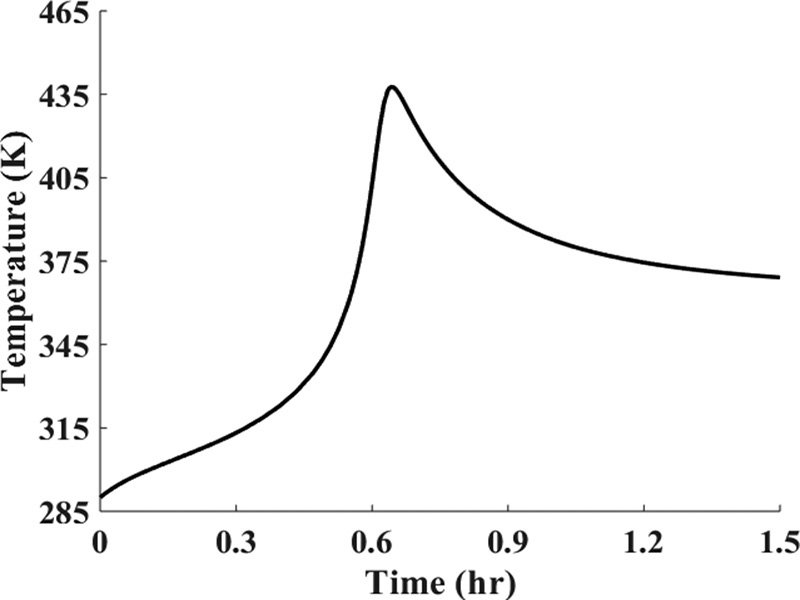
A graph plots temperature against time. — **Figure E13-5.2** Temperature (K)–time (h)

In the graph, the horizontal axis represents time, and is marked from 0 to 1.5 hours in increments of 0.3. The vertical axis represents temperature, and is marked from 285 to 465, in increments of 30. The curve increases from 285 to 436 Kelvin at 0.63 hours, and decreases to 375 Kelvin at 1.5 hours.

Analysis: At the start of the reaction, both C_A and T in the reactor increase because the feed concentrations of C_A0 (4M) and T₀ (305 K) are greater than the initial settings of C_A_i (1 M) and T_i (290 K). This increase continues until the rate of consumption of the reacting species, (–r_AV), is greater than the feed rate to the reactor, F_A0. We note that at about t = 0.2 hours, the reactor temperature exceeds the feed temperature (i.e., 305 K) as a result of the heat generated by the exothermic reaction (Reaction 1). The temperature continues to rise until about t = 0.6 hours, at which point reactant A is virtually all consumed. After this point the temperature begins to drop for two reasons: (1) the reactor is cooled by the heat exchanger and (2) heat is absorbed by the endothermic reaction rate (Reaction 2). The question is, does the maximum temperature (437 K) exceed a temperature that is too high, resulting in a high vapor pressure that then results in evaporation losses or causes a highly exothermic secondary reaction to set in?

Example 13–6 T2 Laboratories Explosion⁴

⁴ This example was coauthored by Professors Ronald J. Willey, Northeastern University, Michael B. Cutlip, University of Connecticut, and H. Scott Fogler, University of Michigan, and published in Process Safety Progress, 30, 1 (2011).

A pictures shows the aftermath of a deadly explosion at T2 laboratories. Debris can be found through out the picture, all covered with ashes. — **Figure E13-6.1** Aerial photograph of T2 taken December 20, 2007. (Courtesy of Chemical Safety Board.)

The aftermath of a deadly explosion at T2 Laboratories is shown in Figure E13-6.1. T2 Laboratories manufactured a fuel additive, methylcyclopentadienyl manganese tricarbonyl (MCMT), in a 2450-gal, high-pressure batch reactor utilizing a three-step batch process. (See http://umich.edu/~safeche/assets/pdf/courses/CRE/344ReactionEngrModule(1)PS-T2.pdf.)

Step 1a. The liquid-phase metalation reaction between methylcyclopentadiene (MCP) and sodium in a solvent of diethylene glycol dimethyl ether (diglyme) to produce sodium methylcyclopentadiene and hydrogen gas is

A chemical reaction shows a 5-membered cyclic diene compound with an alkyl group, undergo metallation. On the addition of sodium, in the presence of diglyme, sodium methylcyclopentadiene is formed with the liberation of hydrogen gas.

Hydrogen immediately comes out of the solution and is vented at the top into the gas head space and then out of the system.

Step 1b. At the end of Step 1a, MnCl₂ is added. The substitution reaction between sodium methylcyclopentadiene and manganese chloride that produced manganese dimethylcyclopentadiene and sodium chloride is

A chemical reaction shows the reaction of sodium methylcyclopentadiene with MnCl2. — The sodium methylcyclopentadiene is a 5-membered cyclic diene compound with sodium. On addition of Manganese chloride, The Mn combines 2 molecules of methylcyclopentadiene to form Manganesedimethylcyclopentadiene and the chlorine combines with sodium to form salt.

Step 1c. At the end of Step 1b, CO is added. The carbonylation reaction between manganese dimethylcyclopentadiene and carbon monoxide produces the final product, methylcyclopentadienyl manganese tricarbonyl (MCMT):

A carbonyl reaction of Manganese dimethylcyclopentadiene is shown. 3 molecules of carbon monoxide attach with the manganese liberating a molecule of cyclopentadiene. The compound is named methylcyclopentadienyl manganese tricarbonyl.

We will only consider Step 1a as this step is the one in which the explosion occurred.

Procedure

First, solid sodium is mixed in the batch reactor with methylcyclopentadiene dimer and a solvent diethylene glycol dimethyl ether (diglyme). The batch reactor is then heated to about 422 K (300°F) with only slight reaction occurring during this heating process. On reaching 422 K, the heating is turned off, as the exothermic reaction is now proceeding, and the temperature continues to increase without further heating. When the temperature reaches 455.4 K (360°F), the operator initiates cooling using the evaporation of boiling water in the reactor jacket as the heat sink (T_a = 373.15 K; 212°F).

Before reading further it might be helpful to view the Chemical Safety Board (CSB) video of the accident (http://umich.edu/~safeche/courses/ChemicalReactionEngineering.html).

It’s a really good video.

What Happened

On December 19, 2007, when the reactor reached a temperature of 455.4 K (360°F), the process operator could not initiate the flow of cooling water to the cooling jacket shown in Figure E13-6.2. Thus, the expected cooling of the reactor was not available and the temperature in the reactor continued to rise. The pressure also increased as hydrogen continued to be produced at an increased rate, to the point that the reactor’s pressure control valve system on the 1-in. diameter hydrogen venting stream could no longer vent the gas and maintain the operating pressure at 50 psig (4.4 atm). As the temperature continued to increase further, a previously unknown exothermic secondary reaction of the decomposition of diglyme solvent, also catalyzed by sodium, accelerated rapidly.

$\begin{matrix} {CH}_{3} - O - {CH}_{2} - O - {CH}_{2} O - {CH}_{3} \underset{Na}{\to} 3 H_{2} + misc (1) & (s) & (D) \end{matrix}$

An illustration shows a full reactor. — **Figure E13-6.2** Reactor.

In the full reactor, the cooling jacket water inlet gives water for cooling the reactor and outlet is placed at the right side of reactor. The gas head space has a filling port at the left side and it has the vent with pressure control valve on the right side through which H2 is let out.

This reaction produced even more hydrogen, causing the pressure to rise even faster, eventually causing the rupture disk which was set at 28.2 atm absolute (400 psig), to break, in the 4-in. diameter relief line for H₂. Even with the relief line open, the rate of production of H₂ was now far greater than the rate of venting, causing the pressure to continue to increase to the point that it ruptured the reactor vessel initiating a horrific explosion. The T2 plant was completely leveled and four personnel lives were lost. Surrounding businesses were heavily damaged and additional injuries were sustained.

I would like to emphasize again, before continuing with this example, it might be helpful to view the 9-minute Chemical Safety Board (CSB) video, which you can access directly from the CRE Web site (under YouTube videos), or you can read the supporting reports (http://www.csb.gov/videos/runaway-explosion-at-t2-laboratories/). Also review the T2 Laboratores Safety Modules (http://umich.edu/~safeche/assets/pdf/courses/Problems/344ReactionEngineeringModule(2)PS050818.pdf ).

Simplified Model

Summarizing the important reactions for Step 1

A reaction shows the compound methylcyclopentadiene react with the sodium metal. This leads to the formation of sodium methylcyclopentadiene and the liberation of hydrogen gas.

$\begin{matrix} {CH}_{3} - O - {CH}_{2} - {CH}_{2} - O- {CH}_{2} - {CH}_{2} O - {CH}_{3} \underset{Na}{\to} 3 H_{2} + misc (1) & (s) & (Reaction 2) \end{matrix}$

Let A = methylcyclopentadiene, B = sodium, S = solvent (diglyme), and D = H₂.

This runaway reaction can be approximately modeled with two reactions. These reactions are

(1) A + B → C + 1/2 D (gas)	(Reaction 1)
(2) S → 3 D (gas) + miscellaneous liquid and solid products	(Reaction 2)

Rate laws

In Reaction (1), A and B react to form products. Reaction (2) represents the decomposition of the liquid-phase solvent diglyme, S, catalyzed by the presence of B, but this reaction only begins to proceed once a temperature of approximately 470 K is reached. The fact that the solvent diglyme would decompose and also explode was unknown to the plant personnel. If they had researched this reaction system using an ARSST (see Chapter 13 Professional Reference Shelf), they might have seen the potential danger.

The rate laws, along with the specific reaction-rate constants at the initial temperature of 422 K, are

$\begin{matrix} - r_{1 A} = & k_{1 A} C_{A} C_{B} \\ A_{l A} = 5.73 \times 1 0^{2} d m^{3} m o l^{- 1} h r^{- 1} with E_{l A} = 128 000 J / m o l K \end{matrix}$

$\begin{matrix} - r_{2 S} = & k_{2 S} C_{S} \\ A_{2 S} = 9.41 \times 1 0^{16} h r^{- 1} with E_{2 S} = 800000 J / m o l K \end{matrix}$

The heats of reaction are constant.

ΔH_Rx1A = –45400 J/mol

ΔH_Rx2S = –320000 J/mol

The sum of products of the moles of each species and their corresponding heat capacities in the denominator of Equation (13-12) is essentially constant at

ΣN_jC_{P_j} = 1.26 × 10⁷ J/K

Assumptions

Assume that the liquid volume, V₀, in the reactor remains constant at 4000 dm³ and that the vapor space, V_H, above the reactor occupies 5000 dm³. Any gas, H₂ (i.e., D), that is formed by Reactions (1) and (2) immediately appears as an input stream F_D to the head-space volume. The dissolved H₂ and the vapor pressures for the liquid components in the reactor will be neglected. The initial absolute pressure within the reactor is 4.4 atm (50 psig). During normal operation, the H₂ generated obeys the ideal gas law. The pressure control system on the H₂ vent stream maintains the pressure, P, at 4.40 atm up to a flow of 11400 mol/hr. The reactor vessel will fail when the pressure exceeds 45 atm or the temperature exceeds 600 K.

Additional information:

UA = 2.77 x 10⁶ J hr^–1 K^–1. The concentrations in the reactor at the end of the reactor heating at 422 K are C_A0 = 4.3 mol/dm³, C_B0 = 5.1 mol/dm³, C_I0 = 0.088 mol/dm³, and C_S0 = 3 mol/dm³. The sensible heat of the two gas venting streams may be neglected.

Problem Statement

Plot the reactor temperature, the reactant concentrations, and the head-space pressure as a funciton of time for the case when the reactor cooling fails to work (i.e., UA = 0).
In Problem P13-1_B (f), you will be asked to redo the problem when the cooling water comes as expected whenever the reactor temperature exceeds 455 K.
Analyze your results and explain why the trajectories look the way they do, for example, sudden increases in temperature and pressure.

Solution Procedure Overview

We will carry out a two-step procedure of our CRE algorithm by adding a mole balance on the reactor head space in order to determine the pressure in the reactor as a function of time. (1) In step 1, we will use the usual mole balance step, coupled with rate laws, stoichiometry, and energy balances to determine the rate of H₂ generation. Because there is no accumulation of H₂ in the reactor, H₂ flows out of the reactor into the head space. (2) In step 2, we perform a mole balance on the head space to determine the pressure in the head space and reactor. The remaining steps are part of our CRE algorithm that will allow us to determine temperature, concentration, and pressure as a function of time.

Step (1) Reactor Mole Balances:

Reactor (Assume Constant-Volume Batch)

Liquid

$\begin{matrix} \frac{d C_{A}}{d t} = r_{1 A} & (E13-6.1) \end{matrix}$

$\begin{matrix} \frac{d C_{B}}{d t} = r_{1 A} & (E13-6.2) \end{matrix}$

$\begin{matrix} \frac{d C_{s}}{d t} = r_{2 S} & (E13-6.3) \end{matrix}$

Step (2) Head-Space Mole Balance:

Let N_D = moles of gas D (i.e., H₂) in the reactor vapor space V_V. The flows in and out of the head space are shown in the figure below.

A balance on species D (H₂) in the head-space volume V_H yields

Accum = In − Out

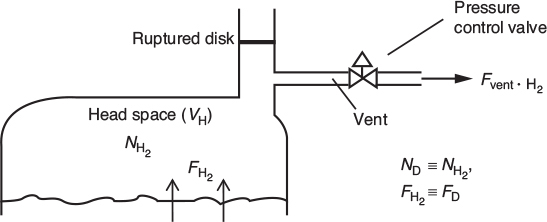
An illustration depicts adding mole balance to reactor head space. — A reactor with ruptured disk is shown. The direction of flow rate, F subscript H2 is shown from bottom to head space. N subscript H2 (moles) is marked near the head space. A vent is present on the right and a pressure control valve is present adjacent to it. The output flow rate through vent is shown as F subscript vent dot H2.

$\begin{matrix} \frac{d N_{D}}{d t} = F_{D} - F_{v e n t} & (E13-6.4) \end{matrix}$

where F_vent is the molar flow rate of gas out of the head space through one or both outlet lines, and F_D (i.e., F₂) is the molar rate of gas leaving the liquid and entering the head space and is equal to the hydrogen generated in the liquid (see relative rates and net rates in the algorithm where V₀ is the liquid reactor volume).

$\begin{matrix} F_{D} = [(- 0.5 r_{1 A}) + (- 3 r_{2 S})] V_{0} & (E13-6.5) \end{matrix}$

The assumptions of a perfect gas in the head-space volume and modest changes in T allow Equation (E13-6.4) to be written in terms of total gas pressure in the reactor head space

$\begin{matrix} N_{D} = N_{H} = \frac{P V_{H}}{R T_{H}} & (E13-6.6) \end{matrix}$

Substituting for N_D in Equation (E13-6.3) and rearranging

$\begin{matrix} \frac{d P}{d t} = (F_{D} - F_{vent}) \frac{R T_{H}}{V_{H}} & (E13-6.7) \end{matrix}$

(3) How the Venting Works:

Gas exits the reactor through the pressure control valve line. At low gas production rates, the pressure control valve maintains set-point pressure at the initial pressure by venting all produced gas until the rate of gas production reaches 11400 mol/hr.

$\begin{matrix} F_{v e n t} = F_{D} when F_{D} < 11, 400 & (E13-6.8) \end{matrix}$

Just a little help in calculating the flow rate of H₂ out the vent.

We now need to know a little more about the venting system for H₂ and the condition for flow out of the vent. As the pressure increases, but is still below the rupture disk setting, the pressure control line vents to the atmosphere (1 atm) according to the equation

$\begin{matrix} F_{vent} = Δ P C_{v 1} = (P - 1) C_{v 1} when P < 28.2 atm & (E13-6.9) \end{matrix}$

where P is the absolute pressure in the reactor (atm), 1 atm is the downstream pressure (atmospheric), and the pressure control correlation constant is 3360 mol/hr · atm. If the pressure P within the reactor exceeds 28.2 atm (400 psig), the relief line activated by the rupture disk breaks and vents gas in the reactor at the rate given F_vent = (P=1)C_v₂ where C_v₂ = 53600 mol/atm · h.

After the rupture disk blowout at P = 28.2 atm, both the pressure control line and the rupture disk lines vent the reactor according to the equation

$\begin{matrix} F_{vent} = (P - 1) (C_{v 1} + C_{v 2}) & (E13-6.10) \end{matrix}$

Equations (E13-6.7)–(E13-6.10) can then be used to describe the F_vent flow rate with time for the appropriate logic for the values of F_D and P.

(4) Rates:

Laws:

(1) $\begin{matrix} - r_{1 A} = k_{l A} C_{A} C_{B} & (E13-6.11) \end{matrix}$

$\begin{matrix} k_{l A} = A_{l A} e^{- E_{l A} / R T} & (E13-6.12) \end{matrix}$

(2) $\begin{matrix} - r_{2 S} = k_{2 S} C_{S} & (E13-6.13) \end{matrix}$

$\begin{matrix} k_{2 S} = A_{2 S} e^{- E_{2 S} / R T} & (E13-6.14) \end{matrix}$

Relative Rates:

(1) $\begin{matrix} \frac{r_{1 A}}{- 1} = \frac{r_{1 B}}{- 1} = \frac{r_{1 C}}{1} = \frac{r_{1 D}}{1 / 2} & (13-6.15) \end{matrix}$

(2) $\begin{matrix} \frac{r_{2 S}}{- 1} = \frac{r_{2 D}}{3} & (E13-6.16) \end{matrix}$

Net Rates:

$\begin{matrix} r_{A} = r_{B} = r_{1 A} & (E13-6.17) \end{matrix}$

$\begin{matrix} r_{s} = r_{2 S} & (13-6.18) \end{matrix}$

$\begin{matrix} r_{D} = - \frac{1}{2} r_{1 A} + - 3 r_{2 S} (gas generated) & (E13-6.19) \end{matrix}$

(5) Stoichiometry:

Neglect reactor-liquid volume change form loss of product gases.

$\begin{matrix} C_{A} = \frac{N_{A}}{V_{0}} & (13-6.20) \end{matrix}$

$\begin{matrix} C_{B} = \frac{N_{B}}{V_{0}} & (13-6.21) \end{matrix}$

$\begin{matrix} C_{s} = \frac{N_{s}}{V_{0}} & (E13-6.22) \end{matrix}$

$\begin{matrix} C_{D} = \frac{P}{R T} & (E13-6.23) \end{matrix}$

(6) Energy Balance:

The batch reactor energy balance is

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{Σ N_{j} C_{P_{j}}} & (E13-6.24) \end{matrix}$

The heat generated, ${\dot{Q}}_{g b}$ , and the heated removed, ${\dot{Q}}_{r b}$ , terms are

$\begin{matrix} {\dot{Q}}_{g b} = V_{0} [r_{1 A} Δ H_{Rx1A} + r_{2 S} Δ H_{Rx2S}] & (\begin{matrix} E13-6.25 \end{matrix}) \end{matrix}$

and

$\begin{matrix} {\dot{Q}}_{r b} = U A (T - T_{a}) & (E13-6.26) \end{matrix}$

Combining the above three equations one obtains

$\begin{matrix} \frac{d T}{d t} = \frac{V_{0} [r_{1 A} Δ H_{R x l A} + r_{2 S} Δ H_{R x 2 S}] - U A (T - T_{a})}{\sum N_{j} C_{P_{j}}} & (E13-6.27) \end{matrix}$

Substituting for the rate laws and ΣN_j C_{P_j}

$\begin{matrix} \frac{d T}{d t} = \frac{V_{0} [- k_{1 A} C_{A} C_{B} Δ H_{R x 1 A} - k_{2 S} C_{s} Δ H_{R x 2 S}] - U A (T - T_{a})}{1.26 \times 1 0^{7} (J / K)} & (E13-6.28) \end{matrix}$

(7) Numerical Solutions: “Tricks of the Trade”

A rapid change of temperature and pressure is expected as Reaction (2) starts to runaway. This typically results in a “stiff” system of ordinary differential equations, which can become numerically unstable and generate incorrect results. This instability can be prevented by using a software switch (SW) that will set all derivates to zero when the reactor reaches the explosion temperature or pressure. This switch can have the form of Equation (E13-6.29) in Poly-math, as shown in Table E13-6.1, and can be multiplied by the right-hand side of all the differential equations in this problem. This operation will halt (or freeze) the dynamics when the temperature T becomes higher than 600 K or the pressure exceeds 45 atm.

$\begin{matrix} SW1 = if (T > 600 o r P > 45) then (0) else (1) & (E13-6.29) \end{matrix}$

See tutorial at http://www.umich.edu/~elements/6e/tutorials/Polymath_Tutorial_to_solve_numerically_unstable_systems.pdf.

Steps to take to prevent your computer from crashing.

TABLE E13-6.1 POLYMATH PROGRAM

Differential equations

1 d(CA)/d(t) = SW1*r1A mol/dm3/hr

2 d(CB)/d(t) = SW1*r1A change in concentration of cyclomethylpentadiene

3 d(CS)/d(t) = SW1*r2S change in concentration of diglyme

4 d(P)/d(t) = SW1*((FD-Fvent)*0.082*T/VH)

5 d(T)/d(t) = SW1*(Qg-Qr)/SumNCp

Explicit equations

1 V0 = 4000 dm3

2 VH = 5000 dm3

3 DHRx1A = -45400 J/mol Na

4 DHRx2S = -3.2E5 J/mol of Diglyme

5 SumNCp = 1.26E7 J/K

6 A1A = 4E14 per hour

7 E1A = 128000 J/kmol/K

8 k1A = A1A*exp(-E1A/(8.31*T)) rate constant reaction 1

9 A2S = 1E84 per hour

10 E2S = 800000 J/kmol/K

11 k2S = A2S*exp)-E2S/(8.31*T)) rate constant reaction 2

12 SW1 = if (T>600 or P>45) then (0) else (1)

13 r1A = -k1A*CA*CB mol/dm3/hour (first order in sodium and cyclomethylpentadiene)

14 r2S = -k2S*CS mol/dm3/hour (first order in diglyme)

15 FD = (-0.5*r1A-3*r2S)*V0

16 Cv2 = 53600

17 Cv1 = 3360

18 Fvent = if (FD<11400) then (FD) else(if (P<28.2) then ((P-1)*Cv1) else ((P-1)*(Cv1 +Cv2)))

19 UA = 0 no cooling

20 Qr = UA*(T-373.15)

21 Qg = V0*(r1A*DHRx1A+r2S*DHRx2S)

Calculated values of DEQ variables

	Variable	Initial value	Final value
1	A1A	4.0E+14	4.0E+14
2	A2S	1.0E+84	1.0E+84
3	CA	4.3	9.919E-07
4	CB	5.1	0.800001
5	CS	3.	2.460265
6	Cv1	3360.	3360.
7	Cv2	5.36E+04	5.36E+04
8	DHRx1A	-4.54E+04	-4.54E+04
9	DHRx2S	-3.2E+05	-3.2E+05
10	E1A	1.28E+05	1.28E+05
11	E2S	8.0E+05	8.0E+05
12	FD	2467.445	7.477E+10
13	Fvent	2467.445	2.507E+06
14	k1A	0.0562573	153.6843
15	k2S	8.428E-16	2.533E+06
16	P	4.4	45.01004
17	Qg	2.24E+08	7.975E+15
18	Qr	0	0
19	r1A	-1.233723	-0.000122
20	r2S	-2.529E-15	-6.231E+06
21	SumNCp	1.26E+07	1.26E+07
22	SW1	1.	0
23	t	0	4.
24	T	422.	538.8048
25	UA	0	0
26	V0	4000.	4000.
27	VH	5000.	5000.

Note: The second reaction took off about 3.6 hours after starting the reactor.

Also see this example on the Web site Process Safety Across the Chemical Engineering Curriculum (http://umich.edu/~safeche) and click on Chemical Reaction Engineering Course.

A trend graph to determine the temperature at the time of explosion is shown. — **Figure E13-6.3(a)** Temperature (K) versus time (h) trajectory.

A trend graph represents the time taken for a reactor to explode. The horizontal axis represents the time in hours ranging from 0.0 to 4.0 in increments of 0.4. The vertical axis represents the temperature in Kelvin ranging from 400 Kelvin to 600 Kelvin in increments of 20 Kelvin. The trend curve begins at a point (0.0, 420) and gradually increases to the point (1.2, 480). From this point the curve gets slightly flattened until it reaches the point (3.6, 482). This point is marked as the explosion point and the curve starts increasing vertically from here. Note: The above-mentioned points are approximate.

A trend graph to determine the pressure at the time of explosion is shown. — **Figure E13-6.3(b)** Pressure (atm) versus time (h) trajectory.

A trend graph represents the time taken for a reactor to explode with respect to the pressure in it. The horizontal axis represents the time in hours ranging from 0.0 to 4.0 in increments of 0.4. The vertical axis represents the pressure (atm) ranging from 0 to 50 in increments of 5. The pressure remains to be at 4 atm for a time of 0.0 to 3.6 hours. From here it increases vertically. Note: The above-mentioned points are approximate.

A trend graph to determine the concentration at the time of explosion is shown. — **Figure E13-6.3(c)** Concentration (mol/dm³) versus time (h) trajectory.

A trend graph represents the time taken for a reactor to explode with respect to the concentration in it. The horizontal axis represents the time in hours ranging from 0.0 to 4.0 in increments of 0.4. The vertical axis represents the concentration C 1(moles over decimeter cubed) ranging from 0.0 to 6.0 in increments of 0.6. There are three curves A, B, and S. The curve A begins at a point (0.0, 4.3) and falls to a point (1.5, 0.2), from here it gets slightly flattened to end at a point (2.2, 0.0). The curve B begins at a point (0.0, 5.0) and falls to the point (1.2, 1.6), from here the curve becomes constant and end at (3.6, 1.1). The curve S remains at a concentration of 3.0 moles per decimeter cubed over the time period of 0.0 to 3.6 hours. After which it begins to fall drastically. This point is marked as the explosion point. Note: The above-mentioned points are approximate.

We now will solve the essential equations from (E13-6.1) through (E13-6.29) for the scenario where there is no cooling and thus UA = 0. Also the switch SW1 must be implemented in all the differential equations as discussed above.

We note from Figures E13-6.3(a)–(b) that the explosion occurred at approximately 3.6 hours after startup and the concentration of diglyme begins to drop sharply before that point, as seen in Figure E13-6.3(c). We also note that numerical instabilities occur at about the point of the arrows in these figures because of the rapid increase in temperature.

Analysis: Runaway would not have occurred if (1) the cooling system had not failed, causing the reactor temperature to rise and initiate a second a reaction, and (2) the solvent dygline had not decomposed at the higher temperature to produce hydrogen gas (D). The rate of production of H₂ gas was greater than the removal of H₂ from the head space, causing the pressure to build up to the point that it ruptured the reactor vessel. Also, had the Advanced Reactor System Screening Tool (ARSST) been used to study this reaction, additional preventative actions could have been implemented. The details with an example for the ARSST are given in the Chapter 13 Professional Reference Shelf on the Web site (http://www.umich.edu/~elements/6e/13chap/pdf/CD_ARSST_ProfRef.pdf ).

Use of an ARSST may have provided information on diglyme that could have prevented this accident.

13.5 And Now… A Word from Our Sponsor–Safety 13 (AWFOS–S13 Safety Analysis of the T2 Laboratories Incident)

In this AWFOS–S, we are going to draw from Safety Module 1 “T2 Laboratories Explosion” from the Chemical Reaction Engineering modules (http://umich.edu/~safeche/courses/ChemicalReactionEngineering.html) on the Process Safety Across the Chemical Engineering Curriculum (http://umich.edu/~safeche/index.html). In going through this module, first view the CSB Video and then analyze the relevance of the Safety Analysis to the video.

Safety Analysis of the Incident

Activity: Production of methylcyclopentadienyl manganese tricarbonyl (MCMT), which involves an exothermic reaction.

Hazard: Dangerous reaction chemistry involving toxic and flammable chemicals, with a high potential for a runaway reaction. Toxicity, flammability, or reactivity hazards were involved in all the production steps of MCMT. Hazardous chemicals used or generated during production steps included sodium metal, carbon monoxide, hydrogen, and organometallic compounds.

Incident: A runaway reaction during production of MCMT resulted in a powerful explosion and fire. Failure of the cooling system caused the explosion. The blast killed 4 employees, and injured 32 other people. It demolished the entire plant and caused extensive damage to local businesses. Decomposition of the diglyme solvent became significant at elevated temperatures that caused a significant increase in temperature and pressure leading to the runaway reaction. The 2500-gal reactor’s pressure relief valve ruptured when it exceeded the set pressure. The reactor pressure continued to increase and eventually led to the explosion and fire.

Initiating Event: Failure of cooling water system led a to a runaway reaction in the metalation step of the process. This runaway resulted in uncontrolled rise in temperature and pressure inside the reactor leading to its rupture.

Preventative Actions and Safeguards: Sole reliance on city water for cooling should have been avoided and additional cooling systems should have been ready to use as a backup. A thorough understanding of reaction chemistry could have prevented the accident. This understanding could have been achieved by carrying out ARSST experiments to learn the ignition temperature of diglyme and the cooling requirement of the system. A complete description of the ARSST is given in the expanded material for Chapter 13 (http://www.umich.edu/~elements/6e/13chap/pdf/CD_ARSST_ProfRef.pdf ). Firefighting procedures and explosion barriers should have been in place to reduce the damage. Different levels of alarms, pressure relief systems, and safety inter-locks should have been installed to give different layers of protection from a potential disaster.

Contingency Plan/Mitigating Actions: Alarm system should be initiated as temperature and pressure increases. Emergency quenching system should be made available. Barrier walls should surround the reactor. Appropriate emergency pressure relief systems and other design safeguards should have been installed. Plan for possible accidents, including evacuation drill and emergency response exercises should have been in place.

Lessons Learned: Improved industry practices and a thorough and complete understanding of the chemistry and hazards of the reaction being carried out can help prevent these kinds of accidents. A Kepner–Tregoe potential problem analysis^† of the system should have been carried out. All incidents must be thoroughly investigated to find the root cause, and corrective actions must be taken immediately. Effective operating procedures and training programs should be developed, and any changes to existing processes should be carefully managed. Management of change and careful analysis of any change in operation should be done before they are implemented.

^† H. S. Fogler, S. E. LeBlanc and B. Rizzo, Strategies for Creative Problem Solving, 3rd ed., p. 208.

The preventative and mitigating actions described above can be put into a BowTie diagram as shown in Figures 13-2 and 13-3.

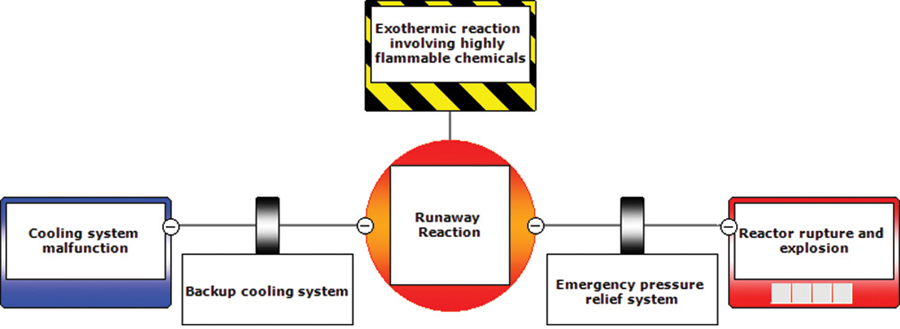
An illustration of the T2 laboratories explosion using a abbreviated BowTie diagram. — **Figure 13-2** Abbreviated BowTie diagram for T2 Laboratories incident.

A BowTie diagram illustrates the preventive and safety measures to be taken as a result of the safety analysis of the T2 Laboratories incident. The hazard in this incident is the exothermic reaction involving highly flammable chemicals. The initiation action is the runaway reaction. The preventive action is backup cooling system and the potential problem is cooling system malfunctioned. The mitigating action is emergency pressure relief system and the consequence is reactor rupture and explosion.

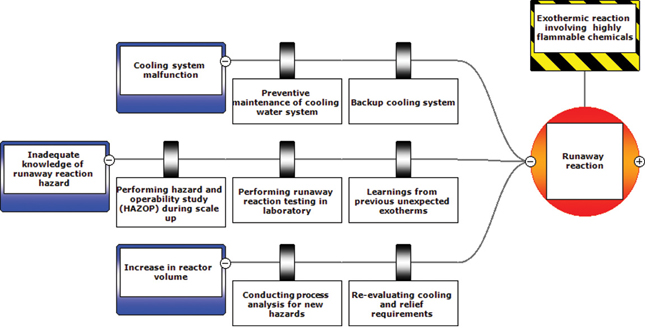
A complete illustration of the preventive measures that could have been taken in the T2 laboratories explosion using a BowTie diagram. — A BowTie diagram illustrates the preventive and safety measures to be taken as a result of the safety analysis of the T2 Laboratories incident in a detailed manner. The hazard in this incident is the exothermic reaction involving highly flammable chemicals. The initiation action is the runaway reaction. The preventive action is a backup cooling system and preventive maintenance of cooling water system to which the potential problem is the cooling system malfunctioned. The other preventive actions are learnings from previous unexpected exotherms, performing runaway reaction testing in the laboratory, and performing hazard and operability study (HAZOP) during scale-up which leads to a potential problem of Inadequate knowledge of runaway reaction hazard. The other preventive measures are re-evaluating cooling and relief requirements, conducting process analysis of new hazards for which the potential problem seems to be the increase in reactor volume.

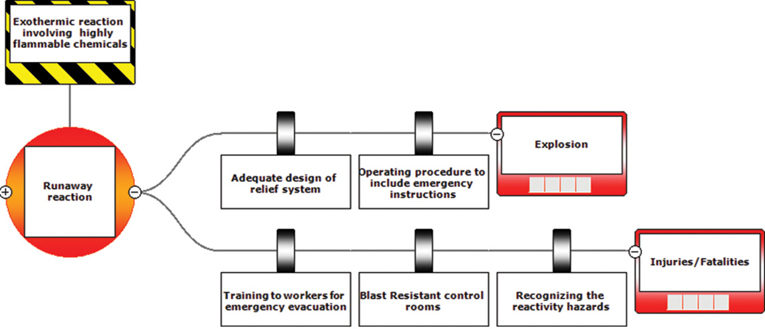
A complete illustration of the mitigation actions in T2 laboratories explosion using a BowTie diagram. — **Figure 13-3** Full BowTie Diagram for T2 Laboratories Incident.

The mitigating actions are an adequate design of relief system and operating procedure to include emergency instructions to which the consequence is an explosion. The other mitigating actions are training to workers for emergency evacuation, Blast Resistant control rooms, and Recognizing the reactivity hazards leading to a decrease in injuries or fatalities.

Closure. After completing this chapter, the reader should be able to apply the unsteady-state energy balance to CSTRs, semibatch, and batch reactors. The reader should also be able to discuss reactor safety using the ONCB and the T2 Laboratories case studies of explosions to help prevent future accidents. Included in the reader’s discussion should be how to start up a reactor so as not to exceed the practical stability limit. After studying these examples, the reader should be able to describe how to operate reactors in a safe manner for both single and multiple reactions.

Summary

1. The energy balance on unsteady operation of a CSTR and semibatch reactors

$\begin{matrix} \frac{d T}{d t} = \frac{\dot{Q} - {\dot{W}}_{s} - Σ F_{i 0} C_{P_{i}} (T - T_{i 0}) + [- Δ H_{Rx} (T)] (- r_{A} V)}{Σ N_{i} C_{P_{i}}} & (S13-1) \end{matrix}$

Using the heat exchange Equation (13-12) and neglecting shaft work

$\begin{matrix} \frac{d T}{d t} = \frac{{\overset{\cdot}{Q}}_{g s} - {\overset{\cdot}{Q}}_{r s}}{\sum N_{i} C_{P_{i}}} & (S13-2) \end{matrix}$

$\begin{matrix} {\overset{\cdot}{Q}}_{rs} = (r_{A^{V}}) (Δ H_{Rx}) & (S13-3) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{r s} = \sum F_{i 0} C_{P_{i}} (T - T_{i 0}) + {\dot{m}}_{c} C_{P_{c}} [T - T_{a 1}] [1 - \exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{c}}})] & (S13-4) \end{matrix}$

For large coolant flow rates, ${\dot{m}}_{c} C_{P_{c}}$ , Equation (13-22) reduces to

$\begin{matrix} \frac{d T}{d t} = \frac{\overset{\dot{Q_{g}}}{\overset{⏞}{(r_{A} V) (Δ H_{Rx})}} - \overset{\dot{Q_{r s}}}{\overset{⏞}{[Σ F_{i 0} C_{P_{i}} (T - T_{i 0}) + U A (T - T_{a})]}}}{Σ N_{i} C_{P_{i}}} & (S13-5) \end{matrix}$

2. Batch reactors

a. Non-adiabatic

$\begin{matrix} \frac{d T}{d t} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{Σ N_{i} C_{P_{i}}} = \frac{{\dot{Q}}_{g b} - {\dot{Q}}_{r b}}{N_{A0} (Σ Θ_{i} C_{P_{i}} + Δ C_{P} X)} & (S13-6) \end{matrix}$

where

$\begin{matrix} {\dot{Q}}_{g b} = (r_{A} V) (Δ H_{Rx}) & (S13-7) \end{matrix}$

$\begin{matrix} {\dot{Q}}_{r b} = {\dot{m}}_{c} C_{P_{C}} (T - T_{a 1}) [1 - exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{C}}})] & (S13-8) \end{matrix}$

b. Adiabatic

$\begin{matrix} X = \frac{C_{P_{s}} (T - T_{0})}{- Δ H_{Rx} (T)} = \frac{Σ Θ_{i} C_{P_{i}} (T - T_{0})}{- Δ H_{Rx} (T)} & (S13-9) \end{matrix}$

$\begin{matrix} T = T_{0} + \frac{[- Δ H_{Rx} (T_{0})] X}{C_{P_{s}} + X Δ C_{P}} = T_{o} + \frac{[- Δ H_{Rx} (T_{0})] X}{Σ_{i = 1}^{m} Θ_{i} C_{P_{i}} + X Δ C_{P}} & (S13-10) \end{matrix}$

3. Semibatch reactors and startup of CSTR

$\begin{matrix} \frac{\begin{matrix} d T \end{matrix}}{d t} = \frac{{\dot{Q}}_{g s} - {\dot{Q}}_{r s}}{Σ N_{i} C_{P_{i}}} & (S13-11) \end{matrix}$

Where ${\dot{Q}}_{g s}$ is the same as Equation (S13-7) and ${\dot{Q}}_{r s}$ (sub rs, i.e., “heat removed” from semibatch) is

$\begin{matrix} {\dot{Q}}_{r s} = \sum F_{i 0} C_{P_{i 0}} (T - T_{i 0}) + {\dot{m}}_{c} C_{P_{c}} [T - T_{a 1}] [1 - \exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{c}}})] & (S13-12) \end{matrix}$

4. Multiple reactions (q reactions and m species)

$\begin{matrix} \frac{\begin{matrix} d T \end{matrix}}{d t} = \frac{\overset{}{\overset{\dot{Q_{g}}}{\overset{⏞}{Σ_{j = 1}^{q} r_{i j} V Δ H_{Rx i j} (T)}} - \overset{\dot{Q_{r s}}}{\overset{⏞}{Σ_{j = 1}^{m} F_{j 0} C_{P_{i}} (T - T_{0}) + {\dot{m}}_{c} C_{p_{c}} (T - T_{a 1}) [1 - exp (\frac{- U A}{{\dot{m}}_{c} C_{P_{C}}})]}}}}{Σ_{j = 1}^{m} N_{i} C_{P_{i}}} & (S13-13) \end{matrix}$

where i = reaction number and j = species.

CRE WEB SITE MATERIALS
(http://www.umich.edu/~elements/6e/13chap/obj.html#/)

A figure depicts the accessible CRE website materials. This includes useful links for living example problems, extra help, additional materials, professional reference shelf, computer simulation problem statements, YouTube videos. Materials for evaluation includes self tests and i>Clicker questions.

Professional Reference Shelf

(http://umich.edu/~elements/6e/13chap/prof.html)

R13.1 The Complete ARSST (http://umich.edu/~elements/6e/13chap/pdf/CD_ARSST_ProfRef.pdf )

In this section, further details are given to size safety valves to prevent runaway reactions.

A graph representing the temperature-time trajectory for hydrolysis of acetic anhydride in an ARRST. — **Figure R13.1** Temperature–time trajectory for hydrolysis of acetic anhydride in an ARRST.

A trend graph represents the time taken for hydrolysis of acetic anhydride with respect to the temperature. The horizontal axis represents the time in hours 0, 3, 5, 8, 10, 13, 15, 18, and 20. The vertical axis represents the temperature in degree Celsius ranging from 0 to 180 in increments of 20. An intermittent dotted curve begins at a point (0, 22) and gradually increases to a point (14, Tf). From this point the curve gradually decreases. A tangent is drawn to the curve. An intermittent line is drawn horizontally from 55 degree Celsius and vertically upwards from 10 minutes to join at a point to determine T Subscript on. Note: The above-mentioned points are approximate.

If an ARSST experiment had been carried out with MCP and diglyme, then precautions may have been taken such that the explosion would most likely not have occurred.

R13.2 Falling Off the Upper Steady State (http://umich.edu/~elements/6e/13chap/prof-uppersteadystate.html)

R13.3 Control of a CSTR (http://umich.edu/~elements/6e/13chap/pdf/controlCSTR.pdf )

In this section, we discuss the use of proportional (P) and integral (I) control of a CSTR. Examples include I and PI control of an exothermic reaction.

An illustration of CSTR. — **Figure R13.3** Reactor with coolant flow-rate control system.

An illustration of the Continuous Stirred Tank Reactor with a coolant flow-rate control system is shown. The tank reactor is at the center with a stirrer in it and is surrounded by the coolant. In the beginning the concentration of the coolant is m subscript c and the temperature is T a1 and at the end its concentration is m subscript c and T subscript a 2. A valve is placed at the start of the coolant to control its flow. In the reactor, the temperature is T0 and the feed flow rate is F subscript A 0. The exit feed flow rate from the reactor is F subscript A and the exit temperature is T. The temperature difference between T and T subscript sp is the charge produced e in the power source which in turn is used to control the valve.

Proportional integral action

$z = z_{0} + k_{c} (T - T_{SP}) + \frac{k_{c}}{τ} \int_{0}^{t} (T - T_{SP}) d t$

R13.4 Linearized Stability Theory (http://umich.edu/~elements/6e/13chap/pdf/CD_CH09Linearized_ProfRef3.pdf)

R13.5 Approach to Steady-State Phase-Plane Plots and Trajectories of Concentration versus Temperature (http://umich.edu/~elements/6e/13chap/prof-steadystate.html)

Startup of a CSTR (Figure R13.5) and the approach to the steady state (CRE Web site). By mapping out regions of the concentration–temperature phase plane, one can view the approach to steady state and learn whether the practical stability limit is exceeded. The steady-state trajectories are shown for the mole balance (MB = 0) and energy balance (EB = 0). Use Wolfram to explore these trajectories shown below.

A graph of concentration versus temperature during the startup of a CSTR. — **Figure R13.5** Startup of a CSTR.

A trend graph represents the steady-state trajectories. The horizontal axis represents the temperature, T and the vertical axis represents C subscript A over C Subscript A 0. There are two curves EB and MB. The EB curve is a gradually increasing curve and the MB curve is a gradually decreasing curve. Both the curves intersect at a point. The regions formed by the intersection of the two curves are marked 1, 2 , 3, and 4 and the direction of the trajectory is marked as anticlockwise.

R13.6 Adiabatic Operation of a Batch Reactor (http://umich.edu/~elements/6e/13chap/prof-adiabaticbatch.html)

R13.7 Unsteady Operation of Plug-Flow Reactor (http://umich.edu/~elements/6e/13chap/prof-unsteadyplug.html)

QUESTIONS, SIMULATIONS, AND PROBLEMS

Questions

Q13-1_A QBR (Question Before Reading). What conditions cause reactions to runaway and explode and what could be done to insure runaway does not occur?

Q13-2_A i>clicker. Go to the Web site (http://www.umich.edu/~elements/6e/13chap/iclicker_ch13_q1.html) and view five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case and explain why the question should not be on the next exam. In either case, explain your reasoning.

Q13-3 Discuss with a classmate what are the most important safety considerations to address for exothermic reactions. To help answer this question, prepare a list of safety considerations for designing and operating chemical reactors. See the August 1985 issue of Chemical Engineering Progress, vol. 81, no. 7, p. 29.

Q13-4 Go to the LearnChemE screencast link for Chapter 13 (http://www.umich.edu/~elements/6e/13chap/learn-cheme-videos.html).

(a) View one of the screencast 5- to 6-minute video tutorials and list two of the most important points.

(b) What are the two mole balances for species B?

Q13-5 AWFOS–S13 Make a list of at least four things you learned from this section.

(a) Were any or all of the things discussed in the Safety Analysis of the Incident and BowTie Diagram in place when the reactor exploded?

(b) Were there any safety issues T2 did address?

Computer Simulations and Experiments

P13-1_B Review the example problems in this chapter and use a software package such as Polymath, Wolfram, or MATLAB to carry out a parameter sensitivity analysis to answer the following “What if…” questions.

What if...

Example 13-1: Batch Reactor with an Exothermic Reaction

Wolfram
1. Adiabatic Case: Use Wolfram to see whether you can find a trajectory that is ready “to ignite” and whose trajectory looks like a “cobra” ready to strike, . Hint: Vary T₀ to learn the point at which the reaction runs away at 2500 s.
2. Heat Exchange Case: (1) Vary UA and T_a1 and suggest conditions at which runaway might occur. (2) Use the plot of Q_r and Q_g as a function of time to describe and explain what you see as you vary T_a₁ and N_A0 from their maximum to minimum values.
3. Write three conclusions on what you found in experiments (i) and (ii).
  
  Polymath
4. How much time would it take to achieve 90% conversion for adiabatic operation if the reaction were started on a very cold day where the initial temperature was 20°F? (Methanol won’t freeze at this temperature.)
5. Now, consider that a heat exchanger is added to the reactor for the propylene oxide reaction; the parameters are: C_A0 = 1 lb-mol/ft³, V = 1.2 ft³, (ΣN_iC_{P_i} = 403 Btu°R), neglect ΔC_P, UA = 0.22 Btu/°R/s, and T_a = 498 K. Plot and analyze the trajectories X, T, Q_g, and Q_r as a function of time.
Example 13-2: Safety in Chemical Plants with Exothermic Runaway Reactions.

This is another Stop and Smell the Roses Simulation.

Wolfram
1. View the temperature trajectory for the base case and then describe how it changes when the charge (i.e., the amount initially in the reactor) is varied above and below the base case value.
2. Show the explosion would not have occurred for the triple production case if the heat exchanger had not failed. Hint: Set the sliders for t₁ and t₂ = 45 minutes in the Wolfram LEP.
3. Does it make any sense to plot the down time, (t₂ – t₁), versus time since the start of the reaction that the reactor fails, (t₁) to identify regions where the explosion will and will not occur? Explain.
  
  If it does make sense, please prepare such a plot; if not, explain why. Hint: Choose t₁ and then find the largest t₂ for which the reaction will not runaway. Choose another larger value of t₁ and repeat. Continue in this manner to construct your plot.
4. Use Wolfram to find a value of N_A0 below which no explosion would occur when all other variables remain as in the base case. Repeat for N_B0.
5. Use Wolfram to find the value of NC_p and also of UA, above which no explosion would occur.
6. Develop a set of guidelines as to how the reaction should be quenched should the cooling fail. Perhaps safe operation could be discussed using a plot of the length of the cooling failure, t₂ – t₁, as a function of the time at which the cooling failed, t₁, for the different charges of ONCB.
7. Write a set of conclusions related to safety from your experiments in (i) and (v).
  
  Polymath
8. Modify the Polymath code to show that no explosion would have occurred if the cooling was not shut off for the 9.04-kmol charge of ONCB, or if the cooling was shut off for 10 minutes after 45 minutes of operation for the 3.17-kmol ONCB charge.
9. Find a set of parameter values that would cause the explosion to occur at exactly 12:18 A.M. For example, include the mass and heat capacities of the metal reactor and/or make a new estimate of UA.
10. Finally, what if a 1/2-in. rupture disk rated at 800 psi had been installed and did indeed rupture at 800 psi (270°C)? Would the explosion still have occurred? Note: The mass flow rate varies with the cross-sectional area of the disk. Consequently, for the conditions of the reaction, the maximum mass flow rate out of the 1/2-in. disk can be found by comparing it with the mass flow rate of 830 kg/min of the 2-in. disk. Go to the Living Example Problems on the Web site and explore on your own the ONCB explosion described in Example 13-2. Explain what you would do to prevent an explosion of this type from ever occurring again while still operating at the triple production specified by management.
This problem was written in honor of Ann Arbor, Michigan’s own Grammy Award–winning artist, Bob Seger (https://www.youtube.com/channel/UComKJVf5rNLl_RfC_rbt7qg/videos).
Example 13-3: Startup of a CSTR

Wolfram
1. What is the minimum coolant flow such that there is no upturn in temperature–concentration profile for Case 2 (T_i = 339 K, C_A_i = 0)?
2. Is it possible to prevent crossing of practical stability limit for Case 3 (T_i = 344 K, C_A_i = 2.26) by varying coolant temperature, coolant flow, or overall heat transfer coefficient? If so, which is the parameter and which should be varied to achieve that?
3. Use Wolfram to find initial temperatures and concentrations that will cause the temperature trajectory to exceed the practical stability limit, and then write a conclusion.
  
  Polymath
4. Consider the case when C_A_i = 0.1 lb mol/ft³ and T_i = 150°F. What is the minimum coolant temperature such that the practical stability limit is not exceeded?
5. Describe what happens to the trajectories for an entering temperature of 70°F, an initial reactor temperature of 160°F, and an initial concentration of propylene oxide of 0.1 M.
6. Try various combinations of T₀, T_i, and C_A_i, and report your results in terms of temperature– time trajectories and temperature–concentration phase planes.
7. Find a set of conditions above which the practical stability limit will be reached or exceeded, and those conditions below which it will not.
8. Vary the coolant flow rate and compare with the base case given in Figures E13-3.1 to E13-3.4. Describe what you find and then write a conclusion.
  
  COMSOL CSTR Startup
  
  Go to the COMSOL hot button on the LEP Web site for Chapter 13 (http://www.umich.edu/~elements/6e/13chap/comsol_lep_tutorial.html) to access this LEP in COMSOL.
9. Vary the tank volume between 1 and 5 m³ and describe the differences in the trajectories and the time to reach steady state and exceeding a practical stability limit of 360 K.
10. Use the base case parameters for the trajectory T_i = 340 K and C_i = 1400 mol/m³ to find the maximum feed temperature you can have that will not exceed the practical stability limit of 360 K?
11. Pick two operating parameters from ν₀, V_tank, T₀, T_a, m_c, and UA to vary from minimum to maximum values, and describe what you find.
12. Vary the activation energy, E_A, and discuss the effect of E_A on the number of oscillations to reach steady state.
13. Write three conclusions from your COMSOL experiments (ix) through (xii).
Example 13-4: LEP Semibatch

Wolfram
1. Use Wolfram to vary C_B0 and describe how the maximum in C_C varies.
2. List the slider variables that have virtually no effect on the temperature trajectory. Repeat for the concentration trajectory.
3. Which parameter, when varied, causes the graphs of T and T_a₂ to overlap each other?
4. What is the minimum inlet temperature such that 100% conversion of A is still achieved?
5. Write three conclusions on what you found from your experiments (i) through (iv).
  
  Polymath
6. At what times will the number of moles of C (N_C = C_CV) and the concentration of species C reach a maximum?
7. Are the times in part (i) that these maximums occur different, and if so, why? What would the X versus t and T versus t trajectories look like if the coolant rate were increased by a factor of 10? Why is the reaction time (252 seconds) so short?
8. Problem. Assume the surface area contacting the reacting fluid changes with time. The initial fluid volume in the reactor is 0.2 m³ and the inlet volumetric flow rate is 0.004 m³/s. Calculate the heat exchanger area as a function of time if the half-pipe jacket on page 684 is 0.5 m in diameter. Repeat for diameters of 1.0 and 0.25 m.
Example 13-5: LEP Multiple Reactions in a Semibatch Reactor

Wolfram
1. Assume a secondary reaction ignites when the reactor temperature reaches 450 K. Find the value (or combination thereof) of C_A0 and ν₀ above which the secondary reaction will ignite.
2. Vary C_A0 and ν₀ between their maximum and minimum values and describe how the concentration trajectories change and why they change the way they do.
3. Which parameter, when varied, results in equal concentration of A, B, and C at some point in time? What is the parameter value? Write two conclusions.
  
  Polymath
4. Vary the volumetric flow rate (between 24 < ν₀ < 1000) and compare with the base case. Describe any trends you find.
5. Plot and analyze the trajectories of N_A = C_AV and N_B = C_BV for long times (e.g., t = 15 hours). What do you observe?
6. Can you show for long times that N_A ≅ C_A0ν₀/k_1A and N_B ≅ C_A0ν₀/2k_2B?
7. If species B is the desired product, how would you maximize N_B?
Example 13-6: LEP T2 Laboratories Explosion

Wolfram

This problem is a Stop and Smell the Roses Simulation. We need to spend more time than usual exploring this problem. First view the video described on the Web site (http://umich.edu/~safeche/assets/pdf/courses/Problems/CRE/344ReactionEngrModule(1)PS-T2.pdf).
1. Vary the liquid volume, V₀, and learn its effect on pressure profile. What is the critical value of V₀ at which pressure shoots up?
2. Which parameter will you vary such that concentration of B is always higher than concentration of C?
3. Vary different parameters and check whether it is possible that the temperature limitation is reached before the pressure limitation.
4. Find a value of the heat of reaction for the secondary reaction of diglyme, below which no explosion would have occurred.
5. Write a set of conclusions and of the lessons learned.
  
  Polymath
6. Review the safety module (http://umich.edu/~safeche/assets/pdf/courses/Problems/344ReactionEngineeringModule(2)PS050818.pdf ) and fill out the safety algorithm. Write a set of conclusions and the lessons learned.
7. (a) What did you learn from watching the video? (b) Suggest how this reactor system should be modified and/or operated in order to eliminate any possibility of an explosion. (c) Would you use backup cooling and, if so, how? (d) How could you learn whether a second reaction could be set in at a higher temperature? Hint: See PRS R13.1 The Complete ARSST.
8. Download the Living Example Polymath E13-6. Plot C_A, C_B, C_C, P, and T as a function of time. Vary UA between 0.0 and 2.77 × 10⁶ J/h/K to find the lowest value of UA that you observe a runaway to find the value of UA below which you would observe runaway. Describe the trends as you approach runaway. Did it occur over a very narrow range of UA values? Hint: The problem becomes very stiff near the explosion condition when T > 600 K or P > 45 atm, so you will need to set all derivatives equal to zero so that the numerical solution will complete the analysis and hold all variables at the explosion point of the reactor.
9. Now let’s consider the actual operation in more detail. The reactor contents are heated from 300 K to 422 K at a rate of = 4 K/minute. At 422 K, the reaction rate is sufficient such that heating is turned off. The reactor temperature continues to rise because the reaction is exothermic, and, when the temperature reaches 455 K, the cooling water turns on and cooling is initiated. Model this situation for the case when UA = 2.77 × 10⁶ J/h/K and when UA = 0.
10. What is the maximum time in minutes that the cooling can be lost (UA = 0) starting at the time when the reactor temperature reaches 455 K so that the reactor will not reach the explosion point? The conditions are those of part (1) of this problem.
11. Vary the parameters and operating conditions and describe what you find.
LEP PRS R13.2 Example CD13-5. Download the Living Example Problem for Falling Off the Upper Steady State. Try varying the entering temperature, T₀, between 80°F and 68°F, and plot the steady-state conversion as a function of T₀. Vary the coolant rate between 10,000 and 400 mol/h. Plot conversion and reactor temperature as a function of coolant rate.
LEP PRS R13.3 Example CD13-2. Download the Living Example Problem. Vary the gain, k_C, between 0.1 and 500 for the integral controller of the CSTR. Is there a lower value of k_C that will cause the reactor to fall to the lower steady state or an upper value to cause it to become unstable? What would happen if T₀ were to fall to 65°F or 60°F?
LEP PRS R13.3 Example CD13-3. Download the Living Example Problem. Learn the effects of the parameters k_C and τ₁. Which combination of parameter values generates the least and greatest oscillations in temperature? Which values of k_C and τ₁ return the reaction to steady state the quickest?
SAChE. Go to the SAChE Web site (www.sache.org). On the left-hand menu, select “SaChe Products.” Select the “All” tab and go to the module titled: “Safety, Health and the Environment (S, H & E).” The problems are for KINETICS (i.e., CRE). There are some example problems marked K and explanations in each of the above S, H & E selections. Solutions to the problems are in a different section of the site. Specifically look at: Loss of Cooling Water (K-1), Runaway Reactions (HT-1), Design of Relief Values (D-2), Temperature Control and Runaway (K-4) and (K-5), and Runaway and the Critical Temperature Region (K-7). Go through the K problems and write a paragraph on what you have learned. Your instructor or department chair should have the username and password to enter the SAChE Web site in order to obtain the module with the problems.

Problems

P13-2_B OEQ (Old Exam Question). The following is an excerpt from The Morning News, Wilmington, Delaware (August 3, 1977): “Investigators sift through the debris from blast in quest for the cause [that destroyed the new nitrous oxide plant]. A company spokesman said it appears more likely that the [fatal] blast was caused by another gas—ammonium nitrate—used to produce nitrous oxide.” An 83% (wt) ammonium nitrate and 17% water solution is fed at 200°F to the CSTR operated at a temperature of about 510°F. Molten ammonium nitrate decomposes directly to produce gaseous nitrous oxide and steam. It is believed that pressure fluctuations were observed in the system and, as a result, the molten ammonium nitrate feed to the reactor may have been shut off approximately 4 minutes prior to the explosion. A starving artist’s conception of the system is shown below

The badge of the member of the hall of fame.

An illustration of a CSTR is shown. Ammonium nitrate and H2O are fed into the CSTR through a valve in liquid state to release H2O and Nitrous Oxide in gaseous form.

Can you explain the cause of the blast?
If the feed rate to the reactor just before shutoff was 310 lb_m of solution per hour, what was the exact temperature in the reactor just prior to shutdown? Use the data to calculate the exact time it took for the reactor to explode after the feed was shut off to the reactor.

Assume that at the time the feed to the CSTR stopped, there was 500 lb_m of ammonium nitrate in the reactor at a temperature of 520°F. The conversion in the reactor is virtually complete at about 99.99%. Additional data for this problem are given in Problem 12-5_C. How would your answer change if 100 lb_m of solution were in the reactor? 310 lb_m? 800 lb_m? What if T₀ = 100°F? 500°F? How would you start up or shut down and control such a reaction?

Safety—Shut Down: An Open-Ended Problem. Rather than shut off the total feed to the reactor, it should be diluted with pure water at a volumetric rate ν_w while reducing the ammonium nitrate reactant feed rate. Keep the same total volumetric feed ν₀ rate and entering temperature. Choose a ν_w and plot the reactor temperature and composition as a function of time. At what time could you shut off the water feed safely?

P13-3_B The liquid-phase reaction in Problems P11-4_A and P12-7_A is to be carried out in a semibatch reactor. There are 500 mol of A initially in the reactor at 25°C. Species B is fed to the reactor at 50°C and a rate of 10 mol/min. The feed to the reactor is stopped after 500 mol of B has been fed.

Plot and analyze the temperature Q_r, Q_g and conversion as a function of time when the reaction is carried out adiabatically. Calculate to t = 2 hours.
Plot and analyze the conversion as a function of time when a heat exchanger (UA = 100 cal/min·K) is placed in the reactor and the ambient temperature is constant at 50°C. Calculate to t = 3 hours.
Repeat part (b) for the case where the reverse reaction cannot be neglected.

New parameter values:

k = 0.01 (dm³/mol · min) at 300 K with E = 10 kcal/mol

V₀ = 50 dm³, υ₀ = 1 dm³/min, C_A0 = C_B0 = 10 mol/dm³

For the reverse reaction: k_r = 0.1 min^-1 at 300 K with E_r = 16 kcal/mol

P13-4_B OEQ (Old Exam Question). Sophia and Nic are operating a batch reactor at their grandfather’s plant in Kärläs, Jofostan. The reaction is first-order, irreversible, liquid-phase, and exothermic. An inert coolant is added to the reaction mixture to control the temperature. The temperature is kept constant by varying the flow rate of the coolant (see Figure P13-4_B).

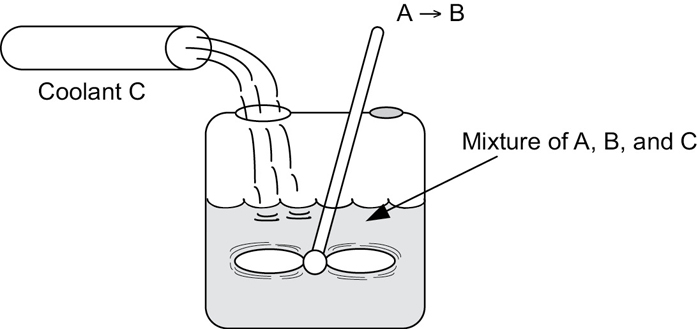
An illustration of a semibatch reactor is shown. — **Figure P13-4_B** Semibatch reactor with inert coolant stream.

A reaction mixture of A and B is in the reactor to which a coolant C is fed making it a mixture of A, B, and C in order to maintain the temperature of the reactor. The stirrer is fully submerged in the mixture.

Help them calculate the flow rate of the coolant 2 hours after the start of the reaction. (Ans: F_C = 3.157 lb/s)
It is proposed that rather than feeding a coolant to the reactor, a solvent be added that can be easily boiled off, even at moderate temperatures. The solvent has a heat of vaporization of 1000 Btu/lb and initially there are 25 lb-mol of A placed in the tank. The initial volume of solvent and reactant is 300 ft³. Determine the solvent evaporation rate as a function of time. What is the rate at the end of 2 hours?

Additional information:

Temperature of reaction: 100°F

Value of k at 100°F: 1.2 × 10^-4 s^–1

Temperature of coolant: 80°F

Heat capacity of all components: 0.5 Btu/lb°F

Density of all components: 50 lb/ft³

${Δ H}_{Rx}^{\circ}$ : – 25000 Btu/lb-mol

Initially:

Vessel contains only A (no B or C present)

C_A0: 0.5 lb-mol/ft³

Initial volume: 50 ft³

W2014 CRE U of M MidTermExamII

P13-5_B The reaction

$A + B \to C$

is carried out adiabatically in a constant-volume batch reactor. The rate law is

$- r_{A} = k_{1} C_{A}^{1 / 2} C_{B}^{1 / 2} - k_{2} C_{C}$

Plot and analyze the conversion, temperature, and concentrations of the reacting species as a function of time.

Additional information:

$\begin{matrix} {Initial Temparature = 100}^{\circ} C \\ k_{1} (373 K) = 2 \times 10^{- 3} s^{- 1} & E_{1} = 100 k J /mol \\ k_{2} (373 K) = 3 \times 10^{- 5} s^{- 1} & E_{2} = 150 k J/mol \\ C_{A0} = 0.1 {mol/dm}^{3} & C_{{p_{A}}_{}} = 25 J/mol \cdot K \\ C_{B0} = 0.125 {mol/dm}^{3} & C_{p_{B}} = 25 J/mol \cdot K \\ Δ H_{Rx}^{\circ} (298 K)= - 40000 J/mol A & C_{p_{C}} = 40 J/mol \cdot K \end{matrix}$

P13-6_B The elementary irreversible liquid-phase reaction

$A + 2 B \to C$

is to be carried out in a semibatch reactor in which B is fed to A. The volume of A in the reactor is 10 dm³, the initial concentration of A in the reactor is 5 mol/dm³, and the initial temperature in the reactor is 27°C. Species B is fed at a temperature of 52°C and a concentration of 4 M. It is desired to obtain at least 80% conversion of A in as short a time as possible, but at the same time the temperature of the reactor must not rise above 130°C. You should try to make approximately 120 mol of C in a 24-hour day, allowing for 30 minutes to empty and fill the reactor between each batch. The coolant flow rate through the reactor is 2000 mol/min. There is a heat exchanger in the reactor.

What volumetric feed rate (dm³/min) do you recommend?
How would your answer or strategy change if the maximum coolant rate dropped to 200 mol/min? To 20 mol/min?

Additional information:

$\begin{array}{l} Δ H_{R x}^{\circ} = - 55, 000 cal/mol A \\ C_{P_{A}} = 35 cal/mol \cdot {K, C}_{P_{B}} = 20 cal/mol \cdot {K, C}_{P_{C}} = 75 cal/mol \cdot K \\ k = 0.0005 \frac{{dm}^{6}}{{mol}^{2} \cdot \min} {at 27}^{\circ} C with E = 8000 cal/mol \\ U A = 2500 \frac{cal}{\min \cdot K} {with T}_{a} = 17^{\circ} C \\ C_{P} (coolant) = 18 cal/mol \cdot K \end{array}$

P13-7_B The irreversible reaction liquid phase in Problems P11-4_A and P12-7_A

$A + 2 B \to C$

is to be carried out in a 10 dm³ batch reactor.

Plot and analyze the temperature and the concentrations of A, B, and C as a function of time for the following cases:

(a) Adiabatic operation.

(b) Values of UA of 10000, 40000, and 100000 J/min · K.

(c) Use UA = 40000 J/min · K and different initial reactor temperatures.

An equal molar feed in A and B enters at 27°C, and the volumetric flow rate is 2 dm³/s and C_A0 = 0.1 kmol/m³.

Additional information:

$\begin{matrix} Δ H_{A}^{\circ} (273 K) = - 20 kcal/mol, Δ & H_{B}^{\circ} (273 K) = - 15 kcal/mol, \\ Δ H_{C}^{\circ} (273 K) = - 41 kcal/mol \end{matrix}$

$\begin{matrix} C_{P_{A}} = C_{P_{B}} = 15 c a l / m o l \cdot K C_{P_{C}} = 30 cal/mol \cdot K \\ k = 0.01 \frac{d m^{3}}{m o 1 \cdot s} at 300 K E = 10000 cal/mol K_{C} = 10 m^{3} / mol at 450 \end{matrix}$

P13-8_B Use the reaction and corresponding parameter values in Problem P12-16_B to describe the startup of a CSTR with T_i = 25°C and C_A_i = 0.0. Hint: Plot the concentration and temperature trajectories as well as the phase-plane plots of C_A versus T for various values of T_i and C_A_i.

P13-9_B OEQ (Old Exam Question). The following reactions are taking place in a 2000-dm³ liquid-phase batch reactor under a pressure of 400 psig:

$\begin{matrix} A + 2 B \overset{k_{1 A}}{\to} C & Δ H_{Rx1B} = - 5000 cal/mol & - r_{1 A} = k_{1 A} C_{A} C_{B}^{2} \\ 3 C + 2 A \overset{k_{2 A}}{\to} D & Δ H_{Rx2C} = + 10000 cal/mol & - r_{2 A} = k_{2 A} C_{A} C_{C} \\ B + 3 C \overset{k_{3 C}}{\to} E & Δ H_{Rx3B} = - 50000 cal/mol & - r_{3 C} = k_{3 C} C_{B} C_{C} \end{matrix}$

The initial temperature is 450 K and the initial concentrations of A, B, and C are 1.0, 0.5, and 0.2 mol/dm³, respectively. The coolant flow rate was at its maximum value so that T_a₁ = T_a₂ = T_a = 400 K, so that the product, the exchange area, and the overall heat transfer coefficient, UA, is UA = 100 cal/s · K.

(a) If Q_r > Q_g at time t = 0, and there is no failure of the heat exchange system, is there any possibility that the reactor will run away? Explain.

(b) What is Q_r at t = 0?

(c) What is Q_g at t = 0?

(d) What is the initial rate of increase in temperature, (i.e., dT/dt) at t = 0?

$\frac{d T}{d t} =__________[N u m e r i c l a A n s w e r]$

(e) Suppose that the ambient temperature T_a is lowered from 400 K to 350 K; what is the initial rate of reactor temperature change?

$\frac{d T}{d t} =__________[N u m e r i c a l A n s w e r]$

Plot the temperatures and all the concentrations as a function of time up to t = 1000 seconds.

(f) A suggestion was made to add 50 moles of inerts at a temperature of 450 K. Will the addition of the inerts make runaway more likely or less likely? How? Show quantitatively.

Additional information:

As a first approximation, assume all heats of reaction are constant (i.e., =C_P_ij ≅ 0). Specific reaction rates at 450 K are

$\begin{matrix} k_{1 A} = 1 \times 10^{- 3} ({dm}^{3} {/mol)}^{2} / s & C_{p_{A}} = 10 cal/mol/k & C_{P_{D}} = 80 cal/mol/K \\ k_{2 B_{}} = \frac{1}{3} \times 10^{- 3} ({dm}^{3} {/mol)}^{2} /s & C_{P_{B}} = 10 {cal/mol/K}_{_{}} & C_{p E} = 80 cal/mol/K \\ k_{3 C} = 0.6 \times 10^{- 3} ({dm}^{3} {/mol)}^{2} / s & C_{P_{C}} = 50 cal/mol/K \end{matrix}$

P13-10_B Synthron Explosion LEP. Read the Synthron example in Chapter 13 Additional Materials on the CRE Web Site (http://www.umich.edu/~elements/6e/13chap/obj.html#/additional-materials/)

Wolfram and Python

Describe and discuss the base case temperature-time trajectory.
What is the critical initial volume of reactants (V₀) above which the reactor will explode? For the sake of simplicity, assume the reactor will explode if the contents of the reactor remain above 350 K at 500 s after the start of the reaction, as the lack of cooling will result in an unsafe pressure increase.
Vary two parameters of your choice that you think will have the most effect on the explosion and describe what you find.
Write a set of conclusions.

Zachary Gdowski, Ayush Agrawal and Mayur Tikmani participated in developing this problem.

P13-11_B STOP THE PRESSES – COVID-19 Analysis. As the final edits to the Sixth Edition were being made, the coronavirus pandemic struck and it was decided to expand Problem P9-7 and apply it to the pandemic. (Mayur Tikmani, Devosmita Sen, Manjeet Singh, and Jagana Janan Sai participated in developing this problem.) We will start the modeling after 770 people have been infected. Let H = Healthy, S = Susceptible, I = Infected, D = Died, and R = Recovered. Treat each of the following interactions as an elementary reaction. The first reaction could result from a healthy person contacting the virus on a surface.

$\begin{matrix} S \overset{K_{1}}{\to} I & (P13-11.1) \end{matrix}$

$\begin{matrix} I + S \overset{K_{2}}{\to} 2 I & (P13-11.2) \end{matrix}$

$\begin{matrix} I \overset{K_{3}}{\to} r & (P13-11.3) \end{matrix}$

$\begin{matrix} I \overset{K_{4}}{\to} D & (P13-11.4) \end{matrix}$

$\begin{matrix} H = r + S & (P13-11.5) \end{matrix}$

Wolfram and Python

(i) Derive equations for the populations of S, I, R, and D as a function of time.

(ii) Use Wolfram to see if the resulting equations can be matched to Figures P13-11_B (a) and P13-11_B (b).

(iii) If we could vary k₁, k₂, k₃, and k₄, at what concentration of infected people does the death rate become critical?

(iv) Compare your model with the data from China for two extreme cases: (1) k₁ = 0 with I(0) = 770, and (2) k₁ = 2 × 10^–7 day^–1 and I(0) = 0.

(v) Vary the parameters k₁, k₂, k₃, and k₄ along with I (t = 0) and S (t = 0) and write a set of conclusions.

(vi) Apply the PSSH to the concentration of ill people and comment on your results.

(vii) Critique the COVID-19 model and initial concentrations and discuss the changes you would make.

Additional Information:

k₁ = 6 × 10^–7 day^–1 (initial infection rate)

k₂ = 10.58 10^–9 (people*day)^–1 (rate of spread of infection)

k₃ = 14.5645 day^–1 (recovery rate)

k₄ = 2 × 10^–3 day^–1 (death rate)

Initial values:

S(0) = 1.3864 × 10⁹ people (population that is not social distancing)

I(0) = 770 people infected at the start of the modeling

R(0) = 0

D(0) = 0

A scatter plot depicts the number of Covid-19 infected cases in China. — **Figure P13-11_B (a)** Infected People as a Function of Time

A scatter plot represents the number of people infected of COVID-19 in China. The horizontal axis represents the time in days ranging from 0 to 90 in increments of 10. The vertical axis represents the number of people ranging from 0 to 6 times 10 to the power 4 in increments of 1 times 10 to the power 4. The infected people are marked as dots and a curve is drawn exhibiting the trend. The number of cases increases to 6 times 10 to the power 4 from 0 in 30 days and then gradually decreases to 0 cases in 75 days. Note: The above-mentioned values are approximate.

A scatter plot depicts the number of Covid-19 death cases in China. — **Figure P13-11_B (b)** Dead People as a Function of Time

A scatter plot represents the number of death cases in China due to COVID-19. The horizontal axis represents the time in days ranging from 0 to 90 in increments of 10 days. The vertical axis represents the number of people ranging from 0 to 4000 times 10 to the power 9 in increments of 500 times 10 to the power 9. The infected people are marked as dots and a curve is drawn along them to exhibit the trend. The number of death cases keeps gradually increasing from day 1 to end at 3500 times 10 to the power 9 in a span of 80 days. Note: The above-mentioned values are approximate.

A scatter plot depicts the number of healthy people despite Covid-19 in China. — **Figure P13-11_B (c)** Healthy People as a Function of Time

A scatter plot represents the number of healthy cases in China despite of COVID-19. The horizontal axis represents the time in days ranging from 0 to 90 in increments of 10 days. The vertical axis represents the number of people ranging from 1.38634 times 10 to the power 9 to 13.3864 times 10 to the power 9. The healthy people are marked as dots and a curve is drawn along them to exhibit the trend. The number of healthy cases keeps gradually decreasing from 1.3864 times 10 to the power 9 in day 1 to 1.38634 times 10 to the power 9 in 30 days. It then gradually increases back to 1.3864 times 10 to the power 9 in 70 days. Note: The above-mentioned values are approximate.

• Additional Homework Problems

A number of homework problems that can be used for exams or supplementary problems or examples are found on the CRE Web site, www.umich.edu/~elements/6e/index.html.

SUPPLEMENTARY READING

1. A number of solved problems for batch and semibatch reactors can be found in

S. M. WALAS, Chemical Reaction Engineering Handbook. Amsterdam: Gordon and Breach, 1995, pp. 386–392, 402, 460–462, and 469.

Safety

DANIEL A. CROWL and JOSEPH F. LOUVAR, Chemical Process Safety: Fundamentals with Applications, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2001.

T. F. EDGAR, “From the Classical to the Postmodern Era,” Chem. Eng. Educ., 31, 12 (1997).

TREVOR A. KLETZ, “Bhopal Leaves a Lasting Legacy: The Disaster Taught Some Hard Lessons That the Chemical Industry Still Sometimes Forgets,” Chemical Processing, p. 15 (Dec. 2009).

Links

1. Be sure to review the author’s Web site Process Safety Across the Chemical Engineering Curriculum (http://umich.edu/~safeche/index.html). In particular, review the tutorials (e.g., the BowTie Diagram).

2. The SAChE Web site has a great discussion on reactor safety with examples (www.sache.org). You will need a username and password; both can be obtained from your department chair. Hit the 2003 Tab. Go to K Problems.

3. The reactor lab developed by Professor Herz and discussed in Chapters 4 and 5 could also be used here: www.reactorlab.net.

4. See the Center for Chemical Process Safety (CCPS) Web site, www.aiche.org/ccps/.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 13. Unsteady-State Nonisothermal Reactor Design

Create new playlist

Sign In

Sign Up

13. Unsteady-State Nonisothermal Reactor Design

13.1 The Unsteady-State Energy Balance

13.2 Energy Balance on Batch Reactors (BRs)

13.2.1 Adiabatic Operation of a Batch Reactor

13.2.2 Case History of a Batch Reactor with Interrupted Isothermal Operation Causing a Runaway Reaction

13.3 Batch and Semibatch Reactors with a Heat Exchanger

13.3.1 Startup of a CSTR

13.3.2 Semibatch Operation

13.4 Nonisothermal Multiple Reactions

13.5 And Now… A Word from Our Sponsor–Safety 13 (AWFOS–S13 Safety Analysis of the T2 Laboratories Incident)

Safety Analysis of the Incident

Summary

CRE WEB SITE MATERIALS(http://www.umich.edu/~elements/6e/13chap/obj.html#/)

QUESTIONS, SIMULATIONS, AND PROBLEMS

Questions

Computer Simulations and Experiments

Problems

SUPPLEMENTARY READING

Table of Contents for
13. Unsteady-State Nonisothermal Reactor Design

CRE WEB SITE MATERIALS
(http://www.umich.edu/~elements/6e/13chap/obj.html#/)