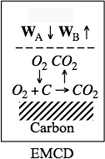
14. Mass Transfer Limitations in Reacting Systems

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

14. Mass Transfer Limitations in Reacting Systems

Giving up is the ultimate tragedy.

—Robert J. Donovan

It ain’t over ’til it’s over.

—Yogi Berra NY Yankees

Overview. Many industrial reactions are carried out at high temperatures where the overall rate of reaction is limited by the rate of mass transfer of reactants between the bulk fluid and the catalytic surface. By mass transfer, we mean any process in which diffusion plays a role. Under these circumstances our generation term becomes a little more complicated as we cannot directly use the rate laws discussed in Chapter 3. Now we have to consider the fluid velocity and the fluid properties when writing the mole balance. In the rate laws and catalytic reaction steps described in Chapter 10 (diffusion, adsorption, surface reaction, desorption, and diffusion), we neglected the diffusion steps.

In this chapter we discuss how to determine the rate of reaction and how to size reactors when the reactions are limited by mass transfer. To do this we

Present the fundamentals of diffusion and molar flux, and then write the mole balance in terms of the mole fluxes for rectangular and for cylindrical coordinates (Section 14.1).
Incorporate Fick’s first law into our mole balance in order to describe flow, diffusion, and reaction (Section 14.2).
Model diffusion through a stagnant film to a reacting surface (Section 14.3).
Introduce the mass transfer coefficient, k_c, and describe how it is used to design mass transfer-limited reactions (Section 14.4).
Focus on one of the engineer’s most important skills, that is, to answer “What if…” questions, as Robert the Worrier does (Section 14.5).

The Algorithm

1. Mole balance

2. Rate law

3. Stoichiometry

4. Combine

5. Evaluate

14A Mass Transfer Fundamentals

14.1 Diffusion Fundamentals

The first step in our CRE algorithm is the mole balance, which we now need to extend to include the molar flux, W_A_z, and diffusional effects. The molar flow rate of A in a given direction, such as the z direction down the length of a tubular reactor, is just the product of the flux, W_A_z (mol/m² • s), and the cross-sectional area, A_c (m²); that is,

F_A_z = A_c W_A_z

In the previous chapters, we have only considered plug flow with no diffusion superimposed, in which case

W_{A z} = \frac{C_{A} υ}{A_{C}}

We now drop the plug-flow assumption and extend our discussion of mass transfer in catalytic and other mass transfer-limited reactions. In Chapter 10, we focused on the middle three steps (3, 4, and 5) in a catalytic reaction shown in Figure 14-1 and neglected steps (1), (2), (6), and (7) by assuming the reaction was surface-reaction limited. In this chapter, we describe the first and last steps (1) and (7), as well as showing other applications in which mass transfer plays a role.

A figure represents the heterogeneous catalytic reaction. — **Figure 14-1** Steps in a heterogeneous catalytic reaction.

An illustration of the step-by-step process of a heterogeneous catalytic reaction is shown. The steps are as follows: Step 1- A undergoes external diffusion; Step 2- A undergoes Internal diffusion; Step 3- A enters the catalytic surface; Step 4- Surface reaction takes place and A turns B; Step 5- B leaves the catalytic surface; Step 6- B undergoes Internal diffusion; Step 7- B undergoes External diffusion. The steps are also categorized as the concepts discussed in chapters 14, 15, and 10.

Where are we going??^†

^† “If you don’t know where you are going, you’ll probably wind up some place else.” Yogi Berra, NY Yankees

We want to arrive at the mole balance that incorporates both diffusion and reaction effects, such as Equation (14-17) on page 746, that is,

{D_{AB} \frac{d^{2} C_{A}}{{d z}^{2}} - U_{z} \frac{{d C}_{A}}{d z} + r}_{A} = 0

We begin with Section 14.1.1 where we write the mole balance on Species A in three dimensions in terms of the molar flux, W_A. In Section 14.1.2 we write W_A in terms of the bulk flow of A in the fluid, B_A and the diffusion flux J_A of A that is superimposed on bulk flow. In Section 14.1.3 we use the previous two subsections as a basis to finally write the molar flux, W_A, in terms of concentration using Fick’s first law, J_A, and the bulk flow, B_A. Next, in Section 14.2 we combine diffusion convective transport and reaction in our mole balance.

14.1.1 Definitions

Diffusion is the spontaneous intermingling or mixing of atoms or molecules by random thermal motion. It gives rise to motion of the species relative to motion of the mixture. In the absence of other gradients (such as temperature, electric potential, or gravitational potential), molecules of a given species within a single phase will always diffuse from regions of higher concentrations to regions of lower concentrations. This gradient results in a molar flux of the species (e.g., A), W_A (moles/area=time), in the direction of the concentration gradient. The flux of A, W_A, is relative to a fixed coordinate (e.g., the lab bench) and is a vector quantity with typical units of mol/m² · s. In rectangular coordinates

W_A = iW_A_x + jW_A_y + kW_A_z

We now apply the mole balance to species A, which flows and reacts in an element of volume ΔV = ΔxΔyΔz to obtain the variation of the molar fluxes in three dimensions.

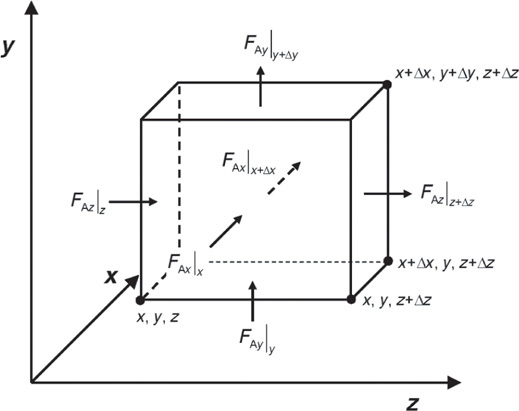
An illustration of the molar flux during diffusion in a rectangular 3 dimensional structure is shown. — A three-dimensional plane is shown. A cuboid is positioned in the plane representing a molecule. The vertex at the left-bottom on the front side of the cuboid is (x, y, z). The vertex at the right-bottom on the front side of the cuboid is (x, y, z plus delta z) and the vertex at the bottom right at the rear end is (x plus delta x, y, z plus delta z) and the vertex vertically above it is (x plus delta x, y plus delta y, z plus delta y). The flux at the face of the cuboid is F subscript A X at x and on the rear side it is F subscript A X at x plus delta x. The flux on the bottom side of the cuboid is F subscript A Y at y and on the upper side it is F subscript A Y at y plus delta y. The flux on the left side of the cuboid is F subscript A Z at z and on the right side it is F subscript A Z at z plus delta z.

F_Az = W_AzΔxΔy

F_Ay = W_AyΔxΔz

F_Ax = W_AxΔzΔy

\begin{array}{l} \begin{matrix} \begin{matrix} {[\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ in \end{matrix}]}_{z} - {[\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ out \end{matrix}]}_{z + Δ z} + [\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ in \end{matrix}] - {[\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ out \end{matrix}]}_{y + Δ y} + \\ {\begin{matrix} Δ x Δ y W \end{matrix}}_{A z | z} - Δ x Δ y W_{A z | z+ Δ z} + {\begin{matrix} Δ x Δ z W \end{matrix}}_{A y | y} - Δ x Δ z W_{Ay | y + Δ y} + \end{matrix} \\ {[\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ in \end{matrix}]}_{x} - {[\begin{matrix} \begin{matrix} Molar \\ flow rate \end{matrix} \\ out \end{matrix}]}_{x + Δ x} + [\begin{matrix} Rate of \\ generation \end{matrix}] = [\begin{matrix} Rate of \\ accumulation \end{matrix}] \end{matrix} \\ {\begin{matrix} Δ z Δ y W \end{matrix}}_{A x | x} - Δ z Δ y W_{A x} |_{x + Δ x} + r_{A} Δ x Δ y Δ z = Δ x Δ y Δ z \frac{\partial C_{A}}{\partial t} \end{array}

Mole balance

where r_A is the rate of generation of A by reaction per unit volume (e.g., mol/m³/h).

Dividing by ΔxΔyΔz and taking the limit as they go to zero, we obtain the molar flux balance in rectangular coordinates

$\begin{matrix} \begin{matrix} \begin{matrix} - \frac{\partial W_{A x}}{\partial x} - \frac{\partial W_{Ay}}{\partial y} - \frac{\partial W_{A z}}{\partial z} + r_{A} = \frac{\partial C_{A}}{\partial t} \end{matrix} \end{matrix} \end{matrix} \begin{matrix} (14-1) \end{matrix}$

The corresponding balance in cylindrical coordinates with no variation in the rotation about the z-axis is

COMSOL

$\begin{matrix} - \frac{1}{r} \frac{\partial}{\partial r} (r W_{A r}) - \frac{\partial W_{A z}}{\partial z} + r_{A} = \frac{\partial C_{A}}{\partial t} \end{matrix} \begin{matrix} (14-2) \end{matrix}$

We will now evaluate the flux terms W_A. We have taken the time to derive the molar flux equations in this form because they are now in a form that is consistent with the partial differential equation (PDE) solver COMSOL, which is accessible from the CRE Web site.

14.1.2 Molar Flux: W_A

The molar flux of A, W_A, is the result of two contributions: J_A, the molecular diffusion flux relative to the bulk motion of the fluid produced by a concentration gradient, and B_A, the flux resulting from the bulk motion of the fluid:

Total flux = diffusion + bulk motion

$\begin{matrix} W_{A} = J_{A} + B_{A} \end{matrix} \begin{matrix} (14-3) \end{matrix}$

The bulk-flow term for species A is the total flux of all molecules relative to a fixed coordinate times the mole fraction of A, y_A; that is, B_A = y_A Σ W_i.

For a two-component system of A diffusing in B, the flux of A is

\begin{matrix} W_{A} = J_{A} + y_{A} (W_{A} + W_{B}) & (14-4) \end{matrix}

The diffusional flux, J_A, is the flux of A molecules that is superimposed on the bulk flow. It tells how fast A is moving ahead of the bulk flow velocity, that is, the molar average velocity.

The flux of species A, W_A, is wrt a fixed coordinate system (e.g., the lab bench) and is just the concentration of A, C_A, times the particle velocity of species A, U_A, at that point

$\begin{matrix} W_{A} = U_{A} C_{A} \\ \frac{mol}{m^{2} S} = (\frac{m}{s}) (\frac{mol}{m^{3}}) \end{matrix}$

By particle velocities, we mean the vector average of millions of molecules of A at a given point. Similarly for species B: W_B = U_BC_B; substituting into the bulk-flow term

B_A = y_A Σ W_i = y_A (W_A + W_B) = y_A (C_A U_A + C_BU_B

Writing the concentration of A and B in the generic form in terms of the mole fraction, y_i, and the total concentration, c, that is, C_i = y_ic, and then factoring out the total concentration, c, the bulk flow, B_A, is

B_A = (c y_A)(y_A U_A + y_B U_B) = C_A U

Molar average velocity U

where U is the molar average velocity: U = Σy_i U_i. The molar flux of A can now be written as

$\begin{matrix} W_{A} = J_{A} + C_{A} U \end{matrix} \begin{matrix} (14-5) \end{matrix}$

We now need to determine the equation for the molar flux of A, J_A, that is superimposed on the molar average velocity.

14.1.3 Fick’s First Law

Experimentation with frog legs led to Fick’s first law.

Our discussion on diffusion will be restricted primarily to binary systems containing only species A and B. We now wish to determine how the molar diffusive flux of a species (i.e., J_A) is related to its concentration gradient. As an aid in the discussion of the transport law that is ordinarily used to describe diffusion, recall similar laws from other transport processes. For example, in conductive heat transfer the constitutive equation relating the heat flux q and the temperature gradient is Fourier’s law, q = −k_t ∇ T, where k_t is the thermal conductivity.

Constitutive equations in heat, momentum, and mass transfer

In rectangular coordinates, the gradient is in the form

$\nabla = i \frac{\partial}{\partial x} + j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z}$

The mass transfer law for the diffusional flux of A resulting from a concentration gradient is analogous to Fourier’s law for heat transfer and is given by Fick’s first law^†

^† Adolf Fick was an interesting character as evidenced by his use of frogs to study diffusion.

$\begin{matrix} {J_{A} = - D_{AB} \nabla C}_{A} & (14-6) \end{matrix}$

D_AB is the diffusivity of A in B $(\frac{m^{2}}{s})$ . Combining Equations (14-5) and (14-6), we obtain an expression for the molar flux of A in terms of concentration for constant total concentration

Molar flux equation

$\begin{matrix} W_{A} = - D_{AB} \nabla C_{A} + C_{A} U \end{matrix} \begin{matrix} (14-7) \end{matrix}$

In one dimension, that is, z, the molar flux term is

$\begin{matrix} {W_{A z} = - D}_{AB} \frac{{d C}_{A}}{d z} + C_{A} U_{Z} & (14-8a) \end{matrix}$

Where U_z is the axial velocity, in radial coordinates with no variations in the angular (θ) direction

$\begin{matrix} {W_{A r} = - D}_{AB} \frac{{d C}_{A}}{d z} + C_{A} U_{r} & (14-8b) \end{matrix}$

Where U_r is the fluid’s radial velocity

14.2 Binary Diffusion

Although many systems involve more than two components, the diffusion of each species can be treated as if it were diffusing through another single species rather than through a mixture by defining an effective diffusivity.

14.2.1 Evaluating the Molar Flux

Now the task is to evaluate the bulk-flow term.

We now consider A diffusing in B. Substituting Equation (14-6) into Equation (14-4) we obtain

$\begin{matrix} W_{A} = - D_{AB} \nabla C_{A} + y_{A} (W_{A} + W_{B}) & (14-9) \end{matrix}$

Before going to Section 14.2.2 it would be helpful to evaluate the bulk flow term (y_A (W_A + W_B)) for five limiting situations. These situations are given by Equations 14-10 through 14-13 in Table 14-1 on page 745.

An illustration of the oxidation of a solid carbon is shown. — TABLE 14-1 EVALUATING W_A FOR SPECIES A DIFFUSING IN SPECIES B

An illustration of a liquid in a test tube is shown. The liquid evaporates into the air and the diffusion process here is highlighted as W subscript A. — TABLE 14-1 EVALUATING W_A FOR SPECIES A DIFFUSING IN SPECIES B

¹ C. N. Satterfield, Mass Transfer in Heterogeneous Catalysis, Cambridge: MIT Press, 1970, pp. 41–42, discusses Knudsen flow in catalysis and gives the expression for calculating D_K.

14.2.2 Diffusion and Convective Transport

When accounting for diffusional effects, the molar flow rate of species A, F_A, in a specific direction z, is the product of molar flux in that direction, W_A_z, and the cross-sectional area normal to the direction of flow, A_c

F_A_z = A_cW_A_z

In terms of concentration, the flux is

{{W_{A Z} = - D}_{AB} \frac{{d C}_{A}}{d z} + C_{A} U}_{z}

The molar flow rate is

$\begin{matrix} F_{A z} = W_{A z} A_{C} = [{- D}_{AB} \frac{{d C}_{A}}{d z} + {C_{A} U}_{z}] A_{C} & (14-14) \end{matrix}$

Similar expressions follow for W_A_x and W_A_y. Substituting for the flux W_A_x, W_A_y, and W_A_z into Equation (14-1), we obtain

Flow, diffusion, and reaction

This form is used in COMSOL Multiphysics.

$\begin{matrix} D_{AB} [\frac{{\partial^{2} C}_{A}}{{\partial x}^{2}} + \frac{{\partial^{2} C}_{A}}{{\partial y}^{2}} + \frac{{\partial^{2} C}_{A}}{{\partial z}^{2}}] - U_{x} \frac{{\partial C}_{A}}{\partial x} - U_{y} \frac{{\partial C}_{A}}{\partial y} - U_{z} \frac{{\partial C}_{A}}{\partial z} + r_{A} = \frac{{\partial C}_{A}}{\partial t} \end{matrix} \begin{matrix} (14-15) \end{matrix}$

In terms of axial and radial coordinates with no angular variation and no radial velocity U_r we have

$\begin{matrix} D_{AB} [\frac{\partial}{\partial r} (\frac{{r d C}_{A}}{\partial r}) + \frac{{\partial^{2} C}_{A}}{{\partial z}^{2}}] - U_{z} \frac{{\partial C}_{A}}{\partial z} + r_{A} = \frac{{\partial C}_{A}}{\partial t} & (14-16) \end{matrix}$

Equation (14-15) and (14-16) are in a user-friendly form to apply to the PDE solver, COMSOL. For one dimension at steady state, Equation (14-15) reduces to

$\begin{matrix} \begin{matrix} D_{A B} \frac{d^{2} C_{A}}{d z^{2}} - U_{z} \frac{d C_{A}}{d z} + r_{A} = 0 \end{matrix} \end{matrix} \begin{matrix} (14-17) \end{matrix}$

In order to solve Equation (14-17) we need to specify the boundary conditions. In this chapter we will consider some of the simple boundary conditions, and in Chapter 18 we will consider the more complicated boundary conditions, such as the Danckwerts’ boundary conditions.

We will now use this form of the molar flow rate in our mole balance in the z direction of a tubular flow reactor

$\frac{{d F}_{A}}{d V} = \frac{d (A_{c} W_{A z})}{d (A_{c} z)} = \frac{{d W}_{A z}}{d z} = r_{A}$

However, we first have to discuss the boundary conditions in solving this equation.

14.2.3 Boundary Conditions

The most common boundary conditions are presented in Table 14-2.

An illustration of the boundary of a reactant is shown. The concentration at the boundary is marked as z equals 0 and C subscript A equals C subscript A0. — TABLE 14-2 TYPES OF BOUNDARY CONDITIONS

An illustration of portion of the boundary of the reactant is shown. It is marked as W subscript A equals 0 indicating there is no mass transfer. — TABLE 14-2 TYPES OF BOUNDARY CONDITIONS

14.2.4 Temperature and Pressure Dependence of D_AB

Before closing this brief discussion on mass-transfer fundamentals, further mention should be made of the diffusion coefficient. Equations for predicting gas diffusivities are given by Fuller and are also given in Perry’s Handbook.^2,3 The orders of magnitude of the diffusivities for gases, liquids, and solids and the manner in which they vary with temperature and pressure are given in Table 14-3.⁴ We note that the Knudsen, liquid, and solid diffusivities are independent of total pressure.

² E. N. Fuller, P. D. Schettler, and J. C. Giddings, Ind. Eng. Chem., 58(5), 19 (1966).

³ R. H. Perry and D. W. Green, Chemical Engineer’s Handbook, 7th ed. New York: McGraw-Hill, 1999.

⁴ To estimate liquid diffusivities for binary systems, see K. A. Reddy and L. K. Doraiswamy, Ind. Eng. Chem. Fund., 6, 77 (1967).

TABLE 14-3 DIFFUSIVITY RELATIONSHIPS FOR GASES, LIQUIDS, AND SOLIDS

	Order of Magnitude
Phase	cm²/s	m²/s	Temperature and Pressure Dependences^a
Gas
Bulk	10⁻¹	10⁻⁵	$D_{AB} (T_{2}, P_{2}) = D_{AB} (T_{1}, P_{1}) \frac{P_{1}}{P_{2}} {(\frac{T_{2}}{T_{1}})}^{1.75}$
Knudsen	10⁻²	10⁻⁶	${D_{A} (T_{2}) = D_{A} (T_{1}) (\frac{T_{2}}{T_{1}})}^{1 / 2}$
Liquid	10⁻⁵	10⁻⁹	$D_{AB} (T_{2}) = D_{AB} (T_{1}) \frac{μ_{1}}{μ_{2}} (\frac{T_{2}}{T_{1}})$
Solid	10⁻⁹	10⁻¹³	$D_{AB} (T_{2}) = D_{AB} (T_{1}) exp [\frac{E_{D}}{R} (\frac{T_{2} - T_{1}}{T_{1} T_{2}})]$

^aμ₁, μ₂, liquid viscosities at temperatures T₁ and T₂, respectively; E_D, diffusion activation energy.

It is important to know the magnitude and the T and P dependence of the diffusivity.

A trend graph on the diffusivity D subscript AB of a gas with respect to pressure P is shown. The diffusivity keeps decreasing with increase in pressure.

A trend graph plots the diffusivity D subscript AB of a liquid with respect to temperature T is shown. The diffusivity keeps increasing with increase in temperature.

14.3 Modeling Diffusion with Chemical Reaction

We now consider the situation where species A does not react as it diffuses through a hypothetical stagnant film to a surface where it does react. In Chapter 15 we consider the case when species A does react as it diffuses through a stagnant film. Table 14-4 provides an algorithm for both of these situations.

TABLE 14-4 STEPS IN MODELING CHEMICAL SYSTEMS WITH DIFFUSION AND REACTION

Define the problem and state the assumptions.
Define the system on which the balances are to be made.
Perform a differential mole balance on a particular species.
Obtain a differential equation in W_A by rearranging your balance equation properly and taking the limit as the volume of the element goes to zero.
Substitute the appropriate expression involving the concentration gradient for W_A from Section 14.2 to obtain a second-order differential equation for the concentration of A.^a
Express the reaction rate r_A (if any) in terms of concentration and substitute into the differential equation.
State the appropriate boundary and initial conditions.
Put the differential equations and boundary conditions in dimensionless form.
Solve the resulting differential equation for the concentration profile.
Differentiate this concentration profile to obtain an expression for the molar flux of A.
Substitute numerical values for symbols.

^aIn some instances it may be easier to integrate the resulting differential equation in Step 4 before substituting for WA.

The purpose of presenting algorithms (e.g., Table 14-4) to solve reaction engineering problems is to give the readers a starting point or framework with which to work if they were to get stuck. It is expected that once readers are familiar and comfortable using the algorithm/framework, they will be able to move in and out of the framework as they develop creative solutions to nonstandard chemical reaction engineering problems.

Use Table 14-4 to Move In ⇄ Out of the algorithm (Steps 1 → 10) to generate creative solutions.

14.3.1 Diffusion through a Stagnant Film to a Particle

We will first discuss the diffusion of reactants from the bulk fluid to the external surface of a particle that is either solid or liquid. Here our attention will focus on the flow past a single particle as shown in Figure 14-2(a) and its corresponding boundary layer shown in Figure 14-2(b). The particle can be either a liquid droplet, a catalyst pellet or a combustible solid grain. The reaction takes place only on the external surface and not in the fluid surrounding it. The fluid velocity in the vicinity of the spherical pellet will vary with position around the sphere. The hydrodynamic boundary layer is usually defined as the distance from a solid object to where the fluid velocity is 99% of the bulk velocity, U₀. Similarly, the mass transfer boundary-layer thickness, =, is defined as the distance from a solid object to where the concentration of the diffusing species reaches 99% of the bulk concentration.

A reasonable representation of the concentration profile for a reactant A diffusing to the external surface is shown in Figure 14-2. As illustrated, the change in concentration of A from C_A_b to C_A_s takes place in a very narrow fluid layer next to the surface of the sphere. Nearly all of the resistance to mass transfer is found in this layer.

A figure depicts the boundary layer around a spherical particle. — **Figure 14-2** Boundary layer around the surface of spherical particle.

Two images are shown. An illustration of a spherical particle and the hydrodynamic boundary layer at a distance along the circumference of the particle is shown, and it is marked with intermittent lines. The concentration of the particle is C subscript As and the concentration of the boundary layer is C subscript Ab. An illustration of a section of the boundary layer of a spherical particle is shown. The thickness (z) of the film in between the spherical particle and the boundary layer is delta. The concentration changes from C subscript A s in the spherical particle to C subscript A b in the boundary layer.

The concept of a hypothetical stagnant film within which all the resistance to external mass transfer exists

A useful way of modeling diffusive transport is to treat the fluid layer next to a solid boundary as a hypothetical stagnant film of thickness δ, which we cannot measure. We say that all the resistance to mass transfer is found (i.e., lumped) within this hypothetical stagnant film of thickness δ, and the properties (i.e., concentration, temperature) of the fluid at the outer edge of the film are identical to those of the bulk fluid. This model can readily be used to solve the differential equation for diffusion through a stagnant film. The dashed line in Figure 14-2(b) represents the concentration profile predicted by the hypothetical stagnant film model, while the solid line gives the actual profile. If the film thickness is much smaller than the radius of the pellet (which is usually the case), curvature effects can be neglected. As a result, only the one-dimensional diffusion equation must be solved, as shown in Figure 14-3.

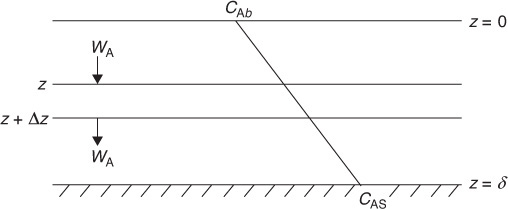
Figure 14-3 Concentration profile for dilute concentration in stagnant film mode.

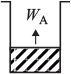
We are going to carry out a mole balance on species A diffusing through the fluid between z = z and z = z + Δz at steady state for the unit cross-sectional area, A_c

$\begin{matrix} In & - & Out & + & Generation & = & Accumulation \\ W_{A z} |_{z} & - & W_{A z} |_{z+ Δ z} & + & 0 & = & 0 \end{matrix}$

dividing by Δz and taking the limit as Δz → 0

$\frac{{d W}_{A z}}{d z} = 0$

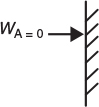
For diffusion through a stagnant film at dilute concentrations

$\begin{matrix} J_{A} ≫ y_{A} (W_{A} + W_{B}) & (14-23) \end{matrix}$

or for EMCD, we have using Fick’s first law

$\begin{matrix} W_{A z} = - D_{AB} \frac{{d C}_{A}}{d z} & (14-24) \end{matrix}$

Substituting for W_A_z and dividing by D_AB we have

$\frac{{d^{2} C}_{A}}{{d z}^{2}} = 0$

Integrating twice to get C_A = K₁z + K₂, using the boundary conditions at

\begin{matrix} z = 0 & C_{A} = C_{A b} \\ z = δ & C_{A} = C_{A s} \end{matrix}

we obtain the concentration profile

\begin{matrix} C_{A} = C_{A b} + (C_{A s} - C_{A b}) \frac{z}{δ} \end{matrix} \begin{matrix} (14 -25) \end{matrix}

To find the flux to the surface we substitute Equation (14-25) into Equation (14-24) to obtain

\begin{matrix} W_{A z} = \frac{D_{AB}}{δ} [C_{A b} - C_{As}] \end{matrix} \begin{matrix} (14-26) \end{matrix}

At steady state the flux of A to the surface will be equal to the rate of reaction of A on the surface. We also note that another example of diffusion through a stagnant film as applied to transdermal drug delivery is given in the Chapter 14 Expanded Material on the CRE Web site.

14.4 The Mass Transfer Coefficient

We now interpret the ratio (D_AB/δ ) in Equation (14-26).

While the boundary-layer thickness will vary around the sphere, we will take it to have a mean film thickness δ. The ratio of the diffusivity D_AB to the film thickness δ is the mass transfer coefficient, k_c, that is,

$\begin{matrix} k_{c} = \frac{D_{AB}}{δ} \end{matrix} \begin{matrix} (14-27) \end{matrix}$

Combining Equations (14-26) and (14-27), we obtain the average molar flux from the bulk fluid to the surface

$\begin{matrix} W_{A z} = k_{c} (C_{A b} - C_{As}) \end{matrix} \begin{matrix} (14-28) \end{matrix}$

The mass transfer coefficient

In this stagnant film model, we consider all the resistance to mass transfer to be lumped into the thickness δ. The reciprocal of the mass transfer coefficient can be thought of as this resistance

$\begin{matrix} W_{A z} = Flux = \frac{Driving force}{Resistance} = \frac{C_{A b} - C_{As}}{(1 / k_{c})} \end{matrix} \begin{matrix} (14-29) \end{matrix}$

Molar flux of A to the surface

How Do I find the Mass Transfer Coefficient? The mass transfer coefficient is found either by experimentation or from correlations analogous to what one finds for a heat transfer coefficient. These correlations are usually in the form of the Sherwood number, Sh, as a function of the Reynolds number, Re, and the Schmidt number, Sc, that is,

$\begin{matrix} Sh = f (Re, Sc) & (14-30) \end{matrix}$

where

Sherwood

$\begin{matrix} Sh = \frac{k_{c} ″ L ″}{D_{AB}} & (14-31) \end{matrix}$

Schmidt

$\begin{matrix} Sc = \frac{υ}{D_{AB}} = \frac{μ / ρ}{D_{AB}} & (14 -32) \end{matrix}$

Reynolds

$\begin{matrix} Re = \frac{U ″ L ″}{υ} = \frac{U ″ L ″ ρ}{μ} & (14-33) \end{matrix}$

where

″L″ is the characteristic length (m) (e.g., d_P, diameter of the particle)

υ = Kinematic viscosity (m²/s) = μ/ρ

μ = viscosity (kg/m · s)

ρ = density (kg/m³)

U = free stream velocity (m/s)

D_AB = diffusivity (m²/s)

As an example, the mass transfer coefficient for flow around a single spherical particle can be found from the Frössling correlation.^†

^†N. Frössling, Gerlands Beitr. Geophys., 52, 170 (1938).

$\begin{matrix} Sh = 2 + 0.6 {Re}^{1 / 2} {Sc}^{1 / 3} & (14-34) \end{matrix}$

For turbulent flow, the number 2 in this equation can be neglected with respect to the second term and the resulting correlation is shown in Table 14-5.^‡

^‡ Just out… An article in August 2019 issue of the AIChE Journal expands this correlation. Y. Wang and J G. Brasseur, “Enhancement of mass transfer from particles by local shear-rate and correlations with application to drug dissolution,” AIChE J., 65 (8), (August 2019). Equation (14-34) is derived for dissolution in an infinite fluid while Professor Wang’s article AIChE J. discusses dissolution in a confined domain. The corrections are particularly important at low Reynolds number and this article guides you through these corrections. However, the nomenclature is different. For example, the Sherwood number is given as Sh = R/δ, so it might help if you referred to Professor Wang’s earlier article 2012 Y. Yang, et.al., Mol. Pharm., 9, 1052 (2012).

The correlation given for low Re is reported as

Sh = Sh₀ + 0.0177 Re^0.46 Sc^0.68

where Sh₀ is a function of the Schmidt number Sc. For example, when

5 < Sc < 100

then

Sh₀ = 1.2 + Sc^0.82

Other values of Sh₀ are given in Professor Wang’s article.

After calculating the numerical value of Sh, given the parameters to calculate Re and Sc, the mass transfer coefficient can be calculated

$\begin{matrix} \begin{matrix} k_{c} = \frac{Sh D_{AB}}{d_{p}} \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} (m/s) \end{matrix} \end{matrix} \end{matrix} (14-35) \end{matrix}$

Correlation for geometries other than a single spherical particle are given in Table 14-5.

TABLE 14-5 MASS TRANSFER CORRELATIONS

Turbulent flow, mass transfer to pipe wall	Sh = .332 (Re)^1/2 (Sc)^1/3
Mass transfer to a single sphere	Sh = 2 = 0.6 Re^1/2 Sc^1/3
Mass transfer in fluidized beds	${ϕ J}_{D} = \frac{0.765}{{Re}^{82}} + \frac{0.365}{{Re}^{0.386}}$
Mass transfer to packed beds	ϕJ_D = 0.453 Re^0.453
	$J_{D} = \frac{Sh}{{ReSc}^{1 / 3}}$

What if I cannot find the mass transfer correlation for my situation or geometry? In this case, see whether a correlation for the heat transfer coefficient exists and then go to (http://www.umich.edu/~elements/6e/14chap/obj.html#/additional-materials/) to learn how to turn that heat transfer correlation into a mass transfer correlation.

The Sherwood, Reynolds, and Schmidt numbers are used in forced convection mass transfer correlations.

14B Applications

14.5 Mass Transfer to a Single Particle

Mass transfer to single particles is important in catalytic reactions and in dust explosions. In this section we consider two limiting cases of diffusion and reaction on a catalyst particle.⁵ In the first case, the reaction is so rapid that the rate of diffusion of the reactant to the surface limits the reaction rate. In the second case, the reaction is so slow that virtually no concentration gradient exists in the gas phase (i.e., rapid diffusion with respect to surface reaction).

⁵ A comprehensive list of correlations for mass transfer to particles is given by G. A. Hughmark, Ind. Eng. Chem. Fund., 19(2), 198 (1980).

14.5.1 First-Order Rate Laws

To easily show the limitations of mass transfer and reaction rate we will consider first order kinetics. For the case of either the burning of a combustible dust particle or for reaction on a catalyst surface at high temperatures, the rate law is taken as apparent first order.

Figure 14-4 shows the mass transfer flux of A to the surface, W_A, the reaction on the surface $r_{A s}^{″}$ , and the mass transfer flux of B away from the surface. In the examples discussed here species A can be thought of as oxygen and B as the combustion products, for example, CO₂. The reaction on the surface is taken as apparent first order.

$\begin{matrix} - r_{A s}^{″} = {k_{r} C}_{As} & (14-36) \end{matrix}$

An illustration depicts the diffusion process on a pellet. — **Figure 14-4** Diffusion to, and reaction on, external surface of pellet.

An illustration depicts the mass transfer and reaction of two particles A and B. The particle B is spherical with a diameter d subscript p. The boundary layer is at a distance delta along the circumference of the particle B. The concentration of the particle B is C subscript A s and the concentration of the boundary layer is C subscript A. It is also mentioned that the concentration of boundary layer is greater than the concentration of the particle. A mass transfer flux of W subscript A r is exerted from the particle A on B for which a reaction force of r subscript A s double prime is shown by the particle B which leads to a mass transfer flux of W subscript B r exiting the particle B.

Using boundary conditions 2b. and 2c. in Table 14-2, we obtain

\begin{matrix} W_{A| surface} = {- r}_{A s}^{″} & (14-37) \end{matrix}

\begin{matrix} W_{A} = k_{c} (C_{A} - C_{A s}) = k_{r} C_{A s} & (14-38) \end{matrix}

The concentration at the surface, C_A_s, is not as easily measured as is the bulk concentration, C_A. Consequently, we need to eliminate C_A_s from the equation for the flux and rate of reaction. Solving Equation (14-38) for C_A_s yields

\begin{matrix} C_{A s} = \frac{k_{c} C_{A}}{k_{r} + k_{c}} & (14-39) \end{matrix}

and the rate of reaction on the surface becomes

Molar flux of A to the surface is equal to the rate of consumption of A on the surface.

$\begin{matrix} W_{A} = {- r}_{A s}^{″} = \frac{{k_{c} k_{r} C}_{A}}{k_{r} + k_{c}} \end{matrix} \begin{matrix} (14-40) \end{matrix}$

One will often find the flux to or from the surface written in terms of an effective transport coefficient k_eff

\begin{matrix} W_{A} = {- r}_{A s}^{″} = k_{eff} C_{A} & (14-41) \end{matrix}

where

\begin{matrix} k_{eff} = \frac{{k_{c} k}_{r}}{k_{c} + k_{r}} & (14-42) \end{matrix}

We will now consider the extremes of rapid and slow reaction at the particle surface.

14.5.2 Limiting Regimes

Rapid Reaction. We first consider how the overall rate of reaction may be increased when the rate of mass transfer to the surface limits the overall rate of reaction. Under these circumstances, the specific reaction-rate constant is much greater than the mass transfer coefficient

$k_{r} ≫ k_{c}$

and

k_eff = k_c

$\begin{matrix} W_{A} = - r_{As}^{″} = \frac{k_{c} C_{A}}{1 + k_{c} / k_{r}} \approx k_{c} C_{A} & (14-43) \end{matrix}$

To increase the rate of reaction per unit surface area of a solid sphere, one must increase C_A and/or k_c. In this gas-phase catalytic reaction example, and for most liquids, the Schmidt number is sufficiently large that the number 2 in Equation (14-34) is negligible with respect to the second term when the Reynolds number is greater than 25. As a result, Equation (14-34) gives

It is important to know how the mass transfer coefficient varies with fluid velocity, particle size, and physical properties.

$\begin{array}{r} \begin{matrix} k_{c} = 0.6 (\frac{D_{AB}}{d_{p}}) {Re}^{1 / 2} {Sc}^{1 / 3} \\ \begin{matrix} = 0.6 (\frac{D_{AB}}{d_{p}}) {(\frac{U d_{p}}{v})}^{1 / 2} {(\frac{v}{D_{AB}})}^{1 / 3} \end{matrix} \end{matrix} & (14-44) \end{array}$

$\begin{matrix} \begin{matrix} \begin{matrix} k_{c} = 0.6 \times \frac{D_{AB}^{2 / 3}}{v^{1 / 6}} \times \frac{U^{1 / 2}}{d_{p}^{1 / 2}} \end{matrix} \\ k_{c} = 0.6 \times (Term 1) \times (Term 2) \end{matrix} & (14-45) \end{matrix}$

Mass Transfer Limited

A trend graph depicts the relation between reaction rate and mass transfer when mass transfer is limited. It is a gradually increasing curve and it has a y-intercept greater than 0.

Term 1 is a function of the physical properties D_AB and ν, which depend on temperature and pressure only. The diffusivity always increases with increasing temperature for both gas and liquid systems. However, the kinematic viscosity ν increases with temperature (ν ∝ T^3/2) for gases and decreases exponentially with temperature for liquids. Term 2 is a function of flow conditions and particle size. Consequently, to increase k_c and thus the overall rate of reaction per unit surface area, one may either decrease the particle size or increase the velocity of the fluid flowing past the particle. For this particular case of flow past a single sphere, we see that if the velocity is doubled, the mass transfer coefficient and consequently the rate of reaction is increased by a factor of

(U₂/U₁)^0.5 = 2^0.5 = 1.41 or 41%

Reaction Rate Limited

Slow Reaction. Here, the specific reaction-rate constant is small with respect to the mass transfer coefficient

$\begin{matrix} k_{r} ≪ k_{c} \\ \begin{matrix} W_{A} = {- r}_{A S}^{″} = \frac{{k_{r} C}_{A}}{1 + k_{r} / k_{c}} \approx {k_{r} C}_{A} & (14-46) \end{matrix} \end{matrix}$

A trend graph depicts the relation between reaction rate and mass transfer when reaction rate is limited. The curve is a horizontal line.

Mass transfer effects are not important when the reaction rate is limiting.

The specific reaction rate is independent of the velocity of fluid and for the solid sphere considered here, independent of particle size. However, for porous catalyst pellets, k_r may depend on particle size for certain situations, as shown in Chapter 15.

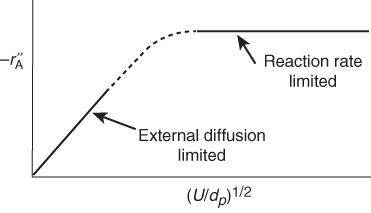
Figure 14-5 shows the variation in reaction rate with Term 2 in Equation (14-45), the ratio of velocity to particle size. At low velocities, the mass transfer boundary-layer thickness is large and diffusion limits the reaction. As the velocity past the sphere is increased, the boundary-layer thickness decreases, and the mass transfer across the boundary layer no longer limits the rate of reaction. One also notes that for a given (i.e., fixed) velocity, reaction-limiting conditions can be achieved by using very small particles. However, the smaller the particle size, the greater the pressure drop in a packed bed. When one is obtaining reaction-rate data in the laboratory, one must operate at sufficiently high velocities or sufficiently small particle sizes to ensure that the reaction is not mass transfer-limited when collecting data.

When collecting rate-law data, operate in the reaction-limited region.

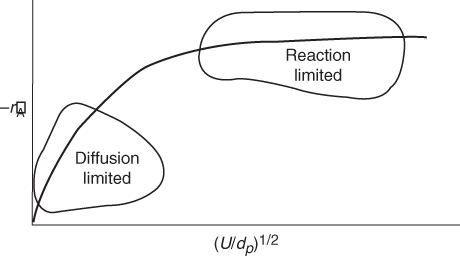
A trend graph depicts the reaction rate for diffusion limited region and reaction limited region. — **Figure 14-5** Regions of mass transfer-limited and reaction-limited reactions.

A trend graph traces the variation of reaction to the ratio of velocity to particle size. The curve initially is an gradually increasing which after a point flattens. An area at the start of the curve is marked diffusion-limited (increasing reaction rate) and an area on the end or the constant part is marked as Reaction limited.

Before we analyze Equation (14-40) in more detail, we will describe examples involving a dust particle fire of granular carbon in air and a catalyst particle in a liquid slurry. In both cases we will use k_r >> k_s so that $- r_{As}^{″} = W_{A} = k_{c} C_{A}$ .

Example 14–1 Mass Transfer of Oxygen to a Burning Carbon Particle

A schematic of the transfer of oxygen to the particle is shown in Figure 14-4. The gas-phase diffusivity in the flame (1000 K) surrounding the particle is taken as 10^–4 m²/s and the particle diameter is 50 μm (5 × 10^–5 m). The concentration of oxygen in the bulk air (21% at 1 atm and 298 K) is 8.58 mol/m³. The reaction is virtually instantaneous so that the concentration of oxygen on the surface of the particle is zero, that is, C_A_s = 0. The heat of reaction is ΔH_Rx = –93.5 kJ/mol carbon.

Calculate molar flux, W_A (mol/m²/s) and molar flow ${\dot{m}}_{A}$ (mol/s) to the particle. For a dust cloud density of 200 g/m³, calculate the heat generated per particle ${\dot{q}}_{p}$ , and the heat generated per volume of cloud.

Solution

The flux to the surface is

$\begin{matrix} W_{A} = k_{c} [C_{A \infty} - C_{As}] ≅ k_{c} C_{A \infty} & (E14-1.1) \end{matrix}$

For particles that are sufficiently small such that they are in Stoke’s flow, (i.e., it follows the fluid) the fluid velocity relative to the particle is zero, (i.e., U ≌ 0). For a single particle in Stoke’s flow, the Sherwood number for a spherical particle

Sh = 2 + 0.61 (Re^1/2 Sc^1/3) ≅ 2

reduces to

$\begin{matrix} Sh = \frac{{k_{c} d}_{p}}{D_{AB}} = 2 & (E14-1.2) \end{matrix}$

The corresponding molar flux of oxygen to the surface where it reacts virtually instantaneously (C_A_s = 0) at the surface

$\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} k_{c} = \frac{Sh}{d_{p} / D_{AB}} = \frac{2 D_{AB}}{d_{p}} = \frac{2 (10^{- 4} m^{2} / s)}{5 \times 10^{- 5} m} = 4 m/s \\ W_{A} = k_{c} (C_{A \infty}) = 2 \frac{D_{AB}}{d_{p}} C_{A \infty} \end{matrix} \end{matrix} \\ W_{A} = \frac{2 (10^{- 4} m^{2} / s)}{{50 \times 10}^{- 6} m} (8.58 \frac{mol}{m^{3}}) = {34.3 mol/m}^{2} \cdot s \end{matrix} & (E14-1.3) \end{matrix}$

The molar flux (mol/m²/s) of oxygen to one particle is

$\begin{matrix} W_{A} = - r_{A}^{″} = 34.3 {mol/m}^{2} \cdot s \end{matrix}$

The molar flow (mol/s) of oxygen, $\dot{m_{A}}$ , to one particle with surface area A_P is

${{\dot{m}}_{A} = {A_{P} W}_{A} = {π d}_{p}^{2} W_{A} = π {(50 \times 10^{- 6} m)}^{2} 34.3 mol/m}^{2} \cdot s$

$\begin{matrix} {{\dot{m}}_{A} = 2.7 \times 10}^{- 7} mol/s \end{matrix}$

Heat Effects

Now let’s estimate the heat generated for this burning particle and then for the dust cloud with n_p, the number of particles per unit volume. Figure 8.40 of Ogle^† gives the minimum dust explosion concentration, in air, Ccloud, as approximately 200 g/m³. The mass of one 50 μm carbon dust particle is

^† Ibid, page 480.

$\begin{array}{l} m_{P} = ρ_{c} V = ρ_{c} \frac{{π d}_{p}^{3}}{6} & = & ({{2.226 \times 10}^{6} g/m}^{3}) \frac{π}{6} {({5 \times 10}^{- 5})}^{3} m^{3} \\ = & {\begin{matrix} 14.5 \times 10 \end{matrix}}^{- 8} g/particle \end{array}$

The corresponding particle concentration is

$n_{P} = \frac{C_{cloud}}{m_{p}} = \frac{{200 g/m}^{3}}{{14.5 \times 10}^{- 8} g/particle}$

$\begin{matrix} {{n_{p} = 1.38 \times 10}^{9} particles/m}^{3} \end{matrix}$

The heat generated by a single particle ${\dot{q}}_{P}$ (kJ/particle) is just the molar flux of O₂ (i.e., ${- r}_{A s}^{″} = W_{A}$ ) times the surface area of particle times the heat of reaction, that is,

${\dot{q}}_{P} = (- r_{A s}^{″} A_{P}) (- {Δ H}_{Rx})$

The heat generated per unit volume of dust cloud, $\dot{Q_{g d}}$ , with a concentration of dust particles, n_P, is

${\dot{Q}}_{g d} = {n_{P} \dot{q}}_{P} = ({- r}_{A s}^{″} n_{P} A_{P}) - ({- Δ H}_{Rx})$

The rate of heat generated per particle, ${\dot{q}}_{P}$ , times the particle concentration, n_P, gives the heat generated per unit volume of dust as

${\dot{Q}}_{g d} = {n_{P} \dot{q}}_{P} = {n_{P} \dot{q}}_{P} = {n_{P} \dot{m}}_{A} ({- Δ H}_{Rx}) = \frac{{1.38 \times 10}^{9}}{m^{3}} \times 2.7 \times 10^{- 7} \frac{mol}{s} \times (93.5 \frac{kJ}{mol})$

$\begin{matrix} Q_{g d} = 34586 kJ/s \cdot m^{3} \end{matrix}$

Analysis: We calculated the molar flux as well as the mass flow of oxygen to the surface of a burning particle. The molar flux of O₂ to the surface is equal to the rate of reaction per unit surface area. Knowing the reaction rate, the dust density, and the heat of reaction we calculated the heat generated per particle and per unit volume of dust cloud.

We will continue our discussion on single dust particles when we discuss the shrinking core model. However, let’s first make a comparison with a larger particle, 0.1 cm, suspended in a body of flowing liquid.

Example 14–2 Rapid Liquid-Phase Reaction on the Surface of a Catalyst

Calculate the molar flux, W_A_r, of reactant A to a single catalyst pellet 1 cm in diameter suspended in a large body of liquid B. The reactant is present in dilute concentrations, and the reaction is considered to take place instantaneously at the external pellet surface (i.e., C_A_s ≃ 0). The bulk concentration of the reactant A is 1.0 M, and the free-stream liquid velocity past the sphere is 0.1 m/s. The kinematic viscosity (i.e., $\frac{μ}{ρ}$ ) is 0.5 centistoke (cS; 1 centistoke = 10^-6 m²/s), and the liquid diffusivity o A in B is D_AB = 10^–10 m²/s at 300 K.

If the surface reaction is rapid, then diffusion limits the overall rate.

Solution

For dilute concentrations of the solute, the radial flux is

$\begin{matrix} W_{A r} = k_{c} (C_{A b} - C_{As}) & (E14-2.1) \end{matrix}$

Because reaction is assumed to occur instantaneously on the external surface of the pellet, C_A_s = 0. Also, C_A_b is given as 1 mol/dm³.

$\begin{matrix} W_{A r} = k_{c} C_{A b} & (E14-2.2) \end{matrix}$

The mass transfer coefficient for single spheres is calculated from the Frössling correlation

$\begin{matrix} \begin{matrix} Sh & = & \frac{{k_{c} d}_{p}}{D_{AB}} = 2 + {{0.6 Re}^{1 / 2} Sc}^{1 / 3} \\ Re & = & \frac{{ρ d}_{p} U}{μ} = \frac{d_{p} U}{v} = \frac{(0.01 m) (0.1 m/s)}{{0.5 \times 10}^{- 6} m^{2} / s} = 2000 \end{matrix} & (14-34) \end{matrix}$

Liquid Phase

Re = 2000

Sc = 5000

Sh = 460

k_c = 4.6 × 10^-6 m/s

$Sc = \frac{v}{D_{AB}} = \frac{{{5 \times 10}^{- 7} m}^{2} / s}{10^{- 10} m^{2 / S}} = 5000$

Substituting these values into Equation (14-34) gives us

$\begin{matrix} {{Sh = 2 + 0.6 (2000)}^{0.5} (5000)}^{1 / 3} = 460.7 & (E14-2.3) \end{matrix}$

$\begin{matrix} \begin{matrix} k_{c} = \frac{D_{AB}}{d_{p}} Sh = \frac{10^{- 10} m^{2} / s}{0.01 m} \times 460.7 = 4.61 \times 10^{- 6} m/s & (E14-2.4) \end{matrix} \\ {\begin{matrix} {\begin{matrix} C_{A b} = 1.0 mol/dm \end{matrix}}^{3} = 10^{3} mol/m \end{matrix}}^{3} \end{matrix}$

Substituting for k_c and C_A_b in Equation (E14-2.2), the molar flux to the surface is

W_A_r = (4.61 × 10⁻⁶) m/s (10³ − 0) mol/m³ = 4.61 × 10⁻³ mol/m² · s

Because $W_{A r} = r_{A S}^{″}$ , this rate is also the rate of reaction per unit surface area of catalyst.

$\begin{matrix} {{{{- r}_{A S}^{″} = 0.0046 mol/m}^{2} \cdot s = 4.6 \times 10}^{- 5} mol/dm}^{2} \cdot s \end{matrix}$

The mass transfer flow to the particle is

$\begin{matrix} {\dot{m}}_{A} = {π d}_{p}^{2} (- r_{A}^{″}) & = & π {(0.01m)}^{2} ({0.0046 mol/m}^{2} \cdot s) \\ {\dot{m}}_{A} & = & 1.45 \times 10^{- 6} mol/s \end{matrix}$

Analysis: In this example we calculated the rate of reaction on the external surface of a catalyst pellet in a liquid reactant when external mass transfer was limiting the reaction rate. To determine the rate of reaction, we used correlations to calculate the mass transfer coefficient and then used k_c to calculate the flux to the surface, which in turn was equal to the rate of surface reaction.

14.6 The Shrinking Core Model

14.6.1 Dust Explosions, Particle Dissolution, and Catalyst Regeneration

Many situations arise in heterogeneous reactions where a gas-phase species reacts with a species contained in an inert solid matrix or solid combustible dust particles. The burning of a combustible dust is shown in Figure 14-6(a). The removal of carbon from catalyst particles that have been deactivated by fouling is shown in Figure 14-6(b) (see Section 10.7.1). The catalyst regeneration process to reactivate the catalyst by burning off the carbon is discussed in the expanded material on the CRE Web site.

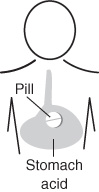
The shrinking core model is used to describe situations in which solid particles are being consumed either by dissolution or reaction and, as a result, the amount of the material being consumed is “shrinking.” For example, to design the time release of drugs into the body’s system, one must focus on the rate of dissolution of capsules and solid pills in the stomach. We now apply the shrinking core model to dust explosions where solid organic particles such as sugar are burned, to the formation of an ash layer around a burning coal particle, to catalyst regeneration. In this section we focus primarily on dust explosions and catalyst regeneration, and leave other applications such as drug delivery as exercises at the end of the chapter.

An illustration depicts burning dust particle and shell progressive regeneration of fouled pellet. — **Figure 14-6** Shell progressive regeneration of fouled pellet.

Two figures are shown. An illustration depicts the burning of a dust particle in a core. The size of the particle keeps decreasing with time. A trend graph represents the progressive regeneration of a burnt particle. The horizontal axis represents time ranging from 0 to 200 in increments of 100 and the vertical axis represents the percentage of coke burned ranging from 0 to 100 in increments of 50. The curve is a gradually increasing curve. The catalyst particle in the carbon is denoted as a shaded portion in a circle. This shaded portion keeps decreasing over time to end at a circle of carbon with no catalyst particle.

To illustrate the principles of the shrinking core model, we shall consider the burning of carbon dust particle. As the carbon continues to burn the radius of dust particles shrink from R₀ initially to R at time t as shown in Figure 14-6(a).

As shown in Figure 14-7, oxygen diffuses from the bulk gas at R_∞ to the radius R, where it reacts with carbon to form carbon dioxide, which then diffuses out from the particle. The reaction

C + O₂ → CO₂

at the solid surface is very rapid, so the rate of oxygen diffusion to the surface controls the rate of carbon removal from the core. Although the core of

Oxygen must diffuse through the porous pellet matrix until it reaches the unreacted carbon core.

An illustration of diffusion of oxygen through a porous pellet matrix. — **Figure 14-7** Sphere of radius R.

An illustration of the diffusion of oxygen through the porous pellet matrix to the surface of the carbon core and form carbon dioxide is shown. The carbon core is denoted as a shaded circle of radius R and there are three concentric circles around it of radius r, r plus delta r, and R infinity. The oxygen molecule diffuses through all these layers to the surface of the carbon core to form carbon dioxide and leaves the core again by diffusing through all the layers.

carbon is shrinking with time (an unsteady-state process), we assume the concentration profiles at any instant in time to be the steady-state profiles over the distance (R_∞ – R) when R_∞ is some larger distance from the surface of the particle, for example, R_∞ ≈ ∞. This assumption is known as the quasi-steady state assumption (QSSA).

QSSA Use steady-state profiles

To study how the radius of unreacted carbon changes with time, we must first find the rate of diffusion of oxygen to the carbon surface. Next, we perform a mole balance on the elemental carbon and equate the rate of consumption of the carbon particle to the rate of diffusion of oxygen to the gas–carbon interface.

In applying a differential oxygen mole balance over the increment Δr located somewhere between R_∞ and R, we recognize that O₂ does not react in this region and reacts only when it reaches the solid carbon interface located at r = R. We shall let species A represent O₂.

Step 1: The mole balance on O₂ (i.e., A) between r and r + Δr is

$\begin{matrix} [\begin{matrix} Rate \\ in \end{matrix}] & - & [\begin{matrix} Rate \\ out \end{matrix}] & + & [\begin{matrix} Rate of \\ generation \end{matrix}] & \begin{matrix} \begin{matrix} = \end{matrix} & [\begin{matrix} Rate of \\ accumulation \end{matrix}] \end{matrix} \\ {\begin{matrix} {\begin{matrix} W_{A r} 4 π r \end{matrix}}^{2} | \end{matrix}}_{r} & - & {\begin{matrix} {\begin{matrix} W_{A r} 4 π r \end{matrix}}^{2} | \end{matrix}}_{r + Δ r} & + & 0 & \begin{matrix} \begin{matrix} = \end{matrix} & 0 \end{matrix} \end{matrix}$

Dividing through by –4πΔr and taking the limit gives

Mole balance on oxygen

$\begin{matrix} \overset{lim}{Δ r \to 0} \frac{{{{W_{A r} r}^{2} |}_{r + Δ r} - W_{A r} r^{2} |}_{r}}{Δ r} = \frac{d ({W_{A r} r}^{2})}{d r} = 0 & (14-47) \end{matrix}$

Step 2: The constitutive equation for constant total molar concentration becomes

$\begin{matrix} W_{A r} = - D_{AB} \frac{{d C}_{A}}{d r} & (14-48) \end{matrix}$

An illustration depicts footsteps, and represents the phrase "following the algorithm".

Combining Equations (14-17) and (14-48) and dividing by (–D_AB) gives

$\begin{matrix} \frac{d}{d r} (r^{2} \frac{{d C}_{A}}{d r}) = 0 \end{matrix} \begin{matrix} (14-49) \end{matrix}$

Step 3: Boundary conditions for burning of a dust particle At a large distance from the dust particle r ~ ∞ then C_A = C_A_∞ At the dust particle’s surface, r = R then C_A = 0

Step 4: Integrating twice yields

$r^{2} \frac{{d c}_{A}}{d r} = K_{1}$

$C_{A} = \frac{{- K}_{1}}{r} + K_{2}$

Using the boundary conditions for a spherical dust particle to eliminate K₁ and K₂, the concentration profiles is

$\begin{matrix} C_{A} = C_{A \infty} (1 - \frac{R}{r}) & (14-50) \end{matrix}$

A schematic representation of the profile of O₂ is shown in Figure 14-8 at a time when the inner core has receded to a radius R. The zero on the r axis corresponds to the center of the sphere

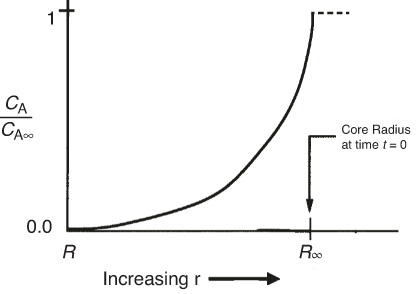
Figure 14-8 Oxygen concentration profile shown from the external radius of the pellet (R) to a large distance R_∞ from the center of the burning particle. The gas–carbon interface is located at R.

Step 5: The molar flux of O₂ to the gas–carbon interface for a dust particle is

$\begin{matrix} W_{A r} = - D_{AB} \frac{{d C}_{A}}{d r} = - \frac{D_{AB} C_{A \infty}}{R} & (14-51) \end{matrix}$

Step 6: We now carry out an overall balance on elemental carbon. Elemental carbon does not enter or leave the particle.

$\begin{matrix} \begin{matrix} [\begin{matrix} Rate \\ in \end{matrix}] & - & [\begin{matrix} Rate \\ out \end{matrix}] & + & [\begin{matrix} Rate of \\ generation \end{matrix}] & = & [\begin{matrix} Rate of \\ accumulation \end{matrix}] \\ 0 & - & 0 & + & {\begin{matrix} r_{A}^{″} \cdot 4 π R \end{matrix}}^{2} & = & \frac{d ({\frac{4}{3} π R}^{3} ρ_{c} ϕ_{c})}{d t} \end{matrix} & (14-52) \end{matrix}$

Where ρ_c is the molar density of the solid carbon, simplifying gives

$\begin{matrix} \frac{d R}{d t} = \frac{r_{A}^{″}}{{ρ_{c} ϕ}_{c}} & (14-53) \end{matrix}$

In terms of particle diameter, d_P,

$\begin{matrix} \frac{{d d}_{p}}{d t} = \frac{2 r_{A}^{″}}{{ρ_{c} ϕ}_{c}} & (14 -54) \end{matrix}$

Step 7: The rate of disappearance of carbon is equal to the flux of O₂ to the gas–carbon interface:

A. Surface reaction limiting

$\begin{matrix} {- r}_{A}^{″} = k_{r} C_{A S} & (14-55) \end{matrix}$

$\begin{matrix} \frac{d d p}{d t} = \frac{2 r_{A}^{″}}{{ρ_{c} ϕ}_{c}} = \frac{{2 k}_{c} C_{A \infty}}{{ρ_{c} ϕ}_{c}} & (14-56) \end{matrix}$

The initial conditions are

Images

$\begin{matrix} d_{p 0}^{2} - d_{p}^{2} = \frac{{2 k}_{r}}{{ρ_{c} ϕ}_{c}} C_{A s} t \end{matrix} \begin{matrix} (14-58) \end{matrix}$

B. Diffusion Limiting

$\begin{matrix} {- r}_{A}^{″} = W_{A} = k_{c} C_{A \infty} \\ \frac{d d p}{d t} = \frac{2 r_{A}^{″}}{{ρ_{c} ϕ}_{c}} = - 2 (\frac{{2 D}_{AB}}{d_{p}}) \frac{C_{A \infty}}{{ρ_{c} ϕ}_{c}} = - \frac{{4 D}_{AB} C_{A \infty}}{{ρ_{c} ϕ}_{c}} \frac{1}{d_{p}} \end{matrix}$

Again using the boundary conditions in Equation (14-57), we obtain

$\begin{matrix} d_{p 0}^{2} - d_{p}^{2} = \frac{{8 D}_{AB} C_{A \infty}}{{ρ_{c} ϕ}_{c}} t = K_{S} t \end{matrix} \begin{matrix} (14-59) \end{matrix}$

$K_{S} = \frac{{8 D}_{AB} C_{A \infty}}{{ρ_{c} ϕ}_{c}}$

where K_S is the burning rate constant, s^-1.^†

^†R. A. Ogle Dust Explosion Dynamics, Amsterdam: Elsevier, 2017.

The time for complete combustion (d_P = 0) of a particle of diameter d_p₀ is

$\begin{matrix} t_{c} = \frac{d_{p 0}^{2}}{K_{S}} = \frac{d_{p 0}^{2} {ρ_{c} ϕ}_{c}}{{{8 D}_{AB} C}_{A \infty}} \end{matrix} \begin{matrix} (14-60) \end{matrix}$

Example 14–3 Combustion Time for a Single Particle

There is a 100 micron carbon dust particle in air at 1 atm. Calculate K_S and the time for the particle to burn completely (d_p = 0). The average value of the diffusivity near the burning particle is 10^–4 m²/s and the density of the carbon particle is 2.26 × 10⁶ g/m³.

Solution

The concentration of gas at 1 atm and 273 K is 0.046 mol/dm³. The corresponding concentration of O₂ at the outside the boundary layer correcting for the temperature at 298 K, that is, C_A_∞ is

$\begin{matrix} C_{O_{2}} = 0.21 & C_{t} = (0.21) (0.0446 \frac{mol}{{dm}^{3}}) \frac{273}{298} {(\frac{10 dm}{m})}^{3} = 8.58 \frac{mol}{m^{3}} \end{matrix}$

The molar density of the solid carbon particle is

$\begin{matrix} ρ_{c} & = & \frac{2.26 \times 10^{6} {g/m}^{3}}{12 g/mol} = 188333 \frac{mol}{m^{3}} \\ ϕ_{c} & = & 1 \\ K_{S} = \frac{{8 D}_{AB} C_{A \infty}}{ρ_{c}} & = & \frac{8 (10^{- 4} m^{2} / S) (\frac{8.58 mol}{m^{3}})}{{0.1883 \cdot 10}^{6} {mol/m}^{3}} = {365 \times 10}^{- 10} m^{2} / s \end{matrix}$

The units used by R. A. Ogle in his book Dust Explosion Dynamic, Elsevier 2017, are μm and ms, in which case K_S becomes

$K_{S} = 365 \times 10^{- 10} m^{2} / s {(\frac{10^{6} μ m}{1 m})}^{2} (\frac{1 s}{10^{3} ms}) = 36.5 μ m^{2} /ms$

This value of K_S is about an order of magnitude smaller than a burning liquid droplet. Calculate, t_c, the time for the dust particle to completely burn

$\begin{matrix} t_{c} = \frac{d_{p 0}^{2}}{K_{S}} = \frac{{(100 μ m)}^{2}}{36.5 {μ m}^{2} / ms} = 274 ms \end{matrix}$

The time for a blink of an eye is approximately 400 ms.

Analysis: This analysis shows how to calculate time to consume a 100 micron carbon particle. The time is quite short, leading to a dust explosion. Be sure to view the Chemical Safety Board (CSB) video on the CRE Web site (http://www.csb.gov/imperial-sugar-company-dust-explosion-and-fire/).

14C Packed-Bed Applications

14.7 Mass Transfer-Limited Reactions in Packed Beds

A number of industrial reactions are potentially mass transfer-limited because they may be carried out at high temperatures without the occurrence of undesirable side reactions. In mass transfer-dominated reactions, the surface reaction is so rapid that the rate of transfer of reactant from the bulk gas or liquid phase to the surface limits the overall rate of reaction. Consequently, mass transfer-limited reactions respond quite differently to changes in temperature and flow conditions than do the rate-limited reactions discussed in previous chapters. In this section the basic equations describing the variation of conversion with the various PBR design parameters (catalyst weight, flow conditions) will be developed. To achieve this goal, we begin by carrying out a mole balance on the following generic mass transfer-limited reaction

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (14-61) \end{matrix}$

carried out in a packed-bed reactor (Figure 14-9). A steady-state mole balance on reactant A in the reactor segment between z and z + Δz is

$\begin{matrix} \begin{matrix} [\begin{matrix} Molar \\ rate in \end{matrix}] & - & [\begin{matrix} Molar \\ rate out \end{matrix}] & + & [\begin{matrix} Molar rate of \\ generation \end{matrix}] & = & [\begin{matrix} \begin{matrix} Molar rate of \\ accumulation \end{matrix} \end{matrix}] \\ F_{A z | z} & - & F_{A z | z + Δ z} & + & r_{A}^{″} a_{c} (A_{c} Δ_{z}) & = & 0 \end{matrix} & (14-62) \end{matrix}$

Figure of the packet-bed reactor is shown. The packet-bed reactor is a horizontal cylindrical tube that consists of the catalyst pellet at the center. The reactor has two segments Z and Z plus delta Z. The entering flow and exiting flow across the cylindrical tube is provided. — **Figure 14-9** Packed-bed reactor.

where $r_{A}^{″}$ = rate of generation of A per unit of catalytic surface area, mol/s · m²

a_c = external surface area of catalyst per volume of catalytic bed, m²/m³

$A_{c} = \frac{Volume of solid}{Volume of bed} \times \frac{Surface area}{Volume of solid} = (1 - ϕ) [{π d}_{p}^{2} / ({π d}_{p}^{3} / 6)]$

= 6(1 = ϕ)/d_p for packed beds, m²/m³

ϕ = porosity of the bed (i.e., void fraction)⁶

⁶ In the nomenclature for Chapter 4, for the Ergun equation for pressure drop.

d_p = particle diameter, m

A_c = cross-sectional area of tube containing the catalyst, m²

Dividing Equation (14-62) by A_cΔz and taking the limit as Δz → 0, we have

$\begin{matrix} - \frac{1}{A_{c}} (\frac{{d F}_{A z}}{d z}) + r_{A}^{″} A_{c} = 0 & (14-63) \end{matrix}$

We now need to express F_A_z and $r_{A}^{″}$ in terms of concentration.

The molar flow rate of A in the axial direction is

$\begin{matrix} F_{A z} = A_{c} W_{A z} = (J_{A z} + B_{A z}) A_{c} & (14-64) \end{matrix}$

Axial diffusion is neglected.

In almost all situations involving flow in packed-bed reactors, the amount of material transported by diffusion or dispersion in the axial direction is negligible compared with that transported by convection (i.e., bulk flow)

${J_{A z} ≪ B}_{A z}$

(In Chapter 18 we consider the case when dispersive effects (e.g., diffusion) must be taken into account.) Neglecting dispersion, Equation (14-14) becomes

$\begin{matrix} F_{A z} = A_{c} W_{A z} = A_{c} B_{A z} = {U C}_{A} A_{c} & (14-65) \end{matrix}$

where U is the superficial molar average velocity through the bed (m/s). Substituting for F_A_z in Equation (14-63) gives us

$\begin{matrix} - \frac{d (C_{A} U)}{d z} + r_{A}^{″} a_{c} = 0 & (14-66) \end{matrix}$

For the case of constant superficial velocity U

Differential equation describing flow and reaction in a packed bed

$\begin{matrix} - U \frac{{d C}_{A}}{d z} + r_{A}^{″} a_{c} = 0 \end{matrix} \begin{matrix} (14-67) \end{matrix}$

For reactions at steady state, the molar flux of A to the particle surface, W_A_r (mol/m² · s) (see Figure 14-10), is equal to the rate of disappearance of A on the surface $- r_{A}^{″}$ (mol/m² · s); that is

$\begin{matrix} - r_{A}^{″} = W_{A r} & (14-68) \end{matrix}$

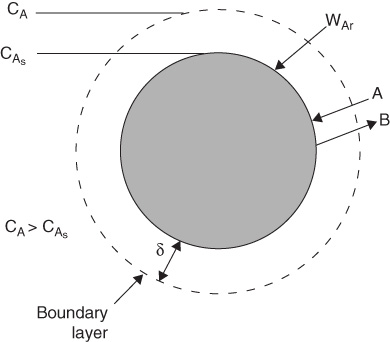
A figure depicts the diffusion across the stagnant film that surrounds the catalyst pellet. — **Figure 14-10** Diffusion across stagnant film surrounding catalyst pellet.

The cross-section of the catalyst pellet represents the diffusion across the stagnant film surrounding it. The catalyst pellet is surrounded by the boundary layer, where the distance between the boundary layer and the catalyst pellet is marked as delta. The particle surface of the catalyst pellet is marked as A and the outer surface is marked as B. The molar flux of A to the particle surface is marked as W subscript Ar. The concentration on the boundary level is marked as C subscript A, and the concentration at the catalytic surface is marked as C subscript As, where its relation is marked as C subscript A is greater than C subscript AS.

A figure depicts the diffusion between two surfaces. — The diffusion between the region are, the bulk concentration of A (C subscript A) and the concentration of A at the catalytic surface (C subscript As). The distance between the two regions is represented as sigma. The particle surface (W subscript Ar) on the C subscript A surface is diffused across the surface on the C subscript As (negative r double prime A).

From Section 14.4, the boundary condition at the external surface is

$\begin{matrix} - r_{A}^{″} = W_{A r} = k_{c} (C_{A} - C_{A s}) & (14 -69) \end{matrix}$

where k_c = mass transfer coefficient = (D_AB/δ), (m/s)

C_A = bulk concentration of A (mol/m³)

C_A_s = concentration of A at the catalytic surface (mol/m³)

Substituting for $- r_{A}^{″}$ in Equation (14-67), we have

$\begin{matrix} - U \frac{{d C}_{A}}{d z} - k_{c} a_{c} (C_{A} - C_{A s}) = 0 & (14-70) \end{matrix}$

In reactions that are completely mass transfer-limited, it is not necessary to know the rate law.

In most mass transfer-limited reactions, the surface concentration is negligible with respect to the bulk concentration (i.e., $C_{A} ≫ C_{A S}$ )

$\begin{matrix} - U \frac{{d C}_{A}}{d z} = k_{c} a_{c} C_{A} & (14-71) \end{matrix}$

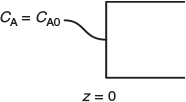
Integrating with the limit, at z = 0, C_A = C_A0

$\begin{matrix} \frac{C_{A}}{C_{A0}} = exp (- \frac{k_{c} a_{c}}{U} z) \end{matrix} \begin{matrix} (14 -72) \end{matrix}$

The corresponding variation of reaction rate along the length of the reactor is

$\begin{matrix} {- r}_{A}^{″} = k_{c} C_{A0} exp (- \frac{k_{c} a_{c}}{U} z) & (14-73) \end{matrix}$

The concentration and conversion profiles down a reactor of length L are shown in Figure 14-11.

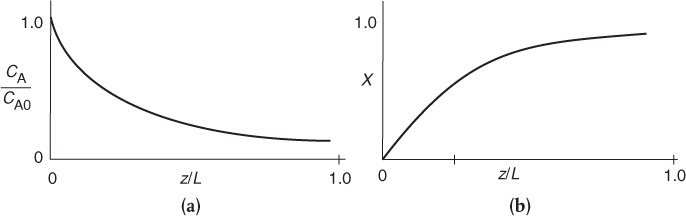
Two graphs compare the concentration and conversion profiles in a packet bed with respect to the reactor of length L. — **Figure 14-11** Axial concentration (a) and conversion (b) profiles in a packed bed.

The first graph depicts the axial concentration profiles in a packed bed. The horizontal axis representing z over L ranging from 0 to 1.0. The vertical axis representing C subscript A over C subscript A0, ranging from 0 to 1.0. A concave up, decreasing curve is drawn from the point (0, 1.0), which steadily decreases and ends at (1.0, 0.2), which denotes that the increase in concentration decreases the reactor of length L. The second graph depicts the conversion profiles in a packed bed. The horizontal axis representing z over L ranging from 0 to 1.0. The vertical axis represents X ranging from 0 to 1.0. A concave up, increasing curve is drawn from the origin (0,0) which steeply increases and ends at (1.0, 1.0), which denotes that the increase in conversion increases the reactor of length L. Note: the mentioned values are approximate.

To determine the reactor length L necessary to achieve a conversion X, we combine the definition of conversion

$\begin{matrix} X = \frac{C_{A0} - C_{AL}}{C_{A0}} & (14-74) \end{matrix}$

Reactor concentration profile for a mass transfer-limited reaction

with the evaluation of Equation (14-72) at z = L to obtain

$\begin{matrix} ln \frac{1}{1 - X} = \frac{k_{c} a_{c}}{U} L \end{matrix} \begin{matrix} (14-75) \end{matrix}$

14.8 Robert the Worrier

Robert is an engineer who is always worried (which is a Jofostanian trait). He always thinks something bad will happen if we change an operating condition such as flow rate or temperature, or an equipment parameter such as particle size. Robert’s motto is “If it ain’t broke, don’t fix it.” We can help Robert be a little more adventuresome by analyzing how the important parameters vary as we change operating conditions in order to predict the outcome of such a change. We first look at Equation (14-75) and see that conversion depends on the parameters k_c, a_c, U, and L. We now examine how each of these parameters will change as we change operating conditions. We first consider the effects of temperature and flow rate on conversion.

To learn the effect of flow rate on conversion, we need to know how flow rate affects the mass transfer coefficient. That is, we must determine the correlation for the mass transfer coefficient for the particular geometry and flow field. For flow through a packed bed, the correlation given by Thoenes and Kramers for 0.25 < ϕ < 0.5, 40 < Re′ < 4000, and 1 < Sc < 4000 is⁷

⁷ D. Thoenes, Jr. and H. Kramers, Chem. Eng. Sci., 8, 271 (1958).

Cartoon image of a person with a worried face.

Thoenes–Kramers correlation for flow through packed beds

$\begin{matrix} {{Sh′ = 1.0 (Re′)}^{1 / 2} Sc}^{1 / 3} \end{matrix} \begin{matrix} (14-76) \end{matrix}$

$\begin{matrix} [\frac{k_{c} d_{p}}{D_{AB}} (\frac{ϕ}{1 - ϕ}) \frac{1}{γ}] = {[\frac{U d_{p} ρ}{μ (1 - ϕ) γ}]}^{1 / 2} {(\frac{μ}{ρ D_{AB}})}^{1 / 3} \end{matrix} \begin{matrix} (14 -77) \end{matrix}$

where $Re′ = \frac{Re}{(1 - ϕ) γ}$

$Sh′ = \frac{Sh ϕ}{(1 - ϕ) γ}$

d_p = particle diameter (equivalent diameter of a sphere of the same volume), m

= [(6/π) (volume of pellet)]^1/3, m

ϕ = void fraction (porosity) of packed bed

γ = shape factor (external surface area divided by ${π d}_{p}^{2}$ )

and

U, ρ, μ, v, and D_AB are as previously defined.

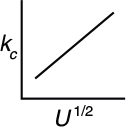
A graph of K subscript c over U superscript 1 over 2 shows an upward slope line.

For constant fluid properties and particle diameter

$\begin{matrix} {k_{c} \propto U}^{1 / 2} & (14-78) \end{matrix}$

We see that the mass transfer coefficient increases with the square root of the superficial velocity through the bed. Therefore, for a fixed concentration, C_A, such as that found in a differential reactor, the rate of reaction should vary with U^1/2

For diffusion-limited reactions, reaction rate depends on particle size and fluid velocity.

${{- r}_{A}^{″} \propto k_{c} C_{A} \propto U}^{1 / 2}$

However, if the gas velocity is continually increased, a point is reached where the reaction becomes reaction rate–limited and, consequently, is independent of the superficial gas velocity, as shown in Figure 14-5.

Many mass transfer correlations in the literature are often reported in terms of the Colburn J factor (i.e., J_D), which is a function of the Reynolds number. The relationship between J_D and the numbers we have been discussing is

$\begin{matrix} J_{D} = \frac{Sh}{{Sc}^{1 / 3} Re} \end{matrix} \begin{matrix} (14-79) \end{matrix}$

Figure 14-12 shows data from a number of investigations for the J factor as a function of the Reynolds number for a wide range of particle shapes and gas-flow conditions. Note: There are serious deviations from the Colburn analogy when the concentration gradient and temperature gradient are coupled, as shown by Venkatesan and Fogler.⁸

⁸ R. Venkatesan and H. S. Fogler, AIChE J., 50, 1623 (July 2004).

Colburn J factor

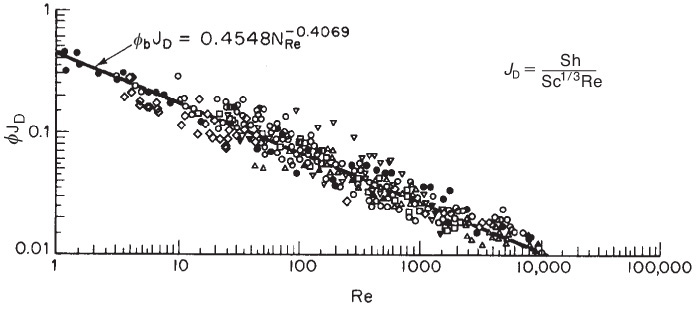
A graph of phi J subscript D over Re depicts the mass transfer correlation for packet beds. — **Figure 14-12** Mass transfer correlation for packed beds. ϕb≡ϕ [Reprinted by permission. Copyright © 1977, American Chemical Society. Dwivedi, P. N. and S. N. Upadhyay, “Particle-Fluid Mass Transfer in Fixed and Fluidized Beds.” *Industrial & Engineering Chemistry Process Design and Development*, 1977, 16 (2), 157–165.]

The scatter plot shows the data from a number of investigations for the J factor as a wide range of particle shapes and gas-flow conditions. The horizontal axis represents Re (Reynolds number), ranging from 1 to 100,000, and the vertical axis represents phi J subscript D, ranging from 0.01 to 1, in increments of 0.1. Several scatter plots (in the shape of circle, square, and triangle) are drawn, where most points are densely plotted between the range (50, 0.1) and (1000, 0.02), few scatter points are plotted in the region between the range (1, 0.7) and (2, 0.5). The scatter plots denote the negative correlation, such that the increase in the Colburn factor increases the Reynolds number of particles. A best-fit line representing Phi subscript b Upper J subscript D (equals 0.4548 N subscript Re superscript negative 0.4069) is drawn from (1, 0.7) to (10,000, 0), where the plots follow the straight line pattern. The Coburn J factor, J D is the ratio of S h over Sc superscript 1 over 3 times Re. Note: the mentioned values are approximate.

A correlation for flow through packed beds in terms of the Colburn J factor

Dwidevi and Upadhyay review a number of mass transfer correlations for both fixed and fluidized beds and arrive at the following correlation, which is valid for both gases (Re > 10) and liquids (Re > 0.01) in either fixed or fluid-ized beds:⁹

⁹ P. N. Dwidevi and S. N. Upadhyay, Ind. Eng. Chem. Process Des. Dev., 16, 157 (1977).

$\begin{matrix} {ϕ J}_{D} = \frac{0.765}{{Re}^{0.82}} + \frac{0.365}{{Re}^{0.386}} \end{matrix} \begin{matrix} (14-80) \end{matrix}$

For nonspherical particles, the equivalent diameter used in the Reynolds and Sherwood numbers is $d_{p} = \sqrt{A_{p} / π} = 0.564 \sqrt{A_{p}}$ , where A_p is the external surface area of the pellet.

To obtain correlations for mass transfer coefficients for a variety of systems and geometries, see either D. Kunii and O. Levenspiel, Fluidization Engineering, 2nd ed. Butterworth-Heinemann, 1991, Chap. 7, or W. L. McCabe, J. C. Smith, and P. Harriott, Unit Operations in Chemical Engineering, 6th ed. New York: McGraw-Hill, 2000. For other correlations for packed beds with different packing arrangements, see I. Colquhoun-Lee and J. Stepanek, Chemical Engineer, 108 (Feb. 1974).

Example 14–4 Mass Transfer Effects in Maneuvering a Space Satellite

Hydrazine has been studied extensively for use in monopropellant thrusters for space flights of long duration. Thrusters are used for altitude control of communication satellites. Here, the decomposition of hydrazine over a packed bed of alumina-supported iridium catalyst is of interest.¹⁰ In a proposed study, a 2% hydrazine in 98% helium mixture is to be passed over a packed bed of cylindrical particles 0.25 cm in diameter and 0.5 cm in length at a gas-phase velocity of 150 m/s and a temperature of 450 K. The kinematic viscosity of helium at this temperature is 4.94 × 10^–5 m²/s. The hydrazine decomposition reaction is believed to be externally mass transfer-limited under these conditions. If the packed bed is 0.05 m in length, what conversion can be expected? Assume isothermal operation.

¹⁰ O. I. Smith and W. C. Solomon, Ind. Eng. Chem. Fund., 21, 374.

Actual case history and current application

Space satellite, space shuttle, and planets icons.

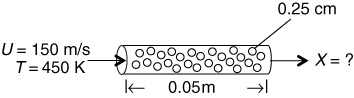
Figure of the Packet-Bed Reactor (PBR) is shown to determine the expected conversion (X). — **Figure E14-4.1** PBR.

The packet-bed reactor (PBR) is a horizontal cylindrical tube with the cylindrical particles of diameter 0.25 centimeters and the length of the PBR is 0.05 meters. On the left, the gas-phase velocity (U) enters the PBR at the speed of 150 meters per second at a temperature of 450 Kelvin. On the right end of the PBR tube, the expected conversion (X) is marked as an unknown value.

Additional information:

D_AB = 0.69 × 10^–4 m²/s at 298 K

Bed porosity: 40%

Bed fluidicity: 95.7%

Solution

The following solution is detailed and a bit tedious, but it is important to know the details of how a mass transfer coefficient is calculated.

Rearranging Equation (14-64) gives us

$\begin{matrix} {X = 1 - e}^{- (k_{c} a_{c} / U) L} \end{matrix} \begin{matrix} (E14-4.1) \end{matrix}$

(a) Using the Thoenes–Kramers correlation to calculate the mass transfer coefficient, k_c

First we find the volume-average particle diameter

$\begin{matrix} {d_{p} = {(\frac{6 V}{π})}^{1 / 3} = (6 \frac{{π D}^{2}}{4} \frac{L}{π})}^{1 / 3} & (E14-4.2) \end{matrix}$
Surface area per volume of bed

$\begin{matrix} a_{c} = 6 (\frac{1 - 0.4}{d_{p}}) = 6 (\frac{1 - 0.4}{3.61 \times 10^{- 3} m}) = {998 m}^{2} {/ m}^{3} & (E14-4.3) \end{matrix}$

Tedious reading and calculations, but we gotta know how to do the nitty–gritty.
Mass transfer coefficient

$Re = \frac{d_{p} U}{v} = \frac{(3.61 \times 10^{- 3} m) (150 m/s)}{{4.94 \times 10}^{- 5} m^{2 / 5}} = 10942$

For cylindrical pellets

$\begin{matrix} \begin{matrix} γ = \frac{{2 π r L}_{p} + {2 π r}^{2}}{{π d}_{p}^{2}} = \frac{{(2) (0.005 / 2) (0.005) + (2) (0.0025 / 2)}^{2}}{({3.61 \times 10^{- 3})}^{- 2}} = 1.20 & (E14-4.4) \end{matrix} \\ Re′ = \frac{Re}{(1 - ϕ) γ} = \frac{10942}{(0.6) (1.2)} = 15173 \end{matrix}$

Correcting the diffusivity to 450 K using Table 14-3 gives us

$\begin{matrix} \begin{array}{l} \begin{matrix} \begin{matrix} {D_{AB} (450 K) = D_{AB} (298 K) \times (\frac{450}{298})}^{1.75} & = \end{matrix} & ({0.69 \times 10^{- 4} m}^{2} / s) (2.06) \end{matrix} \\ D_{AB} (450 K) = 1.42 \times 10^{- 5} m^{2 / s} \end{array} & (E14-4.5) \end{matrix}$

$Sc = \frac{v}{D_{AB}} = \frac{{{4.94 \times 10}^{- 5} m}^{2} / s}{{{1.42 \times 10}^{- 4} m}^{2} / s} = 0.35$

Representative values

Gas Phase

Re′ = 15173

Sc = 0.35

Sh′ = 86.66

k_c = 6.15 m/s

Substituting Re′ and Sc into Equation (14-65) yields

$\begin{matrix} {{Sh′ = (15173.92)}^{1 / 2} (0.35)}^{1 / 3} = (123.18) (0.70) = 86.6 & (E14-4.6) \end{matrix}$

$k_{c} = \frac{D_{AB} (1 - ϕ)}{d_{p} ϕ} γ (Sh′) = (\frac{1.42 {\times 10^{- 4} m}^{2} / s}{{3.61 \times 10}^{- 3} m}) (\frac{1 - 0.4}{0.4}) \times (1.2) (86.66)$

$\begin{matrix} k_{c} = 6.15 m/s \end{matrix} \begin{matrix} (E14-4.7) \end{matrix}$

The conversion is

$\begin{array}{l} \begin{matrix} X = 1 - exp [- (6.15 m/s) (\frac{998 m^{2} / m^{3}}{150 m/s}) (0.05 m)] & (E14-4.8) \end{matrix} \\ = 1 - 0.13 = 0.87 \end{array}$

We find 87% conversion.

(b) Colburn J_D factor to calculate k_c. To find k_c, we first calculate the surface-area-average particle diameter.

For cylindrical pellets, the external surface area is

$\begin{matrix} A = {π d L}_{p} + 2 π (\frac{d^{2}}{4}) & (E14-4.9) \end{matrix}$

$\begin{matrix} d_{p} & = & \sqrt{\frac{A}{π}} = \sqrt{\frac{π d L_{p} + 2 π (d^{2} / 4)}{π}} (E14-4.10) \\ = & \sqrt{(0.0025) (0.005) + \frac{{(0.0025)}^{2}}{2}} = 3.95 \times 10^{- 3} m \\ a_{c} & = & \frac{6 (1 - φ)}{d_{p}} = 910.74 m^{2} / m^{3} \\ Re & = & \frac{d_{p} U}{v} = \frac{(3.95 \times 10^{- 3} m) (150 m/s)}{4.94 \times 10^{- 5} m^{2} / s} \\ = & 11996.04 \end{matrix}$

An illustration shows an unenergetic person seated on a chair and lying down on the book placed on the table in front of him.

Typical values

Gas Phase

Re = 11996

J_D = 0.025

Sc = 0.35

Sh = 212

k_c = 7.63 m/s

$\begin{matrix} ϕ J_{D} = \frac{0.765}{{Re}^{0.82}} + \frac{0.365}{{Re}^{0.386}} & (14-79) \end{matrix}$

$\begin{array}{l} \begin{matrix} = \frac{0.765}{{(11996)}^{0.82}} + \frac{0, 365}{{(11996)}^{0.386}} = 3.5 \times 10^{- 4} + 9.7 \times 10^{- 3} & (E14-4.11) \end{matrix} \\ = 0.010 \end{array}$

$\begin{matrix} J_{D} = \frac{0.010}{0.4} = 0.025 & (E14-4.12) \end{matrix}$

$\begin{array}{l} Sh & = & {Sc}^{1 / 3} Re (J_{D}) & (E14-4.13) \\ = & {\begin{matrix} (0.35) \end{matrix}}^{1 / 3} (11996) (0.025) = 212 \\ k_{c} & = & \frac{D_{AB}}{d_{p}} Sh = \frac{1.42 \times 10^{- 4}}{3.95 \times 10^{- 3}} (212) = 7.63 m/s \end{array}$

$\begin{matrix} \begin{matrix} \begin{array}{l} Then X \end{array} & = & 1 - exp [- (7.63 m/s) (\frac{910 m^{2} / m^{3}}{150 m/s}) (0.05 m)] \\ ≃ & 0.9 \end{matrix} & (E14-4.14) \end{matrix}$

Fluidicity?? Red herring!

If there were such a thing as the bed fluidicity, given in the problem statement, it would be a useless piece of information. Make sure that you know what information you need to solve problems, and go after it. Do not let additional data confuse you or lead you astray with useless information or facts that represent someone else’s bias, and which are probably not well founded.

14.9 What If . . . ? (Parameter Sensitivity)

As we have stressed many times, one of the most important skills of an engineer is to be able to predict the effects of changes of system variables on the operation of a process. The engineer needs to determine these effects quickly through approximate but reasonably close calculations, which are sometimes referred to as “back-of-the-envelope calculations.”¹¹ This type of calculation is used to answer such questions as “What will happen if I decrease the particle size?” “What if I triple the flow rate through the reactor?”

¹¹ Prof. J. D. Goddard, University of Michigan, 1963–1976. Professor Emeritus at the University of California, San Diego.

J. D. Goddard’s

Back of the Envelope

To help answer these questions, we recall Equation (14-45) and our discussion on page 754. There, we showed the mass transfer coefficient for a packed bed was related to the product of two terms: Term 1 was dependent on the physical properties and Term 2 was dependent on the system properties. Re-writing Equation (14-45) as

$\begin{matrix} k_{c} \propto (\frac{D_{AB}^{2 / 3}}{v^{1 / 6}}) (\frac{U^{1 / 2}}{d_{p}^{1 / 2}}) \end{matrix} \begin{matrix} (14 -81) \end{matrix}$

one observes from this equation that the mass transfer coefficient increases as the particle size decreases. The use of sufficiently small particles offers another technique to escape from the mass transfer-limited regime into the reaction-rate-limited regime.

Find out how the mass transfer coefficient varies with changes in physical properties and system properties.

Example 14–5 The Case of Divide and Be Conquered

A mass transfer-limited reaction is being carried out in two reactors of equal volume and packing, connected in series as shown in Figure E14-5.1. Currently, 86.5% conversion is being achieved with this arrangement. It is suggested that the reactors be separated and the flow rate be divided equally among each of the two reactors (Figure E14-5.2) to decrease the pressure drop and hence the pumping requirements. In terms of achieving a higher conversion, Robert is wondering if this is a good idea.

Cartoon image of a person with a worried face.

A figure depicts the series arrangement of two reactors. The flow rate V subscript 0 is passed between the reactors connected in series, which denotes that the flow rate between them is the same, and the conversion X is 0.865. — **Figure E14-5.1** Series arrangement.

A figure depicts the parallel arrangement of two reactors. The flow rate V subscript 0 is divided equally, and v subscript 0 over 2 is passed between the two reactors connected in parallel. The conversion X from the reactors is unknown. — **Figure E14-5.2** Parallel arrangement.

Reactors in series versus reactors in parallel

Solution

For the series arrangement we were given, X₁ = 0.865, and for the parallel arrangement, the conversion is unknown, that is, X₂ = ? As a first approximation, we neglect the effects of small changes in temperature and pressure on mass transfer.

We recall Equation (14-75), which gives conversion as a function of reactor length. For a mass transfer-limited reaction

$\begin{matrix} ln \frac{1}{1 - X} = \frac{k_{c} a_{c}}{U} L & (14-75) \end{matrix}$

For case 1, the undivided system

$\begin{matrix} (\begin{matrix} ln \frac{1}{1 - X_{1}} \end{matrix}) & = & \frac{k_{c 1} a_{c}}{U_{1}} L_{1} & (E14-51) \\ X_{1} & = & 0.865 & \underline{\begin{matrix} Answer 1 \end{matrix}} \end{matrix}$

For case 2, the divided system

$\begin{matrix} \begin{matrix} (ln \frac{1}{1 - X_{2}}) = \frac{k_{c 2} a_{c}}{U_{2}} L_{2} \\ X_{2} = ? \end{matrix} & (E14-5.2) \end{matrix}$

We now take the ratio of case 2 (divided system) to case 1 (undivided system)

$\begin{matrix} \frac{ln \frac{1}{1 - X_{2}}}{ln \frac{1}{1 - X_{1}}} = \frac{k_{c 2}}{k_{c 1}} (\frac{L_{2}}{L_{1}}) \frac{U_{1}}{U_{2}} & (E14-5.3) \end{matrix}$

The surface area per unit volume a_c is the same for both systems.

From the conditions of the problem statement we know that

$\begin{array}{l} L_{2} & = & \frac{1}{2} L_{1}, U_{2} = \frac{1}{2} U_{1}, and X_{1} = 0.865 \\ X_{2} & = & ? \end{array}$

However, we must also consider the effect of the division on the mass transfer coefficient. From Equation (14-81) we know that

k_c ∝ U^1/2

$\begin{matrix} {\frac{k_{c 2}}{k_{c 1}} = (\frac{U_{2}}{U_{1}})}^{1 / 2} & (E14-5.4) \end{matrix}$

Multiplying by the ratio of superficial velocities yields

$\begin{matrix} {\frac{U_{1}}{U_{2}} (\frac{k_{c 2}}{k_{c 1}}) = (\frac{U_{1}}{U_{2}})}^{1 / 2} & (E14-5.5) \end{matrix}$

$\begin{matrix} \begin{matrix} ln \frac{1}{1 - X_{2}} & = & {\begin{matrix} (ln \frac{1}{1 - X_{1}}) \frac{L_{2}}{L_{1}} (\frac{U_{1}}{U_{2}}) \end{matrix}}^{1 / 2} \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} = & (ln \frac{1}{1 - 0.865}) [\frac{\frac{1}{2} L_{1}}{L_{1}} {(\frac{U_{1}}{\frac{1}{2} U_{1}})}^{1 / 2}] \\ = & 2.00 (\frac{1}{2}) \sqrt{2} = 1.414 \end{matrix} & (E14-5.6) \end{matrix}$

Solving for X₂ gives us

X₂ = 0.76 Answer 2

Analysis: Consequently, we see that although the divided arrangement will have the advantage of a smaller pressure drop across the bed, it is a bad idea in terms of conversion. Recall that the series arrangement gave X₁ = 0.865; therefore (X₂ < X₁). Bad idea!! But every chemical engineering student in Jofostan knew that! Recall that if the reaction were reaction rate–limited, both arrangements would give the same conversion.

Bad idea!! Robert was right to worry.

Example 14–6 The Case of the Overenthusiastic Engineers

The same reaction as that in Example 14-5 is being carried out in the same two reactors in series. A new engineer suggests that the rate of reaction could be increased by a factor of 2¹⁰ by increasing the reaction temperature from 400°C to 500°C, reasoning that the reaction rate doubles for every 10 = C increase in temperature. Another engineer arrives on the scene and berates the new engineer with quotations from Chapter 3 concerning this rule of thumb. She points out that it is valid only for a specific activation energy within a specific temperature range. She then suggests that he go ahead with the proposed temperature increase but should only expect an increase on the order of 2³ or 2⁴. What do you think? Who is correct?

Robert worries if this temperature increase will be worth the trouble.

Solution

Because almost all surface reaction rates increase more rapidly with temperature than do diffusion rates, increasing the temperature will only increase the degree to which the reaction is mass transfer-limited.

We now consider the following two cases:

$\begin{matrix} Case 1: T = 400 ° C & X = 0.865 \\ Case 2: T = 500 ° C & X = ? \end{matrix}$

Taking the ratio of case 2 to case 1 and noting that the reactor length is the same for both cases (L₁ = L₂), we obtain

$\begin{matrix} \frac{ln \frac{1}{1 - X_{2}}}{In \frac{1}{1 - X_{1}}} = \frac{k_{c 2}}{k_{c 1}} (\frac{L_{2}}{L_{1}}) \frac{U_{1}}{U_{2}} = \frac{k_{c 2}}{k_{c 1}} (\frac{U_{1}}{U_{2}}) & (E14-6.1) \end{matrix}$

The molar feed rate F_T₀ remains unchanged

$\begin{matrix} F_{T0} = υ_{01} (\frac{P_{01}}{{R T}_{01}}) = υ_{02} (\frac{P_{02}}{{R T}_{02}}) & (E14-6.2) \end{matrix}$

the pressure remains constant so

$\frac{υ_{01}}{T_{1}} = \frac{υ_{02}}{T_{2}}$

Because υ = A_cU, the superficial velocity at temperature T₂ is

$\begin{matrix} U_{2} = \frac{T_{2}}{T_{1}} U_{1} & (E14-6.3) \end{matrix}$

J. D. G.

We now wish to learn the dependence of the mass transfer coefficient on temperature

$\begin{matrix} k_{c} \propto (\frac{U^{1 / 2}}{d_{p}^{1 / 2}}) (\frac{D_{AB}^{2 / 3}}{v^{1 / 6}}) & (E14-6.4) \end{matrix}$

Taking the ratio of case 2 to case 1 and realizing that the particle diameter is the same for both cases gives us

$\begin{matrix} {\frac{k_{c 2}}{k_{c 1}} = {(\frac{U_{2}}{U_{1}})}^{1 / 2} {(\frac{D_{AB2}}{D_{AB1}})}^{2 / 3} (\frac{v_{1}}{v_{2}})}^{1 / 6} & (E14-6.5) \end{matrix}$

The temperature dependence of the gas-phase diffusivity is (from Table 14-3)

$\begin{matrix} D_{AB} \propto T^{1.75} & (E14-6.6) \end{matrix}$

For most gases, viscosity increases with increasing temperature according to the relation

μ ∝ T^1/2

From the ideal gas law

ρ ∝ T^-1

Then

$\begin{matrix} v = \frac{μ}{ρ} {\propto T}^{3 / 2} & (E14-6.7) \end{matrix}$

$\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} {\frac{ln \frac{1}{1 - X_{2}}}{ln \frac{1}{1 - X_{1}}}}^{} & = \end{matrix} & \frac{U_{1}}{U_{2}} (\frac{k_{c 2}}{k_{c 1}}) = {(\frac{U_{1}}{U_{2}})}^{1 / 2} {(\frac{D_{AB2}}{D_{AB1}})}^{2 / 3} (\frac{υ_{1}}{v_{2}})^{1 / 6} & (E14-6.8) \end{matrix} \end{matrix} \end{matrix}$

$\begin{matrix} {\begin{matrix} = & {\begin{matrix} (\frac{T_{1}}{T_{2}}) \end{matrix}}^{1 / 2} {[{(\frac{T_{2}}{T_{1}})}^{1.75}]}^{2 / 3} [{(\frac{T_{1}}{T_{2}})}^{3 / 2}] \end{matrix}}^{1 / 6} \end{matrix}$

$\begin{matrix} \begin{matrix} \frac{U_{1} k_{c 2}}{U_{2} k_{c 1}} & = & {(\frac{T_{1}}{T_{2}})}^{1 / 2} {(\frac{T_{2}}{T_{1}})}^{7 / 6} {(\frac{T_{1}}{T_{2}})}^{1 / 4} = (\frac{T_{2}}{T_{1}})^{5 / 12} \\ = & {\begin{matrix} (\frac{773}{673}) \end{matrix}}^{5 / 12} = 1.059 \end{matrix} & (E14-6.9) \end{matrix}$

It’s really important to know how to do this type of analysis.

Rearranging Equation (E14-6.1) in the form

$\begin{matrix} \begin{matrix} \begin{matrix} ln \frac{1}{1 - X_{2}} = \frac{k_{c 2} U_{1}}{k_{c 1} U_{2}} ln \frac{1}{1 - X 1} \\ ln \frac{1}{1 - X_{2}} = 1.059 (ln \frac{1}{1 - 0.685}) = 1.059 (2) \end{matrix} \\ \begin{matrix} \begin{matrix} X_{2} = 0.88 \end{matrix} \underline{Answer} \end{matrix} \end{matrix} & (E14-6.10) \end{matrix}$

Analysis: Consequently, we see that increasing the temperature from 400°C to 500°C increases the conversion by only 1.7%, that is, X = 0.865 compared to X = 0.88. Bad idea! Bad, bad idea! Both engineers would have benefited from a more thorough study of this chapter.

Bad idea!! Robert was right to worry.

For a packed catalyst bed, the temperature-dependence part of the mass transfer coefficient for a gas-phase reaction can be written as

$\begin{matrix} \begin{matrix} k_{c} \propto U^{1 / 2} & (D_{AB}^{2 / 3} / v^{1 / 6}) \end{matrix} & (14-82) \end{matrix}$

$\begin{matrix} k_{c} \propto U^{1 / 2} T^{11 / 12} & (14-83) \end{matrix}$

Taking the ratio of U to U₀ and T to T₀ and k_c₀ (T₀, U₀) the mass transfer coefficient at any other T and U can be found from the Equation

$\begin{matrix} {{k_{c} = k_{c 0} (\frac{U}{U_{0}})}^{1 / 2} (\frac{T}{T_{0}})}^{11 / 12} & (14-84) \end{matrix}$

One can use Equation (14-81) when studying mass transfer-limited gas-phase reaction.

Depending on how one fixes or changes the molar feed rate, F_T₀, U may also depend on the feed temperature.

As an engineer, it is extremely important that you reason out the effects of changing conditions, as illustrated in the preceding two examples.

Owl icon.

Important concept

Example 14–7 Flow, Diffusion, and Reaction in a Packed Bed

Let’s revisit a packed-bed reactor shown in Figure E14-4.1 in Example 14-4. We want to put the algorithm in a form where one can use Wolfram or Python to vary all the physical parameters and operating variables in order to study a first-order gas-phase reaction in a PBR. The reaction will be carried out isothermally and pressure drop is neglected.

Study the conversion and reaction rate profile for a reaction that is partially diffusion limited by first plotting the conversion as a function of catalyst weight up to a value W = 100 kg. Next use Wolfram to vary all the parameters and describe what you find.

Solution

Mole Balance

$\begin{matrix} \frac{d X}{d W} = {- r}_{A}^{'} / F_{A0} & (E14-7.1) \end{matrix}$
Rate Law

2A. First order, ${- r}_{A}^{″} = k_{r} C_{As}$

$\begin{matrix} {- r}_{A}^{'} = {- r}_{A}^{″} * a_{c}^{'} & (E14-7.2) \end{matrix}$

At steady state the molar flux to the surface is equal to the rate of reaction on the surface

$\begin{matrix} W_{A} = k_{c} (C_{A0} - C_{As}) = k_{r} C_{As} = {- r}_{A}^{″} = \frac{k_{c} k_{r}}{k_{r} + k_{c}} C_{A} = {k C}_{A} & (E14-7.3) \end{matrix}$

where

k_r = reaction-rate constant on the surface (m/s)

k_c = mass transfer coefficient (m/s)

$k = \frac{k_{c} k_{r}}{k_{r} + k_{c}}$ (m/s) overall transfer coefficient

$a_{c}^{'}$ = external surface area of the catalyst per unit mass of catalyst (m²/kg-cat)

2B. Using the Thoenes and Kramer’s correlation, Equations (14-76) and (14-77)

$\begin{matrix} Sh′ = 1.0 {(Re′)}^{1 / 2} {Sc}^{1 / 3} & (14-76) \end{matrix}$

$\begin{matrix} {[\frac{k_{c} d_{p}}{D_{AB}} (\frac{ϕ}{1 - ϕ}) \frac{1}{γ}] = [\frac{{U d}_{p} ρ}{μ (1 - ϕ) γ}] (\frac{μ}{{ρ D}_{AB}})}^{1 / 3} & (14-77) \end{matrix}$

Correlation for k_c is

$\begin{matrix} k_{c} = \frac{Sh′ D_{AB}}{d_{p}} \frac{(1 - ϕ) γ}{ϕ} & (E14-7.4) \end{matrix}$

$\begin{matrix} {{Sh′ = 1.0 (Re′)}^{1 / 2} Sc}^{1 / 3} & (E14-7.5) \end{matrix}$

$\begin{matrix} Re′ = \frac{Re}{(1 - ϕ) γ} & (E14-7.6) \end{matrix}$

$\begin{matrix} Re = \frac{d_{p} U}{v} & (E14-7.7) \end{matrix}$

$\begin{matrix} Sc = \frac{v}{D_{AB}} & (E14-7.8) \end{matrix}$

$\begin{matrix} v = \frac{μ}{ρ} & (E14-7.9) \end{matrix}$

$\begin{matrix} a_{c}^{'} = 6 \frac{(1 - ϕ)}{d_{p}^{*} ρ_{c}} & (E14-7.10) \end{matrix}$
Stoichiometry with P = P₀ and T = T₀

$\begin{matrix} C_{A} = C_{A0} (1 - X) & (E14-7.11) \end{matrix}$
Combine Polymath

We will now combine Equations (E14-7.1) through (E14-7.11) into Polymath, Wolfram, or Python to vary the parameters. The Polymath program is shown in Table E14-7.2 and the Wolfram solution in Figure E14-7.1.

Evaluate

The nominal values of the parameter to be varied are shown in Table E14-7.1.

TABLE E14-7.1 NOMINAL PARAMETER VALUES

Parameters	Liquids	Gases
υ	10^–6 m²/s	10^–5 m²/s
ρ	1000 kg/m³	1 kg/m³
D_AB	10^–8 m²/s	10^–5 m²/s
μ	10^–3 kg/m/s	10^–5 kg/m/s
U	1 m/s	100 m/s
d_p	10^–3 m	10^–2 m
k_r	0.5 m/s	5 m/s
A_c	5*10^–2 m²	5*10^–2 m²
γ	1	1
ϕ	0.4	0.4
ρ_c	3000 kg/m³	3000 kg/m³
C_A0	1 mol/m³	0.01 mol/m³ (Ca 1 atm)

Plot the conversion as a function of catalyst weight.

Images — TABLE E14-7.2 POLYMATH PROGRAM FOR MASS TRANSFER-LIMITED LIQUID-PHASE REACTION IN A PBR

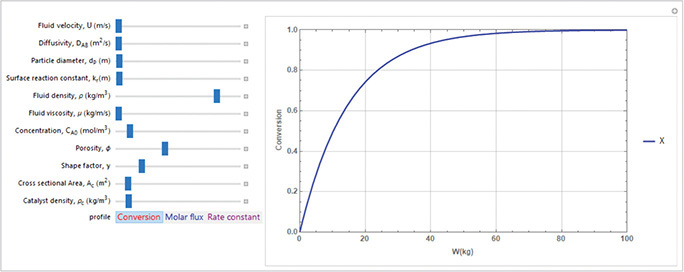
An example of the wolfram solution with an analysis of partially diffusion limited reaction in Packet-Bed Reactor is depicted. — **Figure E14-7.1** Wolfram solution.

The wolfram solution graph shows the conversion of different variables and their respective weights (in kilogram). The horizontal axis represents the weight in kilograms, ranging from 0 to 100 in increments of 20. The vertical axis represents conversion, ranging from 0.0 to 1.0 in increments of 0.2. A curve is drawn from the origin (0, 0.0), which increases rapidly and ends at (100, 1.0). The variables are listed on the left of the graph, such as fluid velocity (U), meter per second; diffusivity (D AB), square meter per second; particle diameter (dp), meter; surface reaction constant (kf), meter; fluid density (rho), kilogram per cubic meter; fluid viscosity (mu), kilogram per meter per second; concentration (C A0), moles per cubic meter; porosity (pi); shape factor (gamma); cross-sectional area (A c), square meter; catalyst density (rho c), kilogram per cubic meter. A scale is present across the variables, which represents the profile as conversion, molar flux, and rate constant. Here, porosity is observed as molar flux, fluid density is observed as rate constant, and others are observed as conversion.

Analysis: In this example we modeled a partially diffusion limited reaction in a PBR. The rest of the example is now up to you, the reader. Go to the LEP 14-7 and vary a number of physical parameters and operating variables, and write a set of observations and conclusions.

14.10 And Now… A Word from Our Sponsor—Safety 14 (AWFOS–S14 Sugar Dust Explosion)

Dust Explosion at Imperial Sugar Company

According to the Chemical Safety Board, the yearly average number of dust explosions has been 5 per year over the last 5 years. In Examples 14-1 and 14-3, we discussed and calculated the rate of mass transfer of oxygen to small carbon dust particles allowing the particle to burn and possibly causing a dust explosion. Dust explosions can produce deadly consequences. On February 7, 2008, combustible fine sugar was ignited at the Imperial Sugar Company causing an explosion. Because the fine granulated sugar has high surface area, it has the potential to rapidly burn and explode. Prior to the explosion the dust collection system was not working properly; as a result fine sugar that had spilled over on the floor and collected on the ceiling and piping became airborne. When the belt transport system was enclosed, the airborne sugar dust found an ignition source and ignited. The explosion was fueled by the large accumulation of airborne sugar dust throughout the packaging plant. The fire and explosion caused 14 deaths and 38 injuries, including life-threatening burns.

Photograph shows the dust or gas explosion inside a factory.

Photograph shows the dust or gas explosion outside a factory.

(https://www.csb.gov/imperial-sugar-company-dust-explosion-and-fire/)

As chemical reaction engineers, it is important that we understand this accident, why it happened, and how it could have been prevented to ensure similar accidents may be prevented. In order to become familiar with a strategy for accident awareness and prevention, view the Chemical Safety Board video on the explosion and determine whether all the important concepts to prevent and mitigate the incident were captured in the BowTie diagram below.

Two other excellent videos on dust explosions are (https://www.chemengonline.com/combustible-dust-fires-explosions-recent-data-lessons-learned/) and (https://www.aiche.org/academy/webinars/dust-explosion). The BowTie diagram for the sugar dust plan explosion is shown in Figure 14-13.

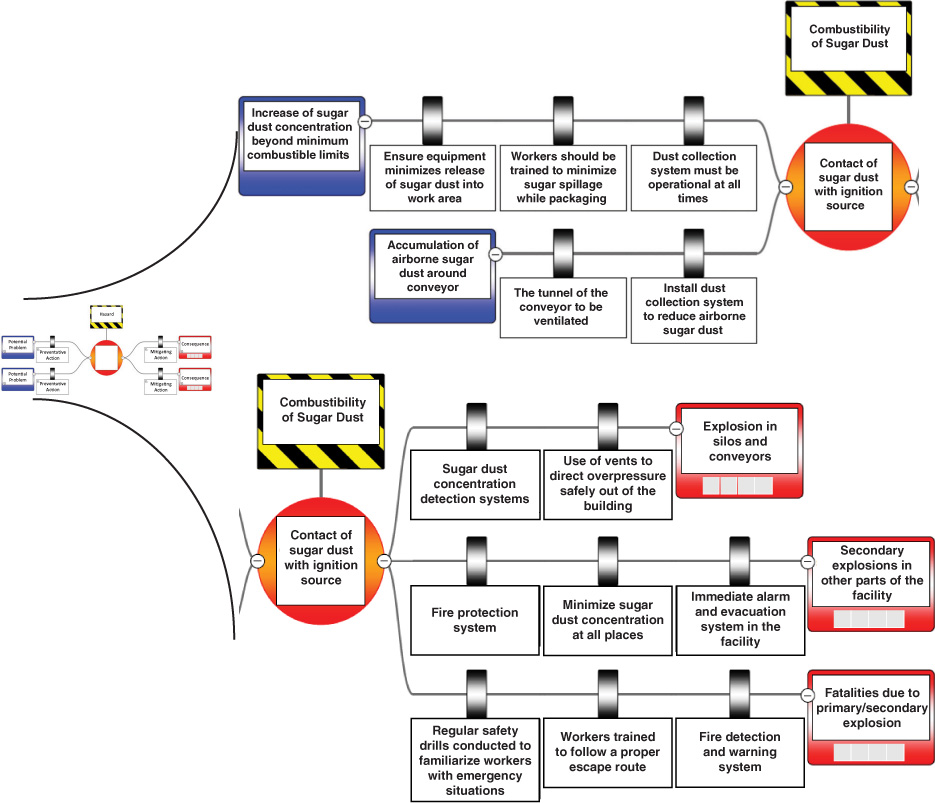
A BowTie diagram depicts the sugar dust plant explosion. — **Figure 14-13** BowTie diagram for dust explosion.

In the BowTie diagram, the starting of the consequence of the potential problem in the hazard zone is shown on the left. At first two potential problems are fed through two separate preventative actions in the hazard zone. After the preventative action, the mitigating action is taken across the hazard zone, which results in consequences. The consequences are divided into two, such as an increase of sugar dust concentration beyond minimum combustible limits and accumulation of airborne sugar around the conveyor. If the consequence of the increase of sugar dust concentration beyond minimum combustible limits, then ensure equipment which minimizes the release of sugar dust into work area. The workers should be trained to minimize sugar spillage during packing and the dust collection system must be operational at all times. If the consequence of the accumulation of airborne sugar dust around the conveyor, the tunnel of the conveyor to be ventilated and install dust collection system to reduce airborne sugar dust. If these consequences are not taken mitigating action, then it results in contact of sugar dust with ignition source due to the combustibility of sugar dust. The consequences of contact of sugar dust with an ignition source can be reduced by the following factors: if the contact of sugar dust with an ignition source, then sugar dust concentration detection systems are used to minimize damage, which is the use of vents to direct overpressure safely out of the building. If these safety measures fail, then the explosion in silos and conveyors are the results. If the contact of sugar dust with an ignition source can be protected by the fire protection system, minimizing sugar dust concentration at all places, and immediate alarm and evacuation system in the facility. If these safety measures fail, then the secondary explosions in the other parts of the facility are possible. If the contact of sugar dust with ignition source is secured by the regular safety drills conducted to familiarize workers with emergency situations, workers trained to follow a proper escape route, and fire detection and warning system. If these measures fail, then the fatalities due to primary or secondary explosion may be at a higher rate.

Closure. After completing this chapter, the reader should be able to define and describe molecular diffusion and how it varies with temperature and pressure, the molar flux, bulk flow, the mass transfer coefficient, the Sherwood and Schmidt numbers, and the correlations for the mass transfer coefficient. The reader should be able to choose the appropriate correlation and calculate the mass transfer coefficient, the molar flux, and the rate of reaction. The reader should also be able to describe the regimes and conditions under which mass transfer-limited reactions occur and when reaction-rate-limited reactions occur, and to make calculations of the rates of reaction and mass transfer for each case. One of the most important areas for the reader to apply the knowledge of this (and other chapters) is in his or her ability to ask and answer “What if . . .” questions.

Summary

The molar flux of A in a binary mixture of A and B is

$\begin{matrix} W_{A} = - D_{AB} \nabla C_{A} + y_{A} (W_{A} + W_{B}) & (S14-1) \end{matrix}$
1. For equimolar counterdiffusion (EMCD) or for dilute concentration of the solute
  
  $\begin{matrix} W_{A} = J_{A} = - D_{AB} \nabla C_{A} & (S14-2) \end{matrix}$
2. For diffusion through a stagnant gas
  
  $\begin{matrix} W_{A} = {c D}_{AB} \nabla ln (1 - y_{A}) & (S14-3) \end{matrix}$
3. For negligible diffusion
  
  $\begin{matrix} W_{A} = y_{A} W = y_{A} (W_{A} + W_{B}) = C_{A} U & (S14-4) \end{matrix}$
The rate of mass transfer from the bulk fluid to a boundary at concentration C_A_s is

$\begin{matrix} W_{A} = k_{c} (C_{A b} - C_{As}) & (S14-5) \end{matrix}$

where k_c is the mass transfer coefficient.
The Sherwood and Schmidt numbers are, respectively,
If a heat transfer correlation exists for a given system and geometry, the mass transfer correlation may be found by replacing the Nusselt number by the Sherwood number and the Prandtl number by the Schmidt number in the existing heat transfer correlation.
Increasing the gas-phase velocity and decreasing the particle size will increase the overall rate of reaction for reactions that are externally mass transfer-limited.

In the graph, the horizontal axis represents the ratio between half of the overall heat transfer coefficient and parameter d p. The vertical axis represents the rate of disappearance of A per unit area of the catalytic surface (r double prime A). A curve is drawn from the initial point, where the region from the initial point to increasing limit on the curve is indicated as external diffusion limited and the region of the maximum constant limit on the curve is indicated as reaction rate limited.
The conversion for externally mass transfer-limited reactions can be found from the equation

$\begin{matrix} ln \frac{1}{1 - X} = \frac{k_{c} a_{c}}{U} L & (S14-8) \end{matrix}$
Back-of-the-envelope calculations should be carried out to determine the magnitude and direction that changes in process variables will have on conversion. What if . . .?

Cre Web Site Materials

(http://www.umich.edu/~elements/6e/14chap/obj.html#/)

In the CRE website, the list of useful links include living example problems, Extra help, Additional Materials, Professional Reference Shelf, and Computer simulation problem statements. A block diagram represents the evaluations for the CRE web site materials. They are self-tests and i greater than clicker questions.

• Additional Material on the Web site

Transdermal Drug Delivery Example

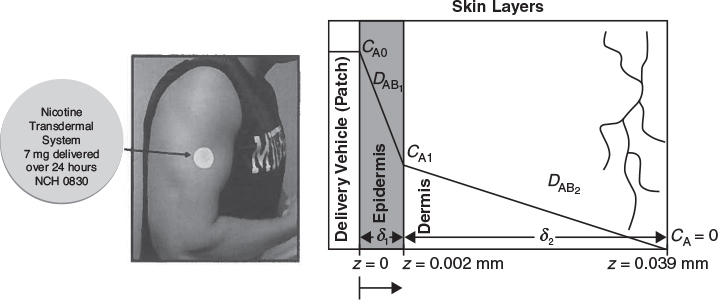
Transdermal drug delivery schematic.

Questions, Simulations, and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

A = • B = ▪ C = ♦ D = ♦♦

Questions

Q14-1_A QBR (Question Before Reading). Under what circumstances will the conversion predicted by mass transfer limitations be greater than that for surface reaction limitations?

Q14-2 Read over the problems at the end of this chapter. Make up an original problem that uses the concepts presented in this chapter. See Problem P5-1_A for the guidelines. To obtain a solution:

Make up your data and reaction.
Use a real reaction and real data.

The journals listed at the end of Chapter 1 may be useful for part (b).

Q14-3 (Sergeant Ambercromby). Capt. Apollo is piloting a shuttlecraft on his way to space station Klingon. Just as he is about to maneuver to dock his craft using the hydrazine system discussed in Example 14-2, the shuttle craft’s thrusters do not respond properly and it crashes into the station, killing Capt. Apollo (Star Wars 7 (fall 2015)). An investigation reveals that Lt. Darkside prepared the packed beds used to maneuver the shuttle and Lt. Data prepared the hydrazine–helium gas mixture. Foul play is suspected and Sgt. Ambercromby arrives on the scene to investigate.

What are the first three questions he asks?
Make a list of possible explanations for the crash, supporting each one by an equation or reason.

Q14-4 How would your answers change if the temperature was increased by 50°C, the particle diameter was doubled, and fluid velocity was cut in half? Assume properties of water can be used for this system.

Q14-5 How would your answers change in Example 14-3 if you had a 50–50 mixture of hydrazine and helium? If you increase d_p by a factor of 5?

Q14-6_A After viewing the video, what was new to you with regard to dust explosions? Could you list three things one should do or have in place to prevent dust explosions?

Q14-7 Go to the LearnChemE screencast link for Chapter 14 (http://www.learncheme.com/screencasts/kinetics-reactor-design). View one or more of the screencast 5- to 6-minute videos and write a two-sentence evaluation of what you learned.

Q14-8 AWFOS–S14 View the CSB video to list two things in which dust explosions are different from those involving flammable liquids.

Computer Simulations and Experiments

P14-1_B

Example 14-1: Mass Transfer of Oxygen to a Burning Carbon Particle

Wolfram and Python
1. Vary each slider to find the parameter to which the flux W_A_r is most sensitive.
2. What happens when the liquid diffusity and viscosity are both increased simultaneously?
3. Vary the velocity as shown in Figure 14-5 and describe its effect on the flux.
4. Write a set of conclusions based on the above experiments.
Example 14-2: Rapid Liquid-Phase Reaction on the Surface of a Catalyst Wolfram

and Python
1. Vary each of the parameters and tell which one the mass transfer coefficient (k_c) is most sensitive.
2. Change D_AB and U simultaneously both up and down and describe what you find.
3. Write a set of three conclusions from your experiments (i) and (ii).
Example 14-3: Combustion Time for a Single Particle

Wolfram and Python
1. Compare the burning time for a 100 μm porous carbon particle with a 10% solid with t_c in Example 14-3.
2. Vary all the parameters you can think of that would give a burning time of 500 ms.
3. Write a set of conclusions from your Wolfram experiments (i) and (ii).
Example 14-4: Mass Transfer Effects in Maneuvering a Space Satellite. What if you were asked for representative values for Re, Sc, Sh, and k_c for both liquid- and gas-phase systems for a velocity of 10 cm/s and a pipe diameter of 5 cm (or a packed-bed diameter of 0.2 cm)? What numbers would you give?
Example 14-5: The Case of Divide and Be Conquered. How would your answers change if the reaction were carried out in the liquid phase where kinematic viscosity, υ, varied as $v (T_{2}) = v (T_{1}) exp [- 400 K (\frac{1}{T_{1}} - \frac{1}{T_{2}})] ?$
Example 14-7: Flow, Diffusion, and Reaction in a Packed Bed

Wolfram and Python
1. Vary k_r and U and view X, W_A, and k as a function of W.
2. Vary D_AB and d_p and view k as a function of W.
3. Vary the ration (D_AB/υ) and describe what you find.
4. Vary the parameters by a factor of 10 above and below their nominal values and describe what you find (e.g., what were the most sensitive and least sensitive parameters? Hint: See Equation (14-81).
5. Write a set of conclusions based on all your experiments.

Problems

Photograph of a squirrel having a peanut.

A figure depicts the trap of a squirrel. — A vertical cylindrical trap of height A is immersed in the ground, where the variables at the initial level are marked as C subscript A0, P subscript r, and L equals 0. The bottom level of the cylindrical trap are marked with the parameters, C subscript AL, P subscript r, and L equals L. A squirrel is trapped at the bottom of the cylindrical trap.

P14-2_B Assume the minimum respiration rate of a chipmunk is 1.5 micromoles of O₂/min. The corresponding volumetric rate of gas intake is 0.05 dm³/min at STP.

What is the deepest a chipmunk can burrow a 3-cm diameter hole beneath the surface in Ann Arbor, Michigan? D_AB = 1.8 × 10^–5 m²/s
In Boulder, Colorado?
How would your answers to (a) and (b) change in the dead of winter when T = 0°F?
Critique and extend this problem (e.g., CO₂ poisoning). Thanks to Professor Robert Kabel at Pennsylvania State University.

Hint: Review derivations and equations for W_A and W_B to see how they can be applied to this problem.

P14-3_B Pure oxygen is being absorbed by xylene in a catalyzed reaction in the experimental apparatus sketched in Figure P14-3_B. Under constant conditions of temperature and liquid composition, the following data were obtained:

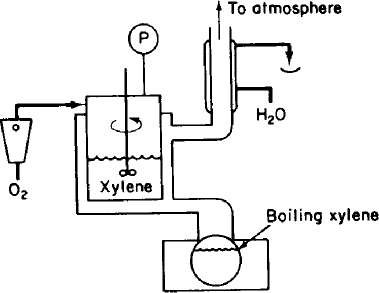
A figure depicts the catalyzed reaction in the experimental apparatus using xylene. — **Figure P14-3_B**

In the experiment, the bottom of the apparatus is heated in a trough consists of xylene. The vapor of boiling xylene is collected in a flask, which is observed by pure oxygen, and also some vapor of the xylene goes to the atmosphere while giving some residues of H2O.

	Rate of Uptake of O₂ (mL/h) for System Pressure (absolute)
Stirrer Speed (rpm)	1.2 atm	1.6 atm	2.0 atm	3.0 atm
400	15	31	75	152
800	20	59	102	205
1200	21	62	105	208
1600	21	61	106	207

No gaseous products were formed by the chemical reaction. What would you conclude about the relative importance of liquid-phase diffusion and about the order of the kinetics of this reaction? (California Professional Engineers Exam)

P14-4_B Derive an equation for the time necessary to completely burn a 100 μm carbon particle as a function of D₀. Also calculate the burning rate constant. Use the K_S values of the parameter values, for example, C_A_∞, given in Example 14-3.

diffusion controlled with D_AB = 10^–4 m²/s
reaction controlled with k_r = 0.01 m/s
combined reaction and diffusion controlled

Additional Information:

ρ_c = 188 mol/m³

P14-5_C In a diving-chamber experiment, a human subject breathed a mixture of O₂ and He while small areas of his skin were exposed to nitrogen gas. After some time, the exposed areas became blotchy, with small blisters forming on the skin. Model the skin as consisting of two adjacent layers, one of thickness δ₁ and the other of thickness δ₂. If counterdiffusion of He out through the skin occurs at the same time as N₂ diffuses into the skin, at what point in the skin layers is the sum of the partial pressures a maximum? If the saturation partial pressure for the sum of the gases is 101 kPa, can the blisters be a result of the sum of the gas partial pressures exceeding the saturation partial pressure and the gas coming out of the solution (i.e., the skin)?

Illustration depicting the diving-chamber experiment shows a fish moving near a container having a mixture of gas under the free water surface.

Before answering any of these questions, derive the concentration profiles for N₂ and He in the skin layers.

Diffusivity of He and N₂ in the inner skin layer = 5 × 10⁻⁷ cm²/s and 1.5 × 10⁻⁷ cm²/s, respectively.

Diffusivity of He and N₂ in the outer skin layer = 10⁻⁵ cm²/s and 3.3 × 10^-4 cm²/s, respectively.

	External Skin Boundary Partial Pressure	Internal Skin Boundary Partial Pressure
N₂	101 kPa	0
He	0	81 kPa
δ₁	20 μm	Stratum corneum
δ₂	80 μm	Epidermis

Hint: See Transdermal Drug Delivery in Expanded Material on the CRE Web site.

P14-6_B The decomposition of cyclohexane to benzene and hydrogen is mass transfer-limited at high temperatures. The reaction is carried out in a 5-cm-ID pipe 20 m in length packed with cylindrical pellets 0.5 cm in diameter and 0.5 cm in length. The pellets are coated with the catalyst only on the outside. The bed porosity is 40%. The entering volumetric flow rate is 60 dm³/min.

Calculate the number of pipes necessary to achieve 99.9% conversion of cyclohexane from an entering gas stream of 5% cyclohexane and 95% H₂ at 2 atm and 500°C.
Plot conversion as a function of pipe length.
How much would your answer change if the pellet diameter and length were each cut in half?
How would your answer to part (a) change if the feed were pure cyclohexane?
What do you believe is the point of this problem? Is the focus really green CRE? How so?

P14-7_C Lead titanate, PbTiO₃, is a material having remarkable ferroelectric, pyroelectric, and piezoelectric properties [ J. Elec. Chem. Soc., 135, 3137 (1988)]. A thin film of PbTiO₃ was deposited in a CVD reactor. The deposition rate is given below as a function of a temperature and flow rate over the film.

Flow Rate (SCCM)	Temperature (°C)	Deposition Rate (mg/cm² · h)
500	650	0.2
	750	0.8
	800	1.2
600	650	0.35
	750	1.0
	800	1.5
750	650	0.53
	750	1.45
	800	2.0
1000	650	0.55
	750	1.5
	800	2.0

What are all the things, qualitative and quantative, that you can learn from these data?

P14-8_B OEQ (Old Exam Question). A plant is removing a trace of Cl₂ from a waste-gas stream by passing it over a solid granulm absorbent in a tubular packed bed (Figure P14-8_B). At present, 63.2% removal is being acomplished, but it is believed that greater removal could be achieved if the flow rate were increased by a factor of 4, the particle diameter were decreased by a factor of 3, and the packed tube length increased by 50%. What percentage of chlorine would be removed under the proposed scheme? (The chlorine transferring to the absorbent is removed completely by a virtually instantaneous chemical reaction.) (Ans: 98%)

Figure of a tubular packed bed is shown. It is a vertical cylindrical tube of length L with a solid granulm absorbent, where the initial reactor volume v subscript 0 is fed by chlorine gas, which passes through the tubular packed bed consists of a solid granular absorbent. — **Figure P14-8_B**

P14-9_B OEQ (Old Exam Question). In a certain chemical plant, a reversible fluid-phase isomerization

$A \underset{\leftarrow}{\to} B$

is carried out over a solid catalyst in a tubular packed-bed reactor. If the reaction is so rapid that mass transfer between the catalyst surface and the bulk fluid is rate-limiting, show that the kinetics are described in terms of the bulk concentrations C_A and C_B by

${- r}_{A}^{″} = \frac{k_{B} [C_{A} - (1 / K) C_{B}]}{1 / K + k_{B} / k_{A}}$

where ${- r}_{A}^{'}$ = moles of A reacting per unit area catalyst per

k_A, k_B = transfer coefficients for A and B

K = equilibrium constant

It is desired to double the capacity of the existing plant by processing twice the feed of reactant A while maintaining the same fractional conversion of A to B in the reactor. How much larger a reactor, in terms of catalyst weight, would be required if all other operating variables are held constant? You may use the Thoenes–Kramers correlation for mass transfer coefficients in a packed bed.

P14-10_B The irreversible gas-phase reaction

$A \overset{cat}{\to} B$

is carried out adiabatically over a packed bed of solid catalyst particles. The reaction is first order in the concentration of A on the catalyst surface

${- r}_{As}^{'} = {k' C}_{As}$

The feed consists of 50% (mole) A and 50% inerts, and enters the bed at a temperature of 300 K. The entering volumetric flow rate is 10 dm³/s (i.e., 10000 cm³/s). The relationship between the Sherwood number and the Reynolds number is

Sh = 100 Re^1/2

As a first approximation, one may neglect pressure drop. The entering concentration of A is 1.0 M. Calculate the catalyst weight necessary to achieve 60% conversion of A for

isothermal operation.
adiabatic operation.

Additional information:

Kinematic viscosity: μ/ρ = 0.02 cm²/s

Particle diameter: d_p = 0.1 cm

Superficial velocity: U = 10 cm/s

Catalyst surface area/mass of catalyst bed: a = 60 cm²/g-cat

Diffusivity of A: D_e = 10⁻² cm²/s

Heat of reaction: $Δ H_{Rx}^{\circ}$ = −10000 cal/g mol A

Heat capacities: C_p_A = C_p_B = 25 cal/g mol · K, C_pS (solvent) = 75 cal/g mol · K

k′ (300 K) = 0.01 cm³/s · g-cat with E = 4000 cal/mol

P14-11_B Transdermal Drug Delivery. See photo on page 781. The principles of steady-state diffusion have been used in a number of drug-delivery systems. Specifically, medicated patches are commonly attached to the skin to deliver drugs for nicotine withdrawal, birth control, and motion sickness, to name a few. The U.S. transdermal drug-delivery is a multibillion dollar market. Equations similar to Equation (14-24) have been used to model the release, diffusion, and absorption of the drug from the patch into the body. The figure shown in the Additional Material and on page 781 shows a drug-delivery vehicle (patch) along with the concentration gradient in the epidermis and dermis skin layers.

Use a shell balance to show

$\frac{{d W}_{A z}}{d z} = 0$
Show the concentration profile in the epidermis layer

$\frac{C_{A0} - C_{A}}{{C_{A}}_{0} - C_{A1}} = \frac{z}{δ_{1}}$
Show the concentration profile in the dermis layer

$\frac{C_{A}}{C_{A1}} = \frac{δ_{2} - z}{{δ_{2}}^{} - δ_{1}}$
Equate the fluxes using $W_{A1} = {- D}_{A1} \frac{{d C}_{A}}{d z}$ and $W_{A2} = {- D}_{A2} \frac{{d C}_{A}}{d z}$ and to show

$C_{A1} = \frac{D_{A1} \frac{C_{A0}}{δ_{1}}}{\frac{D_{A2}}{δ_{2} - δ_{1}} + \frac{D_{A1}}{δ_{1}}}$
What are the concentration profiles in the dermis and epidermis layers?
Show the flux in the dermis layer is

$W_{A z} = \frac{D_{A2}}{δ_{2} - δ_{1}} [\frac{D_{A1} \frac{C_{A0}}{δ_{1}}}{\frac{D_{A2}}{δ_{2} - δ_{1}} + \frac{D_{A1}}{δ_{1}}}]$
What is the flux in the epidermis layer?

P14-12_D(Estimating glacial ages) The following oxygen-18 data were obtained from soil samples taken at different depths in Ontario, Canada. Assuming that all the ¹⁸O was laid down during the last glacial age and that the transport of ¹⁸O to the surface takes place by molecular diffusion, estimate the number of years since the last glacial age from the following data. Independent measurements give the diffusivity of ¹⁸O in soil as 2.64 = 10⁻¹⁰ m²/s.

Sketch of the glaciers on St. Montgomery. — **Figure P14-12_D** Glaciers.

	(surface)
Depth (m)	0	3	6	9	12	18
¹⁸O Conc. Ratio (C/C₀)	0	0.35	0.65	0.83	0.94	1.0

C₀ is the concentration of ¹⁸O at 25 m. Hint: A knowledge of error function solutions may or may not be helpful. (Ans: t = 5,616 years)

P14-13_B OEQ (Old Exam Question). A spherical particle is dissolving in a liquid. The rate of dissolution is first order in the solvent concentration, C. Assuming that the solvent is in excess, show that the following conversion-time relationships hold.

Rate-Limiting Regime	Conversion–Time Relationship
Surface reaction	${1 - (1 - X)}^{1 / 3} = \frac{α t}{D_{i}}$
Mass transfer	$\frac{D_{i}}{2 D *} [1 - {(1 - X)}^{2 / 3}] = \frac{α t}{D_{i}}$
Mixed	${[1 - (1 - X)]}^{1 / 3} + \frac{D_{i}}{2 D *} [1 {- (1 - X)}^{2 / 3}] = \frac{α t}{D_{i}}$

P14-14_C Derive the diffusion and reaction equation in spherical coordinates to describe the dissolution of a drug in the form of a spherical pellet. Plot the drug concentration as a function distance r and time t. Also plot the flux and particle diameter as a function of time.

P14-15_B A powder is to be completely dissolved in an aqueous solution in a large, well-mixed tank. An acid must be added to the solution to render the spherical particle soluble. The particles are sufficiently small that they are unaffected by fluid velocity effects in the tank. For the case of excess acid, C₀ = 2 M, derive an equation for the diameter of the particle as a function of time when

Mass transfer limits the dissolution: –W_A = k_cC_A0
Reaction limits the dissolution: ${- r}_{A}^{″} = k_{r}^{A} C_{A0}$

What is the time for complete dissolution in each case?
Now assume that the acid is not in excess and that mass transfer is limiting the dissolution. One mole of acid is required to dissolve 1 mol of solid. The molar concentration of acid is 0.1 M, the tank is 100 L, and 9.8 mol of solid is added to the tank at time t = 0. Derive an expression for the radius of the particles as a function of time and calculate the time for the particles to dissolve completely.
How could you make the powder dissolve faster? Slower?

Additional information:

$\begin{matrix} \begin{matrix} {D_{e} = 10^{- 10} m}^{2} / s, & {\begin{matrix} k = 10 \end{matrix}}^{- 18} / s \end{matrix} \\ initial diameter = 10^{- 5} m \end{matrix}$

P14-16_B (Pills) An antibiotic drug is contained in a solid inner core and is surrounded by an outer coating that makes it palatable. The outer coating and the drug are dissolved at different rates in the stomach, owing to their differences in equilibrium solubilities.

If D₂ = 4 mm and D₁ = 3 mm, calculate the time necessary for the pill to dissolve completely.
Assuming first-order kinetics (k_A = 10 h^–1) for the absorption of the dissolved drug (i.e., in solution in the stomach) into the bloodstream, plot the concentration in grams of the drug in the blood per gram of body weight as a function of time when the following three pills are taken simultaneously:

$\begin{matrix} Pill 1: & D_{2} = 5 mm, & D_{1} = 3 mm \\ Pill 2: & D_{2} = 4 mm, & D_{1} = 3 mm \\ Pill 3: & D_{2} = 3.5 mm, & D_{1} = 3 mm \end{matrix}$
Discuss how you would maintain the drug level in the blood at a constant level using different-size pills?
How could you arrange a distribution of pill sizes so that the concentration in the blood was constant over a period (e.g., 3 hr) of time?

Additional information:

Amount of drug in inner core = 500 mg

Solubility of outer layer at stomach conditions = 1.0 mg/cm³

Solubility of inner layer at stomach conditions = 0.4 mg/cm³

Volume of fluid in stomach = 1.2 L

Typical body weight = 75 kg

Sh = 2, D_AB = 6 × 10^–4 cm²/min

P14-17_B If disposal of industrial liquid wastes by incineration is to be a feasible process, it is important that the toxic chemicals be completely decomposed into harmless substances. One study carried out concerned the atomization and burning of a liquid stream of “principal” organic hazardous constituents (POHCs) [Environ. Prog., 8, 152 (1989)]. The following data give the burning droplet diameter as a function of time (both diameter and time are given in arbitrary units):

Time	20	40	50	70	90	110
Diameter	9.7	8.8	8.4	7.1	5.6	4.0

What can you learn from these data?

Supplementary Reading

The fundamentals of diffusional mass transfer may or may not be found in

R. B. BIRD, W. E. STEWART, and E. N. LIGHTFOOT, Transport Phenomena, 2nd ed. New York: Wiley, 2002, Chaps. 17 and 18.

S. Collins, Mockingjay (The Final Book of the Hunger Games). New York: Scholastic, 2014.

E. L. CUSSLER, Diffusion Mass Transfer in Fluid Systems, 3rd ed. New York: Cambridge University Press, 2009.

C. J. GEANKOPLIS, Transport Processes and Unit Operations. Upper Saddle River, NJ: Prentice Hall, 2003.

V. G. LEVICH, Physiochemical Hydrodynamics. Upper Saddle River, NJ: Prentice Hall, 1962, Chaps. 1 and 4.
Experimental values of the diffusivity can be found in a number of sources, two of which are

R. H. PERRY, D. W. GREEN, and J. O. MALONEY, Chemical Engineers’ Handbook, 8th ed. New York: McGraw-Hill, 2007.

T. K. SHERWOOD, R. L. PIGFORD, and C. R. WILKE, Mass Transfer. New York: McGraw-Hill, 1975.
A number of correlations for the mass transfer coefficient can be found in

A. L. LYDERSEN, Mass Transfer in Engineering Practice. New York: Wiley-Interscience, 1983, Chap. 1.

W. L. MCCABE, J. C. SMITH, and P. HARRIOTT, Unit Operations of Chemical Engineering, 6th ed. New York: McGraw-Hill, 2000, Chap. 17.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 14. Mass Transfer Limitations in Reacting Systems

Create new playlist

Sign In

Sign Up

14. Mass Transfer Limitations in Reacting Systems

14A Mass Transfer Fundamentals

14.1 Diffusion Fundamentals

14.1.1 Definitions

14.1.2 Molar Flux: WA

14.1.3 Fick’s First Law

14.2 Binary Diffusion

14.2.1 Evaluating the Molar Flux

14.2.2 Diffusion and Convective Transport

14.2.3 Boundary Conditions

14.2.4 Temperature and Pressure Dependence of DAB

14.3 Modeling Diffusion with Chemical Reaction

14.3.1 Diffusion through a Stagnant Film to a Particle

14.4 The Mass Transfer Coefficient

14B Applications

14.5 Mass Transfer to a Single Particle

14.5.1 First-Order Rate Laws

14.5.2 Limiting Regimes

14.6 The Shrinking Core Model

14.6.1 Dust Explosions, Particle Dissolution, and Catalyst Regeneration

14C Packed-Bed Applications

14.7 Mass Transfer-Limited Reactions in Packed Beds

14.8 Robert the Worrier

14.9 What If . . . ? (Parameter Sensitivity)

14.10 And Now… A Word from Our Sponsor—Safety 14 (AWFOS–S14 Sugar Dust Explosion)

Summary

Cre Web Site Materials

Questions, Simulations, and Problems

Questions

Computer Simulations and Experiments

Problems

Supplementary Reading

Table of Contents for
14. Mass Transfer Limitations in Reacting Systems

14.1.2 Molar Flux: W_A

14.2.4 Temperature and Pressure Dependence of D_AB