16. Residence Time Distributions of Chemical Reactors

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

16. Residence Time Distributions of Chemical Reactors^†

Nothing in life is to be feared. It is only to be understood.

—Marie Curie

^† Dr. Peter Danckwerts is considered the father of Residence Time Distributions in Chemical Reactors. After WWII, in which he served defusing unexploded bombs in London, he began developing the concepts of Residence Times, which he published in the early 1950s. Lucky for us he was careful during his WWII service.

Overview. In this chapter, we learn about nonideal reactors; that is, reactors that do not follow the models we have developed for ideal CSTRs, PFRs, and PBRs. After studying this chapter, the reader will be able to describe:

What the residence time distribution (RTD) is and how it can be used in analyzing reactors (Section 16.1).
Measurement of the RTD. How to calculate the concentration curve (i.e., the C-curve) and residence time distribution curve (i.e., the E-curve (Section 16.2)).
Characteristics of the RTD. How to calculate and use the cumulative RTD function, F(t), the mean residence time, t_m, and the variance σ² (Section 16.3).
The RTD in ideal reactors. How to evaluate E(t), F(t), t_m, and σ² for ideal PFRs, CSTRs, and laminar flow reactors (LFRs) so that we have a reference point as to how much our real (i.e., nonideal) reactor deviates from an ideal reactor (Section 16.4).
How to diagnose problems with real reactors by comparing t_m, E(t), and F(t) with ideal reactors. This comparison will help to diagnose and troubleshoot bypassing and dead volume problems in real reactors (Section 16.5).

16.1 General Considerations

The reactors treated in the book thus far—the perfectly mixed batch, the plug-flow tubular, the packed bed, and the perfectly mixed continuous tank reactors—have been modeled as ideal reactors. Unfortunately, in the real world we often observe behavior very different from that expected from the exemplar; this behavior is true of students, engineers, college professors, and chemical reactors. Just as we must learn to work with people who are not perfect,^† so the reactor analyst must learn to diagnose and handle chemical reactors whose performance deviates from the ideal. Nonideal reactors and the principles behind their analysis form the subject of this chapter and the next two chapters.

^† See the AIChE webinar “Dealing with Difficult People”: www.aiche.org/academy/webinars/dealing-difficult-people.

We want to analyze and characterize nonideal reactor behavior.

Peter V. Danckwerts was an interesting character and a number of stories about him can be found in the biography by Peter Varey.^‡ The basic ideas that Danckwerts used in the distribution of residence times to characterize and model nonideal reactions are really few in number. The two major uses of the residence time distribution to characterize nonideal reactors are

^‡ P. Varey, Life on the Edge, London: PFV Publications, 2012.

To diagnose problems of reactors in operation.
To predict conversion or effluent concentrations in existing/available reactors when a new chemical reaction is used in the reactor.

The following two examples illustrate reactor problems one might find in a chemical plant.

Example 1

A packed-bed reactor is shown in Figure 16-1. When a reactor is packed with catalyst, the reacting fluid usually does not flow uniformly through the reactor. Rather, there may be sections in the packed bed that offer little resistance to flow (Path 1) and, as a result, a portion of the fluid may channel through this pathway. Therefore, the molecules following this pathway do not spend much time in the reactor. On the other hand, if there is internal circulation or a high resistance to flow, the molecules could spend a long time in the reactor (Path 2). Consequently, we see that there is a distribution of times that molecules spend in the reactor in contact with the catalyst.

A packed bed reactor with catalyst. — **Figure 16-1** Packed-bed reactor.

Figure shows molecules packed inside a reactor. The molecules inside are packed closelyin most areas. In some areas, there is a pathway formed in between the loosely packed molecule. Path 1 is marked from left to right, along the direction of flow and path 2 is marked from right to left in the pathways present.

Example 2

In many continuous-stirred tank reactors, the inlet and outlet pipes are somewhat close together (Figure 16-2). In one operation, it was desired to scale up pilot plant results to a much larger system. It was realized that some short-circuiting occurred, so the tanks were modeled as perfectly mixed CSTRs with a bypass stream. In addition to short-circuiting, stagnant regions (dead zones) are often encountered. In these regions, there is little or no exchange of material with the well-mixed regions and, consequently, virtually

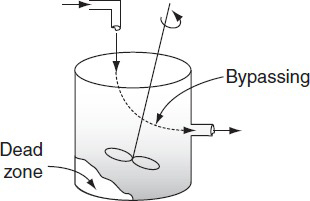
Working of a CSTR is shown. — **Figure 16-2** CSTR.

Figure shows a continuous-stirred tank reactors, with its respective inlet and outlet pipes. The direction of mixing is marked in the counter-clockwise direction. An inlet pipe is present at the top. An arrow is marked from the inlet pipe to the outlet representing the bypassing steam. A small portion at the bottom left of the tank is marked as the dead zone, which is empty.

We want to find ways of determining the dead zone volume and the fraction of the volumetric flow rate bypassing the system.

no reaction occurs there. Experiments were carried out to determine the amount of the material effectively bypassed and the volume of the dead zone. A simple modification of an ideal reactor successfully modeled the essential physical characteristics of the system and the equations were readily solvable.

The three concepts

RTD
Mixing
Model

Three concepts are used to describe nonideal reactors in these examples: the distribution of residence times in the system (RTD), the quality of mixing, and the model used to describe the system. All three of these concepts are considered when describing deviations from the mixing patterns assumed in ideal reactors. The three concepts can be regarded as characteristics of the mixing in nonideal reactors.

One way to order our thinking on nonideal reactors is to consider modeling the flow patterns in our reactors as either ideal CSTRs or PFRs as a first approximation. In real reactors, however, nonideal flow patterns exist, resulting in ineffective contacting and lower conversions than in the case of ideal reactors. We must have a method of accounting for this nonideality, and to achieve this goal we use the next higher level of approximation, which involves the use of macromixing information (RTD) (Sections 16.1–16.4). The next level uses microscale (micromixing) information (Chapter 17) to make predictions about the conversion in nonideal reactors. After completing the first four sections, 16.1–16.4, the reader can proceed directly to Chapter 17 to learn how to calculate the conversion and product distributions exiting real reactors. Section 16.5 closes the chapter by discussing how to use the RTD to diagnose and troubleshoot reactors. Here, we focus on two common problems: reactors with bypassing and dead volumes. Once the dead volumes, V_D, and bypassing volumetric flow rates, v_b, are determined, the strategies in Chapter 18 to model the real reactor with ideal reactors can be used to predict conversion.

Chance Card: Do not pass go, proceed directly to Chapter 17.

Reactor Monoply

16.1.1 Residence Time Distribution (RTD) Function

The idea of using the distribution of residence times in the analysis of chemical reactor performance was apparently first proposed in a pioneering paper by MacMullin and Weber.¹ However, the concept did not appear to be used extensively until the early 1950s, when Prof. P. V. Danckwerts gave organizational structure to the subject of RTD by defining most of the distributions of interest.² The ever-increasing amount of literature on this topic since then has generally followed the nomenclature of Danckwerts, and this will be done here as well.

¹ R. B. MacMullin and M. Weber, Jr., Trans. Am. Inst. Chem. Eng., 31, 409 (1935).

² P. V. Danckwerts, Chem. Eng. Sci., 2, 1 (1953).

Residence time

In an ideal plug-flow reactor, all the atoms of material leaving the reactor have been inside it for exactly the same amount of time. Similarly, in an ideal batch reactor, all the atoms of materials within the reactor have been inside the BR for an identical length of time. The time the atoms have spent in the reactor is called the residence time of the atoms in the reactor.

The “RTD”: Some molecules leave quickly, others overstay their welcome.

The idealized plug-flow and batch reactors are the only two types of reactors in which all the atoms in the reactors have exactly the same residence time. In all other reactor types, the various atoms in the feed spend different times inside the reactor; that is, there is a distribution of residence times of the material within the reactor. For example, consider the CSTR; the feed introduced into a CSTR at any given time becomes completely mixed with the material already in the reactor. In other words, some of the atoms entering the CSTR leave it almost immediately because material is being continuously withdrawn from the reactor; other atoms remain in the reactor almost forever because all the material recirculates within the reactor and is virtually never removed from the reactor at one time. Many of the atoms, of course, leave the reactor after spending a period of time somewhere in the vicinity of the mean residence time. In any reactor, the distribution of residence times can significantly affect its performance in terms of conversion and product distribution.

We will use the RTD to characterize nonideal reactors.

The residence time distribution (RTD) of a reactor is a characteristic of the mixing that occurs in the chemical reactor. There is no axial mixing in a plug-flow reactor, and this omission is reflected in the RTD. The CSTR is thoroughly mixed and possesses a far different kind of RTD than the plug-flow reactor. As will be illustrated later (cf. Example 16-3), not all RTDs are unique to a particular reactor type; markedly different reactors and reactor sequencing can display identical RTDs. Nevertheless, the RTD exhibited by a given reactor yields distinctive clues to the type of mixing occurring within it and is one of the most informative characterizations of the reactor.³

³ There are a number of mixing tutorials on the AIChE Webinar Web site and as an AIChE student member you have free access to all these webinars. See www.aiche.org/search/site/webinar.

16.2 Measurement of the RTD

The RTD is determined experimentally by injecting an inert chemical, molecule, or atom, called a tracer, into the reactor at some time t = 0 and then measuring the tracer concentration, C, in the effluent stream as a function of time, cf. Figure 16-3. In addition to being a nonreactive species that is easily detectable, the tracer should have physical properties similar to those of the reacting mixture and be completely soluble in the mixture. It also should not adsorb on the walls or other surfaces in the reactor. The latter requirements are needed to ensure that the tracer’s behavior will reliably reflect that of the material flowing through the reactor. Colored and radioactive materials along with inert gases are the most common types of tracers. The two most used methods of injection are pulse input and step input.

Use of tracers to determine the RTD

A reactor setup to determine the E(t). — **Figure 16-3** Experimental setup to determine E(t).

The setup contains a reactor present at the middle. On its left, feed is injected into the reactor and on the right, the resulting effluent is detected.

16.2.1 Pulse Input Experiment

The C-curve

In a pulse input, an amount of tracer N₀ is suddenly injected in one shot into the feed stream entering the reactor in as short a time as is humanly possible. The outlet concentration is then measured as a function of time. Typical concentration–time curves at the inlet and outlet of an arbitrary reactor are shown in Figure 16-4 on page 848. The effluent tracer concentration versus time curve is referred to as the C-curve in RTD analysis. We shall first analyze the injection of a tracer pulse for a single-input and single-output system in which only flow (i.e., no dispersion) carries the tracer material across system boundaries. Here, we choose an increment of time Δt sufficiently small that the concentration of tracer, C(t), exiting between time t and time (t + Δt) is essentially the same. The amount of tracer material, ΔN, leaving the reactor between time t and t + Δt is then

$\begin{matrix} Δ N = C (t) υ Δ t & (16 - 1) \end{matrix}$

where v is the effluent volumetric flow rate. In other words, ΔN is the amount of material exiting the reactor that has spent an amount of time between t and t + Δt in the reactor. If we now divide by the total amount of material that was injected into the reactor, N₀, we obtain

$\begin{matrix} \frac{Δ N}{N_{0}} = \frac{υ C (t)}{N_{0}} Δ t & (16 - 2) \end{matrix}$

which represents the fraction of material that has a residence time in the reactor between time t and t + Δt.

For pulse injection we define

$\begin{matrix} E (t) = \frac{υ C (t)}{N_{0}} & (16 - 3) \end{matrix}$

so that

$\begin{matrix} \frac{Δ N}{N_{0}} = E (t) Δ t & (16 - 4) \end{matrix}$

Interpretation of E(t) dt

The quantity E(t) is called the residence time distribution function. It is the function that describes in a quantitative manner how much time different fluid elements have spent in the reactor. The quantity E(t) dt is the fraction of fluid exiting the reactor that has spent between time t and t + dt inside the reactor.

Figure 16-4 shows schematics of the inlet and outlet concentrations for both a pulse input and step input for the experimental setup in Figure 16-3.

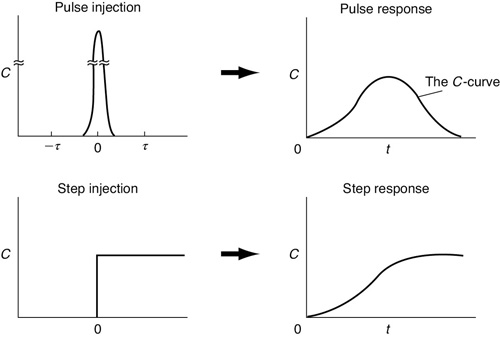
Two sets of graphs show RTD measurements. — **Figure 16-4** RTD measurements..

The graphs for pulse and step injections are shown. The vertical axis represents concentration C in all four graphs. The first graph is shown for pulse injection. The horizontal axis is marked with the values negative tau, 0, and tau. A curve starts on the horizontal axis between negative tau and 0 and ends on the horizontal axis between 0 and tau. It reaches a very high concentration level at 0. The second graph shows pulse response. The curve starts at the origin, increases gradually and reaches a maximum value of concentration at t and again gradually decreases to 0. The second set of graphs show step injection. This curve is called the C-curve. In the third graph, the curve is a vertical line drawn at 0 up to point C and becomes horizontal beyond this point. The next graph shows step response in which an increasing curve is drawn across time t, which is almost constant after a while.

The C-curve is shown. — A graph of C (t) versus t is shown. The curve resembles a bell curve across time t.

If N₀ is not known directly, it can be obtained from the outlet concentration measurements by summing up all the amounts of materials, ΔN, between time equal to zero and infinity. Writing Equation (16-1) in differential form yields

$\begin{matrix} d N = υ C (t) d t & (16 - 5) \end{matrix}$

The area within C-curve. — A graph of C (t) versus t is shown. The curve resembles a bell curve across time t. The area enclosed within the curve is shaded. This area equals integral lower limit 0 upper limit infinity, C(t) dt.

and then integrating, we obtain

$\begin{matrix} N_{0} = \int_{0}^{\infty} υ C (t) d t & (16 - 6) \end{matrix}$

The volumetric flow rate is usually constant, so we can define E(t) as

We find the RTD function, E(t), from the tracer concentration C(t)

The E-curve is shown. — The E-curve is plotted in a graph. The curve resembles a bell curve across time t.

$\begin{matrix} E (t) = \frac{C (t)}{\int_{0}^{\infty} C (t) d t} \end{matrix} \begin{matrix} (16 - 7) \end{matrix}$

The E-curve is just the C-curve divided by the area under the C-curve.

An alternative way of interpreting the residence time function is in its integral form:

$\begin{matrix} [\begin{matrix} Fraction of material leaving the reactor \\ that has resided in the reactor \\ for a time between t_{1} and t_{2} \end{matrix}] = \int_{t_{1}}^{t_{2}} E (t) d t \end{matrix}$

We know that the fraction of all the material that has resided for a time t in the reactor between t = 0 and t = ∞ is 1; therefore

Eventually, all guests must leave.

$\begin{matrix} \int_{0}^{\infty} E (t) d t = 1 \end{matrix} \begin{matrix} (16 - 8) \end{matrix}$

The following example will show how we can calculate and interpret E(t) from the effluent concentrations from the response to a pulse tracer input to a real (i.e., nonideal) reactor.

Example 16–1 Constructing the C(t) and E(t) Curves

A sample of the tracer hytane at 320 K was injected as a pulse into a reactor, and the effluent concentration was measured as a function of time, resulting in the data shown in Table E16-1.1.

Pulse input

TABLE E16-1.1 TRACER DATA

t (min)	0	0.5	1	2	3	4	5	6	7	8	9	10	12	14
C (g/m³)	0	0.6	1.4	5	8	10	8	6	4	3	2.2	1.6	0.6	0

The measurements represent the exact concentrations at the times listed and not average values between the various sampling tests.

Construct a figure showing the tracer concentration C(t) as a function of time.
Construct a figure showing E(t) as a function of time.

Solution

By plotting C as a function of time, using the data in Table E16-1.1, the curve shown in Figure E16-1.1 is obtained.

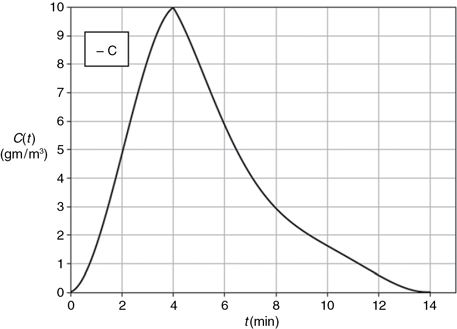
Figure E16-1.1 The C-curve.

The C-curve is plotted in a graph. The horizontal axis representing t (in minutes) ranges from 0 to 14 in increments of 2. The vertical axis representing C(t) (grams per meter cubed) ranges from 0 to 10 in increments of 1. The curve starts from the origin and increases to 10 gm per meter cubed at 4 minutes and decreases up to 3 gm per meter cubed at 8 minutes and decreases to 0 at 14 minutes.

To convert the C(t) curve in Figure E16-1.1 to an E(t) curve we use the area under the C(t) curve. There are three ways we can determine the area using this data.
1. Brute force: calculate the area by measuring the area of the squares and partial squares under the curve, and then summing them up. Who in the world do you think would use this method? Not sure I would.
2. Use the integration formulas given in Appendix A.4 Possibly Method 2 Simpson’s rule.
3. Fit the data to one or more polynomials using Polymath or some other software program. We will choose Polymath to fit the data. Note: A step-by-step tutorial to fit the data points using Polymath is given on the CRE Web site (www.umich.edu/~elements/6e/index.html) LEP 16-1. We will use two polynomials to fit the C-curve, one for the ascending portion, C₁(t), and one for the descending portion, C₂(t), both of which meet at t₁. Like Nike. Just do it.
Using the Polymath polynomial fitting routine (see tutorial), the data in Table E16-1.1 yields the following two polynomials:

$\begin{matrix} For t \leq 4 min then C_{1} (t) = 0.0039 + 0.274 t + 1.57 t^{2} - 0.255 t^{3} & (E16-1.1) \end{matrix}$

$\begin{matrix} For t \geq 4 min then C_{2} (t) = - 33.4 + 37.2 t - 11.6 t^{2} + 1.7 t^{3} - 0.13 t^{4} + 0.005 t^{5} \\ - 7.7 \times 10^{- 5} t^{5} & (E16-1.2) \end{matrix}$

A graph of C (t) versus t is shown. The curve resembles a normal distribution curve. The peak of the curve is marked match, at time t subscript 1. The curve becomes 0 at t subscript 2. The curve is marked as C subscript 1, of t before the match and the curve is marked as C subscript 2, of t beyond the match.

We then use an if statement in our fitted curve.

If (t ≤ 4 and t > 0) then C₁ else if (t > 4 and t < = 14) then C₂ else 0

To find the area under the curve, A, we use the ODE solver.

Let A represent the area under the curve, then

$\begin{matrix} \frac{d A}{d t} = C (t) & (E16-1.3) \end{matrix}$

$\begin{matrix} A = \int_{0}^{14} C (t) d t & (E16-1.4) \end{matrix}$
Construct E(t).

$E (t) = \frac{C (t)}{\int_{0}^{\infty} C (t) d t} = \frac{C (t)}{A}$

The Polymath program and results are shown in Table E16-1.2 where we see A = 51.

Images — TABLE E16-1.2 POLYMATH PROGRAM TO FIND AREA UNDER THE C-CURVE

Now that we have the area, A (i.e., 51 g•min/m³), under the C-curve, we can construct the E(t) curves. We now calculate E(t) by dividing each point on the C(t) curve by 51.0 g·min/m³

$\begin{matrix} E (t) = \frac{C (t)}{\int_{0}^{\infty} C (t) d t} = \frac{C (t)}{51 g \cdot min / m^{3}} & (E 16-1.5) \end{matrix}$

with the following results:

TABLE E16-13 C(t) AND E(t)

t (min)	1	2	3	4	5	6	7	8	9	10	12	14
C(t) (g/m³)	1.4	5	8	10	8	6	4	3	2.2	1.6	0.6	0
E(t) (min^–1)	0.027	0.1	0.16	0.2	0.16	0.12	0.08	0.06	0.043	0.03	0.012	0.0

Using Table E16-1.3 we can construct E(t) as shown in Figure E16-1.2.

**Figure E16-1.2** *E(t)*-Curve.

The E-curve is plotted in a graph. The horizontal axis representing t ranges from 0.0 to 15.0 in increments of 1.5. The vertical axis ranges from 0.00 to 0.20 in increments of 0.02. The curve starts from the origin and increases to 0.19 at 4 minutes and decreases to 0 at 13.5 minutes, approximately.

The E(t) Curve

Analysis: In this example, we fit the effluent concentration data C(t) from an inert tracer pulse input to two polynomials and then used an If statement to model the complete curve. We then used the Polymath ODE solver to get the area under the curve that we then used to divide the C(t) curve in order to obtain the E(t). Once we have the E(t) curve, we ask and easily answer such questions as “what fraction of the modules spend between 2 and 4 minutes in the reactor” or “what is the mean residence time t_m?” We will address these questions in the following sections where we discuss characteristics of the residence time distribution (RTD).

The principal difficulties with the pulse technique lie in the problems connected with obtaining a reasonable pulse at a reactor’s entrance. The injection must take place over a period that is very short compared with residence times in various segments of the reactor or reactor system, and there must be a negligible amount of dispersion between the point of injection and the entrance to the reactor system. If these conditions can be fulfilled, this technique represents a simple and direct way of obtaining the RTD.

Drawbacks to the pulse injection to obtain the RTD

There could be problems in fitting E(t) to a polynomial if the effluent concentration–time curve were to have a long tail because the analysis can be subject to large inaccuracies. This problem principally affects the denominator of the right-hand side of Equation (16-7), that is, the integration of the C(t) curve. It is desirable to extrapolate the tail and analytically continue the calculation. The tail of the curve may sometimes be approximated as an exponential decay. The inaccuracies introduced by this assumption are very likely to be much less than those resulting from either truncation or numerical imprecision in this region. Methods of Fitting the Tail are described in the Professional Reference Shelf R16.1.

16.2.2 Step Tracer Experiment

Now that we have an understanding of the meaning of the RTD curve from a pulse input, we will formulate a relationship between a step tracer injection and the corresponding concentration in the effluent.

The inlet concentration most often takes the form of either a perfect pulse input (Dirac delta function), imperfect pulse injection (see Figure 16-4), or a step input. Just as the RTD function E(t) can be determined directly from a pulse input, the cumulative distribution F(t) can be determined directly from a step input. The cumulative distribution gives the fraction of material F(t) that has been in the reactor at time t or less. We will now analyze a step input in the tracer concentration for a system with a constant volumetric flow rate. Consider a constant rate of tracer addition to a feed that is initiated at time t = 0. Before this time, no tracer was added to the feed. Stated symbolically, we have

A graph is shown for step input concentration. — A graph of C subscript in versus t is shown. The curve is a vertical line up to a point and then becomes horizontal.

A graph shows a C subscript out curve. — A graph of C subscript out versus t is shown. An increasing s-curve is drawn. The ends of the curve are connected using horizontal and vertical dashed lines.

$C_{in} (t) = {\begin{matrix} 0 & t < 0 \\ C_{0}, constant & t \geq 0 \end{matrix} \begin{matrix} (16 - 9) \end{matrix}$

The concentration of tracer in the feed to the reactor is kept at this level until the concentration in the effluent is indistinguishable from that in the feed; the test may then be discontinued. A typical outlet concentration curve for this type of input is shown in Figure 16-4.

Because the inlet concentration is a constant with time, C₀, we can take it outside the integral sign; that is,

$C_{out} (t) = C_{0} \int_{0}^{t} E (t^{'}) d t^{'}$

Dividing by C₀ yields

$\begin{matrix} {[\frac{C_{out} (t)}{C_{0}}]}_{step} = \int_{0}^{t} E (t^{'}) d t^{'} = F (t) \\ F (t) = {[\frac{C_{out} (t)}{C_{0}}]}_{step} & (16 - 10) \end{matrix}$

We differentiate this expression to obtain the RTD function E(t):

$\begin{matrix} E (t) = \frac{d F}{d t} = \frac{d}{d t} {[\frac{C_{out} (t)}{C_{0}}]}_{step} & (16 - 11) \end{matrix}$

The positive step is usually easier to carry out experimentally than the pulse test, and it has the additional advantage that the total amount of tracer in the feed over the period of the test does not have to be known as it does in the pulse test. One possible drawback in this technique is that it is sometimes difficult to maintain a constant tracer concentration in the feed. Obtaining the RTD from this test also involves differentiation of the data and presents an additional and probably more serious drawback to the technique, because differentiation of data can, on occasion, lead to large errors. A third problem lies with the large amount of tracer required for this test. If the tracer is very expensive, a pulse test is almost always used to minimize the cost.

Advantages and drawbacks to the step injection

A graph is shown for negative step input. — Two graphs of C of t versus t are shown. The curve for input is a horizontal line drawn from the vertical axis C(t) up to a point where time is 0 and then drawn vertically to touch the horizontal axis at 0. The second graph for output shows a decreasing-curve that originates on the vertical axis.

Other tracer techniques exist, such as negative step (i.e., elution), frequency-response methods, and methods that use inputs other than steps or pulses. These methods are usually much more difficult to carry out than the ones presented and are not encountered as often. For this reason, they will not be treated here, and the literature should be consulted for their virtues, defects, and the details of implementing them and analyzing the results. A good source for this type of information is Wen and Fan.³

³ C. Y. Wen and L. T. Fan, Models for Flow Systems and Chemical Reactors, New York: Marcel Dekker, 1975.

16.3 Characteristics of the RTD

From E(t) we can learn how long different molecules have been in the reactor.

Sometimes E(t) is called the exit-age distribution function. If we regard the “age” of an atom as the time it has resided in the reaction environment, then E(t) concerns the age distribution of the effluent stream. It is the most used of the distribution functions connected with reactor analysis because it characterizes the lengths of time various atoms spend at reaction conditions.

16.3.1 Integral Relationships

The fraction of the exit stream that has resided in the reactor for a period of time shorter than a given value t is equal to the sum over all times less than t of E(t) Δt, or expressed continuously, by integrating E(t) between time t = 0 and time, t.

$\begin{matrix} \int_{0}^{t} E (t) d t = F (t) = [\begin{matrix} Fraction of effluent \\ that has been in reactor \\ for less than time t \end{matrix}] & (16 - 12) \end{matrix}$

Analogously, we have, by integrating between time t and time t ⇒ ∞

$\begin{matrix} \int_{t}^{\infty} E (t) d t = 1 - F (t) = [\begin{matrix} Fraction of effluent \\ that has been in reactor \\ for longer than time t \end{matrix}] & (16 - 13) \end{matrix}$

Because t appears in the integration limits of these two expressions, Equations (16-12) and (16-13) are both functions of time. Danckwerts defined Equation (16-12) as a cumulative distribution function and called it F(t).⁴ We can calculate F(t) at various times t from the area under the curve of a plot of E(t) versus t, that is, the E-curve. A typical shape of the F(t) curve is shown in Figure 16-5. One notes from this curve that 80% (i.e., F(t) = 0.8) of the molecules spend 8 minutes or less in the reactor, and 20% of the molecules [1 = F(t)] spend longer than 8 minutes in the reactor.

The graph of a cumulative distribution curve. — **Figure 16-5** Cumulative distribution curve, F(t).

The figure shows an F-curve. The vertical axis representing F(t) ranges from 0 to 1.0 in increments of 0.2. The horizontal axis represents time (in minutes). A curve starts at the origin and increases to reach a maximum value of 1 at the end. The curve exhibits that f(t) is 0.8 in 8 minutes.

⁴ P. V. Danckwerts, Chem. Eng. Sci., 2, 1 (1953).

The F-curve is another function that has been defined as the normalized response to a particular input. Alternatively, Equation (16-12) has been used as a definition of F(t), and it has been stated that as a result it can be obtained as the response to a positive step tracer test. Sometimes the F-curve is used in the same manner as the RTD in the modeling of chemical reactors. An excellent industrial example is the study of Wolf and White, who investigated the behavior of screw extruders in polymerization processes.⁵

⁵ D. Wolf and D. H. White, AIChE J., 22, 122 (1976).

The F-curve

16.3.2 Mean Residence Time

In previous chapters treating ideal reactors, a parameter frequently used was the space time or average residence time, τ, which was defined as being equal to (V/ν). It will be shown that, in the absence of dispersion, and for constant volu-metric flow (ν = ν₀) no matter what RTD exists for a particular reactor, ideal or nonideal, this nominal space time, τ, is equal to the mean residence time, t_m.

τ = t_m

As is the case with other variables described by distribution functions, the mean value of the variable is equal to the first moment of the RTD function, E(t). Thus the mean residence time is

The first moment gives the average time the effluent molecules spent in the reactor.

$\begin{matrix} t_{m} = \frac{\int_{0}^{\infty} t E (t) d t}{\int_{0}^{\infty} E (t) d t} = \int_{0}^{\infty} t E (t) d t \end{matrix} \begin{matrix} (16 - 14) \end{matrix}$

We now wish to show how we can determine the total reactor volume using the cumulative distribution function.

In the Additional Material for Chapter 16 on the Web site (http://www.umich.edu/~elements/6e/16chap/expanded_ch16_exampleB.pdf), a proof is given that the mean residence time is equal to the space time, for the case of a constant volumetric flow rate, that is,

$\begin{matrix} t_{m} = τ \end{matrix} \begin{matrix} (16 - 15) \end{matrix}$

This result is true only for a closed system (i.e., no dispersion across boundaries; as is the case in Chapter 18). The exact reactor volume is determined from the equation

$\begin{matrix} V = υ t_{m} \end{matrix} \begin{matrix} (16 - 16) \end{matrix}$

16.3.3 Other Moments of the RTD

It is very common to compare RTDs by using their moments instead of trying to compare their entire distributions (e.g., Wen and Fan).⁶ For this purpose, three moments are normally used. The first is the mean residence time, t_m. The second moment commonly used is taken about the mean and is called the variance, σ², or square of the standard deviation. It is defined by

⁶ C. Y. Wen and L. T. Fan, Models for Flow Systems and Chemical Reactors, New York: Decker, 1975, Chap. 11.

The second moment about the mean is the variance.

$\begin{matrix} σ^{2} = \int_{0}^{\infty} {(t - t_{m})}^{2} E (t) d t \end{matrix} \begin{matrix} (16 - 17) \end{matrix}$

The magnitude of this moment is an indication of the “spread” of the distribution; the greater the value of this moment is, the greater a distribution’s spread will be.

The third moment is also taken about the mean and is related to the skewness, s³. The skewness is defined by

The two parameters most commonly used to characterize the RTD are τ and σ².

$\begin{matrix} S^{3} = \frac{1}{σ^{3 / 2}} \int_{0}^{\infty} {(t - t_{m})}^{3} E (t) d t \end{matrix} \begin{matrix} (16 - 18) \end{matrix}$

The magnitude of the third moment measures the extent that a distribution is skewed in one direction or another in reference to the mean.

Rigorously, for a complete description of a distribution, all moments must be determined. Practically, these three are usually sufficient for a reasonable characterization of an RTD.

Example 16–2 Mean Residence Time and Variance Calculations

Using the data given in Table E16-1.3 in Example 16-1

Construct the F(t) curve.
Calculate the mean residence time, t_m.
Calculate the variance about the mean, σ².
Calculate the fraction of fluid that spends between 3 and 6 minutes in the reactor.
Calculate the fraction of fluid that spends 2 minutes or less in the reactor.
Calculate the fraction of the material that spends 3 minutes or longer in the reactor.

Solution

To construct the F-curve, we simply integrate the E-curve

$\begin{matrix} E (t) = \frac{C (t)}{A} = \frac{C (t)}{51} & (E 16 - 1.5) \end{matrix}$

using an ODE solver such as Polymath shown in Table E16-2.1

$\begin{matrix} \frac{d F}{d t} = E (t) & (16 - 11) \end{matrix}$

The Polymath program and results are shown in Table E16-2.1 and Figure E16-2.1(b), respectively.

TABLE E16-1.3 C(t) AND E(t)

t (min)

0

1

2

3

4

5

6

7

8

9

10

12

14

C(t) (g/m³)

0

1.4

5

8

10

8

6

4

3

2.2

1.6

0.6

0

E(t) (min^–1)

0

0.027

0.1

0.16

0.2

0.16

0.12

0.08

0.06

0.043

0.03

0.012

0

Calculating the mean residence time,

$τ = t_{m} = \int_{0}^{\infty} t E (t) d t$
We also show in Table E16-2.1 the Polymath program to calculate the mean residence time, t_m. By differentiating Equation (16-14), we can easily use Polymath to find t_m, that is,

$\begin{matrix} \frac{d t_{m}}{d t} t E (t) & (E 16 - 2.1) \end{matrix}$

with t = 0 then E = 0 and t = 14 then E = 0. Equation (E16-2.1) and the calculated result is also shown in Table E16-2.1 where we find

t_m = 5.1 minutes

TABLE E16-2.1 POLYMATH PROGRAM AND RESULTS TO CONTRUCT THE E- AND F-CURVES

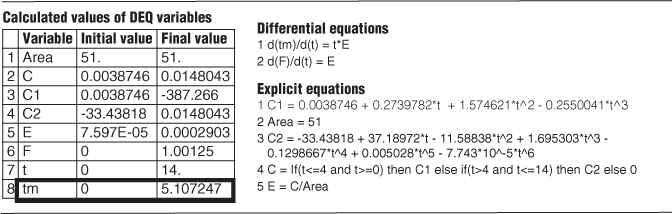
Using the Polymath plotting routines, we can construct Figures E16-2.1(a) and (b) after executing the program shown in the Polymath Table E16-2.1.

The E(t) and F(t) Curves

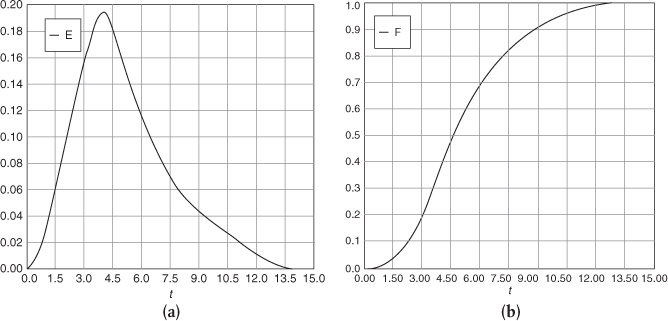
Figure E16-2.1 (a) E-Curve; (b) F-Curve.

The E(t) and F(t) curves are shown. The horizontal axis represents time t (in minutes) ranging from 0 to 15 in increments of 1.5. for both graphs. In graph (a), the vertical axis represents E(t) ranging from 0 to 0.20, in increments of 0.02. The value of E is 0 for the initial time t, which equals 0. Then, the curve gradually increases to a maximum value of E, which is 0.19 in 4 minutes. After this point, the curve decreases, and the value of E becomes 0 in 14 minutes. In graph (b), the vertical axis represents F(t) ranging from 0 to 1, in increments of 0.1. The value of F is 0 for the initial time t, which equals 0. Then, the curve gradually increases to 0.7 at t equals 7 minutes and further increases to a maximum value of 1, when t equals 12 minutes. Note: The mentioned values are approximate.
Now that we have found the mean residence time t_m, we can calculate the variance σ².

Calculating the variance

$\begin{matrix} σ^{2} = \int_{0}^{\infty} {(t - t_{m})}^{2} E (t) d t & (E 16 - 2.2) \end{matrix}$

We now differentiate Equation (E16-2.2) with respect to t

$\begin{matrix} \frac{d σ^{2}}{d t} {(t - t_{m})}^{2} E (t) & (E 16 - 2.3) \end{matrix}$

and then use Polymath to integrate between t = 0 and t = 14, which is the last point on the E-curve.

The results of this integration are shown in Table E16-2.2 where we find σ² = 6.2 minutes², so σ = 2.49 minutes.

TABLE E16-2.2 POLYMATH PROGRAM AND RESULTS TO CALCULATE THE MEAN RESIDENCE TIME, t_m, AND THE VARIANCE σ²
To find the fraction of fluid that spends between 3 and 6 minutes, we simply integrate the E-curve between 3 and 6

$F_{3 - 6} = \int_{3}^{6} E (t) d t$

The Polymath program is shown in Table E16-2.3 along with the output.

TABLE E16-2.3 POLYMATH PROGRAM TO FIND THE FRACTION OF FLUID THAT SPENDS BETWEEN 3 AND 6 MINUTES IN THE REACTOR

We see that approximately 50% (i.e., 49.53%) of the material spends between 3 and 6 minutes in the reactor.

We can visualize this fraction with the use of plot of E(t) versus (t) as shown in Figure E16-2.2. The shaded area in Figure E16-2.2 represents the fraction of material leaving the reactor that has resided in the reactor between 3 and 6 minutes. Evaluating this area, we find that 50% of the material leaving the reactor spends between 3 and 6 minutes in the reactor.

The E-curve

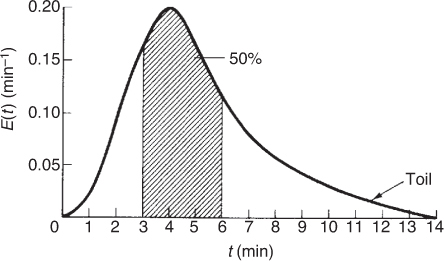
Figure E16-2.2 Fraction of material that spends between 3 and 6 minutes in the reactor.

The E(t) versus t graph is presented. The horizontal axis representing time t (in minutes) ranges from 0 to 14 in increments of 1. The vertical axis representing E(t) (in minutes inverse) ranges from 0 to 0.20 in increments of 0.05. The curve starts at the origin and increases to a maximum value of 0.20 in 4 minutes, after which it decreases gradually to 0.05 in 8 minutes and further decreases to 0 in 14 minutes. The region enclosed by the curve between 3 to 6 minutes is shaded, which represents the time spent by 50 percent of the materials in the reactor. The curve is marked as "Toil" at the decreasing end.
We shall next consider the fraction of material that has been in the reactor for a time t or less; that is, the fraction that has spent between 0 and t minutes in the reactor, F(t). This fraction is just the shaded area under the curve up to t = t minutes. This area is shown in Figure E16-2.3 for t = 3 minutes. Calculating the area under the curve, we see that approximately 20% of the material has spent 3 minutes or less in the reactor.

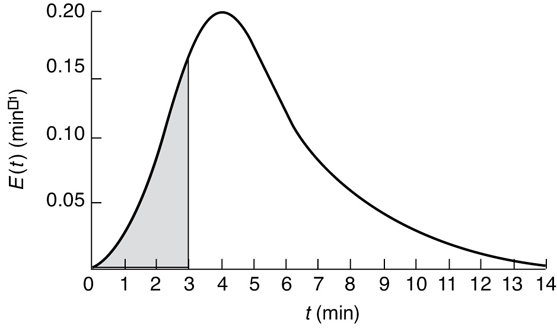
Figure E16-2.3 Fraction of material that spends 3 minutes or less in the reactor.

In the graph, the vertical axis represents E of t (minute inverse) ranging from 0.05 to 0.20 and the horizontal axis represents the time ranging from 0 to 14 minutes. The E-curve is plotted for a material. It starts from the origin, increases to a maximum value at (4,0.20), and decreases gradually to 0 at 14 minutes. The area under the curve corresponding to the first 3 minutes is shaded to indicate the fraction of material that spent 3 minutes or less in the reactor.
The fraction of fluid that spends a time t = 3 min or greater in the reactor is

$[\begin{matrix} Greater \\ than time t \end{matrix}] = 1 - F (t) = 1 - 0.2 = 0.8$

therefore 80% of the fluid spends a time t = 3 min or greater in the reactor.

The standard deviation is σ² = 6.19 min², so σ = 2.49 min.

Analysis: In this example we calculated two important properties of the RTD, the mean time molecules spend in the reactors, t_m, and the variance about this mean, σ². We will calculate these properties from the RTD of other nonideal reactors and then show in Chapter 18 how to use them to formulate models of real reactors using combinations of ideal reactors. We will use these models along with reaction-rate data to predict the conversion in the nonideal reactor we obtained from the reactor storage shed.

16.3.4 Normalized RTD Function, E(Θ)

Frequently, a normalized RTD is used instead of the function E(t). If the parameter Θ is defined as

$\begin{matrix} Θ \equiv \frac{t}{τ} \end{matrix} \begin{matrix} (16 - 19) \end{matrix}$

Why we use a normalized RTD

The quantity Θ represents the number of reactor volumes of fluid, based on entrance conditions, that have flowed through the reactor in time t. The dimensionless RTD function, E(Θ) is then defined as

$\begin{matrix} E (Θ) \equiv τ E (t) & (16 - 20) \end{matrix}$

and plotted as a function of Θ, as shown in the margin.

An E(t) versus time graph is shown. — Two decreasing and intersecting curves representing v subscript 1 and v subscript 2 are drawn in the E(t) versus time graph. Here, v subscript 1 is greater than v subscript 2.

The purpose of creating this normalized distribution function is that the flow performance inside reactors of different sizes can be compared directly. For example, if the normalized function E(Θ) is used, all perfectly mixed CSTRs have numerically the same RTD. If the simple function E(t) is used, numerical values of E(t) can differ substantially for CSTRs different volumes, V, and entering volumetric flow rates, ν₀. As will be shown later in Section 16.4.2, E(t) for a perfectly mixed CSTR

E(t) for an ideal CSTR

$\begin{matrix} E (t) = \frac{1}{τ} e^{- t / τ} \end{matrix} \begin{matrix} (16 - 21) \end{matrix}$

and therefore

$\begin{matrix} E (Θ) = τ E (t) = e^{- Θ} \end{matrix} \begin{matrix} (16 - 22) \end{matrix}$

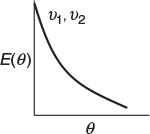
E(theta) versus theta graph is shown. — A graph of E(theta) as a function of theta shows a decreasing curve, representing v subscript 1 and v subscript 2.

From these equations it can be seen that the value of E(t) at identical times can be quite different for two different volumetric flow rates, say ν₁ and ν₂. But for the same value of Θ, the value of E(Θ) is the same irrespective of the size or volumetric flow rate of a perfectly mixed CSTR.

It is a relatively easy exercise to show that

$\begin{matrix} \int_{0}^{\infty} E (Θ) d Θ = 1 & (16 - 23) \end{matrix}$

and is recommended as a 93-s divertissement. (Jofostan University chemical engineers claim they can do it in 87 s.)

16.3.5 Internal-Age Distribution, /(α)

Tombstone jail How long have you been here? I(α)Δα When do you expect to get out?

Although this section is not a prerequisite to the remaining sections, the internal-age distribution is introduced here because of its close analogy to the external-age distribution. We shall let α represent the age of a molecule inside the reactor. The internal-age distribution function I(α) is a function such that (I(α)Δα) is the fraction of material now inside the reactor that has been inside the reactor for a period of time between α and (α + Δα). It may be contrasted with E(α)Δα, which is used to represent the material leaving the reactor that has spent a time between α and (α + Δα) in the reaction zone; I(α) characterizes the time the material has been (and still is) in the reactor at a particular time. The function E(α) is viewed outside the reactor and I(α) is viewed inside the reactor. In unsteady-state problems, it can be important to know what the particular state of a reaction mixture is, and I(α) supplies this information. For example, in a catalytic reaction using a catalyst whose activity decays with time, the internal-age distribution of the catalyst activities in the reactor I(α) can be of use in determining the amount of catalyst decay, a(α) when modeling the reactor.

The internal-age distribution is discussed further on the Professional Reference Shelf (R16.2) where the following relationships between the cumulative internal-age distribution I(α) and the cumulative external-age distribution F(α)

An icon of the reference shelf with books.

$\begin{matrix} I (α) = (1 - F (α)) / τ \end{matrix} \begin{matrix} (16 - 24) \end{matrix}$

and between E(t) and I(t)

$\begin{matrix} E (α) = - \frac{d}{d α} [τ I (α)] \end{matrix} \begin{matrix} (16 - 25) \end{matrix}$

are derived. For a CSTR, it is shown that the internal-age distribution function is

$\begin{matrix} I (α) = - \frac{1}{τ} e^{- α / τ} & (16 - 26) \end{matrix}$

16.4 RTD in Ideal Reactors

16.4.1 RTDs in Batch and Plug-Flow Reactors

The RTDs in plug-flow reactors and ideal batch reactors are the simplest to consider. All the atoms leaving such reactors have spent precisely the same amount of time within the reactors. The distribution function in such a case is a spike of infinite height and zero width, whose area is equal to 1; the spike occurs at t = V/ ν= τ, or Θ = 1, as shown in Figure 16-6.

The E(t) function is shown in Figure 16-6(a), and F(t) is shown in Figure 16-6(b).

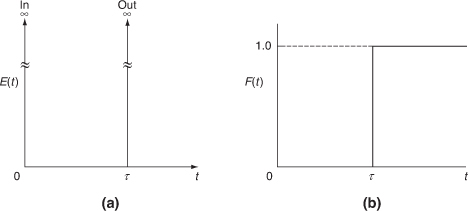
The E(t) and F(t) curves for the RTDs in the plug-flow reactor and ideal batch reactor. — **Figure 16-6** Ideal plug-flow response to a pulse tracer input.

The E(t) versus t graph is presented. The horizontal axis represents time t. The vertical axis representing E(t) ranges from 0 to In infinity. The E(t) value increases from 0 to out infinity at a fixed time, tau. The F(t) versus t graph is also presented. The horizontal axis represents time t. The vertical axis representing F(t) ranges from 0 to 1. The F(t) value increases from 0 to 1 at constant time tau, after which the value of F(t) is constant at 1 as time t increases.

Mathematically, this spike is represented by the Dirac delta function:

E(t) for a plug-flow reactor

$\begin{matrix} E (t) = δ (t - τ) \end{matrix} \begin{matrix} (16 - 27) \end{matrix}$

Properties of the Dirac delta function

The Dirac delta function has the following properties:

$δ (x) = \begin{matrix} {\begin{matrix} 0 & when x \neq 0 \\ \infty & when x = 0 \end{matrix} & (16 - 28) \end{matrix}$

$\begin{matrix} \begin{matrix} \int_{- \infty}^{\infty} & δ (x) \end{matrix} d x = 1 & (16 - 29) \end{matrix}$

$\begin{matrix} \begin{matrix} \int_{- \infty}^{\infty} & g (x) \end{matrix} δ (x - τ) d x = g (τ) & (16 - 30) \end{matrix}$

To calculate τ the mean residence time, we set g(x) = t

$\begin{matrix} t_{m} = \int_{0}^{\infty} t E (t) d t = \int_{0}^{\infty} t δ (t - τ) d t = τ \end{matrix} \begin{matrix} (16 - 31) \end{matrix}$

But we already knew this result, as did all chemical reaction engineering students at the university in Riça, Jofostan. To calculate the variance, we set g(t) = (t – τ)², and the variance, σ², is

PFR RTD

Parameters

t_m = τ and σ² = 0

$\begin{matrix} σ^{2} = \int_{0}^{\infty} {(t - τ)}^{2} δ (t - τ) d t = 0 \end{matrix}$

All material spends exactly a time τ in the reactor, so there is no variance [σ² = 0]!

The cumulative distribution function F(t) is

$\begin{matrix} F (t) = \int_{0}^{t} E (t) d t = \int_{0}^{t} δ (t - τ) d t \end{matrix} \begin{matrix} (16 - 32) \end{matrix}$

16.4.2 Single-CSTR RTD

From a tracer balance we can determine E(t).

In an ideal CSTR, the concentration of any substance in the effluent stream is identical to the concentration throughout the reactor. Consequently, it is possible to obtain the RTD from conceptual considerations in a fairly straightforward manner. A material balance on an inert tracer that has been injected as a pulse at time t = 0 into a CSTR yields for t > 0

$\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} In & - \end{matrix} & Out \end{matrix} & = \end{matrix} & Accumulation \end{matrix} \\ \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \overset{︷}{0} \end{matrix} & - \end{matrix} \end{matrix} & \overset{︷}{\begin{matrix} ν C \end{matrix}} \end{matrix} \end{matrix} & = \end{matrix} \end{matrix} & \overset{︷}{\begin{matrix} V \frac{d C}{d t} \end{matrix}} \end{matrix} \end{matrix} & (16 - 33) \end{matrix}$

Because the reactor is perfectly mixed, C in this equation is the concentration of the tracer both in the effluent and within the reactor. Separating the variables and integrating with C = C₀ at t = 0 yields

$\begin{matrix} C (t) = C_{0} e^{- t / τ} & (16 - 34) \end{matrix}$

The C-curve for an ideal CSTR can be plotted from Equation (16-34), which is the concentration of tracer in the effluent at any time t.

To find E(t) for an ideal CSTR, we first recall Equation (16-7) and then substitute for C(t) using Equation (16-34). That is,

$\begin{matrix} E (t) = \frac{C (t)}{\int_{0}^{\infty} C (t) d t} = \frac{C_{0} e^{- t / τ}}{\int_{0}^{\infty} C_{0} e^{- t / τ} d t} = \frac{e^{- t / τ}}{τ} & (16 - 35) \end{matrix}$

Evaluating the integral in the denominator completes the derivation of the RTD for an ideal CSTR and one notes they are the same as previously given by Equations (16-21) and (16-22)

E(t) and E(Θ) for a CSTR

$\begin{matrix} \begin{matrix} E (t) = \frac{e^{- t / τ}}{τ} \\ E (Θ) = e^{- Θ} \end{matrix} \end{matrix} \begin{matrix} (16 - 21) \\ (16 - 22) \end{matrix}$

the cumulative distribution is

$\begin{matrix} f (t) = \int_{0}^{t} E (t) d t = \int_{0}^{t} \frac{e^{- t / τ} d t}{τ} = 1 - e^{- t / τ} \end{matrix} \begin{matrix} (16 - 32) \end{matrix}$

Recall that Θ = t/τ and E(Θ) = τE(t).

Response of an ideal CSTR

$\begin{matrix} \begin{matrix} E (Θ) = e^{- Θ} \\ F (Θ) = 1 - e^{- Θ} \end{matrix} \end{matrix}$

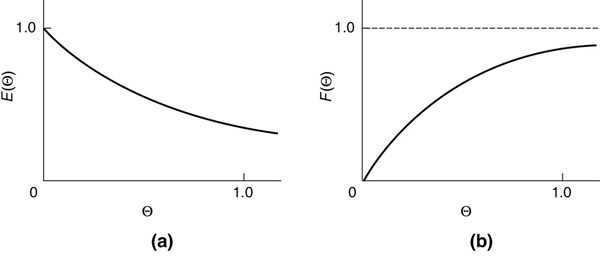
Two graphs depict the E of theta and F of theta curves for an ideal CSTR. — **Figure 16-7** E(Θ) and F(Θ) for an Ideal CSTR.

Graph (a) plots E of theta as a function of theta. The horizontal axis representing theta ranges from 0 to 1 and the vertical axis representing E of theta ranges from 0 to 1. The curve starts at the value 1 on the vertical axis, when theta equals 0, after which the curve decreases gradually with an increase in time. Graph (b) plots F of theta as a function of theta. The horizontal axis representing theta ranges from 0 to 1 and the vertical axis representing F of theta ranges from 0 to 1. The curve starts at the origin and gradually increases with an increase in the value of theta, to reach a maximum value of F of theta, which is less than 1.

The cumulative distribution F(Θ) is

$\begin{matrix} F (Θ) = \int_{0}^{θ} E (Θ) d Θ = 1 - e^{- Θ} & (16 - 36) \end{matrix}$

The E(Θ) and F(Θ) functions for an ideal CSTR are shown in Figure 16-7(a) and (b), respectively.

Earlier it was shown that for a constant volumetric flow rate, the mean residence time in a reactor is equal to (V/v), or τ. This relationship can be shown in a simpler fashion for the CSTR. Applying the definition of the mean residence time to the RTD for a CSTR, we obtain

$\begin{matrix} t_{m} = \int_{0}^{\infty} t E (t) d t = \int_{0}^{\infty} \frac{t}{τ} e^{- t / τ} d t = τ & (16 - 14) \end{matrix}$

Thus, the nominal holding time (space time) τ = (V/v) is also the mean residence time that the material spends in the reactor.

The second moment about the mean is the variance and is a measure of the spread of the distribution about the mean. The variance of residence times in a perfectly mixed tank reactor is (let x = t/τ)

For a perfectly mixed CSTR: t_m = τ

and σ = τ.

$\begin{matrix} σ^{2} = \int_{0}^{\infty} \frac{{(t - τ)}^{2}}{τ} e^{- t / τ} d t = τ^{2} \int_{0}^{\infty} {(x - 1)}^{2} e^{- x} d x = τ^{2} & (16 - 37) \end{matrix}$

Then, σ = τ. The standard deviation is the square root of the variance. For a CSTR, the standard deviation of the residence time distribution is as large as the mean itself!!

16.4.3 Laminar-Flow Reactor (LFR)

Before proceeding to show how the RTD can be used to estimate conversion in a reactor, we shall derive E(t) for a laminar-flow reactor. For laminar flow in a tubular (i.e., cylindrical) reactor, the velocity profile is parabolic, with the fluid in the center of the tube spending the shortest time in the reactor. A schematic diagram of the fluid movement after a time t is shown in Figure 16-8. The figure at the left shows how far down the reactor each concentric fluid element has traveled after a time t.

A laminar flow reactor is shown. — **Figure 16-8** Schematic diagram of fluid elements in a laminar-flow reactor.

The structure of a laminar flow reactor is shown. It has four cylindrical frames of four different radius connected together, ranging from the highest radius to the least. The top view of the reactor resembles four concentric circles of outer radius upper R. The third figure shows a circular frame of outer radius r and inner radius r plus dr. The width of the frame in the middle is marked dr.

Molecules near the center spend a shorter time in the reactor than those close to the wall.

The velocity profile in a pipe of outer radius R is

$\begin{matrix} U (r) = U_{max} [1 - {(\frac{r}{R})}^{2}] = 2 U_{avg} [1 - {(\frac{r}{R})}^{2}] = \frac{2 υ_{0}}{π R^{2}} [1 - {(\frac{r}{R})}^{2}] & (16 - 38) \end{matrix}$

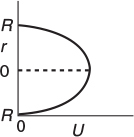
A graph presents the parabolic velocity. — A graph is shown in which the vertical axis is marked from upper R to R and the horizontal axis represents U. The curve is an open leftward parabola, with ends on the vertical axis. The center of the curve is at 0. The distance between the center and the ends of the curve is marked r and the edges are marked at upper R.

Parabolic Velocity Profile

where U_max is the centerline velocity and U_avg is the average velocity through the tube. U_avg is just the volumetric flow rate divided by the cross-sectional area.

The time of passage of an element of fluid at a radius r is

$\begin{matrix} t (r) = \frac{L}{U (r)} = \frac{π R^{2} L}{υ_{0}} \frac{1}{2 [1 - {(r / R)}^{2}]} & (16 - 39) \end{matrix}$

$\begin{matrix} = \frac{τ}{2 [1 - {(r / R)}^{2}]} & (16 - 40) \end{matrix}$

The volumetric flow rate of fluid out of the reactor between r and (r + dr), dv, is

$\begin{matrix} d υ = U (r) 2 π r d r & (16 - 41) \end{matrix}$

We are just doing a few manipulations to arrive at E(t) for an LFR

The fraction of total fluid passing out between r and (r + dr) is dυ/υ₀, that is,

$\begin{matrix} \frac{d υ}{υ_{0}} = \frac{U (r) 2 (π r d r)}{υ_{0}} & (16 - 42) \end{matrix}$

The fraction of fluid between r and (r + dr) that has a flow rate between ν and (ν + dν) and spends a time between t and (t + dt) in the reactor is

$\begin{matrix} E (t) d t = \frac{d υ}{υ_{0}} & (16 - 43) \end{matrix}$

We now need to relate the fluid fraction, Equation (16-43), to the fraction of fluid spending between time t and t = dt in the reactor. First we differentiate Equation (16-40)

$\begin{matrix} d t = \frac{τ}{2 R^{2}} \frac{2 r d r}{{[1 - {(r / R)}^{2}]}^{2}} = \frac{4}{τ R^{2}} {\frac{τ / 2}{[1 - {(r / R)}^{2}]}}^{2} r d r & (16 - 44) \end{matrix}$

and then use Equation (16-40) to substitute t for the term in brackets to yield

$\begin{matrix} d t = \frac{4 t^{2}}{τ R^{2}} r d r & (16 - 45) \end{matrix}$

Combining Equations (16-42) and (16-45), and then using Equation (16-40) that relates for U(r) and t(r), we now have the fraction of fluid spending between time t and t = dt in the reactor

$E (t) d t = \frac{d υ}{υ_{0}} = \frac{L}{t} (\frac{2 π r d r}{υ_{0}}) = \frac{L}{t} (\frac{2 π}{υ_{0}}) \frac{τ R^{2}}{4 t^{2}} d t = \frac{τ^{2}}{2 t^{3}} d t$

$\begin{matrix} E (t) = \frac{τ^{2}}{2 t^{3}} & (16 - 46) \end{matrix}$

The minimum time the fluid may spend in the reactor is

$t = \frac{L}{U_{max}} = \frac{L}{2 U_{avg}} (\frac{π R^{2}}{π R^{2}}) = \frac{V}{2 υ_{0}} = \frac{τ}{2}$

Consequently, the complete RTD function for a laminar-flow reactor is

At last! E(t) for a laminar-flow reactor

$\begin{matrix} E (t) = {\begin{matrix} 0 & t < \frac{τ}{2} \\ \frac{τ^{2}}{2 t^{3}} & t \geq \frac{τ}{2} \end{matrix} \end{matrix} \begin{matrix} (16 - 47) \end{matrix}$

The cumulative distribution function for t ≥ τ/2 is

$\begin{matrix} F (t) = \int_{0}^{t} E (t) d t = 0 + \int_{τ / 2}^{t} E (t) d t = \int_{τ / 2}^{t} \frac{τ^{2}}{2 t^{3}} d t = \frac{τ^{2}}{2} \int_{τ / 2}^{t} \frac{d t}{t^{3}} = 1 - \frac{τ^{2}}{4 t^{3}} & (16 - 48) \end{matrix}$

The mean residence time t_m is

For LFR t_m = τ

$\begin{matrix} t_{m} & = & \int_{τ / 2}^{\infty} t E (t) d t = \frac{τ^{2}}{2} \int_{τ / 2}^{\infty} \frac{d t}{t^{2}} \\ = & \frac{τ^{2}}{2} {[- \frac{1}{t}]}_{τ / 2}^{\infty} = τ \end{matrix}$

This result was shown previously to be true for any reactor without dispersion. The mean residence time is just the space time τ.

The dimensionless form of the RTD function is

Normalized RTD function for a laminar-flow reactor

$\begin{matrix} E (Θ) = {\begin{matrix} 0 & Θ < 0.5 \\ \frac{1}{2 Θ^{3}} & Θ \geq 0.5 \end{matrix} \end{matrix} \begin{matrix} (16 - 49) \end{matrix}$

and is plotted in Figure 16-9.

Comparing LFR, CSTR, and PFR

The RTD function for three reactors are plotted. — **Figure 16-9** **(a)** E(Θ) for an LFR; **(b)** F(Θ) for a PFR, CSTR, and LFR.

In the first graph, the value of LFR is plotted. The vertical axis representing E(theta) ranges from 0 to 4 in increments of 0.5. The horizontal axis ranges from 0 to 1.4 in increments of 0.2. A curve representing LFR is at 0 up to theta equals 0.5 and increases to 4 at theta equals 0.5. The curve then gradually decreases to 0.2 at theta equals 1.4. In the second graph, three curves are drawn for CSTR, LFR, and PFR. The vertical axis representing F(theta) ranges from 0 to 1.2 in increments of 0.2. The horizontal axis ranges from 0 to 1.4 in increments of 0.2. A curve representing CSTR increases from 0 to 0.8 at theta equals 1.4. The curve representing LFR ranges from 0 at theta equals 0.5 and increases to 0.9 at theta equals 1.4. The curve representing PFR is at 0 when theta equals 1 and increases to 1.0 when theta equals 1.0 and remains constant till theta equals 1.4.

The dimensionless cumulative distribution, F(Θ) for Θ ≥ 1/2, is

$F (Θ) = 0 + \int_{\frac{1}{2}}^{Θ} E (Θ) d Θ = \int_{\frac{1}{2}}^{Θ} \frac{d Θ}{2 Θ^{3}} = (1 - \frac{1}{4 Θ^{2}})$

$\begin{matrix} F (Θ) = {\begin{matrix} 0 & Θ < \frac{1}{2} \\ (\begin{matrix} 1 - \frac{1}{4 Θ^{2}} \end{matrix}) & Θ \geq \frac{1}{2} \end{matrix}} \end{matrix} \begin{matrix} (16 - 50) \end{matrix}$

Figure 16-9(a) shows E(Θ) for a laminar-flow reactor (LFR), while Figure 16-9(b) compares F(Θ) for a PFR, CSTR, and LFR.

Experimentally injecting and measuring the tracer in a laminar-flow reactor can be a difficult task if not a nightmare. For example, if one uses as a tracer chemicals that are photoactivated as they enter the reactor, the analysis and interpretation of E(t) from the data become much more involved.⁷

⁷ D. Levenspiel, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999, p. 342.

16.5 PFR/CSTR Series RTD

Modeling the real reactor as a CSTR and a PFR in series

In some stirred tank reactors, there is a highly agitated zone in the vicinity of the impeller that can be modeled as a perfectly mixed CSTR. Depending on the location of the inlet and outlet pipes, the reacting mixture may follow a somewhat tortuous path either before entering or after leaving the perfectly mixed zone—or even both. This tortuous path may be modeled as a plug-flow reactor. Thus, this type of reactor may be modeled as a CSTR in series with a plug-flow reactor, and the PFR may either precede or follow the CSTR. In this section, we develop the RTD for a series arrangement of a CSTR and a PFR.

First consider the CSTR followed by the PFR (Figure 16-10). The mean residence time in the CSTR will be denoted by τ_s and the mean residence time in the PFR by τ_p. If a pulse of tracer is injected into the entrance of the CSTR, the CSTR output concentration as a function of time will be

C = C₀ e^–t/τ_s

Figure shows a real reactor model. — **Figure 16-10** Real reactor modeled as a CSTR and PFR in series.

A stirred tank reactor is shown in which axis of rotation is marked in the counter-clockwise direction. The particles enter the tank through the inlet pipe, follow random paths and leaves the tank via the outlet pipe. This enters the CSTR, from which it is connected to PFR.

This output will be delayed by a time τ_p at the outlet of the plug-flow section of the reactor system. Thus, the RTD of the reactor system is

$\begin{matrix} E (t) = {\begin{matrix} 0 & t < τ_{p} \\ \frac{e^{- (t - τ_{p}) / τ_{s}}}{τ_{s}} & t \geq τ_{p} \end{matrix} \end{matrix} \begin{matrix} (16 - 51) \end{matrix}$

See Figure 16-11.

The RTD is not unique to a particular reactor sequence.

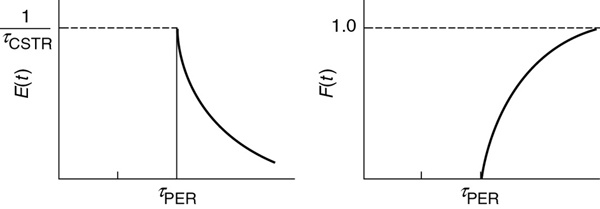
Two graphs of RTD curves are plotted. — **Figure 16-11** RTD curves *E(t)* and *F(t)* for a CSTR and a PFR in series.

In the first graph, the vertical axis represents E(t). A decreasing curve is drawn from 1 over tau subscript CSTR at tau subscript PFR. In the second graph, the vertical axis represents F(t). A steep increasing curve starting from tau subscript PFR on the horizontal axis increases to a maximum value of 1.0.

Next, consider a reactor system in which the CSTR is preceded by the PFR. If the pulse of tracer is introduced into the entrance of the plug-flow section, then the same pulse will appear at the entrance of the perfectly mixed section τ_p seconds later, meaning that the RTD of the reactor system will again be

E(t) is the same, no matter which reactor comes first.

$\begin{matrix} E (t) = {\begin{matrix} 0 & t < τ_{p} \\ \frac{e^{- (t - τ_{p}) / τ_{s}}}{τ_{s}} & t \geq τ_{p} \end{matrix} \end{matrix} \begin{matrix} (16 - 51) \end{matrix}$

which is exactly the same as when the CSTR was followed by the PFR.

It turns out that no matter where the CSTR occurs within the PFR/CSTR reactor sequence, the same RTD results. Nevertheless, this is not the entire story as we will see in Example 16-3.

Example 16–3 Comparing Early and Late Mixing for a Second-Order Reaction

Examples of early and late mixing for a given RTD

Consider a second-order reaction being carried out in a real CSTR that can be modeled as two different reactor systems: In the first system an ideal CSTR is followed by an ideal PFR (Figure E16-3.1); in the second system the PFR precedes the CSTR (Figure E16-3.2). To simplify the calculations, let τ_s and τ_p each equal 1 minute, let the reaction-rate constant equal 1.0 m³/kmol·min, and let the initial concentration of liquid reactant, C_A0, equal 1.0 kmol/m³. Find the conversion in each system.

For the parameters given, we note that in these two arrangements (see Figures E16-3.1 and E16-3.2), the RTD function, E(t), is the same

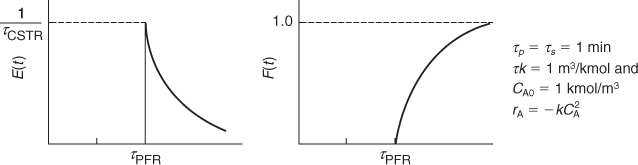
A figure shows an E-curve and F-curve plotted for a PFR reactor. — Two graphs are shown. In the first graph, the vertical axis represents E of t and the horizontal axis represents time. The graph plotted is concave upward decreasing curve. The curve starts at (tau subscript PFR, 1 over tau subscript CSTR) and decreases gradually. In the second graph, the vertical axis represents F of t and the horizontal axis represents time. The curve plotted starts at (tau subscript PFR, 0) and increases gradually to a maximum value of F(t) equals 1. Here, T subscript p equals T subscript s equals 1 minute, tau K equals 1 meter cubed over kilo mole, and C subscript A0 equals 1 kilo mole per meter cubed. Also, r subscript equals negative k times (C subscript A) squared.

Solution

Let’s first consider the case of early mixing when the CSTR is followed by the plug-flow section (Figure E16-3.1).

Early Mixing

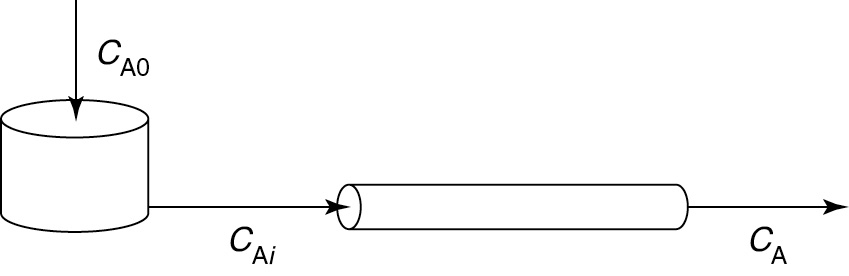
Figure E16-3.1 Early mixing scheme.

An initial concentration of C subscript A0 enters the CSTR. The concentration of C subscript A i is transferred from CSTR to a narrow cylindrical plug flow section. The concentration leaving this section is C subscript A.

A mole balance on the CSTR section gives upon inserting the rate law

$V = \frac{F_{A0} - F_{A i}}{- r_{A i}} = \frac{υ_{0} (C_{A 0} - C_{A i})}{{k C}_{A i}^{2}}$

Rearranging

$\begin{matrix} υ_{0} (C_{A 0} - C_{A i}) = {k C}_{A i}^{2} V & (E16-3.1) \end{matrix}$

Dividing by ν₀ and rearranging, we have quadric equation to solve for the intermediate concentration C_Ai

$τ_{s} {k C}_{A i}^{2} + C_{A i} - C_{A 0} = 0$

Substituting for τ_s and k

$τ_{s} k = 1 min \cdot \frac{m^{3}}{kmol \cdot min} = \frac{1 m^{3}}{kmol}$

Solving for C_A_i gives

$\begin{matrix} C_{A i} = \frac{\sqrt{1 + 4 τ_{s} k C_{A 0} - 1}}{2 τ_{s} k} = \frac{- 1 + \sqrt{1 + 4}}{2} = 0.618 kmol / m^{3} & (E16-3.2) \end{matrix}$

This concentration will be fed into the PFR. The PFR mole balance is

$\begin{matrix} \frac{d F_{A}}{d V} = υ_{0} \frac{d C_{A}}{d V} = \frac{d C_{A}}{d τ_{p}} = r_{A} = - {k C}_{A}^{2} & (E16-3.3) \end{matrix}$

Integrating Equation (E16-3.3)

$\begin{matrix} \frac{1}{C_{A}} - \frac{1}{C_{A i}} = τ_{p} k & (E16-3.4) \end{matrix}$

Substituting C_A_i = 0.618 kmol/m³, τ_p = 1 min, k = 1 m³/kmol/min, and τ_pk = 1 m³/kmol in Equation (E16-3.4) yields

Early Mixing CSTR → PFR

X = 0.618

C_A = 0.382 kmol/m³

as the concentration of reactant in the effluent from the reaction system. The conversion is

$X = (\frac{C_{A0} - C_{A}}{C_{A0}})$

$\begin{matrix} X = (\frac{1 - 0.382}{1}) = 0.618 = 61.8 % \end{matrix}$
Now, let’s consider the case of late mixing.

When the perfectly mixed section is preceded by the plug-flow section (Figure E16-3.2), the outlet of the PFR is the inlet to the CSTR, C_A_i. Again, solving Equation (E16-3.3)

$\frac{1}{C_{A i}} - \frac{1}{C_{A0}} = τ_{p} k$

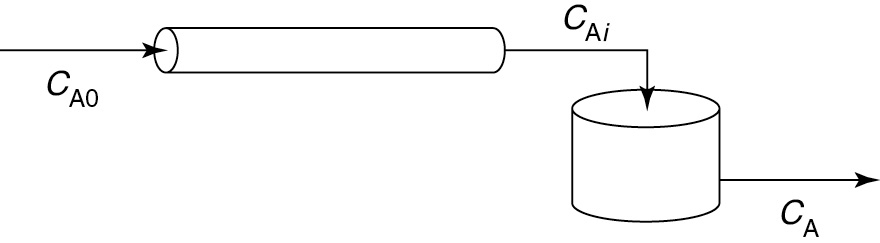
Figure E16-3.2 Late mixing scheme.

An initial concentration of C subscript A0 enters the narrow cylindrical plug flow section. The concentration of C subscript A i is transferred from the plug flow section to CSTR. The concentration leaving this section is C subscript A.

Solving for intermediate concentration, C_A_i, given τ_pk= 1 m³/mol and a C_A0 = 1 mol/m³

C_A_i = 0.5 kmol/m³

Next, solve for C_A exiting the CSTR.

A material balance on the perfectly mixed section (CSTR) gives

$\begin{matrix} τ_{s} k C_{A}^{2} + C_{A} - C_{A i} = 0 & (E 16 - 3.5) \end{matrix}$

$\begin{matrix} C_{A} = \frac{\sqrt{1 + 4 τ_{s} k C_{A i}} - 1}{2 τ_{s} k} = \frac{- 1 + \sqrt{1 + 2}}{2} = 0.366 kmol / m^{3} & (E16-3.6) \end{matrix}$

Late Mixing

PFR → CSTR

X = 0.634

Early mixing

X = 0.618

Late mixing

X = 0.634

as the concentration of reactant in the effluent from the reaction system. The corresponding conversion is 63.4%; that is,

$\begin{matrix} X = 1 - (C_{A} / C_{A 0}) = 1 - \frac{0.366}{1.0} = 63.4 % \end{matrix}$

Analysis: The RTD curves are identical for both configurations. However, the conversion was not the same. In the first configuration, a conversion of 61.8% was obtained; in the second configuration, 63.4%. While the difference in the conversions is small for the parameter values chosen, the point is that there is a difference. Let me say that again, the point is that there is a difference and we must explore it further in Chapters 17 and 18.

While E(t) was the same for both reaction systems, the conversion was

Chance Card: Do not pass go, proceed directly to Chapter 17.

The conclusion from this example is of extreme importance in reactor analysis: The RTD is not a complete description of structure for a particular reactor or system of reactors. The RTD is unique for a particular or given reactor. However, as we just saw, the reactor or reaction system is not unique for a particular RTD. When analyzing nonideal reactors, the RTD alone is not sufficient to determine its performance, and more information is needed. It will be shown in Chapter 17 that in addition to the RTD, an adequate model of the nonideal reactor flow pattern and knowledge of the quality of mixing or “degree of segregation” are both required to characterize a reactor properly.

Reactor Monopoly

At this point, the reader has the necessary background to go directly to Chapter 17 where we use the RTD to calculate the mean conversion in a real reactor using different models of ideal chemical reactors.

16.6 Diagnostics and Troubleshooting

16.6.1 General Comments

As discussed in Section 16.1, the RTD can be used to diagnose problems in existing reactors. As we will see in further detail in Chapter 18, the RTD functions E(t) and F(t) can be used to model the real reactor as combinations of ideal reactors.

Figure 16-12 illustrates typical RTDs resulting from different nonideal reactor situations. Figures 16-12(a) and (b) correspond to “nearly” ideal PFRs and CSTRs, respectively. The RTD for the nonideal reactor in Figure 16-12(c) modeled as a PBR with channeling and dead zones is shown in Figure 16-12(d). In Figure 16-12(d), one observes that a principal peak occurs at a time smaller than the space time (τ = V/ν₀) (i.e., early exit of fluid) and also that some fluid exits at a time greater than space-time τ. This curve is consistent with the RTD for a packed-bed reactor with channeling (i.e., bypassing) and stagnant zones (i.e., not mixed with bulk flow) as discussed earlier in Figure 16-1. Figure 16-12(f) shows the RTD for the nonideal CSTR in Figure 16-12(e), which has dead zones and bypassing. The dead zone serves not only to reduce the effective reactor volume, so the active reactor volume is smaller than expected, but also results in longer residence times for the tracer molecules to diffuse in and out of these “dead or stagnant” zones.

Six graphs for the different values of RTD. — **Figure 16-12** (a) RTD for *near* plug-flow reactor; (b) RTD for *near* perfectly mixed CSTR; (c) packed-bed reactor with dead zones and channeling; (d) RTD for packed-bed reactor in (c); (e) tank reactor with short-circuiting flow (bypass); (f) RTD for tank reactor with channeling (bypassing or short-circuiting) and a dead zone in which the tracer slowly diffuses in and out.

In graph "a," the vertical axis represents E(t) and the horizontal axis representing time has tau marked in between. A bell curve is drawn across tau. A dashed vertical is line is drawn at tau and the curve is symmetrical about the vertical line. The dashed line is marked as ideal and the curve is marked as actual. Graph b shows two decreasing curves representing actual and ideal, drawn across time t. The actual curve is given by a solid line and the ideal curve is given by a dashed line. Comparatively, E (t) is greater for actual case in the beginning and lesser at the end. In figure c, a packed bed reactor is shown in which the channeling and dead zones are marked. The arrows are marked from left to right. It is marked z equals 0 on the left and z equals L on the right end of the reactor. Figure d shows a graph in which E(t) is plotted against time t. A random curve is drawn across time t. A vertical dashed line is drawn at tau. The curve, to the left of tau is marked channeling and the curve to the right of the line is marked as dead zone. Figure e shows a tank reactor in which the channeling and dead zones are marked. Figure f shows a graph in which the E(t) is plotted against time. A curve increases from the origin and then decreases gradually across time t. The curve, at its peak is marked bypassing and the decreasing part of the curve is marked as long tail dead zone. A vertical dashed line is drawn at tau.

RTDs that are commonly observed

What’s wrong with my reactor?

16.6.2 Simple Diagnostics and Troubleshooting Using the RTD for Ideal Reactors

16.6.2A The CSTR

We now consider three CSTRs: (a) one that operates normally, (b) one with bypassing, and (c) one with a dead volume. For a well-mixed CSTR, as we saw in Section 16.4.2, the response to a pulse tracer is

CSTR RTD Functions

Concentration:

$\begin{matrix} C (t) = C_{0} e^{- t / τ} & (16 - 34) \end{matrix}$

RTD function:

$\begin{matrix} E (t) = \frac{1}{τ} e^{- t / τ} & (16 - 35) \end{matrix}$

Cumulative function:

$\begin{matrix} F (t) = 1 - e^{- t / τ} & (16 - 36) \end{matrix}$

$τ = \frac{V}{υ_{0}}$

where τ is the space time—the case of perfect operation.

Perfect Operation (P) Model

Here, we will measure our reactor with a yardstick to find V and our flow rate with a flow meter to find ν₀ in order to calculate τ = V/ν₀. We can then compare the curves for imperfect operation (cf. Figures 16-14 and 16-15) with the curves shown below in Figure 16-13 for perfect (i.e., ideal) CSTR operation

$τ = \frac{V}{υ_{0}}$

Figure 16-13 Perfect operation of a CSTR.

A CSTR reactor is shown in which the input volume and output volume are marked as v subscript 0. The stirring takes place in counter-clockwise direction. The yardstick used to measure the reactor is also shown. The graph of E(t) versus time is a decreasing curve marked transient. It is drawn across time from 1 over tau on the vertical axis. In the curve, e to the power negative t over tau is marked. In the graph of F(t) versus time, an increasing curve is drawn from the origin up to 1.0 across time t. It is marked 1 minus e to the power negative t over tau.

If τ is large, there will be a slow decay of the output transient, C(t), and E(t) for a pulse input. If τ is small, there will be rapid decay of the transient, C(t), and E(t) for a pulse input.
Bypassing (BP) Model

In Figure 16-14, the real reactor on the left is modeled by an ideal reactor with bypassing, as shown on the right.

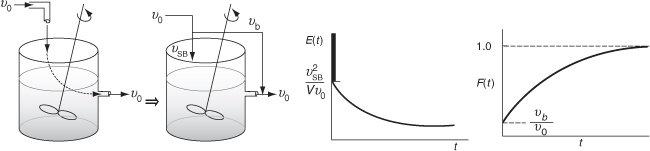
Figure 16-14 Ideal CSTR with bypass.

A CSTR tank is shown in which the entering volumetric flow rate and the exiting volumetric flow rate are marked as v subscript 0. A part of the input bypasses to the outlet. The reacting system is stirred in the counter-clockwise direction. The volumetric flow rate that bypasses is marked as v subscript b and the volumetric flow rate that enters the mixture is marked as v subscript SB. The graph of E(t) is a curve that decreases to v subscript SB squared over the volume V times v subscript 0, at the initial value of t. Then, the E(t) value decreases steadily from v subscript SB, squared over the volume V times v subscript 0 with an increase in time t. The graph of F(t) is a curve that increases from v subscript b, over v subscript 0 to 1, as time t increases.

The entering volumetric flow rate is divided into a volumetric flow rate that enters the reacting system, ν_SB, and a volumetric flow rate that bypasses the reacting mixture system completely ν_b. Where ν₀ = ν_SB = ν_b. The subscript SB denotes a model of a reactor system with bypassing. The reactor system volume V_S is the well-mixed portion of the reactor.

The analysis of a bypass to the CSTR may be elucidated by observing the output to a step tracer input to the real reactor. The CSTR with bypassing will have RTD curves similar to those in Figure 16-15.

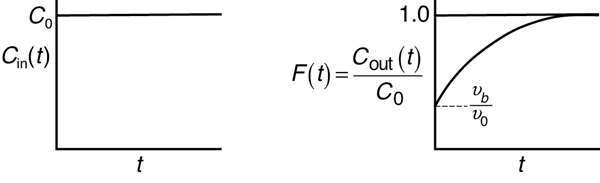
Figure 16-15 Inlet (a) and outlet (b) concentration curves correspond to Figure 16-14.

Two graphs are shown plotting concentration as a function of time. In the first graph, the vertical axis represents C subscript in of t. The concentration is constant at C subscript 0 across time t. In the second graph, an increasing curve is drawn from v subscript b over v subscript 0 to 1.0 across time t. The value of f(t) on the vertical axis equals C subscript out, of (t) over C subscript 0.

We see the concentration output in the form C(t)/C₀ for a step input will be the F-curve and the initial jump will be equal to the fraction bypassed. The corresponding equation for the F-curve is

$F (t) = \frac{υ_{b}}{υ_{0}} + \frac{υ_{SB}}{υ_{0}} [1 - e^{- (\frac{υ_{SB} t}{V})}]$

differentiating the F-Curve we obtain the E-curve

$E (t) = \frac{υ_{b}}{υ_{0}} δ (t - 0) + \frac{υ_{SB}^{2}}{V υ_{0}} e^{- (\frac{υ_{SB} t}{V})}$

Here, a fraction of the tracer (ν_b/ν₀) will exit immediately while the rest of the tracer will mix and become diluted with volume V and exponentially increase up to C_out(t), where F(t) = 1.0.

Because some of the fluid bypasses, the flow passing through the system will be less than the total volumetric rate, υ_SB < ν₀; consequently, τ_SB > τ. For example, let’s say the volumetric flow rate, which bypasses the reactor, ν_b, is 25% of the total (e.g., ν_b = 0.25 ν₀). The volumetric flow rate entering the reactor system, ν_SB, is 75% of the total (ν_SB = 0.75 ν₀) and the corresponding true space time (τ_SB) for the system volume with bypassing is

$τ_{SB} = \frac{V}{υ_{SB}} = \frac{V}{0.75 υ_{0}} = 1.33 τ$

The space time, τ_SB, will be greater than it would be if there were no bypassing. Because τ_SB is greater than τ, there will be a slower decay of the transients C(t) and E(t) than there would be with perfect operation.
Dead Volume (DV) Model

Consider the CSTR in Figure 16-16 without bypassing but instead with a stagnant or dead volume.

Figure 16-16 Ideal CSTR with dead volume.

A CSTR tank is shown in which the input volume is marked as v subscript 0 and the system volume is marked V subscript SD. The dead volume is marked as V subscript DV and the output volume is v subscript 0. The graph of E(t) is a curve starting from 1 over tau subscript SD and decreasing across time t. The graph of F(t) is an increasing curve that increases to 1.0 across time t.

The total volume, V, is the same as that for perfect operation, V = V_DV + V_SD. The subscript DV in V_DV represents the dead volume in the model, and the subscript SD in V_SD is the reacting system volume in the model. Here, the dead volume where absolutely no reaction takes place, V_DV, acts like a fictitious brick at the bottom taking up precious reactor volume. The system volume where the reaction can take place, that is, V_SD, is reduced because of this dead volume and therefore less conversion can be expected.

We see that because there is a dead volume that the fluid does not enter, there is less system volume, V_SD, available for reaction than in the case of perfect operation, that is, V_SD < V. Consequently, the fluid will pass through the reactor with the dead volume more quickly than that of perfect operation, that is, τ_SD < τ.

If

$\begin{matrix} V_{DV} \end{matrix} = 0.2 V, V_{SD} = 0.8 V, then τ_{SD} = \frac{0.8 V}{υ_{0}} = 0.8 τ$

Also as a result, the transients C(t) and E(t) will decay more rapidly than that for perfect operation because there is a smaller system volume.

Summary

A summary for ideal CSTR mixing volume is shown in Figure 16-17.

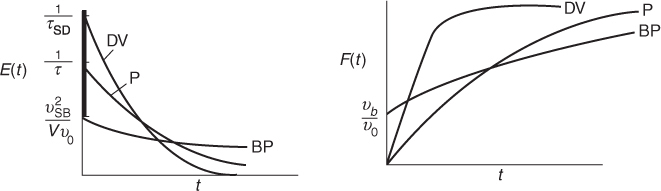
Graphs of E(t) and F(t) are presented for three models of CSTR under perfect operation. — **Figure 16-17** Comparison of E(t) and F(t) for CSTR under perfect operation, bypassing, and dead volume. (BP = bypassing model, P = perfect operation model, and DV = dead volume model).

The graphs of E(t) and F(t) show three curves. In the graph of E(t), the three curves exhibit a decreasing trend. The E(t) curve for bypassing model starts at v subscript SB, squared over the volume V times v subscript 0, and slightly decreases with increase in time. The E(t) curve for the perfect operation model decreases from a value of 1 over tau on the vertical axis with an increase in time and reaches the horizontal axis. The E(t) curve for the dead volume model starts at a maximum value of 1 over tau subscript SD, rapidly decreases with an increase in time, and reaches the horizontal axis. In the graph of F(t), the three curves show an increasing trend. The F(t) curve for bypassing model starts at v subscript b, over v subscript 0, and linearly increases with an increase in time. The F(t) curve for perfect operation model starts at the origin, steadily increases with an increase in time, and reaches a maximum value. The F(t) curve for the dead volume model starts at the origin, increases rapidly for a while, and then remains almost constant at a maximum value of F(t).

Knowing the volume V measured with a yardstick and the flow rate ν₀ entering the reactor measured with a flow meter, one can calculate and plot E(t) and F(t) for the ideal case (P) and then compare with the measured RTD E(t) to see whether the RTD suggests either bypassing (BP) or dead zones (DV).

16.6.2B Tubular Reactor

A similar analysis to that for a CSTR can be carried out on a tubular reactor.

Perfect Operation of PFR (P) Model

We again measure the volume V with a yardstick and ν₀ with a flow meter. The E(t) and F(t) curves are shown in Figure 16-18. The triangles drawn in Figures 16-18 and 16-19 should really be Dirac delta functions with zero width at the base. The space time for a perfect PFR is

τ = V/ν₀
PFR with Channeling (Bypassing, BP) Model

Let’s consider channeling (bypassing), as shown in Figure 16-19, similar to that shown in Figures 16-2 and 16-12(d). The space time for the reactor system with bypassing (channeling) τ_SB is

$τ_{SB} = \frac{V}{υ_{SB}}$

Figure 16-18 Perfect operation of a PFR.

A reactor is shown in which an arrow representing the flow rate v subscript 0 is marked from left to right. A yardstick and a flow meter are also shown. Two graphs are plotted for E(t) and F(t). The E(t) graph has a peak marked across time tau. The F(t) graph has a vertical line drawn at time tau up to 1.0. The line becomes horizontal past tau at 1.0.

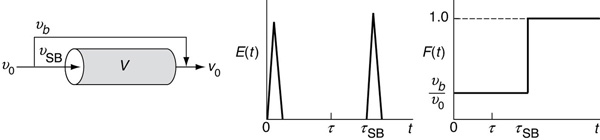
Figure 16-19 PFR with bypassing similar to the CSTR.

A reactor is shown in which an arrow representing flow rate v subscript 0 is marked from left to right, through the reactor. The volumetric flow rates v subscript SB and v subscript b are also marked. Two peaks are marked in an E(t) graph at 0 and at tau subscript SB. The horizontal axis has tau marked at the center, between the two peaks. The F(t) graph is shown in which the vertical axis is marked with 0, v subscript b over v subscript 0, and 1.0 and the horizontal axis representing time marked with tau and tau subscript S B. A horizontal line is drawn from v subscript b over v subscript 0 on the vertical axis up to tau subscript S B and increases vertically to 1.0. At 1.0, the line becomes horizontal past tau subscript S B.

Because ν_SB < ν₀, the space time for the case of bypassing is greater when compared to perfect operation, that is,

τ_SB > τ

If 25% is bypassing (i.e., ν_b = 0.25 ν₀) and only 75% is entering the reactor system (i.e., ν_SB = 0.75 ν₀), then τ_SB = V/(0.75ν₀) = 1.33τ. The fluid that does enter the reactor system flows in a plug flow. Here, we have two spikes in the E(t) curve: one spike at the origin and one spike at τ_SB that comes after τ for perfect operation. Because the volumetric flow rate is reduced, the time of the second spike will be greater than τ for perfect operation.
PFR with Dead Volume (DV) Model

The dead volume, V_DV, could be manifested by internal circulation at the entrance to the reactor as shown in Figure 16-20.

Figure 16-20 PFR with dead volume.

The PFR reactor resembles a horizontal cylinder with opening on both sides. Arrows are marked from left to right and dead zones are marked on either corners of the opening on the left. An arrow representing flow rate v subscript 0 is marked from left to right. The PFR is marked with dead volume V subscript DV and system volume V subscript SD. In the first graph, E(t) is plotted against time. A peak is marked in between the origin and time tau, at tau subscript S D. In the second graph, F(t) is plotted against time. A vertical line is drawn at tau subscript S D and then becomes horizontal till time tau.

The system volume, V_SD, is where the reaction takes place and the total reactor volume is (V = V_SD + V_DV). The space time, τ_SD, for the reactor system with only dead volume is

$τ_{SD} = \frac{V_{SD}}{υ_{0}}$

Compared to perfect operation, the space time τ_SD is smaller and the tracer spike will occur before τ for perfect operation.

τ_SD < τ

Here again, the dead volume takes up space that is not accessible. As a result, the tracer will exit early because the system volume, V_SD, through which it must pass is smaller than the perfect operation case.

Summary

Figure 16-21 is a summary of these three cases.

The comparison of PFR under three categories. — **Figure 16-21** Comparison of PFR under perfect operation, bypassing, and dead volume (DV = dead volume model, P = perfect PFR model, BP = bypassing model).

In the graph, F(t) is plotted against time. The vertical axis is marked with v subscript b and v subscript 0. The horizontal axis is marked with tau subscript S D, tau, and tau subscript S B. The curve representing DV is drawn vertically at tau subscript S D, which extends horizontally after a point. The curve representing P is drawn vertically at tau, which extends horizontally after a point. The curve representing BP is drawn horizontally from a point between v subscript b and v subscript 0 up to tau subscript S B, then increases vertically, and again horizontally. The highest value of F of t is the same for all three curves.

In addition to its use in diagnosis, the RTD can be used to predict conversion in existing reactors when a new reaction is tried in an old reactor. However, as we saw in Section 16.5, the RTD is not unique for a given system, and we need to develop models for the RTD to predict conversion. Examples of these models will be discussed in Chapter 18.

There are many situations where the fluid in a reactor is neither well mixed nor approximates plug flow. The idea is this: We have seen that the RTD can be used to diagnose or interpret the type of mixing, bypassing, and so on, that occurs in an existing reactor that is currently on stream and is not yielding the conversion predicted by the ideal reactor models. Now let’s envision another use of the RTD. Suppose we have a nonideal reactor either on line or sitting in storage. We have characterized this reactor and obtained the RTD function. What will be the conversion of a reaction with a known rate law that is carried out in a reactor with a known RTD?

The question

How can we use the RTD to predict conversion in a real reactor?

In Chapter 17 we show how this question can be answered in a number of ways.

16.7 And Now… A Word from Our Sponsor–Safety 16 (AWFOS–S16 Critical Thinking Actions)

In addition to critical thinking questions discussed in Table 15-3, Chapter 15, we also have Rubenfeld and Scheffer^† seven Critical Thinking Actions (CTAs) shown in Table 16-1. We will use Example 13-2 on the explosion that occurred after the charge to the reactor was tripled in order to hypothesize the CTAs for each of type of action.^*

^† M. G. Rubenfeld and B. Scheffer, Critical Thinking TACTICS for Nurses: Achieving the IOM Competencies, 2nd ed. Sudbury, MA: Jones & Bartlett Publishers, 2010.

^* H. S. Fogler, Elements of Chemical Reaction Engineering, 6th ed. Boston MA: Pearson, 2020.

TABLE 16-1 TYPES OF CRITICAL THINKING ACTIONS (CTAS) AND EXAMPLES MONSANTO EXPLOSION (EXAMPLE 13-2)^**

Types of CTA	Example Phrases of CTA	CTA Safety Examples
Predicting: envisioning a plan and its consequences	I could imagine that happening if I … I anticipated … I was prepared for … I made provisions for … I envisioned the outcome to be … My prognosis was … I figured the probability of … I tried to go beyond the here and now …	I knew that if the cooling system were to fail for more than 9 minutes (cf. Example 13-2), the reaction would run away.
Analyzing: separating or breaking a whole into parts to discover their nature, function, and relationships	I dissected the situation … I tried to reduce things to manageable units … I detailed a schematic picture of … I sorted things out by … I looked for the parts that … I looked at each piece individually …	I dissected the energy balance to find the parameters that were the most sensitive to down time and temperature increases and would cause the reaction to run away.
Information seeking: searching for evidence, facts, or knowledge by identifying relevant sources and gathering objective, subjective, historical, and current data from those sources	I made sure I had all the pieces of the picture … I knew I needed to look up, or study … I wondered how I could find out … I asked myself if I knew the whole story … I kept searching for more data … I looked for evidence of … I needed to have all the facts …	I looked up the heat of reaction to calculate the heat generated Q_g in the reactor at the start of the reaction to see whether it would be greater than the heat removed, Q_r.
Applying standards: judging according to established personal, professional, or social rules or criteria	I judged that according to … I compared this situation to what I knew to be the rule … I thought of/studied the policy for … I knew I had to … There are certain things you just have to account for … I thought of the bottom line that is always … I knew it was unethical to …	I measured the corrosion inside the reactor tubes and determined the tube wall thickness was insufficient to withstand 1,000 psi according to established standards for the pipe material.
Discriminating: recognizing differences and similarities among things or situations and distinguishing carefully as to category or rank	I grouped things together … I put things in categories … I tried to consider what was the priority of … I stood back and tried to see how those things were related … I wondered if this was as important as … I listed the discrepancies in the study and found that … What I heard and what I saw were consistent/inconsistent with … This situation was different from/the same as …	I made a list of all the things that could go wrong when we restarted the cooling system. The reaction runaway occurred after cooling water failure for 10 minutes as the situation was different, that is, reactor was charged three times more than normal charge rate.
Transforming knowledge: changing or converting the condition, nature, form, or function of concepts among contexts	I wondered if that would fit in this situation … I took what I knew and asked myself if it would work … I improved on the basics by adding … At first I was puzzled; then I saw that there were similarities to … I figured if this were true, then that would also be true.	I was puzzled at first because I did not understand why the reactor took so long to explode after the cooling system failed (cf. Example 13-2). Then I calculated and determined that the rate of temperature increase (dT/dt) was so small that it took a long time, 2 hours, to reach a point where the Arrhenius dependence dominated the heat-generated term.
Logical reasoning: drawing inferences or conclusions that are supported in or justified by evidence	I deduced from the information that … I could trace my conclusion back to the data … My diagnosis was grounded in the evidence … I considered all the information and then inferred that … I could justify my conclusion by … I moved down a straight path from the initial data to the final conclusion … I had a strong argument for … My rationale for the conclusion was …	I justified my conclusion that the reaction would not have run away for the increased feed charge by carrying out a number of computer simulations to show that the heat generated, Q_g, was less than the heat removed, Q_r, for a downtime less that 5 minutes.

^** See page 58–59, H. S. Fogler, S. E. LeBlanc, and B. R. Rizzo, Strategies for Creative Problem Solving, 3rd ed. Boston, MA: Prentice Hall, 2014.

HSF favorite actions (1) I envisioned the outcome would be … (2) I dissected the situation … (3) I know I had to look up or study … (4) I judged that according to … (5) I grouped things together … (6) At first I was puzzled; then I saw that there were similarities to … (7) I justified my conclusion with the evidence that …

Closure. After completing this chapter, the reader will be able to use the tracer concentration–time data to calculate the external-age distribution function E(t), the cumulative distribution function F(t), the mean residence time, t_m, and the variance, σ². The reader will be able to sketch E(t) for ideal reactors, and by comparing E(t) from the experiment with E(t) for ideal reactors (PFR, PBR, CSTR, laminar-flow reactor (LFR)), be able to diagnose problems in real reactors. The reader will be able to use the RTD curves to identify the nonideal reactor problems of dead volume and bypassing.

SUMMARY

The quantity E(t) dt is the fraction of material exiting the reactor that has spent between time t and (t + dt) in the reactor.
The mean residence time

$\begin{matrix} t_{m} = \int_{0}^{\infty} t E (t) d t = τ & (S 16 - 1) \end{matrix}$

is equal to the space time τ for constant volumetric flow, ν = ν₀.
The variance about the mean residence time is

$\begin{matrix} σ^{2} = \int_{0}^{\infty} {(t - t_{m})}^{2} E (t) d t & (S 16 - 2) \end{matrix}$
The cumulative distribution function F(t)

$\begin{matrix} F (t) & = & \int_{0}^{t} E (t) d t & = & \begin{matrix} The cumulative distribution function F (t) gives \\ the fraction of effluent material that has been \\ in the reactor for a time t or less \end{matrix} \\ 1 - F (t) & = & \int_{0}^{\infty} E (t) d t & = & \begin{matrix} Fraction of effluent material that has been in \\ the reactor for a time t or longer \end{matrix} & (S16-3) \end{matrix}$
The RTD functions for an ideal reactor are

PFR:

$\begin{matrix} E (t) = δ (t - τ) & (S16-4) \end{matrix}$

CSTR:

$\begin{matrix} E (t) = \frac{e^{- t / τ}}{τ} & (S16-5) \end{matrix}$

LFR:

$\begin{matrix} E (t) = 0 & t < \frac{τ}{2} & (S16-6) \end{matrix}$

$\begin{matrix} E (t) = \frac{τ^{2}}{2 t^{3}} & t \geq \frac{τ}{2} & (S16-7) \end{matrix}$
The dimensionless residence time is

$\begin{matrix} Θ = \frac{t}{τ} & (S16-8) \end{matrix}$

$E \begin{matrix} (Θ) = τ E (t) & (S16-9) \end{matrix}$
Diagnosing nonideal reactors with dead volume and bypassing

Graphs present the F(t) curves for three models of nonideal CSTR and tubular reactor. — In the graph of F(t) for nonideal CSTR, F(t) is plotted against time. The three curves show an increasing trend. The F(t) curve for bypassing model starts at v subscript b, over v subscript 0, and linearly increases with an increase in time. The F(t) curve for perfect operation model starts at the origin, steadily increases with an increase in time, and reaches a maximum value. The F(t) curve for the dead volume model starts at the origin, increases rapidly for a while, and then remains almost constant at a maximum value of F(t). In the graph of F(t) for the nonideal tubular reactor, F(t) is plotted against time. The vertical axis is marked with v subscript b and v subscript 0. The horizontal axis is marked with tau subscript S D, tau, and tau subscript S B. The curve representing F(t) for dead volume model extends vertically at tau subscript S D, which extends horizontally after a point. The curve representing F(t) value for the perfect operation model is drawn vertically at tau, which extends horizontally after a point. The curve representing F(t) value for bypassing model is drawn horizontally from a point between v subscript b and v subscript 0 up to time tau subscript S B, then the curve increases vertically, and again horizontally. The highest value of F of t is the same in all three curves.

CRE WEB SITE MATERIALS

Expanded Material on the Web Site
1. Web Example 16-1 Gas–Liquid Reactor
2. Proof That in the Absence of Dispersion, the Mean Residence Time, t_m, is Equal to Space Time, that is, t_m = τ
3. Side Note on the Medical Uses of RTD
4. Solved Problems WP16-14_C and WP16-15_D
Learning Resources
1. Summary Notes
2. Web Material Links
  
  The Attainable Region Analysis
  
  http://www.umich.edu/~elements/6e/16chap/learn-attainableregions.html
  
  http://hermes.wits.ac.za/attainableregions/
Living Example Problems
1. Living Example 16-1 Determining E(t)
2. Living Example 16-2T: Tutorial to Find E(t) from C(t)
3. Living Example 16-2 (a) and (b) Finding t_m and σ²
Professional Reference Shelf

R16.1. Fitting the Tail

Whenever there are dead zones into which the material diffuses in and out, the C- and E-curves may exhibit long tails. This section shows how to analytically describe fitting these tails to the curves.

E(t) = ae^-bt

b = slope of ln E vs. t

a = be^bt₁ [1–F(t₁)]

R16.2. Internal-Age Distribution

The internal-age distribution currently in the reactor is given by the distribution of ages with respect to how long the molecules have been in the reactor.

The equation for the internal-age distribution is derived and an example is given showing how it is applied to catalyst deactivation in a “fluidized CSTR.”

(http://www.umich.edu/~elements/6e/16chap/obj.html#/)

Links and evaluations in University of Michigan website. — The useful links include the following: living example problems, extra help, additional materials, professional reference shelf, and computer simulation problem statements. The evaluation includes self tests and i>clicker questions.

QUESTIONS, SIMULATIONS, AND PROBLEMS

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

A = • B = ▪ C = ♦ D = ♦♦

Questions

Q16-1_A QBR (Question Before Reading). What concept does RTD add to our CRE algorithm and where does it fit in the algorithm (1) Mole Balance, (2) Stoichiometry, and so on?

Q16-2_A Read over the problems of this chapter. Discuss with a classmate ideas for making up an original problem that uses the concepts presented in this chapter. The guidelines are given in Question Q5-3_A, page 217. RTDs from real reactors can be found in Ind. Eng. Chem., 49, 1000 (1957); Ind. Eng. Chem. Process Des. Dev., 3, 381 (1964); Can. J. Chem. Eng., 37, 107 (1959); Ind. Eng. Chem., 44, 218 (1952); Chem. Eng. Sci., 3, 26 (1954); and Ind. Eng. Chem., 53, 381 (1961).

Q16-3_B

Example 16-1. What fraction of the fluid spends 9 minutes or longer in the reactor? What fraction spends 2 minutes or less?
Example 16-3. How would the E(t) change if the PFR space time, τ_p, was reduced by 50% and τ_s was increased by 50%? What fraction spends 2 minutes or less in the reactor?

Q16-4 Go to the LearnChemE screencast link for Chapter 16 (http://www.learncheme.com/screencasts/kinetics-reactor-design). View one or more of the screencast 5- to 6-minute videos and write a two-sentence evaluation.

Q16-5 AWFOS–S16

List additional QTAs that could have been taken in addition to the ones listed for each CTA in the table.
Apply the seven types of actions of CTA to Example 13-2 and write an action that should have been taken for each type.

Computer Simulations and Experiments

P16-1_A Living Example 16-3 Wolfram and Python

Vary and find the combination of parameters for which the exit conversion is virtually the same for both early mixing and late mixing.
Find the combination of parameters for which there is a maximum difference between early mixing and late mixing.
Explain your findings for (i) and (ii) and then write a set of conclusions.

Problems

P16-2_B (a) (Excellent Exam Problem) Suggest a diagnosis (e.g., bypassing, dead volume, multiple mixing zones, internal circulation) for each of the following real reactors in Figure P16-2_B (a) (1–10 curves) that had the following RTD [E(t), E(Θ), F(t), F(Θ) or (1 – F(Θ))] curves:

Graphs depict 10 RTD curves. — **Figure P16-2_B (a)** RTD curves.

The first graph of F of theta versus theta shows a vertical line drawn from the point 0.5 of the horizontal axis that remains constant on reaching the value 1.0 of the vertical axis. The second graph of E of theta versus theta shows a line starting from the origin that increases to attain a minimum peak and further remains constant touching the horizontal axis. Again, the line increases and declines to attain a maximum peak. The third graph of F of theta versus theta shows a decreasing line that starts from the vertical axis at point In, decreases rapidly, takes a bend and further declines gradually near the horizontal axis. The fourth graph of 1 minus F of theta versus theta shows a line starting from the vertical axis. It remains constant for a while then decreases gradually touching the horizontal axis. The fifth graph of E of theta versus theta shows a line starting from the origin that gradually increases and declines to attain a minimum peak. Then, remains almost horizontal near the horizontal axis and inclines as a vertical line. From a point, it gradually declines. The sixth graph of E of theta versus theta shows a continuous curve with a sequence of peaks, with a maximum peak at the beginning that declines gradually with Area A subscript 1, A subscript 2, A subscript 3, and A subscript 4, respectively. The seventh graph of E of theta versus theta shows a vertical line that declines with two bumps. The eighth graph of F of theta versus theta shows an increasing curve with two bumps. The ninth graph of F of theta versus theta shows an increasing curve in a step-like manner. The tenth graph of F of theta versus theta shows an increasing curve from the origin that takes a bend and further inclines.

P16-2_B (b) Suggest a model (e.g., combinations of ideal reactors, bypassing) for each RTD function shown in Figure P16-2_B(a) (1–10) that would give the RTD function. For example, for the real tubular reactor, whose E(Θ) curve is shown in Figure P16-2_B (a) (5) above, the model is shown in Figure P16-2_B (b) below. The real reactor is modeled as having bypassing, a back mix zone, and a PFR zone that mimics the real CSTR.

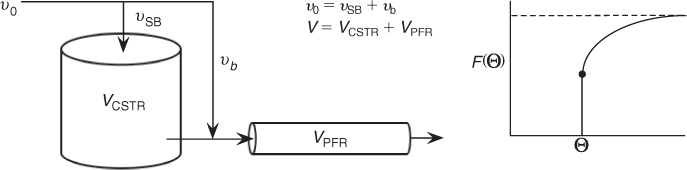
An illustration of the working of a real reactor with CSTR and PFR along with the F of theta curve. — **Figure P16-2_B (b)** Real reactor modeled as CSTR and PFR with bypass.

The figure shows a Continuous-Stirred Tank Reactor of volume V subscript CSTR and a Plug-Flow Reactor of volume V subscript PFR. The volumetric flow rate that enters the reactors represents v subscript 0. The volumetric flow rate that bypasses the CSTR and flows into the PFR tank is marked as v subscript b and the volumetric flow rate that enters the mixture in CSTR tank is marked as v subscript SB. Here, v subscript 0 equals v subscript SB plus v subscript b and volume V equals V subscript CSTR plus V subscript PFR. A graph plots F of theta as a function of theta. The curve initially extends vertically. That is, the F of theta value increases for a constant value of theta. Further, the F of theta value gradually increases with an increase in theta value.

P16-3_C OEQ (Old Exam Question)—Graduate Course. Consider the E(t) curve below.

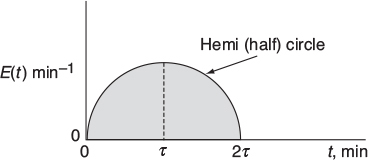
The E(t) curve is shown. — A graph is shown, with t (in minutes) on horizontal axis and E of t (minutes inverse) on vertical axis. A hemi (half) circular curve starts at the origin and ends at 2 tau on the horizontal axis. It is symmetric about the vertical line at tau.

Mathematically this hemi circle is described by these equations:

For 2τ ≥ t ≥ 0, then $E (t) = \sqrt{τ^{2} - {(t - τ)}^{2}} {min}^{- 1}$ (hemi circle)

For t > 2τ, then E(t) = 0

What is the mean residence time?
What is the variance? (Ans: σ² = 0.159 min²)

P16-4_B A step tracer input was used on a real reactor with the following results:

For t ≤ 10 min, then C_T = 0

For 10 ≤ t ≤ 30 min, then C_T = 10 g/dm³

For t ≥ 30 min, then C_T = 40 g/dm³

What is the mean residence time t_m?
What is the variance σ²?

P16-5_B OEQ (Old Exam Question). The following E(t) curves were obtained from a tracer test on two tubular reactors in which dispersion is believed to occur.

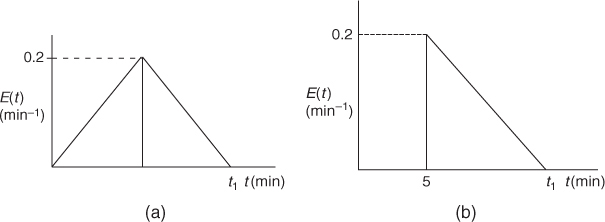
Two graphs show E of t curves for two reactors acquired from a tracer test. — **Figure P16-5_B (a)** RTD Reactor A; (b) RTD Reactor B

The graphs for RTD reactors A and B are shown. The horizontal axis represents time (in minutes) and the vertical axis represents E of t (in minute inverse) in both graphs. The first graph is shown for RTD reactor A. The curve starts at the origin, increases linearly, reaches a maximum value of E of t at 0.2, and again gradually decreases to 0 at time interval t subscript 1. The second graph shows the response of RTD reactor B. The curve is a vertical line, where E(t) value increases from 0 to a maximum of 0.2 for the constant value 5 of t. After this, it linearly decreases and reaches 0 at t subscript 1.

What is the final time t₁ (in minutes) for the reactor shown in Figure P16-5_B (a)?

How about in Figure P16-5_B (b)?
What is the mean residence time, t_m, and variance, =², for the reactor shown in Figure P16-5_B (a)?

How about in Figure P16-5_B (b)?
What is the fraction of the fluid that spends 7 minutes or longer in Figure P16-5_B (a)?

How about in Figure P16-5_B (b)?

P16-6_B An RTD experiment was carried out in a nonideal reactor that gave the following results:

E(t) = 0	for	t <1 min
E(t) = 1.0 min⁻¹	for	1 ≤ t ≤ 2 min
E(t) = 0	for	t > 2 min

What are the mean residence time, t_m, and variance σ²?
What is the fraction of the fluid that spends a time 1.5 minutes or longer in the reactor?
What fraction of fluid spends 2 minutes or less in the reactor?
What fraction of fluid spends between 1.5 and 2 minutes in the reactor? (Ans: Fraction = 0.5)

P16-7 Derive E(t), F(t), t_m, and σ² for a turbulent flow reactor with 1/7 the power law, that is,

$U = U_{max} {(1 - \frac{r}{R})}^{1 / 7}$

P16-8 OEQ (Old Exam Question)—Graduate Course. Consider the RTD function

$E (t) = {\begin{matrix} A - B {(t_{0} - t)}^{3} \\ 0 \end{matrix}} \begin{matrix} for 0 \leq t < 2 t_{0} \\ for t > 2 t_{0} \end{matrix}$

Sketch E(t) and F(t).
Calculate t_m and σ².
What are the restrictions (if any) on A, B, and t₀? Hint: $\int_{0}^{\infty} E (t) d t = 1$ .

P16-9_A Evaluate the first moment about the mean $m_{1} = \int_{0}^{\infty} (t - τ) E (t) d t$ E(t)dt for an ideal PFR, a CSTR, and a laminar-flow reactor.

P16-10_B Gasoline shortages in the United States have produced long lines of motorists at service stations. The table below shows a distribution of the times required to obtain gasoline at 23 Center County service stations.

What is the average time required?
If you were to ask randomly among those people waiting in line, “How long have you been waiting?” what would be the average of their answers?

Total Waiting Time (min)

0

3

6

9

12

15

18

21

Number of Stations Having That Total Waiting Time

0

4

3

5

8

2

1

0
Can you generalize your results to predict how long you would have to wait to enter a five-story parking garage that has a 4-hour time limit?

(Thanks to R. L. Kabel, Pennsylvania State University)

P16-11_B OEQ (Old Exam Question). The volumetric flow rate through a reactor is 10 dm³/min. A pulse test gave the following concentration measurements at the outlet:

t (min)	c × 10⁵
0	0
0.4	329
1.0	622
2	812
3	831
4	785
5	720
6	650
8	523
10	418
15	238
20	136
25	77
30	44
35	25
40	14
45	8
50	5
60	1

The badge of the member of the hall of fame.

Plot the external-age distribution E(t) as a function of time.
Plot the external-age cumulative distribution F(t) as a function of time.
What are the mean residence time t_m and the variance, σ²?
What fraction of the material spends between 2 and 4 minutes in the reactor? (Ans: Fraction = 0.16)
What fraction of the material spends longer than 6 minutes in the reactor?
What fraction of the material spends less than 3 minutes in the reactor? (Ans: Fraction = 0.192)
Plot the normalized distributions E(Θ) and F(Θ) as a function of Θ.
What is the reactor volume?
Plot the internal-age distribution I(t) as a function of time.
What is the mean internal age α_m?
This problem is continued in Problems P17-14_C and P18-12_C.

P16-12_B An RTD analysis was carried out on a liquid-phase reactor (Chem. Eng. J. 1, 76 (1970)). Analyze the following data:

t(s)	0	150	175	200	225	240	250
C × 10³ (g/m³)	0	0	1	3	7.4	9.4	9.7
t(s)	275	300	325	350	375	400	450
C × 10³ (g/m³)	8.2	5.0	2.5	1.2	0.5	0.2	0

Plot the E(t) curve for these data.
What fraction of the material spends between 230 and 270 seconds in the reactor?
Plot the F(t) curve for these data.
What fraction of the material spends less than 250 seconds in the reactor?
What is the mean residence time?
What is the variance σ²?
Plot E(Θ) and F(Θ) as a function of Θ.

P16-13_C (Distributions in a stirred tank) Using a negative step tracer input, Cholette and Cloutier (Can. J. Chem. Eng., 37, 107 (1959)) studied the RTD in a tank for different stirring speeds. Their tank had a 30-in. diameter and a fluid depth of 30 in. indide the tank. The inlet and exit flow rates were 1.15 gal/min. Here are some of their tracer results for the relative concentration, C/C₀ (courtesy of the Canadian Society for Chemical Engineering):

NEGATIVE STEPS TRACER TEST

	Impeller Speed (rpm)
Time (min)	170	10
10	0.761	0.653
15	0.695	0.566
20	0.639	0.513
25	0.592	0.454
30	0.543	0.409
35	0.502	0.369
40	0.472	0.333
45	0.436	0.307
50	0.407	0.276
55	0.376	0.248
60	0.350	0.226
65	0.329	0.205

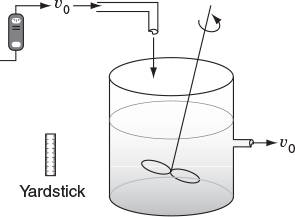
A figure demonstrates the negative step tracer test. — The CSTR tank with a stirrer that rotates counter-clockwise is shown. The negative step tracer input with flow rate v Subscript 0 is fed to the CSTR tank. The outlet from the tank has a resultant flow rate of v Subscript 0. The yardstick used in measuring is also shown.

Calculate and plot the cumulative exit-age distribution, the intensity function, and the internal-age distributions as a function of time for this stirred tank at the two impeller speeds. Can you tell anything about the dead zones and bypassing at the different stirrer rates?

SUPPLEMENTARY READING

Discussions of the measurement and analysis of residence time distribution can be found in

R. L. CURL and M. L. MCMILLIN, “Accuracies in residence time measurements,” AIChE J., 12, 819–822 (1966).

JOFO JACKSON, “Analysis of “RID’ Data from the Nut Cracker Reactor at the Riça Plant,” Jofostan J. Ind. Data, 28, 243 (1982).

O. LEVENSPIEL, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999, Chaps. 11–16.
An excellent discussion of segregation can be found in

J. M. DOUGLAS, “The effect of mixing on reactor design,” AIChE Symp. Ser., 48, vol. 60, p. 1 (1964).
Also see

M. DUDUKOVIC and R. FELDER, in CHEMI Modules on Chemical Reaction Engineering, vol. 4, ed. B. Crynes and H. S. Fogler. New York: AIChE, 1985.

E. B. NAUMAN, “Residence time distributions and micromixing,” Chem. Eng. Commun., 8, 53 (1981).

E. B. NAUMAN and B. A. BUFFHAM, Mixing in Continuous Flow Systems. New York: Wiley, 1983.

B. A. ROBINSON and J. W. TESTER, Chem. Eng. Sci., 41(3), 469–483 (1986).

J. VILLERMAUX, “Mixing in chemical reactors,” in Chemical Reaction Engineering—Plenary Lectures, ACS Symposium Series 226. Washington, DC: American Chemical Society, 1982.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Total Waiting Time (min)	0	3	6	9	12	15	18	21
Number of Stations Having That Total Waiting Time	0	4	3	5	8	2	1	0

Table of Contents for 16. Residence Time Distributions of Chemical Reactors

Create new playlist

Sign In

Sign Up

16. Residence Time Distributions of Chemical Reactors†

16.1 General Considerations

16.1.1 Residence Time Distribution (RTD) Function

16.2 Measurement of the RTD

16.2.1 Pulse Input Experiment

16.2.2 Step Tracer Experiment

16.3 Characteristics of the RTD

16.3.1 Integral Relationships

16.3.2 Mean Residence Time

16.3.3 Other Moments of the RTD

16.3.4 Normalized RTD Function, E(Θ)

16.3.5 Internal-Age Distribution, /(α)

16.4 RTD in Ideal Reactors

16.4.1 RTDs in Batch and Plug-Flow Reactors

16.4.2 Single-CSTR RTD

16.4.3 Laminar-Flow Reactor (LFR)

16.5 PFR/CSTR Series RTD

16.6 Diagnostics and Troubleshooting

16.6.1 General Comments

16.6.2 Simple Diagnostics and Troubleshooting Using the RTD for Ideal Reactors

16.6.2A The CSTR

16.6.2B Tubular Reactor

16.7 And Now… A Word from Our Sponsor–Safety 16 (AWFOS–S16 Critical Thinking Actions)

SUMMARY

CRE WEB SITE MATERIALS

QUESTIONS, SIMULATIONS, AND PROBLEMS

Questions

Computer Simulations and Experiments

Problems

SUPPLEMENTARY READING

Table of Contents for
16. Residence Time Distributions of Chemical Reactors

16. Residence Time Distributions of Chemical Reactors^†