17. Predicting Conversion Directly from the Residence Time Distribution
If you think you can, you can.
If you think you can’t, you can’t.
You are right either way.
—Steve LeBlanc
17.1 Modeling Nonideal Reactors Using the RTD
17.1.1 Modeling and Mixing Overview
Now that we have characterized our reactor and have gone to the lab to take data to determine the reaction kinetic rate-law parameters, we need to choose a model to predict conversion in our real reactor.
The answer
We now present the five models shown in Table 17-1. We shall classify each model according to the number of adjustable parameters. In this chapter, we will discuss the zero adjustable parameter models and the tanks-in-series (T-I-S) model. In Chapter 18, we will discuss the dispersion model and models with two adjustable parameters that will be used to predict conversion.
Ways we use the RTD data to predict conversion in nonideal reactors
TABLE 17-1 MODELS FOR PREDICTING CONVERSION FROM RTD DATA
Real reactors modeled as combinations of ideal reactors |
For the zero adjustable parameter models, we do not need to make any intermediate calculations; we use the E- and F-curves directly to predict the conversion given the rate law and kinetic parameters. For the one-parameter models, we use the RTD to calculate mean residence time, tm, and variance, σ2, which we can then use (1) to find the number of tanks in series necessary to accurately model a nonideal CSTR and (2) calculate the Peclet number, Pe, to find the conversion in a tubular flow reactor using the dispersion model.
For the two-parameter models, we will show in Chapter 18 how to create combinations of ideal reactors to model the nonideal reactor. We then use the RTD to calculate the model parameters such as fraction bypassed, fraction dead volume, exchange volume, and ratios of reactor volumes that then can be used along with the reaction kinetics to predict conversion.
17.1.2 Mixing
The RTD tells us how long the various fluid elements have been in the reactor, but it does not tell us anything about the exchange of matter between the fluid elements (i.e., the mixing). The mixing of reacting species is one of the major factors controlling the behavior of chemical reactors. Fortunately for first-order reactions, mixing is not important, and knowledge of the length of time each molecule spends in the reactor is all that is needed to predict conversion. For first-order reactions, the conversion is independent of concentration (recall Table 5-1, page 162 and Equation (E13-1.4) in Example E13-1)
A model is needed for reactions other than first order.
Consequently, mixing with the surrounding molecules is not important. Therefore, once the RTD is determined, we can predict the conversion that will be achieved in the real reactor provided that the specific reaction rate for the first-order reaction is known. However, for reactions other than first order, knowledge of the RTD is not sufficient to predict conversion. For reactions other than first order, the degree of mixing of molecules must be known in addition to how long each molecule spends in the reactor. Consequently, we must develop models that account for the mixing of molecules inside the reactor.
The more complex models of nonideal reactors necessary to describe reactions other than first order must contain information about micromixing in addition to that of macromixing. To facilitate our discussion on micromixing, we define the age of a molecule as the time a molecule has been inside the reactor. Macromixing produces a distribution of residence times without, specifying how molecules of different ages encounter one another in the reactor. Micromixing, on the other hand, describes how molecules of different ages encounter one another in the reactor. There are two extremes of micromixing:
All molecules of the same age group remain together as they travel through the reactor and are not mixed with any other age until they exit the reactor (i.e., complete segregation).
Molecules of different age groups are completely mixed at the molecular level as soon as they enter the reactor (complete micromixing).
For a given state of macromixing (i.e., a given RTD), these two extremes of micromixing will give the upper and lower limits on conversion in a nonideal reactor.
Late Mixing
Segregation
Early Mixing
Maximum Mixedness
We shall define a globule1 as a fluid particle containing millions of molecules all of the same age. A fluid in which the globules of a given age do not mix with other globules is called a macrofluid. A macrofluid could be visualized as noncoalescent globules where all the molecules in a given globule have the same age. A fluid in which molecules are not constrained to remain in the globule and are free to move everywhere is called a microfluid.2 There are two extremes of mixing of the macrofluid globules—early mixing and late mixing. These two extremes of late and early mixing are shown in Figure 17-1(a) and (b), respectively. The extremes of late and early mixing are referred to as complete segregation and maximum mixedness, respectively. For single reactions with orders greater than one or less than zero, the segregation model will predict the highest conversion. For reaction orders between zero and one, the maximum mixedness model will predict the highest conversion. This concept is discussed further in Section 17.3.1.

Figure 17-1 (a) Macrofluid and (b) microfluid mixing on the molecular level.
1 Pronounced gläbyōōl not Go Blue.
2 J. Villermaux, Chemical Reactor Design and Technology. Boston: Martinus Nijhoff, 1986.
Here represents the mean conversion in the exit stream.
17.2 Zero Adjustable Parameter Models
17.2.1 Segregation Model
In a “perfectly mixed” CSTR, the entering fluid is assumed to be distributed immediately and evenly throughout the reacting mixture. This mixing is assumed to take place even on the microscale, and elements of different ages mix together thoroughly to form a completely micromixed fluid (see Figure 17-1(b)). However, if fluid elements of different ages do not mix together at all, the elements remain segregated from each other, and the fluid is termed completely segregated (see Figure 17-1(a)). The extremes of complete micromixing and complete segregation are the limits of the micromixing of a reacting mixture.
The extremes of micromixing
In developing the segregated mixing model, we first consider a CSTR because the application of the concepts of mixing quality are most easily illustrated using this reactor type. In the segregated flow model, we visualize the flow through the reactor to consist of a continuous series of globules (Figure 17-2).
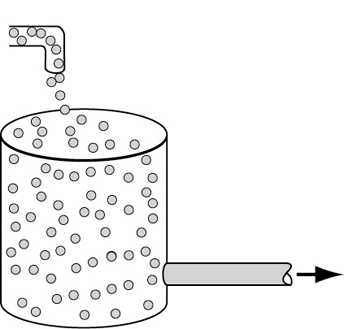
Figure 17-2 Little batch reactors (globules) inside a CSTR.
In the segregation model, globules behave as batch reactors operated for different times.
These globules retain their identity; that is, they do not interchange material with other globules in the fluid during their period of residence in the reaction environment. In other words, they remain segregated until they exit the reactor and mix immediately. In addition, each globule spends a different amount of time in the reactor. In essence, what we are doing is lumping all the molecules that have exactly the same residence time in the reactor into the same globule. The principles of reactor performance in the presence of completely segregated mixing were first described by Danckwerts and Zwietering.3,4
3 P. V. Danckwerts, Chem. Eng. Sci., 8, 93 (1958).
4 T. N. Zwietering, Chem. Eng. Sci., 11, 1 (1959).
The segregation model has mixing at the latest possible point.
Another way of looking at the segregation model for a continuous-flow system is the PFR shown in Figures 17-3(a) and (b). Because the fluid flows down the reactor in plug flow, each exit stream corresponds to a specific residence time in the reactor. Batches of molecules are removed from the reactor at different locations along the reactor in such a manner as to duplicate the RTD function, E(t). The molecules removed near the entrance to the reactor correspond to those molecules having short residence times in the reactor. Physically, this effluent would correspond to the molecules that channel rapidly through the reactor. The farther the molecules travel along the reactor before being removed, the longer their residence time. The points at which the various groups or batches of molecules are removed correspond to the RTD function for the reactor.
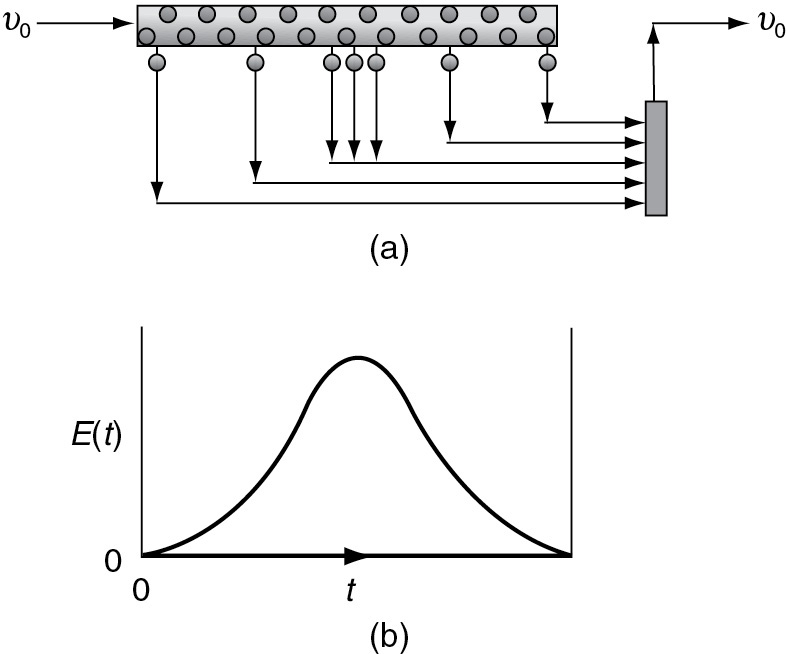
Figure 17-3 Mixing at the latest possible point.
Little batch reactors
E(t) matches the removal of the batch reactors.
Because there is no molecular interchange between globules, each globule acts essentially as its own batch reactor. The reaction time in any one of these tiny batch reactors is equal to the time that the particular globule has spent in the reaction environment and determined by their time of exit. The distribution of residence times among the globules is given by the RTD of the particular reactor.
Now that we have the reactor’s RTD, we will choose a model, apply the rate law and rate-law parameters to predict conversion as shown in the box earlier. We will start with the segregation model.
To determine the mean conversion in the effluent stream, we must average the conversions of all of the various globules in the exit stream:
then
Dividing by dt
Summing over all globules of all different ages, the mean conversion is
Mean conversion for the segregation model
Consequently, if we have the batch reactor equation for X(t) and measure the RTD experimentally, we can find the mean conversion in the exit stream. Thus, if we have the RTD, the reaction-rate law and parameters, then for a segregated flow situation (i.e., model), we have sufficient information to calculate the conversion. An example that may help give additional physical insight to the segregation model is given on the CRE Web site (http://www.umich.edu/~elements/6e/17chap/prof-compare.html and http://www.umich.edu/~elements/6e/17chap/summary.html-top1a1).

Segregation Model for a First-Order Reaction
Consider the following first-order reaction:
We treat the globules that spend different amounts of time in the real reactor as little batch reactors. For a batch reactor we have
For constant volume and with NA = NA0(1 = X)
Solving for X(t), we have for any globule that spends a time t in the real reactor
Because different globules spend different times, we have to add up the conversions from all the globules of all different ages.
Mean conversion for a first-order reaction
We will now determine the mean conversion predicted by the segregation model for an ideal PFR, a CSTR, and an LFR.
Example 17–1 Mean Conversion in an Ideal PFR, an Ideal CSTR, and a Laminar-Flow Reactor
Derive the equation for conversion for a first-order reaction using the segregation model when the RTD is equivalent to (a) an ideal PFR, (b) an ideal CSTR, and (c) a laminar-flow reactor (LFR). Compare these conversions with those obtained from the design equation.
Solution
(a) For the PFR, the RTD function was given by Equation (16-27)
Recalling Equation (17-5)
Substituting Equation (16-27) for the RTD function for a PFR gives
Using the integral properties of the Dirac delta function, Equation (16-30), we obtain
where for a first-order reaction the Damköhler number is Da1 = τk.
Using our PFR algorithm and combining the mole balance, rate law, and stoichiometric relationships (cf. Chapter 5), we had
Integrating yields
Twins!
which is identical to the conversion predicted by the segregation model .
(b) For the CSTR, the RTD function was given in Equation (16-21) as
Recalling Equation (17-5), the mean conversion for a first-order reaction is
The conversion predicted from the segregation model is
As expected, using the E(t) for an ideal PFR and CSTR with the segregation model gives a mean conversion identical to that obtained by using the algorithm in Chapter 5.
Using our algorithm in Chapter 5, we showed that combining the CSTR mole balance, the rate law, and stoichiometry, we have
FA0X = –rAV
v0CA0X = kCA0(1 – X)V
Solving for X, we see the conversion predicted from our Chapter 5 algorithm is the same as that for the segregation model
Another set of twins!!
which is identical to the conversion predicted by the segregation model .
(c) For a laminar-flow reactor, the RTD function is
The dimensionless form is
From Equation (17-5), we have
Integrating twice by parts
The last integral is the exponential integral and can be evaluated from tabulated values. Fortunately, Hilder developed an approximate formula (τk = Da1).5
5 M. H. Hilder, Trans. I. ChemE, 59, 143 (1979).
A comparison of the exact value along with Hilder’s approximation, and also with the conversion in an ideal PFR and an ideal CSTR, is shown in Table E17-1.1 for various values of the Damköhler number for a first-order reaction, τk.
TABLE E17-1.1 COMPARISON OF CONVERSION IN PFR, CSTR, AND LFR FOR DIFFERENT DAMKÖHLER NUMBERS FOR A FIRST-ORDER REACTION
Da1 = τk |
XLFR Exact |
XLFR Approx. |
XPFR |
XCSTR |
0.1 |
0.0895 |
0.093 |
0.0952 |
0.091 |
1 |
0.557 |
0.56 |
0.632 |
0.501 |
2 |
0.781 |
0.782 |
0.865 |
0.667 |
4 |
0.940 |
0.937 |
0.982 |
0.80 |
10 |
0.9982 |
0.9981 |
0.9999 |
0.91 |
We see in Table E17-1.1 XLFR Exact = Exact solution to Equation (E17-1.10) and the approximate solution XLFR Approx. = Equation (E17-1.11). We note that in all cases, the Approximate and Exact solutions are in close agreement.
For large values of the Damköhler number then, there is complete conversion along the streamlines off the center streamline so that the conversion is determined along the pipe axis such that
Figure E17-1.1 shows a comparison of the mean conversion in an LFR, PFR, and CSTR as a function of the Damköhler number for a first-order reaction.
Comparing the conversion profiles for a PFR, a CSTR, and an LFR
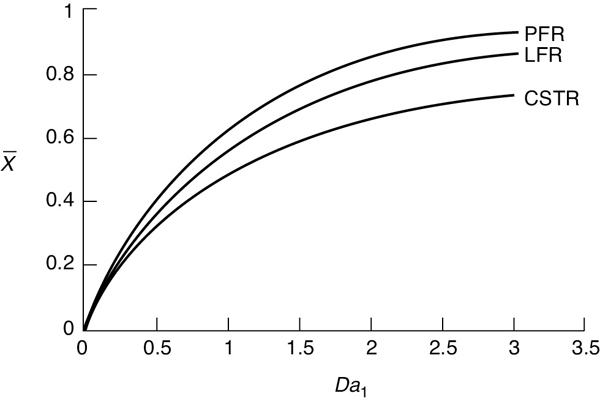
Figure E17-1.1 Conversion in a PFR, LFR, and CSTR as a function of the Damköhler number (Da1) for a first-order reaction (Da1 = τk).
Analysis: One of the first things we observe is that the plug-flow reactor (PFR) and laminar-flow reactor (LFR) conversion profiles as a function of the Damköhler number are quite close for first-order reactions. Secondly, for small Da (Da < 0.5) the mean exit conversion for all the models (PFR, LFR and CSTR) is virtually identical. Finally, we see that the mean conversion for the three models diverges with increasing Da.
Important Point:
For a first-order reaction, knowledge of E(t) is sufficient.
We have just shown for a first-order reaction that whether you assume complete micromixing (Equation (E17-1.7)) or complete segregation (Equation (E17-1.6)) in a CSTR, the same conversion results. This phenomenon occurs because the rate of change of conversion for a first-order reaction does not depend on the concentration of the reacting molecules (Equation (17-3)); it does not matter what kind of molecule is next to it or colliding with it. Thus, the extent of micromixing does not affect a first-order reaction, so the segregated flow model can be used to calculate the conversion. As a result, only the RTD is necessary to calculate the conversion for a first-order reaction in any type of reactor (see Problem P17-3c). Knowledge of neither the degree of micromixing nor the reactor flow pattern is necessary. We now proceed to calculate conversion in a real reactor using RTD data.
Example 17–2 Mean Conversion, X seg, Calculations in a Real Reactor
Calculate the mean conversion in the reactor we have characterized by RTD measurements in Examples 16-1 and 16-2 for a first-order, liquid-phase, irreversible reaction in a completely segregated fluid:
A → products
The specific reaction rate is 0.1 min–1 at 320 K. See Examples 16-1 and 16-2.
Solution
Because each globule acts as a batch reactor of constant volume, we use the batch reactor design algorithm to arrive at the equation giving conversion as a function of time
To calculate the mean conversion, we need to evaluate the integral
These calculations are easily carried out with the aid of a spreadsheet such as Excel or Polymath.
The RTD function for this reactor was determined previously and given in data from Examples 16-1 and 16-2 and are repeated here in Table E17-2.1, that is, E(t) = C(t)/Area.
Polymath Solution
We saw in Example 16-1.1 that C(t) was first fit to a polynomial from which we calculated . We then use this value to calculate the E-curve.
We now combine Equations (E17-2.2), (E17-2.3), and (E17-2.4). The Polymath program and results are given in Table E17-2.1.

TABLE E17-2.1 SEGREGATION MODEL
 |
The conversion would be 75.3% if all the globules spent the same time as the last tracer molecule to exit the reactor (i.e., 14 minutes). However, not all globules spend the same time in the reactor. Instead we have a distribution of times the globules spend in the reactor. Consequently, we use the segregation model to find that the mean conversion for all the globules is 38.2%.
Analysis: We were given the conversion as a function of time for a batch reactor X(t) and the RTD E-curve from Example 16-1. Using the segregation model and a polynomial fit for the E-curve, we were able to calculate the mean conversion using the segregation model, Xseg, in this nonideal reactor. We note there were no model-fitting parameters in making this calculation, just E(t) from the data and X(t).
As discussed previously, because the reaction is first order, the conversion calculated in Example 17-2 would be valid for a reactor with complete mixing, complete segregation, or any degree of mixing between the two. Although early or late mixing does not affect a first-order reaction, micromixing or complete segregation can give significantly different results for a second-order reaction system. We now analyze a second-order reaction using the segregation model.
Example 17–3 Mean Conversion for a Second-Order Reaction in a Laminar-Flow Reactor
The liquid-phase reaction between cytidine and acetic anhydride is carried out isothermally in an inert solution of N-methyl-2-pyrrolidone (NMP) with ΘNMP = 28.9. The reaction follows an elementary rate law. The feed is equal molar in A and B with CA0 = 0.75 mol/dm3, a volumetric flow rate of 0.1 dm3/s, and a reactor volume of 100 dm3. Calculate the conversion in (a) an ideal PFR, (b) a BR, and (c) an LFR.

A + B → C + D
Additional information:6
6 J. J. Shatynski and D. Hanesian, Ind. Eng. Chem. Res., 32, 594.
k = 4.93 × 10–3 dm3/mol · s at 50°C with E = 13.3 kcal/mol, ΔHRX = – 10.5 kcal/mol
Heat of mixing for

Solution
The reaction will be carried out isothermally at 50°C. The space time is
(a) For an ideal PFR
Mole Balance
Rate Law
Stoichiometry, ΘB = 1
Combining
PFR calculation
Evaluating
Integrating and solving with τ = V/ν0 and X = 0 for V = 0 gives
where Da2 is the Damköhler number for a second-order reaction.
(b) Batch reactor
Batch calculation
If the batch reaction time is the same time as the space time, that is, t = τ, the batch conversion is the same as the PFR conversion, X = 0.787.
(c) Laminar-flow reactor
The differential form for the mean conversion is obtained from Equation (17-1)
We use Equation (E17-3.9) to substitute for X(t) in Equation (17-1). Because E(t) for the LFR consists of two parts, we need to incorporate the IF statement in our ODE solver program. For the laminar-flow reaction, we write
Let t1 = τ/2 so that the IF statement now becomes
LFR calculation
One other thing to remember is that the ODE solver will recognize that E2 = ∞ at t = 0 and refuse to run, so we must add a very small number to the denominator such as (0.001); for example,
You won’t be able to carry out the integration of Equation (17-2) with the limit t = ∞ unless you are an honorary resident of Jofostan. However, you can use Poly-math, but the numerical integration time limit, tf should be 10 or more times the reactor space time, τ = 20 τ = 20000 s. The Polymath program for this example is shown in Table E17-3.1.
TABLE E17-3.1 LFR SEGREGATION MODEL
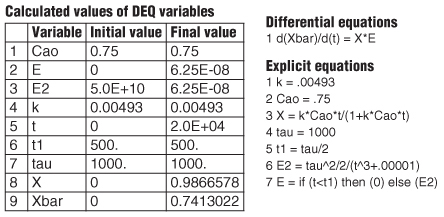 |
We see that the mean conversion Xbar () for the LFR is 74.1%.
In summary,
Compare this result with the exact analytical formula for the laminar-flow reactor with a second-order reaction7
7 K. G. Denbigh, J. Appl. Chem., 1, 227 (1951).
Analytical solution
where Da2 = kCA0τ. For Da2 = 3.70 we get
In many cases, we can approximate the conversion for an LFR with that calculated from the PFR models.
Analysis: In this example involving a second-order reaction, we applied the segregation model to the E-curve for two ideal reactors: the plug-flow reactor (PFR) and the laminar-flow reactor (LFR). We found that the difference between the predicted conversion in the PFR and the LFR reactor was 4.6%. We also learned that the analytical solution for a second-order reaction taking place in an LFR was virtually the same as that for the segregation model.
17.2.2 Maximum Mixedness Model
In the segregation model, mixing occurs at the latest possible point.
In a reactor modeled as a segregated fluid, mixing between particles of fluid does not occur until the fluid leaves the reactor. The reactor exit is, of course, the latest possible point where mixing can occur, and any effect of mixing is postponed until after all reaction has taken place, as shown in Figure 17-3. We can also think of a completely segregated flow as being in a state of minimum mixedness. We now want to consider the other extreme, that of maximum mixedness consistent with a given residence time distribution.
In the maximum mixedness model, mixing occurs at the earliest possible point.
We return again to the plug-flow reactor with side entrances, only this time the fluid enters the reactor along its length (Figure 17-4). As soon as the fluid enters the reactor, it is completely mixed radially (but not longitudinally) with the other fluid already in the reactor. The entering fluid is fed into the reactor through the side entrances in such a manner that the RTD of the plug-flow reactor with side entrances is identical to the RTD of the real reactor.
λ = life expectancy
The globules at the far left of Figure 17-4(a) correspond to the molecules that spend a long time in the reactor, while those at the far right correspond to the molecules that channel through the reactor and spend a very short time in the reactor. In this reactor with side entrances, mixing occurs at the earliest possible moment consistent with the RTD. This situation is termed the condition of maximum mixedness.8 The approach for calculating conversion for a reactor in a condition of maximum mixedness will now be developed. In a reactor with side entrances, let λ = life expectancy be the time it takes for the fluid to move from a particular point to the end of the reactor. In other words, λ is the life expectancy of the fluid in the reactor at that point (Figure 17-5).

Figure 17-4 Mixing at the earliest possible point.
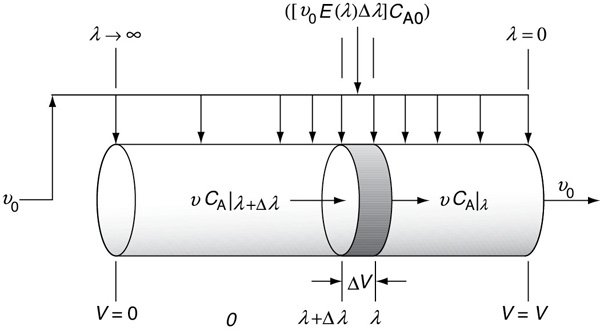
Figure 17-5 Modeling maximum mixedness by a plug-flow reactor with side entrances.
8 T. N. Zwietering, Chem. Eng. Sci., 11, 1 (1959).
Maximum mixedness: mixing occurs at the earliest possible point.
Moving down the reactor from left to right, the life expectancy, λ, decreases and becomes zero at the exit. At the left end of the reactor (i.e., the entrance), λ approaches infinity or the maximum residence time if it is other than infinite.
Consider the fluid that enters the reactor through the sides of volume ΔV in Figure 17-5. The fluid that enters here will have a life expectancy between λ and λ+Δλ. The fraction of fluid that will have this life expectancy between λ and λ+Δλ is E(λ)Δλ. The corresponding volumetric flow rate IN through the sides is [υ0E(λ)Δλ.]
Fluid balance on Δλ In + In = Out

The volumetric flow rate at λ, υλ, is the flow rate that entered at λ+Δλ, that is, υλ+Δλ, plus what entered through the sides υ0 E(λ)Δλ, that is,
Rearranging and taking the limit as Δλ → 0
The volumetric flow rate υ at the entrance to the reactor (V = 0, λ = ∞, and X = 0) is zero (i.e., υλ = 0) because the fluid only enters through the sides along the length.
Integrating Equation (17-7) with limits υλ = 0 at λ = ∞ and υλ = υλ at λ = λ, and then using Equation (16-13) we obtain
The volume of fluid in the reactor, ΔV, with a life expectancy between λ and λ + Δλ is
The rate of generation of the substance A in this volume is
We can now carry out a mole balance on substance A between λ and λ + Δλ
Mole balance
Substituting for υλ + Δλ, υλ and ΔV
Dividing Equation (17-11) by υ0 Δλ and taking the limit as Δλ → 0 gives
Taking the derivative of the term in brackets
Rearranging
We can also rewrite Equation (17-12) in terms of conversion as
or
Maximum mixedness gives the lower bound on X.
The boundary condition is as λ → ∞, then CA = CA0 for Equation (17-12) (or X = 0 for Equation (17-13)). To obtain a solution, the equation is integrated backward numerically, starting at a very large value of λ and ending with the final conversion at λ = 0. For a given RTD and reaction orders greater than one or less than zero, the maximum mixedness model gives the lower bound on conversion as shown in Tables 17-1 and 17-2, pages 888, 909.
Example 17–4 Conversion Bounds for a Nonideal Reactor
The liquid-phase, second-order dimerization
for which k = 0.01 dm3/mol·min is carried out at a reaction temperature of 320 K. The feed is pure A with CA0 = 8 mol/dm3. The reactor is nonideal. The reactor volume is 1000 dm3, and the feed rate for our dimerization is going to be 25 dm3/min.
We wish to know the bounds on the conversion for different possible degrees of micromixing for the RTD of this reactor. What are these bounds?
The Jofostan students carried out a tracer test by throwing 100 g of tracer (N0 = 100 g) into the reactor that had an entering volumetric flow rate of 25 dm3/min (υ0 = 25 dm3/min) and then measured the exit concentration (C(t) as a function of time t) and the results are shown in columns 1 and 2 of Table E17-4.1. The exit concentration, that is, the C-curve, was then fit to a polynomial. A tutorial on how to fit the tracer data points to a polynomial, for example,
C(t) = a0 = a1t = a2t2 = a3t3 = a4t4
is given in the Living Example Problem on the CRE Web site in both Chapters 7 and 16. After finding a0, a1, and so on, we integrate the Ct-curve to find the total amount of tracer, N0, injected
The E-curve
and then divide each concentration by N0, the total tracer concentration to construct the E-curve which is given in column 3, the corresponding polynomial fit for the E-curve is
E2 = -2.64e-9*t^3+1.3618e-6*t^2-.00024069*t+.015011
E1 = 4.44658e-10*t^4-1.1802e-7*t^3+1.35358e-5*t^2-.000865652*t+.028004
E = if (t<=70) then (E1) else (E2)
Solution
The bounds on the conversion are found by calculating conversions under conditions of (a) complete segregation and (b) maximum mixedness.
(a) Conversion if fluid is completely segregated. Using the CRE algorithm we find the batch reactor conversion for a second-order reaction is
TABLE E17-4.1 RAW AND PROCESSED DATA
t (min) |
C (mg/dm3) |
E(t) (min–1) |
X (t) |
X(t)E(t) (min–1) |
X(t)E(t) Δt |
λ(min) |
0 |
112 |
0.0280 |
0 |
0 |
0 |
0 |
5 |
95.8 |
0.0240 |
0.286 |
0.00686 |
0.0172† |
5 |
10 |
82.2 |
0.0206 |
0.444 |
0.00916 |
0.0400 |
10 |
15 |
70.6 |
0.0177 |
0.545 |
0.00965 |
0.0470 |
15 |
20 |
60.9 |
0.0152 |
0.615 |
0.00935 |
0.0475 |
20 |
30 |
45.6 |
0.0114 |
0.706 |
0.00805 |
0.0870 |
30 |
40 |
34.5 |
0.00863 |
0.762 |
0.00658 |
0.0732 |
40 |
50 |
26.3 |
0.00658 |
0.800 |
0.00526 |
0.0592 |
50 |
70 |
15.7 |
0.00393 |
0.848 |
0.00333 |
0.0859 |
70 |
100 |
7.67 |
0.00192 |
0.889 |
0.00171 |
0.0756 |
100 |
150 |
2.55 |
0.000638 |
0.923 |
0.000589 |
0.0575 |
150 |
200 |
0.90 |
0.000225 |
0.941 |
0.000212 |
0.0200 |
200 |
0.610 |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
†For the first point, we have X(t)E(t)Δt = (0 + 0.00686) (5/2) = 0.0172.
Spreadsheets work quite well here.
The conversion for a completely segregated fluid in a reactor is
differentiating
Combining the mole balance, rate law, and stoichiometry for a “little” batch reactor, we obtain the differential equation of X(t).
We now use Polymath to solve Equations (E17-4.3) and (E17-4.4) simultaneously to find Xseg.
The Polymath program and results are given in Table E17-4.2.
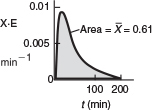
TABLE E17-4.2 SEGREGATION MODEL
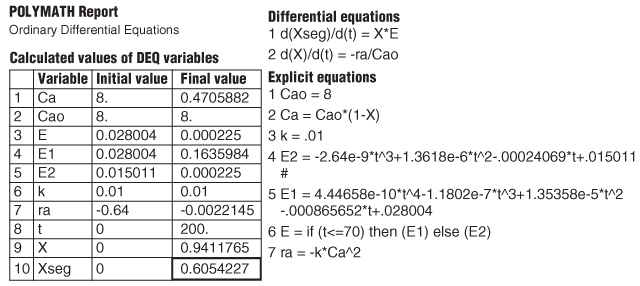 |
The predicted conversion for a completely segregated flow is 0.605 or 61%.
(b) Conversion for maximum mixedness model
Hand Calculation: In practice, we would never carry out step-by-step calculations to predict the conversion from the maximum mixedness model. It is presented here in the hopes that it will give a clearer understanding of maximum mixedness. As we will see in Example 17-5, the Polymath ODE solver is more proficient and unbelievably fast.
Conversion for maximum mixedness. The Euler method will be used for numerical integration

Tedious calculations
Integrating this equation presents some interesting results. If the equation is integrated from the exit side of the reactor, starting with λ = 0, the solution is unstable and soon approaches large negative or positive values, depending on what the starting value of X is. We want to find the conversion at the exit to the reactor, λ = 0. Consequently, we need to integrate backward.
If integrated from the point where λ → ∞, oscillations may occur but are soon damped out, and the equation approaches the same final value no matter what initial value of X between 0 and 1 is used. We shall start the integration at λ = 200 and let X = 0 at this point. If we set Δλ too large, the solution will blow up, so we will start out with Δλ = 25 and use the average of the measured values of E(t)/[(1 = F(t)] where necessary. We will now use the data in column 7 of Table E17-4.1 to carry out the integration.
This calculation (b) is only given to provide insight to maximum mixedness.
At λ = 200, X = 0
λ = 175:
λ = 150:
We need to take an average of E / (1 – F) between λ = 200 and λ = 150.
λ = 125:
X (λ = 125) = 1.46 – (25)[(0.0266)(1.46) – (0.01)(8)(1 – 1.46)2] = 0.912
λ = 100:
λ = 70:
X = 0.372 – (30)[(0.0221)(0.372) – (0.01)(8)(1 – 0.372)2] = 1.071
λ = 50:
X = 1.071 – (20)[(0.0226)(1.071) – (0.01)(8)(1 – 1.071)2] = 0.595
λ = 40:
X = 0.595 – (10)[(0.0237)(0.595) – (0.01)(8)(1 – 0.595)2] = 0.585
Note: Oscillations in X are beginning to be damped out.
Running down the values of X along the right-hand side of the preceding equation shows that the oscillations have now damped out. Carrying out the remaining calculations down to the end of the reactor completes Table E17-4.3. The conversion for a condition of maximum mixedness in this reactor is 0.56 or 56%. It is interesting to note that there is little difference in the conversions for the two conditions of complete segregation (61%) and maximum mixedness (56%). With bounds this narrow, one may question the point in using additional models for the reactor to improve the predictability of conversion.
Calculate backward to reactor exit.
TABLE E17-4.3 MAXIMUM MIXEDNESS MODEL
λ (min) |
X |
200 |
0.0 |
175 |
2.0 |
150 |
1.460 |
125 |
0.912 |
100 |
0.372 |
70 |
1.071 |
50 |
0.595 |
40 |
0.585 |
30 |
0.580 |
20 |
0.581 |
10 |
0.576 |
5 |
0.567 |
0 |
0.564 |
Summary
PFR |
76% |
Segregation |
61% |
CSTR |
58% |
Max. mix |
56% |
Analysis: For comparison, it is left for the reader to show that the conversion for a PFR of this size would be 0.76, and the conversion in a perfectly mixed CSTR with complete micromixing would be 0.58. As mentioned in this example, you probably will never use this kind of hand calculation method to determine the maximum mixedness conversion. It is only presented to help give an intuitive understanding as one integrates the maximum mixedness model backward to the reactor entrance. Instead, an ODE solver such as Polymath is preferred. In Section 17.3, we will show how to solve maximum mixedness problems numerically using Polymath software.
17.3 Using Software Packages Such as Polymath to Find Maximum Mixedness Conversion
The first thing we do when using a software package to solve the ODEs to find either the conversion or the exit concentrations in a nonideal reactor is to fit the tracer concentration measurements to a polynomial C(t) = a0 + a1t + a2t2 + a3t3 + a4t4 to obtain C(t) from the data, such as Polymath. A tutorial on how to obtain an analytical expression is given in the Living Example Problem in both Chapters 7 and 16 on the CRE Web site, http://www.umich.edu/~elements/6e/07chap/Polynomial_Regression_Tutorial.pdf.
Maximum Mixedness Model Computer Calculations
Because software packages won’t integrate backward, we need to change the variable such that the integration proceeds forward as λ decreases from some large value to zero. We do this by forming a new variable, z, which is the difference between the longest time measured in the E(t) curve, , and λ, that is, ( – λ). In the case of Example 17-4, the longest time at which the tracer concentration was measured was 200 minutes (Table E17-4.1). Therefore, we will set .
Realizing
Substituting for λ in Equation (17-14)
changing variables and rearranging
One now integrates between the limits z = 0 and z = 200 to find the exit conversion at z = 200, which corresponds to λ = 0.
Two concerns!!
In fitting E(t) to a polynomial, one very important concern is to make sure that the polynomial does not become negative at large times. Another concern in the maximum mixedness calculations is that the term (1 − F(λ)) does not go to zero. Setting the maximum value of F(t) at 0.999 rather than 1.0 will eliminate this problem. It can also be circumvented by integrating the polynomial for E(t) to get F(t) and then setting the maximum value of F(t) at 0.999. If F(t) is ever greater than 1.0 when fitting a polynomial, the solution will blow up when integrating Equation (17-17) numerically.
Example 17–5 Using Software to Make Maximum Mixedness Model Calculations
Use an ODE solver to determine the conversion predicted by the maximum mixedness model for the E(t) curve given in Example E17-4.
Solution
Because of the shape of the E(t) curve, it is necessary to use two polynomials, a third order and a fourth order, each for a different part of the curve to express the RTD, E(t), as a function of time.
For values of λ less than 70, we use the polynomial
For values of λ greater than 70, we use the polynomial
The resulting E(t) curve is shown in Figure E17-5.1.
First, we fit E(t).
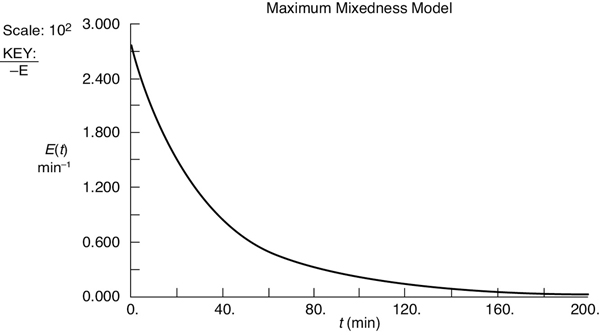
Figure E17-5.1 Polynomial fit of E(t).
To use Polymath to carry out the integration, we change our variable from λ to z using the largest time measurement that was taken from E(t) in Table E17-4.1, which is 200 min:
z = 200 − λ
The equations to be solved are
Maximum Mixedness Model
with z = 0 (λ = 200), X = 0, and F = 1 [i.e., F(λ) =0.999]. Caution: Because [1 – F(λ)]–1 tends to infinity at F = 1, (z = 0), we set the maximum value of F at 0.999 at z = 0.


Polynomials used to fit E(t) and F(t)
TABLE E17-5.1 POLYMATH PROGRAM FOR MAXIMUM MIXEDNESS MODEL
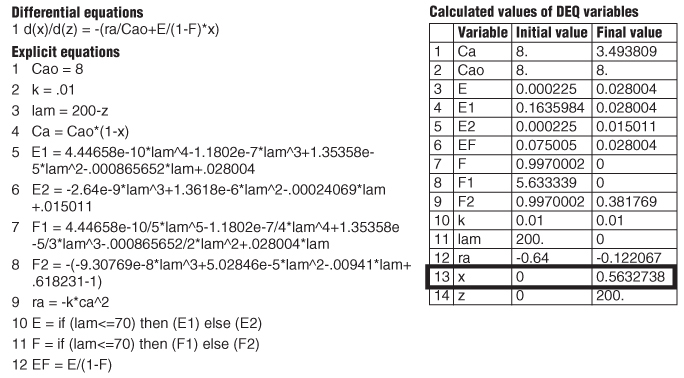
The Polymath equations are shown in Table E17-5.1. The solution is
The conversion predicted by the maximum mixedness model is 56.3%, Xmm = 0.56 while the conversion predicted from complete segregation was Xseg = 0.61.
Summary
XPFR = 0.76
Xseg = 0.61
XCSTR = 0.58
Xmm = 0.56
Analysis: As expected, the conversion Xmm calculated using Polymath or another software package is virtually the same as the hand calculation, but somewhat easier. The most difficult part of the calculation is to fit the E-curve and the F-curve to the polynomials and then to make sure that
for the polynomial parameters chosen.
17.3.1 Comparing Segregation and Maximum Mixedness Predictions

In the previous example, we saw that the conversion predicted by the segregation model, Xseg, was greater than that by the maximum mixedness model Xmm. Will this always be the case? No! To learn the answer is no, we take the second derivative of the rate law as shown in Table 17-2.
Comparing Xseg and Xmm
TABLE 17-2 CRITERIA FOR HIGHEST CONVERSION XSEG OR XMM

We now apply Table 17-2 to power-law rate laws, for an nth order reaction we have
From the product [(n)(n – 1)], we see
TABLE 17-3 COMPARING XSEG OR XMM FOR POWER-LAW MODELS

Important point
We note that in some cases Xseg is not too different from Xmm. However, when one is considering the destruction of toxic waste where X > 0.99 is desired, then even a small difference is significant!!
In this section, we have addressed the case where all we have is the RTD and no other knowledge about the flow pattern exists. Perhaps the flow pattern cannot be assumed because of a lack of information or other possible causes. Perhaps we wish to know the extent of possible error from assuming an incorrect flow pattern. We have shown how to obtain the conversion, using only the RTD, for two limiting mixing situations: the earliest possible mixing consistent with the RTD, or maximum mixedness, and mixing only at the reactor exit, or complete segregation. Calculating conversions for these two cases gives bounds on the conversions that might be expected for different flow paths consistent with the observed RTD.
17.4 Tanks-in-Series One Parameter Model, n
In the previous sections, we showed how to calculate conversion in nonideal reactors using no (zero) adjustable parameters. We now will show two ways to use one adjustable parameter to model the real reactor: (1) the T-I-S model, Section 17.4, (2) the dispersion model, Section 18.2. In this section, we show how to use the tanks-in-series (T-I-S) model to describe nonideal reactors and calculate conversion. The one parameter in T-I-S model is n, the number of tanks. We will use the RTD data to determine the number of ideal tanks, n, in series that will give approximately the same RTD as the nonideal reactor. Next, we will apply the reaction engineering algorithm developed in Chapters 1–5 to calculate the conversion.
We are first going to develop the RTD equation for three tanks in series (Figure 17-6) and then generalize to n reactors in series to derive an equation that gives the number of tanks, n, in series that best fits the RTD data.
17.4.1 Find the Number of T-I-S to Model the Real Reactor

Figure 17-6 Tanks in series: (a) real system; (b) model system.
Figure 17-6 shows a one large CSTR that is modeled as three CSTRs in series. By carrying out sequential mole balances on each reactor in series as shown in the Additional Material on the Web site for Chapter 17, the concentration of tracer exiting the third CSTR is
with
where V is the total reactor volume and v0 is the volumetric flow rate through all three reactors. Extrapolating the exiting conversion from the last of three reactors, Equation (17-21) to n reactors
Substituting for Cn in Equation 16-7, the RTD function is
Using the RTD data to find τ and σ2, the number of tanks-in-series, n, necessary to model the real reactor derived on the Chapter 17 CRE Web site (http://www.umich.edu/~elements/6e/17chap/Fogler_Ch17_Web_17.4_Tanks-in-Series.pdf) and is shown in Equation (17-25)
Number of T-I-S to match RTD
with τ and σ given by
17.4.2 Calculating Conversion for the T-I-S Model
If the reaction is first order, we can use Equation (5-15) to calculate the conversion
It is acceptable (and usual) for the value of n calculated from Equation (18-11) to be a noninteger in Equation (5-15) to calculate the conversion. For reactions other than first order, an integer number of reactors must be used and sequential mole balances on each reactor must be carried out. If, for example, n = 2.53, then one could calculate the conversion for two tanks and also for three tanks to bound the conversion. The conversion and effluent concentrations would be solved sequentially using the algorithm developed in Chapter 5; that is, after solving for the effluent from the first tank, it would be used as the input to the second tank, and so on, as shown on the CRE Web site for Chapter 17 Additional Materials.
17.4.3 Tanks-in-Series versus Segregation for a First-Order Reaction
We have already stated that the segregation and maximum mixedness models are equivalent for a first-order reaction. The proof of this statement was left as an exercise in Problem P17-3C. We can extend this equivalency for a first-order reaction to the tanks-in-series (T-I-S) model
For a first-order reaction, the predicted conversions are the same.
The proof of Equation (17-26) is given in the Additional Materials on the CRE Web site for Chapter 17.
17.5 RTD and Multiple Reactions
As discussed in Chapter 8, when multiple reactions occur in reacting systems, it is best to work in concentrations, moles, or molar flow rates rather than conversion.
17.5.1 Segregation Model
In the segregation model, we consider each of the globules in the reactor to have different concentrations of reactants, CA, and of products, CP. These globules are mixed together immediately upon exiting to yield the exit concentration of A, , which is the average of all the globules exiting
The concentrations of the individual species, CA(t) and CB(t), in the different globules are determined from batch reactor calculations. For a constant-volume batch reactor, where q reactions are taking place, the coupled mole balance equations are
Solving for the exit concentrations using the segregation model for multiple reactions
These equations are solved simultaneously with to give the exit concentration. The RTDs, E(t), in Equations (17-31) and (17-32) are determined from experimental measurements and then fit to a polynomial.
17.5.2 Maximum Mixedness
For the maximum mixedness model, we write Equation (17-12) for each species and replace rA by the net rate of formation
After substitution for the rate laws for each reaction (e.g., r1A = k1CA), these equations are solved numerically by starting at a very large value of λ say , and integrating backward to λ = 0 to yield the exit concentrations CA, CB, ….
We will now show how different RTDs with the same mean residence time can produce different product distributions for multiple reactions.
Example 17–6 RTD and Complex Reactions

Consider the following set of liquid-phase reactions
which are occurring in two different reactors with the same mean residence time, tm = 1.26 minutes. However, the RTD is very different for each of the reactors, as can be seen in Figures E17-6.1 and E17-6.2.
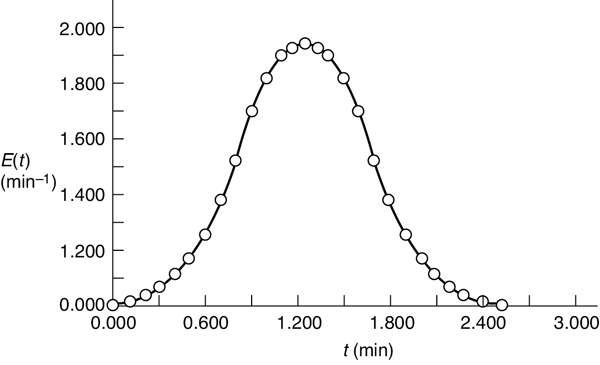
Figure E17-6.1 E1(t): asymmetric distribution.
Two different reactors with different RTDs, but the same mean residence time tm
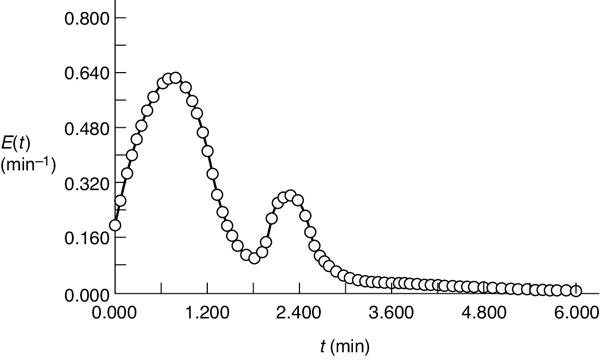
Figure E17-6.2 E2(t): bimodal distribution.
Fit polynomials to the RTDs for each reactor.
Determine the product distribution and selectivities (e.g., ŜC/D, ŜD/E) for
The segregation model.
The maximum mixedness model.
Before carrying out any calculations, what do you think the exit concentrations and conversion will be for these two very different RTDs with the same mean residence time?
Additional information:
k1 = k2 = k3 = 1 in appropriate units at 350 K.
Solution
Segregation Model
Combining the mole balance and rate laws for a constant-volume batch reactor (i.e., globules), we have
and the concentration for each species exiting the reactor is found by integrating the equation
over the life of the E(t) curve. The life of the E(t) curve is from t = 0 to the time at the last data point. For this example, the life of the E1(t) is 2.52 minutes (Figure E17-6.1), and the life of E2(t) is 6 minutes (Figure E17-6.2).
The initial conditions are t = 0, CA = CB = 1, and CC = CD = CE = 0.
The Polymath program used to solve these equations is shown in Table E17-6.1 for the asymmetric RTD, E(t).
With the exception of the polynomial for E(t), the Polymath programs for the bimodal RTD and asymmetric are identical for the segregation model. The Polymath program for the segregation model for the asymmetric distribution is shown in Table E17-6.1 and the program for the maximum mixedness model for the bimodal distribution is shown in Table E17-6.3. A comparison of the exit concentrations and selectivities of the two RTD curves is shown in Table E17-6.2.
TABLE E17-6.1 POLYMATH PROGRAM FOR SEGREGATION MODEL WITH ASYMMETRIC RTD (MULTIPLE REACTIONS)


TABLE E17-6.2 SEGREGATION MODEL RESULTS
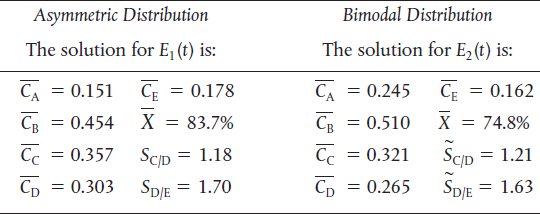
Analysis: We note that while the conversion and the exit concentration of species A are significantly different for the two distributions, the selectivities are not. In Problem P17-6B (b), you are asked to calculate the mean residence time for each distribution to try to explain these differences.
Maximum Mixedness Model
The equations for each species are
The Polymath program for the bimodal distribution, E(t), is shown in Table E17-6.3. The Polymath program for the asymmetric distribution is identical, with the exception of the polynomial fit for E1(t) and is given in the Chapter 17 Living Example Problems, Web 17-1e and Web 17-1h, on the CRE Web site. A comparison of the exit concentration and selectivities of the two RTD distributions is shown in Table E17-6.4.
TABLE E17-6.3 POLYMATH PROGRAM FOR MAXIMUM MIXEDNESS MODEL WITH BIMODAL DISTRIBUTION (MULTIPLE REACTIONS)
ODE Report (RKF45) Differential equations as entered by the user [1] d(ca)/d(z) = -(-ra+(ca-cao)*EF) [2] d(cb)/d(z) = -(-rb+(cb-cbo)*EF) [3] d(cc)/d(z) = -(-rc+(cc-cco)*EF) [4] d(F)/d(z) = -E [5] d(cd)/d(z) = -(-rd+(cd-cdo)*EF) [6] d(ce)/d(z) = -(-re+(ce-ceo)*EF) |
Explicit equations as entered by the user [1] cbo = 1 [2] cao = 1 [3] cco = 0 [4] cdo = 0 [5] ceo = 0 [6] lam = 6-z [7] k2 = 1 [8] k1 = 1 [9] k3 = 1 [10] rc = k1*ca*cb [11] re = k3*cb*cd [12] E1 = 0.47219*lam^4-1.30733*lam^3+0.31723*lam^2+0.85688*lam+0.20909 [13] E2 = 3.83999*lam^6-58.16185*lam^5+366.2097*lam^4-1224.66963*lam^3+2289.84857*lam^2-2265.62125*lam+925.46463 [14] E3 = 0.00410*lam^4-0.07593*lam^3+0.52276*lam^2-1.59457*lam+1.84445 [15] rb = -k1*ca*cb-k3*cb*cd [16] ra = -k1*ca*cb-k2*ca [17] rd = k2*ca-k3*cb*cd [18] E = if(lam<=1.82)then(E1)else(if(lam<=2.8)then(E2)else(E3)) [19] EF = E/(1-F) |
TABLE E17-6.4 MAXIMUM MIXEDNESS MODEL RESULTS
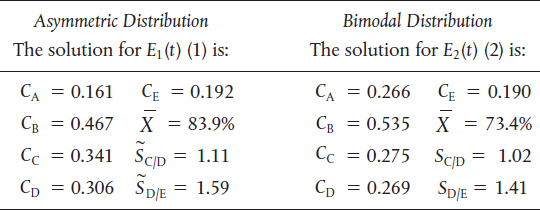
Analysis: In this example, we have applied the segregation model and the maximum mixedness models to complex reactions. While the concentrations of species A exiting the reactors for the two distributions are different, the selectivities are not so different for the same mean residence time.
Calculations similar to those in Example 17-6 are given in an example on the CRE Web site for the series reaction
Living Example CD17-RTD (LEP), parts (a) through (h), explores the earlier series reaction and also multiple reactors with different residence time distributions (e.g., asymmetric, bimodal).
17.6 And Now… A Word from Our Sponsor–Safety 17 (AWFOS–S17 Brief Case History on an Air Preheater)
Crude oil furnace APH fouling: In crude heaters, air preheaters (APHs) are installed to preheat the ambient air using hot flue gas exiting from the furnace. The preheater, shown schematically in Figure 17-7, reduces the heat input required to heat the air and thus increasing heater efficiency. In a turnaround of a crude distillation unit plant, the existing APH was replaced with a new design having a narrow passage on the flue gas side. The purpose of replacing the old design was to increase the heat-transfer surface area so as to increase heat recovery from flue gas and thus heater efficiency. However, after the plant was started-up, heavy and frequent fouling (e.g., depositing of material) was observed in the APH, requiring cleaning once in 2 weeks. The APH was shut down for 3–4 days for cleaning and during this period heaters were aggressively operated at high fuel rates (to maintain same plant rate). This increase in rates caused an increase in tube metal temperatures and increasing risk of tube failures. Further, hot flue gas was released to atmosphere and causing the heater to operate at a lower efficiency. Overall, it was estimated that the heater reliability had decreased and the financial loss from the APH outage outweighed the benefit of increased heat recovery when APH was in service. Management concluded that the narrow passage is leading to fouling and thus design is flawed. It was therefore, proposed to revert to the older design.
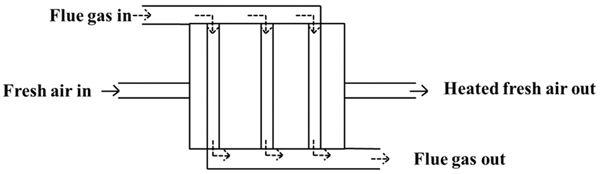
Figure 17-7 Air preheater.
Apply R.W. Paul’s six types of critical thinking questions to this situation to help management decide whether or not to revert to the older design APH.
Solution
1. Questions about the question or problem statement
Manan: Why do you think the APH design is flawed considering design would have been reviewed at various levels before installation?
2. Questions for clarification:
Manan: Are there any other case studies where this new design APH has been installed and performed as per expectations?
3. Questions that probe assumptions
Manan: How did you assume that heater conditions remained the same and there was no change in flue gas quality or temperature?
4. Questions that probe reasons and evidences
Manan: Did the laboratory analysis of foulant show there was no increase in carbon particles or corrosion products (which are known foulant) in flue gas post new APH installation?
5. Questions that probe viewpoints and perspectives
Manan: What is the counterargument that reverting back to the older design will not work?
6. Questions that probe implications and consequences?
Manan: What are the consequences of taking APH offline on environment as hot flue gas is released to atmosphere?
What are the implications on the operator’s behavior/mind-set who now has the additional task of frequently cleaning the APH?
Thanks to Manan Agrawal, Indian Institute of Technology, Bombay, and to Mayur Tikmani, Indian Institute of Technology, Guwahati.
Summary
The RTD functions for an ideal reactor are
PFR:
CSTR:
LFR:
The dimensionless residence time is
and is equal to the number space times. Then
The internal-age distribution, [I(α) dα], gives the fraction of material inside the reactor that has been inside between a time α and a time (α + dα).
Segregation model: The conversion is
and for multiple reactions
Maximum mixedness: Conversion can be calculated by solving the following equations
Tanks-in-series model: Use RTD data to estimate the number of tanks in series,
For a first-order reaction
The exit concentration predicted for multiple reactions using the maximum mixedness model can be found by solving the equation
from λ = λmax to λ = 0. To use an ODE solver, let z = λmax – λ.
CRE Web Site Materials
(http://www.umich.edu/~elements/6e/17chap/obj.html#/)

Questions, Simulations, and Problems
The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.
A = • B = ▪ C = ♦ D = ♦♦

Questions
Q17-1A QBR (Question Before Reading). How does the conversion predicted from the segregation model, Xseg, compare with the conversion predicted by the CSTR, PFR, and LFR models for the same mean residence time, tm?
Q17-2A Read over the problems of this chapter. Make up an original problem that uses the concepts presented in this chapter. The guidelines are given in Problem P5-1B. RTDs from real reactors can be found in Ind. Eng. Chem., 49, 1000 (1957); Ind. Eng. Chem. Process Des. Dev., 3, 381 (1964); Can. J. Chem. Eng., 37, 107 (1959); Ind. Eng. Chem., 44, 218 (1952); Chem. Eng. Sci., 3, 26 (1954); and Ind. Eng. Chem., 53, 381 (1961).
Q17-3 Go to the LearnChemE screencast link for Chapter 17 (http://www.learncheme.com/screencasts/kinetics-reactor-design). View one of the screencast 5- to 6-minute video tutorials and list two of the most important points.
Q17-4 AWFOS–S17. Pick two critical thinking questions and describe why they are the most important questions to ask.
Computer Simulations and Experiments
P17-1B
- Example 17-2: Mean Conversion, Xseg, Calculations in a Real Reactor
Wolfram and Python
How do CA0, n and k affect the trajectories in X for the segregation model and the LFR?
Write a set of conclusions based on your experiments in (i).
Polymath
How does the conversion predicted from the segregation model, Xseg, compare with the conversion predicted by the CSTR, PFR, and LFR models for the same mean residence time, tm?
Example 17-3: Mean Conversion for Second-Order Reaction in a Laminar-Flow Reactor Wolfram and Python
For what value of k are X and the farthest apart? Closest together?
Vary n and describe what you find with regard to Xseg.
Explain how the E-curve varies with n, CA0, and k.
Vary n, τ, CA0, and k and describe what you find.
Write a set of conclusions for your experiments (i) through (iv).
Polymath
(1) Vary k by a factor of 5–10 or so above and below the nominal value given in the problem statement of 4.93 × 10–3 dm3/mol/s. When do XPFR and XLFR come close together and when do they become farther apart? (2) Use the E(t) and F(t) in Examples 16-1 and 16-2 to predict conversion, and compare in parts (a), (b), and (c).
Example 17-4: Conversion Bounds for a Nonideal Reactor
Wolfram and Python
For what value of k are X and the farthest apart? Closest together?
Vary n and describe what you find with regard to Xseg.
Explain how the E-curve varies with n, CA0, and k.
Vary n, τ, CA0, and k and describe what you find.
Write a set of conclusions for your experiments (i) through (iv).
Polymath
(1) Vary the parameter kCA0, whose nominal value is
by a factor of 10 above and below the value nominal of 0.08 s–1 and describe when Xseg and Xmm come closer together and when they become farther apart. (2) How do Xmm and Xseg compare with XPFR, XCSTR, and XLFR for the same mean residence time? (3) How would your results change if T = 350 K with E = 10 kcal/mol? How would your answer change if the reaction was pseudo first order with kCA0 = 4 × 10–3/s?
Example 17-5: Using Software to Make Maximum Mixedness Model Calculations
Wolfram and Python
Individually vary k, CA0 and n and describe how the profile X as a function of Z changes.
Individually vary k, CA0 and n and describe how the rate –rA changes as you vary k, CA0 and n.
Write a set of conclusions.
Polymath
(1) Vary the parameters kCA0, above and below the nominal value 0.08 s–1, by a factor of 10 and describe when Xmm and Xseg come closer together and when they become farther apart. (2) How do Xmm and Xseg compare with XPFR, XCSTR, and XLFR for the same tm? (3) How would your results change if the reaction was pseudo first order with k1 = CA0k = 0.08 min–1? (4) If the reaction was third order with ? (5) If the reaction was half order with ? Describe any trends.
Example 17-6a: RTD and Complex Reaction for an Asymmetric RTD (shown on the CRE Web site at http://www.umich.edu/~elements/6e/17chap/live.html)
Wolfram and Python
Vary k1, k2, and k3 and describe how the conversion changes.
Vary k1, k2, and k3 and describe how the concentration and selectivity change.
Vary k1, k2, and k3 and describe how the rate changes.
Write a set of conclusions.
Polymath
Download the Living Example Problem from the CRE Web site. (1) If the activation energies in cal/mol are E1 = 5000, E2 = 1000, and E3 = 9000, how would the selectivities and conversion of A change as the temperature was raised or lowered around 350 K? (2) If you were asked to compare the results from Example 17-6 for the asymmetric and bimodal distributions in Tables E17-6.2 and E17-6.4, what similarities and differences do you observe? What generalizations can you make?
Example 17-6b: RTD and Complex Reaction with a Bimodal RTD (shown on the CRE Web site at http://www.umich.edu/~elements/6e/17chap/live.html)
Wolfram and Python
Vary k1, k2, and k3 and describe how the conversion changes.
Vary k1, k2, and k3 and describe how the concentration and selectivity change.
Vary k1, k2, and k3 and describe how the rate changes.
Write a set of conclusions.
Problems
P17-2B OEQ (Old Exam Question). An irreversible first-order reaction takes place in a long cylindrical reactor. There is no change in volume, temperature, or viscosity. The use of the simplifying assumption that there is plug flow in the tube leads to an estimated degree of conversion of 86.5%. What would be the actually attained degree of conversion if the real state of flow is laminar, with negligible diffusion?
P17-3C Show that for a first-order reaction
A → B
the exit concentration maximum mixedness equation
is the same as the exit concentration given by the segregation model
Hint: Verify
is a solution to Equation (P17-3.1).
P17-4C OEQ (Old Exam Question). The first-order reaction
A → B
with k = 0.8 min–1 is carried out in a real reactor with the following RTD function:

Mathematically, this hemi circle is described by the equations for 2τ ≥ t ≥ 0 then
For t > 2τ, then E(t) = 0.
What is the mean residence time?
What is the variance?
What is the conversion predicted by the segregation model?
What is the conversion predicted by the maximum mixedness model? (Ans: Xmm = 0.447)
What is the conversion predicted by the tanks-in-series model?
P17-5B OEQ (Old Exam Question). A step tracer input was used on a real reactor with the following results:
For t ≤ 10 min, then CT = 0.
For 10 ≤ t ≤ 30 min, then CT = 10 g/dm3.
For t ≥ 30 min, then CT = 40 g/dm3.
The second-order reaction A → B with k = 0.1 dm3/mol • min is to be carried out in the real reactor with an entering concentration of A of 1.25 mol/dm3 at a volumetric flow rate of 10 dm3/min. Here, k is given at 325 K.
What is the mean residence time tm?
What is the variance σ2?
What conversions do you expect from an ideal PFR and an ideal CSTR in a real reactor with tm?
What is the conversion predicted by
The segregation model?
The maximum mixedness model?
The T-I-S model?
What conversion is predicted by an ideal laminar flow reactor?
Assume now that the reaction is first order with k = 0.4 min–1 and calculate the conversion using the tanks-in-series model.
P17-6B OEQ (Old Exam Question). The following E(t) curves were obtained from a tracer test on two tubular reactors in which dispersion is believed to occur.
A second-order reaction
is to be carried out in this reactor. There is no dispersion occurring either upstream or downstream of the reactor, but there is dispersion inside the reactor.
What is the final time t1 (in minutes) for the reactor shown in Figure P17-6B (a)? In Figure P17-6B (b)?
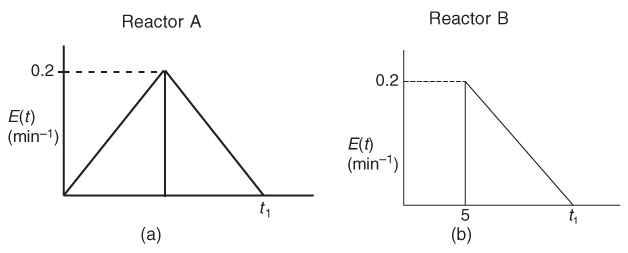
Figure P17-6 B (a) RTD reactor A; (b) RTD reactor B.
What is the mean residence time, tm, and variance, σ2, for the reactor shown in Figure P17-6B (a)? In Figure P17-6B (b)?
What is the fraction of the fluid that spends 7 minutes or longer in Figure P17-6B (a)? In Figure P17-6B (b)?
Find the conversion predicted by the segregation model for reactor A.
Find the conversion predicted by the maximum mixedness model for reactor A.
Find the conversion predicted by the T-I-S model for reactor A.
Repeat (d)–(f) for reactor B.
Now assume the reaction is first order with k1 = 0.2 min–1, what are the conversions predicted by the tanks-in-series, the segregation in the maximum mixedness model?
P17-7B The RTD for a nonideal reactor is shown in Figure P17-6B. What is the conversion predicted by the tanks-in-series model for a first-order reaction?
with k1 = 0.4 min–1?
with k1 = 0.04 min–1?
with k1 = 4 min–1?
P17-8B The following E(t) curve was obtained from a tracer test on a reactor.
The conversion predicted by the tanks-in-series model for the isothermal elementary reaction
A → B
was 50% at 300 K.
If the temperature is to be raised 10°C (E = 25000 cal/mol) and the reaction carried out isothermally, what will be the conversion predicted by the segregation, maximum mixedness models, and the T-I-S models?
P17-9B OEQ (Old Exam Question). The third-order liquid-phase reaction with an entering concentration of 2M
was carried out in a reactor that has the following RTD:
For isothermal operation, what is the conversion predicted by
A CSTR, a PFR, an LFR, T-I-S, XT-I-S, and maximum mixedness, Xmm, the segregation model, Xseg?
Hint: Find tm (i.e., τ) from the data and then use it with E(t) for each of the ideal reactors.
The maximum mixedness model, Xmm? Plot X versus z (or λ) and explain why the curve looks the way it does.
Now calculate the exit concentrations of A, B, and C for the reaction
using (1) the segregation model and (2) the maximum mixedness model.
P17-10A Consider again the nonideal reactor characterized by the RTD data in Example 17-5, where E (t) and F(t) are given as polynomials. The irreversible gas-phase nonelementary reaction
A + B → C + D
is first order in A and second order in B, and is to be carried out isothermally. Calculate the conversion for:
A PFR, a laminar-flow reactor with complete segregation, and a CSTR all at the same tm.
The cases of T-I-S, complete segregation, and maximum mixedness.
Additional information (obtained at the Jofostan Central Research Laboratory in Riça, Jofostan):
CA0 = CB0 = 0.0313 mol / dm3, V = 1000 dm3,
υ0 = 10 dm3/ s, k = 175 dm6/ mol 2 ? s at 320 K.
P17-11A Consider an ideal PFR, CSTR, and LFR.
Evaluate the first moment about the mean E(t)dt for a PFR, a CSTR, and an LFR.
Calculate the conversion in each of these ideal reactors for a second-order liquid-phase reaction with Da = 1.0 (τ = 2 min and kCA0 = 0.5 min–1).
Calculate the conversion predicted by the T-I-S, segregation, and maximum mixedness models.
P17-12B For the catalytic reaction
the rate law can be written as
Which will predict the highest conversion, the maximum mixedness model or the segregation model?
Hint: Specify the different ranges of the conversion where one model will dominate over the other.
P7-13B Use the RTD data in Examples 16-1 and 16-2 to predict XPFR, XCSTR, XLFR, XT-I-S, Xseg and Xmm for the following elementary gas-phase reactions
A → B k = 0.1 min–1
A → 2B k = 0.1 min–1
2A → B k = 0.1 min–1 m3/kmol CA0 = 1.0 kmol/m3
3A → B k = 0.1 m6/kmol2min CA0 = 1.0 kmol/m3
Repeat (a) through (d) for the RTD given by
Problem P16-3B
Problem P16-4B
Problem P16-5B
P17-14C The second-order, elementary liquid-phase reaction
is carried out in a nonideal CSTR. At 300 K, the specific reaction rate is k1A = 0.5 dm3 / mol·min. In a tracer test, the tracer concentration rose linearly up to 1 mg / dm3 at 1.0 minutes and then decreased -linearly to zero at exactly 2.0 minutes. Pure A enters the reactor at a temperature of 300 K.
Calculate the conversion predicted by the segregation and maximum mixedness models.
Now consider that a second elementary reaction also takes place
Compare the selectivities predicted by the segregation and maximum mixedness models.
P17-15C The reaction and corresponding rate data discussed in Example 12-3 are to be carried out isothermally at 613°R in a nonideal reactor where RTD is given by the data (i.e., E(t) and F(t)) in Example 16-2. Determine the exit selectivities
Using the segregation model.
Using the maximum mixedness model.
Compare the selectivities in parts (a) and (b) with those that would be found in an ideal PFR and ideal CSTR in which the space time is equal to the mean residence time.
P17-16C The reactions described in Example 12-7 are to be carried out isothermally at 1000°C in the reactor whose RTD is described in Example 17-4 with CA0 = CB0 = 0.05 mol/dm3.
Determine the exit selectivities using the segregation model.
Determine the exit selectivities using the maximum mixedness model.
Compare the selectivities in parts (a) and (b) with those that would be found in an ideal PFR and ideal CSTR in which the space time is equal to the mean residence time.
What would your answers to parts (a) through (c) be if the RTD curve rose from zero at t = 0 to a maximum of 50 mg/dm3 after 10 minutes, and then fell linearly to zero at the end of 20 minutes?
P17-17B Using the data in Problem P16-11B,
Plot the internal-age distribution I(t) as a function of time.
What is the mean internal age αm?
The activity of a “fluidized” CSTR is maintained constant by feeding fresh catalyst and removing spent catalyst at a constant rate. Using the preceding RTD data, what is the mean catalytic activity if the catalyst decays according to the rate law ?
What conversion would be achieved in an ideal PFR for a second-order reaction with kCA0 = 0.1 min–1 and CA0 = 1 mol/dm3?
Repeat (d) for a laminar-flow reactor.
Repeat (d) for an ideal CSTR.
What would be the conversion for a second-order reaction with kCA0 = 0.1 min–1 and CA0 = 1 mol/dm3 using the segregation model?
What would be the conversion for a second-order reaction with kCA0 = 0.1 min–1 and CA0 = 1 mol/dm3 using the maximum mixedness model?
P17-18B OEQ (Old Exam Question). The relative tracer concentrations obtained from pulse tracer tests on a commercial packed-bed desulfurization reactor are shown in Figure P17-18B. After studying the RTD, what problems are occurring with the reactor during the period of poor operation (thin line)? The bed was repacked and the pulse tracer test again carried out with the results shown in Figure P17-18B (thick line). Calculate the conversion that could be achieved in the commercial desulfurization reactor during poor operation and during good operation (Figure P17-18B) for the following reactions:
A first-order isomerization with a specific reaction rate of 0.1 h–1
A first-order isomerization with a specific reaction rate of 2.0 h–1
What do you conclude upon comparing the four conversions in parts (a) and (b)?
From Additional Home Problem CDP17-IB (3rd ed. P13-5)
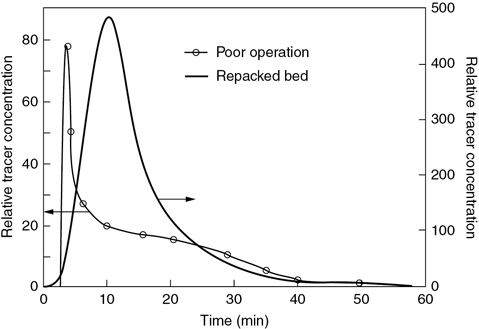
Figure P17-18B Pilot-plant RTD. [Murphree, E. V., A. Voorhies, and F. Y. Mayer, Ind. Eng. Chem. Process Des. Dev., 3, 381 (1964). Copyright © 1964, American Chemical Society.]
Application Pending for a Problem Hall of Fame

Supplementary Reading
Discussions of the measurement and analysis of residence time distribution can be found in
R. L. CURL and M. L. MCMILLIN, “Accuracies in residence time measurements,” AIChE J., 12, 819–822 (1966).
O. LEVENSPIEL, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999, Chaps. 11–16.
An excellent discussion of segregation can be found in
J. M. DOUGLAS, “The effect of mixing on reactor design,” AIChE Symp. Ser., 48, 60, 1 (1964).
Also see
M. DUDUKOVIC and R. FELDER, in CHEMI Modules on Chemical Reaction Engineering, vol. 4, ed. B. Crynes and H. S. Fogler. New York: AIChE, 1985.
E. B. NAUMAN, “Residence time distributions and micromixing,” Chem. Eng. Commun., 8, 53 (1981).
E. B. NAUMAN and B. A. BUFFHAM, Mixing in Continuous Flow Systems. New York: Wiley, 1983.
B. A. ROBINSON and J. W. TESTER, “Characterization of flow maldistribution using inlet-outlet tracer techniques: an application of internal residence time distributions,” Chem. Eng. Sci., 41 (3), 469–483 (1986).
J. VILLERMAUX, “Mixing in chemical reactors,” in Chemical Reaction Engineering—Plenary Lectures, ACS Symposium Series 226. Washington, DC: American Chemical Society, 1982.
