Chapter 6. Techniques for Estimating
“Prediction is very difficult, especially about the future.”
—Niels Bohr, Danish physicist
The more effort we put into something, the better the result. Right? Perhaps, but we often need to expend just a fraction of that effort to get adequate results. For example, my car is dirty, and I need to wash it. If I wash it myself, I’ll spend about an hour on it, which will be enough to wash the exterior, vacuum the interior, and clean the windows. For a one-hour investment, I’ll have a fairly clean car.
On the other hand, I could call a car-detailing service and have them wash my car. They’ll spend four hours on it. They do everything I do but much more thoroughly. They’ll also wax the car, shine the dashboard, and so on. I watched one time, and they used tiny cotton swabs to clean out the little places too small to reach with a rag. That’s a lot of effort for slightly better results. For me, the law of diminishing returns kicks in well before I’ll use a cotton swab on my car.
We want to remain aware, too, of the diminishing return on time spent estimating. We can often spend a little time thinking about an estimate and come up with a number that is nearly as good as if we had spent a lot of time thinking about it. The relationship between estimate accuracy and effort is shown in Figure 6.1. The curve in this graph is placed according to my experience, corroborated in discussions with others. It is not based on empirical measurement.
Figure 6.1. Additional estimation effort yields very little value beyond a certain point.
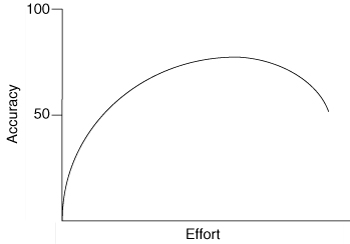
To understand this relationship better, suppose you decide to estimate how many cookies I’ve eaten in the past year. You could put no effort into the estimate and just take a random guess. Mapping this onto Figure 6.1, you’d be completely to the left on the effort axis, and your estimate would be unlikely to be accurate. You could move to the right on the effort axis by spending a half-hour or so researching national averages for cookie consumption. This would improve your accuracy over the pure guess. If you felt the need to be more accurate, you could do some research—call my friends and family, subpoena my past cookie orders from the Girl Scouts, and so on. You could even follow me around for a day—or, better yet, a month—and then extrapolate your observations into how many cookies you think I eat in a year.
Vary the effort you put into estimating according to purpose of the estimate. If you are trying to decide whether or not to send me a box of cookies as a gift, you do not need a very accurate estimate. If the estimate will be used to make a software build versus buy decision, it is likely enough to determine that the project will take six to twelve months. It may be unnecessary to refine that to the point where you can say it will take seven or eight months.
Look carefully at Figure 6.1, and notice a couple of things. First, no matter how much effort is invested, the estimate is never at the top of the accuracy axis. No matter how much effort you put into an estimate, an estimate is still an estimate. No amount of additional effort will make an estimate perfect. Next, notice how little effort is required to move the accuracy up dramatically from the baseline. As drawn in Figure 6.1, about 10% of the effort gets 50% of the potential accuracy. Finally, notice that eventually, the accuracy of the estimate declines. It is possible to put too much effort into estimating, with the result being a less accurate estimate.
When starting to plan a project, it is useful to think about where on the curve of Figure 6.1 we wish to be. Many projects try to be very high up the accuracy axis, forcing teams far out on the effort axis even though the benefits diminish rapidly. Often, this is the result of the simplistic view that we can lock down budgets, schedules, and scope and that project success equates to on-time, on-budget delivery of an up-front, precisely planned set of features. This type of thinking leads to a desire for extensive signed requirements documents, lots of up-front analysis work, and detailed project plans that show every task a team can think of. Then, even after all this additional up-front work, the estimates still aren’t perfect.
Agile teams, however, choose to be closer to the left in a figure like Figure 6.1. They acknowledge that we cannot eliminate uncertainty from estimates, but they embrace the idea that small efforts are rewarded with big gains. Even though they are less far up the accuracy/effort scale, agile teams can produce more reliable plans because they frequently deliver small increments of fully working, tested, integrated code.
Estimates Are Shared
Estimates are not created by a single individual on the team. Agile teams do not rely on a single expert to estimate. Despite well-known evidence that estimates prepared by those who will do the work are better than estimates prepared by anyone else (Lederer and Prasad 1992), estimates are best derived collaboratively by the team, which includes those who will do the work. There are two reasons for this.
First, on an agile project we tend not to know specifically who will perform a given task. Yes, we may all suspect that the team’s database guru will be the one to do the complex stored procedure task that has been identified. However, there’s no guarantee that this will be the case. She may be busy when the time comes, and someone else will work on it. So because anyone may work on anything, it is important that everyone have input into the estimate.
Second, even though we may expect the database guru to do the work, others may have something to say about her estimate. Suppose that the team’s database guru, Kristy, estimates a particular user story as three ideal days. Someone else on the project may not know enough to program the feature himself, but he may know enough to say, “Kristy, you’re nuts; the last time you worked on a feature like that, it took a lot longer. I think you’re forgetting how hard it was last time.” At that point Kristy may offer a good explanation of why it’s different this time. However, more often than not in my experience, she will acknowledge that she was indeed underestimating the feature.
The Estimation Scale
Studies have shown that we are best at estimating things that fall within one order of magnitude (Miranda 2001; Saaty 1996). Within your town, you should be able to estimate reasonably well the relative distances to things like the nearest grocery store, the nearest restaurant, and the nearest library. The library may be twice as far as the restaurant, for example. Your estimates will be far less accurate if you are asked also to estimate the relative distance to the moon or a neighboring country’s capital. Because we are best within a single order of magnitude, we would like to have most of our estimates in such a range.
Two estimation scales I’ve had good success with are
• 1, 2, 3, 5, and 8
• 1, 2, 4, and 8
There’s a logic behind each of these sequences. The first is the Fibonacci sequence.[1] I’ve found this to be a very useful estimation sequence because the gaps in the sequence become appropriately larger as the numbers increase. A one-point gap from 1 to 2 and from 2 to 3 seems appropriate, just as the gaps from 3 to 5 and from 5 to 8 do. The second sequence is spaced such that each number is twice the number that precedes it. These nonlinear sequences work well because they reflect the greater uncertainty associated with estimates for larger units of work. Either sequence works well, although my slight personal preference is for the first.
Each of these numbers should be thought of as a bucket into which items of the appropriate size are poured. Rather than thinking of work as water being poured into the buckets, think of the work as sand. If you are estimating using 1, 2, 3, 5, and 8, and have a story that you think is just the slightest bit bigger than the other five-point stories you’ve estimated, it would be OK to put it into the five-point bucket. A story you think is a 7, however, clearly would not fit in the five-point bucket.
You may want to consider including 0 as a valid number within your estimation range. Although it’s unlikely that a team will encounter many user stories or features that truly take no work, including 0 is often useful. There are two reasons for this. First, if we want to keep all features within a 10x range, assigning nonzero values to tiny features will limit the size of largest features. Second, if the work truly is closer to 0 than 1, the team may not want the completion of the feature to contribute to its velocity calculations. If the team earns one point in this iteration for something truly trivial, in the next iteration their velocity will either drop by one or they’ll have to earn that point by doing work that may not be as trivial.
If the team does elect to include 0 in their estimation scale, everyone involved in the project (especially the product owner) needs to understand that 13 × 0 ≠ 0. I’ve never had the slightest problem explaining this to product owners, who realize that a 0-point story is the equivalent of a free lunch. However, they also realize there’s a limit to the number of free lunches they can get in a single iteration. An alternative to using 0 is to group very small stories and estimate them as a single unit.
Some teams prefer to work with larger numbers, such as 10, 20, 30, 50, and 100. This is fine, because these are also within a single order of magnitude. However, if you go with larger numbers, such as 10 to 100, I still recommend that you pre-identify the numbers you will use within that range. Do not, for example, allow one story to be estimated at 66 story points or ideal days and another story to be estimated at 67. That is a false level of precision, and we cannot discern a 1.5% difference in size. It’s acceptable to have one-point differences between values such as 1, 2, and 3. As percentages, those differences are much larger than between 66 and 67.
User Stories, Epics, and Themes
Although in general, we want to estimate user stories whose sizes are within one order of magnitude, this cannot always be the case. If we are to estimate everything within one order of magnitude, it would mean writing all stories at a fairly fine-grained level. For features that we’re not sure we want (a preliminary cost estimate is desired before too much investment is put into them) or for features that may not happen in the near future, it is often desirable to write one much larger user story. A large user story is sometimes called an epic.
Additionally, a set of related user stories may be combined (usually by a paper clip if working with note cards) and treated as a single entity for either estimating or release planning. Such a set of user stories is referred to as a theme. An epic, by its very size alone, is often a theme on its own.
By aggregating some stories into themes and writing some stories as epics, a team is able to reduce the effort they’ll spend on estimating. However, it’s important that they realize that estimates of themes and epics will be more uncertain than estimates of the more specific, smaller user stories.
User stories that will be worked on in the near future (the next few iterations) need to be small enough that they can be completed in a single iteration. These items should be estimated within one order of magnitude. I use the sequence 1, 2, 3, 5, and 8 for this.
User stories or other items that are likely to be more distant than a few iterations can be left as epics or themes. These items can be estimated in units beyond the 1 to 8 range I recommend. To accommodate estimating these larger items I add 13, 20, 40, and 100 to my preferred sequence of 1, 2, 3, 5, and 8.
Deriving an Estimate
The three most common techniques for estimating are
• Analogy
Each of these techniques may be used on its own, but the techniques should be combined for best results.
Expert Opinion
If you want to know how long something is likely to take, ask an expert. At least, that’s one approach. In an expert opinion-based approach to estimating, an expert is asked how long something will take or how big it will be. The expert relies on her intuition or gut feel and provides an estimate.
This approach is less useful on agile projects than on traditional projects. On an agile project, estimates are assigned to user stories or other user-valued functionality. Developing this functionality is likely to require a variety of skills normally performed by more than one person. This makes it difficult to find suitable experts who can assess the effort across all disciplines. On a traditional project for which estimates are associated with tasks, this is not as significant of a problem, because each task is likely performed by one person.
A nice benefit of estimating by expert opinion is that it usually doesn’t take very long. Typically, a developer reads a user story, perhaps asks a clarifying question or two, and then provides an estimate based on her intuition. There is even evidence that says this type of estimating is more accurate than other, more analytical approaches (Johnson et al. 2000).
Analogy
An alternative to expert opinion comes in the form of estimating by analogy, which is what we’re doing when we say, “This story is a little bigger than that story.” When estimating by analogy, the estimator compares the story being estimated with one or more other stories. If the story is twice the size, it is given an estimate twice as large. There is evidence that we are better at estimating relative size than we are at estimating absolute size (Lederer and Prasad 1998; Vicinanza et al. 1991).
When estimating this way, you do not compare all stories against a single baseline or universal reference. Instead, you want to estimate each new story against an assortment of those that have already been estimated. This is referred to as triangulation. To triangulate, compare the story being estimated against a couple of other stories. To decide if a story should be estimated at five story points, see if it seems a little bigger than a story you estimated at three and a little smaller than a story you estimated at eight.
Disaggregation
Disaggregation refers to splitting a story or feature into smaller, easier-to-estimate pieces. If most of the user stories to be included in a project are in the range of two to five days to develop, it will be very difficult to estimate a single story that may be 100 days. Not only are large things notoriously more difficult to estimate, but also in this case there will be very few similar stories to compare. Asking “Is this story fifty times as hard as that story” is a very different question from “Is this story about one-and-a-half times that one?”
The solution to this, of course, is to break the large story or feature into multiple smaller items and estimate those. However, you need to be careful not to go too far with this approach. The easiest way to illustrate the problem is with a nonsoftware example. Let’s use disaggregation to estimate my golf score this weekend. Assume the course I am playing has eighteen holes each with a par of four. (If you’re unfamiliar with golf scoring, the par score is the number of shots it should take a decent player to shoot his ball into the cup at the end of the hole.)
To estimate by disaggregation, we need to estimate my score for each hole. There’s the first hole, and that’s pretty easy, so let’s give me a three on that. But then I usually hit into the lake on the next hole, so that’s a seven. Then there’s the hole with the sandtraps; let’s say a five. And so on. However, if I’m mentally re-creating an entire golf course it is very likely I’ll forget one of the holes. Of course, in this case I have an easy check for that, as I know there must be eighteen individual estimates. But when disaggregating a story, there is no such safety check.
Not only does the likelihood of forgetting a task increase if we disaggregate too far, but summing estimates of lots of small tasks also leads to problems. For example, for each of the 18 holes, I may estimate my score for that hole to be in the range 3 to 8. Multiplying those by 18 gives me a full round range of 54 to 144. There’s no chance that I’ll do that well or that poorly. If asked for an estimate of my overall score for a full round, I’m likely to say anywhere from 80 to 120, which is a much smaller range and a much more useful estimate.
Specific advice on splitting user stories is provided in Chapter 12, “Splitting User Stories.”
Planning Poker
The best way I’ve found for agile teams to estimate is by playing planning poker (Grenning 2002). Planning poker combines expert opinion, analogy, and disaggregation into an enjoyable approach to estimating that results in quick but reliable estimates.
Participants in planning poker include all of the developers on the team. Remember that developers refers to all programmers, testers, database engineers, analysts, user interaction designers, and so on. On an agile project, this will typically not exceed ten people. If it does, it is usually best to split into two teams. Each team can then estimate independently, which will keep the size down. The product owner participates in planning poker but does not estimate.
At the start of planning poker, each estimator is given a deck of cards. Each card has written on it one of the valid estimates. Each estimator may, for example, be given a deck of cards that reads 0, 1, 2, 3, 5, 8, 13, 20, 40, and 100. The cards should be prepared prior to the planning poker meeting, and the numbers should be large enough to see across a table. Cards can be saved and used for the next planning poker session.
For each user story or theme to be estimated, a moderator reads the description. The moderator is usually the product owner or an analyst. However, the moderator can be anyone, as there is no special privilege associated with the role. The product owner answers any questions that the estimators have. However, everyone is asked to remain aware of the effort/accuracy curve (Figure 6.1). The goal in planning poker is not to derive an estimate that will withstand all future scrutiny. Rather, the goal is to be somewhere well on the left of the effort line, where a valuable estimate can be arrived at cheaply.
After all questions are answered, each estimator privately selects a card representing his or her estimate. Cards are not shown until each estimator has made a selection. At that time, all cards are simultaneously turned over and shown so that all participants can see each estimate.
It is very likely at this point that the estimates will differ significantly. This is actually good news. If estimates differ, the high and low estimators explain their estimates. It’s important that this does not come across as attacking those estimators. Instead, you want to learn what they were thinking about.
As an example, the high estimator may say, “Well, to test this story, we need to create a mock database object. That might take us a day. Also, I’m not sure if our standard compression algorithm will work, and we may need to write one that is more memory efficient.” The low estimator may respond, “I was thinking we’d store that information in an XML file—that would be easier than a database for us. Also, I didn’t think about having more data—maybe that will be a problem.”
The group can discuss the story and their estimates for a few more minutes. The moderator can take any notes she thinks will be helpful when this story is being programmed and tested. After the discussion, each estimator re-estimates by selecting a card. Cards are once again kept private until everyone has estimated, at which point they are turned over at the same time.
In many cases, the estimates will already converge by the second round. But if they have not, continue to repeat the process. The goal is for the estimators to converge on a single estimate that can be used for the story. It rarely takes more than three rounds, but continue the process as long as estimates are moving closer together. It isn’t necessary that everyone in the room turns over a card with exactly the same estimate written down. If I’m moderating an estimation meeting, and on the second round four estimators tell me 5, 5, 5, and 3, I will ask the low estimator if she is OK with an estimate of 5. Again, the point is not absolute precision but reasonableness.
The Right Amount of Discussion
Some amount of preliminary design discussion is necessary and appropriate when estimating. However, spending too much time on design discussions sends a team too far up the effort/accuracy curve of Figure 6.1. Here’s an effective way to encourage some amount of discussion but make sure that it doesn’t go on too long.
Buy a two-minute sand timer, and place it in the middle of the table where planning poker is being played. Anyone in the meeting can turn the timer over at any time. When the sand runs out (in two minutes), the next round of cards is played. If agreement isn’t reached, the discussion can continue. But someone can immediately turn the timer over, again limiting the discussion to two minutes. The timer rarely needs to be turned over more than twice. Over time this helps teams learn to estimate more rapidly.
Smaller Sessions
It is possible to play planning poker with a subset of the team, rather than involving everyone. This isn’t ideal but may be a reasonable option, especially if there are many, many items to be estimated, as can happen at the start of a new project.
The best way to do this is to split the larger team into two or three smaller teams, each of which must have at least three estimators. It is important that each of the teams estimates consistently. What your team calls three story points or ideal days had better be consistent with what my team calls the same. To achieve this, start all teams together in a joint planning poker session for an hour or so. Have them estimate ten to twenty stories. Then make sure each team has a copy of these stories and their estimates and that they use them as baselines for estimating the stories they are given to estimate.
When to Play Planning Poker
Teams will need to play planning poker at two different times. First, there will usually be an effort to estimate a large number of items before the project officially begins or during its first iterations. Estimating an initial set of user stories may take a team two or three meetings of from one to three hours each. Naturally, this will depend on how many items there are to estimate, the size of the team, and the product owner’s ability to clarify the requirements succinctly.
Second, teams will need to put forth some ongoing effort to estimate any new stories that are identified during an iteration. One way to do this is to plan to hold a very short estimation meeting near the end of each iteration. Normally, this is quite sufficient for estimating any work that came in during the iteration, and it allows new work to be considered in the prioritization of the coming iteration.
Alternatively, Kent Beck suggests hanging an envelope on the wall with all new stories placed in the envelope. As individuals have a few spare minutes, they will grab a story or two from the envelope and estimate them. Teams will establish a rule for themselves, typically that all stories must be estimated by the end of the day or by the end of the iteration. I like the idea of hanging an envelope on the wall to contain unestimated stories. However, I’d prefer that when someone has a few spare minutes to devote to estimating, he find at least one other person and that they estimate jointly.
Why Planning Poker Works
Now that I’ve described planning poker, it’s worth spending a moment on some of the reasons why it works so well.
First, planning poker brings together multiple expert opinions to do the estimating. Because these experts form a cross-functional team from all disciplines on a software project, they are better suited to the estimation task than anyone else. After completing a thorough review of the literature on software estimation, Jørgensen (2004) concluded that “the people most competent in solving the task should estimate it.”
Second, a lively dialogue ensues during planning poker, and estimators are called upon by their peers to justify their estimates. This has been found to improve the accuracy of the estimate, especially on items with large amounts of uncertainty (Hagafors and Brehmer 1983). Being asked to justify estimates has also been shown to result in estimates that better compensate for missing information (Brenner et al. 1996). This is important on an agile project because the user stories being estimated are often intentionally vague.
Third, studies have shown that averaging individual estimates leads to better results (Hoest and Wohlin 1998) as do group discussions of estimates (Jørgensen and Moløkken 2002). Group discussion is the basis of planning poker, and those discussions lead to an averaging of sorts of the individual estimates.
Finally, planning poker works because it’s fun.
Summary
Expending more time and effort to arrive at an estimate does not necessarily increase the accuracy of the estimate. The amount of effort put into an estimate should be determined by the purpose of that estimate. Although it is well known that the best estimates are given by those who will do the work, on an agile team we do not know in advance who will do the work. Therefore, estimating should be a collaborative activity for the team.
Estimates should be on a predefined scale. Features that will be worked on in the near future and that need fairly reliable estimates should be made small enough that they can be estimated on a nonlinear scale from 1 to 10 such as 1, 2, 3, 5, and 8 or 1, 2, 4, and 8. Larger features that will most likely not be implemented in the next few iterations can be left larger and estimated in units such as 13, 20, 40, and 100. Some teams choose to include 0 in their estimation scale.
To arrive at an estimate, we rely on expert opinion, analogy, and disaggregation. A fun and effective way of combining these is planning poker. In planning poker, each estimator is given a deck of cards with a valid estimate shown on each card. A feature is discussed, and each estimator selects the card that represents his or her estimate. All cards are shown at the same time. The estimates are discussed and the process repeated until agreement on the estimate is reached.
Discussion Questions
1. How good are your estimates today? Which techniques do you primarily rely on: expert opinion, analogy, or disaggregation?
2. Which estimation scale do you prefer? Why?
3. Who should participate in planning poker on your project?
