A golf club has a limited number of golf balls available for hire. Players can hire golf balls for their game from the club and return them to the club after use. Expert players, who tend not to lose any of their golf balls, only hire one or two. Novice players hire more balls, so that they have spares during the game in case of loss. However, they are required to buy replacements for lost balls so that they return the same number that they originally hired. To simulate the golf club as a Java program, we create a new thread for each player arriving at the golf club and use a monitor to control the hiring of golf balls to players. The display for the program is shown in Figure 9.1.

Figure 9.1. Golf Club applet display.

New players, with their golf ball requirements indicated in parentheses, are created by clicking the buttons at the bottom of the display. Each newly created player is given a name consisting of a letter, allocated consecutively in alphabetic order, and the number of golf balls the player requires. A newly created player appears briefly in the "new" window and then appears in the "wait golf balls" window if there are not enough golf balls available for the player to start playing. When the player acquires golf balls and starts playing, its identity appears in the "playing" window. When finished playing, the player's identity appears briefly in the "end" window. The "SimpleAllocator" window displays the state of the monitor controlling golf ball allocation. The maximum number of golf balls available is set to five.

Figure 9.1 depicts the situation in which there are currently no golf balls available for hire since all five are in use by players c2, f1, e1 and g1. The novice player d4 who requires four golf balls to start playing is thus waiting. Note that the expert players e1, f1 and g1 were created after d4. They have started playing before d4 since at the time they requested golf balls, there were enough to satisfy their requirements but not enough to satisfy d4. In fact, if we keep creating new expert golfers that only require one or two golf balls, then the novice d4 will continue waiting. A continuous stream of expert players arriving at the golf club can cause novices to wait forever. In other words, the program has a liveness problem in which novice players may experience starvation. Before examining this problem in more detail using a model, we describe the program that drives the display of Figure 9.1. The classes involved are depicted in the UML class diagram of Figure 9.2.

Figure 9.2. Golf Club class diagram.

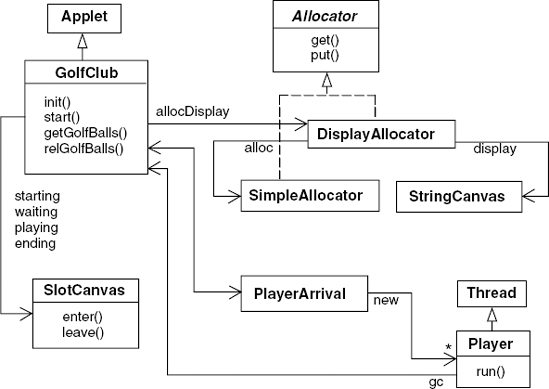
We are going to develop a number of implementations of the golf ball allocator. To allow us to substitute these implementations without modifying the rest of the program, we define the Java interface Allocator as listed in Program 9.1. The DisplayAllocator class implements this interface and delegates calls to get and put golf balls to SimpleAllocator which actually implements the allocation monitor. In addition, DisplayAllocator displays the state of the monitor using the StringCanvas class we have used in previous chapters. The code for the SimpleAllocator monitor is also listed in Program 9.1.

From Program 9.1, it can be seen that a call to get n golf balls will block a calling thread until enough balls become available. When a thread returns golf balls, all blocked threads are awakened so that they can see if there are now sufficient for them to proceed. Notice that this allows a thread trying to get a large number of golf balls to remain blocked while a thread requiring fewer can proceed.

public interface Allocator {
  //get n golf balls
  public void get(int n) throws InterruptedException;
  //put back n golfballs
  public void put(int n);
}

 public class SimpleAllocator implements Allocator {
 private int available;

 public SimpleAllocator(int n)
   { available = n; }

    synchronized public void get(int n)
             throws InterruptedException {
      while (n>available) wait();
      available -= n;
    }

    synchronized public void put(int n) {
      available += n;
      notifyAll();
    }
  }

The PlayerArrival class creates new Player threads in response to button presses. Each newly created thread is passed a reference to the applet class Golf-Club. The thread needs this reference since it calls the golf ball allocator monitor indirectly via the GolfClub methods getGolfBalls() and relGolfBalls(). The program has been organized this way to avoid passing all the display objects to every newly created thread. The code for the Player class is listed in Program 9.2.

Notice that, in contrast to the threads we have defined in previous chapters, the run() method of the Player class does not involve a loop. After it has been started, the player gets the golf balls it requires by calling getGolfBalls(), sleeps for a period of time to simulate playing and then releases the golf balls using relGolfBalls(). The run() method then terminates. Rather than listing the entire code for the class GolfClub, since it is rather lengthy, we have listed below the two methods used by Player:

class Player extends Thread {
  private GolfClub gc;
  private String name;
  private int nballs;

  Player(GolfClub g, int n, String s) {
     gc = g; name = s; nballs =n;
  }

  public void run() {
    try {
      gc.getGolfBalls(nballs,name);
      Thread.sleep(gc.playTime);
      gc.relGolfBalls(nballs,name);
    } catch (InterruptedException e){}
  }
}

void getGolfBalls(int n, String name)
              throws InterruptedException {
       String s = name+n;
       starting.enter(s);
       Thread.sleep(500);
       starting.leave(s);
       waiting.enter(s);
       alloc.get(n);
       waiting.leave(s);
       playing.enter(s);
     }

     void relGolfBalls(int n, String name)
               throws InterruptedException {
       String s = name+n;
       alloc.put(n);
       playing.leave(s);
       ending.enter(s);
       Thread.sleep(500);
       ending.leave(s);
     }

These methods access the allocator monitor using alloc which references the DisplayAllocator object which in turn calls SimpleAllocator as previously explained. The references starting, waiting, playing and ending refer to instances of the SlotCanvas class. This is the first time we have used this display class. An outline of the methods it provides is listed in Program 9.3.

public class SlotCanvas extends Canvas {
  ...
  //create display with slots boxes
  public SlotCanvas
    (String title, Color c, int slots) {...}

  //enter the string name in an empty box
  public synchronized void enter(String name){...}

  //clear the box containing name
  public synchronized void leave(String name) {...}
   ...
}

This completes the description of the golf club program. As discussed previously, it has the problem that novices can wait forever to play while they are continuously overtaken by expert players. In the next section, we investigate a solution to this liveness problem by modeling the golf club.

In modeling the golf club program, we need only be concerned with the player threads and the allocator monitor that embody the concurrent behavior of the golf club. We can abstract away from the details of how the program's display interface is constructed. We first model the allocator monitor and then examine the problem of modeling dynamically created threads. The model for the allocator is listed below:

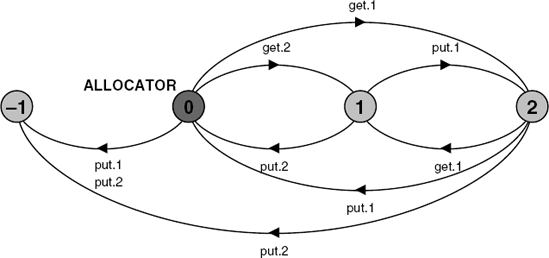
const N=5    //maximum #golf balls
range B=0..N //available range

ALLOCATOR = BALL[N],
BALL[b:B] = (when (b>0) get[i:1..b]->BALL[b-i]
            | put[j:1..N]          ->BALL[b+j]
            ).

Figure 9.3. ALLOCATOR LTS for N = 2.

The ALLOCATOR process initially has N golf balls to allocate. In the state with b golf balls, the process accepts requests for 1..b. In other words, the process blocks requests to get more than b golf balls. The process moves into an ERROR state if more golf balls are put back than were previously requested (i.e. b + j > N). The behavior of ALLOCATOR can be clearly seen in Figure 9.3 where N = 2 to reduce the complexity of the diagram.

How do we model the potentially infinite stream of dynamically created player threads? The straightforward answer is that we cannot since this would involve an infinite state space. However, while we cannot model infinite state spaces, we can model infinite behaviors that are repetitive. In the golf club example, we do not need to model the fact that each player thread is distinct. Instead, we model a fixed population of golfers who continuously repeat the actions involved in playing golf – a situation not too far removed from real life! Effectively, our model constrains the maximum number of golfers who are concurrently trying to play golf. The maximum number of active player threads in the program is only constrained by the available storage. Our model generates an infinite stream of requests from a fixed set of golfers while the program generates a stream of requests with each request originating from a new player.

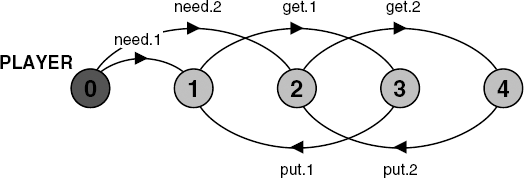
A player is modeled by a process that initially decides the number of golf balls it needs to play golf. Subsequently, the process continuously attempts to get and then put back that number of golf balls. The model for a player process is:

range R=1..N //request range

PLAYER      = (need[b:R]->PLAYER[b]),
PLAYER[b:R] = (get[b]->put[b]->PLAYER[b]).

Figure 9.4. PLAYER LTS for N = 2.

The behavior of PLAYER can be seen in Figure 9.4 where we have again set N = 2 to reduce the complexity of the diagram.

We now need to distinguish between expert players and novices. The difference is, of course, that novices require more golf balls than experts. We define an additional process to constrain the numbers of golf balls requested by both novices and experts. We use named label sets to declare the names of players. Sets of labels were first used explicitly in Chapter 4. FSP also allows named sets to be declared as below:

set Experts = {alice,bob,chris}
set Novices = {dave,eve}
set Players = {Experts,Novices}

FSP does not support sets of sets, simply sets of labels. Consequently, the set named Players is the union of the sets Experts and Novices. With these declarations, we can define the constraint that distinguishes experts from novices as:

HANDICAP =
      ({Novices.{need[3..N]},Experts.need[1..2]}
                -> HANDICAP)
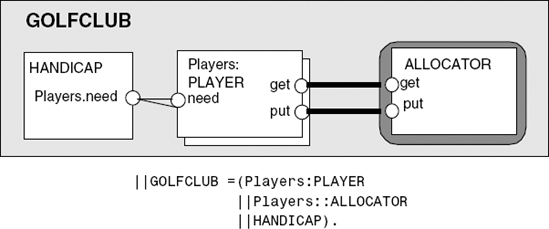
      +{Players.need[R]}.

The alphabet of the process HANDICAP consists of all the need actions that can be performed by all players. However, it only engages in actions in which experts need one or two golf balls and novices need between three and N golf balls. When composed with the PLAYER processes, HANDICAP inhibits these processes from performing any other need actions. The composition of players, allocator and constraint is described in Figure 9.5.

Analysis of the GOLFCLUB model of Figure 9.5 reveals no safety violations. The system is well-behaved in the sense that players return the same number of golf balls they get and consequently the allocator cannot get into the ERROR state. The problem with this system is not safety but liveness. The following progress properties assert for experts and novices that they make progress with respect to getting golf balls.

Figure 9.5. GOLFCLUB composition.

progress NOVICE = {Novices.get[R]}
progress EXPERT = {Experts.get[R]}

Notice that we have not specified any particular number of golf balls. Getting any number satisfies the property. Similarly, we have not specified a specific novice or expert. Consequently, if any novice regularly gets any number of golf balls, the property NOVICE is satisfied and similarly for experts. A progress check against these properties reveals no violations. To reveal the problem that occurred in the program, we must set up adverse scheduling conditions using the technique described in Chapter 7. We make the put action, which releases golf balls, low priority:

||ProgressCheck = GOLFCLUB ≫{Players.put[R]}.

Progress analysis of this system detects a violation of the progress property NOVICE. One of the violating traces produced by the analyzer is listed below:

Progress violation: NOVICE
     Path to terminal set of states:
          alice.need.1
          alice.get.1
          bob.need.1
          bob.get.1
          chris.need.1
          chris.get.1
          dave.need.4
          eve.need.4

Actions in terminal set:
     {alice.get.1, alice.put.1, bob.get.1,
     bob.put.1, chris.get.1, chris.put.1}

This is the situation in which each of the expert players alice, bob and chris needs a single ball and the novices dave and eve need four. The terminal set indicates an infinite execution, in which the experts repeatedly get and put the golf balls they need. However, novices do not get access because the situation does not occur in which two experts put their golf balls without an intermediate get. Consequently, the allocator never has four golf balls to give to a novice. As in the Java program, experts continuously overtake novices and consequently, the novices make no progress.

Having successfully detected the liveness problem in the model, the next step is to look at ways of solving the problem and to check that they work correctly in the model. We can then change the program to reflect the updated model. In the model, we could simply increase the number of golf balls with which the allocator is initialized. Since we have a fixed population of golfers, we can easily increase the number such that there is no contention. This would not be a general solution since it would always be possible for expert players to arrive at a faster rate and, as a result, novices would starve. Instead, we arrange it such that players wait in an orderly line for golf balls such that experts cannot overtake novices.

Rather than make players line up in first-in-first-out (FIFO) order, we use a ticketing scheme. New tickets are generated in ascending numerical order. Players take a new ticket from a dispenser when they arrive at the golf club and they are subsequently served with golf balls in ticket order. In the model, we do not require an infinite number of tickets since, as long as we have at least as many tickets as players, we can restart the numbering sequence when the last ticket has been handed out.

The ticket dispenser is modeled by the following process:

const TM = 5    // maximum ticket
range T = 1..TM // ticket values

TICKET    = NEXT[1],
NEXT[t:T] = (ticket[t]->NEXT[t%TM+1]).

We must modify the PLAYER process to get tickets and modify the ALLOCATOR to only accept requests in ticket order. The modified processes are shown below.

PLAYER     = (need[b:R]->PLAYER[b]),
     PLAYER[b:R]= (ticket[t:T]
                   ->get[b][t]->put[b]->PLAYER[b]).

     ALLOCATOR      = BALL[N][1],
     BALL[b:B][t:T] =
       (when (b>0) get[i:1..b][t]->BALL[b-i][t%TM+1]
       |put[j:1..N]              ->BALL[b+j][t]
       ).

The revised PLAYER process requests a ticket and uses it when requesting golf balls i.e. get[b][t]. The revised ALLOCATOR accepts get actions in ticket order starting with ticket number 1. The ticket scheme increases the size of the model considerably. To compensate for the increase, we modify the HANDICAP constraint such that expert players always request a single golf ball and novices request four:

HANDICAP =
          ({Novices.{need[4]},Experts.need[1]}
                -> HANDICAP)
          +{Players.need[R]}.

The golf club system is now modeled as follows:

||GOLFCLUB =(Players:PLAYER
                  ||Players::(ALLOCATOR||TICKET)
                  ||HANDICAP
                  ).

To analyze progress for this system, the progress properties must be slightly revised to take into account the addition of the ticket value in the get action.

progress NOVICE = {Novices.get[R][T]}
progress EXPERT = {Experts.get[R][T]}

Using ProgressCheck, as defined before, no progress violations are detected. The next section discusses the implementation of the revised allocator.

Fortunately, we can encapsulate the ticketing scheme described in the previous section in a revised implementation of the allocator monitor. Other than using this revised implementation in place of SimpleAllocator, no otherchanges are required to the program. The new implementation, called FairAllocator, is listed in Program 9.4.

public class FairAllocator implements Allocator {
  private int available;
  private long turn = 0; //next ticket to be dispensed
  private long next = 0; //next ticket to be served

  public FairAllocator(int n) { available = n; }

  synchronized public void get(int n)
          throws InterruptedException {
    long myturn = turn; ++turn;
    while (n>available ||  myturn != next) wait();
    ++next; available -= n;
    notifyAll();
  }

  synchronized public void put(int n) {
    available += n;
    notifyAll();
  }
}

We have added two instance variables to implement the ticketing scheme: next records the value of the next ticket to be served, and turn records the value of the next ticket to be dispensed. A thread gets a ticket by recording it in the local variable myturn. Remember that each time a thread calls the method get, a new activation record is created. Consequently, a new copy of myturn is also created which is only used by the calling thread. A thread is now blocked until there are sufficient golf balls and its ticket is the next one to be served. To keep the code simple, we have not dealt with resetting the ticket when the maximum ticket value is reached. However, by using 64-bit ticket values, we have ensured that, with a player arrival rate of one per second, the program will run for 300 billion years before ticket overflow becomes a problem!

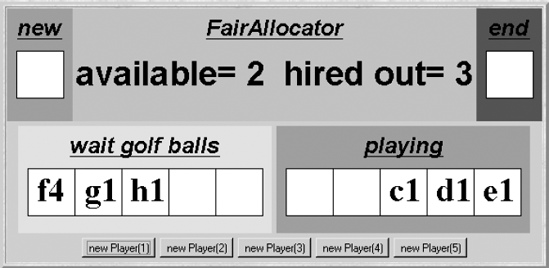
Figure 9.6 shows a screen dump of the revised golf club applet. The changed behavior can clearly be seen. Although two golf balls are available, players g1 and h1 are waiting because they cannot overtake f4 due to the FIFO ordering enforced by the ticketing scheme.

The ticketing scheme ensures that starvation does not occur. However, it does not use the available golf ball resources efficiently. Expert players are kept waiting by novices even though the golf balls they require are available. A modified scheme allows experts to overtake novices but denies starvation by setting an upper bound on the number of times a novice can be overtaken. Once that bound is reached, the novice can no longer be overtaken by an expert and must receive his/her allocation next.

Figure 9.6. Golf Club applet with fair allocation.

The allocator algorithm for bounded overtaking was implemented but not modeled in the first edition of this book. One of our insightful readers pointed out that adverse scheduling by the Java Virtual Machine could result in the bound being violated. The lesson is clear: models are essential in helping to eliminate errors. Below is a new algorithm which has been carefully modeled to support analysis.

In the algorithm, we need to keep track of those players who have overtaken others. This can be modeled as a set, as shown below. Elements of the set are of type T and can be added, removed and checked for set membership. The set is modeled as the parallel composition of elements which preserve the property that an element is only added if it is not already a member of the set, and only removed if it is a member.

const False = 0
const True  = 1
range Bool  = 0..1

ELEMENT(Id=0) = IN[False],
IN[b:Bool]  = ( add[Id]         -> IN[True]
              | remove[Id]      -> IN[False]

| contains[Id][b] -> IN[b]
              ).

       property
         ONEADD(Id=0) = (add[Id]->remove[Id]->ONEADD).

       ||SET = (forall[i:T] (ELEMENT(i) ||  ONEADD(i))).

We model bounded overtaking using tickets as in the fair FIFO allocator, where ticket numbers are used to indicate the order in which players make their requests. The allocator records which ticket number is next. Overtaking occurs when we allocate balls to a player whose turn – indicated by his/her ticket number – is subsequent to a waiting player with the next ticket. The overtaking player is added to the overtaking set, and a count ot is incremented to indicate the number of times next has been overtaken. When the count equals the bound, we allow allocation to the next player only. When allocation is made to the next player, we need to update next to indicate the next (waiting) player. We skip the ticket numbers of those overtaking players who have already received their allocation, remove each of these intervening players from the overtaking set and decrement the overtaking count accordingly. This is achieved in the local process, WHILE, in the ALLOCATOR given below. Note that the maximum ticket value must not be less than the sum of the number of players and the bound so as to avoid ambiguity when the sequence of ticket numbers restarts.

const N  =  5     // maximum #golf balls
const Bd =  2     // bound on overtaking
range B  =  0..N  // available range

const TM = 5 + Bd // maximum ticket
range T  = 1..TM  // ticket values

TICKET    = TURN[1],
TURN[t:T] = (ticket[t]->TURN[t%TM+1]).

ALLOCATOR  = BALL[N][1][0],
BALL[b:B][next:T][ot:0..Bd] =
    (when (b>0 && ot<Bd) get[i:1..b][turn:T] ->
         if (turn!=next) then
            (add[turn] -> BALL[b-i][next][ot+1])

else
                     WHILE[b-i][next%TM+1][ot]
            |when (b>0 && ot==Bd) get[i:1..b][next] ->
                    WHILE[b-i][next%TM+1][ot]
            |put[j:1..N] -> BALL[b+j][next][ot]
            ),
       WHILE[b:B][next:T][ot:0..Bd] =
            (contains[next][yes:Bool] ->
                 if (yes) then
                 (remove[next] ->
                      WHILE[b][next%TM+1][ot-1])
                 else
                      BALL[b][next][ot]
            )+{add[T],remove[T]}.

The golf club system is now modeled as follows:

||GOLFCLUB = (Players:PLAYER
                   || ALLOCATOR||TICKET||SET
                   || HANDICAP
                   )/ {Players.get/get,
                      Players.put/put,
                      Players.ticket/ticket}.

Using ProgressCheck, as defined before, no progress violations are detected for this bounded overtaking golf club. Using animation, we can step through to produce a trace which illustrates the bounded allocation algorithm:

eve.need.4          Novices Eve and Dave
       dave.need.4
       chris.need.1        Experts Alice, Bob and Chris
       alice.need.1
       bob.need.1
       alice.ticket.1
       alice.get.1.1       Alice gets 1 ball, ticket 1
       contains.2.0        Ticket 2 is next
       bob.ticket.2
       bob.get.1.2         Two allocated, three available
       contains.3.0        Ticket 3 is next
       dave.ticket.3       Dave needs four balls: waits
       chris.ticket.4
       chris.get.1.4       Chris overtakes

add.4
       eve.ticket.5        Eve needs four balls: waits
       alice.put.1
       alice.ticket.6
       alice.get.1.6       Alice overtakes
       add.6
       bob.put.1
       bob.ticket.7
       bob.get.1.7         Bob overtakes: bound reached
       add.7
       chris.put.1
       chris.ticket.8      Chris waits: three available
       alice.put.1
       alice.ticket.1      Alice waits: four available
       dave.get.4.3        Dave gets four balls
       contains.4.1        remove intervening overtaker
       remove.4
       contains.5.0        Ticket 5 (Eve) is next
       dave.put.4
       dave.ticket.2
       alice.get.1.1       Alice overtakes: bound reached
       add.1
       bob.put.1
       bob.ticket.3
       eve.get.4.5         Eve gets four balls
       contains.6.1        remove intervening overtakers
       remove.6
       contains.7.1
       remove.7
       contains.8.0        Ticket 8 (Chris) is next
       ...

We can easily add a safety property BALLS to check that players return the same number of balls as allocated. This is shown below.

property
   BALLS = BALLS[N],
   BALLS[b:0..N] =
     (when b>0
          Players.get[i:1..b][turn:T] -> BALLS[b-i]
     |Players.put[j:1..N] -> BALLS[b+j]
     ).

Can we also specify the bounded nature of this allocator as a safety property? This requires more ingenuity in which we check, for each player, that he/she is not overtaken more than bound times. Overtaking is indicated by an allocation to another player whose ticket t lies between the turn of the player and the latest ticket issued.

property
   BOUND(P='alice) =
     ({Players {[P]}}.ticket[T] -> BOUND
     |[P].ticket[t:T]  -> WAITING[t][t][0]
     |[Players].get[R][T]       -> BOUND
    ),
   WAITING[turn:T][latest:T][overtaken:0..Bd] =
     ([P].get[b:R][turn] -> BOUND
     |{Players{[P]}}.get[b:R][t:T] ->
          if ((t>turn && (t<=latest ||  latest<turn))
            || (t<turn && (t<=latest && latest<turn)))
              then WAITING[turn][latest][overtaken+1]
              else WAITING[turn][latest][overtaken]
     |Players.ticket[last:T] ->
                WAITING[turn][last][overtaken]
     ).

The golf club system is now modeled as below, where the property is checked for all players. This is a large model of over 4 million states and 10 million transitions. No safety (or progress) violations are found for CHECKGOLFCLUB.

||CHECKGOLFCLUB = (GOLFCLUB
                         || BALLS
                         || forall [p:Players] BOUND(p)
                         ).

However, if we check for an overtaken bound of 2 in the property BOUND and leave the allocator with Bd set to 3, then we quickly get the violation below in which Alice is overtaken three times, twice by Bob and once by Chris. This confirms that the property BOUND does indeed detect violations in the overtaking bound.

Trace to property violation in BOUND(alice):
        alice.need.1
        alice.ticket.1
        bob.need.1

bob.ticket.2
        bob.get.1.2
        chris.need.1
        chris.ticket.3
        add.2
        bob.put.1
        bob.ticket.4
        bob.get.1.4
        add.4
        chris.get.1.3

Bounded overtaking is implemented in the allocator of Program 9.5. The program follows the algorithm used in our model. Each thread waits if there are insufficient balls available or if the bound has been reached and the player is not next. Overtaking players are added to the overtakers set and removed as necessary when next is updated; the count of those overtaken is incremented and decremented on addition and removal respectively.

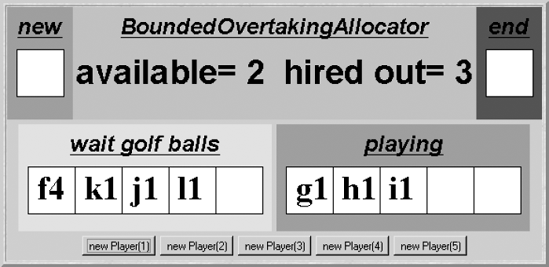
The operation of the bounded overtaking allocator can be seen in the applet display shown in Figure 9.7. This captures the situation in which player f4 has been overtaken by players g1, h1 and i1. Since the overtaking bound, which has been set to three, has been exceeded, players j1 and k1 are blocked although there are two golf balls available. They will remain blocked until f4 has been served.

Figure 9.7. Golf Club with bounded overtaking allocator (bound = 3).

public class BoundedOvertakingAllocator
                     implements Allocator{
  private int TM;
     //must be maximum active threads + bound
  private int available;
  private int bound;
  private int turn = 1;
  private int next = 1;
  private int overtaken =0;
  private BitSet overtakers;

  public BoundedOvertakingAllocator(int n, int b)
    { available = n; bound = b; TM = 10000+b;
      overtakers = new BitSet(TM+1);}

  synchronized public void get(int n)
          throws InterruptedException{
    int myturn = turn; turn = turn%TM + 1;
    while (n>available ||
          (myturn!=next && overtaken>=bound)) {
      wait();
      }
       if (myturn!=next)  {
            overtakers.set(myturn); ++overtaken;
       }
       else  {
            next =  next%TM + 1;
            while (overtakers.get(next)) {
                 overtakers.clear(next);
                 --overtaken;
                 next =  next%TM + 1;
            }
       }
      available -= n;
      notifyAll();
    }

    synchronized public void put(int n) {
      available += n;
      notifyAll();
    }
  }

In the golf club example, when a player thread finished playing and returned its golf balls, it simply terminated. In some concurrent programming situations, we may want to determine a result that is computed by a dynamically created thread. Usually, a slave thread is created to perform some input/output (I/O) activity while the master thread that created it continues with some other activity. At some point, the master must synchronize with the slave to retrieve the result of the I/O activity. This master–slave arrangement is frequently used to allow the master thread to continue executing while the slave waits for a remote communication to complete. When the remote communication completes, the slave thread terminates and the master must obtain the result of the remote communication. We could use a monitor to allow the slave to signal when it is about to terminate. Alternatively, the master could continuously test the status of the slave thread using the isAlive() method. This method returns false when the thread to which it is applied terminates. However, this busy wait would consume CPU cycles that could be put to better use by another thread. To avoid this busy wait, the Java Thread class provides a method to allow one thread to await the termination of another:

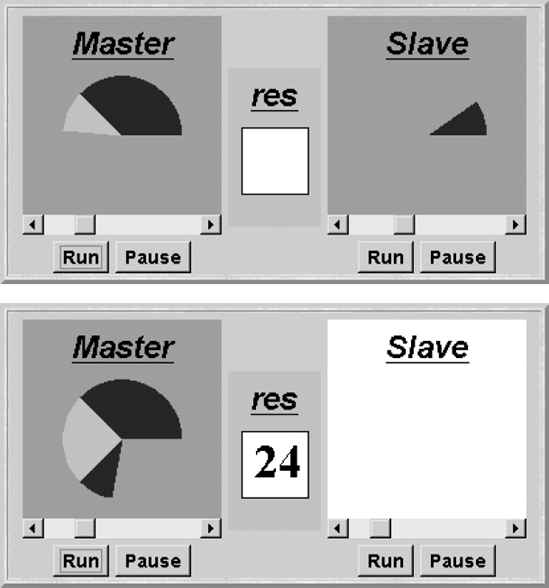
Figure 9.8 is the display of an applet that demonstrates the operation of join(). The upper display shows the master executing concurrently with the slave. The slave was created at the point the master's segment changed color. The bottom display shows the point at which the slave has terminated and the master has obtained the result of its computation. In the demonstration, the result is the amount the slave rotates its display before terminating. The amount of slave rotation can be adjusted by the slider control positioned below its rotating segment. The amount that the master rotates before waiting for the slave to terminate is adjusted using the other slider.

By adjusting the sliders, it is possible to arrange for the master to wait for the slave to terminate or for the slave to terminate before the master gets the result. Thecodeforboth Master and Slave threads is depicted in Program 9.6.

The Slave thread is created and started using the start() method provided by ThreadPanel. This returns a reference to the new thread. The result is obtained from the Slave thread by calling the result() method after the Slave thread has terminated. Note that result() need not be synchronized since, as long as it is only called after termination, there can be no interference between Master and Slave threads.

Figure 9.8. join() demonstration applet.

We can construct a satisfactory model of the master–slave program by observing that, although it creates a sequence of new slave processes, only a single slave thread is active at any one time. Consequently, we use a single slave process, which after it terminates, immediately becomes available to be started again:

SLAVE = (start->rotate->join->SLAVE).

class Master implements Runnable {
    ThreadPanel slaveDisplay;
    SlotCanvas resultDisplay;

    Master(ThreadPanel tp, SlotCanvas sc)
      {slaveDisplay=tp; resultDisplay=sc;}

    public void run() {
      try {
        String res=null;
        while(true) {
          while (!ThreadPanel.rotate());
          if (res!=null) resultDisplay.leave(res);
          // create new slave thread
          Slave s = new Slave();
          Thread st = slaveDisplay.start(s,false);
          // continue execution
          while (ThreadPanel.rotate());
          // wait for slave termination
          st.join();
          // get and display result from slave
          res = String.valueOf(s.result());
          resultDisplay.enter(res);
        }
      } catch (InterruptedException e){}
    }
  }

  class Slave implements Runnable {
    int rotations = 0;

   public void run() {
     try {
       while (!ThreadPanel.rotate()) ++rotations;
     } catch (InterruptedException e){}
   }

   int result(){
      return rotations;
    }
  }

The master thread is modeled by the following process:

MASTER = (slave.start->rotate
              ->slave.join->rotate->MASTER).

The master–slave program can now be modeled as the composition:

||MASTER_SLAVE = (MASTER || slave:SLAVE).

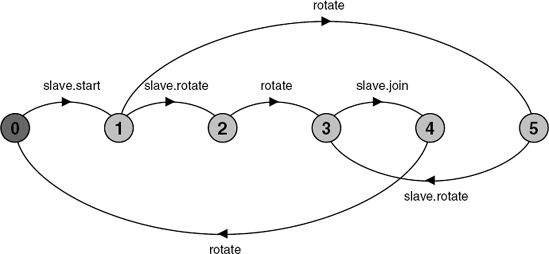
The behavior of this model is depicted in the LTS of Figure 9.9.

Figure 9.9. MASTER_SLAVE LTS.

From the LTS, it can be seen that the slave rotation action, slave.rotate, and the master rotation action, rotate, are concurrent since they can occur in any order. However, after the slave.join action only the master rotation action can take place, as in the applet. The model can easily be generalized to a system in which two or more slave processes are active concurrently.

In this chapter, we have looked at programs in which threads both start and terminate dynamically during program execution. We have shown that it is possible to construct satisfactory finite state models for this sort of program by using a static population of processes with cyclic behavior. The model fixes the maximum number of concurrently active processes while concurrent thread activation in the program is only limited by available storage. We regard a model as satisfactory if it exhibits the same behavior as the program it is modeling with respect to safety and liveness properties. We were able to use the golf club model to investigate and correct a liveness problem and subsequently to implement that correction in the program.

The main example concerned a resource allocator that managed a pool of identical reusable resources. Threads competed for access to these resources. In our example, the resources were golf balls. In computing systems, this form of allocation is required for resources such as memory pages and message buffers.

The results of this chapter show that the models we constructed in previous chapters for resource access also apply to programs in which threads are created dynamically. For example, the Readers–Writers program of Chapter 7 had a fixed number of Reader and Writer threads with cyclic behavior. However, the monitor that controlled read/write access would work equally well in a program with a dynamically varying number of Reader and Writer threads.

Finally, this chapter demonstrated the use of the Java join() method which allows one thread to await the termination of another. The example was a master–slave arrangement in which the master thread obtained the result of the slave computation.

One of the first proposals for thread creation was the fork L command, which transfers control to the statement labeled L and also allows control to pass to the statement after fork. In this way, two concurrently executing threads of control are created. A join command was provided to allow the two threads to rejoin execution. The first thread to reach join blocks until the second thread also executes the command. Only a single thread executes after the join. Unstructured use of fork and join leads to extremely complex multi-threaded programs. The UNIX operating system has a version of the fork command with no label. The fork operating system call creates a complete copy of the calling process and starts it executing. The fork call returns a result, which lets a process determine whether it is the parent or child.

To resolve the problems caused by unstructured use of fork and join, Dijkstra (1965) proposed what later became the cobegin..coend construct:

P and Q are executed concurrently as separate threads until both have terminated. The construct can easily be generalized to more than two threads. It was proposed for use in block-structured languages such as Algol. In these languages, the main structuring tools are procedures and procedure activations rather than classes and objects. Storage for procedure activations is managed as a stack in these languages and the addition of threads created using the cobegin..coend construct requires a tree of stacks, sometimes called a "cactus" stack.

The Java thread model does not enforce this degree of structure on thread execution. A thread can continue executing after the thread that created it has terminated. This is more appropriate in an object-oriented language where we are generally less concerned with the lifetime of objects. Storage is managed by a heap structure. Objects exist until they are garbage collected and threads exist until they terminate, at which point their storage can also be garbage collected. Java provides the ThreadGroup class to manage collections of threads and to enforce security policies by dynamically restricting access to Thread operations. For example, a thread may only stop() another thread if both are in the same group. By default, each thread is created in the same ThreadGroup as its creator. We have been able to ignore ThreadGroups in the examples since all threads are created in the default group provided by browsers for applet execution.

In this chapter, we have dealt with programs where dynamic thread creation and termination can be modeled by a fixed set of cyclic processes. The more general problem is to model programs in which the configuration of threads and monitors evolves as execution proceeds. For this sort of program, using FSP, each configuration must be enumerated. The program can then be modeled as the composition of its possible configurations. To address the problem of describing concurrent systems in which configuration changes dynamically, Robin Milner introduced the π-calculus (Milner, Parrow and Walker, 1992). This permits an elegant and concise description of dynamic systems. However, in general, these π-calculus descriptions are not amenable to the form of state exploration analysis that we use for FSP descriptions.

The idea of bounded delays to provide a class of resource allocation strategies is due to Dijkstra (1972a). These strategies can be characterized as satisfying a set of safe scheduling rules for resource allocation to a fixed pool of m processes from a pool of n reusable resources:

The first two rules avoid resource starvation for an individual process and the third rule preserves resource integrity. Allocation from a pool of reusable resources was used as an exercise in rigorous program design at Imperial College in the late 1970s. Students were required to design, verify and implement a resource allocator in SIMULA (Birtwistle, Dahl, Myhrhaug, et al., 1973). The rules were used by Cunningham and Kramer (1978) as an invariant to guide the development and verification of the program. Rule two was subsequently modified as follows to permit simpler implementations and to cater for dynamic systems where there is no bound on the number of processes (Kramer and Cunningham, 1979):

The golf club problem and the particular formulation described in this book evolved from that experience.

We are grateful to Alexander Höher for his insight into potential problems with the implementation given in the first edition of this book.