CHAPTER 22

Key-Exchange Algorithms

22.1 DIFFIE-HELLMAN

Diffie-Hellman was the first public-key algorithm ever invented, way back in 1976 [496]. It gets its security from the difficulty of calculating discrete logarithms in a finite field, as compared with the ease of calculating exponentiation in the same field. Diffie-Hellman can be used for key distribution—Alice and Bob can use this algorithm to generate a secret key—but it cannot be used to encrypt and decrypt messages.

The math is simple. First, Alice and Bob agree on a large prime, n and g, such that g is primitive mod n. These two integers don't have to be secret; Alice and Bob can agree to them over some insecure channel. They can even be common among a group of users. It doesn't matter.

Then, the protocol goes as follows:

1. (1) Alice chooses a random large integer x and sends Bob

   

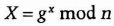
2. (2) Bob chooses a random large integer y and sends Alice

   

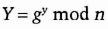
3. (3) Alice computes

   

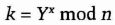
4. (4) Bob computes

   

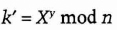
Both k and k are equal to g^xy mod n. No one listening on the channel can compute that value; they only know n, g, X, and Y. Unless they can compute the discrete logarithm and recover x or y, they do not solve the problem. So, k is the secret key that both Alice and Bob computed independently.

The choice of g and n can have a substantial impact on the security of this system. The number (n - 1)/2 should also be a prime [1253]. And most important, n should be large: The security of the system is based on the difficulty of factoring numbers the same size as n. You can choose any g, such that g is primitive mod n; there's no reason not to choose the smallest g you can—generally a one-digit number. (And actually, g does not have to be primitive; it just has to generate a large subgroup of the multiplicitive group mod n.)

Diffie-Hellman with Three or More Parties

The Diffie-Hellman key-exchange protocol can easily be extended to work with three or more people. In this example, Alice, Bob, and Carol together generate a secret key.

1. (1) Alice chooses a random large integer x and sends Bob

   

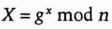
2. (2) Bob chooses a random large integer y and sends Carol

   

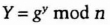
3. (3) Carol chooses a random large integer z and sends Alice

   

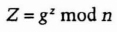
4. (4) Alice sends Bob

   

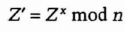
5. (5) Bob sends Carol

   

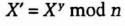
6. (6) Carol sends Alice

   

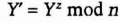
7. (7) Alice computes

   

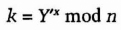
8. (8) Bob computes

   

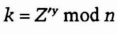
9. (9) Carol computes

   

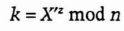
The secret key, k, is equal to g^xyz mod n, and no one else listening in on the communications can compute that value. The protocol can be easily extended to four or more people; just add more people and more rounds of computation.

Extended Diffie-Hellman

Diffie-Hellman also works in commutitive rings [1253]. Z. Shmuley and Kevin McCurley studied a variant of the algorithm where the modulus is a composite number [1442,1038]. V. S. Miller and Neal Koblitz extended this algorithm to elliptic curves [1095,867]. Taher ElGamal used the basic idea to develop an encryption and digital signature algorithm (see Section 19.6).

This algorithm also works in the Galois field GF(2^k) [1442,1038]. Some implementations take this approach [884,1631,1632], because the computation is much quicker. Similarly, cryptanalytic computation is equally fast, so it is important to carefully choose a field large enough to ensure security.

Hughes

This variant of Diffie-Hellman allows Alice to generate a key and send it to Bob [745].

1. (1) Alice chooses a random large integer x and generates

   

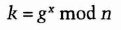
2. (2) Bob chooses a random large integer y and sends Alice

   

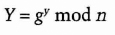
3. (3) Alice sends Bob

   

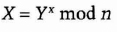
4. (4) Bob computes

   

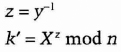
If everything goes correctly, k = k′.

The advantage of this protocol over Diffie-Hellman is that k can be computed before any interaction, and Alice can encrypt a message using k prior to contacting Bob. She can send it to a variety of people and interact with them to exchange the key individually later.

Key Exchange without Exchanging Keys

If you have a community of users, each could publish a public key, X = g^x mod n, in a common database. If Alice wants to communicate with Bob, she just has to retrieve Bob's public key and generate their shared secret key. She could then encrypt a message with that key and send it to Bob. Bob would retrieve Alice's public key to generate the shared secret key.

Each pair of users would have a unique secret key, and no prior communication between users is required. The public keys have to be certified to prevent spoofing attacks and should be changed regularly, but otherwise this is a pretty clever idea.

Patents

The Diffie-Hellman key-exchange algorithm is patented in the United States [718] and Canada [719]. A group called Public Key Partners (PKP) licenses the patent, along with other public-key cryptography patents (see Section 25.5). The U.S. patent will expire on April 29, 1997.

22.2 STATION-TO-STATION PROTOCOL

Diffie-Hellman key exchange is vulnerable to a man-in-the-middle attack. One way to prevent this problem is to have Alice and Bob sign their messages to each other [500].

This protocol assumes that Alice has a certificate with Bob's public key and that Bob has a certificate with Alice's public key. These certificates have been signed by some trusted authority outside this protocol. Here's how Alice and Bob generate a secret key, k.

1. (1) Alice generates a random number, x, and sends it to Bob.
2. (2) Bob generates a random number, y. Using the Diffie-Hellman protocol he computes their shared key based on x and y: k. He signs x and y, and encrypts the signature using k. He then sends that, along with y, to Alice.

   

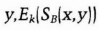
3. (3) Alice also computes k. She decrypts the rest of Bob's message and verifies his signature. Then she sends Bob a signed message consisting of x and y, encrypted in their shared key.

   

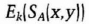
4. (4) Bob decrypts the message and verifies Alice's signature.

22.3 SHAMIR'S THREE-PASS PROTOCOL

This protocol, invented by Adi Shamir but never published, enables Alice and Bob to communicate securely without any advance exchange of either secret keys or public keys [1008].

This assumes the existence of a symmetric cipher that is commutative, that is:

Alice's secret key is A; Bob's secret key is B. Alice wants to send a message, M, to Bob. Here's the protocol.

1. (1) Alice encrypts M with her key and sends Bob

   

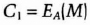
2. (2) Bob encrypts C₁ with his key and sends Alice

   

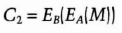
3. (3)Alice decrypts C₂ with her key and sends Bob

   

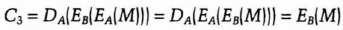
4. (4) Bob decrypts C₃ with his key to recover M.

One-time pads are commutative and have perfect secrecy, but they will not work with this protocol. With a one-time pad, the three ciphertext messages would be:

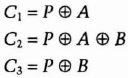
Eve, who can record the three messages as they pass between Alice and Bob, simply XORs them together to retrieve the message:

This clearly won't work.

Shamir (and independently, Jim Omura) described an encryption algorithm that will work with this protocol, one similar to RSA. Let p be a large prime for which p - 1 has a large prime factor. Choose an encryption key, e, such that e is relatively prime to p - 1. Calculate d such that de ≡ 1 (mod p - 1).

To encrypt a message, calculate

To decrypt a message, calculate

There seems to be no way for Eve to recover M without solving the discrete logarithm problem, but this has never been proved.

Like Diffie-Hellman, this protocol allows Alice to initiate secure communication with Bob without knowing any of his keys. For Alice to use a public-key algorithm, she has to know his public key. With Shamir's three-pass protocol, she just sends him a ciphertext message. The same thing with a public-key algorithm looks like:

1. (1) Alice asks Bob (or a KDC) for his public key.
2. (2) Bob (or the KDC) sends Alice his public key.
3. (3) Alice encrypts M with Bob's public key and sends it to Bob.

Shamir's three-pass protocol will fall to a man-in-the-middle attack.

22.4 COMSET

COMSET (COMmunications SETup) is a mutual identification and key exchange protocol developed for the RIPE project [1305] (see Section 25.7). Using public-key cryptography, it allows Alice and Bob to identify themselves to each other and also to exchange a secret key.

The mathematical principle behind COMSET is Rabin's scheme [1283] (see Section 19.5). The scheme itself was originally proposed in [224]. See [1305] for details.

22.5 ENCRYPTED KEY EXCHANGE

The Encrypted Key Exchange (EKE) protocol was designed by Steve Bellovin and Michael Merritt [109]. It provides security and authentication on computer networks, using both symmetric and public-key cryptography in a novel way: A shared secret key is used to encrypt a randomly generated public key.

The Basic EKE Protocol

Alice and Bob (two users, a user and the host, or whoever) share a common password, P. Using this protocol, they can authenticate each other and generate a common session key, K.

1. (1) Alice generates a random public-key/private-key key pair. She encrypts the public key, K′, using a symmetric algorithm and P as the key: E_p(K′). She sends Bob

   

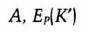
2. (2) Bob knows P. He decrypts the message to obtain K′. Then, he generates a random session key, K, and encrypts it with the public key he received from Alice and P as the key. He sends Alice

   

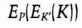
3. (3) Alice decrypts the message to obtain K. She generates a random string, R_A, encrypts it with K, and sends Bob

   

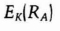
4. (4) Bob decrypts the message to obtain R_A. He generates another random string, R_B, encrypts both strings with K, and sends Alice the result.

   

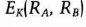
5. Alice decrypts the message to obtain R_A and R_B. Assuming the R_A she received from Bob is the same as the one she sent to Bob in step (3), she encrypts R_B with K and sends it to Bob.

   

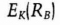
6. Bob decrypts the message to obtain R_B. Assuming the R_B he received from Alice is the same one he sent to Alice in step (4), the protocol is complete. Both parties now communicate using K as the session key.

At step (3), both Alice and Bob know K and K. K is the session key and can be used to encrypt all other messages between Alice and Bob. Eve, sitting between Alice and Bob, only knows EP(K), E_P(E_K(K)), and some messages encrypted with K. In other protocols, Eve could make guesses at P (people choose bad passwords all the time, and if Eve is clever she can make some good guesses) and then test her guesses. In this protocol, Eve cannot test her guess without cracking the public-key algorithm as well. And if both K and K are chosen randomly, this can be an insurmountable problem.

The challenge-response portion of the protocol, steps (3) through (6), provides validation. Steps (3) through (5) prove to Alice that Bob knows K; steps (4) through (6) prove to Bob that Alice knows K. The Kerberos protocol timestamp exchange accomplishes the same thing.

EKE can be implemented with a variety of public-key algorithms: RSA, ElGamal, Diffie-Hellman. There are security problems with implementing EKE with a knapsack algorithm (aside from the inherent insecurity of knapsack algorithms): The normal distribution of the ciphertext messages negates the benefits of EKE.

Implementing EKE with RSA

The RSA algorithm seems perfect for this application, but there are some subtle problems. The authors recommend encrypting only the encryption exponent in step (1) and sending the modulus in the clear. An explanation of the reasoning behind this recommendation, as well as other subtleties involved in using RSA, is in [109].

Implementing EKE with ElGamal

Implementing EKE with the ElGamal algorithm is straightforward, and there is even a simplification of the basic protocol. Using the notation from Section 19.6, g and p are parts of the public key and are common to all users. The private key is a random number r. The public key is g^r mod p. The message Alice sends to Bob in step (1) becomes

Note that this public key does not have to be encrypted with P. This is not true in general, but it is true for the ElGamal algorithm. Details are in [109].

Bob chooses a random number, R (for the ElGamal algorithm and independent of any random numbers chosen for EKE), and the message he sends to Alice in step (2) becomes

Refer back to Section 19.6 for restrictions on choosing the variables for ElGamal.

Implementing EKE with Diffie-Hellman

With the Diffie-Hellman protocol, K is generated automatically. The final protocol is even simpler. A value for g and n is set for all users on the network.

1. (1) Alice picks a random number, r_A, and sends Bob

   

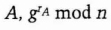
   With Diffie-Hellman, Alice does not have to encrypt her first message with P.

2. (2) Bob picks a random number, r_B, and calculates

   

   He generates a random string R_B, then calculates and sends Alice:

   

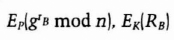
3. (3) Alice decrypts the first half of Bob's message to obtain g^rB mod n. Then she calculates K and uses K to decrypt R_B. She generates another random string, R_A, encrypts both strings with K, and sends Bob the result.

   

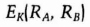
4. (4) Bob decrypts the message to obtain R_A and R_B. Assuming the R_B he received from Alice is the same as the one he sent to Alice in step (2), he encrypts R_A with K and sends it to Alice.

   

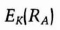
5. (5) Alice decrypts the message to maintain R_A. Assuming the R_A she received from Bob is the same as the one she sent to Bob in step (3), the protocol is complete. Both parties now communicate using K as the session key.

Strengthening EKE

Bellovin and Merritt suggest an enhancement of the challenge-and-response portion of the protocol—to prevent a possible attack if a cryptanalyst recovers an old K value.

Look at the basic EKE protocol. In step (3), Alice generates another random number, S_A, and sends Bob

In step (4), Bob generates another random number, SB, and sends Alice

Alice and Bob now can both calculate the true session key, S_A ' S_B. This key is used for all future messages between Alice and Bob; K is just used as a key-exchange key.

Look at the levels of protection EKE provides. A recovered value of S gives Eve no information about P, because P is never used to encrypt anything that leads directly to S. A cryptanalytic attack on K is also not feasible; K is used only to encrypt random data, and S is never encrypted alone.

Augmented EKE

The EKE protocol suffers from one serious disadvantage: It requires that both parties possess the P. Most password-based authentication systems store a one-way hash of the user's password, not the password itself (see Section 3.2). The Augmented EKE (A-EKE) protocol uses a one-way hash of the user's password as the superencryption key in the Diffie-Hellman variant of EKE. The user then sends an extra message based on the original password; this message authenticates the newly chosen session key.

Here's how it works. As usual, Alice and Bob want to authenticate each other and generate a common key. They agree on some digital signature scheme where any number can serve as the private key, and where the public key is derived from the private key, rather than being generated along with it. The ElGamal and DSA algorithms work well for this. Alice's password P (or perhaps some simple hash of it) will serve as the private key and as P.

1. (1) Alice picks her random exponent R_a and transmits

   

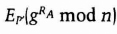
2. (2) Bob, who knows only P′ and cannot derive P from it, chooses R_b and sends

   

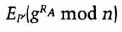
3. (3) Both Alice and Bob calculate the shared session key K = g^r_A*^r_B mod n. Finally, Alice proves that she knows P itself, and not just P′, by sending

   

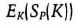
Bob, who knows both K and P′, can decrypt and validate the signature. Only Alice could have sent this message, since only she knows P; an intruder who obtains a copy of Bob's password file can try guessing at P, but cannot otherwise sign the session key.

The A-EKE scheme does not work with the public-key variant of EKE, since in it one party chooses the session key and imposes it on the other. This permits a man-in-the-middle attack by an attacker who has captured P′.

Applications of EKE

Bellovin and Merritt suggest using this protocol for secure public telephones [109]:

EKE's primary strength is that both symmetric and public-key cryptography work together in a manner that strengthens them both:

EKE is patented [111].

22.6 FORTIFIED KEY NEGOTIATION

This scheme also protects key-negotiation schemes from poorly chosen passwords and man-in-the-middle attacks [47,983]. It uses a hash function of two variables that has a very special property: It has many collisions on the first variable while having effectively no collisions on the second variable.

Here's the protocol. Alice and Bob share a secret password, P, and have just exchanged a secret key, K, using Diffie-Hellman key exchange. They use P to check that their two session keys are the same (and that Eve is not attempting a man-in-the-middle attack), without giving P away to Eve.

1. (1) Alice sends Bob

   

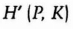
2. (2) Bob computes H′ (P, K) and compares his result with what he received from Alice. If they match he sends Alice

   

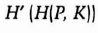
3. (3) Alice computes H′ (H(P, K)) and compares her result with what she received from Bob.

If Eve is trying a man-in-the-middle attack, she shares one key, K₁, with Alice, and another key, K₂, with Bob. To fool Bob in step (2), she has to figure out the shared password and then send Bob H′ * (P, K₂). With a normal hash function she can try common passwords until she guesses the correct one, and then successfully infiltrate the protocol. But with this hash function, many passwords are likely to produce the same value when hashed with K₁. So when she finds a match, she will probably have the wrong password, and hence Bob will not be fooled.

22.7 CONFERENCE KEY DISTRIBUTION AND SECRET BROADCASTING

Alice wants to broadcast a message, M, from a single transmitter. However, she doesn't want it to be intelligible by every listener. In fact, she only wants a select subset of listeners to be able to recover M. Everyone else should get nonsense.

Alice can share a different key (secret or public) with each listener. She encrypts the message in some random key, K. Then she encrypts a copy of K with each of the keys of her intended recipients. Finally, she broadcasts the encrypted message and then all of the encrypted Ks. Bob, who is listening, either tries to decrypt all the Ks with his secret key, looking for one that is correct, or, if Alice doesn't mind everyone knowing who her message is for, he looks for his name followed by an encrypted key. Multiple-key cryptography, previously discussed, also works.

Another method is suggested in [352]. First, each listener shares a secret key with Alice, one that is larger than any possible encrypted message. All of those keys should be pairwise prime. She encrypts the message in a random key, K. Then, she computes a single integer, R, such that R modulo a secret key is congruent to K when that secret key is supposed to decrypt the message, and R modulo a secret key is otherwise congruent to zero.

For example, if Alice wants the secret to be received by Bob, Carol, and Ellen, but not by Dave and Frank, she encrypts the message with K and then computes R such that

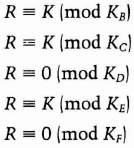
This is a straightforward algebra problem, one that Alice can solve easily. When listeners receive the broadcast, they compute the received key modulo their secret key. If they were intended to receive the message, they recover the key. Otherwise, they recover nothing.

Yet a third way, using a threshold scheme (see Section 3.7), is suggested in [141]. Like the others, every potential receiver gets a secret key. This key is a shadow in a yet-uncreated threshold scheme. Alice saves some secret keys for herself, adding some randomness to the system. Let's say there are k people out there.

Then, to broadcast M, Alice encrypts M with key K and does the following.

1. (1) Alice chooses a random number, j. This number serves to hide the number of recipients of the message. It doesn't have to be very large; it can be as small as 0.
2. (2) Alice creates a (k + j + 1, 2k + j + 1) threshold scheme, with:

   K as the secret.

   The secret keys of the intended recipients as shadows.

   The secret keys of nonrecipients not as shadows.

   j randomly chosen shadows, not the same as any of the secret keys.

3. (3) Alice broadcasts k + j randomly chosen shadows, none of which is any of the shadows listed in step (2).
4. (4) All listeners who receive the broadcast add their shadow to the k + j shadows they received. If adding their shadow allows them to calculate the secret, then they have recovered the key. If it does not, then they haven't.

Another approach can be found in [885,886,1194]. For yet another approach, see [1000].

Conference Key Distribution

This protocol allows a group of n users to agree on a secret key using only insecure channels. The group shares two large primes, p and q, and a generator g the same size as q.

1. (1) User i, where i goes from 1 to n, chooses a random r_i less than q, and broadcasts

   

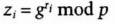
2. (2) Every user verifies that z_j^q ≡ 1 (mod p), for all i from 1 to n.
3. (3) User i broadcasts

   

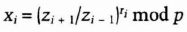
4. (4) User i computes

   

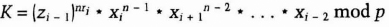
All index computations in the above protocol—i − 1, i − 2, and i + 1—should be computed mod n. At the end of the protocol, all honest users have the same K. No one else gets anything. However, this protocol falls to a man-in-the-middle attack. Another protocol, not quite as pretty, is in [757].

Tatebayashi-Matsuzaki-Newman

This key distribution protocol is suitable for networks [1521]. Alice wants to generate a session key with Bob using Trent, the KDC. All parties know Trent's public key, n. Trent knows the two large primes that n factors to, and hence can easily take cube roots modulo n. A lot of the details are left out of the following protocol, but you get the idea.

1. (1) Alice chooses a random number, r_A, and sends Trent

   

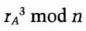
2. (2) Trent tells Bob that someone wants to exchange a key with him.
3. (3) Bob chooses a random number, r_B, and sends Trent

   

4. (4) Trent uses his private key to recover r_A and r_B. He sends Alice

   

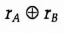
5. (5) Alice calculates

   

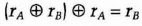
   She uses this r_B to communicate securely with Bob.

This protocol looks good, but it has a horrible flaw. Carol can listen in on step (3) and use that information, with the help of an unsuspecting Trent and another malicious user (Dave), to recover r_B [1472].

1. (1) Carol chooses a random number, r_C, and sends Trent

   

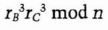
2. (2) Trent tells Dave that someone wants to exchange a key with him.
3. (3) Dave chooses a random number, r_D, and sends Trent

   

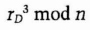
4. (4) Trent uses his private key to recover r_C and r_D. He sends Carol

   

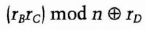
5. (5) Dave sends r_D to Carol.
6. (6) Carol uses r_C and r_D to recover r_B. She uses r_B to eavesdrop on Alice and Bob.

This is not good.