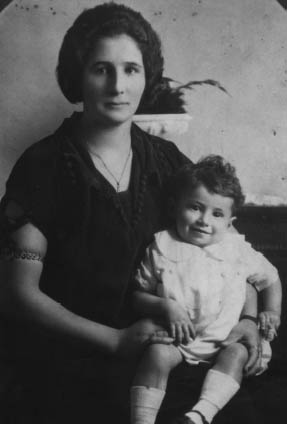Two
Tom Apostol
Tom M. Apostol is professor emeritus of mathematics at the California Institute of Technology. His writing talents blossomed in graduate school in the late forties at UC Berkeley, in large part because textbooks were rarely used by the UC faculty, and he felt compelled to transform his class notes into text form. He is especially well known for his pathbreaking Calculus in two volumes, first published in 1961, and his Mathematical Analysis, published in 1957. Both have been translated into several languages, and both are still in print! These books have had a strong influence on an entire generation of mathematicians. His other books include Introduction to Analytic Number Theory, Modular Functions and Dirichlet Series in Number Theory, Selected Papers on Pre-calculus (with Chakerian, Darden, and Neff), The Mechanical Universe: Introduction to Mechanics and Heat (with Olenick and Goodstein), The Mechanical Universe: Mechanics and Heat for Science and Engineering Students (with Frautschi, Olenick, and Goodstein), and Beyond the Mechanical Universe (with Olenick and Goodstein). In 1982 Apostol was initiated into the world of television production. Over the past ten years, he has developed a prizewinning series of videos titled Project MATHEMATICS! Although he has received considerable praise for his writing, he says that “of all the things I’ve done in my fifty years as a mathematician, the most satisfying has been producing and directing the videos for Project MATHEMATICS! . . . Making a video is like solving a puzzle.”
The Immigrant Experience
MP: Where did you start life?
Apostol: I was born in Helper, Utah, in 1923. My mother, whose maiden name was Efrosini Pappathanasopoulos, was a mail-order bride from Greece. My father, Emmanouil Apostolopoulos, whose name was shortened to Mike Apostol when he became an American citizen, traveled from Utah to New York to meet her. She had been eager to come to the United States, but ending up in the mountains of Utah was not exactly what she had expected.
MP: How long had your father been in America before your mother arrived?
Apostol: My father came around 1916 and she came in 1922, so it was about six years.
MP: What drew him here?
Apostol: He had two brothers working in mine smelters in Montana, and they paid his way to come join them. They earned seventy-five cents a day. When his brothers had saved enough money they returned to Greece. But my father heard that the coal mines in Utah were paying a dollar and a quarter a day, and he thought, “Well, that’s a great deal.” So he went to Utah by himself in 1918, and he worked in a coal mine—but only for one day! When he climbed on the elevator and it descended 5,000 feet into the mine, he got claustrophobic. He just couldn’t stand it.
MP: But what else could he do?
Apostol: The coal mine was at Castle Gate, about four miles north of a hamlet called Helper, the hub of Carbon County, and he saw an opportunity there. Since most of the miners had their shoes repaired in Price, seven miles south of Helper, he thought it would be a good idea to open a shoe shop in Helper. Back in Greece he had been apprenticed as a shoemaker from the age of eight, so he knew how to repair and to make shoes by hand. He had even brought a few hand tools with him. He rented a store-front, lived in the back room, and started repairing shoes.
MP: Did his idea work out all right?
Apostol: He put all the money he earned in a coffee can, and at the end of the first month he dumped it on the bed. There was $200—and for somebody who had been earning 75 cents a day, that was a small fortune. Most of it he sent back to Greece for his sisters’ dowries. Then after all his sisters were married off, he decided it was his turn. Now, my father couldn’t write very well, since he had only gone to the first or second grade, so he had a Greek friend write a letter to my mother’s older brother in Egion asking for the hand of one of the daughters. Which one didn’t matter, because he didn’t really know them. He knew it was a good, respectable family with several daughters. They had a nice home with a lemon orchard and olive groves. My father’s letter, which still exists, explained that he had paid the dowries of his sisters and wanted to start his own family now. So the letter arrived, but the eldest daughter, who normally would be the first to be married, didn’t want to go to America by herself. My mother was the youngest daughter. She had heard great things about America, and she immediately spoke up and said, “I’ll go.” So her brothers put her on a steamship and off she went.
MP: She must have had a lot of courage.
Apostol: Yes, indeed. My father traveled across the country by train and met her in New York City. They were married promptly and took the train back to Utah. My mother told me that as they crossed the beautiful green fields of the Midwest she would say, “Oh, this looks like a nice place to live.” And my father would say, “Oh, that’s nothing. Wait until you see Utah.”
Figure 2.1 Efrosini Pappathanasopoulos bidding farewell to her brother before she left Greece in 1922.
MP: So they landed in Helper, Utah. That’s a pretty desolate place.
Apostol: Right, about 5,500 feet elevation, in the middle of nowhere, not too many trees around—my mother was pretty upset when she got there. She had left this beautiful place in Greece overlooking the Gulf of Corinth. She shed a lot of tears in the next few months.
MP: How much younger than your father was your mother?
Apostol: She was 22 when she came to America, six years younger than my father. He had bought a small house on Main Street, but it was only about 50 yards from the railroad tracks. Trains went by all day and night pumping out soot on her clean laundry. It was not really a happy time for her at first. And then I was born, the first child. She lavished all her attention on me, and the tears stopped flowing. All four of her children, two boys and two girls, were born in that house. Being the first child, and a boy, I got a lot of special attention. My mother was very sharp. She had finished the fifth or sixth grade in school—about as far as Greek girls could go in those days—so she could read and write much better than my father. She loved poetry and had memorized many poems, some of them quite lengthy. She also composed long poems of her own, most of them with a touch of humor. She taught me to memorize them, and she also taught me to read Greek. By the age of three I could read the Greek newspaper.
Figure 2.2 Apostol (age 14 months) with his mother.
MP: Amazing. So she thought that reading was important?
Apostol: There was no question about it. She wanted me to be educated and to do well in school, so she taught me to read, even though there weren’t many books in the house. I was a precocious child, so when I was five she thought I should start school. You had to be six to start first grade, and there was no kindergarten in Helper. But she sent me anyway.
MP: Did you misrepresent your age?
Apostol: Not very well. When the teacher asked, “How old are you?” I said, “I’m five, but my mother told me to say I was six.” They sent me home in tears.
MP: Was Greek your first language?
Apostol: Yes. My father was picking up English from his customers at his shoe shop, but he and my mother spoke Greek at home. She began to learn some English from our neighbors. That’s also how I learned most of my English, from the kids in the neighborhood and from talking with my first sister. She was born three years after me, and the two of us learned English very quickly.
Math Is Number One
MP: Did you attend a one-room schoolhouse?
Apostol: No. Helper Central School was a big two-story brick building with grades one through six. I remember it very well. Looking back, I am impressed at the high quality of the teachers. I had a very good elementary education there.
By the time I reached sixth grade the Depression was going strong, and good teachers had a hard time finding jobs. Many ended up in places like Helper. Our arithmetic teacher was very good and strict; you really had to learn your multiplication tables and arithmetical skills. The principal had the theory that math was number one. If kids were good at mathematics, they would be good at everything else.
MP: Revolutionary idea!
Apostol: It was revolutionary. He and the math teacher made up sheets of multiplication and addition problems that we had to solve, day after day after day. It just became second nature after a while.
MP: Did you like most subjects you encountered?
Apostol: Yes. I was very good at reading, which made it easy to learn everything. I also enjoyed learning practical skills as a Boy Scout. I joined at age twelve and became an Eagle Scout at age sixteen. Also, the kids in school were an interesting group to be with. There were Italians, Poles, Greeks, Japanese, and Mormons. Most of their fathers worked either for the Denver & Rio Grande Railroad or in the nearby coal mines.
Figure 2.3 Apostol (first row, fourth from right) with the sixth grade class of Helper Central School.
MP: Do you think that your mathematical genes come from your mother’s side or your father’s?
Figure 2.4 Tom as a Boy Scout, 1935.
Apostol: My mother had an uncle who was a mathematics professor in Greece. She herself was very good at arithmetic. My parents often played cards at home with friends, and my mother kept score, doing all the addition in her head. She figured out shortcuts by herself, like rounding off to ten and then deciding how much to add or subtract. She had innate intelligence and also good common sense.
She had a keen sense of humor, too, and was a marvelous story teller, with an excellent memory. Sometimes she would retell a story we had heard years before, but I swear she would relate it word for word, exactly as she told it the first time. We always wondered what she would have done had she been more fully educated. She was a remarkable woman and would have accomplished great things.
MP: The Depression was a hard time to raise a family.
Apostol: My mother took in laundry to help out. For example, she did laundry in exchange for piano lessons for me and my sister. All four children provided delivery service, picking up and delivering laundry. My mother seemed to be always washing and ironing, or cooking and baking bread. She was a very busy woman.
MP: And your father?
Apostol: He worked hard in his shoe shop. One evening a week he would drive to nearby coal-mining camps to pick up and deliver shoes. He loved Helper and the American way of life. Business picked up around 1939 when the Depression began to lessen, and he hired a worker, a deaf man, with whom he communicated by sign language. He also apprenticed several young brothers, the Arlottis, who later started their own chain of shops in Southern California.
Figure 2.5 Apostol with his father and younger sister at the Helper Shoe Shop, 1936.
Apostol: Not really. He tried to teach me to drive, and it was an awful experience. He had tried to teach my mother to drive, and she gave up. He was impatient. If you didn’t catch on right away, he would say, “Here, I’ll show you. I’ll do it for you”—hardly the best teaching method. But his heart was in the right place, and he was certainly hard working and set a good example. My father never took a day’s vacation, except to close his shop on Sundays. He was a goodhearted man who continued to send money back to his family in Greece.
MP: Working six days a week, probably from eight o’clock in the morning to six o’clock at night, does not leave much time for recreation.
Apostol: We did things together as a family and with other Greek families in the community. We would often take Sunday drives in the countryside, usually up Price Canyon beyond Castle Gate, where we would picnic near springs with fresh running water. That was fun. My mother sang songs while we drove, and everyone joined in. She always livened things up with her songs and her anecdotes. My dad made his own wine in our cellar. He ordered grapes from California, and we wore rubber boots and smashed the grapes in large tubs. I don’t know if he learned how from other Greeks or perhaps from our Italian neighbor, who happened to be the town marshal.
MP: That may have posed a problem.
Apostol: My dad also had a slot machine in the shoe shop. Every fifth nickel would fall into a drawer at the back of the machine; the rest were used to pay off the players. At the end of the day, my father would unlock the drawer and find at least a dollar’s worth of nickels. Sometimes the slot machine earned more than the shoe shop. But slot machines were illegal in Utah, so once a year he would get hauled in and pay the $25 fine. The marshal never confiscated the machines because he knew that people needed the income.
MP: Your dad sounds like an enterprising guy.
Apostol: He was. Besides repairing shoes, he sold new ones, and he also cleaned and blocked hats in the shop. He set up all the equipment himself. The naphtha used for cleaning hats was flammable and rather dangerous, but there were no accidents. Eventually he rented a space at the rear of the store for a beauty parlor. His own rent was $55 a month. Some days the shop took in only a couple of dollars, so there were some hard times.
MP: It sounds like your mother brought a lot of joy into the house.
Apostol: She was the best thing that ever happened to my dad. We never knew till we were grown up how unhappy she had been when she first came to the United States. My parents never argued, at least not in front of the children. Here were two complete strangers who had a very long and happy marriage. The whole family celebrated their sixtieth wedding anniversary a few years ago.
MP: It sounds like your parents were a good match. You can look at your mother and see some qualities you may have gotten from her. What do you think you got from your dad?
Apostol: His work ethic, and to some extent I guess you might consider me entrepreneurial.
MP: Considering all your mathematical projects, I certainly do. As a boy at school, were you interested in math?
Apostol: Just as I finished sixth grade, Helper built a new junior high school. I had a very good mathematics teacher there, Mr. Pisa, who taught me algebra in the eighth grade and geometry in the ninth.
MP: Did you take any mathematics in seventh grade?
Apostol: Yes, but it was a waste of time—more of the arithmetic we had learned in elementary school, with applications to business. Geometry in ninth grade was the most interesting. Mr. Pisa had kids go to the board to present proofs and work geometry problems. He was a hard taskmaster, really severe, but I just loved all of the theorems and proofs. For the first time, mathematics began to make sense, because he followed the classical Euclidean geometry. We started out with axioms and definitions, and it all seemed perfectly logical. And we did the standard two-column proofs. Mr. Pisa could explain things very well, and I always felt he got me off to a good start. For tenth grade I went to Carbon Senior High School in Price, which then became a combination high school and junior college that I attended for one more year. I finished my last year of high school in Salt Lake City after my family moved there.
Entrepreneurs in Salt Lake City
MP: What prompted the move to Salt Lake City?
Apostol: My mom wanted me to go to a university. She saw what happened to the kids who stayed in Helper. They worked either in the mines or on the railroad; that’s about all that was open to them. If we moved to Salt Lake I could attend the University of Utah while living at home. We used to visit distant relatives in Salt Lake from time to time. It is a beautiful city, and we liked it a lot. Of course, my dad did not want to move; he was quite content in Helper. He had convenient barter arrangements; for example, in exchange for dental work the dentist and his family would have their shoes repaired. My dad knew almost everyone in town, and he certainly knew all his customers. If we went to the big city, all those personal contacts would be lost. But my mother insisted, and finally my parents took a trip to Salt Lake. They found a combination shoe shop and dry cleaning shop that was for sale. My mother was delighted. She said she could run the dry cleaning business.
MP: Did she know anything about dry cleaning?
Apostol: No, but she was smart and was confident that she could learn. After all, she had been doing laundry all those years in Helper. So we moved to Salt Lake, and I helped out in the business, just as I had been doing in Helper, where almost every day after school I stayed at the shop while my father walked home for a coffee break. It wasn’t that busy, so I could do homework until a customer came in. I would shine shoes and do minor shoe repairs. I never learned to attach soles on the heavy-duty stitching machine, but I could put on heels. My brother helped, too, when he was old enough. We both helped out in Salt Lake during my last year at high school.
MP: Was the high school a big change from Price?
Apostol: It was a very big change. South High was a huge school with 700 in the senior class. I took what they called college algebra, and the teacher was awful. At the beginning of each class she would work the illustrative examples in the text and then assign homework while she sat there and read novels. We spent most of the class time doing homework. When people would ask her how to do a problem, she would send them to me. Since I had studied the book and figured everything out at home by myself, I was able to do all the problems and explain them to my fellow students. The teacher realized that and exploited my talents. She was really bad news, but I enjoyed the subject matter—and I was also happy to be admired by my classmates.
MP: Did you take any other math there?
Apostol: The next semester I took trigonometry and solid geometry. The teacher for both was an old gentleman named Mr. Bird who made things interesting and taught us very well. I also had a good chemistry teacher, Mr. Decker. I had taken chemistry in Price, but it was taught by the football coach, who didn’t know beans about chemistry. He just had us work problems out of a workbook; then he would read the answers aloud while the students graded each other’s work. But Mr. Decker gave interesting lectures and demonstrations. He was really a good teacher. I loved the subject so much that I wanted to become a chemist. So I did very well that year.
MP: But you had liked math, too, if not as much.
Apostol: I liked math, and I was always good at it. But I didn’t realize at the time that you could make a career out of it. Besides, I was interested in all kinds of things. One was aeronautical engineering. I loved model airplanes, and I built lots of them and sold them to other kids in Helper. When I was about fifteen I sold model airplane kits through my dad’s shop. My wholesaler in Salt Lake gave me a 40 percent discount, and to save shipping costs I would hitchhike 100 miles to Salt Lake and back to get the materials.
MP: So you were a real entrepreneur. Imagine if you had gone to business school!
Apostol: Unfortunately, our new shop in Salt Lake was just a block away from the model airplane dealer, so I got out of the airplane business. Besides, I was getting ready to go to the university.
Figure 2.6 Apostol with his first gasoline-powered model airplane, 1938.
MP: So you enrolled at the University of Utah. Was the war on yet?
Apostol: The Second World War started when I was a sophomore at the University of Utah. There was a military base, Fort Douglas, in Salt Lake, and many soldiers would stop at our shop to have their shoes shined or their pants pressed. This was a gold mine for my parents, because they didn’t have to invest in any materials. I helped out with that when I wasn’t in class. The university was only fifteen minutes by bus from the shop.
MP: What was the University of Utah like in those days?
Apostol: I attended for two years. My best mathematics teacher was Anna Henriques, who taught me college algebra and analytic geometry. She’s in her nineties now and lives in a retirement complex in Virginia. I telephoned her recently, and she remembers me very well. I also sat in on a course on complex variables my freshman year. I don’t know why; the subject seemed fascinating, but very little of it made any sense to me at the time. In my sophomore year my first semester of calculus was taught by the head of the department, a nice old gentleman who really didn’t understand the subject very well. Every time I asked him to explain something he would say, “Work some more problems in the book.” I just wasn’t satisfied with that. I felt there was something fundamental behind all this formal manipulation, and I wanted to know what it was. The second semester I had a new young faculty member, Frederick Biesele, who was very good. He understood the subject and knew how to explain it.
MP: So you were interested in math. Was that your major?
Apostol: I was more interested in chemistry and became a chemistry major. A young chemistry teacher named Hammond, who had just gotten his PhD from the University of Washington, impressed me with his knowledge and teaching ability. I thought, “I’d like to go where he learned chemistry,” and I talked to him about that possibility. In 1941, after Pearl Harbor, when everybody began leaving school to enlist, I thought I should join up, too. Since I was still interested in aeronautical engineering, I applied for officers’ candidate school in the Air Force. But at the interview they said, “Sorry, we can’t take you. Insufficient calculus.” Well, I was just beginning to take calculus in my sophomore year, and I was terribly upset. What could I do? I didn’t want to join the infantry. Then some administrator at the university said, “Look, the country needs engineers to help the war effort and to rebuild after the war. We’ll try to get you guys deferments to stay in school and study engineering.” Since I was not too keen on the engineering school at Utah, I switched to the University of Washington, where I majored in chemical engineering.
MP: But your mother’s original motivation for moving to Salt Lake was that you could go to the university there and also save money by staying at home.
Apostol: Right. I had to convince her that Washington was a better school for me. I also realized that I was going to have to find work. During my first year at Washington, I was a houseboy in a sorority, with free room and board in exchange for washing dishes for ninety girls; it was great. My dad paid my tuition, which was not very much in those days. In my senior year, I worked nights at Boeing Aircraft. They were mass-producing B-17s, Flying Fortresses, at that time, and every time a wing was assembled someone had to check the alignment of the jigs before the next wing was started. That was my job: an inspector for wing jigs. It was simple, trivial, and periodic. I just waited till someone needed an inspector, then I did my duty. It was great, because I had a desk and could get all kinds of homework done on the job.
Mathematics, by Golly
MP: At the University of Washington, did you study mathematics or only chemical engineering?
Apostol: My BS degree was in chemical engineering, but I had taken so many math courses that I was effectively a math major as well. In my junior year I encountered Herbert Zuckerman, and he turned my whole life around. He taught advanced calculus, and it was the first time I had ever seen advanced mathematics done properly. He explained things well, made it interesting, and made everything look so easy. I never thought of switching to mathematics, but I took number theory from Zuckerman the next year. He used Uspensky and Heaslett as a textbook. There were other good people in the department as well. I took differential equations from C. M. Cramlet, complex variables from L. H. McFarlae, and projective geometry from Roy Winger.
MP: All this while working nights?
Apostol: Yes. When I got my bachelor’s degree in chemical engineering in May 1944, the war was still on, and there were no job openings for chemical engineers in the Seattle area. That summer I worked at Kaiser Shipyards in Portland, Oregon, designing layouts for plumbing systems for thirty Liberty Ships. They were mass-produced, but so many modifications were made that no two were exactly alike. As summer came to a close, I decided to go back to the University of Washington as a graduate student in mathematics.
MP: What motivated you to switch? You still liked chemistry, didn’t you?
Apostol: One day while riding the bus to work, I pondered about my future. I thought, “What am I going to do with my life?” I asked myself, “Of everything I’ve studied, what is it I like the most?” And I decided it was mathematics. I told myself, “By golly, I’m going to get a master’s degree in mathematics and study with Zuckerman!” I thought I would have only a few months of classes before being drafted. But it turned out that my draft board in Salt Lake had misfiled my papers, and I wasn’t called for a physical exam until January 1945. By then the Army knew the war was almost over, so they were raising the standards. Since my eyes were bad, I was classified 4-F. And that was that.
MP: Back to school for you, then. Tell me more about what math was like at the University of Washington.
Apostol: Most of the male students were military personnel in the V-12 program. There was only one other mathematics graduate student at that time, a fellow named Marvin Stippes. Zuckerman was not eager to teach a course with only two students, so I said, “I’ll make a deal with you. I’ve come across Knopp’s book, Theory and Applications of Infinite Series, and I’d love to go through it. Why don’t we do this as a kind of seminar? Stippes and I will do all the lecturing and you just sit there and keep us on track.” Zuckerman loved that.
MP: Did it actually work?
Apostol: It was the best training I’ve ever had. I was the first speaker on day one, and Zuckerman demolished me. He kept asking, “What is the reason for this?”—and I didn’t know. “Why is this true?”—and I didn’t know. I had read the book carefully and thought I understood it, but it was clear that I was completely unprepared when it came to details. There were proofs about convergence, with epsilons, deltas, and all that stuff that I had never really understood before. That was the last time that happened. From then on, I really studied the book line by line, making sure I understood all the details. Zuckerman was extremely helpful, and I could visit him in his office for assistance. I felt as if I had a personal tutor for a year, learning basic analysis. Knopp’s book is marvelous; it has all kinds of great mathematics in it. One of us would lecture each day, sometimes half an hour each, sometimes for the full hour. Zuckerman quizzed us as if we were taking a PhD exam. Nothing got by him. He made sure we understood everything that was going on. Later, when I was a graduate student at Berkeley, my father lost his lease in Salt Lake and bought a new shop in Oakland. My parents loved California; it reminded them of Greece. Anyway, I was working in the shop one day when a customer brought in his shoes, and I asked, “What’s the name?” He said, “Knopp.” I said, “Oh, are you by any chance related to Konrad Knopp, the mathematician?” “Yes,” he replied, “that’s my uncle. How do you know about him?” He was stunned. Here was a young guy working in a shoe repair shop who knew the work of his uncle in Germany!
Figure 2.7 Konrad Knopp.
MP: What else did you do with Zuckerman?
Apostol: Every math major there had to write a master’s thesis, and I did mine with Zuckerman on magic squares. It was an extension of work done in 1929 by D. N. Lehmer, the father of D. H. Lehmer. It was the first research I had ever done. Years later Zuckerman and I published a joint paper on the topic. It was so exciting to discover something new in mathematics by digging away at it. The first time you discover a new result in mathematics, it is a religious experience. I don’t know how else to describe it. I decided that mathematics was the field I wanted to work in for the rest of my life, and it has been very satisfying to do that.
No Books at Berkeley
MP: After your thesis, were you excited about number theory in particular? Or did you just generally want to be in mathematics?
Figure 2.8 D. H. Lehmer was Apostol’s thesis advisor.
Apostol: At that point, I wasn’t sure. When I asked Zuckerman about working with him for a PhD, he said, “It’s not good to stay at the same school all the time. Why don’t you go to Berkeley? D. H. Lehmer is there, and you can tell him about your work with his father’s paper.” As it turned out, Berkeley had a special one-year scholarship for students from Utah, which I got, and the next year I became a teaching assistant. I showed Lehmer my results on magic squares, and he was very pleased. It almost brought tears to his eyes to see the congruences his father had worked on many years before. He said, “I’ll be happy to guide your research when you find a suitable problem to work on.”
MP: He left that up to you?
Apostol: Right. I sat in on his number theory course and registered for his number theory seminar, where I got the idea for my dissertation. Lehmer and I would meet from time to time as I worked on it, but he would just sit there and nod, “Yeah, that looks good. Go ahead, keep working.” He did not make a single suggestion about what to do or which way to go. Months later I asked him, “Do I have enough for a thesis? I have to know when to stop.” Lehmer said, “Yeah, I think that’s enough. Write it up.”
MP: Your experience with Zuckerman probably helped a lot.
Apostol: The other thing that helped was that they did not use many textbooks in the graduate courses at Berkeley. A lot of good mathematics was being taught, but there weren’t any textbooks on analysis or algebra, just lecture notes. The professors were fast lecturers, so we all took notes like mad. I would rewrite my notes at home in little notebooks as a record for myself and as something to review. I would fill in all the details that were not quite finished in class to satisfy myself that I understood the material. This really helped later in writing textbooks, because I learned how to be an expositor, writing so that students could understand.
MP: Virtually no texts were being used in the graduate courses? How times change!
Apostol: I do not remember buying a single text. I took a course in complex analysis from Frantisek Wolf, who had just acquired a copy of Widder’s book on the Laplace transform. Wolf loved it and began lecturing out of it. After a while, the students formed a little committee and went to see him. “Professor Wolf, this is very interesting, but we signed up for a course in complex analysis.” He replied, “This is complex analysis.” “Well, it’s interesting, but it’s not what was advertised in the catalog.” I said, “We want a course in complex function theory.” “Okay,” he said. “You guys prepare the talks, and we’ll do it that way.”
MP: The Zuckerman method.
Apostol: Same thing again. I started preparing some lectures on elliptic functions because this material related to my area of research. And that was when I learned a lot of topics that eventually went into the second volume of my number theory book.
MP: This explains a lot about your writing.
Apostol: Very little was available in English in those days. For complex analysis there was Hurwitz-Courant in German, so I studied that and learned German at the same time, which also enabled me to pass the German language exam. I translated portions of Hurwitz-Courant and recast it to fit the modern approach to mathematics that we had been taught at Berkeley, and I started producing lectures on elliptic functions and other topics in complex analysis. I also translated much of the Pólya and Szegő problem books. That was complex analysis. For real variables, I had a very abstract course from Anthony P. Morse, which I didn’t particularly care for. Raphael Robinson’s symbolic logic course was great; I still have my notes from that. And Cesari was also there.
MP: The expert on summability?
Apostol: No, Lamberto Cesari, not Ernesto Cesàro. Cesari gave a course in classical real analysis. He was a character. To begin each lecture, he would call someone to the board and say, “Please tell your colleagues what we discussed last time.” This forced students to review their notes before coming to class. If you could not remember all the details, he would say, “Tell us about the theorem on absolute continuity,” or whatever, to remind you. He got the students to break the ice and make the transition to his next lecture. Cesari was such a pleasant, outgoing fellow that no one took offense at being asked to do something.
MP: These sound like lots of strongly supportive teaching experiences.
Apostol: Yes. Another class that helped me a lot was Alfred Tarski’s algebra course. Again, not a scrap of notes and no text—and he wrote very little on the board. On some days he would say, “Let big A be an algebra,” and then a big German “A” stood there all by itself. “Okay, theorem one,” and then he would write the number “1” on the board—and that was all you saw. He would recite the theorem and proof orally while we wrote everything down as fast as we could. Then, “Theorem two.” And the number “2” went on the board.
MP: To lecture that way is actually very hard to do.
Apostol: It is hard, although not all his lectures were like that. Tarski never referred to lecture notes. He had it all in his head. I’m not sure how much algebra I learned in that class, because he played around a lot with axiomatic systems. One day he said, “You can describe an abelian group with one axiom and one operation, division.” He gave that as a homework problem, to show that this does indeed define a group. I worked at least forty hours on it! One day he asked, “Has anyone done this problem?” So I raised my hand and went to the board. It took nearly the whole hour to write out the details. He told me later that he had published a paper on this problem years ago in some obscure Polish journal.
MP: So it was really a research problem.
Apostol: Yes. He gave us stuff like that all the time, research quality problems. So he was good in making real demands on us.
MP: How big was the graduate group when you were at Berkeley?
Apostol: About 200 graduate students. There were about twenty students in Tarski’s class. After I got my PhD in 1948 I stayed on another year as a lecturer at the University of California. Then I received a C.L.E. Moore Instructorship at the Massachusetts Institute of Technology and went to Cambridge in 1949.
Boston and Back
MP: Was MIT a pretty inspiring place?
Apostol: It was a very good school, and I enjoyed teaching there for a year. I taught advanced calculus and a course in my own field, analytic number theory. Murray Gell-Mann, who was a physics graduate student at MIT at the time and later became one of Caltech’s Nobel Laureates, took my number theory course. I had forgotten this until he reminded me of it some forty years later at Caltech.
MP: Did you get to know Norbert Wiener?
Apostol: He was quite a character. You would often see him striding up and down the halls accompanied by military people. But he was a terrible teacher. He offered a course on Fourier analysis, one of his fundamental contributions to mathematics, so I sat in on it with Earl Coddington, a fellow instructor. The first day there were two instructors and one student in the audience; after the first lecture the audience went down to zero, because he was such a poor lecturer. He was unaware of who was in the audience, and he talked about whatever he wanted to. He might spend twenty minutes arguing with himself at the blackboard over what symbol to use. But he was a brilliant man. At the weekly colloquium at Harvard, Wiener would sit in the front row and promptly fall asleep, snoring, no matter who the speaker was. The minute the speaker stopped, Wiener would get up and ask a sensible question. As a lecturer, though, he just floundered.
MP: Did you know Norman Levinson?
Apostol: Coddington and I sat in on his course in differential equations. Levinson was famous, and the room was packed to overflowing on the first day. But he gave a terrible lecture, just awful, and at the end he said, “This is probably the clearest lecture you’ll hear all year.” Next time, only about a third of the audience came back, and he began all over again and gave an excellent lecture. That was his way of getting rid of people who did not have a real interest in mathematics. He was a very good mathematician and an excellent lecturer.
MP: How did Caltech come to recruit you?
Apostol: I don’t know for sure. In a letter to Lehmer about some mathematical question, I mentioned that I did not care for the climate or the living conditions in the Boston area, that I wanted to return to California, and that I had heard of an opening at Caltech. I asked if he knew anything about it, but he never responded to this question. Soon after that, Robert F. Bacher wrote to offer me an assistant professorship at Caltech. I immediately accepted, even though I could have stayed another year at MIT as a Moore Instructor.
MP: Berkeley was a high-powered place. How did Caltech feel in comparison?
Apostol: Many faculty members were retiring, and the department started recruiting young, active mathematicians. When I arrived in 1950 the department was very small, with only a handful of full professors—E. T. Bell, H. F. Bohnenblust, Arthur Erdélyi, A. D. Michal, and Morgan Ward. Bell retired a couple of years later. But there was a lot of activity because so many young people were being hired. There were parties and get-togethers; the whole department would turn out for picnics. It was a fun place to be. What I liked best was the high caliber of the students. If anything has kept me at Caltech all these years, it has been the quality of the undergraduate student body.
Figure 2.9 Apostol with Caltech colleague Olga Taussky-Todd, 1978.
MP: What were you interested in doing when you arrived?
Apostol: I didn’t have any grandiose plans. I wanted to be a good researcher and a good teacher, and the atmosphere here was very good for that. I had just published my PhD thesis and was making good progress on related topics. The teaching load was fairly heavy. We had to teach two courses, which takes a lot of time when you are starting out. I often taught courses I had never taken myself, so I had to learn the material and teach it at the same time. I also used to participate in seminars, both actively and passively. E. T. Bell and I conducted a private seminar for just the two of us for a couple of years before he retired.
Calculus for Caltech
MP: What made you decide to write your first calculus text?
Apostol: I was asked to teach the advanced calculus course, which had been using volume two of Courant’s Differential and Integral Calculus from the 1920s. It was a very good book, but too low-level for that kind of course. There was no book in English that was intermediate between elementary calculus and real variable theory, sort of an introduction to both real and complex analysis. When Morgan Ward and I were assigned to teach the course for 1953 and 1954, we couldn’t find an appropriate text, so I said, “Morgan, you and I could probably write such a book.” We made a tentative plan to write up a few chapters over the summer and then get together in September to see what we had come up with. I spent the summer in Oregon working like crazy, and when I came back I found that Morgan had forgotten all about it. So I offered to write up a set of lecture notes by myself, which I did. I managed to keep three months ahead of the students during the year. Warren Blaisdell, who was then vice-president of Addison-Wesley, heard about those notes and asked if he could have them refereed, with the idea of publishing them as a book. I said, “Well, you know, they’re just sketchy notes. They’re in no form for a book.” But he got some very enthusiastic responses from the reviewers and sent me their critiques. So I spent another summer working like crazy to transform them into a publishable manuscript. Mathematical Analysis was published in 1957 and became somewhat of a classic in its field. A whole generation of mathematicians was raised on that book, and it has been translated into several languages.
MP: Tell us about the process you went through in writing your two-volume Calculus textbook. You had weekly development meetings with math colleagues and physicists, I understand.
Figure 2.10 Apostol after his promotion to full professor, 1962.
Apostol: It took about five years overall. Caltech students were coming here better and better prepared—not only bright but with a lot of background. There was no book on the market that was suitable for these more sophisticated kids. First we tried a preliminary edition of George Thomas’s Calculus, which used vectors and other things that had never been in a calculus book before. But the students didn’t like it, so we decided to write our own book. Some of us sat down and discussed what would make sense to teach these bright kids. We considered all kinds of possibilities, but in the end we decided that calculus was the best thing we could offer them. We met for a year, one hour every week, thrashing ideas around until we developed a sort of master plan for an integrated course in freshman mathematics. The physicists were made aware of the changes, why we were doing things differently, and how the mathematics would mesh with freshman physics. Then came the question of who would transform our plan into useful notes. I had already published one book, so I had some experience. And actually I was eager to do it! So I wrote little booklets of mimeographed notes, keeping one term ahead of the course, just following the plan from our meetings, filling in all the details, and adding suitable exercises. At the end of the year it dawned on us that we had not discussed the follow-up course in sophomore mathematics. So I modified the Math 2 course to fit what we had done in Math 1, and again it was discussed with the physicists. Then I wrote another set of notes the same way as before, keeping one term ahead of the students. This eventually became my Calculus, volumes one and two.
Figure 2.11 Apostol delivering a transparent lecture.
MP: It must have been well received by the students, since they refer to your calculus volumes as “Tommy 1” and “Tommy 2.”
Apostol: They knew this was something new, and they liked the approach. There was a sense of excitement, because this was “the book written for Caltech.” It took into account the needs of other departments, physics primarily, and it also satisfied the mathematicians, who were happy to teach this material.
MP: How important is it for mathematics students to learn physics?
Figure 2.12 Tom and his calculus class celebrating Gauss’s 133rd birthday, 1988.
Apostol: To have some kind of physical feeling for what things mean—that’s good for everybody. I have always felt that applications are an important part of a mathematics education. Don’t forget, I’m an upward bound engineer! And I had a minor in physics when I got my MS at Washington. That’s why my calculus book has a lot of applications to physics and engineering. Anything that helps increase understanding and insight is important. If you can see something from two or three points of view, that is valuable. I try to give my freshmen the message that great achievements are made by people who see these connections, not by those who specialize in just one field.
Figure 2.13 Tom and Jane Apostol hamming it up at a Democratic fundraising party in 1960.
MP: So they should be willing to study even abstract concepts, because they might apply someday?
Apostol: Yes, although it is difficult to get freshmen to feel that way. They want something utilitarian, and they don’t really care why it works, as long as it works—like driving a car. It is a constant challenge to convince them that you also have to think about why it works. What if your car breaks down?
MP: Other departments that require mathematics often complain, “The math department is just completely out of touch with us.” Many institutions have people teaching calculus who probably never had anything beyond a high school physics course.
Apostol: It is important for mathematics students to understand how mathematics is used in other fields. You are depriving them of an education if you don’t teach them that.
MP: Your teaching experience at Caltech has largely been positive, in part because the students are good. What makes a good teacher?
Apostol: Output is proportional to input, so if you work hard at it, you can do a good job. If you are not interested and don’t prepare your material, you won’t do a good job—unless you are an exceptional person. But I always put a lot of effort into the courses I taught because I felt it was important. Mostly, I wanted to make sure that what I said was understandable to the students and that it motivated them to want to learn more. I tried to anticipate their difficulties. Remember, sometimes my teachers in high school and college did not understand what was going on, and it disturbed me when they could not explain it. I was always interested enough in mathematics to try to understand everything, and in my books I always tried to communicate my own concerns to the students.
The Grecian Formula
MP: Have you ever visited your parents’ homeland, Greece?
Apostol: Many times. My wife and I first went there in 1962 as tourists and then again in 1965. I met some Greek mathematicians on these visits and was invited to be a visiting professor at the University of Athens in 1967. But the military dictatorship took over, and since the Greek government runs the universities, I did not want to work for someone who suppressed academic freedom.
MP: Did the best Greek mathematicians tend to stay in Athens?
Apostol: The young talented people would usually leave Greece. The universities followed the old German system that everyone else in Europe gave up long ago. The professors were autocratic and had a lot of power. People with talent couldn’t break into the system or get promotions unless they had family connections or some tie with the government. The situation improved when new legislation was passed in the 1980s. In 1978, after the dictatorship ended, I went for a four-month stay at the University of Patras, a new school. I worked hard preparing to deliver my lectures in Greek—and when I arrived the students were on strike, so there were no classes.
MP: Why were they on strike?
Apostol: It seems like a strange reason. They wanted the right to be promoted from year to year even if they had not passed any exams. Under their system, once you were admitted to the university, you could stay forever. Students got a daily food allowance, free books, free tuition. Most had outside jobs for extra income and just went to class occasionally. But their outside salary depended on the class they were in, so they all wanted to be upperclassmen to get more money.
Figure 2.14 In 2001 Apostol was elected a Corresponding Member of the Academy of Athens. In May 2001, he gave his inaugural lecture to the Academy.
I ended up just giving a small seminar in English every week to some faculty members. This was not announced publicly for fear that the striking students would disrupt it. The only undergraduate I talked to was a young lady who was thinking of going to America and wanted my advice.
MP: Was there any movement to change the system?
Apostol: In the early 1980s new legislation was passed to establish a new university in Crete. It was going to be set up more like the American system: departments instead of chairs for life, department members voting on new members, and so on. I served on an electoral committee that selected the initial mathematics faculty, based on merit. We met eight to ten hours a day in grueling discussions to fill all the positions established by law. When excavations began on the site for the new campus, antiquities were unearthed, and construction was halted. Of course, there are antiquities everywhere in Greece. So this grand new place had to start out in temporary buildings. The mathematics office was once located in downtown Irakleion directly above a pizza parlor. In time, the academic atmosphere improved throughout Greece as new legislation was passed requiring all Greek universities to emulate the Cretan model. Some new universities have been formed in outlying provinces, but political considerations seem to play a role in the way they are structured because everyone wants to share in the benefits that flow from government funding. For example, a new campus may be fragmented so that the engineering school is in one province but the medical school is in another. It is difficult for the faculty to exercise control over a university system that is owned and operated by the Ministry of Education and Religion. But the Greeks are intelligent and hardworking, and I’m sure they will figure out a way to overcome these difficulties.
Project MATHEMATICS!
MP: Ten years ago you started the award-winning video series, Project MATHEMATICS! How did you get involved with film making?
Apostol: It all began in 1982 when a Caltech physicist, David Goodstein, invited me to be part of the academic team for The Mechanical Universe, a fifty-two-episode telecourse in college physics that was calculus based. Goodstein wanted me aboard to make sure the physicists didn’t botch the mathematics, but as time went on I became more heavily involved, both as a scriptwriter and as a co-author of three textbooks. The turning point for me was when I saw the first example of Jim Blinn’s computer animation. It was clear that this was a new and powerful tool that could be exploited for mathematics education. It brought mathematics to life in a way that cannot be done in a textbook or at the chalkboard. I was hooked, and for the next five years I devoted nearly all my energies to this physics project, learning new skills such as scriptwriting, television production and editing, the use of original historical documents, and other techniques well known to the television industry but rarely encountered among research mathematicians.
As the Mechanical Universe project began to wind down in 1985, I asked Blinn if he would be interested in working on another project for mathematics at the high school level in which his animation would play an even greater role. He agreed, and the rest is history. Suddenly I had to learn a new skill, fundraising. It took a long time and a great deal of effort to find money to launch Project MATHEMATICS! The success of The Mechanical Universe helped me to obtain some seed money from the Caltech administration to get organized. I wrote an article for FOCUS in 1986 describing our plans, and this helped generate our first major grant from SIGGRAPH. The rest of the story is described in an update I wrote for FOCUS in 1994. By the way, there is an amusing story about the name of the project. In the 1986 FOCUS article it was called Project MATHEMATICA, and our first video was produced under that name in May 1988. In June 1988 Steve Wolfram announced his new software called MATHEMATICA. I immediately telephoned to let him know we had just completed a video under that same name and asked if he could choose another name, because some people might confuse the two projects. He declined, explaining that he had already spent a small fortune registering a trademark for MATHEMATICA in several countries. To avoid a legal dispute, I notified Wolfram a few days later that we were changing our name to Project MATHEMATICS! (with an exclamation point). He replied, “I wish I had thought of that. I never did like the name MATHEMATICA.”
MP: What have been the joys of making videos? The low points?
Apostol: Of all the things I’ve done in my fifty years as a mathematician, the most satisfying has been producing and directing the videos for Project MATHEMATICS! All mathematicians love to solve puzzles. Making a video is like solving a puzzle. You have all the ingredients for a great story—the mathematics itself, heroes and history, applications to real life, computer animation, and a vast resource of visual images. The challenge is to blend all these together with a sprinkling of music and sound effects to reveal the beauty of mathematics and to provide understanding and motivation for learning more. The enthusiastic response we have received from viewers of all ages and from all walks of life tells me that we have succeeded in creating something of lasting value.
The down side of this endeavor is the constant search for funds to support the effort. Fundraising takes a great deal of my time and energy that could be better spent in more creative ways. The funding problem was the primary reason that Jim Blinn left Project MATHEMATICS! and went to work for Microsoft.
MP: So, over the years, you have been a shoe repairman, a houseboy, a teacher, a writer, a curriculum developer, a maker of videos, and in Greece an administrator of sorts. Like your parents, you keep busy! What do you want to do next?
Apostol: If I had my way, I would continue to make mathematics videos. But it’s not easy without an animator like Jim Blinn to work with. Currently we have a grant from the National Science Foundation to produce an interactive version of Project MATHEMATICS! The idea is to provide discovery-based interactivity where students can discover things like the Pythagorean theorem by themselves. This is a completely new challenge, both pedagogically and technologically. Fortunately, I have a couple of creative people working with me, Benedict Freedman and Mamikon Mnatsakanian, and together we will give it our best shot.
MP: Tell us a little about your mathematical research.
Apostol: Most of it has been in analytic number theory. Number theory deals with the integers—prime numbers and other special sequences of integers. Analytic number theorists study them using tools from real and complex analysis, such as Dirichlet series, infinite products, and elliptic functions. Most of my work has been on these tools and their interrelationships. It is the kind of research that is competent and needed, but if I didn’t do it, someone else would.
Looking back on my career, I think my strength lies in mathematical exposition rather than research. I have tried to tell students what is going on through my books and videos in a way that is both interesting and understandable. I’ve always followed the old principle: Tell them what you want to do, do it, and then tell them what you’ve done. It’s a very good formula to use in teaching.
![]()