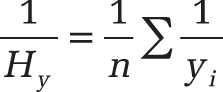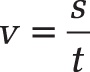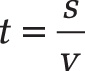Syntax. HARMEAN(number1,number2,...)
Definition. This function returns the harmonic mean of a data set. The harmonic mean is the reciprocal of the arithmetic average of reciprocals.
Arguments
number1 (required) and number2 (optional). At least one and up to 255 arguments (30 in Excel 2003 and earlier versions) for which you want to calculate the harmonic mean. You can also use a single array or a reference to an array instead of arguments separated by commas.
Note
Arguments can be numbers, names, arrays, or references containing numbers. If an array or a reference argument contains text, logical values, or empty cells, those values are ignored. However, cells with the value 0 are included. If one of the numbers is less than or equal to 0, the function returns the #NUM! error.
Background. Statistics use different means including the geometric, arithmetic, square, and harmonic mean. The harmonic mean is mostly used to calculate the mean of quotients and when the observed values are defined as ratios or references. A typical example is the averaging of speeds; in other words, the calculation of the quotient of distance/time, assuming that the distance is known.
The equation for the harmonic mean is:
Important
The harmonic mean is always less than the geometric mean, which is always less than the arithmetic average.
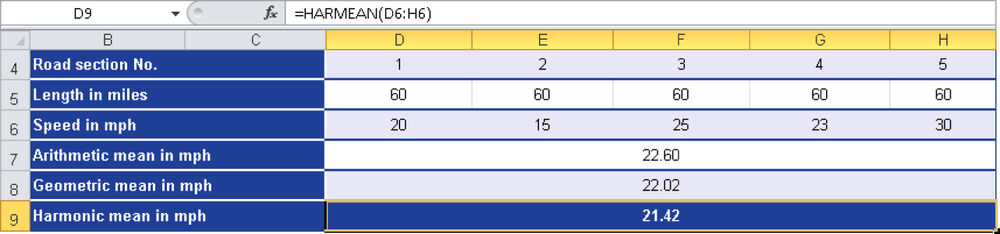
Example. To explain how the harmonic mean is calculated, use the previously mentioned example of speed and time. A bicyclist travels 300 miles through the Alps. The distance is divided into five legs, for which he measures the speed of each.
Now the bicyclist wants to calculate the average speed from the speeds reached in each leg. The result should show the consistent speed at which he could have traveled the same distance in the same time (see Figure 12-73).
To get a better overview, he also calculated the arithmetic average and the geometric mean.
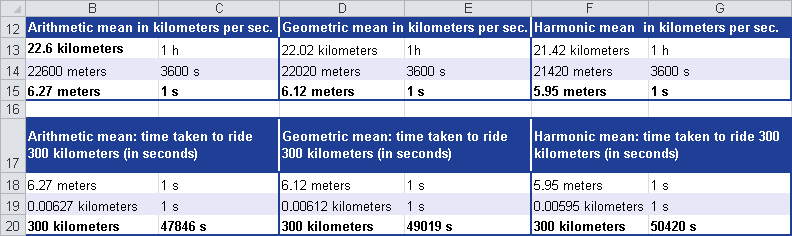
To find out what calculation returns the best result, he transforms the results of the arithmetic, geometric, and harmonic means in meters/seconds and then calculates the time it would take to travel the 300 miles at the average speed (see Figure 12-74).
Figure 12-74. The time in seconds to ride 300 miles calculated for the arithmetic, geometric, and harmonic means.
This calculation also confirms that the geometric mean is smaller than the harmonic mean, and the arithmetic mean is smaller than the geometric mean.
Next, you prove that the harmonic mean returns the best result. First you have to calculate speed v in m/s for the actual miles traveled at speed v for each leg in an hour. At a steady speed, the cyclist could have traveled 20 miles per hour in the first leg. If you divide 20 miles by 3,600 seconds, you get the speed v (see Figure 12-75).
The formula is:
Then you use the result for the speed in m/s in the same formula for t (time) to calculate the time for each leg in seconds. The formula is:
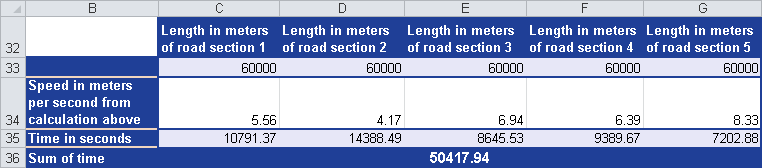
Figure 12-76 shows the result.
The sum of the times in seconds for the legs shows that the value is approximately the same as the harmonic mean. The difference of three seconds is based on the rounded values.
The comparison of the actual result of 50,417.94 seconds with the calculated results of the different means shows that the harmonic mean returns the best result.