A priority queue is a queue that supports accessing items from the largest to the smallest. Unlike a simple queue that supports accessing items in the same order that they were added to the queue, or a stack, which supports accessing the items based on how recently they were added to the stack, a priority queue enables much more flexible access to the objects contained in the structure.

A priority queue allows a client program to access the largest item at any time. (Don't be concerned about the term largest, as a simple reverse comparator can switch that around to be smallest at no cost.) The point is that the priority queue has a mechanism to determine which item is the largest (a comparator) and provides access to the largest item in the queue at any given time.

A priority queue is a more general form of queue than an ordinary first-in, first-out (FIFO) queue or last-in, first-out (LIFO) stack. You can imagine a priority queue in which the comparator supplied to it was based on time since insertion (FIFO) or time of insertion (LIFO). A priority queue could be used in this way to provide exactly the same feature set as a normal stack or queue.

A Simple Priority Queue Example

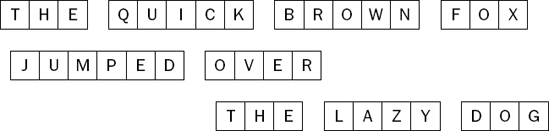
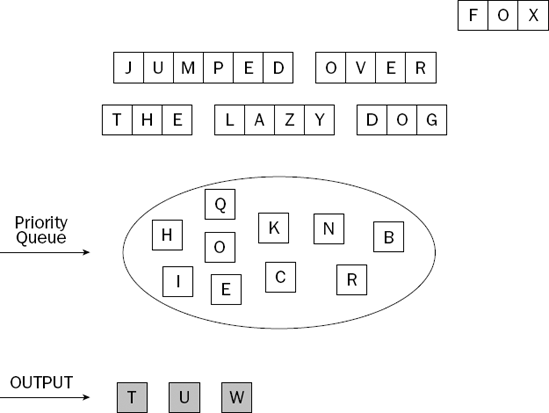
Imagine you have a priority queue that contains letters. Your imaginary client program is going to insert the letters from a series of words into the queue. After each word is inserted, the client will remove the largest letter from the queue. Figure 8-1 shows the letters to use.

Figure 8.1. Input to the example priority queue.

You begin by adding the letters from the first word into the priority queue. Figure 8-2 shows the situation after you do this.

Figure 8.2. The letters from the first word have been added to the priority queue.

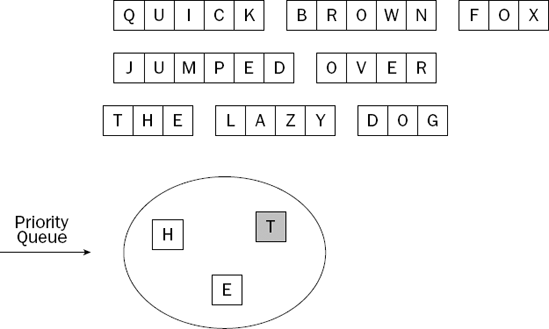
The largest letter in the priority queue is highlighted. When the client program removes the largest item, it becomes the item that is returned. We depicted the priority queue as a pool of letters, rather than as a list of letters with a specific order. Most priority queues hold their elements as a list, but it is important to understand that this is an implementation detail, and not part of the priority queue abstraction.

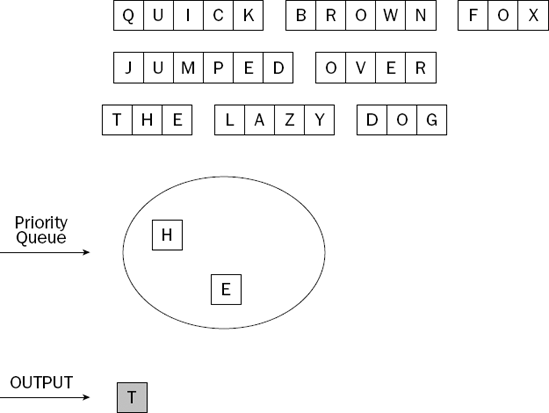
Figure 8-3 shows the situation after the client takes the largest item off the priority queue.

Figure 8.3. The largest letter is removed from the priority queue.

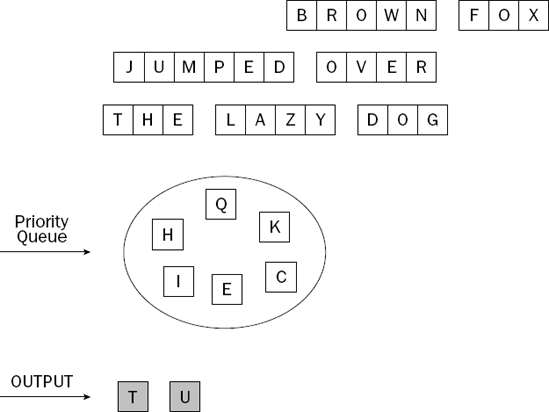
The client program adds all the letters from the second word into the priority queue; then it removes the largest one, leading to the situation shown in Figure 8-4.

Figure 8.4. The second word is added to the queue and the largest letter is removed.

The process is repeated for the third word, as shown in Figure 8-5.

Figure 8.5. The third word in the example is processed.

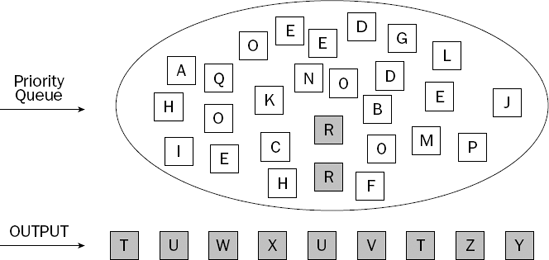
By now, you'll be getting the idea of how the priority queue works, so we'll skip to the result in the example, after all the words have been processed in the same way (see Figure 8-6).

Figure 8.6. The final state of the example priority queue.

In this final state, two items that are the equal largest among the remaining items are highlighted in the priority queue. The next call by the client program to remove the largest item could remove either of these two items.

In the Try It Out examples that follow, you implement three priority queues. They all implement the Queue interface from Chapter 4, and vary from the very simple to a quite complex version based on a heap structure. There is no need to add operations to the Queue interface; all a priority queue does, in effect, is alter the semantics of the dequeue() method to return the largest item currently in the queue.

Start by declaring the test case with a few specific values to use and an instance member to hold the queue itself:

public abstract class AbstractPriorityQueueTestCase extends TestCase {
    private static final String VALUE_A = "A";
    private static final String VALUE_B = "B";
    private static final String VALUE_C = "C";
    private static final String VALUE_D = "D";
    private static final String VALUE_E = "E";

    private Queue _queue;
    ...
}

Next, you define the setUp() and tearDown() methods. setUp() calls the abstract factory method createQueue() that follows. This is the method that each specific test needs to implement:

protected void setUp() throws Exception {
        super.setUp();

        _queue = createQueue(NaturalComparator.INSTANCE);
    }

    protected void tearDown() throws Exception {
        _queue = null;

        super.tearDown();
    }

    protected abstract Queue createQueue(Comparator comparable);

The first test establishes the behavior of an empty queue. This is exactly the same test shown in Chapter 4 for testing other types of queues. You could have avoided duplicating this code by having a more complex hierarchy of test cases, but we opted for simplicity and clarity. We do not recommend making this choice in production code!

public void testAccessAnEmptyQueue() {
        assertEquals(0, _queue.size());
        assertTrue(_queue.isEmpty());

        try {
            _queue.dequeue();
            fail();
        } catch (EmptyQueueException e) {
            // expected
        }
    }

The next method is the major test of your priority queue behavior. You begin by adding three items to the queue and making sure that the size() and isEmpty() methods are working as expected:

public void testEnqueueDequeue() {
        _queue.enqueue(VALUE_B);
        _queue.enqueue(VALUE_D);
        _queue.enqueue(VALUE_A);

        assertEquals(3, _queue.size());
        assertFalse(_queue.isEmpty());

Next, you make sure that the largest of the three items you added (in this case, the string D) is returned from the dequeue() method. In the preceding code that adds the items to the queue, this was the second of the three items, so a normal FIFO queue or LIFO stack fails this test straightaway. Having removed the item, you again verify that the other operations are still making sense:

assertSame(VALUE_D, _queue.dequeue());
        assertEquals(2, _queue.size());
        assertFalse(_queue.isEmpty());

The string B is the largest of the two remaining items, so you make sure that it is returned from the next call to the dequeue() method:

assertSame(VALUE_B, _queue.dequeue());
        assertEquals(1, _queue.size());
        assertFalse(_queue.isEmpty());

Add a couple more items to the queue. It is common in applications that use priority queues to have a mixture of enqueue() and dequeue() invocations, rather than simply building and then emptying the queue:

_queue.enqueue(VALUE_E);
        _queue.enqueue(VALUE_C);

        assertEquals(3, _queue.size());
        assertFalse(_queue.isEmpty());

You now have three elements in your priority queue: the strings A, E, and C. They should come off the queue in order from largest to smallest, so your test completes by removing each one of them in turn, while also ensuring that size() and isEmpty() remain consistent with your expectations:

assertSame(VALUE_E, _queue.dequeue());
        assertEquals(2, _queue.size());
        assertFalse(_queue.isEmpty());

        assertSame(VALUE_C, _queue.dequeue());
        assertEquals(1, _queue.size());
        assertFalse(_queue.isEmpty());

        assertSame(VALUE_A, _queue.dequeue());
        assertEquals(0, _queue.size());
        assertTrue(_queue.isEmpty());
    }

You complete the test case with another generic queue test to verify the behavior of the clear() method, as shown here:

public void testClear() {
        _queue.enqueue(VALUE_A);
        _queue.enqueue(VALUE_B);
        _queue.enqueue(VALUE_C);

        assertFalse(_queue.isEmpty());

        _queue.clear();

        assertTrue(_queue.isEmpty());
    }

That's it for our general priority queue test. You can now move on to the first implementation, a very simple list-based queue that searches for the largest item when required.

public class UnsortedListPriorityQueueTest extends AbstractPriorityQueueTestCase {
    protected Queue createQueue(Comparator comparator) {
        return new UnsortedListPriorityQueue(comparator);
    }
}

public class UnsortedListPriorityQueue implements Queue {
    private final List _list;
    private final Comparator _comparator;

    public UnsortedListPriorityQueue(Comparator comparator) {
        assert comparator != null : "comparator cannot be null";
        _comparator = comparator;
        _list = new LinkedList();
    }
    ...
}

public void enqueue(Object value) {
        _list.add(value);
    }

public Object dequeue() throws EmptyQueueException {
        if (isEmpty()) {
            throw new EmptyQueueException();
        }
        return _list.delete(getIndexOfLargestElement());
    }

private int getIndexOfLargestElement() {
        int result = 0;

        for (int i = 1; i < _list.size(); ++i) {
            if (_comparator.compare(_list.get(i), _list.get(result)) > 0) {
                result = i;
            }
        }

        return result;
    }

public void clear() {
        _list.clear();
    }

    public int size() {
        return _list.size();
    }

    public boolean isEmpty() {
        return _list.isEmpty();
    }

public class SortedListPriorityQueueTest extends AbstractPriorityQueueTestCase {
    protected Queue createQueue(Comparator comparator) {
        return new SortedListPriorityQueue(comparator);
    }
}

public class SortedListPriorityQueue implements Queue {
    private final List _list;
    private final Comparator _comparator;

    public SortedListPriorityQueue(Comparator comparator) {
        assert comparator != null : "comparator cannot be null";
        _comparator = comparator;
        _list = new LinkedList();
    }
    ...
}

public void enqueue(Object value) {
        int pos = _list.size();
        while (pos > 0 && _comparator.compare(_list.get(pos − 1), value) > 0) {
            −−pos;
        }
        _list.insert(pos, value);
    }

public Object dequeue() throws EmptyQueueException {
        if (isEmpty()) {
            throw new EmptyQueueException();
        }
        return _list.delete(_list.size() − 1);
    }

public void clear() {
        _list.clear();
    }

    public int size() {
        return _list.size();
    }

    public boolean isEmpty() {
        return _list.isEmpty();
    }

Understanding Heap-ordered Priority Queues

A heap is a very useful and interesting data structure, so we will take our time in this section explaining how it works. After you grasp the concept, you can use a heap to implement an effective priority queue.

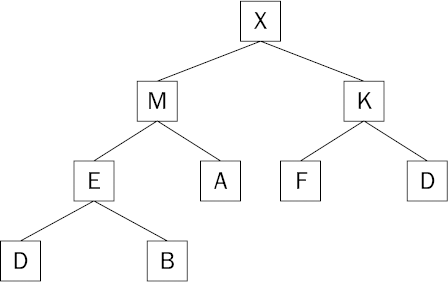
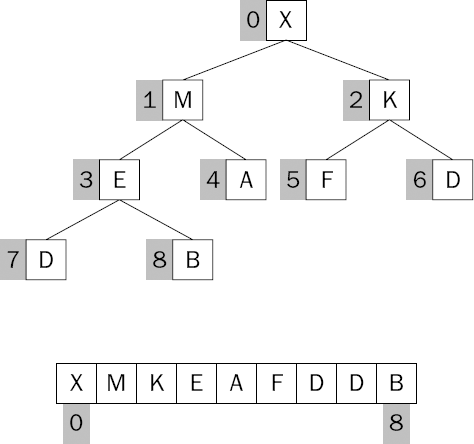
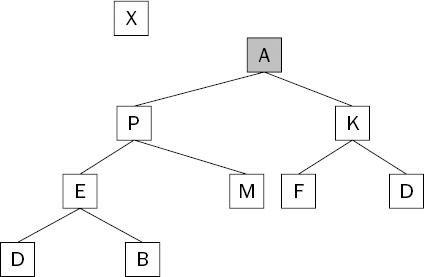
A heap is simply a binary tree structure in which each element is larger than its two children. This is known as the heap condition. In Figure 8-7, note that whichever node you look at, the element is larger than its children (if it has any).

Figure 8.7. A heap.

Be careful not to think of a heap as being sorted, however, as it is not sorted at all. It does have a useful property that is of interest, however: By definition, in a heap, the largest item is sitting right at the top of the tree. The arrangement of the other items is of little interest to us. For example, notice that the smallest element in the heap (in this case, an A) is not on the bottom row of the tree as you might expect.

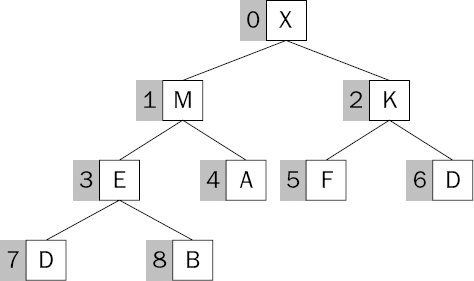
You might be wondering if there is a Heap interface or a Tree interface about to be defined and implemented. In this example, that won't be our approach. This case uses a simple list to contain the heap structure. Figure 8-8 demonstrates a technique of numbering the elements in the heap such that you can easily find them by their index. You start at the top of the tree with index zero, and work top to bottom and left to right, counting as you go.

Figure 8.8. Numbering the items in a heap for storage in a list.

This approach enables you to have a mental model of a tree structure in an implementation in which no tree structure exists at all. Figure 8-9 shows what the list would look like that contains our sample heap structure.

Figure 8.9. The heap structure contained in a list.

To use your heap, you must be able to navigate the structure upwards and downwards. Therefore, if you know the index of an item, you need to be able to determine the index of its left child item and its right child item. You also need to be able to determine the index of its parent item. Here's the way you do it:

• The left child of the item at index X is at index (2 × X + 1).

• The right child of the item at index X is at index (2 × X + 2).

• The parent of the item at index X is at index ((X – 1) / 2); the item at index 0 has no parent, of course!

Refer to the figures in this section to satisfy yourself that these formulas work as you expect. The formula for the parent index of an item relies upon truncation of the result if the item in question is the right child of the parent. You'll realize this if you try to access a list at index "3.5"!

Sink or Swim

To use the heap to build a priority queue, you need to be able to add items to it and remove items from it. That might sound obvious, but in order to perform each of those operations, you need to maintain the heap condition—that is, you need to make sure the heap is still a heap after you add or remove items from it.

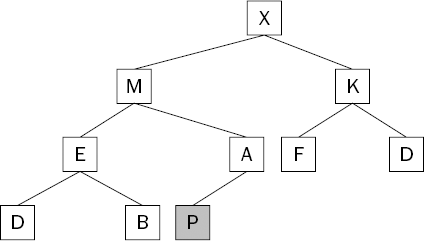
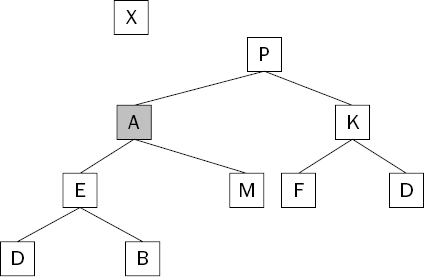
Let's extend the sample heap by adding the letter P to it. You start by simply adding it to the bottom of the tree structure, as shown in Figure 8-10.

Figure 8.10. A new item is added to the heap, breaking the heap condition.

The heap is going to be stored as a simple list, so you just add the new item to the end. The problem is that now the heap is no longer a heap! This is because the parent (A) of the new item (P) is smaller than the item itself. To fix the heap and reestablish the heap condition, the new item must work its way up the tree structure until the heap condition is restored. This is called swimming to the top.

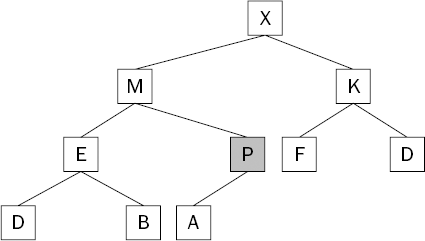
Swimming is a matter of exchanging an item with its parent if the parent is smaller, and continuing until the top of the heap is reached or a parent is found that is equal to or larger than the item doing the swimming. Figure 8-11 shows the situation after the new item has been swapped with its parent item.

Figure 8.11. The new item is exchanged with its parent.

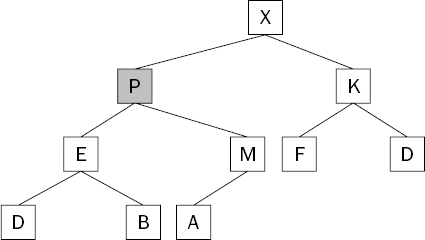
The heap condition is still not met because the new item (P) is larger than its parent (M). It needs to keep swimming. Figure 8-12 shows what happens when the new item is again swapped with its parent item.

Figure 8.12. The new item moves into final position in the heap.

The heap condition is now restored, and the heap is one element larger than it was before you added an item and maintained the heap condition. The next challenge is to do the same when removing the largest item from the heap.

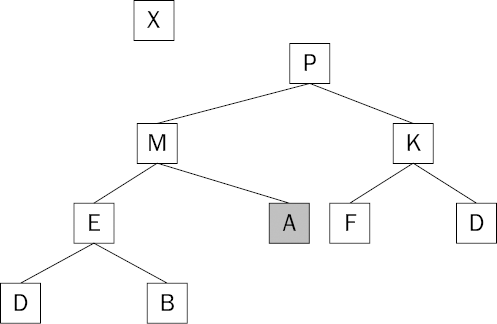
Locating the largest item is easy, but removing it is not so easy. If you just delete it from the underlying list, the tree structure is completely destroyed and you have to start again. (Feel free to try this as an experiment for your own enjoyment!) Instead, you can swap in the item at the bottom right of the tree, as shown in Figure 8-13.

Figure 8.13. The largest item is removed and the last item is put at the top.

Although the tree structure itself is still intact, the heap condition is once again violated; the smallest item of all is now at the top of the tree. It is going to have to make its way down the tree until the heap condition is restored. This process is known as sinking to the bottom.

Sinking is the process of repeatedly exchanging an item with the larger of its children until the heap condition is restored or the bottom of the tree is reached. In this example, the larger of the children of the sinking item is P, so the A is exchanged with it. Figure 8-14 shows the state of the heap after this first exchange is made.

Figure 8.14. The top element has been sunk down one level.

The heap condition is still violated because the A is larger than both of its children. The larger of the children is M, so the swap is made with that item. Figure 8-15 shows the state of the heap after this exchange is made.

Figure 8.15. The heap condition is restored after sinking.

The heap condition has been restored and the largest item is removed, leaving the heap one item smaller than it was. Armed with your new understanding, you can now use this concept to implement a priority queue.

In the next Try It Out, you test and implement a priority queue that stores the elements in the queue in a heap-ordered list—that is, a list arranged logically as a heap. This is the most complex of the three implementations covered in this chapter.

Try It Out: Testing and Implementing a Heap-ordered Priority Queue

First create a test case that is specific to your heap-ordered implementation, as shown here:

public class HeapOrderedListPriorityQueueTest extends AbstractPriorityQueueTestCase {
    protected Queue createQueue(Comparator comparator) {
        return new HeapOrderedListPriorityQueue(comparator);
    }
}

You structure the implementation just as you did with the other two priority queues, with a list to hold the items and a Comparator to order them appropriately:

public class HeapOrderedListPriorityQueue implements Queue {
    private final List _list;
    private final Comparator _comparator;

    public HeapOrderedListPriorityQueue(Comparator comparator) {
        assert comparator != null : "comparator cannot be null";
        _comparator = comparator;
        _list = new ArrayList();
    }
    ...
}

You create the enqueue() method to add the new item to the underlying list and then swim it up the heap:

public void enqueue(Object value) {
        _list.add(value);
        swim(_list.size() − 1);
    }

You create the swim() method, which accepts a parameter that is the index of the item that is swimming up the heap. You compare it with its parent (if it has one), swapping them if the parent is smaller. You call swim() recursively to continue the process further up the heap:

private void swim(int index) {
        if (index == 0) {
            return;
        }
        int parent = (index − 1) / 2;
        if (_comparator.compare(_list.get(index), _list.get(parent)) > 0) {
            swap(index, parent);
            swim(parent);
        }
    }

You have seen numerous swap() methods before, so this should cause you no trouble:

private void swap(int index1, int index2) {
        Object temp = _list.get(index1);
        _list.set(index1, _list.get(index2));
        _list.set(index2, temp);
    }

Next you create the dequeue() method. That returns the item at the front of the list. You then swap the item at the end of the list to the front of the list, and sink it down through the heap to restore the heap condition:

public Object dequeue() throws EmptyQueueException {
        if (isEmpty()) {
            throw new EmptyQueueException();
        }
        Object result = _list.get(0);
        if (_list.size() > 1) {
            _list.set(0, _list.get(_list.size() − 1));
            sink(0);
        }
        _list.delete(_list.size() − 1);
        return result;
    }

Create the sink() method that is used to swap the item with the largest of its children. Be careful to cater to cases in which the item has two, one, or no children at all:

private void sink(int index) {
        int left = index * 2 + 1;
        int right = index * 2 + 2;

        if (left >= _list.size()) {
            return;
        }

        int largestChild = left;
        if (right < _list.size()) {
            if (_comparator.compare(_list.get(left), _list.get(right)) < 0) {
                largestChild = right;
            }
        }

        if (_comparator.compare(_list.get(index), _list.get(largestChild)) < 0) {
            swap(index, largestChild);
            sink(largestChild);
        }
    }

You'll be exhausted after looking at that bit of code, so the good news is that the remaining methods are as simple as can be:

public void clear() {
        _list.clear();
    }

    public int size() {
        return _list.size();
    }

    public boolean isEmpty() {
        return _list.isEmpty();
    }

How It Works

The enqueue() method is simple because it passes most of the hard work off to the swim() method after adding the new item to the underlying list. The parameter passed to the swim() method is the index of the item that needs to swim up the heap. The swim() method has the task of comparing the item at the index provided with its parent item in the heap, and exchanging it if the item is larger than its parent. If an exchange is required, the method calls itself recursively to continue the process higher up the heap. The method stops when the index is 0, as this means we are at the top of the heap. Notice also that the formula used to identify the index of the parent element matches the explanation given earlier in the chapter.

The implementation of dequeue() begins by locating the item to be returned, which is simple; it is already at index 0 in the list. Although this is the item you return, it is not necessarily the item you delete from the underlying list. The only item that ever gets deleted is the one at the very end of the list. If there is only one item in the queue, the item you return is the one you delete; in all other cases, you need to exchange the last item with the first item and sink it down through the heap to reestablish the heap condition.

sink() is unfortunately a lot more complex than swim() because there are a couple of interesting cases to consider. The item in question might have no children, or it may only have one child. If it has a right child, it must also have a left child, so having only a right child is one case we can ignore.

You start by calculating the index of your children. If these indices fall outside the valid range of items in the queue, you are done, as the item cannot sink any lower. Next, figure out which of your children (you have at least one child now) is the larger. It is the larger of the children that you exchange with the item in question if required. You start by assuming that the left child is the larger, and change your assumption to the right child only if you have a right child and it is larger than the left child.

At this point, you know which of your children is the larger one. All that remains is to compare the item itself with the larger of the children. If the child is larger, swap them and recursively call sink() to continue the process down the heap until the heap condition is restored.

The heap-ordered implementation of the priority queue is the final version included in this chapter. It is interesting because it adds items to the queue and removes them from the queue in a manner that is O(log N). Any algorithm that is proportional to the depth of a binary tree of the elements in question has this characteristic, and has a great advantage over those that treat the items in a long linear fashion. In the next section, we will compare our three priority queue implementations to see how they stack up against each other.

As in previous chapters, we will opt for a practical, rather than a theoretical, comparison of the various implementations. Once again, we will use CallCountingComparator to gain an understanding of how much effort the various implementations take to achieve their results. Remember not to take this single dimension of evaluation as total or definitive. Rather, use it to gain insight and to inspire further investigation. Many theoretically sound comparisons are available, so check Appendix B for resources if you're interested in delving further into that area.

As when comparing sorting algorithms in the previous two chapters, this chapter considers best, worst, and average cases for each of the three priority queue implementations. We perform a mixed set of operations to add and remove items from the queues under test. The best case consists of adding data in sorted order. The worst case consists of adding the data in reverse sorted order, and the average case consists of adding randomly generated data to the queue.

The basic structure of the test driver class is shown here. You declare a constant to control the size of the tests, and then declare the lists for each of the best, worst, and average cases. Finally, you declare CallCountingComparator to collect the statistics:

public class PriorityQueueCallCountingTest extends TestCase {
    private static final int TEST_SIZE = 1000;

    private final List _sortedList = new ArrayList(TEST_SIZE);
    private final List _reverseList = new ArrayList(TEST_SIZE);
    private final List _randomList = new ArrayList(TEST_SIZE);

    private CallCountingComparator _comparator;
    ...
}

The setUp() method instantiates the comparator and fills the three lists with the appropriate test data:

protected void setUp() throws Exception {
        super.setUp();
        _comparator = new CallCountingComparator(NaturalComparator.INSTANCE);

        for (int i = 1; i < TEST_SIZE; ++i) {
            _sortedList.add(new Integer(i));
        }

        for (int i = TEST_SIZE; i > 0; −−i) {
            _reverseList.add(new Integer(i));
        }

        for (int i = 1; i < TEST_SIZE; ++i) {
            _randomList.add(new Integer((int)(TEST_SIZE * Math.random())));
        }
    }

Next are the three worst-case scenarios, all of which delegate to the runScenario() method:

public void testWorstCaseUnsortedList() {
        runScenario(new UnsortedListPriorityQueue(_comparator), _reverseList);
    }

    public void testWorstCaseSortedList() {
        runScenario(new SortedListPriorityQueue(_comparator), _reverseList);
    }

    public void testWorstCaseHeapOrderedList() {
        runScenario(new HeapOrderedListPriorityQueue(_comparator), _reverseList);
    }

Now you define the three best-case scenarios, one for each of the priority queue implementations:

public void testBestCaseUnsortedList() {
        runScenario(new UnsortedListPriorityQueue(_comparator), _sortedList);
    }

    public void testBestCaseSortedList() {
        runScenario(new SortedListPriorityQueue(_comparator), _sortedList);
    }

    public void testBestCaseHeapOrderedList() {
        runScenario(new HeapOrderedListPriorityQueue(_comparator), _sortedList);
    }

Finally, you have the three average-case scenarios:

public void testAverageCaseUnsortedList() {
        runScenario(new UnsortedListPriorityQueue(_comparator), _randomList);
    }

    public void testAverageCaseSortedList() {
        runScenario(new SortedListPriorityQueue(_comparator), _randomList);
    }

    public void testAverageCaseHeapOrderedList() {
        runScenario(new HeapOrderedListPriorityQueue(_comparator), _randomList);
    }

The runScenario() method is shown next. It is provided with two parameters: a queue to test and a list of input data. Its approach is to iterate through the input data, adding the elements to the queue under test. However, every 100 items, it stops and takes 25 items off the queue. These numbers are entirely arbitrary and serve only to give you a mixture of both the enqueue() and dequeue() operations to better simulate how priority queues are used in practice. Before the method finishes, it completely drains the queue and calls reportCalls() to output a line summarizing the test:

private void runScenario(Queue queue, List input) {
        int i = 0;
        Iterator iterator = input.iterator();
        iterator.first();
        while (!iterator.isDone()) {
            ++i;
            queue.enqueue(iterator.current());
            if (i % 100 == 0) {
                for (int j = 0; j < 25; ++ j) {
                    queue.dequeue();
                }
            }
            iterator.next();
        }

        while (!queue.isEmpty()) {
            queue.dequeue();
        }
        reportCalls();
    }

The final method in the driver program is a simple dump of the number of comparisons made during the test run:

private void reportCalls() {
        int callCount = _comparator.getCallCount();
        System.out.println(getName() + ": " + callCount + " calls");
    }

The following results of the comparison of the three priority queue implementations are for the worst case:

testWorstCaseUnsortedList:   387000 calls
testWorstCaseSortedList:     387000 calls
testWorstCaseHeapOrderedList: 15286 calls

The heap-ordered version is a clear winner here, with no difference at all between the two simpler versions. Next are the best-case results:

testBestCaseUnsortedList:   386226 calls
testBestCaseSortedList:        998 calls
testBestCaseHeapOrderedList: 22684 calls

That's interesting, although if you recall that insertion sort is excellent on already sorted data, you'll understand why these results show the sorted list version doing the least amount of work. The brute-force version is almost no different, and the heap version is performing about 50 percent more operations by this measure.

Finally, look at the results that most indicate what is likely to happen in the real world:

testAverageCaseUnsortedList:   386226 calls
testAverageCaseSortedList:     153172 calls
testAverageCaseHeapOrderedList: 17324 calls

You can see that the sorted list version is doing about half as many comparisons as the brute-force version, whereas the heap-ordered implementation remains a clear leader again. The implementation based on the heap structure is clearly the most effective based on this simple test; however, whether to use it depends on your specific circumstances. You need to balance the extra complexity with the extra efficiency to determine which implementation suits your application.

This chapter covered a few key points:

To test your understanding of priority queues, try the following exercises: