Discounting Present Values of Cash Flow Streams

As individual consumers, we are always trying to maximize our intertemporal utilities by trading off future and present consumption. That is, we will consume a dollar's worth of goods today if we feel that the satisfaction we receive from doing so exceeds the satisfaction we'd get had we saved that dollar and consumed it somewhere in the future. The decision to consume intertemporally therefore depends on our abilities to compare wealth today with future wealth, which is what we mean when we talk about the time value of money. A dollar cash amount invested in the future will be worth after, say, one year. Therefore, the present value P of a cash flow C to be received one period from now is the future C discounted at rate r:

Alternatively, investing P for one period at rate r will generate value equal to . The present value of a cash flow received two time periods from now is therefore:

If the cash flow is received more than once (say, three periods), then it has present value:

An example of discrete discounting is net present value (NPV), which is present value minus the initial outlay. The NPV function in Excel is: = NPV(rate, cash flow 1, cash flow 2,...). Suppose, for instance, that you were to undertake an investment that requires an initial cash outlay of $100 but will return dividends over the next two years in the amount of $100 per year with certainty. Suppose the opportunity cost of capital is 10 percent (this is the return you could have received had you invested your $100 in the market instead). Then the net present value is:

What exactly is the discount rate? It is the rate at which we are willing to trade present for future consumption. For example, suppose you are waiting to receive one year from now. Rather than wait, you agree to receive a smaller amount now. The smaller amount is consistent with consumers’ preference for present versus future consumption; it suggests we are impatient, that we discount future gains (for a whole host of reasons) or more specifically, that we have our own set of time preferences that determine our individual decisions to consume our wealth intertemporally. We examine derivation of the discount rate in more rigorous detail in Chapter 4. The implication in this example is that the interest rate that is consistent with your time preferences is 11 percent and that your discount rate is , which is your willingness to trade the future $100 for current consumption worth $90. That is, you discount the future at 10 percent. The converse argument is that you would be willing to give up $90 today only if you knew you'd receive in exchange an amount of $100 one year from now.

Discount rates and market returns are obviously linked. Returns are determined by changes in the market prices of assets that more fundamentally reflect market participants’ utility preferences that manifest themselves through the interaction of supply and demand. In this sense, returns can be thought of as an aggregate of all of our revealed preferences, that is, our attitudes regarding present over future consumption. We discount cash flows using observed market rates and we use different market rates to discount different types of cash flows, for example, risk-free Treasury rates to discount riskless bond coupons and more risky equity returns to discount private equity cash flows. For now, we will abstract from these details and study only the process of discounting. Generalizing the cash flow discounting problem, then, to t periods, we get a sum of periodic discounted cash flows:

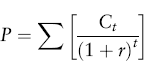
Note how we index C by time. Suppose, now, that the rate r is compounded discretely m times per year (that is, you receive a fraction percent, m times each year). Instead of t periods, we now have periods to discount, each at percent. Thus,

The quantity has a limit as m goes to infinity, that is, as interest is paid continuously. This limit is very important. It is

More fundamentally, recall that

Therefore,

Continuous compounding is therefore the limit of discrete compounding. For example, semiannual compounding (that is, interest paid twice each year) is

Compounding interest quarterly over the year,

Finally, paying interest monthly over the year is equal to the already familiar geometric return, or annual equivalent, equal to .

Taking the compounding frequency to the limit results in continuous compounding, . This means that an amount C received at the end of time t with continuous compounding has a present value:

The discount rate in this case is . Let me digress a bit on this concept. Assume I have capital to be invested right now in the amount , and at the end of one period, it grows to . Thus, . Taking natural logs and noting that for this example gives us the following:

Equivalently,

where r in this case is the rate of return on the investment. It also determines the discount rate in the sense that it represents the opportunity cost of investment, that is, r is what I give up if I choose to consume today. Had I invested (saved) it, it would have grown to in one period.

In general then, an equivalent amount C earns the following over time t with continuous compounding:

Thus, the process of evaluating future obligations as a present value problem is referred to as discounting. The present value of the future monetary amount (C) to be received is less than the face value of that amount because the future is discounted, reflecting, among other things, time preferences (a dollar today is worth more to me than a dollar to be received sometime in the future).

I define the k-period discount rate in discrete time as

In continuous time, we have

It should be obvious that future value is the inverse function of present value. For example, let refer to a cash flow stream. Assume each cash flow is received at the beginning of the period and that the interest rate is constant at r. Then the future value (FV) is the sum of the compounded cash flow values:

Likewise, it should be clear that FV has present value P equal to , that is,

And, therefore, with compounding m times per period:

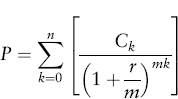
This relationship can be written more compactly with continuous compounding:

Although we develop this concept more fully in Chapter 2, this is our first pricing model. It is a simple discounted cash flow model with certain (riskless) cash flows.