Swaps
Let me motivate this important class of derivatives with an example. Suppose a mining company receives spot price for bauxite (an aluminum ore) but would like to hedge out the risk of prices falling. Since the mining company is naturally long bauxite, it could engage in a continuing sequence of short forward contracts with an aluminum producer who takes the long forward position. Alternatively, if there was an active futures market for bauxite, the company could hedge their price exposure by writing short futures contracts for delivery every period (which they would close out before the delivery date). In either case, the company would need to manage their exposure to price risk continuously and assume the administrative costs of doing so. More importantly, if output from the mine is variable, then the amount of exposure to hedge would be unknown ahead of time, further complicating the hedging strategy. In truth, what the mining company wants to receive is a fixed price of bauxite. They could achieve this by entering into an agreement with a counterparty to swap their variable spot price for a fixed price. Thus, they receive spot, which they trade for fixed. Their cash flows would therefore become (S1 – x), (S2 – x),..., (ST – x), which they can scale by any desired notional amount N. This commodity swap would have value therefore, equal to:
![]()
Since future spot prices are unknown, we use the futures relationship to value this contract, for example:
![]()
Now consider a plain vanilla interest rate swap. Imagine that you are making payments on a variable rate loan in which the rate is tied to an index of Treasury yields (or LIBOR) and you desire to hedge the risk of rising rates. An interest rate swap would entail you receiving the floating rate (which offsets your variable loan payment) and paying a fixed rate. Letting c represent the floating rate and r the fixed rate, then this swap has a theoretical value equal to:
![]()
The problem again is that ci is unknown; its value, however, can be derived from the forward rate structure. Intuitively, we can value the floating leg of the swap contract by appealing to the algebra of floating rate bonds. To see this, think of a standard bond formula but one in which the coupon rate floats across the life of the bond, to wit:
![]()
To simplify further, assume the price P and the face value M are both $1 (equivalent to a $1 notional amount). Then, immediately, we have the value of the floating portion:
![]()
It follows that the value of the vanilla interest rate swap is:
![]()
Notice that we are computing the discounted present value of the fixed interest payments that we pay, given by ![]() and subtract those from the floating rate portion that we receive. This difference is scaled by the notional N. It is instructive to think about what fixed rate you would be willing to pay to make this a fair swap, sometimes referred to as the breakeven rate. That is, given the forward rate structure, which fixed rate payment r makes us indifferent between the fixed and floating legs of the swap? This is easy to solve—I will do the algebra first and then follow with a numerical example. The fixed rate that makes us indifferent between floating and fixed is:
and subtract those from the floating rate portion that we receive. This difference is scaled by the notional N. It is instructive to think about what fixed rate you would be willing to pay to make this a fair swap, sometimes referred to as the breakeven rate. That is, given the forward rate structure, which fixed rate payment r makes us indifferent between the fixed and floating legs of the swap? This is easy to solve—I will do the algebra first and then follow with a numerical example. The fixed rate that makes us indifferent between floating and fixed is:
![]()
Suppose, now, that we add some details, which are summarized in Table 15.4. Specifically, let's study a six-year swap and assume that the forward curve is given in the first column and the discount rates in the third column.
Table 15.4 Swaps Discount Rates.
| Rate | Time | d(0,i) | |||
| 0.07 | 1 | 0.934579 | |||
| 0.073 | 2 | 0.868561 | |||
| 0.077 | 3 | 0.800484 | |||
| 0.081 | 4 | 0.732314 | |||
| 0.084 | 5 | 0.668119 | |||
| 0.088 | 6 | 0.602874 | |||
|
|
∑d(0, i) | 4.606932 |
Substituting d(0,6) = 0.602 and ![]() suggests that the fixed rate we'd be willing to pay would be 8.62 percent. Since we receive floating, then any fixed rate below 8.62 percent would generate positive value to us; otherwise, the swap would have positive value to the counterparty receiving fixed and paying floating. To prove this, we can compare the net present value of the sum of the difference in the cash flows as shown in Table 15.5. (The spreadsheet can be found in Chapter 15 Examples.xlsx.)
suggests that the fixed rate we'd be willing to pay would be 8.62 percent. Since we receive floating, then any fixed rate below 8.62 percent would generate positive value to us; otherwise, the swap would have positive value to the counterparty receiving fixed and paying floating. To prove this, we can compare the net present value of the sum of the difference in the cash flows as shown in Table 15.5. (The spreadsheet can be found in Chapter 15 Examples.xlsx.)
Table 15.5 Vanilla Swap.
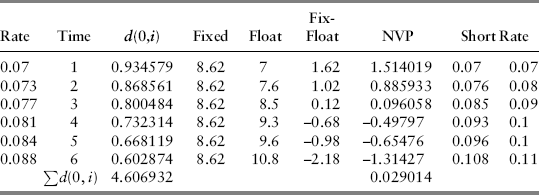
The net present value of the swap computed using 8.62 percent for the fixed payment is about 2.9 cents. You can confirm from the chapter spreadsheet that the floating payment is computed from the short rates (last column), which are estimated from the forward rate structure given in the first column. The short rates are the rate earned on money during the period in question (one year in this example) and are given by the forward rate algebra discussed in Chapter 3. For example, the short rate for year two is computed (assuming continuous compounding) as:
![]()
As a final swap example, let's think about a U.S. mining company that ships bulk ore to Japan and receives yen. (I am going to illustrate this type of swap using an example from Hull 2008.) The mining company is exposed to currency risk, specifically, that the yen may depreciate against the dollar. Rather than short the yen forward to hedge this risk, let's explore the possibility of achieving the same objective using a currency swap. Intuitively, the mining company wants to construct a swap that neutralizes its exposure and it does that by paying yen to a counterparty in exchange for dollars through a separate swap agreement. Here's how they might set up this trade.
The mining company approaches an investment bank to find a counterparty to a currency swap. Suppose the company agrees to deposit $10 million in an account paying 8 percent with the counterparty agreeing to deposit 1,100 million yen in an account paying 5 percent interest. (These rates are negotiated by the parties to the swap.) Thus, the mining company agrees to pay the counterparty 0.05(1100) = 55 million yen annually, which is swapped for the counterparty's annual payment of $0.8 million. Broadly speaking, then, the mining company is paying yen and receiving dollars on these notional amounts. So, for example, if the mining company were receiving 55 million yen annually from the Japanese firm, it is now also paying that amount back out through the swap agreement to the counterparty. Let's add a few more details. Suppose that dollars cost 110 yen, the annual rate of interest in the United States is 4.5 percent and 4 percent in Japan and that the swap agreement is for three years. The mining company therefore pays yen for three years while receiving dollars and at the end of the swap term, it collects the $10 million it deposited and simultaneously reimburses the 1,100 million yen. That way, the transactions consist solely of the swap payments. We can present the value of the respective cash flows as given in Table 15.6.
Table 15.6 Three-Year Currency Swap.
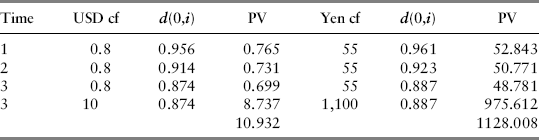
The present value of the dollar portion of the swap is $10.93 million, while the present value of the yen portion is 1128/110 = $10.25 million. Since the mining company pays yen and receives dollars, the net present value of the swap is $10.93 – $10.25 = $0.68 million.
A couple of items of interest center on the interest rate differential and the exchange rate. In this example, because the interest rate is higher in the United States, the swapped dollars are going to be discounted more heavily. Put differently, the opportunity cost of dollars is relatively high and the mining company is bearing that cost. If U.S. interest rates were to fall, then so would this cost and that would improve the value of the swap to the counterparty receiving dollars. Secondly, if the exchange rate rises (yen/USD), then so would the value of this swap. This is the major point of the example, as it illuminates to us why the mining company would engage in the swap to begin with. That is, the mining company wants to lay off yen, so to speak, as they are received in exchange for dollars. This swap achieves that purpose directly. In any case, it is important to realize that the value of the swap is symmetric (one party's gain is the other's loss) depending on a host of parameters, including the payment rates, the cost of money in each country, and the exchange rate.
