Deriving the Parameters of the Binomial Lattice

This is a good point to stop and fit what we've learned into a one-period option model and finally answer the question about the origin of the parameters u and d. We have, from before, a model of log price changes (that is, returns):

This shows the one-period movement in the stock price attributable to a single shock with volatility σ. In our lattice, this shock takes the form up (u) or down (d); that is, it is a binomial outcome. Assuming that S₀ is $1, then for this single-period model, we'd have the expected price equal to the probability weighted average of the two possible outcomes (that is, u or d)

The variance of the expected stock price is therefore (we make use of the result in statistics that Var(X) = E(X²) – [E(X)]²):

This expression factors to the following result:

In sum, we have the mean and variance of stock prices in our lattice given by the two relations:

Note that we set d = 1/u in our work from before. Doing that now simplifies these relationships as follows:

Therefore, we have two equations in two unknowns, p and ln u. Start by solving for the probability p. Squaring the first equation (to get a term in (ln u)²) and adding this to the second equation gets us . If we substitute this back into the first equation, we can solve directly for p as:

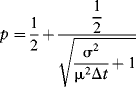
And, substituting this term back in to either equation allows us to solve for ln u as follows:

which, in turn, implies that:

As Δt → 0, the squared term goes to zero, indicating that . Therefore, . Finally, we see that . The conclusion is that the magnitude of the up and down movements in the stock price in our lattice depends on the underlying volatility of the stock return scaled by the time interval Δt. In the call and put option lattices depicted earlier, we assumed u = 1.06 and that Δt = 1/12. Now, we know that this would be consistent with an annual returns volatility of 20 percent.

Go to the companion website for more details.

In general, as the asset's volatility rises, so does the value of the option. To see this, just change the value of sigma in the Chapter 16 spreadsheet from its current value of 0.20 to, say, 0.30. You will readily see that the binomial lattice values have expanded, indicating a much wider range of possible spot prices in the future and, with these, higher likelihoods that the options will be in the money. It is also the case that option values fall as the discount rate rises. The one-month discount rate was based on a 10 percent annual rate—this is the assumed risk-free rate with a flat term structure. In reality, we would replace the one-month rate with the one-month short rates and discount accordingly.