Appendix 17.1: Derivation of Ito's Lemma

Let X be a generalized Wiener process whose law of motion is described by:

Now, define f(x) as a real valued function of X—for example, f(x) is a derivative of X whose law of motion we wish to determine. Expand f(x) using a Taylor series:

Then, in the limit, as we get:

We are recognizing here that this result holds because the higher order terms go to zero faster as Δ approaches zero. This is the fundamental theorem of calculus. But in stochastic calculus, the second order term does not vanish because X is normally distributed with positive variance, which converges in probability to . This can be conceptualized from the Wiener process itself, where the term has variance , since .

So, while the fundamental theorem of calculus is:

we must extend this to include functions of time (where ) so that for f = f(X,t), we get:

Equivalently,

because , since t is deterministic and vanishes.

This is the simplest form of Ito's lemma. If we have a model for the law of motion for X, then we can derive a model of the law of motion for a derivative of X.

Therefore, taking our generalized Wiener process from before and permitting the parameters μ and σ each to also be functions of X and t, then it follows by definition that:

And, substituting for , dX² and then dX,

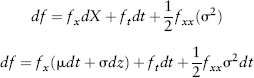
Rearranging, we solve for the law of motion for the derivative: