Pension Logic

Here is a practical savings problem that involves compounding. Suppose you are 25 years old and earn a salary set at the beginning of the year to $Y. Your plan for retirement is to save a fraction, d, of each year's salary. This savings, $dY will earn interest each year equal to r. Also, your salary is expected to grow at rate g annually. Derive an expression for the cumulative savings if you work N years.

It makes sense to break this problem into parts. The first year's savings is dY dollars, and this earns interest, compounded annually, for N years. Therefore at the end of N years, you should have . At the beginning of the second year, your salary has grown to and you save the same fraction of this salary, which earns interest for N – 1 years (and so on). Thus, this part grows to . Let's now extend this logic. The total S of all your savings over the N years until retirement will be equal to the sum:

We solve this like any other geometric series (see the appendix to this chapter). In this case, we multiply both sides of this relation by yielding:

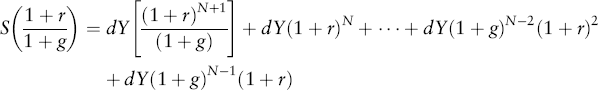
Now, subtract this equation from the first equation, and because the bulk of these two equations cancel, we get:

The chapter spreadsheet contains an example (labeled DC, for defined contributions) which states that for a 30-year career with a starting salary of $31,000, growth rate of 4 percent, rate of return of 7 percent, and an annual contribution rate of 15.2 percent, you would have saved a total of $749,519 for retirement.

Let's shift the problem a bit and consider the idea of income replacement. Now, you contemplate retirement thinking you will require an annuity of $A per year to begin with but which will have to grow by π percent to keep your purchasing power constant (COLA adjustment). Mortality tables indicate that you should expect to live T years in retirement. You think you will need a nest egg equal to $R to draw from and that any savings that remain each year are invested at r percent. How much should R be?

Assume that both interest and annual annuity withdrawal occur at the end of each year. The following schedule shows that at the end of year one, your savings have grown to and that you withdraw your first payment equal to . The entries in the table show the balance to your savings.

Table 2.7 Pension Logic.

Time	Net Savings
0	R
1
2
3
4

Generalizing to time T, we see that the compounded value of the nest egg R must be sufficient to cover the sum of all the annuity payments.

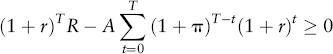
The ratio is the multiple required in savings over the annual annuity. Given the expected time in retirement (T), the return on savings (r), and the expected COLA (π), then one can solve for the required nest egg (given an annual annuity target).

While this equation is solvable using a spreadsheet, it is tedious. Let's simplify the math by assuming continuous compounding. This will give us an equivalent expression in continuous time that we can integrate easily:

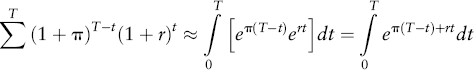
Solving the integral yields the solution:

Therefore R/A must equal this expression:

If, for example, savings earn 5 percent and the COLA is 2.5 percent and he wishes to receive the annuity for years, then the multiple would be equal to:

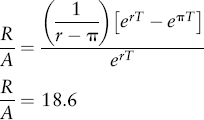
The chapter spreadsheet contains an example illustrating this problem (labeled DB, for defined benefit). If you require $50,000 per year to begin retirement and expect to earn 7 percent on any balance to your retirement fund and expect 2.5 percent inflation (COLA adjustment), then with 25 years of expected longevity in retirement, you would have required a nest egg of $750,386.

Workers often contemplate how much they'd need to retire. Given the rates suggested here and the 25-year life expectancy after retirement, an individual who needs to replace 50 percent of an ending salary equal to $150,000, will require A = $75,000 to start with. With these assumptions, savings, R, will need to be $1.4 million. If, at retirement, all savings are invested in Treasury bonds yielding 4 percent, then savings will have to increase to approximately $1.56 million. This solution requires that r > π.

Let's compare this to an annuity. Suppose for simplicity that there is no inflation and therefore π = 0 and bonds yield 4 percent. (You can substitute these numbers into the pension logic spreadsheet for details.) In this case, with 25 years’ life expectancy, the nest egg required is $1,185,226. Consider, instead, an annuity that the retiree could purchase that pays $75,000 in perpetuity. This would hedge longevity risk (living past his 25-year post-retirement life expectancy). We priced this annuity earlier; it is P = c/r, where c now = $75,000. The annuity costs $1,875,000.

Many public and private pension plans are defined benefits (DB), in which employees receive credit for service equal to some fixed percentage of their salary for every year of service. Suppose that service credit is 2 percent. Thus, after N years of service, the liability to the state pension plan is N∗2 percent times some average of ending salary. Therefore, an individual who works 30 years and ends with an average ending salary of $125,000 will be entitled to $75,000 until death (there are survivorship options that we will ignore for simplicity). This amount is also typically adjusted for an annual COLA.

What is interesting here is that the DB has a market value to the employee of $1,875,000; it is the amount of his savings that would equal his defined benefit.