Capital Market Line and the CAPM
We have been analyzing an optimization problem whose solution resolves the Markowitz problem, specifically, what combination of weights in a k-asset portfolio return a targeted portfolio mean return at minimum variance.
The Two-Fund theorem basically states that for any two efficient portfolios (hence, two sets of weights corresponding to two targeted returns ![]() and
and ![]() ), any other efficient portfolio can be constructed as a linear combination of these two.
), any other efficient portfolio can be constructed as a linear combination of these two.
Now, we derive the One Fund. Add a risk-free asset to our analysis earning a rate of return rf. Then, suppose we have a proportion α in this asset and the remainder ![]() in the risky asset(s). The mean return on this portfolio will be
in the risky asset(s). The mean return on this portfolio will be
![]()
where r is the mean return to the risky portfolio with variance
![]()
Var is a scalar because both the variance and covariance of returns on the riskless asset is zero by definition. The standard deviation on this new portfolio is then ![]() . What is the relationship between the mean (u) and the risk in this portfolio as the relative share, α, changes? To find out, take two derivatives;
. What is the relationship between the mean (u) and the risk in this portfolio as the relative share, α, changes? To find out, take two derivatives; ![]() and
and ![]() . Divide the first by the second to get
. Divide the first by the second to get ![]() . This is the slope of a line in
. This is the slope of a line in ![]() space. Its intercept is rf (that is, the return on the portfolio when
space. Its intercept is rf (that is, the return on the portfolio when ![]() is rf because with no risk, we cannot be holding any of the risky asset).
is rf because with no risk, we cannot be holding any of the risky asset).
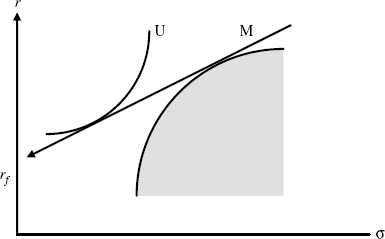
The shaded region in Figure 5.4 is the feasible set depicted in Figure 5.3 bordered by the efficient frontier. The line from rf through M is the capital market line. M is the One Fund (the market portfolio below) and U represents a representative investor's utility. Note that utility is increasing to the northwest. The point at which U is tangent with the capital market line represents a combination of M and the riskless asset that maximizes utility. The inclusion of the riskless asset therefore permits lending (or borrowing); it allows the investor to purchase a single fund of the risky asset M and lend or borrow to maximize utility. Points to the right of M along the line represent borrowing (hence buying more of the risky asset M and therefore increasing risk). Points between M and rf represent lending. Either way, points along the line dominate points on the efficient frontier since they generate higher utility.
Figure 5.4 Capital Market Line
What is the One Fund? The concept is a little abstract, but think of it this way: if all investors had the same beliefs about returns and risks associated with each risky asset, and all are aware of a risk-free asset with return rf, and everyone is a mean-variance optimizer (like Markowitz), then M is a fund of risky assets that contain every asset in the market in proportion to that asset's market capitalization. For example, if the market consists of only two risky assets, X and Y, with valuations of $100 and $200, respectively, then the market has capital value of $300 and X's capitalization weight is ![]() and Y's is
and Y's is ![]() . In equilibrium, M will contain each of theseα assets in these proportions. If market participants’ expectations change, then so will demand and supply of each asset, which, in turn, alters their respective values, and hence, their capitalization weights. Thus, M is still the market portfolio, the One Fund. All investors will buy shares of M and borrow or lend, or both, to maximize utility. (This is the logic of various index funds in the mutual fund industry.)
. In equilibrium, M will contain each of theseα assets in these proportions. If market participants’ expectations change, then so will demand and supply of each asset, which, in turn, alters their respective values, and hence, their capitalization weights. Thus, M is still the market portfolio, the One Fund. All investors will buy shares of M and borrow or lend, or both, to maximize utility. (This is the logic of various index funds in the mutual fund industry.)
From our discussion of the capital market line, in slope-intercept form, the risk-return trade-off is ![]() . Here, σm is the risk on the portfolio M (the market portfolio). The term in the brackets is the price of risk and σ is the amount of risk. For zero risk, obviously, the return is
. Here, σm is the risk on the portfolio M (the market portfolio). The term in the brackets is the price of risk and σ is the amount of risk. For zero risk, obviously, the return is ![]() .
.
The capital market line represents a set of portfolios consisting of the market portfolio M and the risk-free asset. It is silent, however, on informing us on how to price risky assets. The capital asset pricing model (CAPM) combines the capital market line with investors’ mean-variance optimizing behavior to arrive at an equilibrium-inspired model that prices risky assets.
In a word, the CAPM implies that if M is efficient, then the mean return ri for all securities i satisfies ![]() , where ri and rm are mean returns and
, where ri and rm are mean returns and ![]() . The question CAPM addresses is this: if M is a diversified portfolio and ri is the return to a risky asset, then for this risky asset to be included in the portfolio, it should have an excess return over the risk-free asset that is proportional to the excess return of M over the risk-free asset. The factor of proportionality is the asset's beta β. Generalizing, the returns to all risky assets should be proportional to their betas—this is the notion underlying the security market line that we will derive shortly.
. The question CAPM addresses is this: if M is a diversified portfolio and ri is the return to a risky asset, then for this risky asset to be included in the portfolio, it should have an excess return over the risk-free asset that is proportional to the excess return of M over the risk-free asset. The factor of proportionality is the asset's beta β. Generalizing, the returns to all risky assets should be proportional to their betas—this is the notion underlying the security market line that we will derive shortly.
The intuition is that there is a portfolio of asset i and the market portfolio M with weights α and ![]() , respectively, given by:
, respectively, given by:
![]()
This portfolio has standard deviation (risk) given by:
![]()
As we saw while constructing the efficient frontier, changes in α will trace out a curve in return-risk space (![]() in particular corresponds to M, the market portfolio). Since the capital market line contains M, then this bounded set of opportunities involving M and the risky asset, with portfolio weights α and
in particular corresponds to M, the market portfolio). Since the capital market line contains M, then this bounded set of opportunities involving M and the risky asset, with portfolio weights α and ![]() share a common point (M). Therefore, the capital market line is a tangent to this set of portfolios containing M and the risky asset. We want to find the relationship that satisfies this tangency because it will connect the concept of the risk-return trade-off between a diversified portfolio M and the riskless asset with the concept of the relationship between risky assets, in general, and the conditions for their conclusion in a well-diversified portfolio M. To begin with, the trade-off between the return to this portfolio of any risky asset and M with respect to small changes in α is defined by:
share a common point (M). Therefore, the capital market line is a tangent to this set of portfolios containing M and the risky asset. We want to find the relationship that satisfies this tangency because it will connect the concept of the risk-return trade-off between a diversified portfolio M and the riskless asset with the concept of the relationship between risky assets, in general, and the conditions for their conclusion in a well-diversified portfolio M. To begin with, the trade-off between the return to this portfolio of any risky asset and M with respect to small changes in α is defined by:
![]()
Likewise, the trade-off between the risk and the allocation weight α is:
![]()
If we evaluate the risk at the point of tangency (α = 0 meaning the location of M on the capital market line), then:
![]()
And finally, the risk-return trade-off:
![]()
This slope must be equal to the slope of the capital market line. Setting them equal:
![]()
Finally, solving for the return on the risky asset that is to be added to the diversified market portfolio M, we get:
![]()
That completes the derivation of the CAPM.
This means that the excess return ![]() to the risky asset is proportional to the excess market return
to the risky asset is proportional to the excess market return ![]() . The factor of proportionality is the asset's beta. For each asset i, we can plot the relation between the mean return ri and the asset's beta. This relationship is the security market line and has slope equal to the excess market return. This is the same thing as saying that any risky asset return ri is linear in its beta and the trade-off between the two is the market excess return. So if the market excess return is 5 percent, for example, then the excess return to the risky asset is five times whatever its beta is. As beta rises, so does this excess return. Why? Because beta is a normalized covariance between the asset return and the market. The more they covary in a positive way, the greater the contribution to risk in the portfolio through inclusion of the risky asset. The investor needs therefore to be compensated for this and that is why the CAPM indicates that the excess return to the risky asset must increase.
. The factor of proportionality is the asset's beta. For each asset i, we can plot the relation between the mean return ri and the asset's beta. This relationship is the security market line and has slope equal to the excess market return. This is the same thing as saying that any risky asset return ri is linear in its beta and the trade-off between the two is the market excess return. So if the market excess return is 5 percent, for example, then the excess return to the risky asset is five times whatever its beta is. As beta rises, so does this excess return. Why? Because beta is a normalized covariance between the asset return and the market. The more they covary in a positive way, the greater the contribution to risk in the portfolio through inclusion of the risky asset. The investor needs therefore to be compensated for this and that is why the CAPM indicates that the excess return to the risky asset must increase.
The CAPM is an idealized relationship. At any point in time, however, an asset's excess return is not always exactly equal to the product of its beta and the market excess return. That is, there is some mean zero error ε in the relationship that captures the asset's idiosyncratic error—the volatility of this error is its specific or nonsystematic risk. Unlike β, which is systematic and compensated risk, specific risk is uncompensated and must be diversified away. We write the empirical CAPM as
![]()
Note that ε is the asset's idiosyncratic error (what we're calling specific risk) and is uncorrelated with the market excess return and ![]() . Therefore, the variance is:
. Therefore, the variance is:
![]()
The first term on the right-hand side is the systematic error (systematic risk), which must be compensated for if the asset is to be priced correctly. The second term, ![]() , is the idiosyncratic error, which can be diversified away. Why can it be diversified away? Because it is uncorrelated with the market return. Any asset that lies on the security market line must, by definition, have risk equal to
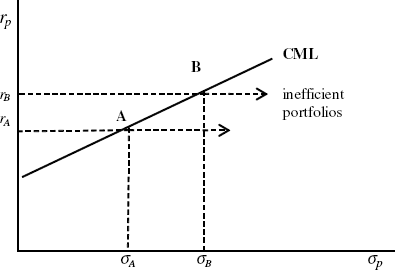
, is the idiosyncratic error, which can be diversified away. Why can it be diversified away? Because it is uncorrelated with the market return. Any asset that lies on the security market line must, by definition, have risk equal to ![]() . Therefore, assets that have nonsystematic risk will lie horizontally to the right of a point on the capital market line. This is illustrated in Figure 5.5.
. Therefore, assets that have nonsystematic risk will lie horizontally to the right of a point on the capital market line. This is illustrated in Figure 5.5.
Figure 5.5 Capital Market Line with Inefficient Portfolios