Portfolio 1: Minimum Variance Portfolio (Fully Invested)
Go to the companion website for more details.
There are two assets and we wish to solve for the portfolio (this is a vector of weights) that minimizes the portfolio's risk. Risk is the standard deviation of the time series of returns on the portfolio, which is a weighted average of the individual risks on the two assets and their covariances. That is, we want to minimize the scalar quantity (by scalar, I mean a single value, that is w′Vw is a number; a 1 × 1 matrix) given by:
Expanding this as we did in Chapter 5 is equivalent to optimizing the following objective function:
Written out, the summation is:
This is the portfolio's risk for a given set of weights and covariances. We want to minimize this quantity subject to the constraint that the portfolio is fully invested, that is, that the weights sum to unity,
. We set this up as a Langrangian:
Write out the summation and take derivatives with respect to the wi to get the first order conditions as we did in Chapter 5. There are three first order conditions. The first two are:
And the third (with respect to the constraint λ is:
Factor the first order conditions and write them in matrix format (see Appendix 6.1 for a review of matrix operators and simple matrix algebra) as:
We wrote this system as 
. We want the vector x. Let's substitute the numbers from the spreadsheet, that is, from the sample data sheet assuming the two returns are uncorrelated for now:
The zero covariances imply that the returns are independent. (This makes the math more transparent, as you will see shortly.) With this information, the system is:
The solution is (look at the formula bar in the spreadsheet for the Excel instructions):
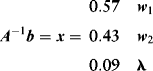
It is easy to verify that these weights are the reciprocals of the variances on the two assets. For example: 
; 
; 
and 
. Thus, the minimum variance portfolio selected assets in inverse proportion to their individual risks—the riskier, the lower the weight. That establishes the basic intuition of portfolio optimization. There are other ways of framing the objective as we shall see but the intuition remains unchanged. Constraints will, of course, restrict the space in which we look for the solution, but within that constrained space, we still seek allocations inversely proportional to their risks.
Recall that returns were assumed independent in the preceding example. This makes the covariances zero and highlights the relationship between optimization and individual asset risks. In general, however, covariances among asset returns are nonzero as asset prices evolve over the business cycle and respond to unanticipated shocks. As such, the off-diagonal elements in the covariance matrix are nonzero and the risk to each asset is a weighted average of its own risk and its covariance with the other assets in the portfolio. If, for example, the covariation in returns in the preceding example was 0.10, then the solution would change as follows:
Verify this for yourself. The weight to the first asset has now increased at the expense of the weight to the second asset. The reason is that the positive covariance increases the total risk to investing in both assets but proportionately more for the second asset. Since the objective is to minimize portfolio risk, the optimizer now puts more weight on asset 1 and less on asset 2.
Note that portfolio 1 finds the left-most point on the efficient frontier.