Model Estimation

(1) Factors are first standardized. These are time series, so standardization for a factor involves differencing the time-t value from the time series mean and dividing by the standard deviation of the macro factor. (2) Then a time series for each stock's returns is regressed on the standardized factors (also called factor exposures) and the estimated factor sensitivities (also referred to as beta, factor return, or factor loading) are saved. (3) This time series regression is then repeated for the universe of stocks. The resulting population factor sensitivities are saved. (4) Individual factor sensitivities are standardized, that is, the standardized factor sensitivity for the ith asset on the jth factor is given by (b_ij – b_j)/s_bj where b_j and s_bj are the estimated sensitivity and standard error for the jth factor, using the universe of stocks.

A factor sensitivity with value zero means that the stock has average sensitivity to that particular factor. Standardized factor sensitivities can be positive or negative. Output from this model is called a score. For example, output is the sum of the standardized factors and sensitivities products for a firm. For the ith firm,

where denotes the score, β_ik are the factor returns or sensitivities, and the factors, f_i, are standardized exposures across time. This is a predicted return, conditional on the factor exposures and their estimated sensitivities and, in principle, can be used as the mean return in the mean-variance portfolio optimization. If the factors are orthogonal, then the covariance matrix is diagonal; in this case, the variance of the asset's return is the sum of the factor variances weighted by the squares of their betas (see the following discussion on principal components).

Factor sensitivities measure the estimated response to a one-standard deviation in the factor. Standardized factor sensitivities can be ranked across factors to ascertain which factors are more or less important in driving returns. Scenarios can then be devised whereupon the manager takes action based on the estimated response in the stock's return to contrived factor values. Essentially, the same analysis can be conducted using BIRR (though for BIRR, the output is an expected excess return). Both methodologies use time series. The entire set of factor sensitivities is the portfolio's risk profile—the weighted average of the factor sensitivities of the individual stocks that compose the portfolio. This analysis is then replicated for the benchmark, or index portfolio (for example, S&P 500), and risk profiles can be compared allowing managers to assess relative risk exposures, compute expected returns, and reallocate accordingly.

The BARRA methodology is cross-sectional. Although factors are still standardized (for the current time cross-section of firms) and factor sensitivities are still ordinary least squares (OLS) estimates, there are econometric implications for cross-sectional models, which differ from time series methods. Some of these are covered in the next section. BARRA begins with firm fundamentals, not macroeconomic variables, as raw descriptors, and combines them to obtain risk indices to capture company attributes. For example, debt-to-asset ratio, debt-to-equity ratio, and fixed rate coverage can be combined to obtain the risk index for financial leverage. BARRA's GEM2 global model, for example, covers 54 countries and currencies, 34 industry groups, and a host of risk factors, including value, growth, size, momentum, volatility, liquidity, and leverage.

As with the macroeconomic factor models, the raw descriptors are standardized and then the indices are standardized (as functions of the standardized raw descriptors). Factor sensitivities are standardized as well after estimation. In general, estimation is a cross-sectional regression across n firms at time t. If, for example, data are of monthly frequency, then we could write the model as follows:

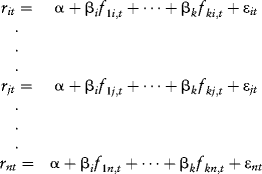
The factor sensitivities are OLS estimates from a cross-sectional regression of the n firms’ returns at time t. While all firms share the factor sensitivity, they have different exposures. Therefore β_k measures the impact of a one-standard deviation change in firm i's exposure to factor k.

It is convenient to work with this model in matrix format, which we can write as:

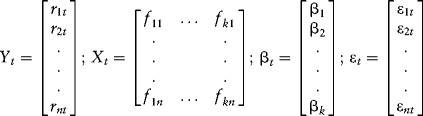
It follows therefore that:

The vector β_t is estimated using least squares. This is a cross-sectional regression model whose factor sensitivities are estimated for each time period. We can collect these vectors over time T into a matrix,

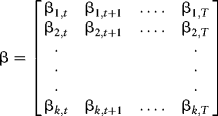
These factor sensitivities have a covariance relationship over T given by:

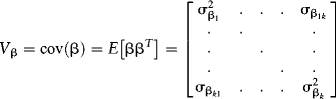
Therefore, the cross-sectional variation in returns is closely tied to the covariances of the β's. Let's write the total variance in returns as follows:

Think about the dimensions of this result and what they mean. Since there are n firms and k factors, we first note that X_t is an n × k matrix of standardized factor exposures observed at time t, and V_β is the estimated k × k covariance matrix of factor sensitivities using information up to time t. Therefore, is of dimension n × n. Likewise, V_ε is the n × n idiosyncratic risk matrix (referred to also as specific risk):

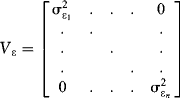
Therefore, Var(Y_t)—the cross-section variation in returns—is the sum of a systematic component, , which is conditional on the standardized factor exposures plus an unsystematic component embodied in the cross-section of specific risks. Furthermore, merely scales V_β with the current observed factor matrix.

Now, of what importance is this to mean-variance optimization? Well, first recall that any minimum variance portfolio (for a stated return) is also the maximum return portfolio for a stated level of risk. We therefore want ̀the vector w (the portfolio) that solves the following problem:

This problem takes two arguments (r, V), the vector of N returns to the assets and the covariance matrix of those returns: the risk matrix. In previous chapters, these parameters were estimated using sample means and variances. For example, was the simple sample mean returns and V was the returns covariances. Two problems arise with this approach. First, these are unconditional moment estimates and are therefore entirely driven by historical data. Factor models yield conditional moments for us. For example, instead of the unconditional mean return, we use the estimated factor model return:

The second problem relates to estimating V. For small portfolios, V is estimated using historical returns, as we've shown in previous chapters. However, if the number of firms N exceeds the length of the time series t, then V cannot be estimated from sample returns at all. Recall that V has covariance estimates as well as N variances along the diagonal. Monthly historical data going back 50 years will consist of roughly 600 observations, which is insufficient to estimate the required 780 covariances in a 40-asset portfolio! Portfolio analysts who estimate V under this condition will find that their optimizations routinely return computational errors based on V having less than full rank, the end result being that V is not invertible. The factor model, however, gives an estimate of V, which consists of two components, that are tied to estimating the K × K matrix V_β and V_ε, which is a diagonal matrix requiring N individual specific risk estimates. Since K is small relative to T, then V_β will not violate the rank condition based on any degrees of freedom restriction. And, since the specific risk estimates are often estimated from the residuals of the factor model, then V_ε will also have full rank. Therefore, we substitute for r and V using:

This is a powerful result and one that we need to fully comprehend. Factor models have moved portfolio management from unconditional moment estimates to estimates conditional on the underlying risk factors. This development allows managers to condition returns estimates on subsets of factors, effectively tilting the portfolio in the direction of, or away from, chosen factors (that is, basing on a subset of factors) and, more importantly, provides a methodology to handling large portfolios. Nonetheless, these improvements do not come without their own set of problems, foremost of which is estimation of specific risks. In most applications, specific risk dominates V. The reason is that factors often leave much of the cross-sectional variation in returns unexplained, which means that residual variation (the source of specific risk) must now be modeled. This is not an easy task, as these residuals often do not have ideal time series properties. Approaches to specific risk estimates are varied and complicated. One time series approach would be to collect the time series of factor model residuals for each firm and then model these using GARCH. On the other hand, a naïve estimate would be the firm-specific residual variances. Managers must be aware that optimal portfolios may be quite sensitive to the properties of V, a topic beyond the scope of this book but a very important one nevertheless.

Manager performance can then be evaluated by comparing the risk profile of the portfolio to that of the benchmark, say the set of risk exposures to the S&P 500. Differences in factor sensitivities highlight bets and identify their sources vis-à-vis the risk factor. Managers can then rebalance or tilt the portfolios according to their investment objectives.